Abstract
When plated onto a substrate, cells spread. Many cell types, including smooth muscle cells and fibroblasts, spread more effectively on stiffer substrates, and a simple empirical relationship has been determined that relates a cell's spread area to the substrate stiffness. In addition, some crawling cells when plated onto a stiff substrate will not migrate onto soft substrate, a process called “durotaxis”. Here we show that the resistive force predicted previously for dynamic adhesion molecules can account for both of these mechanosensory effects.
The ability of a cell to sense the physical properties of its environment is likely to be crucial in organism development and disease, as well as many other biological processes (1). For example, cardiac myocytes respond to the stiffness of the environment (1, 2). Cells plated on a substrate that is too soft do not spread well and do not form visible actin bundles. On stiff substrates, cells spread and form large actomyosin bundles but do not beat. Only when the substrate is of similar stiffness to heart tissue do cardiac myocytes develop functional myofibrils and contract periodically (3). Pertinent to this finding, the spread area of a cell, A, is directly related to the Young's modulus of the substrate, E, with an empirically determined relationship A = aEm/(Km + Em) + c, where a, c, and K are constants and m ∼ 1 (4). Crawling cells also respond to the stiffness of the substrate. Cells can crawl from a soft substrate onto a hard one; however, they do not migrate from a hard substrate to a soft one. This mechanosensing response is known as “durotaxis” (5).
Cells adhere to substrates via adhesion proteins, such as integrins, that bind and unbind from the substrate (6). In the case of integrin, the turnover time is ∼1 min (7). Recent work by Walcott and Sun (8) considered the dynamics of adhesion molecules interacting with a surface and found that these molecules exert a resistive force fr on actin filaments sliding above a substrate that is proportional to the velocity of the actin with respect to the substrate; i.e., fr = ζv. The drag coefficient ζ depends on the Young's modulus of the substrate and the total number of adhesion molecules per unit area, n:
| (1) |
In Eq. 1, the coefficient ζ0 depends on the stiffness and the binding and unbinding rates of the adhesion proteins, κ, kon, and koff, respectively:
| (2) |
The constant K in Eq. 1 is equal to the effective stiffness of the adhesion proteins divided by the perimeter of the surface contact between the adhesion molecule and the substrate P, K = κ/P.
In this Letter, we use the Walcott-Sun drag coefficient (Eq. 1) to show that adhesion protein dynamics can quantitatively account for the spread area of a cell as a function of substrate stiffness and also explains durotaxis. We consider that a spreading cell and a crawling cell have many of the same fundamental features (Fig. 1) and construct simple models based on this (see Supporting Material for a discussion of the assumptions that we use). Actin polymerization at the cell membrane along with internal forces that contract the actin network produce actin flows that are directed away from the cell membrane. The actin flow transmits force to the substrate via adhesion proteins, and an equal, but opposite drag force is exerted back on the cell. Equation 1 predicts that harder substrates produce larger resistive forces for the same actin flow speed. For either the crawling or spreading cell, the net force on the cell must be equal to zero. In a crawling cell, graded adhesion protein density can convert equal internal actin flow at the front and rear of the cell into larger resistive forces at the front than at the rear. This imbalance is offset by net movement of the cell across the substrate at speed V in the direction of the adhesion protein gradient.
Figure 1.
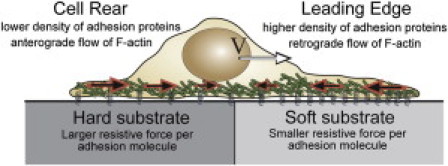
A cell crawls across a substrate at speed V, driven by the flow of actin, which is forward at the rear of the cell and backward at the front of the cell. The density of adhesion molecules is higher at the leading edge than at the rear. Substrate stiffness is predicted to increase the resistance that an adhesion molecule exerts back on to the cell (8).
We first consider the case of how the spread area of a cell is affected by the stiffness of the substrate. We propose that cell spreading is dominated by the actin motion at the periphery of the cell. At the leading edge, actin polymerizes at a rate Vp (Fig. 2). The membrane pushes back on the polymerizing actin with a force that is proportional to the membrane tension T and inversely proportional to the radius of curvature of the membrane R. In many spreading cells, the thickness of the lamellipod h is very thin compared to the other dimensions of the cell. Therefore, the mean radius of curvature of the membrane is largely determined by the thickness of the lamellipod, R ∼ h/2. In addition to the force from the membrane, the actin network also experiences contractile forces from inside the cell, Fc. The membrane and contractile forces push the actin network away from the membrane, which leads to a retrograde flow of actin at the cell membrane Vr. Force balance sets the value of the retrograde flow in terms of the forces:
| (3) |
When the retrograde flow rate is less than the polymerization rate, the cell spreads. When the retrograde flow rate is equal to the polymerization speed everywhere along the cell membrane, the cell has reached its full spread area. To finish the analysis, we make two simplifying assumptions. First, we assume that the actin dynamics (polymerization rate and contractile force) and membrane tension are constants, and are not affected by the substrate stiffness or spread area. Second, we use that an individual cell has a roughly constant lamellipodial volume and assume that the spread area is roughly equal to /h.
Figure 2.
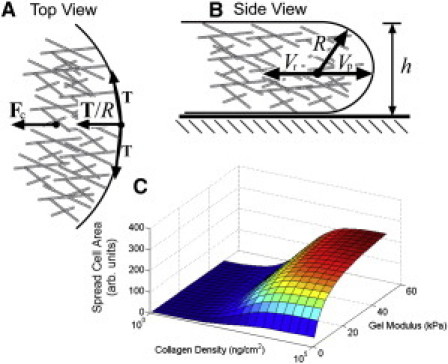
(A and B) Cell spreading is driven by actin polymerization at the leading edge. The actin polymerizes with speed Vp. The tension in the membrane T pushes on the actin with a force that is inversely proportional to the radius of curvature R, which is roughly equal to the thickness of the membrane h. Contractile forces inside the cell also pull the actin away from the leading edge with a speed Vr. (C) The spread area of the cell as a function of substrate stiffness and collagen density.
Then, combining the drag coefficient (Eq. 1) with the force balance equation (Eq. 3) gives that the spread area of a cell is
| (4) |
where a = nκVp/2Tkoff and c is a constant. Equation 4 is identical to the empirically determined formula for the spread area of a cell as a function of substrate stiffness. In addition, we can estimate the value of K using that an estimate for the effective stiffness of integrin is κ ∼ 0.2 pN/nm (9). If we assume an integrin diameter of 4 nm, then K ∼ 15 kPa, which is in fair agreement with the experimentally determined value of 7.5 kPa (4). Furthermore, if the on-rate kon is proportional to the ligand density on the substrate, then the spread area, −c, is a function of substrate stiffness and ligand density, as was found in Engler et al. (4). In fact, the model provides semiquantitative agreement with the experimental data (Fig. 2 C); however, the model does not recapture the decrease in spreading that is observed at high collagen densities. It is likely that the actin density is larger at higher ligand concentration (10), which could lead to increases in the contractile force that would decrease the spread area.
We now consider the case of durotaxis. We use a simplified, one-dimensional picture of a crawling cell (see Supporting Material for generalization to two dimensions). The F-actin in the cell flows forward at the cell rear and rearward at the cell front (11). Therefore, as a first-order approximation, we treat the F-actin speed in the cell frame of reference, vact, as proportional to the distance from the cell center x; i.e., vact = −αx. Adhesion proteins are preferentially localized near the leading edge. Therefore, the density of adhesions is n = n0 + δn(x), where n0 is a constant and δn is an arbitrary function of position, which we assume has zero mean. On a substrate of uniform stiffness, the actin flow produces a larger resistive drag force in regions where δn is positive. Because the net force on the cell (i.e., the integral of ζv over the cell-substrate contact area) must be zero, the cell migrates with velocity
where L is the length of the cell and V0 is the velocity of the cell with respect to the substrate at x = 0.
On a substrate where the stiffness changes abruptly, there is the potential for competing effects. Because the drag coefficient increases with increases in either the density of adhesion molecules or with substrate stiffness (Eq. 1), a cell that is crawling from a region of high stiffness to a region of low stiffness will experience a reduction in the propulsive force that comes from the actin flow at the front of the cell as it invades the softer region. If the change in stiffness is sufficiently large, the cell's progress can be halted, and the cell will be unable to cross into the soft region. Using Eq. 1, we can quantify this effect. In general, we must have that
| (5) |
This equation can be used to calculate the crawling speed of a cell on a substrate with graded stiffness. It is straightforward to show that this equation predicts that a cell with uniform adhesion density on a substrate with a constant stiffness gradient will crawl with a speed roughly proportional to the relative gradient of the stiffness, (1/E)dE/dx, as was found in Harland et al. (12). Here we consider the case of a crawling cell with graded adhesion δn = n1 for x < x1 and δn = n2 for x < x2 on a substrate with a sharp transition in stiffness, E = E0 (x < x2) or E = E0 + ΔE (x > x2). The crawling velocity is then calculated for given values of ΔE and x2, using L = 10 μm, α = 0.5 h−1, n2/n0 = 0.4, x1 = 2.5 μm, and E0 = 14 kPa, which are parameter values that are consistent with experiments (4) and give a crawling velocity of roughly 10 μm/h and a retrograde flow at the leading edge of 1 μm/h. We find that cells speed up as they cross from a soft substrate to a stiff one, and conversely they slow down moving from a stiff substrate onto a soft substrate (Fig. 3). If the soft substrate is half as stiff as the hard substrate, the cell cannot cross the boundary (the velocity goes to zero before the cell crosses the boundary). In Engler et al. (4), they found that a cell could only move ∼30% of its length across the transition from a 30 kPa substrate to a 14 kPa substrate, which is quantitatively consistent with our findings (Fig. 3).
Figure 3.
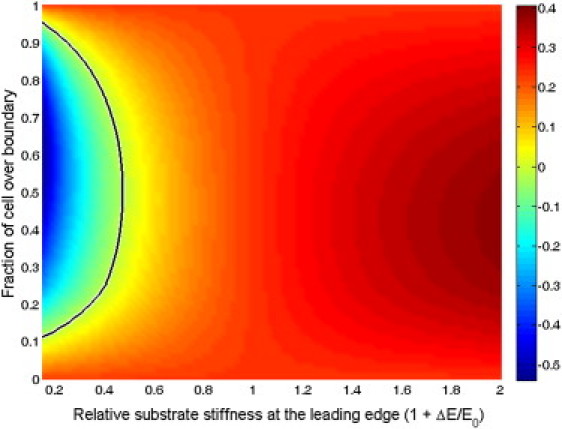
Crawling velocity of a cell crossing a boundary between substrates of different stiffnesses. Cells crawl faster when they move from a soft to stiff substrate and slow down when moving from a stiff to soft substrate. (Black contour line) Point where the crawling velocity is zero, which gives the furthest distance a cell can invade into a soft substrate. (Colorbar) Arbitrary units are used.
Here we have shown that adhesion protein dynamics is sufficient to account for the mechanosensing behavior of cells during spreading and durotaxis. We used very simple reasoning to reach this conclusion and did not implement any feedback between the substrate stiffness and actomyosin dynamics. However, there is evidence that there is feedback, such as an increase in actin density at points of applied force. Based on our findings, we suggest that this feedback acts to accentuate mechanosensing, but, in general, it is a natural by-product of cell adhesion. This model leads to the experimentally testable predictions that cell-speed changes across the boundary between substrates of different stiffnesses and also predicts the magnitude of the stiffness difference that is required to halt a crawling cell.
Acknowledgments
This work was supported by National Institutes of Health grant No. NIH U54 CA143868.
Editor: Denis Wirtz.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Additional information with supporting equations is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(11)01190-8.
Supporting Material
References and Footnotes
- 1.Discher D.E., Janmey P., Wang Y.-L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 2.Bischofs I.B., Schwarz U.S. Cell organization in soft media due to active mechanosensing. Proc. Natl. Acad. Sci. USA. 2003;100:9274–9279. doi: 10.1073/pnas.1233544100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Engler A.J., Carag-Krieger C., et al. Discher D.E. Embryonic cardiomyocytes beat best on a matrix with heart-like elasticity: scar-like rigidity inhibits beating. J. Cell Sci. 2008;121:3794–3802. doi: 10.1242/jcs.029678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Engler A., Bacakova L., et al. Discher D. Substrate compliance versus ligand density in cell on gel responses. Biophys. J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lo C.-M., Wang H.B., et al. Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Choi C.K., Vicente-Manzanares M., et al. Horwitz A.R. Actin and α-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 2008;10:1039–1050. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cluzel C., Saltel F., et al. Wehrle-Haller B. The mechanisms and dynamics of αvβ3 integrin clustering in living cells. J. Cell Biol. 2005;171:383–392. doi: 10.1083/jcb.200503017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Walcott S., Sun S.X. A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells. Proc. Natl. Acad. Sci. USA. 2010;107:7757–7762. doi: 10.1073/pnas.0912739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Taubenberger A., Cisneros D.A., et al. Franz C.M. Revealing early steps of α2β1 integrin-mediated adhesion to collagen type I by using single-cell force spectroscopy. Mol. Biol. Cell. 2007;18:1634–1644. doi: 10.1091/mbc.E06-09-0777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wehrle-Haller B., Imhof B.A. The inner lives of focal adhesions. Trends Cell Biol. 2002;12:382–389. doi: 10.1016/s0962-8924(02)02321-8. [DOI] [PubMed] [Google Scholar]
- 11.Dembo M., Wang Y.-L. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Harland B., Walcott S., Sun S.X. Adhesion dynamics and durotaxis in migrating cells. Phys. Biol. 2011;8:015011. doi: 10.1088/1478-3975/8/1/015011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


