A Conformational Transition in the Myosin VI Converter Contributes to the Variable Step Size

Abstract

Myosin VI (MVI) is a dimeric molecular motor that translocates backwards on actin filaments with a surprisingly large and variable step size, given its short lever arm. A recent x-ray structure of MVI indicates that the large step size can be explained in part by a novel conformation of the converter subdomain in the prepowerstroke state, in which a 53-residue insert, unique to MVI, reorients the lever arm nearly parallel to the actin filament. To determine whether the existence of the novel converter conformation could contribute to the step-size variability, we used a path-based free-energy simulation tool, the string method, to show that there is a small free-energy difference between the novel converter conformation and the conventional conformation found in other myosins. This result suggests that MVI can bind to actin with the converter in either conformation. Models of MVI/MV chimeric dimers show that the variability in the tilting angle of the lever arm that results from the two converter conformations can lead to step-size variations of ∼12 nm. These variations, in combination with other proposed mechanisms, could explain the experimentally determined step-size variability of ∼25 nm for wild-type MVI. Mutations to test the findings by experiment are suggested.

Introduction

Myosin VI (MVI) is an ATP-powered cellular transporter that is capable of forming dimers that move processively along actin filaments in the minus direction (1). Each MVI molecule in a dimer possesses a globular motor domain to which a lever arm is attached. The lever arm is followed by a three-helix bundle, a coiled-coil region, and a globular cargo-binding domain (2, 3). MVI dimers have been shown to walk along actin filaments in a hand-over-hand fashion, i.e., while one motor domain is bound to actin, the other steps forward in search of its next binding site (4). Taking steps with an average length of 36 nm (5), which corresponds to the pitch of the actin filament (6), an MVI dimer is capable of transporting cellular cargoes along actin filaments for distances of up to 2 $\mu \text{m}$ before dissociation occurs (1).

The swinging lever arm hypothesis (7, 8) is the most widely accepted model of myosin function and is believed to apply to all myosins. In dimeric MVI, the release of ATP hydrolysis products from the actin-bound lead head is translated into a large mechanical motion of the converter subdomain. This motion, called the powerstroke, is amplified by the lever arm of the lead head and accounts for part of the forward displacement of the trailing head. The remainder of the MVI step appears to involve a diffusive search by the former trailing head for a binding site on actin in front of what was the lead head (9). Hydrolysis of ATP by the unbound MVI head occurs spontaneously in the prepowerstroke (PPS) state, but the release of ADP and P_i is inhibited until the head binds to actin as the new lead head. The release of P_i from the actin-bound lead head is thought to trigger the powerstroke (10, 11). Additional conformational changes in the head allow the release of ADP and result in a strong actin-binding interface. ATP binds to the rear head, which is strongly attached to actin in the nucleotide-free rigor (R) state, and induces its dissociation from actin. The cycle repeats with the roles of the heads interchanged.

MVI is the first myosin that has been shown to move toward the pointed (minus) end on the actin filament, opposite to the direction of motion of other myosins (12). The converter subdomain of MVI contains a 53-residue insert at its C-terminal end that is unique to MVI. The x-ray structure of MVI in the R state revealed that the converter insert reorients the lever arm by ∼120° relative to myosin V (MV) or myosin II (13) (Fig. 1). Park et al. (5), who studied recombinant MVI/MV chimeras with and without the converter insert, reported minus-directed motion of the dimers if the insert was present, and plus-directed motion otherwise, thus proving that the converter insert is the cause of the reversal of motion. MVI has a surprisingly large average step size (36 nm) given its short lever arm, which contains only two calmodulin light chains (compared with six in MV, which also takes 36-nm steps (14, 15)). The x-ray structure of MVI in the PPS state in the absence of actin, solved by Ménétrey et al. (16) (see their Fig. 5 C), indicates that the large step size can in part be explained by a novel conformation of the converter domain, in which the converter insert (and the lever arm) is rotated compared with the R converter conformation (Fig. 1). We henceforth call the R conformation “conventional” because it is very similar to all known converter structures except for that in the MVI PPS state. Because the PPS conformation of the MVI converter is different from that seen in the PPS state of other myosins (17), we refer to it as “novel” in the following text.

Figure 1.

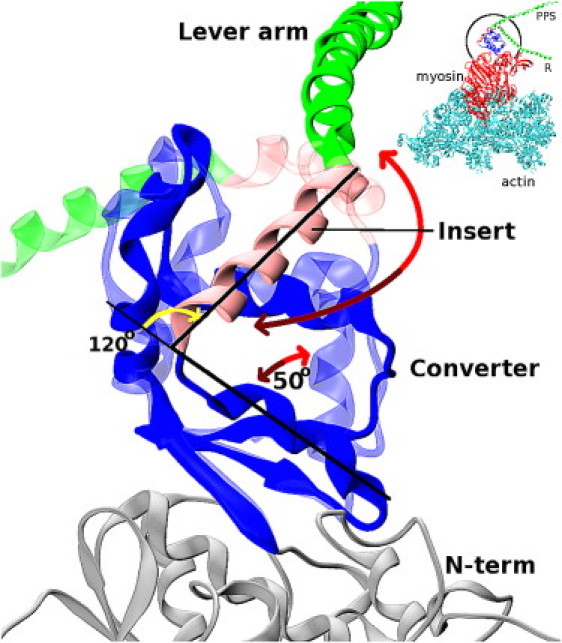
Superposition of the converter domain in the R (conventional) conformation onto the PPS structure of MVI, in which the converter adopts a novel conformation. The alignment minimizes the RMSD between the backbone atoms in the converter β-sheet (see Materials and Methods) rather than the helix that precedes the converter insert, as was done previously in Fig. 4B of reference (16). It is necessary to use the β-sheet for alignment to avoid steric clashes between the converter domain and the N-term of MVI. The converter is shown in blue, the converter insert is in pink, the lever arm is in green, and the N-term in the PPS conformation is in gray. Transparent and solid colors correspond to the R and PPS conformers of the converter, respectively. The 120° angle indicated by a yellow arrow corresponds to the reorientation of the lever arm by the converter insert. The long red arrow indicates the movement of the insert that results from the R↔PPS converter rearrangement (see text). The rearrangement involves a 50° rotation of the converter helix N-terminal to the converter insert. Light red and dark red arrowheads indicate the conformational change in the PPS→R and R→PPS directions, respectively.

Figure 5.

(A) Models of MVI/MV chimeras docked to actin. The rear head is modeled in the rigor-like state with the converter in the conventional conformation (44), shown in gray at position 0. The leading heads are modeled in the PPS state (16), drawn in purple, red, yellow, cyan, and black, and placed at actin positions 11, 13, 15, 17, and 19, respectively. The numbers indicate the actin monomers relative to position 0. The corresponding distances are 30.7 nm, 36.1 nm, 41.5 nm, 47.1 nm, and 52.7 nm. The converter is in the conventional conformation in the gray, purple, and red structures (positions 0, 11, and 13), and in the novel conformation in the other structures. Structures in B are taken from MD simulations in which the lever arms of each of the five dimers shown in A were brought together by biasing forces (see text). In B, the actin filament is rotated around its axis relative to panel A to reduce the overlap of the lever arms in the figure.

Rock et al. (18) found the step size of processive MVI dimers to be highly variable compared with MV dimers, i.e., the step distribution was considerably broader for MVI (30 ± 12 nm) than for MV (35 ± 6 nm). Park et al. (5) attached a lever arm from MV to the converter subdomain of MVI without the insert, and observed that the step-size distribution of the resulting chimeric dimers (36.0 ± 14.7 nm) remained as variable as with the converter insert (39.7 ± 15.6 nm). This result showed that the variability is not due to the MVI lever arm or the adjoining converter insert. Yildiz et al. (4) observed high fluctuations in the lever arm position corresponding to an actin-bound MVI head of a processive dimer, and Sun et al. (19) reported a large variable tilting of the MVI lever arms during processive motion, although the findings of Sun et al. were challenged by a later study (20). To explain the experimental observations, Ménétrey et al. (16) suggested that the converter of the rear head attached to actin may undergo transitions between the PPS and the R conformation while the free lead head searches for its next binding site. In this state, the rear head could be either in the Sleep-Hutton state observed for myosin II (21), which has weak-to-moderate affinity for actin, and from which Pi is probably released (10), or in a strong-actin strong-ADP binding state, which evolves from the Sleep-Hutton state and probably corresponds to the state observed in cryoEM by Whittaker et al. (22). Both of these states are believed to occur before the powerstroke (10), suggesting that their corresponding structures are similar to the actin-free PPS structure, which can accommodate the converter in the R conformation without steric clashes (Fig. 1). Additionally, the moving head, which is the PPS conformation, may be able to bind to actin with its converter in either the R or PPS conformation. A variable step size would be achieved via variable angles between the lever arm and the actin filament (19) (see Fig. 5).

In this study, we obtained quantitative thermodynamic information about the relative stability of the two converter conformers with the rest of the globular head having the prepowerstroke structure. Using the string method, a path-based free-energy simulation tool (23, 24), we computed the minimum free-energy pathway (MFEP) for the R↔PPS isomerization of the converter, the free-energy profile along this transition pathway, and an estimate of the interconversion rate. The structures of MVI in the PPS conformation shown in Fig. 2, A and B, suggest that the PPS converter fold is stabilized by interactions between the converter and the motor N-terminal domain (N-term) that involve residues S119, T122, and D767 (discussed in Results). We performed string calculations to evaluate the importance of these interactions (see Table S3 in the Supporting Material). We constructed atomic models of the chimeric MVI/MV dimers of Park et al. (5) bound to actin to show that R↔PPS converter transition is expected to have a significant effect on the step size. The results indicate that the two conformations of the converter of MVI can contribute to the step-size variability.

Figure 2.

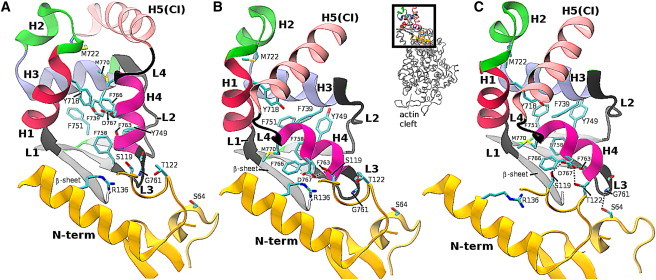
MVI converter in the R (A) and PPS (B and C) conformations. The secondary structure elements are helices 1–5 (H1–H5), loops 1–4 (L1–L4), and the β-sheet (see Table S1). CI (helix 5) denotes the converter insert. (A) The R converter docked into the MVI PPS structure. (B) The x-ray crystal structure. (C) The structure obtained after 28 ns of MD. The dotted lines in B and C show possible stabilizing interactions between the converter and the N-term. The interactions in the x-ray structure and the structure obtained after MD simulation (see text) are somewhat different.

The string method is summarized in Materials and Methods. An additional methodology for applying the string method to a large-scale biomolecular transition was previously described in a study by Ovchinnikov et al. (25), which also includes preliminary calculations for the isolated converter domain of MVI.

Materials and Methods

Preparation of structures

In this study we used several structures, two of which are based directly on the x-ray crystal structures of MVI in the R and PPS states (PDB entries 2BKH and 2V26, respectively). Parts of the structures were undefined and required modeling by structural homology. Details of the procedure used to produce complete structures are given in Section S1 and Section S2 in the Supporting Material. We obtained the PPS structure with the converter in the rigor conformation (PPS-RC) by performing a best-fit alignment between the backbone atoms of the β-sheet of the converter (see Fig. 1) of the R and PPS crystal structures, and copying the coordinates of the R converter to the PPS structure. Minimization and dynamics were performed with the use of the CHARMM (26) program and the FACTS implicit solvation model (27). The CHARMM27 force field with CMAP correction was used in all simulations. Before performing transition path calculations (see below), we ascertained the long-time stability of each starting structure by molecular dynamics (MD) simulation in the NVT ensemble. For comparison, an equilibrium MD simulation of the MVI in the PPS state was performed in explicit solvent. Details are given in Section S4. Structures of the MVI/MV chimeras were built in accord with Park et al. (5). The model of the complete MV lever arm (28) was joined to the structures of MVI in the R, PPS, or PPS-RC conformations at K771 of MVI followed by A764 of MV. To place myosin heads on actin, we performed a best-fit alignment between the structures presented here and the model of the MV rigor complex of Holmes et al. (29). Additional details on the modeling are given in Section S2.

Calculation of transition path by the string method

In the following, we summarize the essential aspects of the string method. A more detailed description is provided in Section S7. The string method computes an MFEP in the space of collective variables that connects two local minima of a free energy $G\left(\mathit{\theta }\right)$ defined by

$$G\left(\mathit{\theta }\right)=-{\beta }^{-1}\text{ln}\langle \delta (\mathit{\theta }-\hat{\mathit{\theta }}\left(\mathit{x}\right))\rangle ,$$ (1)

in which $\hat{\mathit{\theta }}\left(\mathit{x}\right)$ is a vector of collective variables defined over the configurational space. The MFEP is everywhere tangent to the vector $M\left(\mathit{\theta }\right)\nabla G\left(\mathit{\theta }\right)$, where $M_{ij}\left(\mathit{\theta }\right)=\langle \nabla {\hat{\theta }}_i\left(\mathit{x}\right)·\nabla {\hat{\theta }}_j{\left(\mathit{x}\right)\rangle }_{\hat{\theta }\left(\mathit{x}\right)=\theta }$ is a metric tensor associated with the collective variables (23). The MFEP lies near the center of a tube in which the transition is most likely to occur. The significance of the MFEP has been established in transition path theory (30, 31, 32, 33). The selection of the collective variables for the MVI converter domain was previously described in detail by Ovchinnikov et al. (25) and is summarized in Section S8. Locally around the MFEP, the isosurfaces of the committor function viewed as a one-dimensional reaction coordinate (34, 35, 36) are approximated by the surfaces $g\left(\mathit{x},\alpha \right)=0$, where

$$g\left(\mathit{x},\alpha \right)={\mathit{\theta }}^{\prime }\left(\alpha \right)·M^{-1}\left(\mathit{\theta }\left(\alpha \right)\right)\left(\mathit{\theta }\left(\alpha \right)-\hat{\mathit{\theta }}\left(\mathit{x}\right)\right),$$ (2)

and $\mathit{\theta }\left(\alpha \right)$ is a point along the MFEP for every $\alpha \in \left[0,1\right]$,), and ($\prime$) denotes derivative w.r.t to α. The one-dimensional free energy of the reaction is defined as

$$F\left(\alpha \right)=-{\beta }^{-1}\text{ln}\langle \delta \left(g\left(\mathbf{x},\alpha \right)\right)\rangle .$$ (3)

To evaluate $F\left(\alpha \right)$, the converged values of $\mathit{\theta }$ along the MFEP were used to construct a tessellation of the configurational space (25). Concurrent MD simulations were performed in which one all-atom replica was constrained to remain in each cell of the tessellation. A time record of collisions of the replicas with the corresponding cell boundaries was used to extract both the free energy (24) and the reaction rate (37). Further details on the string method calculations can be found in Section S7 and in Ovchinnikov et al. (25). The string simulations performed in this study are summarized in Table S3 and discussed below.

Results

Calculations of free-energy profiles

First, we computed the MFEP between the two converter conformations with the rest of the motor domain removed (simulation 1 in Table S3). Thus, the computed free-energy profile, which is shown in Fig. 3, excludes contributions from possible interactions between the converter and the N-term (Fig. 2, A and B), and indicates that the conventional (R) conformation of the isolated converter in solution is more favorable than the novel (PPS) conformation by 7 kcal/mol (the errors in the free-energy values quoted here are ∼2 kcal/mol, based on three different free-energy profiles computed by Ovchinnikov et al. (25)). We obtained a similar value (9 ± 1 kcal/mol) using the very different confinement technique (38, 39), which validates the results. Such a large free-energy difference in favor of the conventional conformation implies that in the absence of additional stabilizing interactions, the novel conformation would (almost) never be populated if it were stable in solution isolated from the motor domain.

Figure 3.

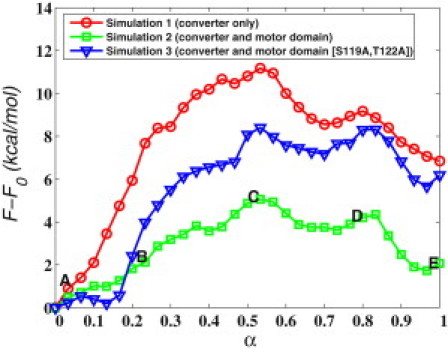
Free-energy profile of the R↔PPS transition of the converter domain, with the motor core in the PPS conformation. Labels A–E correspond to the structures in Fig. 4; A and E correspond to the R and PPS states of the converter, respectively. The progress coordinate α is the normalized string length (25).

In simulation 2, the entire motor domain in the PPS conformation was explicitly included in the calculation. The computed free-energy difference was found to decrease to 2 ± 2 kcal/mol (Fig. 3), demonstrating that the motor domain provides interactions that stabilize the PPS conformation. The relatively low value of the free-energy difference suggests that when the MVI head is in the PPS state, the converter domain can populate both the conventional R and the novel PPS conformation with a significant probability. Given that in the crystal the PPS converter has the novel conformation, it is possible that crystal contacts stabilize that conformation relative to the standard conformation. We calculated the mean first passage time for the PPS→R conformational transition using Markovian milestoning (37) and obtained a value of $\simeq 0.4\mu s$. The reciprocal of this quantity, $\simeq 2.5\times {10}^6$ s⁻¹, is an estimate of the rate of interconversion via the computed pathway. This estimate is four orders of magnitude higher than the experimental rate of phosphate release from MVI monomers interacting with actin ($\le$90 s⁻¹) (40). Thus, the converter in the lead (PPS) head is expected to interconvert rapidly between the conventional and the novel structures while the head is bound to actin. This result may explain in part the lever arm fluctuations observed by Yildiz et al. (4), as described in the Introduction.

Interactions between the converter and the N-terminal domain

To examine the properties of the interface between the converter and the rest of the motor domain in the PPS structure, and to identify possible interactions that could be responsible for the stabilization of the novel conformation (see above), we performed a 28 ns equilibrium MD simulation of MVI in the PPS state using the FACTS implicit solvent model (27). The simulation structure was stable during the entire 28 ns with a root mean-square distance (RMSD) to the x-ray MVI-PPS structure of 2.8 Å (computed between heavy atoms in the final 10 ns of simulation; see Fig. S2). The RMSD of the converter domain was 1.6 Å, and that of the rest of the motor domain was 2.3 Å. The higher overall RMSD of 2.8 Å is due primarily to a rigid motion of the converter domain relative to the N-term, accompanied by changes at the interface between the two domains (Fig. 2 B). These changes are quantified by five center-of-mass distances, P1–P5, as defined in Table S2. In particular, distance P1 between D767 (converter) and R136 (N-term) increased from 4.8 Å to 9.5 Å, and distance P5 between loop L4 of the converter and the N-term increased from 16 Å to 19 Å. In addition, distance P3 between D767 and T122 (N-term) decreased from 8.7 Å to 5.2 Å, and distance P4 between G761 (converter) and S64 (N-term) decreased from 7.3 Å to 3.9 Å. Distance P2 between D767 and S119 was $\simeq 4\AA$ in both the MD simulation and the x-ray structure. To rule out the possibility that the changes to the converter/N-term interface were due to the implicit solvent approximation, we performed a 65 ns MD simulation of MVI in the PPS state with explicit solvent (see Section S4 and Section S5). The structural changes observed in the simulation are qualitatively consistent with those in the implicit solvent simulation, although the changes in the distance parameters were smaller (Table S2 and Fig. S3). We note that the effective duration of the implicit solvent simulation is significantly longer than 28 ns (simulation time), because the absence of friction from explicit water molecules accelerates conformational sampling. We suggest that the increase in the converter/N-term distance observed in the MD simulations represents an actual difference between the solution structure and the crystal structure. It is likely to be of entropic origin, because the converter domain will be able to explore more configurations in solution by rotating relative to the N-term as a quasi-rigid body if it is farther away from the motor core. In the crystal, rotation of the converter is precluded by steric constraints, and therefore an increase in the distance between the converter and the motor core would not increase the entropy. This entropic stabilization is partially offset by the potential energetic penalty of increasing the converter/N-term separation, arising from, e.g., the loss of interactions between R136 and D767.

The interactions D767/S119 and D767/T122 that were observed in the MD simulation of the PPS state (Fig. 2 B) cannot form if the converter is modeled in the R state (D767 is too far away from the N-term domain; see Fig. 2 C). Therefore, we hypothesized that these interactions play a role in stabilizing the PPS converter conformation by the N-term in the PPS structure. To evaluate the contribution of these interactions to the free-energy difference between the R and PPS converter conformations, we introduced residue mutations S119A and T122A (in silico) and recomputed the free-energy profile (simulation 3). Interactions between R136 and the converter were not considered because R136 moved too far away from the converter in the implicit solvent MD simulation (see above). We computed the free-energy profile for the mutant using the optimized path (MFEP) obtained from simulation 2 of the wild-type MVI. Because the MFEP is not reoptimized for the mutant, simulation 3 can be considered a first-order perturbation analysis (41) relative to the MFEP from simulation 2 (i.e., the potential energy and forces are computed on the basis of the mutant structure, but the configurational space is partitioned according to the path obtained in simulation 2). This perturbation approach is analogous to the computational method used for a mutation analysis of catalysis in triosephosphate isomerase (42) and in the standard mutation analysis of protein folding based on ϕ values (43). The use of the MFEP computed for the wild-type MVI avoids the need to recompute the MFEP for the mutant (which would require $\simeq 13\text{ns}$ per system replica in addition to the $\simeq 10\text{ns}$ for the free-energy simulation; see Table S3).

Fig. 3 shows that the free-energy difference increases to ≃6 kcal/mol in favor of the R conformation, indicating that the D767/S119 and D767/T122 interactions are crucial for the stabilization of the PPS converter conformation. The error in the computed free-energy difference, however, is probably higher than the ≃2 kcal/mol quoted for the other values, due to the use of the MFEP from simulation 2, which leads to a poorer approximation of the reaction coordinate isosurfaces and causes a small fraction (0.1) of spurious transition events. These events are discarded in postprocessing a posteriori, as discussed by Ovchinnikov et al. (25).

Transition pathway between R and PPS converter conformers

The string method provides a transition pathway between the R and PPS conformations in which the free energy is optimized. Using such a pathway, one can identify interactions that give rise to the free-energy barriers. These interactions can be tested by mutagenesis.

Two prominent qualitative differences between the PPS and R converter structures (see Fig. 2) are 1), the orientation of helix 4 (H4), which is vertical and approximately perpendicular to the β-sheet in the R structure, and inclined at $\simeq$45° to the β-sheet in the PPS structure; and 2), the conformation of loop 4 (L4), which is α-helical in the R structure and unwound in the PPS structure. In addition, going from the R structure to the PPS structure, H4 rotates about its axis, moving the side chains of M770 and F766 from the interior to the outside of the converter domain. Five snapshots from the MFEP obtained in simulation 2 ordered in the R→PPS direction are shown in Fig. 4, A–E, to illustrate the transition mechanism.

Figure 4.

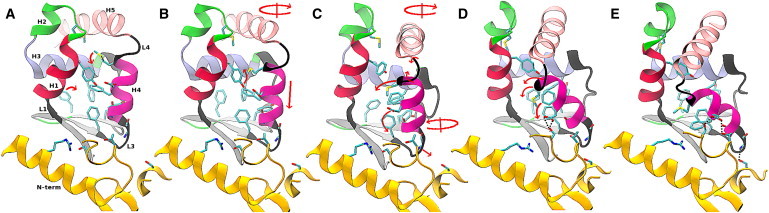
Snapshots from simulation 2 (see text) that illustrate the transition mechanism. Arrows indicate the conformational change associated with the snapshot that leads to the structure in the next snapshot. Circular arrows indicate a rigid rotation around the axis drawn through the arrow. The free energy corresponding to each snapshot is indicated in Fig. 3. Panels A and E show the rigor (R) and PPS converter structures, respectively. Panels B–D correspond to intermediate structures along the transition path. Stabilizing interactions between the converter and the N-term of the motor core in the PPS state (see text) are indicated by dotted black lines. Residues and secondary structure elements are labeled in Fig. 2.

Transition in the converter domain

The conformational change in the converter domain in the R→PPS direction begins with a downward motion of H4, which positions M770 in the middle of the converter interior and causes H5 to rotate (Fig. 4, A and B). H4 continues its downward motion, and M770 moves between the aromatic rings of Y718 and F766 (C). The resulting structure (C) corresponds to the global free-energy maximum (see Fig. 3) due primarily to the repulsive interactions between M770, Y718, and F766. Loop L4 begins to twist into its PPS conformation, and H4 begins to tilt and rotate, accompanied by the motion of M771 and F766 to the outside of the converter interior (D). This structure (D) is near to a local free-energy maximum (Fig. 3) because loop L4 is in a strained state (as it twists from the R into the PPS conformation). H4 continues to tilt, and H5 rotates into its final PPS position.

Interactions between the converter and the N-terminal domains

After H4 has partially tilted and rotated (Fig. 4, C and D), D767 moves toward S119 and T122, and loop L3 approaches closer to the N-term (D). The newly formed hydrogen bonds D767OD/S119OG, D767OD/T122OG, and G761N/S64OG stabilize the converter in the PPS conformation (E). Movie S1 is an animation of this MFEP.

Models of dimers bound to actin

To determine the effect that the R↔PPS converter transition is expected to have on the step size, we built all-atom models of MVI/MV chimeric dimers in which the converter domain in the lead head was in either the conventional or novel conformation and the trailing head was in the rigor-like state (44) in accord with Park et al. (5). Park et al. constructed an MVI/MV chimera in which a lever arm from MV was fused to the converter domain of MVI without the converter insert. In their Fig. 2, they assumed that the converter is in the conventional conformation, probably because their work predates the novel converter structure (16). The step-size distribution of the chimeras recorded by Park et al. (5) remained broad, indicating that the step-size variability is not caused by the converter insert. In the work presented here, we chose to use models for the chimeras and not the wild-type MVI primarily because an atomic model of the complete MV lever arm is available (28), and there is no model for the MVI lever arm. In addition, the MV lever arm lacks the domains that have been proposed to act as lever arm extensions in MVI (2, 3, 45), which could contribute to the step-size variability. Thus, the chimera is the ideal system for investigating the contribution of the converter transition to the step-size variability.

In Fig. 5 A we show sites on actin that the two motor heads could occupy for the chimeric dimers in which the lead head converter is in the novel conformation versus the conventional conformation. Five configurations are shown in which the two MVI heads are separated by 11, 13, 15, 17, and 19 actin monomers. These distances are within the experimental range of 13 ± 6 (5). In each configuration, the conformation of the converter in the lead head is chosen such that the distance between the C-termini of the individual lever arms is minimal. For the 11- and 13-monomer separation distances, the lead head converter is modeled in the R state, and for the other distances, the converter is in the PPS state. The corresponding distances between the centroids of the last 11 residues of the lever arms are 16.6, 9.6, 5.0, 12.0, and 21.0 nm. On the other hand, if the lead head converter is modeled in the conventional (R) state for the 15-, 17-, and 19-monomer separation distances, the distances between the lever arms increase to 14.2, 24.5, and 35.1 nm, respectively. If the lead head converter is modeled in the PPS state for the 11- and 13-monomer separation distances, the increases in the distance between the lever arm termini are smaller (2.6 and 0.6 nm, respectively). However, in this case, the light chain bound to the last IQ motif (IQ6) of the lead head is at the same axial position as the light chain bound to IQ2 and IQ4 of the rear head for the 11- and 13-monomer separations, respectively. Because the formation of a dimer requires proximity between the IQ6 motifs in the two heads, such structures did not appear to be plausible. In contrast, with the lead head converter modeled in the R state, the light chain in the rear head that is closest to IQ6 in the lead head also corresponds to IQ6. The choice of the lead head converter conformation in the 11-monomer separated dimer is illustrated in Fig. 1. The dependence of the optimal conformation of the lead head converter on the separation distance between the two heads on actin (e.g., 11 monomers versus 17 monomers, spanning ∼16 nm) illustrates how the MVI converter can contribute to step-size variability. If MVI dimers can bind to actin with the lead head converter in either conformation, one should expect to see variation in the step size beyond that of wild-type MV (i.e., 22–50 nm based on 2× SD (5)), which would be absent if only one conformation were allowed (but see below). We note that the larger step sizes shown in Fig. 5 were observed experimentally for the MV dimers as well, but with a significantly lower probability relative to the average step size (36 nm) (5).

The fact that a configuration in which the lever arms of the individual myosins connect was not found indicates that modifications to the modeled structures are necessary to construct a dimer. A possible modification, consistent with the existence of pliant regions as reported by Terrak et al. (28), is to bend the lever arms to bring their termini into contact (see below and Fig. 5 B); for other modifications, see Discussion.

To generate hypothetical dimer conformations with the lever arm termini in proximity, we performed biased MD simulations (46) of the MVI structures in Fig. 5 A (Section S6). The final MD structures are shown in Fig. 5 B. The structures in which the heads are 11, 13, and 15 actin subunits apart appear similar to electron micrographs of actin-bound MV (see Fig. 1 in Walker et al. (47)). No distortions of the light chains were observed in the simulations. Although these simulation structures appear plausible, an estimate of the reversible work required to decrease the distance between lever arms in the 13-monomer separated MVI structure (obtained from a free-energy simulation; see Section S6) indicates that the distance can be reduced by only a few nanometers at a small free-energy cost. For example, reducing the distance by ≃4 nm from 10.5 nm to 6.5 nm requires 8 ± 6 kcal/mol (Fig. S4). Reducing the distance between the lever arms further, as appears to be required for the chimeras in which the heads are separated by large distances (e.g., 17 monomers), would require prohibitively high free-energy values (>20 kcal/mol). The results therefore imply that other sources of lever arm extension or compliance, such as coiled-coil unwinding (15, 48) are necessary to permit step sizes larger than 13 actin monomers. Because the two types of dimers have identical lever arms and coiled-coils, unwinding by itself could not explain the different distributions for wild-type MV and the MV/MVI chimeras observed by Park et al. (5).

Discussion

The step size of a MVI dimer walking toward the minus end of actin varies over a surprisingly wide range (from ≃10 nm to ≃60 nm based on 2 × SD) with an average of 36 nm (5). It has been suggested that the variability arises from intermittent uncoupling of the converter insert (18), flexibility of the lever arm (9), or variable conformations involving converter positioning (5). X-ray structural studies have shown that the converter domain of MVI can adopt two structures: a conventional one that is similar to those found in myosins I, II, and V, and a novel one that is observed only in the PPS configuration of MVI. In this study we used MD simulations to investigate the contribution of the conformational transition between the conventional and novel structures of the converter domain to the step-size variability. Park et al. (5) attached a lever arm from MV to the motor domain of MVI without the converter insert, and showed that the step-size distribution for the chimeric construct was as broad as that for wild-type MVI. Modeling of the chimeric dimer shows that the conformation of the converter determines the most probable step size (see Fig. 5 A). The main result of our study is that the calculated free-energy difference between the two converter conformations is sufficiently small for both to be accessible at room temperature ($\Delta F$= 2 ± 2 kcal/mol in favor of the conventional conformation). Given the uncertainty in the calculations, this value is sufficiently low that the role of the PPS↔R transition is very likely to be important for modulating the step size. If the free-energy difference were larger, the conformer that is at a higher free energy would be populated rarely, and the step-size distribution for the MVI/MV chimeras would be narrower, as it is for the wild-type MV dimers. In this work, we used an implicit solvent model together with a low friction constant of 1 ps⁻¹ (Section S1) to accelerate conformational sampling. With such low friction, we expect the rate of converter isomerization computed from the simulations (≃2.5 $\times {10}^6$ s⁻¹) to be overestimated by an order of magnitude. Even with the overestimation taken into account, a value on the order of 10⁵ s⁻¹ suggests that in the absence of preferential stabilization of either converter structure by actin, the converter domain in the lead head can interconvert rapidly enough between the two conformations to explain the lever arm fluctuations observed by Yildiz et al. (4).

The presence of the two converter conformations alone cannot explain the very large step sizes (≥70 nm) that have been recorded in experiments (4, 5, 18). Therefore, additional mechanisms of step-size extension and variability must exist, such as the unwinding of a coiled-coil motif into separated α-helices (2, 15, 47), unfolding of a three-helix bundle (3), or uncoupling of insert 2 from the motor domain (20). Although all three proposals apply to wild-type MVI dimers, only the first one applies to the myosin chimeras studied here and by Park et al. (5), for which 70-nm-sized steps were recorded. The existing studies do not provide a definitive answer as to whether coiled-coil unwinding is necessary for myosin function. Unwinding of unstable coiled-coil motifs was proposed as a requirement to ensure sufficient separation between two heads of heavy meromyosin II so as to allow binding to adjacent sites on actin (49, 50, 51), although this proposal was challenged in another study (52). It was also suggested that predicted coiled-coil domains of myosins VI, VIIa and X form single α-helices in solution (2, 48), which could result in a longer lever arm. Unwinding of the coiled-coil in MVI was challenged on the basis of a high dissociation free energy, which was calculated in MD simulations to be ≃16 kcal/mol for a relatively short dimer (5 nm) of α-helices (45). Unwinding of coiled-coil was observed in dimeric actomyosin V, with both myosin heads bound to actin in ATP-free conditions, and was suggested to relieve internal strain in the dimer (15). It is unclear from that study whether unwinding can also occur during stepping, which would be necessary to generate a broad step-size distribution. Further work is thus needed to explore the role of coiled-coil separation in the function of dimeric myosins.

Sweeney et al. (53) used a mant nucleotide analog to investigate the kinetics of ATP binding to dimeric actomyosin. The increase in mant fluorescence upon addition of nucleotide could be resolved into two phases. The fast phase was dependent on the ATP concentration, with an apparent second-order rate constant of 0.78 ± 0.08 μM⁻¹s⁻¹, and the slow phase was characterized by an ATP-independent rate constant of 2–3 s⁻¹. The authors suggested that the ATP-independent slow phase corresponds to the binding of ATP to the lead head in the MVI dimer, and that the ATP-independence facilitates gating between the two heads, which prevents the lead head from binding ATP and dissociating from actin before the rear head. Ménétrey et al. (16) proposed that binding of ATP to the lead head could be delayed by the isomerization of the converter from the novel (PPS) to the conventional (R) conformation. Our estimate for the rate $\simeq {10}^5$ s⁻¹ appears to be too high to explain the low rate of binding of ATP to the lead head (3 s⁻¹) solely on the basis of the converter transition (correcting for the overestimation of the rate). Additional conformational rearrangements, which may involve another insert near the nucleotide-binding domain (also suggested by Ménétrey et al. (16)), are likely to be important.

In our calculations we identified the atomic origins of the free-energy difference and the free-energy barrier between the two states of the converter domain. Mutagenesis can be used to test these results. The stabilization of the PPS converter conformer by the motor domain can be investigated by making the mutations S119A, T122A, and D767A. The present results indicate that these mutations would weaken the favorable interactions between the N-term and the PPS converter, and make the PPS converter structure too high in free energy to be populated. As a consequence, the mutant MVI heads in processive dimers would take shorter steps, and the step-size variability would decrease. We note that although R136 moves away from D767 after a relatively short equilibration period (28 ns with the FACTS implicit solvent and 18 ns in explicit solvent; see Results), it may still interact with D767 transiently on a longer timescale and contribute to stabilization of the PPS conformer. Thus, it may be useful to test the effect of the R136 mutation as well. We note that the above residues are generally conserved across MVI sequences (see Section S9 and Fig. S6), suggesting that they are crucial for proper MVI function.

The mechanism of transition between the PPS and R converter states was shown to involve the transfer of M770 from the hydrophobic core of the converter domain to the interface between the converter and the N-term (Fig. 4). This suggests that one could make the barrier to the transition prohibitively large by substituting a bulky residue for M770 (e.g., Phe, Trp, or Arg) with the expectation that only the R state will be populated (because the rigor-like MVI structure cannot accommodate the PPS converter conformation (16)). On the other hand, because M770 is located near Y718 and F766 at the transition state, a substitution of either aromatic residue by a smaller residue may reduce the transition barrier. Of interest, myosins II and V, for which the MVI PPS converter conformation has not been observed (see, e.g., PDB IDs 1VOM and 1OE9), have an Arg in place of M770. Other differences between MV and MVI converter sequences, which are believed to stabilize the conventional converter conformation, involve substitutions at positions equivalent to 709, 717, and 767 (see Fig. S5 and Table S5).

The simulation methods employed here provide insight into the converter transition in MVI. We expect that these methods will be useful for studying conformational transitions in motor proteins more generally.

Editor: Claudia Veigel.