Protein fluxes along the filopodium as a framework for understanding the growth-retraction dynamics

Abstract

We present a picture of filopodial growth and retraction from physics perspective, where we emphasize the significance of the role played by protein fluxes due to spatially extended nature of the filopodium. We review a series of works, which used stochastic simulations and mean field analytical modeling to find the concentration profile of G-actin inside a filopodium, which, in turn, determines the stationary filopodial length. In addition to extensively reviewing the prior works, we also report some new results on the role of active transport in regulating the length of filopodia. We model a filopodium where delivery of actin monomers toward the tip can occur both through passive diffusion and active transport by myosin motors. We found that the concentration profile of G-actin along the filopodium is rather non-trivial, containing a narrow minimum near the base followed by a broad maximum. For efficient enough actin transport, this non-monotonous shape is expected to occur under a broad set of conditions. We also raise the issue of slow approach to the stationary length and the possibility of multiple steady-state solutions.

Introduction

One of the most important processes used by cell motility is the filopodium.¹ It is an elongated cell organelle with primarily sensorial function. It grows out of the cell to probe the environment for mechanical obstacles or chemical cues. Types of motile cells employing filopodia for functioning include fibroblasts, the wound-healing cells;² neurons growing axons during embryonic development;³ metastatic cancer cells.⁴ Structurally, a filopodium is a set of parallel actin filaments bundled together and enveloped by the cell's membrane. The bundle is rooted in the lamellipodium—a three-dimensional mesh of actin filaments at the cell's leading edge.⁵ The polymerization dynamics and mechanics of actin filaments are the key factors setting up a rich dynamical behavior of the whole filopodium.^6,7 The filopodium can grow, pause or retract, at a range of speeds,^8–14 switching between these dynamical regimes due to internal regulation and in response to changes in chemical or mechanical environment.^12,15

Filopodia and lamellipodia are not only biologically and medically significant but are also fascinating physico-chemical phenomena. They are part of the cell motility subsystem, which is a collection of different processes working together through an intertwined web of chemical reactions, mechanical interactions and diffusion. Many different proteins are involved in these processes. Chemical reactions between them create or disassemble structural elements of cell motility circuits, such as meshes or bundles of actin filaments or focal adhesions. Chemical reactions also have regulatory and signaling purposes, such as inhibiting or promoting other reactions like actin polymerization. These processes are extended in space, so the transport of involved protein molecules across the region where the processes are occurring may be of crucial importance. Both passive diffusion and active transport by molecular motors are involved in cell motility organelles, and filopodia in particular. Like other biological signaling networks, cell motility circuits are highly subject to random noise. One obvious source of noise is fluctuating numbers of interacting protein molecules.

The outstanding complexity of cell motility web of interactions makes their theoretical and computational studying invaluable. Computational models can help to better understand experimental results, which are sometimes contradictory, and lay out theoretical foundations for physically meaningful interpretations.

The main purpose of this paper is to review some of the recent efforts in constructing such theoretical framework for modeling and interpreting experiments on filopodia. To make it more interesting, we then employ this framework, through stochastic simulation and look at how active transport of actin by molecular motors can influence G-actin distribution inside a filopodium and, hence, dynamically regulate the filopodial length.

Stochastic Chemical Kinetics

It should be emphasized that the sequence of chemical reactions coupled to mechanical evolution in cell motility processes are fundamentally stochastic at the microscopic level. However, coupled chemical reactions are usually described through chemical kinetics formalism—a set of ordinary differential equations (ODEs) for concentrations of all the species evolving in time. Concentrations in these equations are average numbers of molecules of each species divided by the reaction volume. Historically, chemists always worked with samples containing extremely large numbers of molecules, on the order of 10²⁴. Estimating the fluctuations to be on the order of square root of the total number, one can find that relative fluctuations are on the order of 10⁻¹². Therefore, the fluctuations can be neglected, while averages provide sufficient description of the process and chemical kinetics equations for these averages have enough precision.

In the biochemical signaling networks, including filopodia, numbers of molecules are often very small. For instance, in many cases, there is on average just 1–2 G-actin molecules in the immediate vicinity of F-actin barbed ends at the filopodial tip.⁶ Fluctuations in this case constitute 50–100% of the average number. For molecular motors or regulatory molecules, such as capping proteins, the average number can even be much smaller than 1 (which means, most of the time, there are no molecules in the particular region), so when there are any molecules, they are all noise.¹⁵ In this case, neglecting noise may be unphysical and potentially lead to qualitatively wrong conclusions; hence, noise has to be treated explicitly to get the full picture. Many examples of interesting biological phenomena, where noise was responsible for a qualitatively different dynamics than the one predicted by corresponding chemical kinetics equations, have been reported in the literature.^16–22

In order to fully describe a stochastic mechano-chemical process of interest, one has to represent it in terms of different variables. Instead of average concentrations of species (A(t), B(t), etc.), one writes equations for the probability P(n_A,n_B,…,t), that at certain moment t, the number of molecules of species A is n_A, number of molecules of species B is n_B, where protein copy numbers take only discrete values. This formalism also yields a set of coupled ODEs, but the number of equations in this set is enormously larger than the number of different species (technically, infinite, as the copy number of each species can vary from 0 to infinity, so there will be an infinite number of functions P(n_A,n_B…,t) at time t). The set of ODEs describing the temporal evolution of P(n_A,n_B,…,t) is generally called the Master Equation, or, in this case of chemical reactions, Chemical Master Equation. It is much more complicated to solve compared with ODEs found in ordinary chemical kinetics. To see the jump in complexity, one notes that the relation between stochastic kinetics (Master Equation) and ordinary chemical kinetics turns out to be rather analogous to that between classical mechanics and quantum mechanics.²³ In both cases, the simpler theory is an averaged version of the more complex one, which calculates the whole distribution of trajectories rather than just the averages. In fact, Chemical Master Equation can be directly mapped to quantum field theory.^18,23,24 The Master Equation becomes analytically intractable even for moderately large systems. For filopodia, solving it analytically is not possible, but one can instead employ stochastic kinetics computer simulations, which require large-scale computational resources.

When spatial resolution needs to be taken into account, that is, to keep track of where in space are the reactions occurring and the positions of proteins, the formalisms become even more complicated. It is then necessary to consider diffusion of reacting molecules, and deterministic chemical kinetics becomes reaction-diffusion formalism, described by a set of partial differential equations (PDEs). But diffusion is also a stochastic process. The most microscopic approach would be to calculate Brownian dynamics of each individual protein molecule and allow them to react with certain probability if they collide. The next approximation is to discretize space into the reaction volumes. Each molecule travels on average a certain distance before it reacts with another molecule. This distance is called the Kuramoto length.²⁵ Hence, a discretization to reaction volumes of sizes smaller than Kuramoto length assumes well-mixing below that length-scale, which is a relatively accurate approximation. Now diffusion can be added to the Chemical Master Equation as reaction of hopping between reaction volumes. The resulting formalism is called Reaction-Diffusion Master Equation (RDME). Obviously, it cannot be solved analytically for almost any practical problem, but it is possible to simulate it albeit at very significant computational expense. In this work, we use RDME approach to carry out computer simulations of filopodia growth-retraction dynamics.

Structure and Protein Fluxes in the Filopodium

The filopodial diameter is thought to be set up by the elastic properties of the membrane²⁶ and to be around 100–200 nm. The bundle of F-actin, growing out of three-dimensional lamellipodial mesh at the cell's leading edge, typically consists of 10–30 filaments. They are cross-linked by different cross-linking proteins, which increase mechanical rigidity of the filopodium.

The main processes in filopodial growth are transport and interconversion of different forms of actin, so the latter is the key protein for describing and understanding filopodial growth dynamics. The main physical variables governing the dynamics are the fluxes of actin (and to a lesser extent, other proteins) along the filopodial tube. However, there is no straightforward way to directly observe complete actin fluxes experimentally. On the other hand, filopodial length (along with the protrusion force) is the essential result of the growth-retraction dynamics, and can be observed directly in a microscope. Therefore, it is physically insightful to develop models of filopodial dynamics around the concepts of how protein fluxes govern the filopodial length. Models constructed in such way are predictive, and can be readily related to the experimental results.

There are three main actin fluxes in a formed filopodium.⁶ First, since there is ample G-actin in the cell bulk, and hence at the filopodial base, and lack of it at the tip, where they are constantly consumed for polymerization, a concentration gradient of G-actin develops along the filopodium.^6,7,15,27 The gradient drives the diffusion of G-actin to the tip, which is an example of a transport flux. Second, there is the conversion of G-actin to F-actin through polymerization, a reaction flux. Finally, retrograde flow pulls F-actin back to the cell bulk, again a transport flux. These fluxes are regulated by chemistry (such as reactions between actin and other proteins), mechanics (such as pulling from the lamellipodium or pushing of the membrane or an obstacle) and transport (such as active or passive delivery of actin and regulatory proteins).

For the examples of chemical regulation of actin fluxes, we concentrate on the polymerization flux, created by the basic and the most important reaction in filopodia. Special proteins called formins can bind to the barbed ends and increase the polymerization rate (and thus polymerization flux) several fold.²⁸ They also prevent capping of the barbed ends by capping proteins, which stop the polymerization,²⁹ decreasing the total polymerization flux. Capped filaments retract because of retrograde flow, and if they are not uncapped before they fully retract into the cell bulk, the number of filaments decreases, thus lowering the total retrograde flow flux.¹⁵ Sequestering the amount of available G-actin monomers can also regulate polymerization, for instance, via binding of G-actin to thymosin-β4.³⁰ Alternatively, profilin binding to G-actin promotes its association specifically at the barbed ends.³¹

The main mechanical regulatory mechanisms of the fluxes are interactions with the membrane and focal adhesions.³² Barbed ends push the membrane, which makes it harder for G-actin monomers to go in between the barbed end and the membrane and attach to the filament. Therefore, according to the Brownian ratchet hypothesis, these force-dependent steric interactions diminish the polymerization flux.⁷ They also are an example of the regulation of chemistry by mechanics in filopodia. Conversely, chemistry influences mechanics by forming the focal adhesions, which are the attachments of the filaments to the surface on which the cell crawls. They pull on the filaments counteracting the retrograde flow, thus slowing down its transport flux. As the focal adhesion stretch, their disengagement rate increases, again an example of regulation of filopodial chemistry by mechanics.³³ Mechanics can also regulate reaction fluxes by purely steric interactions between proteins, for instance, in the dense filopodial tip complex.^34,35 Another important mechanical aspect is buckling of the filopodium, either under the load from pushing an external obstacle or just randomly.^7,36–38

Finally, transport fluxes can be enhanced by active transport of proteins by molecular motors.³⁹ Again, chemistry is an integral part of it starting from the ATP hydrolysis reaction, which drives the active transport, and binding reactions between the motors and cargo or between the motors and filament tracks on which motors are walking.

Summarizing the points above, the filopodial dynamics is an intricate heavily intertwined web of chemistry, mechanics and transport, interacting stochastically. Many of the important biochemical regulations act through the modifications of protein fluxes, which are the key quantities governing the growth-retraction dynamics. Next, we quantify the statements above using a mean-field approach, trying to distill some basic laws of filopodial growth-retraction dynamics.

The most basic scenario of the filopodial growth includes just G-actin diffusion, polymerization and depolymerization at the tip and retrograde flow of the F-actin bundle back to the bulk of the cell.⁶ By Fick's law, for spatially varying G-actin concentration a, the diffusional flux is

$$J_D=-D\frac{\partial a}{\partial x^{\text{'}}}$$ Eqn. 1

which with the continuity equation yields the diffusion equation for a(x,t):

$$\frac{\partial a}{\partial t}=-D\frac{{\partial }^{2}a}{\partial x^2}.$$ Eqn. 2

The first thing to find out is the stationary filopodial length, or, the maximal length it can grow. In the stationary case, the time derivative on the left hand side is zero, and the solution of Equation 2 is linear:

$$\begin{array}{c}a(x)=a_{\text{base}}-\frac{J_D}{D}x,\\ J_D=-D\frac{a_{\text{tip}}-a_{\text{base}}}{L},\end{array}$$ Eqn. 3

where L is the stationary length we are looking for, but which is undetermined at this point. It is reasonable to assume that the concentration of G-actin at the filopodial base, a_base, is kept equal to that in the bulk of the cell (the cell's volume is much larger than that of the filopodium). Equations 1 and 3 essentially mean that diffusion provides a constant flux J_D of G-actin toward the tip. As the solution is stationary, the flux does not change in time and is the same everywhere along the filopodium.

At the tip, G-actin converts into F-actin via the polymerization reaction. The flux of this conversion or the polymerization flux, is

$$J_P=\frac{N(k^{+}{a}_{\text{tip}}-k^{-})}{\pi R^2},$$ Eqn. 4

where N is the number of actin filaments in a bundle, k⁺ and k⁻ are polymerization and depolymerization rates and R is filopodial radius. In the stationary state, all the G-actin flux delivered by diffusion gets converted to F-actin, since the filopodial tip is closed and the flux cannot be directed anywhere else, so J_D = J_P. Also, each of these fluxes is equal to retrograde flow flux, as all actin incorporated into a filament will flow back with that filament and eventually go through the filopodial base into the bulk of the cell. Retrograde flow flux is

$$J_r=\frac{N{\nu }_r}{\pi R^2\delta }$$ Eqn. 5

where v_r is retrograde flow velocity (which can be reasonably assumed to be constant as the first approximation) and δ is half the monomer size (there are two protofilaments, so when filament moves by a size of a monomer, there is a flux of one monomer in each of the protofilaments).

Next, we recall that in the stationary state, the total flux of all forms of actin should be zero at any point inside the filopodium. When considering the flux balances specifically at the base and the tip, one realizes that at steady-state all of J_D is converted to J_r through J_P (for example, all G-actin entering the filopodial base through diffusion exits the filopodium through retrograde flow as F-actin). Hence, the three fluxes must be equal, J_D = J_r = J_P (as in Eqns. 3–5), which, in turn, leads to the G-actin monomer concentration at the tip being,

$$a_{\text{tip}}=({\nu }_r/\delta +k^{-})/k^{+}$$ Eqn. 6

and the stationary length:⁶

$$L=\frac{\pi R^{2}D}{N}\left(\frac{\delta }{{\nu }_r}\left(a_{\text{base}}-\frac{k^{-}}{k^{+}}\right)-\frac{1}{k^{+}}\right).$$ Eqn. 7

Another way to put it is that a filopodium grows while G-actin concentration at the tip is greater then a_tip from Equation 6, which is governed by the retrograde flow rate. The stationary length occurs exactly at that concentration of G-actin from Equation 6, and if the instantaneous concentration of G-actin at the tip drops below a_tip, the filopodium will start retracting. This is a very fundamental result, independent of approximations of the model: in order to grow, the polymerization flux (depending on the monomer concentration at the tip) should be larger than the retrograde flow flux. Additionally, the monomer concentration at the tip depends on diffusion: as the filopodium grows, the G-actin gradient becomes shallower, and the diffusional flux along with the tip concentration diminishes until the latter hits the value of a_tip given in Equation 6. In other words, in this basic scenario, the maximal filopodial length is essentially limited by the diffusional flux.

To take into account various corrections to the general behavior described by Equation 7, the model can be easily generalized in different ways. For instance, to account for the membrane force pushing on the polymerizing barbed ends of the bundle, k⁺ can be based on the instantaneous membrane load, leading to exponential dampening according to the Brownian ratchet mechanism.^6,40 To account for the effects of formin anticapping and boosting the polymerization rate one can just increase k⁺ (formins are processive motors with a low off-rate, so it is reasonable to assume that most of the filaments are anticapped when formin is present). The approximation of a constant speed retrograde flow fully generated inside of the lamellipodial mesh can also be improved. Membrane pushing on the barbed ends contributes to it as well, so with additional parameter (r), indicating fraction of monomer length contributing to the tube growth, and with (1 − r) indicating a contribution to retrograde flow, it is easy to take the filament recoiling effect into account by modifying Equation 7. For ranges of parameter values reported in the experimental literature, Equation 7 yields the filopodial stationary length on the order of 1 µm.

Indeed, the lengths of the experimentally observed filopodia are generally on the order of several microns. However, in some rare cases they can grow up to a 100 µm.⁴¹ According to the above mean-field model, such lengths can only be achieved if the G-actin flux forward is much greater or the retrograde flow flux is much smaller than the values we used in our estimation. Experimentally observed values of retrograde flow do not really allow for the latter scenario, and diffusion is too slow to do much for the former. Even at very high (but still realistic) bulk G-actin concentrations and diffusion coefficient, and on the lower side of real range of retrograde flow velocities, the filopodial length from Equation 7 falls considerably short of the 100 µm. Regardless of the accuracy of the approximations of the mean-field model described above are, there is no escaping the fact that G-actin has to be delivered to the tip and the corresponding fluxes should be balanced in the stationary state.

One of the common motifs uniting a series of works on filopodia from our group is a focus on this discrepancy between theoretical and experimental lengths and explaining how these long filopodia may be possible.^6,15,27 As an addition to the review of prior works, in this paper we also report on our new analysis of the way active transport flux regulates filopodial growth. This analysis highlights an important, complex issue of coupling of active transport by molecular motors to passive diffusional transport and polymerization and retrograde flow fluxes. We discovered surprising G-actin distributions along the filopodial tube and not-trivial dynamics of reaching the stationary state.

The Stochastic Simulation Model Taking into Account Chemistry, Transport and Mechanics

The simulation model of the filopodium that we use is based on chemical reactions between proteins. Our model is spatially resolved (1D). The filopodium is divided into compartments, and we keep track of discrete number of molecules of each kind in each of the compartments. On each simulation step, a time period and a reaction are randomly chosen based on reaction rates (via Gillespie alogorithm⁴²). Diffusion of different proteins along the filopodium is also modeled as a reaction of hopping back and forth between adjacent compartments (like a unary chemical reaction where species from one compartment turns into the same species in an adjacent compartment). After the reaction is chosen, the copy numbers of the corresponding reactants and products are updated according to the stoichiometric coefficients of the reaction, and then mechanical variables are updated (e.g., retrograde flow is applied corresponding to the expired time period). The reaction rates depending on mechanical variables (e.g., polymerization rates damped by membrane fluctuations or focal adhesion disengagement rates ramped up by stretching) are updated next, and then the cycle goes to the next simulation step.

On top of the basic model, which only contains G-actin diffusion, retrograde flow, membrane force and polymerization,⁶ one can add regulatory proteins, such as formins and capping proteins¹⁵ or myosin molecular motors.²⁷ As mentioned above, capping proteins can decrease the retrograde flow flux J_r, by decreasing the number of filaments (a capped filament retracts due to retrograde flow and will fully disapper into the cell bulk unless randomly uncapped while still retracting). Lower J_r means J_D can be lower and still sustain growth. This allows for shallower G-actin gradient and thus a longer filopodium (Eqn. 3). However, with less filaments in its bundle, the filopodium will be more prone to buckling instability. Also, there is a minimum amount of filaments required to sustain the membrane elastic force (3–4 for our parameters and force of 10 pN). If less than 3–4 filaments remain uncapped, the filopodium retracts as a whole, although it is likely to undergo a mechanical catastrophe before that occurs.¹⁵ Capping proteins are present in very low concentration (40–50 nM), which means that capping or uncapping of a barbed end is a rare random binary event, or, in other words, a highly discrete and slow random noise. In contrast, polymerization (especially, formin-assisted) and retrograde flow are fast processes, so capping acts as a random switch between the two. The switching results in macroscopic filopodial growth-retraction oscillations which have been observed in stochastic computer simulations.¹⁵ Large fluctuations are indicative of high susceptibility of system dynamics to external perturbations, which can be potentially beneficial for performing the sensorial function of a filopodium.

Even with lower number of filaments, the diffusional transport limit on the length falls far short of the 100 µm. When the diffusion is too slow, a living cell often employs transport of cargo by molecular motors. In a previous work based on the stochastic simulations model described above, we followed the consequences of addition of myosin X motors, which could carry the G-actin monomers.²⁷ One would expect that with the addition of motors the G-actin flux forward would greatly increase, however, a naïve throwing of the motors into the mix does not solve the transport limit problem, and the length can only increase for about 30%. The limit is not elevated for two main reasons. First, if freely floating and diffusing motors in the cytosol can also bind G-actin (as cargo), they will also sequester the latter in the cytosol, so the concentration of G-actin at the filopodial tip will not increase, comparing to the situation without the motors. In fact, at high concentration of motors, it can even decrease. Second, high amount of motors and their high processivity lead to socalled “traffic jamming” or clogging of the filaments by motors, which drastically decreases the additional influx of G-actin due to active transport.²⁷ If the sequestration is alleviated either artificially or through plausible biochemical circuits, the filopodia in simulations can grow up to several microns, compared with the submicron length in the situation without the motors.²⁷

In the current work, we investigate how motor transport regulates the filopodial length and determines G-actin distribution along the filopodium, in case when the binding between a motor in cytosol (not on a filament) and a G-actin monomer is forbidden. This requirement, which is one way to solve the sequestration problem discussed above, may not be as artificial as it seems. For instance, it is known that kinesin tail can interact with its head domain in an auto-inhibitory way.^43,44 This may serve not only to inhibit the ATP hydrolysis, but also to prevent cargo binding by those motors that are on the cytosol and not on the tracks. The biological reason for that would be the prevention of cargo sequestration by freely floating motors. One may hypothesize that similar or analogous mechanisms may exist for some myosins as well.

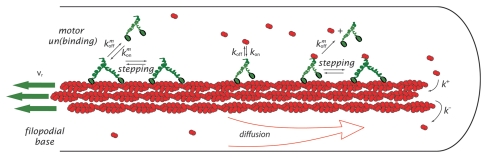
To investigate the effect of non-sequestering motor transport of actin on G-actin concentration profiles and consequently, the filopodial length, we employ the following computational setup (Fig. 1). There are N = 16 actin filaments in the cylindrical filopodial tube with radius R (75 nm).^8,35 G-actin is diffusing along the filopodium (D = 5 µm²/s),⁴⁵ while its concentration at the filopodial base is maintained by the cell at a constant bulk level (10 µM).^27,46–48 At the tip, G-actin monomers can react with the N barbed ends with the rate 11.6 µM⁻¹s⁻¹ and depolymerize with rate 1.4 sec⁻¹.⁴⁹ Retrograde flow moves the filaments backward with a constant speed v_r = 70 nm/s.^50–53 Myosin motors also diffuse along the filopodium, but in addition they can bind to a filament with the rate k^m_on (for all the binding and on-rates we use the diffusion-limited value of 10 µM⁻¹s⁻¹), unbind with the rate k^m_off (10–100 sec⁻¹) and perform right and left steps on filaments with the rates k_→ = 50 s⁻¹ and k_← = 5 s⁻¹. If a motor is bound to a filament, it can also load actin with the rate k_on = 10 µM⁻¹s⁻¹ and unload it with the rate k_off (10–30 sec⁻¹). To prevent sequestration, when a loaded motor unbinds from a filament, it simultaneously releases its G-actin cargo. Motors cannot step on or bind to an F-actin monomer unit occupied by another motor. Model parameters used in this work are summarized in Table 1.

Figure 1.

A representation of the filopodial model is shown with kinetics scheme of chemical reactions. The motors can walk on filaments (with speed v determined by forward and backward stepping rates) or diffuse in the solution (with diffusion constant of 5 µm²/s). They can bind and unbind to the filaments (with rates k^m_on and k^m_off) and, when on filaments, load and unload G-actin (with rates k_on and k_off). A loaded motor can detach from the filament simultaneously releasing G-actin. Thus, there is no G-actin bound to motors in the solution, fulfilling the non-sequestrating regime condition.

Table 1.

The values of parameters used in stochastic simulations

Filopodial radius, R	75 nm
Protein diffusion constant, D	5 µm2/s
Bulk actin concentration, abase	10 µM
Polymerization rate constant, k+	11.6 µM−1s−1
Depolymerzation rate constant, k−	1.4 sec−1
Retrograde flow speed, vr	70 nm/s
Binding/loading rate constants, kon, kmon	10 µM−1s−1 (diffusion-limited)
Stepping rate constants, k→, k←	50; 5 sec−1
Motor unbinding form F-actin, kmoff	10–100 sec−1
G-actin unloading from a motor, koff	10–30 sec−1
Motor speed, vm = 32.4 nm (k→, − k←)	1,458 nm/s
Binding site concentration, N/πR2δ	558 µM

G-Actin Transport by Myosin-X Sets up a Non-Monotonic G-Actin Profile

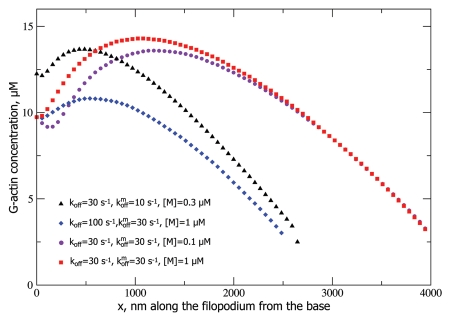
Using stochastic simulations we found that our model of filopodial growth assisted by non-sequestering molecular motor transport predicts an interesting, non-monotonic G-actin concentration profile along the filopodial tube. The profiles are shown in Figure 2, where, for all given parameter values, one can observe a dip in the G-actin concentration followed by a growth to a maximum, followed by a decline. This result is far from obvious, but it can be rationalized through the following arguments. At any point along the filopodium, there are three fluxes: the diffusional flux J_D, the retrograde flow flux J_r, and the active transport flux J_AT. Just like before, in the stationary state, they have to sum up to zero, the only difference being the additional active transport flux. Since in our model motors can only diffuse into the filopodium, but not come on the filament tracks, J_AT at the base is zero. Therefore, J_r has to be balanced by J_D alone which then has to be positive, so the slope of a(x) has to be negative at the filopodial base. The negative slope is in practice achieved by empty motors “vacuuming up” of the diffusing G-actin near the base, then transporting these bound G-actin molecules forward into the tube. As the motors do so, they pump up the G-actin concentration farther from the base, so a(x) should start increasing at some point, hence, explaining the minimum in a(x) profile near the base. Next, as the motor traffic jam builds up, the efficiency of the motor transport decreases, and a(x) starts to drop again, after reaching a maximum (Figs. 2 and 3). In other words, the a(x) slope has to be negative both at the base (to balance J_r) and at the tip (because at the tip a(x) = a_tip (Eqn. 6), and a(x) cannot be lower than that value anywhere in the filopodium or the filopodium would not grow past that point). Without the motors (or with inefficient motor transport) we would see a monotonic, nearly linear decrease in a(x) toward the value of a_tip at the tip. However, in case of efficient motor transport, the motors suck up G-actin near the base, creating a minimum, and pump it up toward the tip, until they jam. Figure 3 shows the active transport flux, which gradually decreases because of this jamming. Therefore, in this case, we generally expect a local minimum followed by a local maximum in the actin concentration profile along the filopodial tube, which is indeed observed in the stochastic simulations (Fig. 2).

Figure 2.

G-actin concentration profiles for different parameter values are shown. All the profiles end when the concentration drops below a_tip (Eqn. 6) which is about 2.3 µM for our parameter values, which, in turn, is determined by v_r = 70 nm/s substituted into Equation 6.

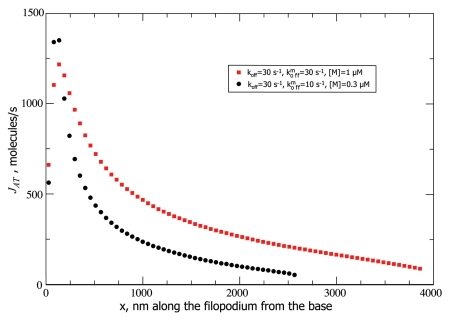
Figure 3.

Active transport fluxes for different parameter values are shown. The flux decreases after the traffic jam is formed. The retrograde flow flux J_r of 415 molecules/s determines the flux of G-actin monomers which need to be delivered to the tip at steady-state.

Because of the broad maximum in the G-actin concentration profile (Fig. 2), J_D is negative and counteracts the positive active transport flux J_AT on the left hand side of the maximum. As J_AT decreases after the jam builds up, J_D correspondingly increases since J_AT + J_D = J_r = constant, and diffusive flux assumes the burden of actin delivery toward the tip, where J_AT can be almost negligible compared with J_D (53 molecules/second vs. 360 molecules/second for one set of parameters, see Fig. 3). Figure 4 shows the how the jamming builds up. The filaments are fully jammed at the concentration of 558 µM. This concentration sharply builds up to more than 500 µM in the first few hundred nanometers of the filopodium. Interestingly, despite the fact, that the maximum in J_AT occurs very close to the base, where jam quickly develops, J_AT is nevertheless still considerable far from the base (Fig. 3), even though the filaments become almost fully jammed (Fig. 4). This is partially explained by high “bare” speed of motors, on the order of micron per second, which even when diminished by an order of magnitude due to jamming, can still deliver noticeable flux. However, in longer filopodia, the final stretch of monomeric actin delivery to the polymerizing tip is done mainly by diffusion. Interestingly, the corresponding filopodia can still be much longer than without active transport, because the latter greatly aids the overall flux to the tip by building up G-actin concentration in the middle of the filopodial tube.

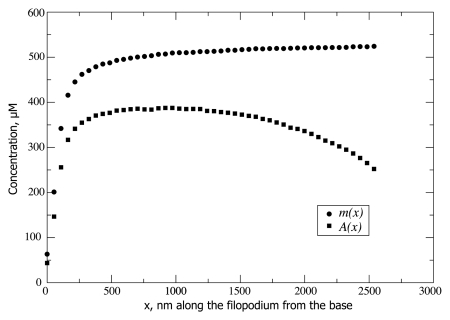
Figure 4.

Concentration profiles for actin-on-the-motors A(x) and motors-on-the-filaments m(x) are shown for k_off = 30 s⁻¹, k^m_off = 30 s⁻¹, [M] = 0.3 µM (corresponding to the black curve on Fig. 2). The concentration of F-actin binding sites N/πR²δ = 558 µM caps m(x), while A(x) is in turn capped by m(x).

There doesn't seem to be a straightforward experimental way to obtain these G-actin concentration profiles. The main complication for fluorescence microscopy is that one would have to discriminate between three forms of actin: F-actin, G-actin on the motors and free G-actin. Also, at this point, there is no evidence that G-actin is in fact transported by motors, which is the first issue to be resolved. In that case, one would still have to discriminate between G-actin and F-actin, but that seems to be possible, for example through labeling only a small fraction of actin or labeling a protein that only binds to G-actin.⁵⁴ We have discussed this issue in Zhuravlev et al.²⁷

Another important observation is that the relaxation to the stationary state in stochastic simulations is rather slow, especially, for longer filopodia (up to 15 min). This is higher than the order of average filopodial lifetime,^41,55–57 however some filopodia are longer-lived^41,57 and thus may reach the stationary state before they are switched to retraction by other regulatory proteins. A more important implication of the slow relaxation is that filopodial dynamics and the outcome of a particular protrusion may be extremely sensitive to, or even largely defined by, the initial condition of that particular filopodium formation. In one case we observed relaxation to two close (within 10–15%), but distinctly different stationary lengths for the filopodium of the same set of parameters but with simulations starting with different initial lengths. If an analogy may be drawn between filopodial growth-retraction dynamics and exploration of an energy landscape,^58,59 such observation may imply that the energy landscape is somewhat rugged (like in glasses),^60–64 with kinetic traps, where the filopodium can reside for extended periods of time appearing stable, but then continue to grow or retract, when pushed by a fluctuation or new regulatory proteins coming into play. Interestingly, if a_tip could be tuned to be large enough (e.g., by increasing further the retrograde flow rate), the corresponding horizontal line would cross the G-actin concentration curves at two points, leading to two locally stable steady-state filopodial lengths, indicating a potential for bifurcation in this system. At this point it is not clear whether real filopodia always develop into a unique steady-state, or whether multiple steady-state lengths might exist, with the possibility of transitions from one state to another.

Conclusion

Spatially extended nature of the filopodium makes structural and regulatory protein transport in it crucially important. To shed light on this transport, we were able to distill key physical observables in the very complex stochastic signaling network of mechano-chemical interactions and transport governing the filopodial growth-retraction dynamics. It is advantageous to think about the latter dynamics in terms of protein fluxes and their regulation. For instance, through the balance of actin fluxes one can explain the non-trivial result of non-monotonic conentration of G-actin inside the filopodium, predicted by our stochastic model for filopodial growth. Together, stochastic simulations and theoretical models are invaluable for understanding the mechanisms of filopodial regulation, highlighting roles and potentials of particular proteins. Experiments on filopodia can only be conducted in vivo, which makes them hard to interpret. Filopodial modeling is helpful both in interpretation of prior experiments and building intuition to guide future experiments.