Model-Based Analysis and Control of a Network of Basal Ganglia Spiking Neurons in the Normal and Parkinsonian States

Abstract

Controlling the spatiotemporal firing pattern of an intricately connected network of neurons through microstimulation is highly desirable in many applications. We investigated in this paper the feasibility of using a model-based approach to the analysis and control of a Basal Ganglia (BG) network model of Hodgkin–Huxley (HH) spiking neurons through microstimulation. Detailed analysis of this network model suggests that it can reproduce the experimentally observed characteristics of BG neurons under a normal and a pathological Parkinsonian state. A simplified neuronal firing rate model, identified from the detailed HH network model, is shown to capture the essential network dynamics. Mathematical analysis of the simplified model reveals the presence of a systematic relationship between the network’s structure and its dynamic response to spatiotemporally patterned microstimulation. We show that both the network synaptic organization and the local mechanism of microstimulation can impose tight constraints on the possible spatiotemporal firing patterns that can be generated by the microstimulated network, which may hinder the effectiveness of microstimulation to achieve a desired objective under certain conditions. Finally, we demonstrate that the feedback control design aided by the mathematical analysis of the simplified model is indeed effective in driving the BG network in the normal and Parskinsonian states to follow a prescribed spatiotemporal firing pattern. We further show that the rhythmic/oscillatory patterns that characterize a dopamine-depleted BG network can be suppressed as a direct consequence of controlling the spatiotemporal pattern of a subpopulation of the output Globus Pallidus internalis (GPi) neurons in the network. This work may provide plausible explanations for the mechanisms underlying the therapeutic effects of Deep Brain Stimulation (DBS) in PD and pave the way towards a model-based, network level analysis and closed-loop control and optimization of DBS parameters, among many other applications.

1. Introduction

Microstimulation of biological neural networks through extracellular current injection has been clinically regarded as a way to evoke patterns of neural activity that could ultimately lead to a desirable functional outcome. Examples include Functional Electrical Stimulation (FES) in the peripheral [1, 2], and Deep Brain Stimulation (DBS) in the central nervous systems [3, 4], as well as inducing perception with sensory prosthetic devices such as Cochlear and retinal implants [5, 6]. In many brain areas, information is widely believed to be encoded in the precise spiking patterns of densely connected networks of neurons with distinct morphologies and cell types, and precise spatiotemporal control of the output of these networks through microstimulation is highly desirable in many applications. This control, however, is challenging, in part due to the large number of unobserved elements in the area being stimulated, the complexity underlying the local mechanisms of microstimulation, and the interplay between the intrinsic network structure and its dynamic response to external stimulation.

Electrical microstimulation activates not only the neuronal elements near the electrode tip, but also networks of numerous neurons that are connected to those elements being directly stimulated. It was suggested in [7] that extracellular electrical microstimulation causes sparse and spatially distributed patterns of activation that depends on the axonal projection patterns in the cortex. At low current levels (subthreshold excitation), neural elements-most likely axons within tens of microns from the electrode tip-are mainly activated via direct depolarization and then propagate in both antidromic and orthodromic directions, consistent with previous computational studies [8, 9, 10] and in vitro experimental investigations [11, 12]. This effect, however, does not rule out the possibility that at high current (suprathreshold excitation) through a single electrode or at low currents (subthreshold) through multiple microelectrodes more neurons could be indirectly activated via synaptic connections [13, 14]. Indeed, previous studies have suggested that microstimulation can elicit postsynaptic potentials, which, together with antidromic activation, are expected to have major influence on spatially diffuse networks [13, 15]. Taken together, the sparse and distributed pattern of activation evoked by microstimulation makes it critical to precisely control the delivery of microstimulation, both in space and time, in order to achieve a desired outcome.

Despite the progress made to date, it remains difficult to formally characterize how densely connected networks of neurons respond differentially to arbitrary spatiotemporal stimulation patterns, let alone optimize them for a given application. Lack of analytical tractability is one major obstacle that precludes characterizing the effects of patterned microstimulation at the network level, particularly in the case of large networks of intricately interconnected spiking neurons such as those in the Basal Ganglia (BG) system involved in motor control. The objective of this work is to investigate the feasibility of a model-based approach to the analysis and control of neural microcircuits from a Multiple-Input-Multiple-Output (MIMO) systems perspective. In the BG system, such approach may be substantially important to provide plausible explanation of the enigmatic mechanisms of DBS in Parkinson’s disease treatment, and to provide more effective ways to optimize stimulation parameters.

The paper is organized as follows. Section 2 provides necessary background on the simulated BG neural circuit, the structure of the simplified firing rate model, and the use of Singular Value Decomposition (SVD) for the analysis of the system. The results of the analysis and control design based on the simplified model are detailed in Section 3. We discuss in Sec. 4 practical issues related to spatiotempral control of the BG neural circuit in normal and diseased states and devise some strategies for the control of these circuits. Section 5 summarizes our conclusion and suggestions for future work.

2. Methods

2.1. A Biologically Realistic Network of Spiking Neurons

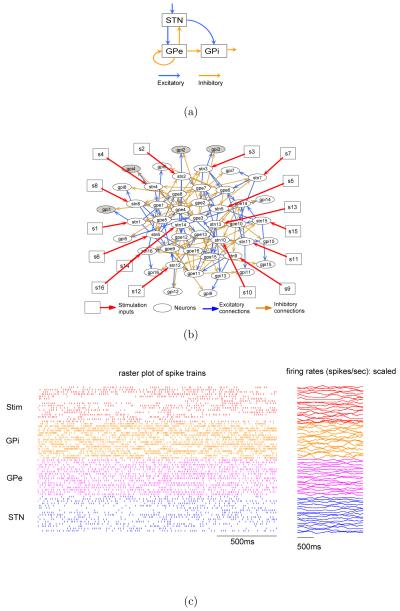
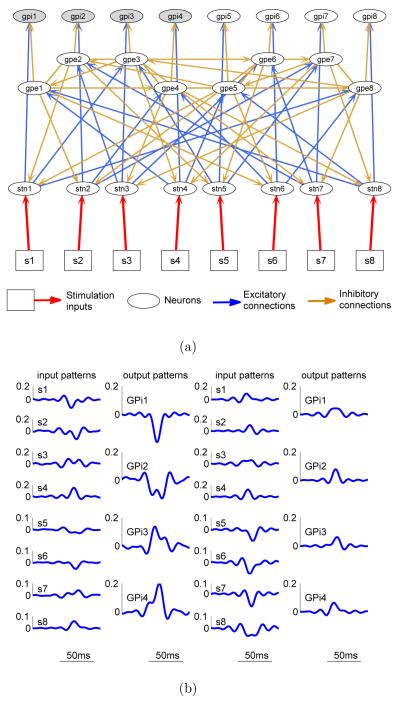
A Matlab/Simulink model was implemented based on the Basal Ganglia (BG) circuit used in [16]. Figure 1(a) shows the high level block digram of the BG circuit and Figure 1(b) shows its detailed synaptic connectivity. The model consists of three populations of neurons (see Figure 1(a)): Subthalamic Nucleus (STN), Globus Pallidus externalis (GPe), and Globus Pallidus internalis (GPi). Each population consists of 16 single-compartment Hodgkin-Huxley (HH) type spiking neurons whose membrane potentials are governed by a selection of ionic channels to match the in-vitro electrophysiological recordings. More precisely, for a microcircuit consisting of N neurons, we have

$$C_i{\stackrel{.}{V}}_i=-\sum _k{I}_k^{\text{ion}}-\sum _{j\ne i}{I}_{i,j}^{\mathit{syn}}+I_i^{\mathit{inj}},i=1,2,\dots ,N$$ (1)

where C_i and V_i are the membrane capacitance and the membrane potential of neuron i, respectively. $I_k^{\text{ion}}$ is the ionic current, $I_{i,j}^{\mathit{syn}}$ is synaptic current from neuron j to neuron i, and $I_i^{\mathit{inj}}$ is the intracellularly injected current at neuron i (See [17, 16] for the composition of ionic channels for each type of neurons).

Figure 1.

A Basal Ganglia microcircuit. (a) High level block diagram of the BG circuit. (b) Detailed synaptic connectivity of the BG circuit. The external microstimulation inputs are marked by squares and red arrows. (c) BG microcircuit under patterned stimulation. Episodes of stimulation pulse trains are randomly generated according to a Poisson distribution with randomly reinforced silence period between successive episodes. Left panel shows a two-second raster plots of the stimulation pulse trains and the spike trains from all neurons in the network. Right panel shows the firing rates (scaled to fit the window) computed from the spike trains shown in left panel over a sliding window of 200ms.

All neurons are firing spontaneously through a constant current injection. Each STN neuron provides excitatory inputs to a subpopulation of GPe and GPi neurons. In addition to the self inhibitory connections within the GPe neuron population, each GPe neuron also inhibits neurons in the STN and GPi population. Each STN neuron accepts temporally patterned electrical pulse (square shape with duration = 0.6 ms and amplitude = 200 pA/μm²) trains that are either randomly generated or controller optimized. Note that each STN neuron will subsequently excite a network of neurons due to synaptic coupling. We chose to control the spatiotemporal firing pattern of GPi neurons because they constitute the major outputs of the BG system to motor nuclei in the thalamus that leads to activation of cortical premotor circuitry [18], and because controlling this activity is hypothesized to underlie the therapeutic mechanisms of DBS in Parkinson’s Disease (PD) [3]. The stimulation inputs are denoted by s₁ to s₁₆ as shown in Figure 1(b). Spike trains were extracted by simple thresholding of the membrane potentials.

2.2. System Identification for Model Simplification

For simplicity we assume that neuronal outputs are expressed in terms of their firing rates instead of precisely timed sequences of action potentials (similarly for the stimulation pulse trains). We first smooth the original discrete event observations by calculating the firing rates over a sliding window of length T (e.g. see Figure 1(c) where T = 200ms). We then use the following model to characterize the input-output relationship of each individual neuron

$$\begin{array}{cc}\hfill & x_i\left(t_k\right)=\sum _{j\ne i}\frac{B_{i,j}^r\left(q^{-1}\right)}{F_{i,j}^r\left(q^{-1}\right)}{r}_j\left(t_k\right)+\sum _{j=1}^p\frac{B_{i,j}^s\left(q^{-1}\right)}{F_{i,j}^s\left(q^{-1}\right)}{s}_j\left(t_k\right)\hfill \\ \hfill & r_i\left(t_k\right)=h\left(x_i\right(t_k);{\theta }_i)\hfill \end{array}$$ (2)

where t_k = kT_s is the discrete time stamps and T_s is the sample time. r_i(t_k) is the firing rate of neuron i over a sliding window of length T, s_j(t_k) is the j^th stimulation input, q⁻¹ is the unit delay operator, x_i(t_k) is an intermediate variable; The term $\frac{B_{i,j}^r\left(q^{-1}\right)}{F_{i,j}^r\left(q^{-1}\right)}$ models the direct (monosynaptic) dynamic influences of the spiking rate of neuron j on that of neuron i via x_i(t_k), and the term $\frac{B_{i,j}^s\left(q^{-1}\right)}{F_{i,j}^s\left(q^{-1}\right)}$ captures the dynamic interaction between input s_j and the firing rate of neuron i via x_i(t_k); h(x_i(t_k); θ_i) is the static output function parameterized by θ_i, which, for example, can be used to account for the background level of spiking and the nonlinearity in spiking frequency characteristics [19, 20, 21, 22].

If we choose to use a first order polynomial for the output function, i.e., h(x_i(t_k); θ_i) = k_ix_i(t_k) + c_i, by eliminating the intermediate variables x_i(t_k), we can explicitly express the firing rates r(t_k) = [r₁(t_k), … , r_n(t_k)]^T (assuming n neurons) as a function of the stimulation inputs s(t_k) = [s₁(t_k), … , s_p(t_k)]^T (assuming p stimulation inputs) and other variables as follows

$$\begin{array}{cc}\hfill \mathbf{r}\left(t_k\right)& ={[\mathbf{I}-\mathbf{KW}(q^{-1}\left)\right]}^{-1}\left[\mathbf{KH}\right(q^{-1}\left)\mathbf{s}\right(t_k)+\mathbf{c}]\hfill \\ \hfill & ={[\mathbf{I}-\tilde{\mathbf{W}}(q^{-1}\left)\right]}^{-1}\left[\tilde{\mathbf{H}}\right(q^{-1}\left)\mathbf{s}\right(t_k)+\mathbf{c}]\hfill \end{array}$$ (3)

where c = [c₁; … ; c_n]^T ; K is a diagonal matrix with each diagonal element equal to k_i; The transfer functions $\frac{B_{i,j}^r\left(q^{-1}\right)}{F_{i,j}^r\left(q^{-1}\right)}$ and $\frac{B_{i,j}^s\left(q^{-1}\right)}{F_{i,j}^s\left(q^{-1}\right)}$ are the (i, j)^th elements of matrices W(q⁻¹) and H(q⁻¹), respectively. Choosing a first order polynomial as the output function linearizes the microcircuit and makes the resulting model mathematically tractable. The model, however, becomes valid only in a limited operation regime. The cost and benefits of model simplification from the perspective of control analysis and design are further discussed in Section 4.

It is worthwhile to emphasize the importance of the expression ${\left[\mathbf{I}-\tilde{\mathbf{W}}\left(q^{-1}\right)\right]}^{-1}$, which describes how the monosynaptic (first-order/direct/open-loop) interaction, $\tilde{\mathbf{W}}\left(q^{-1}\right)=\mathbf{KW}\left(q^{-1}\right)$, translates into polysynaptic (higher-order/indirect/closed-loop) interaction among neurons across the entire network. Each panel of ${\left[\mathbf{I}-\tilde{\mathbf{W}}\left(q^{-1}\right)\right]}^{-1}$ characterizes how the effects of changing the firing rate of one neuron dynamically propagate to other neurons through synaptic coupling. Therefore, pre-multiplying $\tilde{\mathbf{H}}\left(q^{-1}\right)$ by ${\left[\mathbf{I}-\tilde{\mathbf{W}}\left(q^{-1}\right)\right]}^{-1}$, denoted as $\mathbf{G}\left(q^{-1}\right)={\left[\mathbf{I}-\tilde{\mathbf{W}}\left(q^{-1}\right)\right]}^{-1}\tilde{\mathbf{H}}\left(q^{-1}\right)$, represents network effects of multi-site microstimulation.

2.3. Singular Value Decomposition

By replacing q⁻¹ with e^−jwT_s, we obtain the frequency domain representation of the transfer function $\mathbf{G}\left(e^{-jw{T}_s}\right)={\left[\mathbf{I}-\tilde{\mathbf{W}}\left(e^{-jw{T}_s}\right)\right]}^{-1}\tilde{\mathbf{H}}\left(e^{-jw{T}_s}\right)$, where T_s is the sample time, and w here has the units of rad/sec (note $\frac{1}{2\pi }\mathit{rad}∕\mathit{sec}=1\mathrm{Hz}$). G(e^−jwT_s) describes the system response to sinusoidal stimulation patterns with frequency w. Since the model is a firing rate model, w is therefore the oscillation frequency of the firing rates and should not be confused with the actual values of the firing rates (or the instantaneous stimulation frequency). Fixed period pulse trains under this framework are constant vector signals with w = 0 and amplitude equal to the corresponding fixed frequency.

For a Single-Input-Single-Output (SISO) linear time invariant (LTI) system, applying a sinusoidal signal s(t_k) = A_ssin(wT_sk + α_s) (or s(w) = A_se^jα_s in phasor notation) at the input, the output will also be a sinusoidal signal but scaled by a factor ∣G(e^−jwT_s)∣ and phase shifted by $\angle G\left(e^{-jw{T}_s}\right)$

$$r\left(t_k\right)=A_s\mid G\left(e^{-jw{T}_s}\right)\mid \sin (w{T}_{s}k+{\alpha }_s+\angle G(e^{-jw{T}_s}\left)\right)$$

or in phasor notation because

$$r\left(w\right)=A_s\mid G\left(e^{-jw{T}_s}\right)\mid e^{j({\alpha }_s+\angle G(e^{-jw{T}_s}\left)\right)}=G\left(e^{-jw{T}_s}\right)s\left(w\right)$$

because $G\left(e^{-jw{T}_s}\right)=\mid G\left(e^{-jw{T}_s}\right)\mid e^{j\angle G\left(e^{-jw{T}_s}\right)}$. Therefore, the gain at a given frequency is simply

$$\frac{\mid r\left(w\right)\mid }{\mid s\left(w\right)\mid }=\frac{\mid G\left(e^{-jw{T}_s}\right)s\left(w\right)\mid }{\mid s\left(w\right)\mid }=\mid G\left(e^{-jw{T}_s}\right)\mid$$

If we use the vector 2-norm, denoted as ∥·∥₂, then at a given input frequency w, the gain of the MIMO system G(e^−jwT_s) for a specific input signal s(w) is given by the ratio

$$\frac{{\Vert \mathbf{r}\left(w\right)\Vert }_2}{{\Vert \mathbf{s}\left(w\right)\Vert }_2}=\frac{{\Vert \mathbf{G}\left(e^{-jw{T}_s}\right)\mathbf{s}\left(w\right)\Vert }_2}{{\Vert \mathbf{s}(w\Vert }_2}$$

Unlike the case of SISO systems, the system gain of a MIMO system additionally depends on the direction of the input vector, denoted by s(w) = [s₁(w), … , s_p(w)]^T, which can vary from $\underset{¯}{\sigma }\left(\mathbf{G}\right(e^{-jw{T}_s}\left)\right)$ to $\stackrel{‒}{\sigma }\left(\mathbf{G}\right(e^{-jw{T}_s}\left)\right)$, where $\underset{¯}{\sigma }(\cdot )$ is the smallest singular value and $\stackrel{‒}{\sigma }(\cdot )$ is the largest singular value of the transfer function matrix G(e^−jwT_s). In other words, the system responds differentially depending on relative amplitudes and phase shifts of the sinusoidal stimulation inputs across stimulation electrodes.

To gain more insight into the mathematical tractability of the transfer function from stimulation input to neural output, let’s consider the SVD of the transfer functionmatrix G(e^−jwT_s) from s to r evaluated at a fixed frequency w. The SVD of the transfer function matrix is given by

$$\mathbf{G}\left(e^{-jw{T}_s}\right)=\mathbf{U}\left(w\right)\Sigma \left(w\right)\mathbf{V}{\left(w\right)}^H$$ (4)

where ∑(w) is a n by p matrix whose main diagonal elements are the non-zero singular values σ_i(w), i = 1, … , min {n, p} arranged in descending order; U(w) = [u₁(w), … , u_n(w)] is a unitary matrix of output singular vectors, and V(w) = [v₁(w), … , v_p(w)] is a unitary matrix of input singular vectors. ^H denotes the complex conjugate transpose. Note that elements in the input singular vector u_i(w) or output singular vector v_i(w) can also be written in phasor notation and they represent the relative amplitudes and phase shifts of the input and the output signals. If we rewrite Equation (4) as G(e^−jwT_s)V(w) = U(w)∑(w), then for column i we would have

$$\mathbf{G}\left(e^{-jw{T}_s}\right){\mathbf{v}}_i\left(w\right)={\sigma }_i\left(w\right){\mathbf{u}}_i\left(w\right)$$ (5)

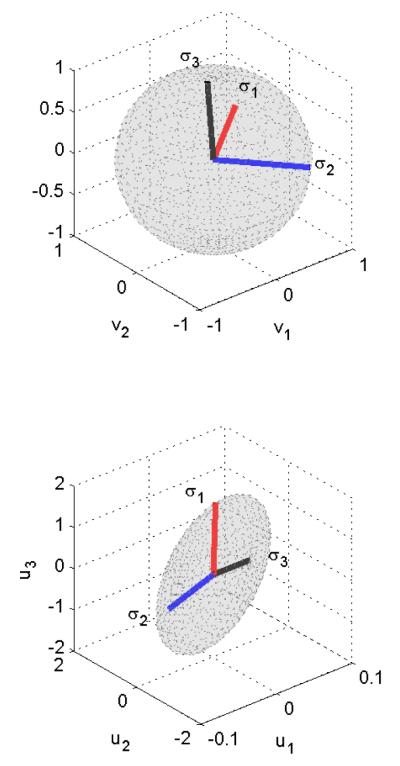
Note that if we consider a stimulation input in the direction v_i(w), then the output is in the direction u_i(w) and the gain is the corresponding singular value σ_i(w). Figure 2 illustrates the singular value decomposition of a 3-input-3-output system at w = 0. The input directions corresponding to σ₁ and σ₂ are amplified whereas the input direction corresponding to σ₃ is attenuated. In the case when ∑(w) is dominated by very few large singular values, the network tends to produce very specific response patterns only when specific input patterns are presented, and thus exhibits strong spatiotemporal selectivity. We will drop the term e^−jwT_s and w from now on for simplicity, but note that SVD is frequency dependent.

Figure 2.

Directions in MIMO systems. The figure illustrates the singular value decomposition of a 3-input-3-output system at w = 0. The input directions corresponding to σ₁ and σ₂ are amplified whereas the input direction corresponding to σ₃ is attenuated.

The number of directions with significantly nonzero singular values can be considered as “vocabularies” that the circuit can generate. This imposes spatiotemporal constraints that may limit the information that could be carried by both timing and rates in a population of neurons [23]. Under this simple SVD framework, we can argue that increasing the number of neurons will generally lead to an increase, albeit at a slower rate, in the number of “vocabularies”, because the dynamics of the local cortical circuit can result in varying degrees of correlation among interconnected neurons. This is consistent to the experimental observations presented in [23].

2.4. Functional Controllability

Given a set of neurons to be controlled, it is important to determine whether their firing activity can be independently manipulated using a given set of stimulation inputs, which brings the concept of functional controllability. A system is said to be functionally controllable if the normal rank of the input-output transfer function is equal to the number of outputs, which naturally requires the number of inputs to be no less than the number of outputs [24]. The minimum singular value of the input-output transfer function matrix can be used as an indicator of how close the system is to be functionally uncontrollable [24]. We note that $\underset{¯}{\sigma }\left({\left[\mathbf{I}-\tilde{\mathbf{W}}\right]}^{-1}\tilde{\mathbf{H}}\right)$ is bounded as follows

$$\frac{\underset{¯}{\sigma }\left(\tilde{\mathbf{H}}\right)}{\underset{¯}{\sigma }(\mathbf{I}-\tilde{\mathbf{W}})}\ge \underset{¯}{\sigma }\left({\left[\mathbf{I}-\tilde{\mathbf{W}}\right]}^{-1}\tilde{\mathbf{H}}\right)\ge \frac{\underset{¯}{\sigma }\left(\tilde{\mathbf{H}}\right)}{\stackrel{‒}{\sigma }(\mathbf{I}-\tilde{\mathbf{W}})}$$

which depends not only on the network synaptic coupling $\tilde{\mathbf{W}}$ but also on the local mechanisms of microstimulation $\tilde{\mathbf{H}}$

High levels of input signal “spreading” onto large number of neurons disregarding their existing anatomical connectivity can potentially cause $\tilde{\mathbf{H}}$ to be ill-conditioned (or rank deficient), and thus lead to smaller $\underset{¯}{\sigma }\left(\tilde{\mathbf{H}}\right)$. For example, in the extreme case when each stimulation electrode activates all STN neurons, we are effectively dealing with a system with only one degree of control freedom. In other words, we can only drive the firing patterns of the STN neurons in one direction. As a result, increasing the level of current spread can shrink the space of spatiotemporal patterns we can evoke through multi-channel microstimulation. This effect is similar to that of reducing the number of stimulation inputs.

2.5. Relative Gain Array

Closing the loop between certain set of inputs and outputs in the feedback control mode can have many undesired system responses. This is primarily due to the presence of dynamic coupling among various inputs and outputs as a result of synaptic connectivity and actuation dynamics. It is, therefore, important to quantify the degree of coupling of various Input/Output (I/O) combinations. This is especially useful when we are faced with an exceedingly large parameter space of potential inputs and corresponding outputs, which would actually be the case when stimulating hundreds or possibly thousands of neurons simultaneously. The Relative Gain Array (RGA) [24, page 90] is one such measure of interaction that is commonly used in the MIMO control literature. The RGA of the input-output transfer function matrix G is defined by

$$\mathit{RGA}\left(G\right)\doteq \mathbf{G}\times {\left({\mathbf{G}}^{†}\right)}^T$$ (6)

where × denotes element-by-element multiplication, and G^† is the pseudo inverse of G. Each element of the RGA matrix represents the ratio between the open-loop and the “closed-loop” gains for the corresponding input-output pair. By “closed-loop” we mean partial control with all other outputs perfectly controlled (set to constant values)[24]. RGA is a very useful tool for localized/decentralized control. The objective is to pair up the specific stimulation inputs and neuron outputs whose corresponding RGA elements are close to 1, because the corresponding transfer function in such case is less affected by closing the other loops.

3. Results

3.1. The Simplified Firing Rate Model Captures the Essential Dynamics of the Network in Response to External Inputs

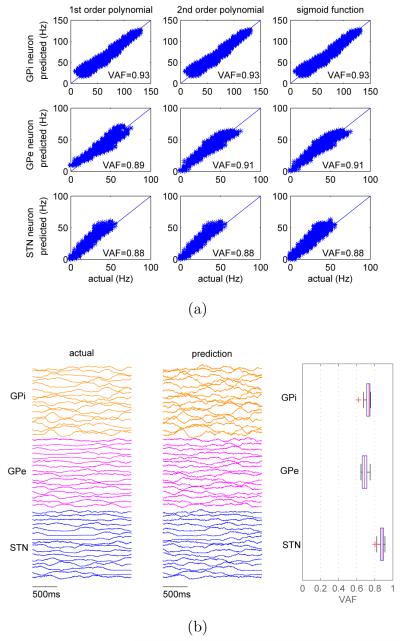
The parameters of each individual firing rate neuron model (see equation (2)) were estimated by fitting the model to the data collected from the simulation of the Hodgkin-Huxley BG circuit as described in Section 2.1 (see Figure 1(c) for examples of simulated data). The parameter estimation was performed using the system identification toolbox in Matlab where iterative prediction-error minimization methods are available. The search method is one or a combination of Gauss-Newton method, adaptive Gauss-Newton method, gradient method, or Levenberg-Marquardt method. The search method was automatically chosen by the Matlab function. The output function was chosen to be the first order polynomial, and the resulting simplified model was linear (see Equation (3)). Note that other types of output functions have been tested, but no significant performance improvement was observed (see Figure 3(a)).

Figure 3.

Prediction performance of the simplified model. (a) The impact of different types of output functions on the prediction accuracy of single neuron model evaluated over ten seconds. (b) Prediction accuracy of network model. Left panel plots the actual spiking rates from the BG circuit of spiking neurons over two seconds. Middle panel plots the predicted spiking rates using the simplified circuit model. Right panel shows the statistics of prediction accuracy ($\mathit{VAF}=1-\frac{\mathit{var}\left(\widehat{r}\right(t_k)-r(t_k\left)\right)}{\mathit{var}\left(r\right(t_k\left)\right)}$) for three different types of neurons.

The simplified network model was then constructed by interconnecting individual simplified neuron models based on the actual network topology of Hodgkin-Huxley BG circuit. The prediction accuracy of the firing rate network model is shown in Figure 3(b), in which the simplified circuit was driven by the same external patterned stimulation inputs. There is high level of correlation between actual spiking rates and the predicted ones (left and middle panels in Figure 3(b)). The statistics of the Variance Accounted For ($\mathit{VAF}=1-\frac{\mathit{var}\left(\widehat{r}\right(t_k)-r(t_k\left)\right)}{\mathit{var}\left(r\right(t_k\left)\right)}$, where $\widehat{r}\left(t_k\right)$ is the predicted firing rate) for three different types of neurons are shown on the right panel. Note that the prediction performance decreases from single neuron models to network models, which is likely due to the error accumulation when neuron models are interconnected into a network. Despite the apparent simplicity of the model structure (see equation (3)), the results demonstrate that the simplified circuit model indeed captures the essential features of the dynamic interactions among different neurons as well as the spatiotemporal dynamics of the neural circuit in response to external stimulation inputs.

3.2. Functional Controllability is Largely a Structural Property of the Network

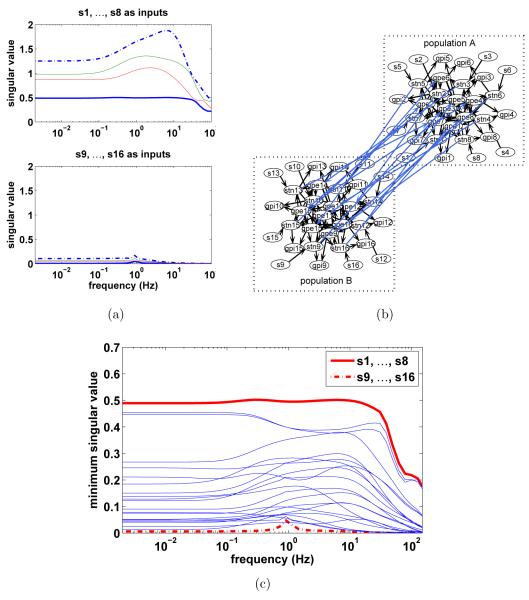
We use a few examples in this section to demonstrate that functional controllability is largely a property of the network structure and the relative connection strength. For example, consider the problem of controlling the firing activities of GPi neurons 1 to 4 using two separate groups of stimulation inputs, {s₁, … , s₈} or {s₉, … , s₁₆}. Figure 4(a) shows the singular values of the transfer function matrices from {s₁, … , s₈} (upper panel) and from {s₉, … , s₁₆} (lower panel) to the outputs of the four GPi neurons (sub-matrices of ${\left[\mathbf{I}-\tilde{\mathbf{W}}\right]}^{-1}\tilde{\mathbf{H}}$). The minimum singular value of the system with inputs {s₁, … , s₈} is much larger than that of the system with inputs {s₉, … , s₁₆}. Therefore, the system with inputs {s₉, … , s₁₆} is much closer to be functionally uncontrollable, meaning that stimulating these specific STN neurons does not permit exercising the most effective control of the spiking of the four GPi neurons. On the other hand, using inputs {s₁, … , s₈} offers much better controllability across all frequencies for these GPi neurons. Closer inspection of the Hodgkin-Huxley BG circuit reveals that this is likely due to the weak synaptic connectivity between two populations of neurons as shown in Figure 4(b), in which the maximum conductance of the synaptic coupling between-population from STN neurons to GPe neurons is only one-fifth of those within each population. The four output GPi neurons belong to population A that inputs {s₁, … , s₈} directly influence. As a result, the influence of inputs {s₉, … , s₁₆} on the firing pattern of the four GPi neurons through these weak between-population synaptic connections is less effective than that of inputs {s₁, … , s₈}.

Figure 4.

Functional controllability is largely a property of the network synaptic coupling and their relative strength. (a) Example of a functionally controllable system indicated by the singular values of the transfer function matrices from {s₁, … , s₈} to GPi neurons 1 to 4 (upper panel); example of a almost functionally uncontrollable system with {s₉, … , s₁₆} as inputs(lower panel). (b) Network is redrawn from Figure 1(b) to demonstrate the two clusters of weakly connected populations. The four output GPi neurons to be controlled belong to population A that inputs {s₁, … , s₈} directly influence while {s₉, … , s₁₆} indirectly influence. (c) The minimum singular values of systems with random combinations of 8 out of 16 available simulation inputs to demonstrate the selectivity of the system across frequencies and inputs. Total 20 different random combinations are shown. The output GPi neurons are kept the same.

The practical implications of this observation can be stated as follows: stimulation inputs have to directly influence neurons that project to the output neurons for the system to have better functional controllability. As expected, the functional controllability of systems with any random combinations of 8 different stimulation inputs, out of the 16 available, largely falls between the two extreme cases discussed above (see Figure 4(c)). In terms of the ability to independently manipulate the firing activity of the four output GPi neurons, input combination {s₁, … , s₈} would be the best choice among all different combinations of 8 out of the 16 available stimulation inputs. The condition of functional controllability guarantees that the system outputs can be controlled to follow arbitrary spatiotemporal patterns. This can be rather restrictive if the desirable output patterns are known to belong to the subspace spanned by directions with large singular values.

3.3. Spatiotemporal Selectivity of the Neural Circuit

We now examine the circuit from the eight stimulation inputs {s₁, … , s₈} to the four output GPi neurons and denote the system transfer function matrix as G₁. We provide here a numerical example to make an important point. The SVD of the DC gain matrix of G₁, which characterizes the system response to stimulation pulse trains with fixed frequency (in other words, when there is no oscillation in the stimulation pattern), is given by

$$\begin{array}{cc}\hfill {\mathbf{G}}_1\left(1\right)=& {\mathbf{U}}_1{\Sigma }_1{\mathbf{V}}_1^H=\hfill \\ \hfill & \left[\begin{array}{cccc}\hfill -0.55& \hfill 0.15& \hfill -0.65& \hfill 0.51\\ \hfill -0.40& \hfill -0.44& \hfill 0.63& \hfill 0.50\\ \hfill 0.31& \hfill 0.75& \hfill 0.31& \hfill 0.50\\ \hfill 0.67& \hfill -0.48& \hfill -0.29& \hfill 0.48\end{array}\right]\left[\begin{array}{cccccccc}\hfill 1.25& \hfill 0& \hfill 0& \hfill 0& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0& \hfill 0.98& \hfill 0& \hfill 0& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0& \hfill 0& \hfill 0.87& \hfill 0& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0& \hfill 0& \hfill 0& \hfill 0.49& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\hfill \\ \hfill & {\left[\begin{array}{cccccccc}\hfill -0.43& \hfill -0.23& \hfill -0.62& \hfill 0.45& \hfill -0.05& \hfill 0.18& \hfill 0.03& \hfill 0.36\\ \hfill -0.50& \hfill -0.01& \hfill 0.64& \hfill 0.41& \hfill 0.15& \hfill -0.08& \hfill 0.38& \hfill 0.00\\ \hfill 0.29& \hfill 0.75& \hfill -0.06& \hfill 0.45& \hfill 0.32& \hfill 0.08& \hfill -0.09& \hfill 0.19\\ \hfill 0.60& \hfill -0.51& \hfill 0.10& \hfill 0.41& \hfill 0.13& \hfill 0.36& \hfill 0.20& \hfill -0.13\\ \hfill -0.12& \hfill -0.19& \hfill -0.13& \hfill -0.27& \hfill 0.92& \hfill -0.03& \hfill -0.01& \hfill -0.02\\ \hfill -0.22& \hfill 0.17& \hfill 0.15& \hfill -0.28& \hfill -0.02& \hfill 0.90& \hfill -0.03& \hfill 0.01\\ \hfill 0.11& \hfill 0.20& \hfill -0.28& \hfill -0.25& \hfill -0.04& \hfill -0.01& \hfill 0.90& \hfill 0.02\\ \hfill 0.19& \hfill -0.14& \hfill 0.27& \hfill -0.22& \hfill -0.01& \hfill -0.05& \hfill 0.01& \hfill 0.90\end{array}\right]}^H\hfill \end{array}$$

Carefully examining the column vectors of U₁, we note that each element corresponds to the amount of change in the firing rate of the corresponding GPi output neuron. For example, the first column vector u₁ is [−0.5, −0.4, 0.31, 0.67]^T means that the firing rates of the first two GPi neurons would change by approximately similar amounts in the opposite direction to the firing rates of the other two GPi neurons. Because this vector corresponds to the largest singular value, small changes in the corresponding input direction would lead to large changes in the output. On the other hand, the last column vector u₄ is [0.51, 0.50, 0.50, 0.48]^T means that changes in the firing rates of the output neurons will occur in similar directions. This, however, would require larger changes in the corresponding input direction because u₄ corresponds to the smallest singular value.

To see if this interpretation is consistent with the network structure, the detailed local synaptic connectivity of the BG circuit that contains the 4 GPi neurons is redrawn in Figure 5(a). As we can observe from this figure, each output GPi neuron (highlighted in grey) accepts one excitatory input from one STN neuron and one inhibitory input from one GPe neuron. To increase the firing of all four GPi neurons, we would naturally want to increase the firing of the excitatory presynaptic STN neurons (indexed from 1 to 4) and simultaneously suppress the firing of inhibitory presynaptic GPe neurons (indexed 1 to 4). This creates a control conflict since each of the presynaptic STN neurons also strongly excite the presynaptic GPe neurons, which subsequently cancels part of the excitatory effects of the presynaptic STN neurons. On the other hand, consider the input/output direction corresponding to the largest singular value, increasing (suppressing) the firing of STN neurons 1 and 2 has similar effects on the firing of the four GPi neurons to that of suppressing (increasing) STN neurons 3 and 4 (Figure 5(a)). Therefore, similar changes in this stimulation input direction can produce larger changes in the corresponding neural output direction.

Figure 5.

Network spatiotemporal selectivity. (a) Detailed view of the local synaptic connectivity of the BG circuit. Same circuit drawn from population A in Figure 4(b) with inter-population weak connections omitted for clarity. (b) Reconstruction of the input and output temporal patterns corresponding to the largest and the smallest non-zero singular values. The total energy of the inputs was normalized to 1. The first and second (third and fourth) column show the input and output temporal patterns associated with the largest (smallest) singular value.

It is important to bring this theoretical analysis to practical observations during DBS of the BG system. Typically, electrical pulses are delivered at a fixed frequency across all stimulation sites [3, 25]. Mathematically, this corresponds to evaluating the transfer function matrix G₁(e^−jwT_s) at w = 0, i.e., G₁(1), which is the DC gain matrix we have previously analyzed. At a fixed stimulation frequency f₀ across all stimulation sites, the stimulation input can be expressed as a vector signals v_s(w)|_w=0 = f₀[1; 1; 1; 1; 1; 1; 1; 1]^T, and applying this input to the system we have

$$\frac{{\Vert {\mathbf{G}}_1\left(1\right){\mathbf{v}}_s\Vert }_2}{{\Vert {\mathbf{v}}_s\Vert }_2}=\frac{{\Vert {\mathbf{U}}_1{\Sigma }_1{{\mathbf{V}}_1}^H{\mathbf{v}}_s\Vert }_2}{{\Vert {\mathbf{v}}_s\Vert }_2}=0.13⪡\underset{¯}{\sigma }\left({\mathbf{G}}_1\right(1\left)\right)=0.49$$ (7)

The gain in the input direction v_s is much smaller than the smallest singular value. This is because the projections of v_s along the last four columns vectors of V₁ occupy 93.65% of the total variance in the stimulation inputs without affecting the firing rates of the output GPi neurons. This shows that progressive changes in the firings rates of GPi neurons will be seen when the frequency of the electrical pulse train is progressively higher than zero.

The small system gain (0.13 << 1) corresponding to stimulation with fixed period/frequency pulse trains suggests that the changes in the GPi neurons’ patterns can be quite insignificant compared to the spontaneous activity at lower fixed stimulation frequencies. In other words, the network dynamics are more likely to be dominated by the spontaneous activity at lower stimulation frequencies. Therefore, low fixed frequency stimulation is unlikely to suppress the rhythmic firing patterns that might exist in the spontaneous network activity that are eventually manifested in the abnormal PD motor behavior. At high stimulation frequencies, the effect of stimulation-induced changes in the network dynamics starts to dominate over the spontaneous network activity and thus potentially suppresses the detrimental effects of any rhythmic patterns that might exist. This could be a plausible explanation of why only high frequency stimulation is effective in suppressing the symptoms of PD [26].

The analysis of the DC matrix G₁(1) shows the importance of the spatial distribution of the stimulation pattern on the network selectivity. To study both the spatial and the temporal aspects of the network dynamics, we need to examine the transfer function matrix G₁(e^−jwT_s(1) across different frequencies (G₁(e^−jwT_s(1) characterizes the system response when the system is subject to sinusoidal stimulation with frequency w). The spatiotemporal selectivity to arbitrary stimulation patterns can be better illustrated by reconstructing the corresponding input and output patterns in the time domain. We use the inverse Fast Fourier Transform (iFFT) by uniformly sampling the frequency domain response (consider (5) and let $w=\frac{2k\pi }{N{T}_s}$, k = 1, … ,N). Figure 5(b) shows the reconstructed time domain stimulation input and output patterns corresponding to the largest and the smallest non-zero singular values. Higher frequency contents greater than 300 rad/s (around 48 Hz) are discarded since the functional controllability of the system degrades significantly at higher frequencies (see Figure 4(a)).

Figure 5(b) shows the response of the GPi neurons under two different sets of spatiotemporal stimulation patterns that correspond to the largest (first panel in Figure 5(b)) and the smallest singular values (third panel in Figure 5(b)). At the same level of variation in the inputs (the total variance in all inputs is kept the same for both scenarios), the total variance in all outputs is 1.71 for the largest singular value (second panel in in Figure 5(b)) and 0.21 for the smallest singular values (fourth panel in in Figure 5(b)). The system amplifies the effect of the input patterns associated with the largest singular value and attenuates the effect of the inputs patterns associated with the smallest singular values. The difference is large (1.71 >> 0.21) and is quite visible from the plotted output patterns for the two different scenarios. The circuit therefore is more sensitive to certain spatiotemporal patterns of variation in the inputs and thus exhibits strong spatiotemporal selectivity.

3.4. Control Structure Selection and Spatiotemporal Feedback Control

In this section, we design a localized/decentralized feedback controller that drives the spatiotemporal firing patterns of the four GPi neurons to follow prescribed reference patterns using eight stimulation inputs s₁, … , s₈. Due to the lack of experimentally validated model that links the observed motor behavior to the firing patterns of GPi, desired reference patterns associated with normal motor behavior were not available. We therefore use reference signals obtained from the open loop simulation of the BG circuit under random pulse trains (see Figure 1(c)). This would maximally probe the system to be controlled, and that helps assessing the ”modes” in the outputs to a broad range of ”modes” in the inputs.

For a given output neuron, we first select a set of stimulation sites that are effective in controlling its firing activity and introduce less close-loop interactions. We accomplish this by using the concept of relative gain arrays (see Section 2.5). We note that the RGA array is frequency dependent and the pairing suggested by RGA can be different at different frequencies. In our case, however, the pairing suggested by the RGA at different frequencies were largely the same and we picked the RGA evaluated at 100 rad/sec as an illustrative example. The relative gain array for transfer function G₁ evaluated around 100 rad/sec is calculated according to Equation (6) and its values are shown in Table 1. This angular frequency corresponds to 16 Hz and it is the frequency at which the singular values started to decrease significantly. The matrix G₁ is of dimension 4 by 8 and it characterizes the system response to various 16 Hz sinusoidal stimulation patterns. The rows and columns correspond to the outputs and inputs, respectively. Each element in the matrix represents the ratio between the open-loop and closed-loop gains for the corresponding input-output pair. If the value is close to 1, the corresponding input is preferred to be used for the control of the corresponding output because closing the loop does not significantly impact the dynamic relationship between the corresponding input and output pair.

Table 1.

Relative gain array of the transfer function matrix G₁ evaluated around 100 rad/sec (or 16 Hz)

	s1	s2	s3	s4
GPi 1	0:47 + 0:04i	−0:01 + 0:01i	−0:00 + 0:00i	0:13 − 0:07i
GPi 2	−0:01 + 0:02i	0:52 + 0:04i	0:09 − 0:04i	−0:00 − 0:01i
GPi 3	0:14 − 0:03i	−0:01 − 0:00i	0:58 + 0:03i	−0:01 + 0:01i
GPi 4	−0:00 − 0:02i	0:16 − 0:04i	−0:01 + 0:00i	0:48 + 0:07i
	s 5	s 6	s 7	s 8
GPi 1	−0:00 − 0:04i	−0:02 − 0:01i	0:00 − 0:00i	0:44 + 0:06i
GPi 2	−0:01 − 0:01i	−0:01 − 0:05i	0:42 + 0:05i	0:00 + 0:00i
GPi 3	0:30 + 0:04i	0:02 + 0:00i	−0:01 − 0:04i	−0:01 − 0:00i
GPi 4	0:02 + 0:01i	0:39 + 0:05i	−0:02 − 0:01i	−0:01 − 0:06i

From Table 1, we can observe that none of the RGA elements is very close to 1 suggesting that there are strong closed-loop interactions within the neuron circuit and all the input-output gains change significantly from open-loop to closed-loop. The RGA elements whose values are relatively close to 1 are highlighted using bold font in Table 1. The corresponding inputs and outputs are thus paired up and only the corresponding inputs can be most effectively used to control the corresponding outputs [24]. Therefore, we use s₁ and s₈ to control GPi neuron 1, s₂ and s₇ to control GPi neuron 2, s₃ and s₅ to control GPi neuron 3, and s₄ and s₆ to control GPi neuron 4. This give rise to the following controller structure

$$\left(\begin{array}{c}\hfill s_1\hfill \\ \hfill s_2\hfill \\ \hfill s_3\hfill \\ \hfill s_4\hfill \\ \hfill s_5\hfill \\ \hfill s_6\hfill \\ \hfill s_7\hfill \\ \hfill s_8\hfill \end{array}\right)=\left(\begin{array}{cccc}\hfill K_0\left(q^{-1}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill K_0\left(q^{-1}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill K_0\left(q^{-1}\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill K_0\left(q^{-1}\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -K_0\left(q^{-1}\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -K_0\left(q^{-1}\right)\hfill \\ \hfill 0\hfill & \hfill -K_0\left(q^{-1}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -K_0\left(q^{-1}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill e_1\hfill \\ \hfill e_2\hfill \\ \hfill e_3\hfill \\ \hfill e_4\hfill \end{array}\right)$$ (8)

where [s₁, … , s₈]^T are the 8-channel stimulation inputs and [e₁, … , e₄]^T are the differences between the references and the measured responses of the 4 GPi neurons; $K_0\left(q^{-1}\right)=P_0^P+P_0^I\frac{T_s{q}^{-1}}{1-q^{-1}}$ in which $P_0^P$ and $P_0^I$ are the proportional and integral gains of the PI controller; T_s is the sampling period. Note that we use the same K₀(q⁻¹) for all and this leaves us only two parameters ( $P_0^P$ and $P_0^I$) to be tuned. The controller has a decentralized structure, for example, only the firing activity of GPi neuron 1 is used to calculate the control signals for s₁ and s₈.

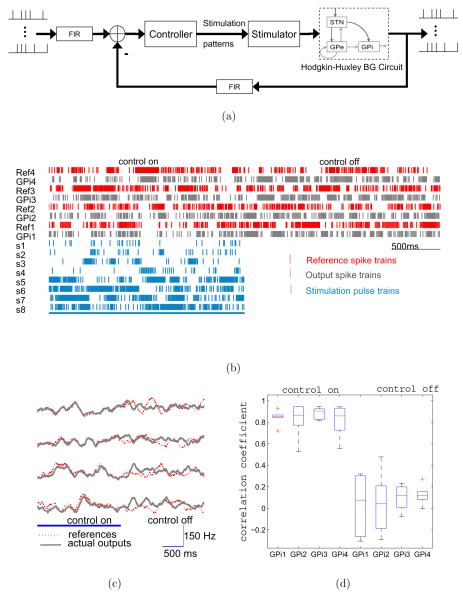
The controller parameter tuning was first carried out using the simplified model. After satisfactory performance was achieved, the same controller was then implemented with the detailed BG circuit of Hodgkin-Huxley neurons. Figure 6(a) shows the block diagram of the detailed implementation of the feedback control system. The Finite Impulse Response (FIR) filter calculates the spiking rates over a sliding window of 200ms. The differences between the filtered reference and output spike trains are used to generate the prototyped stimulation pulse trains that are delivered to s₁, … , s₈ as marked by square in Figure 1(b). The stimulator is a pulse generator with variable frequency inputs, which are continuously adjusted by the controller.

Figure 6.

Tracking performance of the decentralized closed-loop feedback controller. (a) Block diagram of the detailed implementation of the closed-loop feedback control system. (b) The raster plot of the reference and output spike trains before and after the controller is switched off. The raster plot of the stimulation input spike trains are also shown. (c) Same results as in (b) but plotted in firing rates (sliding window of 200 ms). (d) The box plot of the correlation coefficients for each output GPi neuron with and without feedback control.

Figure 6(b) and 6(c) shows an example raster plot of the reference spike trains and the responses of the output GPi neurons (indexed from 1 to 4). Switching on the feedback controller makes the firing patterns of the output GPi neurons to follow the references. Correlation analysis (Figure 6(d)) shows that the correlation coefficients (as in [27]) between the reference and the evoked spike trains under closed-loop control are significantly higher than those when the controller is switched off. This indicates that the closed-loop feedback controller is indeed effective in modulating the spatiotemporal firing patterns of the output neurons.

3.5. Feedback Control of a Parkinsonian BG Circuit

In the previous example, we have shown that the firing activity of the output GPi neurons can be forced to follow a given spatiotemporal firing pattern. Here, we investigate whether this effect might be useful to suppress the existing spontaneous activity patterns in the network such as the rhythmic/oscillatory patterns that characterize PD. We study in this section the effect of feedback tracking in a Parkinsonian BG circuit.

A Parkinsonian BG circuit was simulated by increasing the striatal inhibition to GPe neurons and decreasing the intrapallidal inhibition among GPe neurons to mimic dopamine loss [16]. For the purpose of simplicity, we adopted the same controller design based on the simplified model of the healthy circuit to control the Parkinsonian BG circuit. Note that further adjustment of the controller structure and parameters might produce better results because the controller we used was not specifically designed for the Parkinsonian BG circuit. We used the spike trains collected from the simulation of the healthy circuit under random stimulation inputs as reference signals.

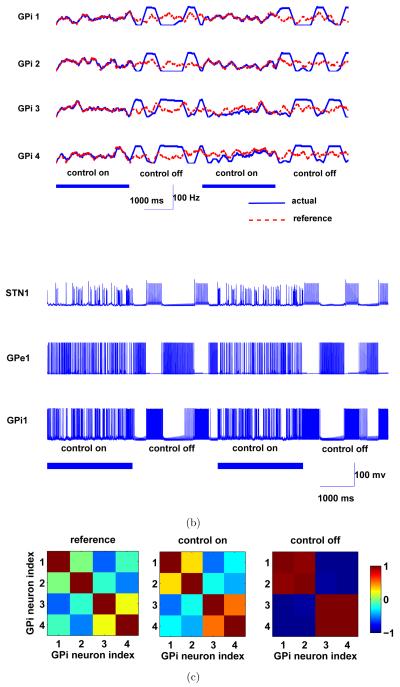
All three types of neurons in the Parkinsonian BG circuit exhibit rhythmic/oscillatory firing patterns once the control was switched off (Figure 7(b)). Two pairs of GPi neurons (GPi neuron 1 and 2, GPi neuron 3 and 4) exhibit high levels of correlation/synchronization and the firing activity of the two pairs is negatively correlated in the Parkinsonian BG circuit when the control was off (see Figure 7(a) and the right panel of Figure 7(c)). Once the controller was switched on, it drove the outputs of the GPi neourns to follow the reference patterns. In doing so, desynchronization of the GPi neurons resulted and the correlation structure among them resembled that of the reference signals (the left and middle panels of Figure 7(c)). In addition, the rhythmic/oscillatory firing patterns also disappeared from all the neurons in the Parkinsonian BG circuit (Figure 7(b)).

Figure 7.

Desynchornization performance of a Parkinsonian BG circuit. (a) The firing rates (sliding window of T = 200 ms) of the references and output GPi neurons during ON-OFF modes of the feedback controller. (c) Sample traces of the membrane potentials of STN, GPe and GPi neurons in the BG circuit during the two modes. (c) Correlation among the reference signals, and the firing rates of the four output GPi neurons when the control is on and off

4. Discussion

4.1. Simplified Model-Based Analysis and Control

In this work, we have shown that closed-loop control of neural activity using neural feedback provides an effective way for precise spatiotemporal control of a complex network of BG spiking neurons. Without any insight into the relationship between the circuit connectivity and network dynamics that can be provided by the analysis of a simplified circuit model, we can easily lose tractability in a myriad of signals. We provided a strategy to build a simplified model-based approach to deal with large scale systems when trial-and-error approaches become increasingly unmanageable [28, 29].

Using a simplified model, however, comes at a cost. Simplified circuit models offer a compromise between modeling accuracy and analytical tractability. As a result, simplified models may only be valid within a limited operation regime. For example, the simplified firing rate model used in our study does not capture the transient spiking dynamics of neurons at the very short (sub-millisecond) time scale. Therefore, it is anticipated to be of most relevance to study the dynamic interactions among neurons through synapses with time constants in the ranges of milliseconds or tens of milliseconds. Even though the simplified model used in our study is sufficient for the investigation of the spatiotemporal network dynamics in response to patterned stimulation, the use of a first order polynomial as the output function prevents it from capturing the subtle features of the self-sustained activity patterns in a spontaneously active neural circuit, such as oscillations, unless they are externally driven. The simplified model only approximates this type of self-sustained neural activity as constant background firing rates. The model, however, does capture the susceptibility or enhanced sensitivity of the network to spatially patterned oscillations in the firing rates within certain frequency bands (note that the largest singular values peaks around 7 Hz as shown in Figure 4(a)).

4.2. Limited Number of Observable Neurons and Stimulation Sites

From a practical standpoint, the invasive nature of microelectrodes implies that simultaneous stimulation and recording from a large number of neurons may inevitably increase tissue damage and thus limit the number of stimulation sites as well as the number of recorded neurons [30]. This may impose difficulties in model identification and fundamentally limit how much could be achieved using controlled microstimulation. As required by functional controllability, the number of inputs has to be no less than the number of outputs. If the number of stimulation inputs p is smaller than the number of output neurons n, the system will have at least n – p output directions u_p+1, … , u_n that are not controllable. In other words, it is only possible for the stimulation inputs to generate spatiotemporal patterns distributed along a specific set of directions u₁, … , u_p (if all the p singular values are non-zero). Therefore, limited by the number of stimulation sites, it is clearly difficult, if not impossible, to independently manipulate the activity of all measured neurons, let alone thousands of unobserved ones.

Despite the apparent difficulty, some factors might help in using smaller number of stimulation sites to control the spatiotemporal activity of larger number of neurons. First, neural activity in local cortical circuits is known to be correlated and the structure of this correlation seems to be critical for shaping the information flow across many pathways [31, 32]. Achieving a spatiotemporally correlated firing pattern does not necessarily require independently manipulating the firing activity of every output neuron and thus impose less restriction on the number of stimulation inputs. Second, a small fraction of neurons in a large cell assembly might be more influential or relevant in producing the desired output than others [33]. Therefore, a “good enough” outcome might be achieved by just controlling the activities of the key members in a cell assembly. This is particularly the case when we have access to neural elements belonging to a strongly connected structure [34, 35, 36].

4.3. On the Use of Feedback

The use of feedback can be very versatile depending on the nature of the application. Neural feedback has been demonstrated, albeit at an elementary level, to be effective in creating functional links between spatially distant brain areas [37]. A number of computational [38, 39, 52] and biological studies [40, 41] have also demonstrated that feedback can be highly effective in regulating ensemble neural activity, particularly in the control of synchronized cell assemblies. Because the control goal in such cases was to desynchronize/regularize the entire population dynamics using a few macroelectrodes with broad spatial current/voltage spread, they are fraught with generalization ability to cases in which precise and more delicate spatiotemporal control of spiking through more localized and less intense multi-channel microstimulation is sought, such as evoking perceptual experience through stimulation of sensory areas.

4.4. Effects of Choosing Different Stimulation Targets

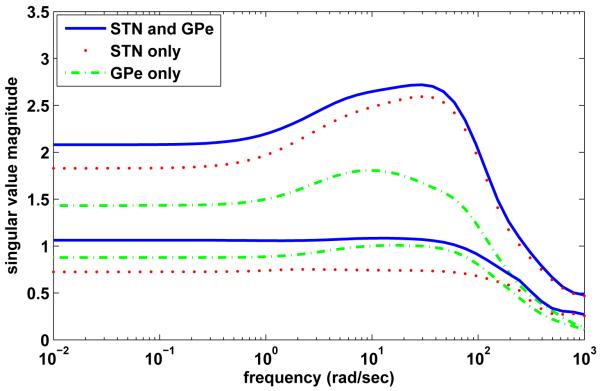
STN and Gllobus Pallidus (GP) of the basal ganglia are the two common targets of stimulation for Parkinson’s Disease (PD) [42]. Mathematical analysis of the matrix ${[\mathbf{I}-\tilde{\mathbf{W}}]}^{-1}$ indicates that the spatiotemporal control of GPi neurons is generally more difficult if we are confined to only one target nuclei: STN or GPe. For example, consider the problem of controlling the spatiotemporal patterns of the four GPi neurons (1 to 4) using different stimulation targets: STN neurons (1 to 8, same system as in the upper panel of Figure4(a)) alone, GPe neurons (1 to 8) alone, or both STN (1 to 4) and GPe (1 to 4) neurons. Figure 8 shows the smallest and the largest singular values of the transfer function matrices for the three different scenarios. The smallest singular value when stimulating both STN and GPe neurons is the largest among the three scenarios and the singular values also cover a higher range. This suggests that simultaneously influencing both STN and GPe neurons may offer better overall controllability with less stimulation energy. This observation, however, is not conclusive since the simulation energy is highly dependent on the output spatiotemporal patterns one would like to evoke. Nevertheless, our analysis is consistent with experimental findings [53] suggesting that, in addition to local effects, GPi stimulation has direct effects on efferent axons, thereby enabling more complex polysynaptic responses to dominate over monosynaptic ones, which eventually leads to changes in baseline firing rates in postsynaptic neurons.

Figure 8.

Profile of the smallest and the largest singular values of the transfer function matrices as a function of frequency for different stimulation input targets: STN neurons (1 to 8) alone, GPe neurons (1 to 8) alone, and combined STN (1 to 4) and GPe (1 to 4) neurons. The output neurons are the four GPi neurons marked by gray in Figure 1(b). The dynamic range between the smallest and largest singular values in the case of STN and GPe stimulation indicates that the control is most effective compared to stimulation of STN or GPe only.

4.5. Implications for DBS

With highly complex anatomical and functional connectivity patterns in many brain areas, the effect of extracellular electrical microstimulation can be profound at the network level. Although the therapeutic mechanisms of DBS remain largely unclear [3], it is now commonly accepted that axons in the vicinity of the DBS electrodes are likely to be directly activated first and the effect of the stimulation on neural activity at the stimulation site would be increased or decreased depending on neurotransmitters of the afferent fibers projecting to that site [4, 43, 14]. Based on this account, high frequency stimulation can “hijack” the pathological neural firing patterns, such as the rhythmic, oscillatory activity patterns that characterize the movement [44], and thus prevents the transmission of pathological activity patterns to other parts of the network [45]. Studies based on functional magnetic resonance imaging (fMRI) provide additional evidence that there is much more to the effects of DBS than just around the electrode [26]. It has been found that DBS induces widespread hemodynamic changes both in the cortical and subcortical areas when applied to patients with Parkinson’s disease [46] and compulsive disorders [47]. Different effects of high frequency stimulation of various targets in the BG system also suggest that the intrinsic network connectivity may play an important role in deciphering the mechanism of DBS, and subsequently other unsolved mysteries, such as therapeutic latencies during DBS onset and with cessation [3, 48].

Without a clear consensus in the clinical community on the exact mechanisms of DBS [48], a model-based network level analysis such as the one proposed here might be helpful in providing plausible explanations [26]. For the BG circuit under study, the response of the output GPi neurons was significantly attenuated when we indiscriminately applied fixed frequency stimulation pulse trains across all stimulation sites at the STN. This may provide a plausible network level explanation of why high frequency stimulation is therapeutically effective. In addition, the BG network model was shown to be susceptible to certain firing patterns with low-frequency oscillations, and as a result the rhythmic activity in the firing rates could be further amplified at the network level.

The strong spatiotemporal selectivity exhibited by the BG circuit under multi-channel microstimulation suggests that both the spatial and the temporal aspects of the stimulation patterns play an important role in shaping the response of the output GPi neurons. A model-based approach becomes beneficial when progressive knowledge of the inferred functional connectivity of the local neural circuit [49, 50, 51] becomes available. As we improve our understanding of the network mechanisms of DBS, it might be possible to develop model-based closed-loop feedback control systems capable of adjusting the stimulation patterns across multiple stimulation sites “on the fly” based on simultaneously recorded neural activity elsewhere to achieve an optimal therapeutic outcome while minimizing the stimulation energy and side effects.

5. Conclusion

We investigated in this paper the feasibility of using a model-based approach to the analysis and control of a network of spiking BG neurons in the normal and pathological states. Our results suggest that a simplified firing rate model, identified from a detailed Hodgkin-Huxley BG microcircuit model, captures the essential network dynamics in response to external stimulation. The use of linearization (first order polynomial approximation of the output function) is not as restrictive as it appears for the purpose of analysis and control design, particularly in the case when the spatiotemporal neural activity is strongly modulated by external stimulation inputs. The mathematical analysis revealed a systematic relationship between the network’s structure and its dynamic response under spatiotemporally patterned stimulation, which was otherwise difficult to characterize. A number of observations drawn from the analysis of the simplified firing rate model were found to be consistent with the detailed Hodgkin-Huxley BG circuit. In particular, the functional controllability was found to be largely decided by the network synaptic coupling and its strength. And the spatiotemporal selectivity of the neural circuit could be readily explained by examining directions in the input-output mapping. Most importantly, once the control objective was given the mathematical analysis helped to evaluate various combinations of stimulation inputs, and a decentralized feedback control architecture suggested by the simplified model was shown to be effective in driving the output neurons to follow a prescribed spatiotemporal firing pattern in the detailed BG circuit. Finally, we demonstrated that it is possible to use the proposed approach to control the activity pattern of the network in a pathological state, effectively shaping its output to follow an arbitrary reference activity pattern that could cause a normal motor function to emanate. This preliminary work can pave the way towards a model-based, multilevel network analysis and closed-loop control of PD, among many other applications.