Is N-acetyl-d-glucosamine a rigid ⁴C₁ chair?

Abstract

Understanding microsecond-timescale dynamics is crucial to establish three-dimensional (3D) structure–activity relationships in sugars but has been intractable to experiments and simulations. As a consequence, whether arguably the most important chemical scaffold in glycobiology, N-acetyl-d-glucosamine (GlcNAc), deviates from a rigid ⁴C₁ chair is unknown. Here, conformer populations and exchange kinetics were quantified from the longest aqueous carbohydrate simulations to date (0.2 ms total) of GlcNAc, four derivatives from heparan sulfate and their methylglycosides. Unmodified GlcNAc took 3–5 μs to reach a conformational equilibrium, which comprised a metastable ⁴C₁ chair that underwent ⁴C₁ ↔ ¹C₄ transitions at a predicted forward rate of 0.8 μs⁻¹ with an average ¹C₄-chair lifetime of 3 ns. These predictions agree with high-resolution crystallography and nuclear magnetic resonance but not with the hypothesis that GlcNAc is a rigid ⁴C₁ chair, concluded from previous experimental analyses and non-aqueous modeling. The methylglycoside was calculated to have a slower forward rate (0.3 μs⁻¹) and a more stable ⁴C₁ conformer (0.2 kcal mol⁻¹), suggesting that pivotal 3D intermediates (particularly ²S_O, ¹S₅ and B_2,5) increased in energy, and water was implicated as a major cause. Sulfonation (N-, 3-O and 6-O) significantly augmented this effect by blocking pseudorotation, but did not alter the rotational preferences of hydroyxl or hydroxymethyl groups. We therefore propose that GlcNAc undergoes puckering exchange that is dependent on polymerization and sulfo substituents. Our analyses, and 3D model of the equilibrium GlcNAc conformer in water, can be used as dictionary data and present new opportunities to rationally modify puckering and carbohydrate bioactivity, with diverse applications from improving crop yields to disease amelioration.

Introduction

Understanding carbohydrate three-dimensional (3D) structure–activity relationships (SARs) is a difficult but critical milestone in glycomics. Elucidating molecular details of glycan equilibrium 3D structure, presently in its infancy, are central to realizing accurate SARs and will enable rational exploitation of the vast medicinal and industrial potential of polysaccharides. The hexosamine chemical scaffold of N-acetyl-d-glucosamine (GlcNAc) is ubiquitous and mediates some of the most important processes in glycobiology. Consequently, establishing SARs in GlcNAc and its derivatives will engender innumerable opportunities to impact some of the most challenging scientific problems of our time. For example, as well as being a versatile scaffold for novel drug discovery (Wang et al. 2009), chemically modified GlcNAc is present in chitin and glycosaminoglycans, which hold great potential as novel biomaterials and medicines (Gama et al. 2006; Murrey and Hsieh-Wilson 2008; Khoushab and Yamabhai 2010).

The 3D structures of GlcNAc polysaccharides are defined by two dynamic conformational determinants: glycosidic linkage geometry and pyranose ring conformation (or pucker). Nanosecond gycosidic-linkage dynamics are better understood because they are amenable to study by both nuclear magnetic resonance (NMR) spectroscopy and simulation. However, while puckering is central to glycobiology, e.g. ribose differs from deoxyribose by having different equilibrium conformations (Rich 2003), whether substituents affect the ensemble of pyranose ring conformers remains enigmatic because exchange occurs on microsecond timescales, which has been problematic for NMR and simulations, until recently (Sattelle et al. 2010).

There is circumstantial experimental evidence to suggest that pyranoses, such as glucose and GlcNAc (considered to exist as exclusively stable ⁴C₁ chairs), are not as stable as once thought. For example, atomic force microscopy has inferred that glucose polymers contain non-⁴C₁ geometries (Marszalek et al. 1998; Heymann and Grubmuller 1999; Li et al. 1999), and non-⁴C₁ GlcNAc is observed in high-resolution crystallographic 3D structures of diverse (non-enzyme) protein co-complexes (Ikemizu et al. 1999; Chang et al. 2003; Maveyraud et al. 2009; Xu et al. 2010). Furthermore, studies have also shown that apparently stable ⁴C₁ chairs can be perturbed by chemical modifications, e.g. glucuronic acid (β-d-GlcA) deviates from a ⁴C₁ chair in fully O-sulfonated chondroitin and hyaluronan (Wessel and Bartsch 1995; Maruyama et al. 1998; Toida et al. 1999, 2000).

While NMR would be an ideal technique to explore these observations, puckering exchange occurs on the microsecond timescale, which is fast-enough to ensure that standard experiments cannot discriminate between conformers (resonances represent “average” puckers) and interpretation of anything but the simplest situation is difficult. Under ideal conditions, using scalar couplings, the minimum percentage of perceptible conformers is around 10%. Simulations are crucially important in this microsecond “blind spot,” but have not been routinely possible with explicit solvent due to lack of processing power (most previous simulations are <100 ns). Recently, implementation of molecular dynamics (MD) programs to run on graphics processing units have made it possible to perform deterministic unperturbed explicit solvent simulations on microsecond timescales (Harvey et al. 2009; Klepeis et al. 2009). Extended molecular mechanics studies are currently restricted to single chemistries but have recently revealed biologically relevant insight into carbohydrate puckering populations and exchange kinetics (Sattelle et al. 2010). Measurements from NMR (e.g. pyranose ring vicinal couplings) can then be usefully applied to test the simulations.

The potential rewards of understanding SARs in GlcNAc-containing polysaccharides are exemplified by heparan sulfate (HS) and structurally related heparin (Powell et al. 2004; Lamanna et al. 2007; Turnbull 2010). Localized in the extracellular matrix, HS mediates of some of the most important processes in biology, e.g. neuronal development (Zhu et al. 2010), anticoagulation (Liu and Pedersen 2007) and angiogenesis (Sasisekharan et al. 2002). In vivo, heterogeneous HS polymers of variable length are bound to proteins via rigid sulfonated (S-)domains (Bishop et al. 2007), which are flanked by flexible unsulfonated (NA-)regions (Mobli et al. 2008). The monosaccharides GlcA and GlcNAc comprise the disaccharide repeat in NA domains, while sulfonated derivatives of α-l-iduronic acid (IdoA) and GlcNAc predominate in S-domains; IdoA can be 2-O-sulfonated (IdoA2S) and GlcNAc can be N-, 6-O- and 3-O-sulfonated, leading most commonly to GlcNS, GlcNS6S, GlcNS6S3S and GlcNS3S (Figure 1). Anticoagulant heparin is one of the oldest and most widely used natural product drugs; synthetic alternatives are highly desirable due to clinical dangers associated with impure material (Liu et al. 2009). Heparin potency is dependent on the charged carboxyl and sulfo substituents of its uronic acid and hexosamine residues (Hricovini et al. 2001; Avci et al. 2003). Puckering is also a key contributor, the protein antithrombin (ATIII) binds the ²S_O pucker of the heparin IdoA2S residue (Hricovini et al. 2001) and derivatives exhibiting ²S_O-biased IdoA2S are highly efficacious (Das et al. 2001; Boltje et al. 2009). Exactly how different sulfonation patterns impart functional diversity in HS and heparin remains unclear; however, they are well characterized and therefore provide excellent model systems for chemically modified carbohydrates in general.

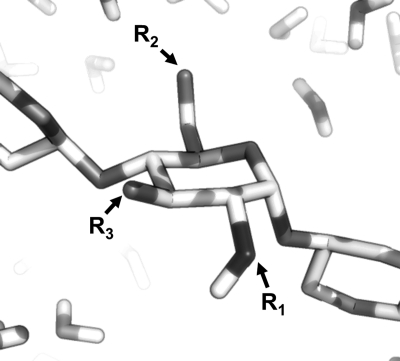
Fig. 1.

Schematic of the GlcNAc scaffold in biological conditions. This ubiquitous carbohydrate building block, four derivatives from HS and their methylglycosides were studied using 20 μs simulations and 900 MHz NMR. For GlcNAc, R₁ = Ac, R₂ = H, R₃ = H; for GlcNS, 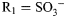, R₂ = H, R₃ = H; for GlcNS6S, 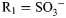, , 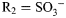R₃ = H; for GlcNS6S3S, 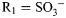, , 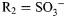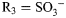; for GlcNS3S, 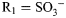, R₂ = H, .

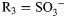In this study, we aim to explore the equilibrium populations and exchange kinetics of GlcNAc puckers and also the effects of sulfo substituents and methylglycosides on them. The most extensive all-atom explicit solvent carbohydrate simulations to date were performed (0.2 ms in total), and experimentally validated, for GlcNAc, GlcNS, GlcNS6S, GlcNS6S3S and GlcNS3S as free α-anomers and methylglycosides. Our findings suggested that in water, despite being a metastable ⁴C₁ chair, the GlcNAc pyranose ring explores the majority of conformational phase space and undergoes microsecond-timescale ⁴C₁ ↔ ¹C₄ puckering, the kinetics of which are modified by substituents. These predictions were consistent with our observations from NMR and the Protein Data Bank (PDB), which suggest that non-⁴C₁ GlcNAc puckers are important in protein interactions. The simulations complete our computational studies of equilibrium puckering for the major hexosamine and uronic acid (Sattelle et al. 2010) constituents of HS. They also provide fundamental information to the wider glycobiology field by demonstrating the great potential of extended unperturbed aqueous simulations to facilitate rational modification of carbohydrate puckering kinetics and concomitant bioactivity. Our detailed analysis and 3D model of the equilibrium GlcNAc conformation in water can be used to drive the development of novel biotechnologies.

Results

Pyranose ring puckering kinetics were investigated in O-sulfonated, N-sulfonated and O-methylated GlcNAc using microsecond all-atom explicit solvent MD simulations. Calculations were performed on the monosaccharides GlcNAc, GlcNS, GlcNS6S, GlcNS6S3S and GlcNS3S as free reducing sugars (the α-anomer) and α-1-O-methylglycosides (1-OMe). The simulations were initiated in both the ⁴C₁ and ¹C₄ chairs and performed for 10 µs each. Thermodynamic equilibrium was confirmed by comparing averages of the Cremer–Pople θ-parameter (Sattelle et al. 2010); when convergence had occurred, both simulations (a total of 20 μs) were used in further analysis.

Microsecond-conformational exchange in GlcNAc

In the GlcNAc simulations, equilibrium of ring pucker was realized within 3–5 μs. As expected, the ⁴C₁ chair was the dominant conformer, present for 99.6% of the trajectory. The average Cremer–Pople puckering parameters for these ⁴C₁ conformers were: Q = 0.54 (±0.04) and θ = 10.1° (±5.5°). The hydroxyl groups were calculated to have the following preferences: O1 (t, 69%; g+, 19%; g−, 12%), O3 (t, 65%; g+, 22%; g−, 13%), O4 (t, 71%; g+, 18%; g−, 11%) and O6 (t, 67%; g+, 20%; g−, 13%). The hydroxymethyl populated the gg (59%), gt (39%) and tg (2%) conformers and the acetamido group was trans (165 ± 25°). For comparison, the experimental hydroxymethyl rotamer populations were estimated from the two experimental measurements (J_5,6proR and J_5,6proS, Table I) and a three-site model to be: gg (96%), gt (4%) and tg (0%).

Table I.

Observed (Obs.) and calculated (Calc.) three-bond proton–proton vicinal couplings (J_H,H, Hz) for the five α-d-monosaccharides in water

Hexosamine	Coupling	Obs.	Calc.
GlcNAc	J1,2	3.5	3.2
GlcNAc	J2,3	10.7	10.1
GlcNAc	J3,4	9.9	9.9
GlcNAc	J4,5	9.3	10.0
GlcNAc	JHN,H2	8.8	9.7
GlcNAc	J5,6proR	5.2a	4.5
GlcNAc	J5,6proS	2.3a	3.2
GlcNS	J1,2	3.5	2.6
GlcNS	J2,3	10.4	10.2
GlcNS	J3,4	9.0	9.9
GlcNS	J4,5	10.2	10.0
GlcNS6S	J1,2	3.5	2.6
GlcNS6S	J2,3	10.4	8.8
GlcNS6S	J3,4	9.1	9.8
GlcNS6S	J4,5	10.1	9.9
GlcNS6S3S	J1,2	3.3	2.7
GlcNS6S3S	J2,3	10.7	10.2
GlcNS6S3S	J3,4	8.9	8.3
GlcNS6S3S	J4,5	10.1	10.0
GlcNS3S	J1,2	3.3	2.7
GlcNS3S	J2,3	10.7	10.2
GlcNS3S	J3,4	8.8	9.9
GlcNS3S	J4,5	10.1	8.5

The Karplus equations of Hricovini and Bizik, Altona and Haasnoot (1980) and Mobli and Almond (2007) were used for pyranose ring, hydroxymethyl and acetamido vicinal couplings, respectively. Experimental errors were estimated to be ±0.2 Hz and standard deviations of calculated ring vicinal couplings were estimated to be at most 0.01 Hz. (except GlcNAc J_5,6proR which was ±0.1 Hz).

^aData from a previous NMR study (Blundell et al. 2009).

Ring and acetamido vicinal couplings of the free reducing GlcNAc α-anomer were accurately measured from 900 MHz [¹H]-1D NMR spectra in water. The ³J_2,3, ³J_3,4,³J_4,5 and ³J_HN,H2 values were in the range 8–10 Hz, the ³J_1,2 coupling was ∼3 Hz (Table I). Compared with experimental values, the computed ring vicinal couplings ³J_1,2 and ³J_2,3 were smaller, ³J_3,4 was identical and ³J_4,5 and ³J_HN,H2 were greater in magnitude. Computed values of ³J_5,6 were also very similar to NMR measurements, one being smaller and one larger. Since the calculated values were all within 1 Hz of experiment and the deviations were not systematic, errors could be assumed to propagate from either the Karplus equations used or the force-field parameters (less likely as these would be expected to be systematic across sets of couplings). Calculation of ring vicinal couplings from only GlcNAc ⁴C₁ conformers (99.6% of the trajectory) gave identical results. This comparison suggested that the simulation and the ensemble of predicted puckers were consistent with experiment.

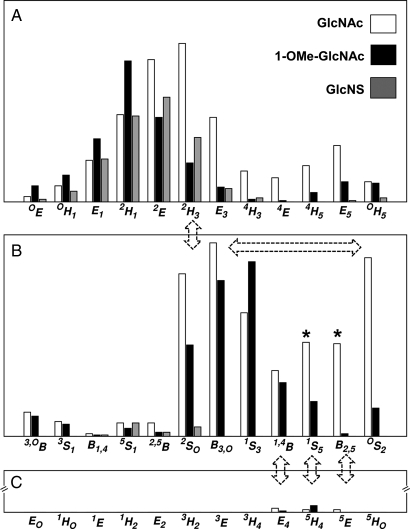
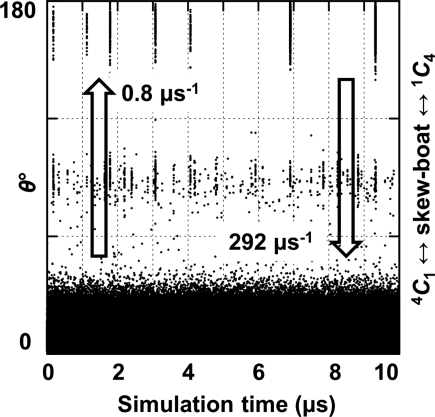
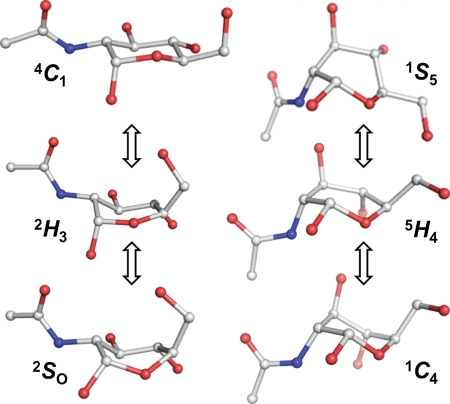
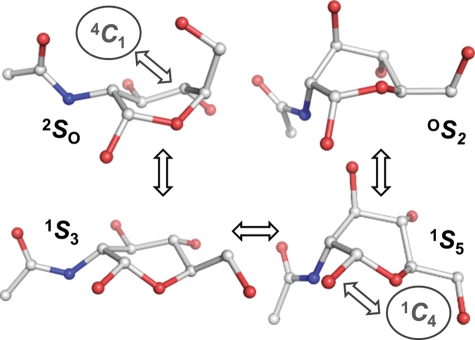
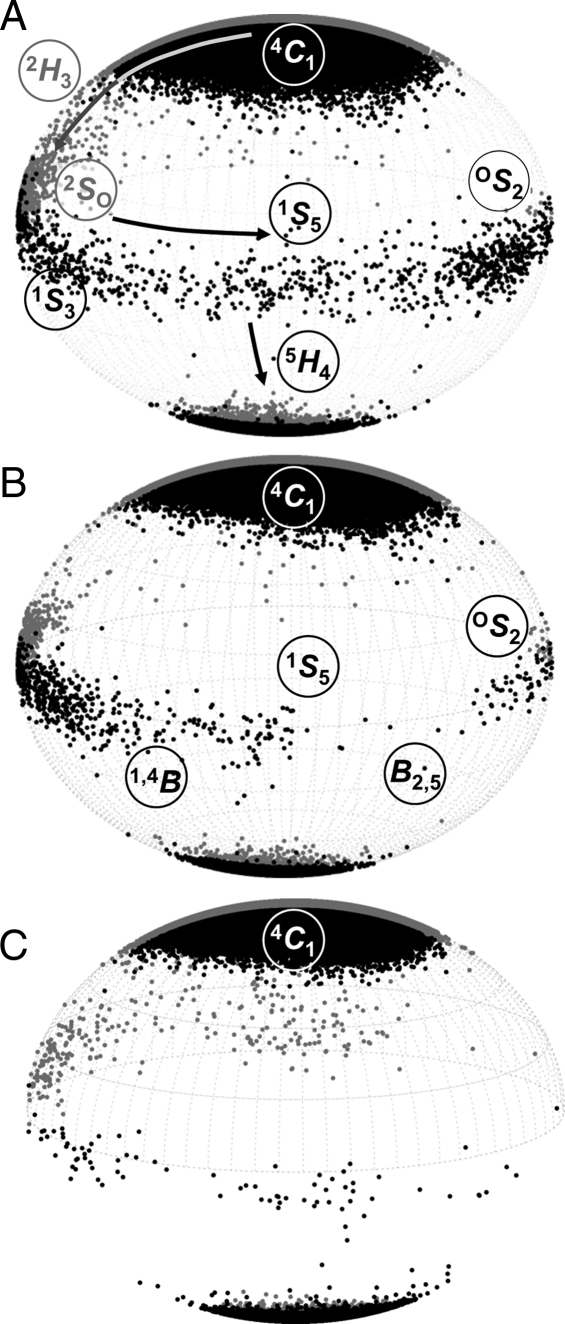
All of the ⁴C₁ hemisphere and boat and skew boat (equatorial) canonical puckers were populated in the simulation of GlcNAc. Although the ⁴C₁ pucker was dominant, the ¹C₄ chair was also transiently occupied, with averages Q = 0.52 (±0.04) and θ = 166.3° (±6.5°). The computed pathway between the two chairs involved predominantly ⁴C₁ ↔ ²H₃ ↔ ²S_O ↔ ¹S₃ ↔ ¹S₅ ↔ ⁵H₄ ↔ ¹C₄; however, 27 of the 36 canonical non-chair puckers were populated (Figure 2). A total of 16 ⁴C₁ → ¹C₄ transitions were observed (Figure 3), occurring at a computed (forward) rate of 0.8 μs⁻¹. The average lifetime of the GlcNAc ¹C₄-chair puckers was ∼3 ns, giving a ¹C₄ → ⁴C₁ (backward) rate of 292 μs⁻¹ and an equilibrium constant of K_eq = 2.9 × 10⁻³ (assuming first-order kinetics). Using the simulated equilibrium data, the GlcNAc ⁴C₁ chair was lower in free energy than the ¹C₄ chair, by ΔG = 3.5 kcal mol⁻¹. The dominant non-chair puckers in the ⁴C₁ hemisphere were half-chairs and envelopes with either C2 up or C3 down (²H₃, ²E, ²H₁ and E₃). Three transition states between skew boats and the ¹C₄ chair were predicted; namely, the unstable envelopes and half-chair conformers E₄, ⁵H₄ and ⁵E. Representative 3D structures of the key ⁴C₁- and ¹C₄-hemisphere intermediates from the simulation are illustrated in Figure 4. Transition to the ²S_O-conformer allowed facile pseudorotation in the equatorial region. The primary boat and skew boat puckers were those with φ-values in the range 150–330°; the most populated were ²S_O, B_3,O, ¹S₃ and ^OS₂ (Figure 5). However, conversion to the ¹C₄ chair occurred from the much less populated ^1,4B, ¹S₅ and B_2,5 conformers (Figure 6).

Fig. 2.

Relative occupancy (y-axis, arbitrary units) of the 36 canonical non-chair conformers in the 20 μs explicit solvent simulations of GlcNAc, 1-OMe-GlcNAc and GlcNS. (A) ⁴C₁ hemisphere, (B) equatorial region and (C) ¹C₄ hemisphere. Dashed arrows highlight predicted transitions between polar and equatorial regions and pseudorotation. Asterisks denote intermediates notably suppressed by 1-O-methyl and N-sulfo substituents.

Fig. 3.

Evidence for microsecond-timescale puckering in aqueous GlcNAc. The ⁴C₁ ↔ ¹C₄ transitions, computed exchange rates and short-lived (∼3 ns) ¹C₄-chair puckers are shown on a time-series plot of the Cremer–Pople parameter θ. Data are from the 10 μs ⁴C₁-initiated explicit solvent GlcNAc simulation.

Fig. 4.

Representative GlcNAc conformers from the 20 μs explicit solvent simulation involved in transitions between chairs and skew boats. Hydrogen atoms are hidden for clarity.

Fig. 5.

Representative GlcNAc skew boat conformers involved in pseudorotation; the structures were derived from a 20 μs explicit solvent simulation. Hydrogen atoms are hidden for clarity.

Fig. 6.

Conformers explored by hexosamines that underwent ⁴C₁ ↔ ¹C₄ transitions during 20 μs explicit solvent simulations: (A) GlcNAc, (B) 1-OMe-GlcNAc and (C) GlcNS6S. Puckers are plotted in spherical Cremer–Pople phase space with the ¹S₅-conformer orientated at the front. Hence, data points at the front (black) and back (gray) of the sphere denote puckers with φ-values in the range 180–360° and 0–180°, respectively. The skew boat and boat labels (S and B, respectively) are situated above or below their positions on the equator. The half-chairs (H) are labeled adjacent to their positions on the sphere.

The effect of 1-O-methylation: a model for polymerization

Simulations of 1-OMe-GlcNAc reached a conformational equilibrium after ∼3–5 μs. Consistent with the free reducing α-anomer simulation, a range of puckers were predicted (28 of the 36 non-chair canonical conformers, Figure 2) with the ⁴C₁ chair as the major conformer. The average ⁴C₁ pucker for 1-OMe-GlcNAc had values of Q = 0.56 (±0.04) and θ = 9.7° (±5.3), similar to GlcNAc. Five ⁴C₁ → ¹C₄ transitions were predicted and their computed pathway was similar to that of the free α-anomer; however, differences in the population of conformers were predicted (Figure 6B). Neighboring the ⁴C₁ pucker, envelopes and half-chairs with either O5 up or C1 down (^OE, ^OH₁, E₁ and ²H₁) were more populated in the 1-OMe-GlcNAc simulation. Those with C2 up or C3 on down (²E, ²H₃, E₃ and ⁴H₃) and with C4 up or C5 down (⁴E, ⁴H₅, E₅ and ^OH₅) were less populated than in GlcNAc. This trend in equatorial conformer populations was identical to GlcNAc; however, all puckers except ¹S₃ were less populated. In particular, the population of B_2,5 was almost precluded by the 1-O-methylsubstitution (Figures 2 and 6B). In the ¹C₄ hemisphere, compared with the GlcNAc simulation, the envelope E₄ was less populated, ⁵H₄ was more populated and ⁵E was absent in the methylglycoside simulation. Calculated orientations of the hydroxyl, hydroxymethyl and acetamido groups were identical to those computed for GlcNAc. In contrast, the rate of ⁴C₁ ↔ ¹C₄ transition was reduced in the 1-OMe-GlcNAc simulation (cf. GlcNAc). Forward and backward rates were computed to be 0.3 and 146 μs⁻¹, respectively, which resulted in a calculated equilibrium constant of K_eq = 1.9 × 10⁻³. Using this equilibrium data, the ⁴C₁ chair was calculated to be ΔG = 3.7 kcal mol⁻¹ lower in free energy than the ¹C₄ chair. Therefore, the two chair conformers in GlcNAc and 1-OMe-GlcNAc had similar equilibria and relative free energies, but methylation slowed the conformational exchange kinetics.

Quantum mechanical (QM) energy calculations were performed to further explore the relative energies of the chair puckers and the energy barriers separating them, in the absence of explicit solvent. The GlcNAc ⁴C₁ pucker was predicted by QM to be 19.1 kcal mol⁻¹ lower in energy than the ¹C₄ conformer and the lowest energy equatorial pucker, ¹S₃ (φ = 213°), was 11.4 kcal mol⁻¹ above the ⁴C₁ chair. For 1-OMe-GlcNAc, the two chairs were separated by 16.8 kcal mol⁻¹ and the lowest energy equatorial pucker, ¹S₅ (φ = 270°), was 11.4 kcal mol⁻¹ above the ⁴C₁ pucker energy. The QM calculations trended in agreement with the MD simulations with respect to the most likely predicted pathway of ⁴C₁ ↔ ¹C₄ exchange. The magnitude of predicted relative energies was lower in MD than QM calculations and inclusion of implicit solvent exacerbated the disagreement (the energy difference between chairs increased to 21.6 and 20.3 kcal mol⁻¹ for GlcNAc and 1-OMe-GlcNAc, respectively). Furthermore, QM predicted the ²S_O pucker (abundantly populated in aqueous simulations) to be the highest energy equatorial pucker (30 kcal mol⁻¹ above the ⁴C₁ chair energy) in both GlcNAc and 1-OMe-GlcNAc.

The effects of sulfonation on microsecond dynamics

In the case of GlcNS (N-sulfonated free α-anomer), the simulations equilibrated to an essentially 100% ⁴C₁ conformation (Figure 7A), which had an average pucker of Q = 0.55 (±0.04) and θ = 9.5° (±5.2). When initiated in the ¹C₄ pucker, the molecule rapidly exchanged to the ⁴C₁ chair (during the 250 ns discarded equilibration phase) and did not return to the ¹C₄ conformation. The N-sulfo substitution did not significantly perturb the distribution of rotamer states at the hydroxyl and hydroxymethyl groups (cf. GlcNAc) and the N-sulfonyl occupied three distinct acetamido rotamer states, centered on +60, −90 and −160°. Computed and experimental pyranose ring vicinal couplings were in excellent agreement. As for GlcNAc, all calculated values were within 1 Hz of the experimentally measured value (Table I). In contrast to the GlcNAc simulation, only a small number of canonical puckers were observed other than ⁴C₁ (Figure 2); the most populated of these were the envelopes and half-chairs with C2 up (²E, ²H₁ and ²H₃). The only GlcNS boats and skew boats had φ-values in the rather limited range 90–150°, which were ⁵S₁, ²S_O, ^2,5B and B_1,4. No transition states were predicted between these puckers and the (unpopulated) ¹C₄ chair. For 1–OMe-GlcNS, the ¹C₄-initiated trajectory remained in the ¹C₄ chair for several hundred nanoseconds. During the remaining simulation time, no transitions were observed from ⁴C₁ to ¹C₄. Thus, it was concluded that the kinetic rate for exchange between the two chair forms had been slowed significantly due to N-sulfonation and further still by methylation.

Fig. 7.

Conformational space of free α-anomer hexosamines that explored only the ⁴C₁ hemisphere of Cremer–Pople phase space during the 20 μs explicit solvent simulations: (A) GlcNS, (B) GlcNS3S and (C) GlcNS6S3S. Each hemisphere is orientated, labeled and colored as in Figure 6.

Using QM, the relative energy of the two GlcNS chairs was 3.0 kcal mol⁻¹ (cf. 13.8 kcal mol⁻¹ using implicit solvent), with the ⁴C₁ chair lower in energy. Notably, the GlcNS ⁴C₁ chair and the equatorial B_2,5 pucker (φ = 300°) were predicted by QM to be energetically degenerate, which was at odds with the explicit solvent MD simulations. The ^1,4B conformer (φ = 240°) was just 1.6 kcal mol⁻¹ above the ⁴C₁ chair and three ⁴C₁-hemisphere puckers (with θ in the range 150–170° and φ in the range 240–270°) were computed by QM to be within 3.0 kcal mol⁻¹ of the ⁴C₁ chair.

In the case of the GlcNS6S free α-anomer, this molecule was predicted to be a stable ⁴C₁ chair with average Q- and θ-values of 0.55 (±0.04) and 9.5° (±5.2), respectively. In the ⁴C₁-initiated simulation of GlcNS6S, a single ⁴C₁ ↔ ¹C₄ transition occurred after ∼6 μs (Figure 6C), in which the ¹C₄ chair was populated for ∼160 ns. Thus, the backward exchange rate was estimated to be ∼6 μs⁻¹. Assuming the equilibrium constant remained at 3 × 10⁻³, the rate of ⁴C₁ ↔ ¹C₄ conformational exchange was estimated to be ∼50 times slower in GlcNS6S than in GlcNAc, suggesting a forward rate of 0.02 μs⁻¹ and explaining why so few transitions had been observed within even 20 μs. This finding also suggested that the activation free energy barrier was increased in GlcNS6S (cf. GlcNAc) by ∼2.3 kcal mol⁻¹. Although the non-equilibrium GlcNS6S simulations precluded calculation of the relative energy between chairs, prediction of an accessible ⁴C₁ ↔ ¹C₄ pathway in the ⁴C₁-initiated trajectory allowed further investigation by QM. The prediction that the two conformers and the equatorial B_2,5 pucker (φ = 300°) had the same energy was at odds with the MD simulations, in which B_2,5 was rather minimally populated compared with the ⁵S₁ and ²S_O conformers (φ = 90 and 150°, respectively), both of which were predicted to be very unfavorable by QM (>30 kcal mol⁻¹ above the ⁴C₁-chair energy).

For 3-O-sulfonated GlcNS3S and GlcNS6S3S, only the ⁴C₁ conformer was observed (Figure 7B and C). Again, exchange from the ¹C₄ pucker occurred rapidly during the equilibration phase. Average Q-values for the ⁴C₁ conformers of these hexosamines were identical, 0.56 (±0.04), and the θ-values were 9.5 (±5.2) and 9.6 (±5.3) for GlcNS3S and GlcNS6S3S, respectively. All of the di- and tri-sulfonated hexosamines had computed vicinal couplings within 1 Hz of the measured value (Table I) with two exceptions, ³J_2,3 of GlcNS6S and ³J_4,5 of GlcNS3S, which were smaller than the corresponding experimental data by 1.2–1.6 Hz, suggesting that the abundance of sulfate groups had made the general Karplus equations used less accurate. Again, the hydroxyl rotamer states and hydroxymethyl conformations were identical in GlcNS3S and GlcNS6S3S compared with unsulfonated GlcNAc. In the 3–O-sulfonated GlcNS3S and GlcNS6S3S simulations, the N-sulfonyl group was different from GlcNS, being predicted to populate only two rotamer states (+60 and −160°), rather than the three found in GlcNS.

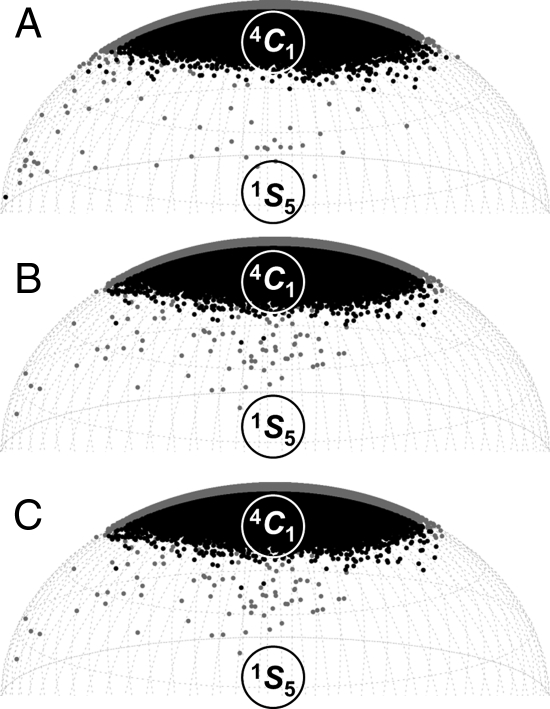
None of the ⁴C₁- or ¹C₄-initiated sulfonated methylglycoside simulations reached conformational equilibrium. This was attributed to the extended time taken for the ¹C₄-initiated trajectories to undergo the ¹C₄ → ⁴C₁ exchange. The ¹C₄-pucker lifetime was correlated with the degree of sulfonation and estimated to be: 1-OMe-GlcNAc (<250 ns), 1-OMe-GlcNS (600 ns), 1–OMe-GlcNS3S (1.2 μs), 1-OMe-GlcNS6S (2.8 μs) and 1-OMe-GlcNS6S3S (5.7 μs). A lifetime of 5 μs corresponds to a back transition rate of 0.2 μs⁻¹ or ∼1000 times slower than in GlcNAc. Assuming the equilibrium constant was similar to GlcNAc, this equates to an increase in activation energy of ∼4.1 kcal mol⁻¹. For the ⁴C₁-initiated simulations, which did not populate any ¹C₄-hemisphere puckers, increased sulfonation resulted in an increased population of ⁴C₁-hemisphere envelopes and half-chairs. The ²H₁ half-chair was the most populated intermediate in all ⁴C₁-initiated simulations and envelopes E₁ and ²E were the next most populated. Only boats and skew boats with φ-values in the range 60–150° (B_1,4, ⁵S₁, ^2,5B and ²S_O) were occupied. Here, the ⁵S₁ conformer of 1-OMe-GlcNS6S3S was significantly more stable than in any of the other sulfonated methylglycosides. In the ¹C₄-initiated trajectories, the distribution of transition states between skew boats and the ¹C₄ chair was similar for the mono- and di-sulfonated hexosamines. However, for 1-OMe-GlcNS6S3S, the puckers ⁵H₄ and ⁵E were much more populated. At the equator, puckers with φ-values in the range 270–330° (¹S₅, B_2,5 and ^OS₂) were occupied by all of the sulfonated methylglycosides, although the ¹S₃ and ^1,4B conformers were comparatively inaccessible to 1-OMe-GlcNS6S3S. The 1-OMe-GlcNS and 1–OMe-GlcNS6S3S ¹C₄-initiated simulations were predicted to populate B_2,5 and ^OS₂ almost equally and much more so than in 1-OMe-GlcNS6S and 1-OMe-GlcNS3S.

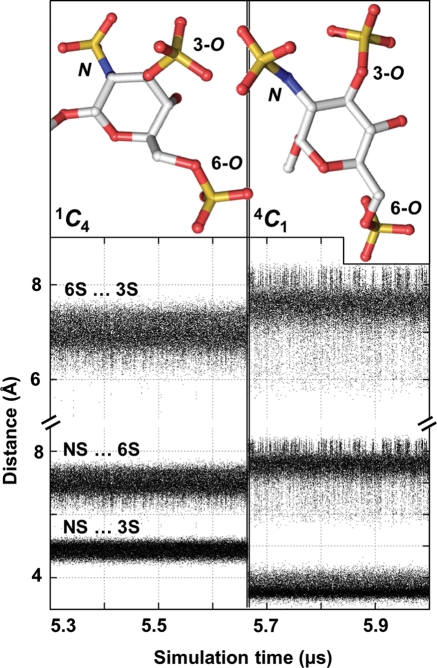
In the di- and tri-sulfonated free reducing and methylglycoside hexosamines (¹C₄-initiated trajectory), the sulfo moieties rearranged during the single transition to the favored ⁴C₁ pucker. This transition brings all of the sulfo groups from the axial to the equatorial position with a consequent increase in the distance from the 6-O-sulfo to both N- and 3-O-sulfo. For example, in 1–OMe-GlcNS6S3S, these distances increased on average by ∼1 Å (Figure 8) and the distance between the adjacent N- and 3-O-sulfo moieties decreased slightly following the transition. These observations indicate that solvation forces and electrostatic repulsion between sulfo groups play an important role in favoring the ⁴C₁ pucker over ¹C₄.

Fig. 8.

Evidence that electrostatic repulsion contributes to stabilization of the ⁴C₁ chair in highly sulfonated hexosamines. In the case of the 10 μs ¹C₄-initiated methylglycoside GlcNS6S3S explicit solvent simulation, time-series plots illustrate the change in distances between sulfur atoms resulting from the single ¹C₄ → ⁴C₁ transition after ∼5.6 μs. Representative 3D structures of ¹C₄ and ⁴C₁ chairs show how conformational rearrangement increased the distance between NS/6S and 3S/6S sulfate pairs. Hydrogen atoms were hidden for clarity.

Analysis of crystallographic data

In an analysis of crystallographic high-resolution (≤2.0 Å) PDB GlcNAc depositions, 96.9% of the 3137 occurrences were in the ⁴C₁ conformation. However, 0.5% were ¹C₄ puckers and 2.6% were boats or skew boats, such as in the non-enzyme structures of viral hemagglutinin, SNA-II, CD2 and interlukin-19 (Ikemizu et al. 1999; Chang et al. 2003; Maveyraud et al. 2009; Xu et al. 2010). For the ⁴C₁ conformers, average puckering parameters were Q = 0.57 and θ = 9.1°; in the ¹C₄ conformers, the averages were Q = 0.59 and θ = 163°. For reference, average values from our simulations were as follows: ⁴C₁ puckers: Q = 0.54 (±0.04), θ = 10.1° (±5.5°); and ¹C₄ puckers: Q = 0.52 (±0.04), θ = 166° (±6.5°). From the Cambridge Structural Database (CSD), the two entries for free α-d-GlcNAc [ACGLUA10 (Johnson 1966) and ACGLUA11 (Mo and Jensen 1975)] are ⁴C₁ chairs; they exhibit Q-values of 0.62 and 0.58, with respective θ-values of 7.6 and 3.1°. In the recent 1 Å resolution crystal structure of chitin (Nishiyama et al. 2011), the GlcNAc θ parameter is identical to the simulation ⁴C₁ average (10°). Sulfonated hexosamines were also found in these repositories. For GlcNS6S, 16 ligands were identified in 13 crystallographic PDB depositions (≤2.0 Å resolution), 12 were ⁴C₁ chairs, 3 were ¹C₄ chairs and 3 were equatorial conformers. Average puckering parameters in the ⁴C₁ conformers were Q = 0.59 and θ = 10.3°; our computed data for this GlcNS6S pucker were Q = 0.55 (±0.04) and θ = 9.5° (±5.2°). In the CSD, two GlcNS molecules were identified [ZULPIF (Ojala et al. 1995) and ZULPIF01 (Yates et al. 1995)], which exist as ⁴C₁ chairs and have Q-values of 0.56 and 0.55 and θ-values 4.0 and 2.9°, respectively.

Discussion

Extended-timescale simulations can exaggerate even small force-field inaccuracies and lead to errors in 3D-structural ensembles (Orozco et al. 2008; Klepeis et al. 2009). Comparison with experiment suggested that our simulations, using GLYCAM06, did not suffer from this phenomenon (Table I) and, in the cases of GlcNAc and 1-OMe-GlcNAc, equilibration of puckering in took ∼3–5 µs. Although in polymers the timescale of equilibration may differ, this finding suggests that previous (nanosecond) GlcNAc simulations explored only a small fraction of conformational phase space. Consequently, previous thermodynamic and kinetic interpretations of simulated GlcNAc puckering should be treated with caution. Importantly, the predicted microsecond-timescale exchange between GlcNAc chair puckers was not in disagreement with NMR measurements reported here (Table I) and elsewhere (Mulloy and Johnson 1987; Jin et al. 2009).

Average Q- and θ-values for chair puckers of GlcNAc and GlcNS6S from the simulations were similar to their respective values derived from the PDB, whereas GlcNAc was identical to a 1 Å resolution 3D structure of chitin (Nishiyama et al. 2011). The CSD data for GlcNAc and GlcNS, derived from crystals devoid of water and protein, were slightly more rigid than our predictions. The trend for non-⁴C₁ puckers of GlcNAc in the PDB and our simulations was similar. Our comparisons of calculated and experimental data provide confidence that the simulated puckering was representative of real conformational exchange in GlcNAc and its derivatives. Furthermore, these similarities support the view that, while GlcNAc exists predominantly as a ⁴C₁ chair in water, other puckers may be biologically important, particularly in unsulfonated GlcNAc.

Our QM data of GlcNAc conformers (without explicit solvent) were consistent with previous studies, such as those of glucose (Barrows et al. 1995; Appell et al. 2004), but in general provided larger relative chair energies than MD and also predicted a different set of boat and skew boat intermediates. However, it should be noted that energies computed without water may be sensitive to small geometrical perturbations due to unnatural intramolecular hydrogen bonding and the large relative QM energies may be a consequence of this. For example, QM predicted GlcNAc to be a rigid ⁴C₁ chair, whereas MD suggested the barrier height was ∼5 times the thermal energy at room temperature, which is in close agreement with many other studies of pyranoses (Dowd et al. 1994; Barnett and Naidoo 2010; Barnett et al. 2010; Spiwok et al. 2010). The finding that the majority of conformational phase space was computed to be accessible in GlcNAc, including the ¹C₄ chair, also challenges the notion that GlcNAc is rigid. We now propose that aqueous GlcNAc undergoes microsecond-timescale conformational exchange, which would not be concluded from straightforward interpretation of NMR vicinal couplings, sub-microsecond unequilibrated MD and gas-phase QM energy calculations. Whether similar conclusions would be made for other biologically important hexosamines, such as N-acetyl-d-galactosamine, remains to be seen.

The hypothesis that GlcNAc undergoes room-temperature-accessible microsecond timescale ⁴C₁ ↔ ¹C₄ transitions (separated by ΔG = 3.5 kcal mol⁻¹) that are consistent with protein co-crystals, but which cannot be predicted by gas phase or implicit solvent QM calculations (in which the chair forms were predicted to be 19.1 kcal mol⁻¹ different), suggests a major role for water in stabilizing the ensemble of GlcNAc puckers. It has been theorized that water is essential to predict carbohydrate conformation (Kirschner and Woods 2001) and our data concurs. As concluded previously (Sattelle and Almond 2010), we again found that extensive empirical simulations were preferential to restricted studies at higher levels of theory for carbohydrates, due to their ability to resolve microsecond dynamics. Figure 9 illustrates the 3D structure of GlcNAc with the pucker and substituents in the most frequently encountered conformation in the 20 µs simulation. This 3D model (available as Supplementary data) could be used as ⁴C₁-dictionary data for structural refinement, protein docking or structure-based design.

Fig. 9.

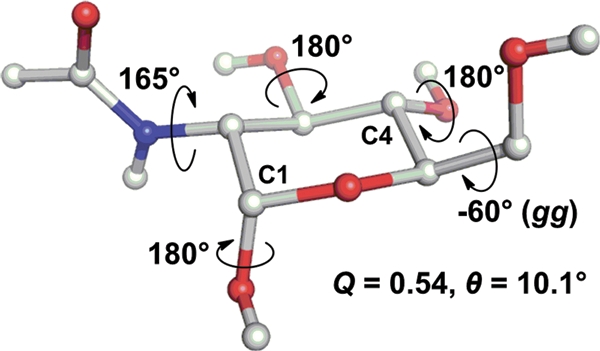
A 3D model for the equilibrium GlcNAc conformation in water. The pucker is a ⁴C₁ chair, the pyranose conformation and rotamer states (hydroxyl, hydroxymethyl and acetamido) represent the most populated in a 20 μs explicit solvent simulation. Non-polar hydrogen atoms are hidden for clarity and the 3D coordinates are provided in Supplementary data S4.

In the absence of unambiguous atomic-resolution experimental data and extended aqueous simulations, it has not been possible to robustly quantify equilibrium conformer populations or the kinetics of puckering exchange at the molecular level. Our simulations of GlcNAc and uronic acid derivatives (Sattelle et al. 2010) clearly demonstrate that recent progress in computer hardware and software (Harvey et al. 2009; Klepeis et al. 2009) has enabled conformationally equilibrated simulations to be performed for carbohydrates involved in microsecond-puckering exchange without the need for enhanced sampling (i.e. artificial perturbation of the simulation temperature or Hamiltonian; Gao et al. 2008). Although enhanced sampling is useful for predicting equilibrium populations, biological interpretation of kinetic phenomena should be treated with caution (Schlick 2009).

Neither the methylglycoside nor the N- or O-sulfo derivative was predicted to alter the rotational preferences of hydroyxl or hydroxmethyl groups. The simulations suggested that the effect of these substituents was instead to add steric bulk and charge, and hence to modify pyranose ring puckering. The methylglycoside has previously been shown to influence pyranose conformation (Marszalek et al. 1998; Heymann and Grubmuller 1999; Li et al. 1999), and this reinforces our thesis that knowledge of equilibrium populations and kinetics are crucial for a complete understanding of carbohydrate 3D SARs. For example, the slower rate of ⁴C₁ → ¹C₄ transition in 1-OMe-GlcNAc (three times cf. GlcNAc) implied a 0.4 kcal mol⁻¹ increase in activation energy. This was found to be due to the relative inaccessibility of several intermediates in 1-OMe-GlcNAc, and in particular ²S_O, ¹S₅ and B_2,5 (Figures 2 and 6), indicating a higher-energy barrier to pseudorotation. Sulfonation further increased this energy barrier, making it more difficult for the ¹C₄-initiated methylglycosides to the exchange from this pucker to the ⁴C₁ chair.

The equilibrium of GlcNS puckers was shifted toward the ⁴C₁ chair (cf. GlcNAc). Puckers involved in the transition between GlcNAc ⁴C₁ and ¹C₄ chair conformers were largely precluded in GlcNS (except for ²S_O), implying that N-sulfonation significantly slows the rate of ⁴C₁ ↔ ¹C₄ conformational exchange by blocking these intermediates. The N-sulfo substituent is ubiquitous in HS, where GlcNAc is sequentially modified by N-deacetylase and N-sulfotransferase enzymes prior to sequential O-sulfotransferase-catalyzed sulfonation at the 6-O- and 3-O-positions (Rabenstein 2002). Our results intimate that this modification both rigidifies and stabilizes the ⁴C₁ pucker of HS GlcNAc residues.

Rearrangement of sulfo groups from the axial to the more solvent-favorable equatorial orientation is probably a major driver of the ¹C₄ → ⁴C₁ transition in the di- and tri-sulfonated hexosamines orientations. However, the distance between sulfo groups also increased as a result of this transition, suggesting that it was partially driven by electrostatic repulsion (Figure 8). Together, these observations infer that puckering of the GlcNAc pyranose scaffold is strongly dependent on sulfo substituents and polymerization, but further studies are required to confirm this. Such insights will facilitate molecular design by making it possible to predict substitutions that perturb the aqueous conformational equilibrium, rates of puckering and concomitant bioactivity. For example, based on our simulations, we now hypothesize that GlcNAc glycosides more bulky than a methyl group would further decrease the rate of ⁴C₁ ↔ ¹C₄ conformational exchange in water.

Equilibration of pucker was realized on the same timescale as seen previously for uronic acids (Sattelle et al. 2010), but the predicted 1-OMe-GlcNAc forward (⁴C₁ → ¹C₄) exchange rate (0.3 μs⁻¹) was much slower than in 1-OMe-IdoA (19 μs⁻¹), again indicating that epimerization at the C5 position significantly lowers the barrier to kinetic exchange of pucker. In both GlcNAc and IdoA, the ¹C₄ conformer was computed to be accessible at room temperature; the key difference was the kinetics of exchange, which was slower in GlcNAc due to the relatively-higher free energy of the ¹C₄ pucker (∼3 kcal mol⁻¹ higher than in IdoA). The effect of IdoA2S on 1-OMe-IdoA was to shift the equilibrium conformation toward the ¹C₄ pucker (1-OMe-IdoA and 1-OMe-IdoA2S were predicted to be 76 and 91% ¹C₄, respectively), whereas in C5-epimerised and N-acetylated GlcNAc, N-, 6-O- and 3-O-sulfonation favored the ⁴C₁ chair. Furthermore, the studies performed here suggest that our previous work on methylglycosides of uronic acids may be more representative of puckering exchange rates in polysaccharides than monosaccharides. Together, these data provide a basis for understanding glycosaminoglycan 3D structure.

Characterization of glycosaminoglycan 3D structures will enable the design of biotechnological devices and medicines (Gama et al. 2006; Ghosh et al. 2009). The predicted substituent dependence of GlcNAc puckering, and that of uronic acids (Sattelle et al. 2010), leads us to hypothesize that the slower exchange kinetics of sulfonated GlcNAc residues (favoring a more rigid ⁴C₁ chair) may, in concert with electrostatic repulsion of sulfo moieties, contribute to the observation that HS S-domains are more rigid than NA-domains (Mobli et al. 2008). The simulations also suggest that puckering could have a significant effect on HS-domain structure by altering chain direction, and it is conceivable that it has a more dominating effect on bioactivity than the glycosidic linkage motions, which are unperturbed by sulfonation (Mulloy and Forster 2000). Insight into the relative contribution of microscopic uronic acid and hexosamine puckering to macroscopic HS-domain 3D structure will be gained from future conformationally equilibrated (microsecond-timescale) co-polymer simulations. It will be interesting to establish if bioactivity of the therapeutically relevant HS motif (GlcNS6S-IdoA2S)₃ (Smits et al. 2010) and the heparin pentasaccharide are modulated by incorporation of conformationally locked GlcNAc derivatives, as is the case for heparin derivatives exhibiting ²S_O-biased IdoA2S (Das et al. 2001; Boltje et al. 2009). It has been proposed that IdoA flexibility does not affect the molecular shape of heparin (Jin et al. 2009). Although not inconsistent with our data, this conclusion was derived from 4 ns of restrained MD or 0.1% of the ∼3 μs now known to be required to equilibrate puckering (explore all conformational phase space) in monosaccharides studied to date, and the analogous effect of GlcNAc puckering has not yet been considered.

Substituent-dependent microsecond-timescale puckering in GlcNAc has important ramifications in wider glycobiology. Despite being rare events, the proposed ⁴C₁ ↔ ¹C₄ transitions equate to ∼1 million s⁻¹ in GlcNAc and we therefore hypothesize that they may be an important factor in protein selectivity. In total, 75% of canonical non-⁴C₁ puckers were predicted to be accessible for this hexosamine in water at room temperature. High-resolution data from the PDB suggest that non-⁴C₁ puckers may play an important role in protein recognition and carbohydrate catalysis. For example, ATIII prefers the ²S_O-skew boat of IdoA2S in heparin (Hricovini et al. 2001), β-mannosidases bind their substrate in the ¹S₅ conformation (Ardevol et al. 2010) and cellobiohydrolase I of Trichoderma reesei drives the envelope and half-chair conformations (⁴E and ⁴H₃) of glucose and renders both chair conformers highly unfavorable (Barnett et al. 2010).

Knowledge of puckering in GlcNAc will lead to new molecular design opportunities. For example, GlcNAc is an essential constituent of protein post-translational modifications (Marino et al. 2010; Nothaft and Szymanski 2010). Rational modification of epitope GlcNAc puckering kinetics can be expected to modulate protein recognition and thereby facilitate development of therapeutics (Jefferis 2009). Also, there are no available 3D structures of Rhizobium nodulation factors, which are characterized by a backbone of between three and five substituted (sulfonated) GlcNAc residues. Recent work has begun to address this knowledge gap with NMR and nanosecond-simulations (Morando et al. 2011). Definition of nodulation factor SARs and generation of synthetic derivatives will accelerate production of non-leguminous plants that can fix nitrogen themselves, toward which our extended microsecond-simulations now contribute. Our predictions also provide a new avenue for development of novel peptidoglycans (for amelioration of bacterial pathogenicity) and biomaterials from marine carbohydrates and chitin (Khoushab and Yamabhai 2010). Furthermore, understanding equilibrium conformer populations and the kinetics of exchange in atomic detail, as has been described, will rationalize decision-making in structure-based design and facilitate generation of increasingly high-affinity, typically weak-binding, carbohydrate-based ligands.

Conclusions

The longest carbohydrate simulations to date were performed on the ubiquitous monosaccharide GlcNAc and biologically important derivatives to investigate microsecond dynamics that cannot currently be quantified by experiments or other computational approaches. In water, at equilibrium, GlcNAc underwent microsecond-timescale exchange between chair puckers, in good agreement with NMR measurements and high-resolution crystallographic data for protein-bound GlcNAc ligands, where an appreciable number are not ⁴C₁ conformers. These results challenge the hypothesis that GlcNAc is a perfectly rigid ⁴C₁ chair, as predicted by high-level energy calculations without explicit water, straightforward interpretation of NMR data and non-equilibrium nanosecond-simulations.

A major role for water in defining the equilibrium ensemble of GlcNAc puckers is proposed. Conformational exchange kinetics may therefore be difficult to predict without detailed and extended simulations. We re-iterate that for carbohydrates, longer empirical aqueous simulations are preferable to higher-level computation on short timescales and without water. Recent progress in computer hardware and software is enabling this for many carbohydrates without the need for artificial perturbation of systemic physical properties, as in enhanced sampling.

Substitution of the GlcNAc chemical scaffold did not affect rotamer preferences but did impact equilibrium ring puckering conformer populations and kinetics. Methylglycosides (a model for the glycosidic linkage) had slowed exchange kinetics due to reduced accessibility of biologically important skew boat intermediates. Sulfonation shifted the ensemble of puckers toward ⁴C₁, likely due to electrostatic repulsion and favorable solvation of equatorial sulfo groups.

Our 3D-structural and kinetic insights have extensive ramifications for understanding and exploiting 3D SARs in glycobiology. The importance of puckering in a myriad of GlcNAc-containing sugars (e.g. glycosaminoglycans, nodulation factors and glycosylation fragments) can now be tested experimentally. This iterative interdisciplinary approach, identification of pivotal kinetic 3D intermediates and concomitant-directed chemical modification of equilibrium conformer populations and exchange kinetics, has great potential to revolutionize glycan design.

Materials and methods

MD simulations

The monosaccharides were prepared using the AMBER tool Leap (Case et al. 2005) and in-house software (to define ⁴C₁ and ¹C₄ puckers). Each of the 10 initial configurations was explicitly solvated in a cubic water box (∼25 × 25 × 25 Å) and neutralized with the appropriate number of Na⁺ counter-ions, followed by 1000 steps of energy minimization. MDs were performed with ACEMD (Harvey et al. 2009) on NVIDIA graphics processors using the force-fields GLYCAM06g (Kirschner et al. 2008) and TIP3P (Jorgensen et al. 1983). Hydrogen atoms were constrained using the M-SHAKE algorithm (Krautler et al. 2001). The velocity-Verlet integration algorithm and a hydrogen mass repartitioning scheme were used to achieve a 4 fs time-step without affecting the equilibrium distribution (Buch et al. 2010). Electrostatic and van der Waals interactions were truncated at 9 Å and the recommended scaling factor for carbohydrate 1–4 interactions (1.0) was used. Parameters not present in GLYCAM06 (the angle O-S-O and the torsion C2-O2-S-O) were appended from the General Amber Force-field (Wang et al. 2004). Merz–Singh–Kollman (Singh and Kollman 1984) electrostatic potential-derived partial charges for the sulfonated monosaccharides were computed using Gaussian 03 (Frisch et al. 2004) following gas-phase geometry optimization at the HF/6-31G(d)//HF/6-31G(d) level of theory (consistent with GLYCAM06). Following 20 ns of heating and 250 ns of thermal equilibration at 298 K (which were discarded), MD simulations of each monosaccharide were performed for 10 µs in the NVT ensemble. Data were saved to file every 10 ps.

NMR spectroscopy

Natural abundance samples were prepared from lyophilized material (Dextra, Reading, UK) reconstituted in 594 µL of D₂O, 99.990% (w/v) and 6 µL of DSS (4,4-dimethyl-4-silapentane-1-sulfonic acid). Samples were adjusted to pD = 7.0 and final concentrations were in the range 41–56 mM. All spectra were recorded at 25°C. Chemical shifts of ¹H and ¹³C atoms were assigned from the following standard heteronuclear NMR spectra recorded with a ¹H frequency of 600 MHz on a Bruker spectrometer equipped with a z-gradient TXI cryoprobe: [¹H–¹³C] HSQC, [¹H–¹H] COSY, [¹H–¹H] TOCSY and a [¹H–¹³C] HSQC–TOCSY. [¹H] 1D spectra were also recorded with a ¹H frequency of 900 MHz (Varian INOVA 900), 32,768 points, an acquisition time of 2949.17 ms and a dwell time of 45.5 µs. Vicinal couplings were measured from 900 MHz [¹H] 1D spectra unless otherwise stated. Spectra were processed with NMRPipe (Delaglio et al. 1995) and analyzed with Sparky (Goddard and Kneller 2006) and Analysis (Vranken et al. 2005). Proton chemical shifts were referenced relative to internal DSS and heteronuclei were referenced indirectly. As detailed previously (Blundell et al. 2004; Blundell, Deangelis, et al. 2006; Blundell, Reed, et al. 2006), appropriate linear prediction, window functions and zero-filling were used to achieve the maximum possible resolution from each data set.

QM calculations

Conformers representative of the complete pyranose Cremer–Pople (Cremer and Pople 1975) conformational space (74 in total) were built using in-house software, which systematically increments θ- and φ-parameters (by 30°) and then performs constrained gas-phase energy minimization (to maintain the pucker) using the UFF force field (Rappe et al. 1992). Single-point energy density functional theory calculations were performed on each geometry optimized conformer using Gaussian 03 (Frisch et al. 2004) at the B3LYP/6-311++G(d,p) level of theory in the gas phase and using the self-consistent reaction field polarizable continuum model (Cances et al. 1997; Cossi et al. 2002), whereby the electrostatic shielding effect of bulk solvent is treated as a continuous medium. The dielectric constant was set to 78.38, representative of water at 298.15 K. Charge and multiplicity values of 0/1, −1/1, −2/1 and −3/1 were used for GlcNAc and the mono-, di- and tri-sulfonated hexosamines, respectively.

Computed vicinal couplings and rotamer populations

Vicinal couplings were calculated using torsional data from the full 20 µs simulations for GlcNAc and 1-OMe-GlcNAc and from the 10 µs ⁴C₁-initiated trajectories for all other molecules. The sulfate-adjusted Karplus equation of Hricovini and Bizik (Altona and Haasnoot 1980; Hricovini and Bizik 2007) was used for ring vicinal couplings. The relationships of Altona and Haasnoot (1980) and Mobli and Almond (2007) were used for hydroxymethyl and acetamido (HN-N2-C2-H2) vicinal couplings, respectively. Values and standard deviations were obtained by computing the vicinal coupling for each 1 μs sub-trajectory and averaging. Hydroxyl orientations were binned as gauche(−), anti(t) or gauche(+) centered on −60, 180 and 60°, respectively. Hydroxymethyl conformations (tg, gt and gg) were defined by the torsions O6-C6-C5-O5 and O6-C6-C5-C4. To estimate hydroxymethyl rotamer populations directly from NMR data, the scalar couplings H5 to H6proR/S were fitted to a rigid three-site model (Poppe 1993) comprising variable populations of tg, gt and gg conformers using the relationships of Altona and Haasnoot.

Cremer–Pople analysis

Puckers were classified (using the pyranose ring atoms O5, C1, C2, C3, C4 and C5) by analysis of the Cremer–Pople (Cremer and Pople 1975) parameters Q, θ and φ, which are the radius, azimuthal and meridian angles (respectively) of the spherical puckering coordinate system describing all possible puckers for a six-membered ring. The Q-value represents the puckering magnitude (deviation from a flat ring), θ describes the type of pucker (chair, half-chair, boat, etc.) and φ is a phase angle describing pseudorotation. In the text and Supplementary data, a value of θ = 0° corresponds to ⁴C₁ and θ = 180° to ¹C₄. Plots of each parameter, for each simulation, are reported in the Supplementary data S1. Equilibration of the simulations was assessed by comparing the convergence of the Cremer–Pople polar angle ácosθñ (which represents the average ring pucker, see Supplementary data S1), for simulations started in ⁴C₁ and ¹C₄ puckers, as described previously (Sattelle et al. 2010). For analysis of GlcNAc 3D structures from the PDB, 794 and 13 GlcNAc and GlcNS6S crystallographic depositions were identified with resolution ≤2.0 Å, containing, respectively, 3137 and 16 3D structures. Acceptable limits of Q were defined as 0.8 (maximum) and 0.4 (minimum).

Free energy and rate constant and calculations

Free energies were derived from the relationship ΔG = |RT ln(p1/p2)|, where p1 and p2 are the equilibrium populations of ⁴C₁ and ¹C₄ conformers, respectively, R the gas constant and T the temperature. Conformational exchange rates (k₁ and k₂) were derived by calculating the average time for transitions (⁴C₁ → ¹C₄ and ¹C₄ → ⁴C₁) and taking the reciprocal. The reported equilibrium constants are the ratio of the rates, K_eq = k₁/k₂. The relationship ▵G = |RT ln K_eq| was used to confirm computed free energies. These equations can be found in standard chemistry textbooks.

Supplementary data

Supplementary data for this article is available online at http://glycob.oxfordjournals.org/. Simulation data (S1 and S2), chemical shifts from NMR (S3) and 3D coordinates of the equilibrium GlcNAc conformer in water (S4) are provided.

Funding

This work was supported by the BBSRC UK (grant number BBG006768).

Conflict of interest

None declared.

Abbreviations

CSD, Cambridge Structural Database; COSY, correlation spectroscopy; 3D, three-dimension; DSS, 4,4-dimethyl-4-silapentane-1-sulfonic acid; GlcA, β-d-glucuronic acid; GlcNAc, N-acetyl-d-glucosamine; HS, heparan sulfate; HSQC, heteronuclear single quantum coherence; IdoA, α-l-iduronic acid; IdoA2S, IdoA 2-sulfate; MD, molecular dynamics; Me, methyl; NMR, nuclear magnetic resonance; 1-OMe, α-1-O-methylglycosides; PDB, Protein Data Bank; QM, quantum mechanics; SAR, structure–activity relationship; TOCSY, total correlation spectroscopy.