Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Dec 1.
Published in final edited form as: Otol Neurotol. 2011 Dec;32(9):1559–1567. doi: 10.1097/MAO.0b013e31822e94f3

New Data on the Motion of the Normal and Reconstructed Tympanic Membrane

JJ Rosowski *, JT Cheng *, SN Merchant *, E Harrington †, C Furlong *,†
PMCID: PMC3219815  NIHMSID: NIHMS319699  PMID: 21956597

Abstract

Hypothesis

The sound-induced motion of the tympanic membrane has features that are most consistent with modal responses to a uniform stimulus.

Background

Conceptual models of the coupling of tympanic-membrane motion to the ossicular chain can be classified as either modal responses to a uniform stimulation of the entire membrane, or traveling wave models in which sound energy is captured at the membrane’s rim and travels along the surface to the umbo. The stroboscopic holography technique we employ can separate strongly modal or traveling-wave dominated motions of the tympanic membrane surface.

Methods

We use computer-aided opto-electronic holography with stroboscopic illumination to measure the magnitude and phase of the sound-induced motion of over 40000 points on the surface of the tympanic membrane in cadaveric human temporal bones. Our techniques are sensitive to motions of the membrane as small as 0.01 microns, and allow determinations of membrane displacement at frequencies as large as 20 kHz.

Results

We report clear signs of both modal tympanic membrane responses and traveling waves on the human tympanic membrane. Modal responses are seen throughout the frequency range, while the traveling waves are most apparent between 2 and 8 kHz. In general, the magnitudes of the traveling waves are small compared to the modal magnitudes.

Conclusion

Much of the motion of the tympanic membrane is well approximated by modal motions of the TM surface. This conclusion has implications for ear drum pathology and its treatment.

Introduction

While work performed over the past 50 years has greatly increased our knowledge of the workings of the normal and pathological middle ear (1–7) there are still notable unknowns. One area of current controversy concerns the precise mechanisms by which sound energy from the ear canal is coupled to the ossicular chain by the tympanic membrane (TM). The controversy is crystallized by two extreme views. One view suggests modal motions excited by near uniform stimulation of the entire membrane surface determine the motion of the TM surface: Modal motion has features in common with standing waves, including the presence of nodal regions of near zero displacement (see Video, Supplemental Digital Content 1, which demonstrates standing waves and nodes on a string rigidly supported at its ends). Modal motions depend on the local mechanical properties of the membrane and more global properties such as the stiffness of the membrane support, and are strongly influenced by the boundary conditions that limit membrane motion at the tympanic ring and along the manubrium. The second view is that the motion of the TM is dominated by surface waves that are initiated at the edge of the TM and travel toward the umbo (see Video, Supplemental Digital Content 2, which illustrates a centripetal traveling wave on a simple model of the TM). Such surface waves depend strongly on the local mechanical properties of the membrane.

The modal model of TM motion

A modal model of TM motion is an older view that is consistent with the pioneering work of Tonndorf and Khanna (3,8,9) who were the first to report detailed holographic pictures of the magnitude of the sound-driven motion of the TM in live animals and cadaveric human temporal bones. Their measurements led to several concepts of TM motion: (a) With stimulus frequencies of 1 kHz and below the sound-induced motions of the TM surface produced a small number of peak displacement regions in the posterior and anterior regions of the TM that grew out of regions of smaller displacement magnitude. (b) In response to sounds of frequency between 1 and 8 kHz the spatial patterns of TM motion became complicated with an increasing number of regions with local motion maxima surrounded by nodal regions of near zero displacement; the arrangement of the peaks and the surrounding nodes appeared disordered or complex. While their methods could not determine the phase of TM motion, Tonndorf and Khanna (3) suggested these patterns were consistent with standing-wave-like modes of TM motion, where the small number of spatially distinct peaks on top of a smaller more uniform displacement observed at low frequencies suggested in-phase motion of the TM, as expected for a low-order modal motion (the order of a modal motion depends on the number of nodes), and at higher frequencies any one of the increasing number of spatial maxima moved precisely out-of-phase with adjacent maxima that are separated from each other by nodal boundaries. A third finding of these studies was that the manubrium of the malleus embedded in the TM moved much less than the regions of the TM where the local maxima occurred, regardless of stimulus frequency.

These findings have been interpreted as evidence that the TM responds to sound in a modal fashion, where the entire TM surface is equally stimulated by sound pressure, and the induced motion of individual points on the TM surface depends on the mechanical properties and shape of the TM, the load of the ossicular chain on the TM and the boundary of the membrane at the TM ring. In such a system sound transduction to the ossicular chain depends on how well the modal patterns effect motion of the manubrium. The modal hypothesis is consistent with views of the frequency-dependent response of microphones and speakers (examples of man-made acoustic-mechanical transducers). In the low-frequency range, the entire sound-responsive surface moves in phase. This uniform motion of the transducer’s receiver area (or generator area) allows more efficient transfer of sound energy between air and the microphone or speaker (10,11). At some higher frequency the modal responses become more complex, nodal regions become apparent and the motion of the sound-responsive surface ‘breaks-up’ into regions that move out-of-phase with other regions (see Video, Supplemental Digital Content 3, which demonstrates modal motion of a simple membrane with one nodal diameter). The result of the break-up may be less efficient acoustic-mechanical transduction at higher sound frequencies (10–13).

A somewhat different view of the contribution of modal motions to TM function, was put forward by Fay et al. (14) who made use of the common observation that the number of possible modes in a geometrically-constrained system increases dramatically as stimulus frequency increases. They suggested that the ear’s response to high-frequency sound is the summed response to a collection of modal patterns that are excited by near-by frequencies. They further argue that summing across a collection of modal responses will act to smooth the frequency response of the TM and increase the frequency range over which it operates.

Traveling waves on the TM surface

The main competing model of TM motion has its roots in descriptions of a middle-ear delay that first surfaced about 15 years ago. Olson (15) in 1998 noted that much of the data she collected on middle-ear sound transfer in gerbil were consistent with a simple delay mechanism that induced a time delay between motions of the gerbil TM and stapes of on the order of 20 μs. Simultaneously, Puria and Allen (16) published a model analysis arguing for the presence of a significant delay in middle-ear mechanics, where the bulk of the delay is in the response of the TM to sound. Since a traveling wave is one physical response that introduces delay (the travel time of the disturbance), Puria and Allen suggested the presence of traveling waves on the TM surface. This idea has been formalized in the more recent models of TM function of Parent and Allen (17,18) where they ascribe a ‘horn-like’ function to the conical TM, such that the wide outer rim is better-matched to the air in the ear canal and that waves of motion progress from the edges of the TM toward the umbo. They also hypothesize that the horn-shape of the TM helps with the transformation process with the relatively low-impedance of the tympanic ring better matched to the impedance of air than the higher impedance at the umbo. The primary evidence for the presence and significance of surface traveling waves are repeated demonstrations of delays in middle-ear sound-transfer where larger tympanic membrane areas correlate with longer delays (15,16,19–21).

In this paper we measure the magnitude and phase of the surface displacement of the human TM and use those data to quantify both modal patterns of TM displacement and traveling waves. The data we gather will be compared to the two models of TM motion we have introduced. The discussion will include the significance of these findings in tympanoplasty and middle-ear reconstruction.

Methods

We apply the previously described techniques of stroboscopic-illumination in computer-aided opto-electronic holographic interferometry (22–24). The holographic technique depends on the interference between two laser beams, a fixed reference beam, and a coherent reflection from the moving surface of the TM. Both beams are “strobed” (turned on and off via a high-speed optoacoustic modulator) at selected phases of the acoustic stimulus with an illumination duty cycle of 5–10% of the period of the stimulus tone. The measurements were made in a dozen cadaveric temporal bones that were otoscopically normal. The temporal bones were unfixed and either prepared and used within 48 hrs post-mortem or frozen and thawed prior to use. The bones were kept moist during the preparation and measurements, and were stored in saline at 4° C or in a freezer. The bony external meatus is drilled away to expose 90% of the surface of the TM. A posterior tympanotomy is performed to assess and confirm the normality of the ossicular chain. The lateral surface of the TM is painted with zinc oxide (ZnO) suspended in saline at a concentration of 60 to 90 mg per cc. The paint is necessary to increase the light reflected from the translucent TM surface. Control measurements have demonstrated that the paint has no significant effect on the motion of the TM or the ossicles (25). The data associated with a single frequency-level combination are gathered over the period of about a second. Measurements at multiple frequencies and levels are taken over the period of several hours. In order to prevent excessive drying of the preparation during the measurement process, the temporal bone is periodically soaked in saline for several minutes. While we summarize our results with measurements from a few individual bones, all bones showed similar patterns. The range of stimulus frequencies and levels we used varied from 200 Hz to 20 kHz and 80 to 120 dB SPL. The relatively high sound levels were needed because our methods are only sensitive to displacements that are larger than 10–20 nm and the magnitude of TM displacements for a given sound pressure falls regularly with frequencies above 1 kHz. Nonetheless, these high sound pressures are still within the linear response range of the TM and middle ear (2,4,25).

Results

Displacements of the TM Surface

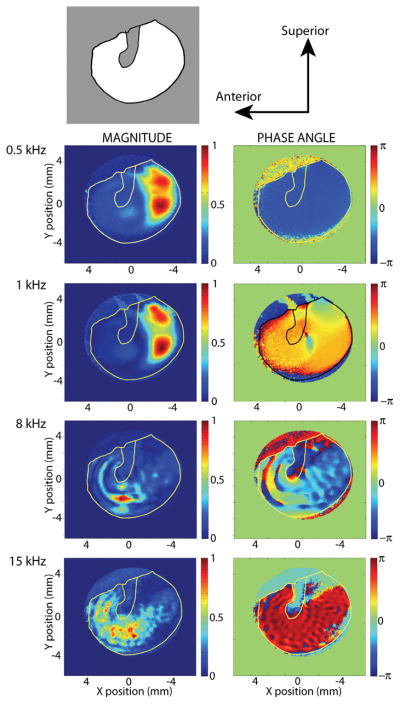
Maps of the magnitude and phase of displacement at over 40000 points on the surface of the TM are illustrated in Figure 1. The first row of the figure shows the orientation of the TM specimen and the manubrium of the malleus. Rows 2–5 show the relative magnitude (left side) and phase (right side) of the surface displacements in response to 4 different stimulus frequencies. The left-hand panel in the second row indicates that with a 500 Hz tonal stimulus the largest displacements observed on the TM are in the posterior half of the TM (the paired red areas), and the right-hand panel illustrates the entire surface is moving with the same phase (the uniform blue area). The third row shows a 1 kHz stimulus produces a similar magnitude pattern but a less uniform phase pattern. The fourth and fifth rows illustrate some ordered patterns of varying displacement and phase that appear as scalloped patterns, where the distance between the scalloped ridges is smaller at the higher frequency. Data like those shown in Figures 1 can be used to produce stroboscopic videos of TM motion that show similar patterns of motion (see Videos, Supplemental Digital Content 4, which illustrates the in-phase motion of the entire TM surface of a different temporal bone in response to a 500 Hz stimulus; Supplemental Digital Content 5, which illustrates the combination of modal and traveling-wave displacements on a TM surface in response to a 4 kHz stimulus, and Supplemental Digital Content 6, which illustrates the combination of modal and traveling-wave displacements on a TM surface in response to a 10 kHz stimulus)

Figure 1.

Figure 1

Open in a new tab

A series of displacement maps of the TM surface, measured with stroboscopic holography tonal sound stimuli of either 0.5, 1, 8 or 15 kHz. The top row describes the view and orientation of the tympanic membrane with the gray outline of the manubrium. Rows 2 through 5 show maps of the normalized magnitude (left-hand column) and phase (right-hand column) of the different locations on the TM. The displacement magnitudes have been scaled by the largest displacement produced by each stimulus. The stimulus sound pressures varied between 80 and 110 dB SPL. The largest displacements are on the order of 500 nm, the smallest measurable displacement is about 20 nm. The phase is scaled in radians.

Comparisons to previous quantitative measurements: Displacements of the Umbo

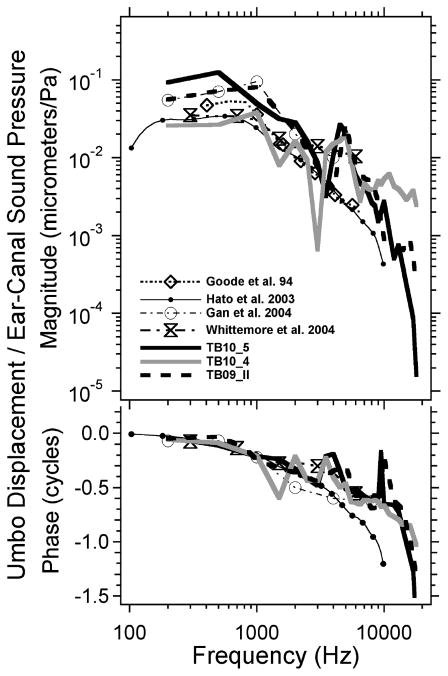
Our holographic measurements are consistent with previous quantitative measurements of TM displacement. Figure 2 compares the magnitude and phase angle of the displacement of the umbo (extracted from displacement maps like those in Figure 1) with measurements from the literature made in cadaveric (4,26,27) and live (6) human ears. There is a good match between the stroboscopic holography data and those gathered with other means.

Figure 2.

Figure 2

Open in a new tab

Comparison of the displacement of the umbo, defined by stroboscopic holography and data from the literature. The comparison data include those of Goode et al. (4), Hato et al. (26), Gan et al. (27) measured in cadaveric temporal bones and Whittemore et al. (6) measured in live humans. The results from stroboscopic holography in three temporal bones are illustrated.

Wave motion on the Tympanic Membrane

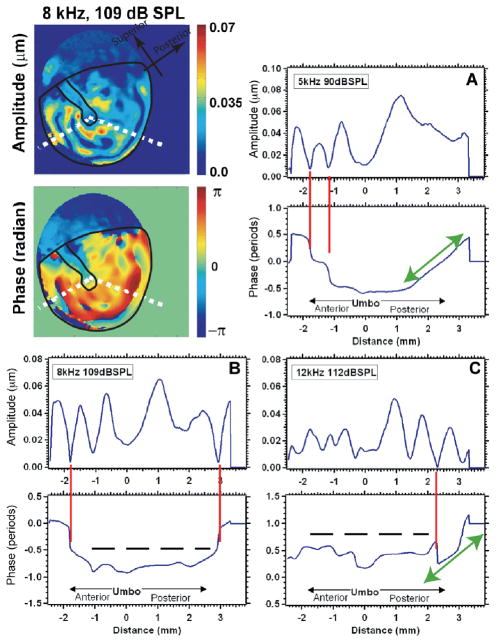
Evidence for both standing-wave-like modal patterns and traveling-waves of displacement on the TM surface is contained in Figure 3. Illustrated are measurements of the magnitude and phase of the displacement of locations that fall on two radii on the TM surface; both radii emanate from the umbo at the center of the TM. The radii used in these examples are illustrated by the white dotted lines in the displacement magnitude and angle maps on the upper left. The plots in panels A, B and C illustrate the magnitude and phase of displacement as one travels from near the tympanic rim on the left-hand radial arm (coded as −2.5 mm on the plot panels) to the umbo (coded as zero) and then onto the posterior-inferior rim of the TM (coded as +3 mm). Each plot panel contains a separate plot of magnitude and angle, where panel A shows results from 5 kHz stimulation, panel B 8 kHz and panel C 12 kHz. The plots illustrate several instances of nodes (deep, sharp minima in motion that are associated with rapid half-cycle phase changes) marked with red vertical lines. Nodes are strong indicators of modal patterns of displacement, and we see one to two nodes (usually near the TM rim) at each of the three frequencies. Panel A and C also show regions (marked by green arrows) where the phase changes regularly and gradually with space; such phase changes are hallmarks of traveling waves. The long gradual phase transition in panel A indicates a dominant traveling wave moving from the rim towards the umbo. The shorter phase transition in panel C, which is punctuated with a node-like phase step and magnitude minima, suggest a combination of near equal magnitude modal and traveling displacements. Note that in both cases the gradual phase transitions do not reach the umbo. The regions marked by dashed horizontal lines in panel B and C, are regions where we observe repeated magnitude peaks with a slowly varying almost oscillating phase; these regions correspond to the scalloped regions of the displacement maps. Since the phase variations in these oscillations are less than ¼ cycle, the scalloped patterns are consistent with the combination of a modal displacement of relatively large magnitude and a traveling wave of smaller magnitude.

Figure 3.

Figure 3

Open in a new tab

Displacement magnitude and phase angle along radii from the umbo to the center. The images in the upper left are displacement magnitude and phase maps of the motion of a human TM stimulated at 8 kHz and 109 dB SPL. The white dotted lines show the radii used in defining the displacement vs. distance in the other plots. (A) The response to a 5 kHz 90 dB SPL tone. (B) The response to a 8 kHz 109 dB SPL tone. (C) The response to a 12 kHz 112 dB SPL tone.

Effect of cartilage sheets on TM wave motion

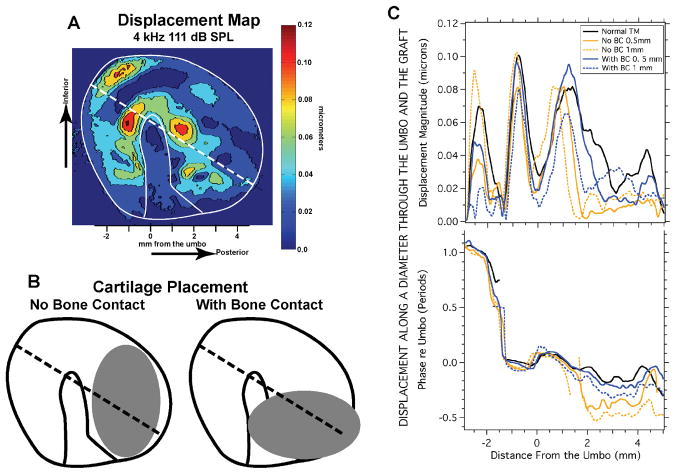
While we have previously published several holographic analyses of the effect of placing cartilage sheets on the TM (28-9), a topic highly relevant to tympanoplasty, Figure 4 illustrates a new analysis of the relative phase of TM motion in response to sound before and after cartilage placement. Fig. 4a shows the displacement map obtained by stroboscopic measurements of a human cadaveric TM stimulated at 4 kHz with 111 dB SPL (29). Displacement measurements were made in this ear, both before (Fig 4a) and after the placement of cartilage ovals that were either 0.5 or 1 mm thick. The ovals had an area of about 1/3 of the TM area and were placed on the posterior medial surface of the TM in one of two orientations (Fig. 4B): either parallel to the manubrium with ‘No Bone Contact’ or nearly perpendicular to the manubrium in contact with the manubrium and the superior-posterior tympanic ring: ‘With Bone Contact’. Panel C illustrates the displacement magnitude and phase measured in each condition along the diameter illustrated by the dotted lines in panels A and B. The placement of the cartilage disks causes relatively large (factor of 3 to 5) changes in the magnitude of the motion of the membrane at the locations under the cartilage (from 2 to 4.5 mm from the umbo). A factor of 4 reduction in magnitude is also seen in the anterior-inferior part of the membrane (between −3 and −1.5 mm), but this later reduction occurs anterior and inferior to a node marked by a sharp minimum and rapid phase change that occurs at −1.5 mm. The displacements of the central part of the membrane surface (between −1.5 and 1.5 mm) are much less affected by the manipulations. Regarding the phase, the only areas with consistent phase alterations are those directly beneath the cartilage oval (between 2 and 4.5 mm), where the phase lags by as much as 1/2 period after the cartilage is placed. The small effect of the cartilage in the central potion of the membrane and the introduction of a significant phase lag in sections in contact with the cartilage sheet is consistent with a modal model of TM motion. In fact, we see little evidence of traveling waves before or after the placement of the cartilage sheet (see Videos, Supplemental Digital Content 7, which shows the TM displacements after placing a 1 mm cartilage sheet in the no bone contact position).

Figure 4.

Figure 4

Open in a new tab

Displacement magnitude on the surface of the TM before and after the placement of ovals of cartilage on the posterior medial surface of the TM. A. The displacement of the TM surface produced by a 4 kHz 111 dB SPL tone. The dotted line shows a diameter that goes through the umbo; the diameter is oriented 30 degrees to the horizontal. B. Schematics showing the placement of oval cartilage disks with thickness of either 0.5 or 1 mm. The disk was placed in the posterior half of the TM either with ‘No Bone Contact’ or ‘With Bone Contact’. C. Graphs of the Magnitude and angle of the displacement of locations along the 30-degree diameter illustrated in A and B. The X-coordinate is distance from the umbo. The upper panel plots the magnitude in microns. The lower panel plots the displacement phase relative to the phase at the umbo. The different line types are for the normal membrane (black line), and after placing cartilage with no bone contact (orange lines), with bone contact (blue lines). The solid orange and blue lines show the effect of a 0.5 mm thick cartilage oval, the dashed lines show the effect of 1 mm thick ovals. Some of these data were presented in a different form in Aarnisalo et al. (28,29).

Discussion

The Motion of the TM Surface: Stimulus frequency less than or equal to 1 kHz

The data we present here and in other publications (24,25) are consistent with in-phase low-order modal motions (no nodes are apparent but the magnitude of displacement varies in space) of the surface of the human TM in response to stimulus frequencies less than or equal to 1 kHz (Supplemental Digital Content 4). The spatial variations in displacement magnitude result from the interaction of the graded mechanical properties of the TM, e.g. TM thickness (30), the boundary conditions that limit TM motion (the suspension of the TM at its rim (31)), the three-dimensional shape of the TM (32-4), and the mechanical load of the ossicular chain and cochlea that limits motion of the manubrium (34,35). The forces that drive the ossicular chain in this frequency range also depend on these structural features, where the important physical parameters include the stiffness of the TM support, and the internal stiffness of the TM, which helps couple the motion of different TM locations together; the area of the TM probably plays a significant role, and the shape also contributes, but to a lesser extent.

The Motion of the TM Surface: Stimulus frequencies between 2 and 8 kHz

Our data point out that the motion of the TM surface with stimuli in the 2–8 kHz range contains a combination of somewhat higher-order modal displacements (we see several nodes) and traveling waves (Supplemental Digital Content 5). The phase gradients in Figures 3A&C are the best indicators of traveling waves of significant magnitude; however, those gradients stop well short of the umbo, indicating that even in the presence of a significant peripheral traveling wave modal patterns dominate umbo motion. If the modal action of the TM is the driving force for ossicular motion, then the total area of the TM does not likely contribute to TM-ossicular sound transformation, since the area that contributes to manubrial motion is the central area that is demarcated by the inner-most nodal boundary. Put another way: we can replace a nodal boundary on the TM surface by a rigid support and not affect the motion of the remaining membrane. If the traveling waves we observe contribute to TM motion they seem to play a lesser role, since we see little wave travel near the manubrium.

The motion of the TM Surface: Stimulus frequencies of 8 kHz and higher

The maps of displacement magnitude and phase that we measure in response to sound stimuli of frequencies of 8 kHz and above also suggest a combination of somewhat higher-order modal patterns (with several apparent nodes) and a traveling wave component of smaller magnitude, where the most prominent indications of traveling waves are small oscillations in displacement phase about some background phase (panels B and C of Figure 3), as well as the scalloped spatial patterning observed in the displacement magnitude and phase maps (the bottom panels of Figure 1). These patterns indicate that the traveling component, while real, is smaller in magnitude than the modal component of TM motion (Supplemental Digital Content 6).

Overall description of TM motion: Additional insight from the measured phase of motion

Our data clearly show that at frequencies less than 1 kHz, all points on the TM move in phase and the surface displacements are well described by a low-order modal motion. At higher frequencies, our data suggest that TM motion patterns are still primarily determined by modal motions, but there is a fundamental difference between our measurements and the earlier interpretations of Tonndorf and Khanna’s data (3,8,9). The magnitude maps that Khanna and Tonndorf and others (25) produced in response to high-frequency sound were consistent with extremely high-order modal patterns, and it was predicted that each modal maximum was separated from the surrounding maxima by nodal boundaries: An interpretation consistent with the break-up of the TM surface motion into multiple independently moving sections. The displacement phase measurements made possible by our stroboscopic techniques, however, point out that many of the multiple local magnitude maxima that we see at frequencies above a few kHz results from the interaction of a modal maxima of larger magnitude and relatively large spatial extent with a traveling wave component of smaller magnitude and smaller wavelength (multiple traveling wave wavelengths fit into the area of a single modal maxima). The new data suggest that the traveling wave components are producing small modulations of a larger, relatively low-order, modal displacement pattern, with the result that even at frequencies of 8 to 12 kHz, large areas of the human TM are generally moving in phase (Figure 3). A similar description of the motion of the gerbil TM has been published (36).

Clinical significance of different TM models

The pure modal and traveling wave models have different implications for the effect of TM pathology and reconstruction. The TM may become altered in many otologic disorders, where examples of TM pathology include tympanosclerosis or fibrosis within the TM, dimeric areas, formation of TM retraction pockets, and formation of adhesive scar bands between the TM and other structures in the middle ear (37). In general, the modal motion model suggests that any local pathology (unless it is close to the manubrial attachment to the TM) will have limited effects on manubrium and ossicular motion. The traveling wave model, on the other hand, suggests that pathology near the rim of the TM will be nearly as effective in disrupting the coupling of sound energy to the umbo as pathology near the center. The modal model predicts that TM pathology might change the shape of the displacement pattern, but have limited effect on ossicular motion unless it significantly affected the more global mechanical properties of the TM, such as the stiffness of the TM support. Clinical observations with various types of TM pathology (e.g., tympanosclerosis, fibrosis, dimeric membrane, retraction pocket, etc.) often reveal little or no conductive hearing loss, which is more consistent with the predictions of the modal model.

The two extreme models also suggest different sensitivities to variations in tympanic-membrane reconstructions. The traveling wave model suggests the need for more precise reconstruction of TM shape and material properties. The modal model is more forgiving, suggesting that maintenance of the more global TM properties, such as the stiffness of the support and the material stiffness of the graft material are of primary importance in tympanoplasties. Our measurements of the magnitude and phase of TM surface displacements favor the modal model of TM function, with the exception that the modal motion patterns are limited to a few lower-order modes, such that the TM does not break up as predicted by earlier investigators. A large number of materials have been used in clinical practice for TM reconstruction including various types of fascial grafts, perichondrium, fat, cartilage, etc (38), with wide variation in shape and thickness of the resulting TM reconstructions. The fact that good clinical results can be obtained with many different materials argues in favor of the modal model.

The models also have a bearing on the placement of tympanostomy tubes. Tubes, especially those with large flanges such as T-tubes, can be expected to interfere with the propagation of traveling waves. However, clinical observations have shown that tubes generally do not cause a significant conductive hearing loss, beyond what is expected from the tube lumen acting as a small perforation (39), a result that is more consistent with the modal model. The modal model does predict that the area of the TM close to the umbo should not be used as a location for tube placement, since this could have a significant effect on manubrial motion.

Caveats

There are several methodological caveats with our measurements that need to be raised. The primary caveat is our use of fresh or thawed temporal bones with widely opened middle-ear air spaces. We, and others, have demonstrated many similarities between live humans and cadaveric temporal bones in the mechanical responses of the normal and pathologic middle ear (40-3); however, there is still a need to demonstrate similarities in TM displacement patterns between live and cadaveric ears. Also, while the effects of the middle-ear cavity in humans are generally small (1,44) there is a suggestion in the literature that opening the middle-ear air spaces can affect TM displacement patterns (45).

A second caveat is the unknown effect of the removal of the bony ear canal to observe the tympanic ring and the generation of a stimulus sound wave front that is parallel to the tympanic ring. The proponents of the TM traveling wave model suggest that part of the process that initiates wave travel on the membrane surface is wave travel within the ear canal from the closer posterior edge of the TM to the more distant anterior edge of the TM. An issue with such travel within the canal is that the TM width is less than 1/3 of a wavelength of sound in air at 10 kHz, and smaller than that at lower frequencies. Also the speed of sound in air (345 m/s) is much larger than even the highest traveling wave velocities predicted by these models (50 m/s). Therefore it seems unlikely that our removal of the ear canal will greatly affect the balance of traveling wave and modal displacement magnitudes.

A third caveat is the effect of the paint we place on the TM surface. While we have been able to demonstrate that painting has little effect on ossicular motion, and that we can see similar levels of holographic responses in painted and unpainted TMs (25), the poor reflections we get from unpainted TMs preclude our ability to measure displacement phase. Therefore it is possible, although unlikely, that the paint we use drastically reduces the significance of surface traveling waves.

A fourth caveat is that our holographic measurements are most sensitive to displacements parallel to the illumination beam. Because of the three-dimensional shape of the TM we may not be sensing all of the important motional components of the TM.

Conclusions

The displacements of the surface of the human TM in response to sound result from a combination of lower-order modal responses patterns and traveling waves. The magnitudes of the modal responses are in general larger than those of the traveling waves, especially near the umbo. Many clinical results based on pathology and reconstruction techniques are consistent with the alterations producing small changes in modal displacement patterns, and are inconsistent with the more drastic alteration predicted by the traveling wave model of TM function.

Supplementary Material

1
Download video file (694KB, mpg)
2
Download video file (188KB, mpg)
3
Download video file (318KB, mpg)
4
Download video file (280KB, mpg)
5
Download video file (262KB, mpg)
6
Download video file (294KB, mpg)
7
Download video file (254KB, mpg)

Acknowledgments

We wish to thank our colleagues Maria del Socorro Hernandez-Montes, Annti Aarnisalo and Christopher Scarpino for their contributions to this work. This work was supported by grants from the NIDCD, and funding from the Massachusetts Eye and Ear Infirmary, the Worcester Polytechnic Institute and L. Mittal.

Work Supported By NIDCD grant R01 DC008642 & F32DC009949

Footnotes

For presentation at the 2011 Meeting of the American Otological Society, Chicago Il, 30 April - 1 May

References

  • 1.Zwislocki J. Analysis of the middle-ear function. Part I: Input impedance. J Acoust Soc Am. 1962;34:1514–1523. [Google Scholar]
  • 2.Guinan JJ, Jr, Peake WT. Middle-ear characteristics of anesthetized cats. J Acoust Soc Am. 1967;41:1237–1261. doi: 10.1121/1.1910465. [DOI] [PubMed] [Google Scholar]
  • 3.Tonndorf J, Khanna SM. The role of the tympanic membrane in middle ear transmission. Ann Otol. 1970;79:743–753. doi: 10.1177/000348947007900407. [DOI] [PubMed] [Google Scholar]
  • 4.Goode RL, Killion M, Nakamura K, Nishihara S. New knowledge about the function of the human middle ear: Development of an improved analog model. Am J Otol. 1994;15(2):145–154. [PubMed] [Google Scholar]
  • 5.Puria S, Peake WT, Rosowski JJ. Sound-pressure measurements in the cochlear vestibule of human cadavers. J Acoust Soc Am. 1997;101:2745–2770. doi: 10.1121/1.418563. [DOI] [PubMed] [Google Scholar]
  • 6.Whittemore KR, Merchant SN, Poon BB, Rosowski JJ. A normative study of tympanic membrane motion in humans using a laser Doppler vibrometer (LDV) Hear Res. 2004;187:85–104. doi: 10.1016/s0378-5955(03)00332-0. [DOI] [PubMed] [Google Scholar]
  • 7.Nakajima HH, Ravicz ME, Merchant SN, Peake WT, Rosowski JJ. Experimental ossicular fixations and the middle-ear’s response to sound: Evidence for a flexible ossicular chain. Hear Res. 2005;204:60–77. doi: 10.1016/j.heares.2005.01.002. [DOI] [PubMed] [Google Scholar]
  • 8.Khanna SM, Tonndorf J. Tympanic membrane vibrations in cats studied by time-averaged holography. J Acoust Soc Am. 1972;51:1904–1920. doi: 10.1121/1.1913050. [DOI] [PubMed] [Google Scholar]
  • 9.Tonndorf J, Khanna SM. Tympanic-membrane vibrations in human cadaver ears studied by time-averaged holography. J Acoust Soc Am. 1972;52:1221–1233. doi: 10.1121/1.1913236. [DOI] [PubMed] [Google Scholar]
  • 10.Beranek LL. Acoustics. New York: Acoustical Society of America; 1993. [Google Scholar]
  • 11.Fletcher NH. Acoustic Systems in Biology. New York: Oxford Univ. Press; 1992. [Google Scholar]
  • 12.Shaw EG, Stinson MR. The human external and middle ear: Models and concepts. In: deBoer E, Viergever MA, editors. Mechanics of Hearing. Delft University Press; 1983. pp. 3–10. [Google Scholar]
  • 13.Tonndorf J, Khanna SM. Mechanics of the auditory system. In: Hinchcliffe R, Harrison D, editors. Scientific Foundations of Otolaryngology. London: William Heineman; 1976. pp. 237–252. [Google Scholar]
  • 14.Fay JP, Puria S, Steele CR. The discordant eardrum. PNAS. 2006;103(52):19743–19748. doi: 10.1073/pnas.0603898104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Olson ES. Observing middle and inner ear mechanics with novel intracochlear pressure sensors. J Acoust Soc Am. 1998;103(6):3445–3463. doi: 10.1121/1.423083. [DOI] [PubMed] [Google Scholar]
  • 16.Puria S, Allen JB. Measurements and model of the cat middle ear: Evidence of tympanic membrane acoustic delay. J Acoust Soc Am. 1998;104(6):3463–3481. doi: 10.1121/1.423930. [DOI] [PubMed] [Google Scholar]
  • 17.Parent P, Allen JB. Wave model of the cat tympanic membrane. J Acoust Soc Am. 2007;122(2):918–931. doi: 10.1121/1.2747156. [DOI] [PubMed] [Google Scholar]
  • 18.Parent P, Allen JB. Time-domain “wave” model of the human tympanic membrane. Hear Res. 2010;263:152–167. doi: 10.1016/j.heares.2009.12.015. [DOI] [PubMed] [Google Scholar]
  • 19.Overstreet EH, III, Ruggero MA. Development of wide-band middle-ear transmission in the Mongolian gerbil. J Acoust Soc Am. 2002;111(1):261–270. doi: 10.1121/1.1420382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Ravicz ME, Cooper NP, Rosowski JJ. Gerbil middle-ear sound transmission from 100 Hz to 60 kHz. J Acoust Soc Am. 2008;124(1):363–380. doi: 10.1121/1.2932061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Nakajima HH, Dong W, Olson ES, Merchant SN, Ravicz ME, Rosowski JJ. Differential intracochlear sound pressure measurements in normal human temporal bones. JARO. 2009;10:23–36. doi: 10.1007/s10162-008-0150-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Furlong C, Rosowski JJ, Hulli N, Ravicz ME. Preliminary analyses of tympanic-membrane motion from holographic measurements. Strain. 2009;45:301–309. doi: 10.1111/j.1475-1305.2008.00490.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Hernández-Montes MdS, Furlong C, Rosowski JJ, et al. Optoelectronic holographic otoscope for measurement of nano-displacements in tympanic membrane. J Biomed Optics. 2009 May;14:034023. doi: 10.1117/1.3153898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Cheng JT, Aarnisalo AA, Harrington E, et al. Motion of the surface of the human tympanic membrane measured with stroboscopic holography. Hear Res. 2010;263:66–77. doi: 10.1016/j.heares.2009.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Rosowski JJ, Cheng JT, Ravicz ME, et al. Computer-assisted time-averaged holography of the motion of the surface of the tympanic membrane with sound stimuli of 0.4 to 25 kHz. Hear Res. 2009;253:83–96. doi: 10.1016/j.heares.2009.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Hato N, Stenfelt S, Goode RL. Three-dimensional stapes footplate motion in human temporal bones. Audiol Neurootol. 2003;8(3):140–152. doi: 10.1159/000069475. [DOI] [PubMed] [Google Scholar]
  • 27.Gan RZ, Wood MW, Dormer KJ. Human middle ear transfer function measured by double laser interferometry system. Otol & Neurotol. 2004;25(4):423–435. doi: 10.1097/00129492-200407000-00005. [DOI] [PubMed] [Google Scholar]
  • 28.Aarnisalo AA, Cheng JT, Ravicz ME, et al. Middle ear mechanics of cartilage tympanoplasty evaluated by laser holography and vibrometry. Otol Neurotol. 2009;30(8):1209–1214. doi: 10.1097/MAO.0b013e3181bc398e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Aarnisalo AA, Cheng JT, Ravicz ME, Furlong C, Merchant SN, Rosowski JJ. Motion of the tympanic membrane after cartilage tympanoplasty determined by stroboscopic holography. Hear Res. 2010;263:78–84. doi: 10.1016/j.heares.2009.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Kuypers LC, Decraemer WF, Dirckx JJJ. Thickness distribution of fresh and preserved human eardrums measured with confocal microscopy. Otol Neurotol. 2006;27(2):256–264. doi: 10.1097/01.mao.0000187044.73791.92. [DOI] [PubMed] [Google Scholar]
  • 31.Gea SLR, Decraemer WF, Funnell RWJ, Dirckx JJJ, Maier H. Tympanic membrane boundary deformations derived from static displacements observed with computerized tomography in human and gerbil. J Assoc Res Otolaryngol. 2010;11:1–17. doi: 10.1007/s10162-009-0192-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Funnell WR, Laszlo CA. Modeling of the cat eardrum as a thin shell using the finite-element method. J Acoust Soc Am. 1977;63:1461–1467. doi: 10.1121/1.381892. [DOI] [PubMed] [Google Scholar]
  • 33.Funnell WR. On the undamped natural frequencies and mode shapes of a finite-element model of the cat eardrum. J Acoust Soc Am. 1983;73:1657–1661. doi: 10.1121/1.389386. [DOI] [PubMed] [Google Scholar]
  • 34.Koike T, Wada H, Kobayashi T. Effect of depth of conical-shaped tympanic membrane on middle-ear sound transmission. JSME. 2001;44(4):1097–1102. [Google Scholar]
  • 35.Funnell WR, Decraemer WF, Khanna SM. On the damped frequency response of a finite-element model of the cat eardrum. J Acoust Soc Am. 1987;81:1851–1859. doi: 10.1121/1.394749. [DOI] [PubMed] [Google Scholar]
  • 36.de La Rochefoucauld O, Olson ES. A sum of simple and complex motions on the eardrum and manubrium in gerbil. Hear Res. 2010;263:9–15. doi: 10.1016/j.heares.2009.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Nadol JB., Jr . Chronic otitis media. In: Nadol JB, McKenna MJ, editors. Surgery of the Ear and Temporal Bone. 2. Lippincott, Williams and Wilkins; Philadelphia: 2004. pp. 199–218. [Google Scholar]
  • 38.Poe D. Perforations of the tympanic membrane. In: Nadol JB, McKenna MJ, editors. Surgery of the Ear and Temporal Bone. 2. Lippincott, Williams and Wilkins; Philadelphia: 2004. pp. 163–178. [Google Scholar]
  • 39.Rosowski JJ, Merchant SN, Ravicz ME, Voss SE, Caradonna D, Cunningham MJ, Peake WT. Analysis of acoustic mechanisms in middle-ear pathology and reconstruction. In: Huttenbrink Karl-Bernd., editor. Middle Ear Mechanics in Research and Otosurgery; Proceedings of the first International Workshop on Middle Ear Mechanics in Research and Otosurgery; Dept of ORL, Univ Hosp Carl Gustav Carus, Dresden Univ of Technology; 1997. pp. 183–190. [Google Scholar]
  • 40.Rosowski JJ, Davis PJ, Merchant SN, Donahue KM, Coltrera MD. Cadaver middle ears as models for living ears: Comparisons of middle-ear input immittance. Ann Otol Rhinol Laryngol. 1990;99:403–412. doi: 10.1177/000348949009900515. [DOI] [PubMed] [Google Scholar]
  • 41.Goode RL, Ball G, Nishihara S, Nakamura K. Laser Doppler vibrometer (LDV) a new clinical tool for the otologist. Am J Otol. 1996;17:813–822. [PubMed] [Google Scholar]
  • 42.Chien W, Ravicz ME, Rosowski JJ, Merchant SN. Measurements of human middle- and inner-ear mechanics with dehiscence of the superior semicircular canal. Otol & Neurotol. 2007;28:250–257. doi: 10.1097/01.mao.0000244370.47320.9a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Chien W, Rosowski JJ, Ravicz ME, Rauch SD, Smullen J, Merchant SN. Measurements of stapes velocity in live human ears. Hear Res. 2009;249:54–61. doi: 10.1016/j.heares.2008.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Stepp CE, Voss SE. Acoustics of the human middle-ear air space. J Acoust Soc Am. 2005;118(2):861–871. doi: 10.1121/1.1974730. [DOI] [PubMed] [Google Scholar]
  • 45.Wada H, Ando M, Takeuchi A, et al. Vibration measurement of the tympanic membrane of guinea pig temporal bones using time-averaged speckle pattern interferometry. J Acoust Soc Am. 2002;111:2189–2199. doi: 10.1121/1.1467671. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
Download video file (694KB, mpg)
2
Download video file (188KB, mpg)
3
Download video file (318KB, mpg)
4
Download video file (280KB, mpg)
5
Download video file (262KB, mpg)
6
Download video file (294KB, mpg)
7
Download video file (254KB, mpg)

RESOURCES