Network anticorrelations, global regression, and phase‐shifted soft tissue correction

Abstract

Synchronized low‐frequency BOLD fluctuations are observed in dissociable large‐scale, distributed networks with functional specialization. Two such networks, referred to as the task‐positive network (TPN) and the task‐negative network (TNN) because they tend to be active or inactive during cognitively demanding tasks, show reproducible anticorrelation of resting BOLD fluctuations after removal of the global brain signal. Because global signal regression mandates that anticorrelated regions to a given seed region must exist, it is unclear whether such anticorrelations are an artifact of global regression or an intrinsic property of neural activity. In this study, we demonstrate from simulated data that spurious anticorrelations are introduced during global regression for any two networks as a linear function of their size. Using actual resting state data, we also show that both the TPN and TNN become anticorrelated with the orbits when soft tissues are included in the global regression algorithm. Finally, we propose a technique using phase‐shifted soft tissue regression (PSTCor) that allows improved correction of global physiological artifacts without global regression that shows improved anatomic specificity to global regression but does not show significant network anticorrelations. These results imply that observed anticorrelations between TNN and TPN may be largely or entirely artifactual in the resting state. These results also imply that differences in network anticorrelations attributed to pathophysiological or behavioral states may be due to differences in network size or recruitment rather than actual anticorrelations. Hum Brain Mapp, 2011. © 2010 Wiley‐Liss, Inc.

INTRODUCTION

The discovery of correlated spontaneous BOLD fMRI fluctuations in functionally related brain regions [Biswal et al., 1995] has subsequently led to the observation of distributed networks of synchronized BOLD signal [Damoiseaux et al., 2006; Fox and Raichle, 2007]. Seed‐based correlation and independent component analysis techniques have allowed dissociation of dorsal and ventral attentional [Fox et al., 2006], default mode [Greicius and Menon, 2004; Greicius et al., 2003, 2008; Raichle et al., 2001], visual [Golland et al., 2007; Nir et al., 2006], sensorimotor [Biswal et al., 1995; Cordes et al., 2000, 2001], subcortical [Di Martino et al., 2008], memory [Vincent et al., 2006], salience [Seeley et al., 2007], and executive control networks [Seeley et al., 2007; Sridharan et al., 2008]. Such networks show consistent anatomical boundaries correlated with measures of structural connectivity [Greicius et al., 2008; Hagmann et al., 2008; Honey et al., 2009] and task‐related activation [Smith et al., 2009].

Studies of higher level cerebral network architecture have suggested a modular organization of the brain into five primary modules corresponding to default mode or task‐negative network (TNN), attentional or task‐positive network (TPN), occipital/visual, sensorimotor/auditory, and limbic/paralimbic networks [He et al., 2009], with reproducible cortical hubs of connectivity in heteromodal association cortex [Buckner et al., 2009]. Of these functional connectivity networks, the TNN [Fair et al., 2008; Fox and Raichle, 2007; Fransson, 2006; Greicius et al., 2003; Raichle and Snyder, 2007; Raichle et al., 2001] and TPN [Fox et al., 2005, 2006; Golland et al., 2007; Seeley et al., 2007; Tian et al., 2007] have received greatest attention.

The TNN, consisting of regions in the posterior cingulate/precuneus, temporoparietal junction, medial prefrontal, hippocampi, and anterior middle temporal gyrus, reproducibly shows decreases in activity across a wide array of attentionally demanding tasks [Gusnard and Raichle, 2001; McKiernan et al., 2003]. The TPN typically shows increased activity for similar demanding tasks and includes frontal eye fields, dorsolateral prefrontal cortex, intraparietal sulcus, lateral parietal, frontoinsular, anterior cingulate, and lateral occipital regions [Corbetta and Shulman, 2002; Fox et al., 2006]. Independent observations suggest that these networks not only show opposite task‐associated activity, but may also show anticorrelated fluctuations at rest [Fox et al., 2005; Fransson, 2005]. Such anticorrelations, however, were masked by a strong global signal resulting in high correlation of BOLD fluctuations in nearly all brain regions [Macey et al., 2004].

This global signal represents a fundamental problem in elucidating functional connectivity networks in that physiological artifacts such as heart rate, respiration, and scanner noise that are seen throughout the brain artificially obscure synchronous correlations between brain regions. This global signal results in most areas of the brain showing significant correlation with each other, and a method for removing this signal is necessary to improve anatomic specificity of connectivity networks. By removing this global signal through a technique such as global regression or related strategy, TPN and TNN anticorrelations have been observed. Also using this kind of technique, others have studied network anticorrelations as a tool to understand high‐level neural architecture [Kelly et al., 2008; Tian et al., 2007; Uddin et al., 2008] and as a probe for neuropathology [Bluhm et al., 2007; Wang et al., 2007; Williamson, 2007].

However, the validity of global signal regression has been questioned as a preprocessing technique [Murphy et al., 2009]. Global regression mathematically requires some brain regions to become anticorrelated [Fox et al., 2009; Murphy et al., 2009], allowing for the possibility that such anticorrelations may be artifactual. Simulations indicated that pure noise voxels may become anticorrelated with a fluctuation of interest, and the effect increased as the size of the network containing the fluctuation increased [Murphy et al., 2009]. Therefore, areas that may be anticorrelated after global regression simply reflect areas that are uncorrelated or least correlated before global regression [Murphy et al., 2009].

Subsequently, it has been argued that although such spurious anticorrelations are possible, a neural basis for network anticorrelations is likely [Fox et al., 2009]. Fox and colleagues proposed three primary arguments for the validity of observed network anticorrelations. First, they observe that the global signal is not preferentially seen in areas that become anticorrelated after global regression and argue that the characteristic spatial distribution of observed anticorrelations requires a biological basis. Second, they demonstrate that improved anatomic specificity is seen in connectivity maps following global regression, suggesting that the technique improves detection of neural‐based connectivity. Finally, they demonstrate that anticorrelations are seen even in the presence of a modified regression algorithm using as little as 5% of the global signal as a regressor [Fox et al., 2009].

To evaluate these interpretations of the validity of global regression and network anticorrelations, we performed simulations by varying the size and noise of two separate networks of interest to determine under what conditions uncorrelated networks will become anticorrelated following global regression. These results can explain why anticorrelations are observed in a reproducible spatial distribution.

Soft tissue voxels do not contain neuronal elements as the brain does and thus do not contribute to the BOLD signal components related to neural activity. Yet, these tissues are perfused and may allow characterization of global signal contaminants related to physiological sources, scanner drift, or other variation in time of blood oxygenation levels not easily assessed with standard physiological monitoring techniques. Using actual resting state data, we also evaluated the effect of introducing such soft tissue voxels of the face, calvarium, and scalp to the global regression analysis and propose that similarly induced anticorrelations in the soft tissues are a model for introduction of spurious anticorrelations, lending support to the claim that network anticorrelations after global regression are artifactual.

Finally, we propose an alternate method for correction of the global signal that makes use of physiological waveforms as well as regressors obtained from subject motion parameters, white matter, CSF, and soft tissues of the face and calvarium (phase‐shifted soft tissue correction [PSTCor]) that shows improved anatomic specificity to global regression, but does not exhibit significant network anticorrelations.

MATERIALS AND METHODS

Simulated Whole‐Brain BOLD Time Series

To evaluate the conditions under which global signal regression may artifactually induce network anticorrelations, it is helpful to have a system where the actual relationship of the networks in question are known. We therefore devised a simulation in which artificially generated BOLD data could be analyzed to observe the effects of global regression. The simulated datasets included a noise signal that varied from voxel to voxel, a superimposed global signal shared between all voxels, and signal from two internally correlated networks, analogous to the TPN and TNN (Fig. 1).

Figure 1.

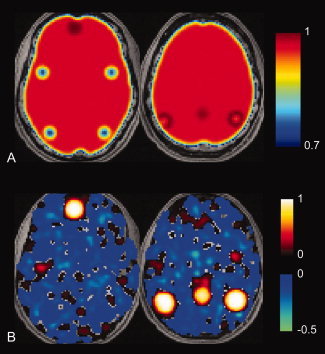
Areas of least correlation to default mode network do not necessarily become anticorrelated after global regression. A: Location of regions of interest corresponding to simulated TNN and TPN show highest correlation to posterior cingulate seed in TPN and lowest correlation in TNN prior to global regression. Scale bar shows correlation values to posterior cingulate seed. B: Following global regression, the TNN is strongly correlated, but the remaining brain shows patchwork pattern of correlation and anticorrelation that is unrelated to presence of uncorrelated TNN signal. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Brain noise was included in the simulation because it is present in actual BOLD data, and because components of the noise may be correlated or anticorrelated by chance to a signal of interest, making noise an important parameter in understanding the behavior of correlated networks. To best approximate actual noise in the brain, we modeled the frequency distribution of the noise after the frequency content of spontaneous BOLD fluctuations [Anderson, 2008; Cordes et al., 2001], which is comprised of frequencies ranging from approximately 0.005 Hz to 0.1 Hz, with a 1/frequency distribution (“pink noise”). For each voxel in an in‐brain mask (brainmask.nii from SPM8, resampled at 3 × 3 × 3 mm³ voxels), we generated three sine waves of equal amplitude, with frequency selected from the interval [0.005, 0.1] with probability weighting of 1/frequency. Phase for each of the components was randomly selected. The resulting time series was sampled every 2 s, to produce 240 volumes, similar to the actual BOLD data we describe below.

To simulate the global signal, we added an additional sine wave of equal amplitude to the noise signal to every voxel's time series. This “global” signal had frequency of 0.375/2π (0.06 Hz). To simulate the effects of correlated networks, four spherical regions of interest were selected to represent the TNN (MNI coordinates: Precuneus 0, −52, 40; left parietal −48, −61, 34; right parietal 42, −58, 34; medial prefrontal −3, 56, −5). A 10 mm diameter region of interest around each of these coordinates was identified and to these voxels were added a sine wave of frequency 0.25/2π (0.04 Hz). An additional four regions of interest were selected to represent the TPN, also 10 mm diameter spherical regions. To these 4 regions, a sine wave of frequency 0.5/2π (0.08 Hz) was added. Frequencies were selected to create uncorrelated (orthogonal) signals between the TPN and TNN, and between both networks and the global signal. The amplitude of the TPN and TNN signals were equal to the global signal.

After adding each of the component signals to the simulated BOLD images, the images were spatially smoothed (FWHM 8 × 8 × 8 mm³) and a correlation analysis was performed to a posterior cingulate seed region. Pearson correlation coefficients were obtained between each voxel's time series and the seed region's time series, and an image of correlation values was obtained.

Global regression was then performed on the simulated dataset by obtaining the mean time series from a single whole‐brain ROI. For each voxel, a general linear model was performed to estimate the optimal component of this whole‐brain time series present in the voxel's time series, and this component was subtracted from the voxel's time series [Fox et al., 2009; Murphy et al., 2009]. Correlation analysis was then repeated on the global regression dataset to a posterior cingulate seed region, and an image of correlation values was obtained.

Simulated Whole‐Brain BOLD Time Series Using Actual TPN/TNN Boundaries

An analogous, but more realistic simulation was then performed, using actual boundaries of the TPN and TNN. This simulation was identical to that described above, except that instead of four small ROI's selected to introduce a simulated TPN and TNN, voxels belonging to the TPN and TNN were selected based on actual resting state data. The resting state BOLD acquisition and postprocessing is described below. Briefly, voxels showing significant correlation to a posterior cingulate seed region after global regression (q < 0.05, FDR) were selected for the TNN and voxels showing significant anticorrelation to a posterior cingulate seed with statistical threshold of q < 0.05, false discovery rate (FDR) was selected for the TPN. (Fig. 2)

Figure 2.

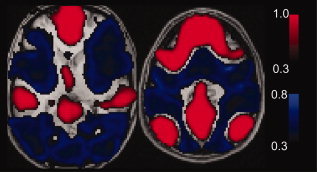
Large networks become anticorrelated after global regression. Simulation is identical to Figure 1 except that actual boundaries of TPN and TNN were used from resting state data obtained from 27 subjects. In this case, the TPN becomes strongly anticorrelated to the TNN. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Otherwise, noise, global, TPN, and TNN were introduced into simulated BOLD data as above. An image of each voxel's correlation to a posterior cingulate seed ROI was obtained before and after global regression procedure on the simulated dataset as above.

Simplified Simulation to Model Effects of Network Size, Noise, and Anticorrelations

A simplified model analogous to the simulations above was performed to allow computationally tractable repetition of the simulation while varying three parameters: Size of the TPN and TNN, amplitude of the noise signal, and actual anticorrelations of the TPN and TNN. (Fig. 3)

Figure 3.

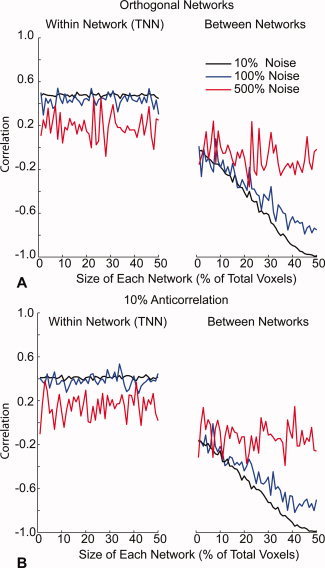
Network anticorrelations after global regression are a linear function of the size of the networks. A: 100 voxel simulation with similar parameters to those above shows little effect of increased network size on correlation within the TNN (left). But TPN and TNN (right) become increasingly anticorrelated following global regression as network size increases. B: Similar results are seen in simulations for which a 10% anticorrelated signal was introduced into the TPN. The initial baseline anticorrelation is greater, but a similar linear trend towards greater anticorrelations with network size is seen. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

For this simulation, instead of using whole brain datasets, only 100 voxels were included. The size of the TPN and TNN was studied by allowing each network to comprise a fixed number of voxels ranging from 2 voxels each to 50 voxels each (the entire dataset). For all simulations, TPN and TNN had the same size. The amplitude of the noise signal was varied logarithmically higher and lower relative to the global signal to study effects of noise on network correlations. Finally, an inverted (anticorrelated) version of the TNN signal was added to the TPN with systematically varied amplitude to represent true anticorrelations of varying magnitude.

Correlation values were obtained between each of the 100 voxels in the dataset and a single voxel belonging to the TNN. Global regression was performed as above by estimating for each voxel's time series the best fit to the mean time series of all 100 voxels using general linear model, and subtracting this component from each voxel's time series. Then, correlation values between each of the 100 voxels and a single voxel belonging to the TNN was repeated.

Subject Characteristics—Actual BOLD Data

Twenty‐seven normal healthy adult participants were examined after informed consent, in accordance with procedures approved by the University of Utah Institutional Review Board. Subjects ranged in age from 17 to 54 (mean 23.7 ± 7.7 s.d., 14 male, 13 female). Healthy subjects had no DSM‐IV Axis I diagnoses based on diagnostic semistructured psychiatric interview. All participants underwent psychiatric screening via the Structured Clinical Interview for DSM‐IV Patient Version (SCID‐P), which is a widely used diagnostic instrument to reliably determine Axis I disorders in clinical populations [First et al., 1996]. All subjects were screened for anxiety by Hamilton Anxiety Rating Scale [Hamilton, 1969] and depression by Hamilton Depression Rating Scale [Hamilton, 1960] immediately prior to MRI scanning. Exclusion criteria for all subjects included: Major sensorimotor handicaps; full scale IQ <70, learning disability, history of claustrophobia, head trauma, loss of consciousness, autism, schizophrenia, anorexia or bulimia nervosa, alcohol or drug dependence/abuse based on DSM‐IV criteria (during 2 months prior to scan, or total past history of ≥12 months), electroconvulsive therapy; active medical or neurological disease; metal fragments or implants; and current pregnancy or lactation. Data from two additional subjects were discarded prior to analysis due to excessive patient motion.

Data Acquisition

Images were acquired on Siemens 3 Tesla Trio scanner with 12‐channel head coil. The scanning protocol consisted of initial 1 mm isotropic MPRAGE acquisition for an anatomic template. BOLD echoplanar images (TR = 2.0 s, TE = 28 ms, GRAPPA parallel acquisition with acceleration factor = 2, 40 slices at 3 mm slice thickness, 64 × 64 matrix) were obtained during the resting state, where subjects were instructed to “Keep your eyes open and remain awake and try to let thoughts pass through your mind without focusing on any particular mental activity.” Prospective motion correction was performed during BOLD imaging with PACE sequence. An 8‐min scan (240 volumes) was obtained for each subject. An additional field map scan was obtained for each subject for the purposes of distortion correction.

For each subject, an additional BOLD fMRI scan was obtained of 4‐min duration (125 volumes) using identical parameters to the resting BOLD data during a bilateral finger movement task. The task consisted of a block design with the word “TASK” or “REST” alternately displayed via LCD projector on a screen within the bore of the scanner every 20 s. During “TASK” blocks, subjects were instructed to alternately touch their thumbs to each of the other four fingers of each hand in succession throughout the task period. During “REST” blocks, subjects were instructed to stop all movement of their fingers.

For all BOLD sequences, simultaneous plethysmograph (pulse oximeter) and chest excursion (respiratory belt) waveforms were recorded for offline analysis. Waveforms were recorded directly on the scanning computer, allowing synchronization of images with physiological waveforms. Stimulus computer was synchronized to the onset of the first BOLD image via fiber optic pulse emitted by the scanner.

fMRI Postprocessing

The following sequence was used for image postprocessing of all BOLD image datasets.

• 1RETROICOR [Glover et al., 2000] was performed using AFNI software package [Cox, 1996] for initial correction of signal components due to respiratory and cardiac artifacts.
• 2Slice timing correction was performed in SPM8 software (Wellcome Trust, London) for Matlab (Mathworks, Natick MA) to correct for timing differences attributable to interleaved MRI acquisition and slice acquisition timing within each TR.
• 3Realign and unwarp procedure (SPM8) was used for distortion correction and concurrent motion correction of all BOLD images using field map sequence to create voxel displacement map. Motion parameters were stored for later use in regression analysis.
• 4Coregistration (SPM8) of BOLD images to MPRAGE anatomic image for each subject
• 5Segmentation (SPM8, thorough clean) of gray matter, white matter, and CSF components for each subject's MPRAGE image.
• 6Normalization (SPM8) by registering MPRAGE scans to the MNI template brain (T1.nii) in SPM8 allowing additional registration of coregistered gray matter, white matter, CSF, and BOLD images to MNI space. Gray matter, white matter, CSF, and BOLD images were sampled at 3 × 3 × 3 mm³ resolution in this step corresponding to acquisition resolution of BOLD images.

Global Regression

After the above postprocessing steps, resting BOLD images for each subject were then subjected to a global signal regression analysis [Fox et al., 2009; Murphy et al., 2009] using in‐house software written in Matlab. For each subject, an in‐brain binary mask was used to extract the mean value of in‐brain voxels (brainmask.nii in SPM8 toolbox) for each image in the time series. This mean time series was then used as a regressor in a general linear model (glmfit.m in Matlab Statistics Toolbox) for the time series at each voxel in the brain, and the best fit was subtracted from the voxel's time series data, producing the global signal corrected time series images. Prior to regression, each voxel's time series was bandpass filtered with a frequency window of 0.005 Hz to 0.1 Hz [Cordes et al., 2001] and linearly detrended to correct for scanner drift. These images were used for subsequent analysis.

Components for PSTCor

An alternate procedure (PSTCor) to global regression was performed using 12 signal components instead of the global signal for general linear model regression analysis. These components were:

• 1White matter time series obtained from the mean time series of voxels within two regions of interest in the bilateral centrum semiovale (MNI coordinates: Left: x = −27, y = −7, z = 30; right: x = 27, y = −7, z = 30, each ROI had 10 mm radius). Before extracting time series, an exclusive mask was performed with the gray matter segmented image from each subject to eliminate voxels containing gray matter.
• 2CSF time series obtained from the lateral ventricles. This was obtained from selecting voxels from the CSF segmented image for each subject within the bounding box defined by MNI coordinates: −35 < x < 35, −60 < y < 30, 0 < z < 30.
• 3Soft tissue time series. The soft tissue restriction mask was created by averaging normalized MPRAGE scans for all 27 subjects and thresholding to obtain a binary image consisting of the face, calvarium, and brain. From this brain and soft tissue binary mask, the in‐brain mask (brainmask.nii in SPM8) was subtracted to obtain a soft tissue only mask. From this mask, the top five slices were zeroed out because these slices showed small variations in coregistration across subjects near the vertex where the calvarium slopes in rapidly on axial slices. The same soft tissue mask was used for all subjects to obtain soft tissue time series.
• 4
  Respiration volume per time convolved with respiration response function (RVT/RRF). Details are obtained from previous reports [Birn et al., 2008b; Chang et al., 2009]. Briefly, maxima and minima were determined from a respiratory belt measurement. These maxima and minima were interpolated to the imaging TR. Respiration period was obtained as the difference between successive maxima, and time series of respiration period was interpolated to the imaging TR. RVT was calculated by subtracting the maxima and minima and dividing by the period for each time point [Birn et al., 2006]. This time series was then convolved with respiration response function [Birn et al., 2008b]:

  

  and the convolved time series was used as a regressor.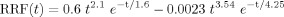
• 5Respiratory belt measurement, integrated over each TR to obtain average position of chest during each imaging volume.
• 6Pulse oximeter, integrated over each TR.
• 7–12Time series of motion parameters from automated realignment procedure (realign and unwarp step from postprocessing, above).

Phase Shifting

For the first six components above, the time series were phase shifted to achieve optimal correlation with the mean gray matter signal. Several of these components, most notably the soft tissue component, exhibited peak correlation with the gray matter signal at a time offset other than zero lag. For the soft tissue component, this may represent differences in timing between perfusion from the external carotid and internal carotid circulations, or changes in the speed at which perfusion occurs in the microvasculature due to alterations in vascular resistance between intracranial and extracranial circulation.

Each of these first six components was shifted by obtaining a cross‐correlogram:

for time series x _i and y _i and time lag m corresponding to the time series of interest and the mean time series of gray matter voxels obtained from segmented gray matter image for each subject. This correlogram reduces to the Pearson correlation coefficient at zero lag. Correlograms were computed for time lags between −16 and +16 s. The 16 s time window was chosen based on a prior report that respiratory fluctuations were maximally correlated with the BOLD signal within a 15 s lag time frame [Birn et al., 2006].

The peak correlation (positive or negative) was identified for each cross‐correlogram. We then phase‐shifted the time series of the soft tissue, CSF, white matter, and physiological waveforms in time by the measured lag to obtain time series for each regressor of optimal synchrony with the gray matter signal. The first eight volumes and last eight volumes of each BOLD run were discarded to ensure that regressor time series overlapped with remaining BOLD images. No phase shifting was performed for motion parameters because these are measured at zero lag from image data.

PSTCor

Once the 12 component time series were computed for each subject, and WM, CSF, soft tissue, and physiological signals were phase‐shifted for optimal correlation, a general linear model was used with these 12 time series as regressors to compute for each voxel's time series the optimal contribution of each of the components. Prior to this analysis, a linear detrend operation was performed on each time series. Best fits for each component were then subtracted from the voxel's time series and resulting PSTCor‐adjusted images were used for subsequent analysis.

Correlation Images

Correlation images were computed for each of four different postprocessed datasets, all of which were processed with RETROICOR, slice timing correction, motion and distortion correction, coregistration, and spatial normalization:

• No regression (RETROICOR only).

• Global regression.

• Global + soft tissue regression (Fig. 4), identical to global regression but including both soft tissue and in‐brain masks in global time series.

• PSTCor.

Figure 4.

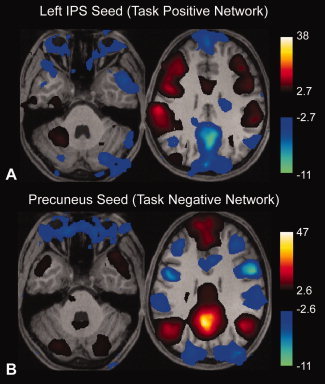
Global regression to combined brain and soft tissue mask induces anticorrelations between the orbits and both task‐positive and task‐negative networks. Results are thresholded at q < 0.05, FDR. A: Correlation to left intraparietal sulcus seed region. B: Correlation to posterior cingulate seed region. Images are shown in radiological format (subject left is on image right). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

For these four sets of images, correlation images were computed to the following seed regions.

• Precuneus/posterior cingulate (MNI: x = −5, y = −52, z = 40) [Fox et al., 2005].

• Left intraparietal sulcus (MNI: x = −50, y = −41, z = 52) [Fox et al., 2005].

• Right primary visual cortex (MNI: x = 9, y = −91, z = −8). These coordinates were obtained from peak activation to visual checkerboard stimuli [Anderson, 2008].

• Left primary auditory cortex (MNI: x = −57, y = −16, z = 1). These coordinates were obtained from peak activation from an auditory language task [Anderson et al., 2010].

• Left primary motor cortex (MNI: x = −48, y = −24, z = 60). These coordinates were obtained from peak activation from bilateral finger movement task obtained as part of this study.

• Prefrontal cortex. Seed mask was obtained from Brodmann areas 8, 9, and 10 obtained from SPM8 Anatomy Toolbox [Eickhoff et al., 2005], masked to include only gray matter regions within these regions using SPM8 gray matter mask (gray.nii).

• Soft tissue mask. The same mask was used as described above for PSTCor. Correlation to this mask was compared with correlation to other seeds for improved anatomic specificity.

Correlation images were calculated by computing Pearson correlation coefficients (zero lag) between mean time series of voxels within the seed region with time series of every voxel in the brain. Except for prefrontal cortex, all other seed time series were obtained from 5 mm radius ROI. Correlation values were converted into Z‐scores by Fisher Transformation by taking the hyperbolic arctangent at each voxel [Fox et al., 2009; Murphy et al., 2009]. Group‐level analysis was performed in SPM8 on the Z‐score images to obtain significance maps of correlation and anticorrelation with the seed regions.

Smoothing was performed on Z‐score maps with full‐width half‐maximum parameter of 8 × 8 × 8 mm³ to reduce pixelated noise in images and improve intersubject registration of functional data prior to group analyses.

Bilateral Finger Movement Task Activation

Activation maps to bilateral finger movement task described above were computed using block design with general linear model in SPM8. Activation maps were obtained for each subject, and contrast images were used for second‐level group analysis with statistical thresholding at q < 0.05, FDR correction for multiple comparisons.

RESULTS

Simulated data was constructed to evaluate under what circumstances network anticorrelations could arise in uncorrelated networks. Data consisted of 240 whole‐brain images, where time series for individual voxels were constructed from a superposition four signals: A noise signal unique to each voxel, a shared global signal common to all voxels, a task‐positive network signal (only in voxels designated as TPN) and a task‐negative network signal (only in voxels designated as TNN). The global, TPN, and TNN components were constructed from sine waves of differing frequencies such as to be mutually orthogonal or uncorrelated. The noise signal, equal in amplitude to the other components, was constructed from three sine waves with frequency selected from a 1/frequency distribution that mirrors frequency content in actual resting state BOLD fluctuations [Anderson, 2008; Cordes et al., 2001].

Anticorrelations Arise in Largest Networks, Not Least Correlated Networks

The regions comprising the TPN and TNN are shown in Figure 1A, before global regression was performed. There is strong global correlation with a posterior cingulate seed region, highest among voxels in the TNN, and lowest among voxels in the TPN. Following global regression, a similar correlation analysis with the posterior cingulate seed region was performed on the simulated data (Fig. 1B). The TNN remains highly correlated, but there is a spatially heterogeneous pattern of correlation and anticorrelation among remaining brain voxels with no relationship to the TPN.

This data shows that simply being uncorrelated or least correlated with the TNN is not sufficient to induce anticorrelations in the TPN. In the presence of even small amounts of noise (tested at 1% of the global signal amplitude), many brain voxels have small components that by chance are slightly anticorrelated with the TNN signal, and it is these voxels that become strongly anticorrelated, rather than the orthogonal TPN signal, following global regression. The TPN regions, by contrast, showed correlation values close to zero with the TNN following global regression.

A very different result was obtained when the size of the networks in the simulation was increased. Instead of using small regions of interest to simulate the TPN and TNN, actual boundaries obtained from resting state data from 27 subjects were used in the simulation. Noise and global signal were identical to the simulation in Figure 1. In this case, shown in Figure 2, the areas that became anticorrelated following global regression matched precisely the boundaries of the TPN and TNN, with anticorrelated regions exclusively within the TPN. Moreover, the heterogeneous pattern of noise observed in the prior simulation was not seen. Rather, the strong anticorrelations induced in the TPN showed only minimal fluctuation from voxel to voxel.

Effect of Network Size on Induced Anticorrelations

To systematically examine the effect of network size on induced anticorrelations from global regression, a simplified simulation consisted only of 100 voxels, with the size of the TPN and TNN varying from 2 voxels each to 50 voxels each. Thus, at their largest size, the two networks occupy the entire volume of the dataset, while at the lower limit of size, occupy only 4% of the volume. Global, noise, and orthogonal TPN and TNN signals were otherwise identical to the prior simulations. Noise amplitude was varied at 10, 100, and 500% of the global signal amplitude.

Results for this simulation are shown in Figure 3A. As the size of the networks increases, there is a linear trend in induced anticorrelations between the TPN and TNN that becomes completely anticorrelated when the networks consume all the voxels in the simulation. Increasing noise decreases these induced anticorrelations, and decreasing noise approaches a straight line where the anticorrelation between the two networks is exclusively determined by the size of the networks. In contrast, network size has almost no effect on correlation within the TNN.

When true anticorrelations exist prior to global regression, a similar pattern is seen (Fig. 3B). In this case, where an inverted TNN signal was added to the TPN of 10% amplitude of the global signal, the anticorrelations of the networks starts below zero, and shows a linear increasing trend with increased network size as before. Higher levels of true anticorrelation shifted the baseline anticorrelation down when the networks were small, but similarly showed a linear trend toward higher anticorrelation as network size increased.

Anticorrelations can be Induced in Soft Tissues by Global Regression

As a further illustration of this process, we included soft tissues in the global regression algorithm by taking the mean of all in‐brain and soft tissue voxels as the global regressor for all 27 subjects and performed a correlation analysis to the TPN using a left intraparietal sulcus seed. Results are shown in Figure 4A. In this case, there is a large cluster of voxels in the orbits including extraocular muscles, globes, and vitreous that exhibit anticorrelations. Within the brain parenchyma, anticorrelated TPN and TNN boundaries are similar to those seen without including the soft tissues in the global signal.

Anticorrelations within the orbits were highly significant across the 27 subjects, with FDR‐corrected q‐value of 0.00027. When a posterior cingulate seed was used, a similar region in the globes was also anticorrelated to the TNN. (FDR, q < 6.8 E‐06, Fig. 4B). Thus global regression induced anticorrelations in the orbits to both the TPN and TNN. No significant anticorrelations with either seed were observed prior to global regression.

Given that no brain voxels are within this anticorrelated cluster in the orbits, it is biologically implausible to interpret these tissues as having a time course that is actually anticorrelated to the neural‐based fluctuations giving rise to both the TPN and TNN time series. A much more likely explanation is that the orbits constitute a self‐correlated group of voxels with time series related to eye movements during the scan. Because this “network” is of sufficient size, it contributes to the global signal used in the regression analysis. When components of the global signal are subtracted from brain voxels in the TPN or TNN during the regression analysis, a component of this signal attributable to the orbits is also subtracted, resulting in anticorrelations between the TPN and TNN with the orbits. We propose that a similar mechanism contributes substantially to the anticorrelations seen between the TPN and TNN after global regression.

PSTCor: An Alternative to Global Regression

If global regression can introduce large, spurious anticorrelations between networks, an alternative technique less susceptible to these artifacts would be desirable. Alternative techniques using signals from white matter, CSF, and physiological waveforms have been proposed as an alternate correction technique [Fox et al., 2009; Murphy et al., 2009]. Yet using these signals as regressors results in poor anatomic specificity of connectivity maps [Fox et al., 2009], with most of the brain still exhibiting substantial positive correlations that limit the ability to define boundaries of functional connectivity networks.

An improvement to this technique can be attained by including additional regressors to the technique, but stopping short of using the mean brain or gray matter signals as regressors. Improved techniques for extracting physiological noise related to cardiac and respiratory fluctuations and aliasing could be included [Chang et al., 2009]. In addition, there is substantial information about global artifacts within voxels in the soft tissues of the face and calvarium that may represent a particularly useful regressor.

We show results from a combination regression technique (PSTCor) that uses regressors from white matter, CSF, soft tissues, physiological waveforms, and motion parameters. The white matter, CSF, and soft tissue masks used to extract time series for regression are shown in Figure 5A. After RETROICOR, substantial correlation between these time series and the global gray matter time series persists. Mean cross‐correlograms for each of the parameters above with the mean gray matter signal are shown in Figure 5B.

Figure 5.

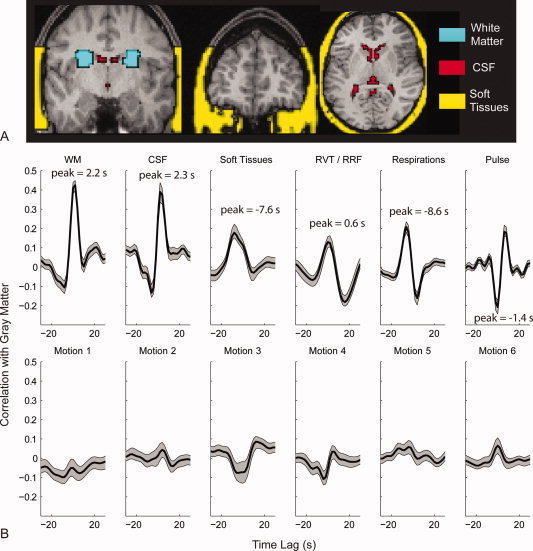
Phase‐shifted Soft Tissue Regression (PSTCor). A: White matter, CSF, and soft tissue masks used as regressors for one subject. B: Average cross‐correlograms of the mean gray matter time series to the time series for white matter (WM), CSF, soft tissues, respiration volume per time convolved with respiratory response function (RVT/RRF), chest expansion (Respirations, integrated over 2 s epochs to correspond to each image volume), pulse oximetry (Pulse, integrated over 2 s epochs), and six motion parameters from realignment procedure. Cross‐correlograms were averaged for 27 subjects, and shaded areas show one standard error of the mean above and below the cross‐correlograms. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In addition to significant correlation with the gray matter signal from each of these regressors (although contribution of motion parameters is very small), there are significant phase shifts relative to the gray matter signal in several components. Respiratory belt and pulse oximeter signals were most commonly negatively correlated with the gray matter signal at lags between 4 and 8 s. Gray matter time series preceded soft tissue time series variably between subjects at lags between 2 and 10 s, with secondary peak at zero lag. Respiration volume per time after convolution with a respiratory response function [Birn et al., 2008a] was positively correlated with BOLD signal at close to zero lag. CSF and WM were generally optimal at zero lag in most subjects.

To facilitate an optimal correction from these components, the phase of each component was allowed to vary to best coincide with mean gray matter signal, except for motion parameters which were obtained at zero lag from measured realignment parameters unlikely to be improved by phase shifting. After regression with these components, correlation images with various seed regions were computed and compared with the same images postprocessed with global regression.

Network Anticorrelations With PSTCor Compared With Global Regression

Correlation to a posterior cingulate seed showed characteristic pattern [Fox et al., 2005] of significant positive correlation in the precuneus, medial prefrontal, middle temporal, temporoparietal junction, and hippocampal regions, with significant negative correlation in the frontal eye fields, intraparietal sulci, mid/anterior cingulate, frontoinsula, lateral occipital, and dorsolateral prefrontal regions (Fig. 6A). When averaged across subjects, most TPN regions showed anticorrelation values to the seed exceeding −0.5.

Figure 6.

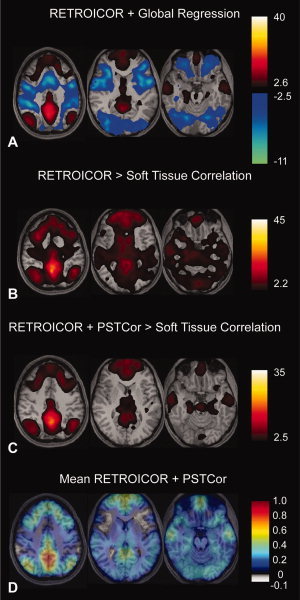
Resting state fMRI data—default mode network. Slice locations are at z = −18, 10, 48, MNI coordinates. A: Correlation to posterior cingulate/precuneus seed following global regression (q < 0.05, FDR). B: Following RETROICOR, images show voxels with significantly greater correlation to posterior cingulate seed than to soft tissue mask. (Paired t‐test, FDR corrected, q < 0.05). C: Following RETROICOR and PSTCor, images show voxels with significantly greater correlation to posterior cingulate seed than to soft tissue mask. (Paired t‐test, FDR corrected, q < 0.05). D: Following RETROICOR and PSTCor, images show mean correlation to posterior cingulate seed. Correlation values were converted using Fisher z‐transform prior to averaging across subjects, then converted back to correlation values after averaging. Subject left is on image right for all images.

No voxels showed significant anticorrelation in data processed with RETROICOR only (Fig. 6B) or PSTCor (Fig. 6C). For additional specificity, the RETROICOR and PSTCor correlation images were compared with correlation to the soft tissue mask. Mean correlation values (converted to Z‐scores prior to averaging and converted back to correlation after averaging) for PSTCor processed data to posterior cingulate seed is shown in Figure 6D. Although no significant anticorrelations were seen in this sample, a slight trend toward anticorrelation was present in a few regions of the TPN, most notably the bilateral frontoinsula. An additional weak trend toward anticorrelation was seen in the atrium of the right lateral ventricle, which may represent small introduced anticorrelations in the CSF, given its presence as a regressor in PSTCor. These anticorrelation values were about −0.05, an order of magnitude less than those seen with global regression.

It is also noted that correlation values in PSTCor processed data in areas outside the TNN seen with global regression did show weakly positive correlation values, generally less than 0.1. This may indicate incomplete removal of the global signal, and may suggest that genuine anticorrelations in the TPN may exist that are underrepresented by this technique. Yet these residual correlation values are very small, substantially smaller than the large global correlation values of around 0.4 seen without PSTCor. Using the correction of comparing correlation values to seed regions to correlation values to the soft tissue mask resulted in exclusion of voxels with these weak residual correlations, as shown in Figure 6C. This was not the case for data processed with RETROICOR only (Fig. 6B), which even after comparison to soft tissue mask correlation still showed poor anatomic specificity of TNN regions.

When correlation images in global regression‐processed data were compared with correlation to the soft tissue mask (not shown), the result was poor identification of the TNN, with many of the classical regions of the TNN no longer significant after multiple comparison correction. In general, correlation T‐scores were higher for both RETROICOR and PSTCor for all regions of the TNN than with global regression.

Thalamocortical Specificity After PSTCor

The superior anatomic specificity in connectivity networks seen after global regression has been argued as a validation of the technique [Fox et al., 2009]. We used a similar approach to Fox et al. to assess thalamocortical specificity of connectivity maps after PSTCor compared with global regression. Seed masks of right primary visual cortex (V1), left primary auditory cortex (A1), and prefrontal cortex are shown in Figure 7, left, analogous to Fox et al. Figure 4. As in Figure 6, the PSTCor results of correlation to anatomic seeds are shown compared with correlation to the soft tissue mask, and global regression results are not because this additional step resulted in no detectable signal in the thalamus for global regression results at significance levels as low as P = 0.05, uncorrected. As in Fox et al., significance levels were allowed to vary to identify areas within the thalamus with highest correlation to the seed.

Figure 7.

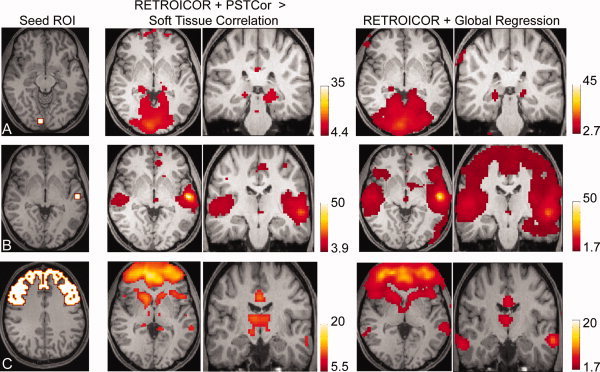
Resting state fMRI data—anatomic specificity of thalamocortical connectivity. Significance levels were varied to show areas within the thalamus of greatest correlation to the seed region. A: Correlation to right primary visual cortical seed (slice location z = −8, MNI). Center images show correlation to V1 seed greater than correlation to soft tissue mask following RETROICOR and PSTCor (Paired t‐test, q < 0.001, FDR). Right images show correlation following global regression (q < 0.05, FDR. Slice locations: z = 1, y = −29, MNI.) B: Correlation to left primary auditory cortical seed (slice location z = 1, MNI). Center images show correlation to seed greater than correlation to soft tissue mask following RETROICOR and PSTCor (Paired t‐test, q < 0.01, FDR). Right images show correlation following global regression (P < 0.05, uncorrected. Slice locations: z = 1, y = −20, MNI.) C: Correlation to prefrontal cortical mask (slice location z = 40). Center images show correlation to seed greater than correlation to soft tissue mask following RETROICOR and PSTCor (Paired t‐test, q < 0.00001, FDR). Right images show correlation following global regression (P < 0.05, uncorrected. Slice locations: z = 1, y = −20, MNI.) All images show subject left on image right. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Correlation with V1 seed showed significant correlation using both techniques in the expected location of the lateral geniculate nuclei, similar in location for both techniques (Fig. 7A). Correlation with A1 seed showed similar localization of peak thalamic activity in the expected location of the medial geniculate nuclei (Fig. 7B). However, for the global regression data, no correlation was seen in the thalamus after multiple comparison correction, with thalamic correlation shown for P < 0.05, uncorrected. Similarly, correlation to a prefrontal cortex mask showed correlation in the anterior thalamus for both techniques (Fig. 7C), but this was not significant in the global regression data after multiple comparison correction.

Correspondence of Correlation Maps to Motor Task Activation

As an additional test of anatomic specificity, correlation maps for global regression and PSTCor data were obtained to a seed in the left primary motor cortex. This seed was chosen as the peak activation in a bilateral finger movement task performed in the same subjects during the same scan sessions in which the resting state data was acquired. The seed used is shown in Figure 8A, and the activation map to the task is shown in Figure 8D.

Figure 8.

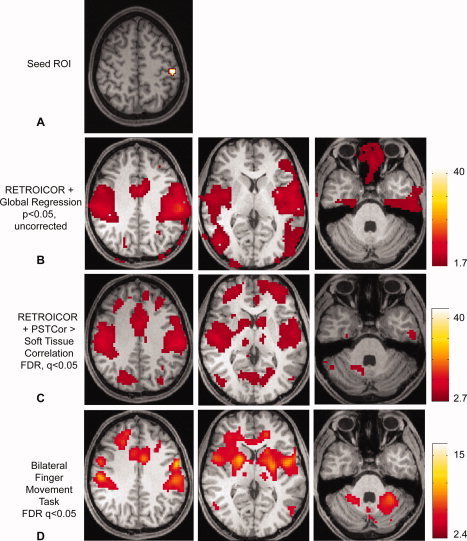
Task‐activated compared with resting fMRI data—Anatomic specificity of connectivity compared with motor task activation. A: Seed region in left primary motor cortex (MNI coordinates: −48, −24, 60) obtained from peak activation in bilateral finger movement task. B: Correlation to seed region following global regression (P < 0.05, uncorrected. Slice locations at z = 41, z = 10, z = −35, MNI.) No significant correlation was seen in the basal ganglia, thalami, or cerebellum. C: Correlation to seed region greater than to soft tissue mask following RETROICOR and PSTCor (q < 0.05, FDR.) D: Activation to a bilateral finger movement task in the same 27 subjects produced by general linear model (q < 0.05, FDR). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Significant activation was seen in bilateral primary sensorimotor cortex, supplementary motor area, bilateral basal ganglia, ventral posterior nucleus of the thalamus, posterior middle temporal cortex, dorsolateral prefrontal cortex, and bilateral superior lateral cerebellum regions.

Both global regression Figure 8B and PSTCor Figure 8C correlation maps showed correlation with bilateral sensorimotor, supplementary motor area, posterior middle temporal, and dorsolateral prefrontal cortex. Only PSTCor showed additional areas of significant (FDR, q < 0.05) correlation in the basal ganglia, thalamus, and superior cerebellum, in anatomic locations closely matching those seen with motor task activation. Although only right‐sided cerebellar correlation was observed in PSTCor data, this might be expected to have stronger connectivity to left motor cortex given contralateral activation. Bilateral activation was seen in the motor task because the task involved similar activation of both hands. Global regression data did not show basal ganglia, thalamic, or cerebellar correlation even when significance threshold was relaxed to P = 0.05, uncorrected (shown in Fig. 8B).

DISCUSSION

We demonstrate with simulated data that two networks with uncorrelated (orthogonal) signals will become anticorrelated following global regression as a linear function of the size of the networks relative to brain volume. Yet global regression has no significant effect on positive correlation values within a network defined by a seed time series. This effect is more pronounced at lower noise levels, but is seen even at noise levels of an order of magnitude greater than the signals of interest.

Heuristically, this can be understood in terms of signal components. When a global signal common to all voxels is present, this signal is “contaminated” by TPN and TNN signals as a function of the size of the network [Murphy et al., 2009]. When global regression is performed, voxels in the TPN will have a nontrivial component of the global signal, so some of the contaminated global signal will be subtracted from the voxel's time series. As a result, an inverted copy of the TNN “contamination” will be subtracted from the voxel's time series, inducing anticorrelations. This effect becomes very strong when the size of the networks are nontrivial compared with total brain volume, as is the case for observed TPN and TNN from resting state data.

This observation accounts for one of the primary objections to an artifactual explanation for network anticorrelations [Fox et al., 2009]. Because the TPN has a shared signal component in the time series across the network which is preserved from subject to subject, and comprises a relatively large brain volume, induced anticorrelations are expected in precisely this region. Moreover, these anticorrelations would be in the same regions across subjects, accounting for consistent location of anticorrelations in random effects analyses. Thus, it may be expected to have strong, consistent observed anticorrelations in the TPN even if the TPN and TNN time courses were completely uncorrelated, simply based on the size of the network and the consistent boundaries of the TPN.

In data acquired from healthy subjects, we also show that spurious anticorrelations can arise in precisely this manner by showing consistent anticorrelations across subjects in the orbits to both the TPN and TNN. This is likely mediated by a shared signal component in the orbits, presumably related to eye movements, that allows induced anticorrelations in this region. This result also demonstrates how a shared signal comprising a region even as small as 5% of the total brain volume is sufficient to induce significant anticorrelations, and may explain why anticorrelations were persistently observed even after exclusion of much of the TPN and TNN by restriction mask when calculating the global signal [Fox et al., 2009].

As an alternative to global regression, we propose an enhanced regression procedure (PSTCor) that includes motion parameters, white matter, CSF, soft tissues, respiration volume per time, respiratory belt, and pulse oximeter signals. Although techniques such as RETROICOR already incorporate physiological waveform correction, the addition of optimally phase‐shifted physiological waveforms as well as soft tissue, CSF, white matter and motion signals allows for improved correction of the global signal. This technique showed only a weak trend toward anticorrelations in the TPN and TNN, with nonsignificant anticorrelation values an order of magnitude smaller than those seen with global regression.

It is possible that our combined regression procedure is simply inadequate in removing global contaminants, and that anticorrelations are stronger than we observe. In fact, some level of under‐representation of anticorrelations may be suggested by small residual positive correlation values of about 0.1 between posterior cingulate seed and white matter or areas of the cortex not generally associated with the TNN.

Yet it seems unlikely that this weak residual correlation is masking the much larger anticorrelations seen with global regression, particularly with a clear alternate explanation shown in simulated data that anticorrelations are produced by global regression for networks of this size. Nevertheless, it is well known that the TPN and TNN have an anticorrelated relationship during execution of complex tasks [Raichle et al., 2001]. A neural architecture where the TNN and TPN show some moment to moment anticorrelation within the resting state is possible even given our results. Future studies, including those involving brain electrical or magnetic activity, may help quantify the extent to which some anticorrelations may be present in brain networks in the resting state.

If the large anticorrelations seen with global regression, however, are substantially artifactual, this makes problematic studies using this technique for assessment of functional network connectivity, quantitative comparison of network anticorrelations between healthy and disease states, or inferences about neural architecture based on the magnitude of these anticorrelations.

The alternative procedure, PSTCor, we demonstrate using soft tissues, white matter, CSF, and physiological parameters as regressors additionally shows improved anatomic specificity to global regression compared with activation results from a motor task and comparable or better thalamocortical specificity of correlation networks. Using this technique with the additional step of comparing seed‐based correlation results to analogous correlation to soft tissues, allows highly specific definition of functional network boundaries without the introduction of salient artifacts in relationships between brain networks.

Murphy et al., note that another common technique for evaluating resting state networks, independent component analysis, may inherently involve something analogous to global regression in that the global signal is typically identified with one component [Murphy et al., 2009]. It is unclear the effect that size of correlated networks may have on functional network connectivity measurements obtained with independent component analysis.

CONCLUSION

Network anticorrelations after global signal removal can be introduced even in completely uncorrelated networks if the networks are of sufficient size, detectable above 5% of brain volume. Such anticorrelations do not necessarily arise in the least correlated regions to a given network, but rather as a linear function of the size of the networks. Because spurious anticorrelations can be introduced following global regression, interpretation of quantitative network anticorrelations as a measurement of neural architecture, or assessment of anticorrelation strength between diseased and healthy populations may be problematic. An alternate correction technique, PSTCor, is described that shows improved anatomic specificity to global regression but does not exhibit large network anticorrelations.