Spatio-temporal control of the heart rate in the rabbit heart

Abstract

Sinoatrial node is responsible for the origin of the wave of excitation, which spreads throughout the heart and orchestrates cardiac contraction via calcium-mediated excitation-contraction coupling. P-wave represents the spread of excitation in the atria. It is well known that the autonomic nervous system controls the heart rate by dynamically altering both cellular ionic fluxes and the anatomic location of the leading pacemaker. In this study we used isolated rabbit right atria and mathematical model of the pacemaker region of the rabbit heart. Application of isoproterenol resulted in doze-dependent acceleration of the heart rate and superior shift of the leading pacemaker. In the mathematical model such behavior could be reproduced by a gradient of expression in β1-adrenergic receptors along the superior-inferior axis. Application of acetylcholine resulted in preferentially inferior shift of pacemaker and slowing of the heart rate. The mathematical model reproduced this behavior with imposing a gradient of expression of acetylcholine-sensitive potassium channel. We conclude that anatomical shift of the leading pacemaker in the rabbit heart could be achieved through gradient of expression of β1-adrenergic receptors and I_K,ACh.

Introduction

Sinoatrial node is the primary pacemaker of the mammalian heart.¹ It leads the heart in every normal heartbeat by generating an action potential, which first excites nearby atrial myocardium, then spreads over the atria, atrio-ventricular node, the specialized conduction system, and finally excites ventricular myocardium.^{2, 3} Pattern of atrial excitation determines morphology of the P-wave of the electrogram.⁴ Early studies by Meak and Eyster⁵ employing string galvanometer presented evidence of dynamic anatomical displacement of the pacemaker during vagal stimulation. A century of reductionist and integrative research of the sinoatrial node has enjoyed several technological advances, which provided deepening understanding of the pattern of excitation and its molecular and cellular foundation. Pioneering point-by-point extracellular electrode mapping conducted by Lewis et al.^{1, 3} provided the first map of excitation in the atria and established the sinoatrial node as the leading pacemaker. Simultaneous recordings by multielectrode arrays provided the first evidence of dynamic changes in the pacemaker site on a beat-to-beat basis.^{6, 7} However, extracellular electrodes which capture earliest activation site as “primary negativity” may fail to capture the leading pacemaker site due to the slow upstrokes of sinoatrial action potentials, which could be reliably detected by intracellular microelectrodes.⁸ Bleeker et al.⁹ conducted point-by-point microelectrode mapping, which allowed characterization of not only timing of excitation, but also action potential characteristics such as action potential upstroke velocity and duration, diastolic dollarization, etc. This work led to recognition of profound electrophysiological complexity of the right atrial myocardium within the anatomical pacemaker region. Numerous groups have engaged over the last 30 years in the studies of molecular and cellular foundation of pacemaker activity (reviewed in Boyett et al.¹⁰). These studies focused on gene and protein expression, ion channel biophysics and interaction among numerous intracellular counterparts, which constitute the profoundly complex cellular pacemaker. Current understanding of the cellular pacemaker mechanisms center at the closely coupled two oscillators, termed “voltage clock” and “calcium clock”,¹¹ which accurately explains autonomic control of the pacemaking at the cellular level. Numerous mathematical models have captured growing complexity of ionic mechanisms of sinoatrial nodal cell activity.¹² Furthermore, many mathematical models have captured anatomically heterogeneous ionic properties of the atrial myocardium and attempted to predict tissue and organ level conduction of action potentials from the sinoatrial node.^13–15

However, a reductionist ion-channel-centric or cell–centric approach cannot fully capture the profound complexity of atrial pacemaker complex, which consist of tissues far beyond the anatomically defined sinoatrial node. Single cell framework cannot explain the dramatic beat-to-beat variability on the leading pacemaker site during autonomic modulation of the heart rate.^16–18 Mapping techniques have been used to address the tissue level mechanisms of pacemaker activity, but they have their limitations. Bleeker described that it takes 3–5 hours of experiment to acquire 150–300 recordings from individual cells, which are needed to reconstruct a normal excitation map.⁹ However, during this time of perfusion with crystalloid solution, the sinoatrial node will slow down at a rate of 10 beat-per-minute/hour, and could change the location of the primary pacemaker.⁹ This method is obviously not applicable to study dynamic changes of the pacemaker complex. Extracellular electrodes provide a better spatial-temporal resolution and could help resolving dynamic changes in the pacemaker complex during autonomic stimulation. However, the interpretation of extracellular signals from the pacemaker complex are not always defendable with respect to activation time, defined by “primary negativity”.⁸

Optical mapping has been able to resolve limitations of both electrode mapping techniques: microelectrode and macroelectrode. Like microelectrode techniques, optical action potential captures the morphology of cellular action potentials.^{19, 20}. This resolves issue of interpretation of extracellular recordings. Moreover, a modern optical imaging system allow simultaneous recordings of 10,000 action potentials in contrast to a single microelectrode recording.²¹ However, optical signals carry signature of electrical activity from hundreds or thousands of cells, depending of magnification. Thus, a careful interpretation of signals is also required as with extracellular electrodes. We have previously presented high-resolution optical mapping studies of pacemaker activity in the mouse,²² rabbit,^{18, 20} canine,²³ and human¹⁷ sinoatrial node.

The goal of this study was to define a minimum spatial variation of ionic channels and pumps that would explain experimentally observed anatomic variation in the primary pacemaker region. The combined experimental and computational study was designed to provide a comparison between anatomically distributed mathematical model of the rabbit sinus node and optical mapping of the sinus node in vitro.

Methods

Rabbit right atrium preparations

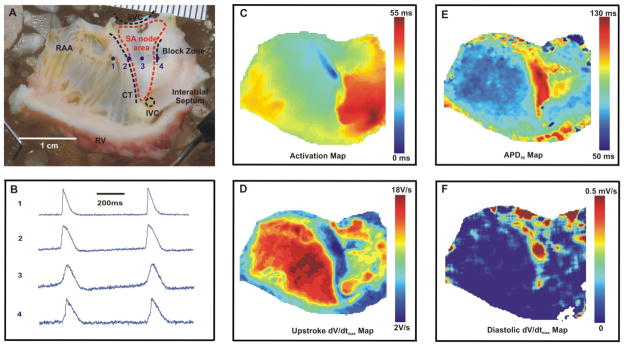
All procedures complied with the standards for the care and use of animal subjects as stated in the Guide of the Care and Use of Laboratory Animals. The animal protocol was approved by the Washington University Animal Care and Use Committee. The isolated rabbit right atrial preparation has been previously described.^{18, 20} Briefly, New Zealand White rabbits (n=5) of either sex weighting 2 to 3 kg were anesthetized by an intravenous injection of sodium pentobarbital (50 mg/kg) with 2000 U heparin. After a midsternal incision was made, the heart was removed and placed onto a Langendorff apparatus, followed by retrogradely perfusion with oxygenated (95% O₂ – 5% CO₂) Tyrode solution of constant-temperature (37°C). After the fat and lung were removed, the heart was stained by voltage-sensitive dye di-4-ANEPPS and removed from the Langendorff apparatus. The right atrium preparation was dissected in the temperature-controlled perfusion chamber. The ventricle was dissected. The right atrium was cut through from tricuspid valve to superior vena cava (SVC) via the right atrial appendix, and then it was flattened, slightly stretched and pined as shown in Figure 1A. The preparation was superfused with Tyrode solution. The pH was monitored and kept at 7.35 ± .05. The sinoatrial node (SAN) region located between the opened SVC and inferior vena cava (IVC) near the crista terminalis (CT),⁹ labeled with red dashed line (Figure 1A).

Figure 1.

Preparation and optical mapping of the isolated right atrium of the rabbit heart. (A) The preparation of the right atrium, and the SAN region in the intercaval area is labeled by the red dashed line. (B) The raw optical action potentials recorded from 4 representative locations labeled in (A), (data was binned 3×3). (C) The activation map under control conditions (based on dV/dt_max). (D) Upstroke dV/dt_max amplitude map, (E) APD50 Map and (F) Diastolic depolarization (dV/dt) map.

Optical mapping

Excitation-contraction uncoupler Blebbistatin (10 μM) was used to suppress motion artifacts in optical signals.²⁴ Until the suppression was completed, the preparation was additionally stained by direct application of a voltage-sensitive dye di-ANEPPS (1 uM) on the tissue. Optical mapping apparatus consisted of a MiCAMUltima-L CMOS camera that have high spatial (100×100 pixels, 350±20 μm per pixel) and temporal (1,000–3,000 frames/sec) resolution. A long-pass emission filter (>650 nm, Thorlabs, Newton, NJ) was positioned in front of the camera. The excitation light was generated by a halogen lamp and was passed through a heat filter, shutter, and excitation band-pass filter (520±45). A flexible light guide directed the band-pass filtered light onto the preparation, and a shutter was used to ensure that the preparation is exposed to light only during image acquisition to avoid photobleaching of the dyes. The acquired fluorescent signal was digitized, amplified, and visualized using custom software (SciMedia, CA).

Experimental protocol

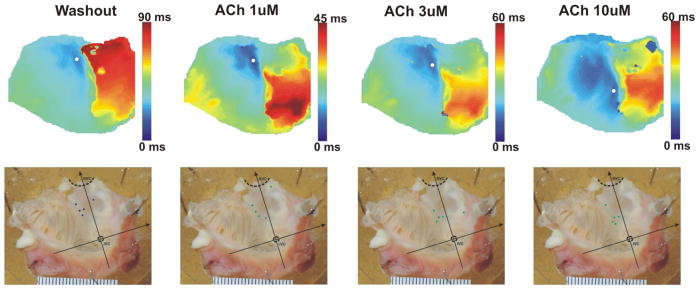
After isolation, dissection, motion suppression and staining, preparations were equilibrated for 5 to 10 min before being imaged. Then we recorded control maps of atrial activation during spontaneous sinus rhythm using detection of activation time in each point as previously described.^{18, 20} To quantify the regulation of heart rate and pacemaker anatomic shift during autonomic stimulations, the location of the leading pacemaker site was plotted with orthogonal axes defined based on anatomical landmarks: Y-axis passing from SVC to IVC, and the other orthogonal to it (Figure 3). After control measurements, progressively increasing concentrations (10, 30 and 100 nM) of isoproterenol (ISO) were tested. ISO was delivered by superfusion and was applied for 10 min at each concentration to reach steady state. The location of the leading pacemakers were also determined and plotted as described for control condition. After ISO measurements, preparations were washed out for 1 h before mapping the control washout location, and then application of progressively increasing concentrations (1, 3 and 10 μM) of acetylcholine (ACh) (Figure 4). After washout, additional staining and application of blebbistatin were performed as needed.

Figure 3.

The leading pacemaker shift induced by ISO. The upper panels show typical activation maps under different conditions. The lower panels show anatomic location of the leading pacemakers under control and ISO conditions in all studied hearts (n=5).

Figure 4.

The leading pacemaker shift due to ACh. The upper panels show typical activation maps under different conditions. The lower panels show anatomic location of the leading pacemakers under control and ACh conditions in all studied hearts (n=5).

Data processing and statistical analysis

A customized Matlab-based program was used to analyze the optical signals.¹⁸ Signals were filtered using low-pas Butterworth algorithm at 256 Hz. The maximum upstroke derivative (dV/dt_max), diastolic dV/dt_max and action potential duration (APD) were calculated for each action potential using normalized optical signals. Activation maps were constructed from activation times.

Values of the data are expressed as means ± SE. Hypothesis testing was carried out using an unpaired Student t-test. Values of P<0.05 were considered statistically significant.

Mathematical Modeling

Biologically relevant models of cardiac sinoatrial node cells were applied to simulate the effect of the leading pacemaker shift in-silico. As a model of the SAN pacemaking cell we used the model of Maltsev and Lakatta.^{12, 25} This model consists of 30 variables and takes into account 13 cell membrane currents. The detailed dynamics of calcium cycling is also introduced in the model.

To introduce anatomic heterogeneity in the model, we used three major parameters in the single cell model, which varied spatially. We used one of the main control parameters of the model, the maximum conductance of the sodium-potassium exchanger ${\text{i}}_{\text{Nak}}^{max}$, to vary pacemaker properties. Different values of this parameter correspond to different values of the cell oscillation frequency, namely, the less the value is the higher the frequency.

The influence of the ACh in the model is described by the additional current:

$$\begin{array}{c}{\text{i}}_{\text{kACh}}=\text{a}·{\text{g}}_{\text{kACh}}·(\text{V}-{\text{E}}_{\text{K}})\\ \stackrel{.}{\text{a}}=({\text{a}}_{\infty }-\text{a})/{\tau }_{\text{a}}\end{array}$$

where a is the current gate variable, g_kACh is the current maximum conductance, V is the cell membrane voltage and E_K is the potassium Nernst potential. Parameter g_kACh here describes the sensitivity of a cell to ACh. If the value of this parameter is large then the cell is more sensitive to the ACh. The influence of the ISO on a cell was introduced in the original paper¹² as several scaling factors for the model parameters. Particularly, the stimulation by β-AR receptors was simulated by the following changes in parameters: 1) P_up (sarcoplasmic reticulum calcium pumping rate) from 12 mM/s to 24, 2) g_CaL (L-type calcium current maximum conductance) from 0.58 nS/pF to 1.015, 3) V_if,1/2 (funny current half saturation parameter) from −64 mV to −56.2 and 4) g_Kr (rapid rectifier potassium current maximum conductance) from 0.08113 nS/pF to 0.1217. In order to simulate the SAN cells with different sensitivity to ISO we introduced the following scaling to the model parameters based on the data from:²⁵

$$\begin{array}{l}{\text{P}}_{\text{up}}={\text{P}}_{\text{up}}^{\text{basal}}·(1+{\beta }_1·[\text{ISO}]),\\ g_{\mathit{CaL}}=g_{\mathit{CaL}}^{\mathit{basal}}·(1+{\beta }_2·[\mathit{ISO}]),\\ V_{if,1/2}=V_{if,1/2}^{\mathit{basal}}·(1+{\beta }_3·[\mathit{ISO}]),\\ g_{Kr}=g_{Kr}^{\mathit{basal}}·(1+{\beta }_4·[\mathit{ISO}]).\end{array}$$

We used the β₁ parameter to simulate various sensitivities of the SAN cells to ISO. The addition of ISO to the system in this case is performed by triggering the parameter [ISO] from 0 to 1.

As a model of the normal atrial cell we choose the Lindblad et al.²⁶ model because it is the most recent one among the models of a rabbit atrial cell. It has 28 variables and describes 13 ionic currents. The whole set of the parameters for the model that we used in simulations was the same as in the original paper. The equations were solved using forward Euler scheme with 0.01 ms time step.

Results

Optical mapping of SAN

In rabbit, SA node area from the intercaval region rises up the endocardial face of the crista terminalis and terminates at the right branch of the sinoatrial ring bundle (Figure 1A), as described by Bleeker et al.⁹ We located the SAN as the leading pacemaker in the anatomically defined SAN area using optical mapping technique. We mapped several electrophysiological characteristics of pacemaker and atrial cells and correlated them to locate the leading pacemaker. Figure 1 illustrates optical mapping signals from four points along the line crossing the SAN area from RAA to block zone. Point 1 represents a typical atrial action potential characterized by sharp upstroke and flat diastolic base line, presence of resting potential. Points 2 and 3 clearly show diastolic depolarization slope, as approaching to SAN leading pacemaker, the slope was steeper (compare point 2 and point 3). Point 4 represents the action potential morphology typical for the block zone.⁹ Two components were observed in the signals, in the inferior part of SAN, depolarization only had small amplitudes followed by a larger upstroke, which is the result of the collision of two wavefronts. The first small and slow component corresponds to electrotonic depolarization of a wavefront which attempted to propagate across the block zone from the SAN towards the septum and failed, because this block zone lacks excitable myocytes.¹⁸ The second fast component of the signal corresponds to atrial cells excitation that travelled around the region of the block zone and is invading the block zone from the inferior and/or superior directions.^{9, 20}

Figure 1C shows a representative activation map reconstructed based on dV/dt_max, and the leading pacemaker was located at the dark blue area which corresponds to the earliest activation time. Action potential duration at 50% repolarization (APD50) was mapped as shown in Figure 1E. Significantly longer APD50 was detected at the SAN region (the red area). The leading pacemaker had the longest APD50 value. The working atrial myocardium had relatively short APD50. The leading pacemaker region is characterized by the slowest rate of phase 0 depolarization.²⁷ The lower rate of depolarization indicated the slower conduction velocity in this area due to its dependence on L-type calcium channels in contrast to sodium channels elsewhere. We detected the upstroke velocity dV/dt_max and confirmed smallest value in the leading pacemaker area (Figure 1D). Another important characteristic of the leading pacemaker is the highest rate of diastolic depolarization due to I_F current. Figure 1F showed the map of diastolic dV/dt_max values, and the highest rate of diastolic depolarization was found in the leading pacemaker area while elsewhere in the right atrium, the values are near 0. Thus, all these electrophysiological characteristics (earliest activation, slowest upstroke velocity, fastest diastolic depolarization, and longest APD) allow independently locate the leading pacemaker and investigate its shift under autonomic stimulations.

Autonomic regulation of the heart rate

Optical mapping of control condition, progressively increasing concentrations of ISO and ACh were performed as described in the methods section. Heart rates under different conditions were calculated and statistically analyzed (Figure 2). Heart rate was does-dependently increased by ISO from 120.75 ± 6.93 beat/min to 184.12 ± 9.31 beat/min, 239.97 ±10.28 beat/min and 251.45 ± 7.97 beat/min for 10, 30 and 100 nM respectively. And after washing out, the heart rate came back to 135.84 ±6.26 beat/min and dose-dependently decreased by 1, 3 and 10 μM ACh to 118.15 ± 7.64 beat/min, 99.56 ±3.14 beat/min and 84.94 ±2.61 beat/min respectively. Heart rate at 1 μM ACh was not significantly decreased compared to washout condition. These measurements are in agreement with previous studies and thus confirm that optical mapping and blebbistatin do not alter SAN physiology.

Figure 2.

Heart rates under different conditions. Heart rate increased by ISO (10, 30 and 100 nM) and decreased under ACH 3 and 10 μM. Heart rate did not change at 1 μM ACh.

Anatomic shift of the leading pacemaker induced by sympathetic and parasympathetic stimulation

The leading pacemakers under different conditions were located as described above and plotted in the orthogonal system of coordinate figures as shown in Figures 3–4, as discussed in “Optical mapping of SAN” section. Leading pacemaker shift was observed in all conditions of autonomic stimulation. Figure 3 shows an example of activation maps recorded under control and ISO conditions in one preparation (upper panels) and location of the leading pacemakers in all 5 studied preparations. Under control condition, leading pacemaker was located in the central part of the anatomically defined SAN region labeled by blue dots. Administration of 10 nM ISO resulted in a shift of the leading pacemaker in the superior direction towards SVC in 3 preparations and in the inferior direction towards AV groove in 2 preparations. Downward shift of the leading pacemaker induced by sympathetic stimulation was relatively rare observation, but it was observed at the lowest concentration of ISO, 10 nM. When high concentrations of ISO (30 and 100 nM) were administered, the leading pacemakers invariably shifted upwards toward SVC as shown in Figure 3.

Washout of ISO resulted in the return of the leading pacemakers back to central region (Figure 4) and the control heart rates restored (Figure 2). Administration of 1 μM ACh slowed the heart rate and shifted the leading pacemaker downwards in 4 hearts, while upwards in 1 heart. Higher concentrations of ACh (3 and 10 μM) resulted in downward shift of the leading pacemakers in all the preparations (Figure 4).

2D mathematical modeling

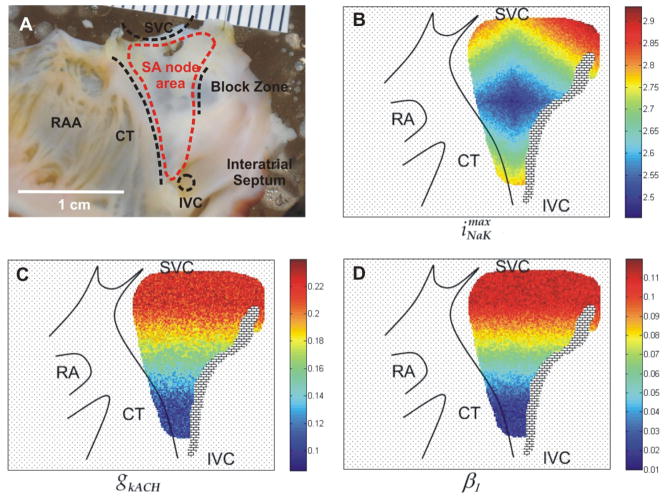
Numerous molecular and structural heterogeneities contribute to functional heterogeneity of the pacemaker properties and responsiveness to autonomic stimulation. Among the main factors are electrical heterogeneities of expression of proteins responsible for G-protein coupled receptor signaling, various exchangers, calcium handling, I_f, I_Ca,L, I_Ca,T, I_Na, I_K,r, and I_K,s. We hypothesized that observed behavior could be recapitulated by heterogeneous expression of only three parameters $i_{\mathit{NaK}[i,j]}^{\mathit{max}}$, g_kACH[i,j] and β_1[i,j]. We constructed a mathematical model with anatomically heterogeneoius distribution of these paratemrents, which could control the observed leading pacemaker shift under autonomic stimulations.

In this section the results of simulations of the two-dimensional model are presented. We modeled the SAN region including the atrial tissue and SAN using the real topology presented by Bleeker et al.⁹ The anatomical landmarks and distribution of $i_{\mathit{NaK}[i,j]}^{\mathit{max}}$, g_kACH[i,j] and β_1[i,j] is shown in Figure 5. The parameter ${\text{i}}_{\text{NaK}[\text{i},\text{j}]}^{max}$ was distributed over the SAN cells in such a way that in control state the leading pacemaker of the SAN was located in the middle of the region, Figure 5B. We also introduced two gradients of the parameters g_kACH[i,j] and β_1[i,j]. They are shown in Figure 5C and Figure 5D, respectively. Both gradients were linear. For g_kACH[i,j] the gradient covered the range of the parameter from 0.2 to 0.085 with the random error Δ = 0.04 in the direction from SVC to IVC (Figure 5C). As for the β_1[i,j] parameter, the maximum and minimum values of the gradient were 0.1 and 0.01 respectively with random Δ = 0.02 in the same direction.

Figure 5.

Mathematic model based on heterogeneity distributions of three parameters $i_{\mathit{NaK}[i,j]}^{\mathit{max}}$, g_kACH[i,j] and β_1[i,j].

The system was discretized on a regular grid of 200×200 points. The calculations were performed for 15000 ms of the model time. The first 5000 ms there was the control system with no additional drugs. After that ISO was added into the system for the following 5000 ms. Then ISO was switched off and ACh was added again for 5000 ms. For all three cases (“control”,”ISO”,”ACh”) the distributions of the action potential generation time delay were obtained. They illustrated the relative time delay of firing between the cells in the system. The results are shown in Figure 6.

Figure 6.

Simulations and experimental data of the leading pacemaker shift.

One can see from Figure 6 that in control the simulated leading pacemaker was located in the middle of the SAN (pink dot), as in experimental conditions. When ISO was administered the leading pacemaker moved in towards SVC against the gradient of β_1[i,j] parameter. And when ACh was added to the system the leading pacemaker shifted in the opposite direction along the gradient of g_kACH[i,j]. In case of ISO, the area of the SAN where the sensitivity to ISO was larger (the area in the direction of SVC) had the greater increase in the individual frequencies of the cells. Thus, the synchronous regime in the ensemble was dominated by this area and the leading pacemaker moved up. In case of ACh the situation was opposite. The area of the SAN with smaller sensitivity to ACh was less affected by it and, consequently, had the higher frequency, resulting in the shift of the leading pacemaker towards the IVC.

As seen in Figure 6, mathematical modeling reproduced general behavior of the real rabbit heart with respect to anatomic shift of pacemaker in response to sympathetic and parasympathetic stimulation.

Dynamics of the leading pacemaker coordinates

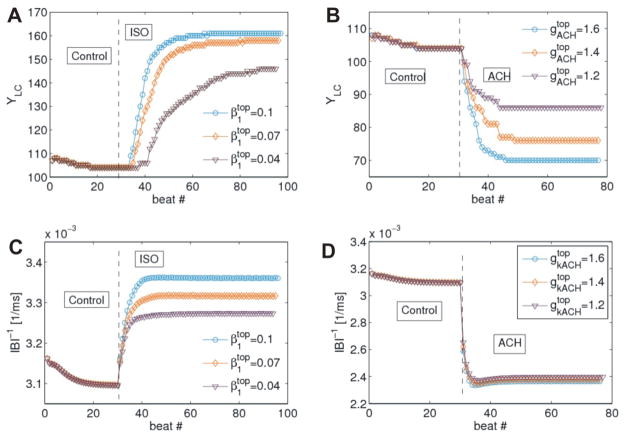
In order to study the dynamics of the leading pacemaker we obtained the dependencies of the leading pacemaker coordinates on the beat number. It was done for several realizations of the parameters gradients. We denote the maximum value of β₁ and g_kACH gradients as ${\beta }_1^{\text{top}}$ and ${\text{g}}_{\text{kACH}}^{\text{top}}$ respectively. Figure 7A shows the anatomic dynamics of the leading pacemaker shift in case of ISO. The system was simulated for 30000 ms where first 10000 ms there was the control state. At each beat cycle in the system the leading pacemaker was located and its coordinates were defined. The three curves in Figure 7A correspond to the dependencies of the y coordinate of the leading pacemaker on the beat number for three different gradients of ${\beta }_1^{\text{top}}=0.1;0.07;0.04$ (circle, diamond and triangle markers respectively). The y-axis is assumed to be along the direction from IVC to SVC.

Figure 7.

Dynamics of the leading pacemaker coordinates and the inverse of the interbeat interval (IBI-1).

One can see from Figure 7A that the larger the gradient of β₁ is, the farther shifts the leading pacemaker. Moreover, for higher gradients it takes less number of beats to reach the final leading pacemaker position. Similar observations were obtained for ACh (Figure 7B).

We also calculated the dependencies of the inverse of the interbeat interval IBI-1 (which is an analogue of the immediate frequency) on the beat number for both cases of ISO and ACh (Figure 7C–D). It is seen that the higher values of gradients result in higher and lower frequencies for ISO and ACh respectively. Note, that final synchronization frequency for ACh establishes in fewer beats that for ISO.

Discussion

The two branches of autonomic nervous system tightly control the mammalian heart rate. It is well known that the anatomic location of the leading pacemaker shift in response to sympathetic and parasympathetic stimulation in the superior and inferior directions, respectively.^{10, 18} A number of sophisticated mathematical models have been developed to explain the sinus node pacemaker activity at the cellular level.¹¹ However, anatomically distributed models the pacemaker complex lack the necessary details due to insufficient experimental information about gene expression in the pacemaker complex and the surroundingatrial myocardium. Here we present a mathematical model, which consists of most up-to-date rabbit sinoatrial cell model¹² and atrial cell model.²⁸ The model was constructed to include anatomic heterogeneity of three parameters, $i_{\mathit{NaK}[i,j]}^{\mathit{max}}$, g_kACH[i,j] and β_1[i,j], which were shown to be able to control the anatomic location of the leading pacemaker during sympathetic and parasympathetic stimulation.

Thus, in this study we present two new observations:

1. Sympathetic and parasympathetic stimulation control the heart rate in widely distributed pacemaker complex, which includes tissues well beyond the anatomically defined sinoatrial node.

2. Three parameters distributed in a gradient along the SVC-IVC direction can control experimentally observed behavior of the leading pacemaker in the rabbit heart.

Future studies will be carried out to map gene expression at high spatial resolution to assess the possible contribution of various ion channels, pump, and receptors in spatial and temporal control of the pacemaker complex. Meanwhile, our data showed that distribution of the major action potential characteristics (APD, upstroke dV/dt_max, diastolic depolarization dV/dt, activation maps, etc) can be used to estimate relative expression of channels and pumps responsible for the observed differences in the phenotype of cells at different anatomic location. Unfortunately, high resolution cellular mapping of ion channel, calcium handling and pumps biophysics in the right atrium does not appear to be feasible due to profound heterogeneity of the phenotype of different cell types with the atrium. Recent regression analyses of various mathematical models pointed in the direction of possible feedback between the experimentally acquired data from the tissue preparations and mathematical models.²⁹ One has to estimate what parameters need to be measured at the tissue level and with what resolution in order to provide reasonable estimates of cellular biophysics in major cell types composing the distributed pacemaker complex and surrounding tissues of the right atrium.