Computational Modeling of Phagocyte Transmigration during Biomaterial-Mediated Foreign Body Responses

Abstract

One of the major obstacles in computational modeling of a biological system is to determine a large number of parameters in the mathematical equations representing biological properties of the system. To tackle this problem, we have developed a global optimization method, called Discrete Selection Levenberg-Marquardt (DSLM), for parameter estimation. For fast computational convergence, DSLM suggests a new approach for the selection of optimal parameters in the discrete spaces, while other global optimization methods such as genetic algorithm and simulated annealing use heuristic approaches that do not guarantee the convergence. As a specific application example, we have targeted understanding phagocyte transmigration which is involved in the fibrosis process for biomedical device implantation. The goal of computational modeling is to construct an analyzer to understand the nature of the system. Also, the simulation by computational modeling for phagocyte transmigration provides critical clues to recognize current knowledge of the system and to predict yet-to-be observed biological phenomenon.

I. Introduction

Computational modeling and simulation have been highlighted in biomedical research for decades due to biological systems’ complexity and intractability by human. The modeling and quantitative simulation have played an important role in not only discovering biological components’ nature but also providing quantitative prediction.

Phagocyte transmigration is one of the processes involved in fibrosis formed around an implanted biomedical device. Deep understanding of this process will disclose the contributing components and predict the evolution of foreign body responses, which will eventually lead to reducing the failure rate of implantation. The goal of this paper is to provide computational modeling for phagocyte transmigration and to suggest a new optimization method, Discrete Selection Levenberg-Marquardt Algorithm (DSLM), to estimate optimal parameters of the mathematical equations for the fittest model to the data. It is proved that the new method should be satisfied with a global non-linear optimization solution and computational convergence in feasible time.

The paper is organized as follows. In Section II, the biological hypothesis based on current existing knowledge is assimilated. The computational modeling using control theory and biological insights is depicted in Section III. The DSLM method for system modeling parameter estimation is illustrated in Section IV. Finally, in Section V, we show how the computational models are used to simulate the phagocyte transmigration with and without biological observation.

II. Hypothesis for Phagocyte Transmigration

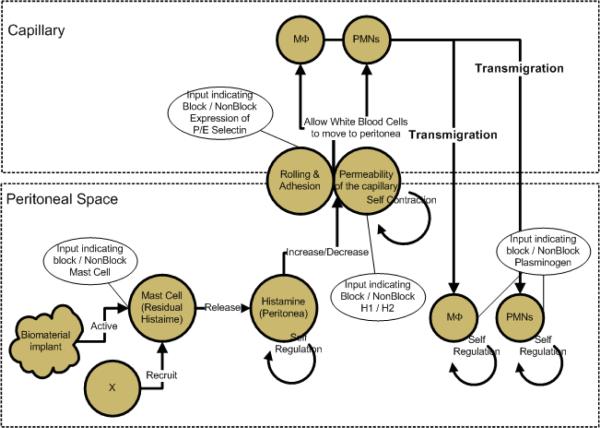
Based on current biological experiments and reportings, we believe that diverse components - mast cells, histamine, histamine receptors, and P/E selectins - are involved in the process of phagocyte transmigration with mutual interactions, as shown in Fig. 1. As one of the major factors comprising phagocyte transmigration, previous studies hypothesized that histamine might play an important role in the recruitment of inflammatory cells to implants [2]. Mast cells are known for the majority source of histamine, and there exists a large amount of mast cells in the peritoneal space [1]. After injecting histamine receptors antagonist, pyrilamine (an H1 receptor antagonist) and famotidine (an H2 receptor antagonist) to implanted bio-materials in the mice, it is verified that histamine enhances phagocyte transmigration via both H1 and H2 receptors. In addition, the hypothesis that mast cells influence histamine releasing was clarified by the experiment using mast cell-deficient mice [3]. It is also reported that histamine augments the expression of P and E selectins [3], which eventually cause phagocytes’ rolling and adhesion on endothelial cells. In the following section, we will introduce how to model different components involved in the transmigration process.

Fig 1.

System Organization for Phagocyte Transmigration.

III. Phagocyte Transmigration as a Dynamic System

A. Residual Histamine

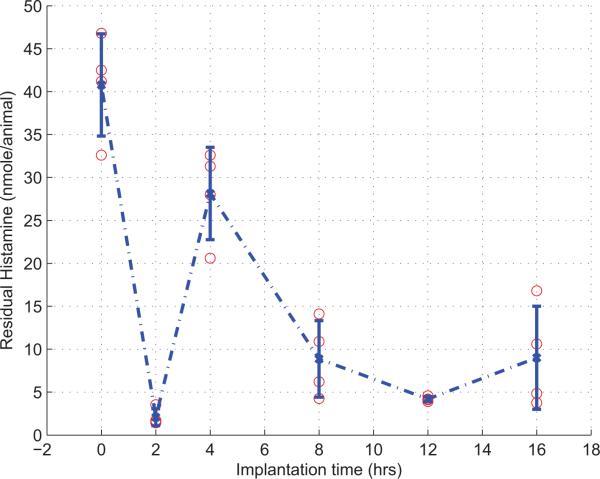
According to our biological measurements as shown in Fig. 2, it is legitimate to assume that the temporal residual histamine may have a regular pattern. In the biological sense, the phenomenon that residual histamine decreases dramatically for the first two hours can be described as residual histamine's degranulation from mast cells for histamine releasing. With the decreasing of residual histamine, another reasonable assumption is that the number of new mast cells is increased by an unknown external source after two hours. For this reason, the external source is modeled by a damped harmonic oscillator,

$${\ddot{U}}_{xrmc}\left(t\right)+2\beta {\stackrel{.}{U}}_{xrmc}\left(t\right)+{\omega }_0^2\left(t\right)U_{xrmc}\left(t\right)=0,$$ (1)

where U_xrmc is the function of the external input source to release new mast cells, β is a non-negative constant for resistance of friction and mass, and ω₀ indicates the oscillator frequency.

Fig. 2.

Experiment Data for Residual Histamine.

Considering biological half-life cycle, residual histamine can be modeled by the following equation,

$${\stackrel{.}{C}}_{rh}\left(t\right)=-k_{rhch}{C}_{rh}\left(t\right)+U_{xrmc}\left(t\right),$$ (2)

where C_rh(t) is the concentration function of residual histamine, k_rhch is the rate that residual histamine decayed, and U_xrmc(t) is the input function defined above.

B. Histamine

The concentration of histamine is increased as much as residual histamine's decreasing.

$${\stackrel{.}{C}}_h\left(t\right)=k_{rhch}{C}_{rh}\left(t\right)I_{mc}\left(t\right)-k_{hs}{C}_h\left(t\right),$$ (3)

where C_h(t) is the concentration function of histamine, k_rhch is the rate that histamine released from residual histamine given from residual histamine (2), k_hs is the rate that histamine regulates itself, and I_mc(t) is an input parameter indicating block/non-block mast cells. The first term on the right hand side of (3) represents the increasing of histamine released from mast cells. The second term on the right hand side of (3) represents the decay of histamine itself.

C. Histamine Receptor and Selectins

Histamine receptors enhance the permeability of the endothelial cell barrier of capillaries for phagocyte to transmigrate into the peritoneal space. It is modeled as,

$${\stackrel{.}{C}}_{hr}\left(t\right)=\frac{k_{hchrt}{C}_h\left(t\right)}{k_{hchrb}+C_h\left(t\right)}-k_{hrs}{C}_{hr}\left(t\right),$$ (4)

where C_hr(t) is the concentration function of histamine receptors, k_hchrt and k_hchrb are the rate bounds that histamine receptors are combined by histamine, k_hrs is the rate that histamine receptors regulate themselves.

In a similar way, selectins are modeled as,

$${\stackrel{.}{C}}_s\left(t\right)=\frac{k_{hcst}{C}_h\left(t\right)}{k_{hcsb}+C_h\left(t\right)}-k_{ss}{C}_s\left(t\right),$$ (5)

where C_s(t) is the concentration function of selectins, k_hcsb and k_hcst are the rate bounds for hyperbolic form, k_ss is the rate that selectins regulate themselves.

D. Phagocytes

For modeling of polymorphonuclear neutrophils (PMN) and monocytesy/macrophages (MΦ), we consider capillary permeabilities for both of them, which are related to the transmigration rate of phagocytes,

$${\stackrel{.}{C}}_{pmnp}\left(t\right)=\frac{k_{pmnipt}{C}_{hr}\left(t\right)C_s\left(t\right)I_{pmns}\left(t\right)I_{pmnhr}\left(t\right)}{k_{pmnipb}+C_{hr}\left(t\right)C_s\left(t\right)I_{pmns}\left(t\right)I_{pmnhr}\left(t\right)}-k_{pmnps}{C}_{pmnp}\left(t\right),$$ (6)

where C_pmnp(t) is the capillary permeability function for PMN to move into peritonea, k_pmnipb and k_pmnipt are the rate bounds for histamine receptors and selectins to increase permeability for PMN, C_hr(t) is the concentration function of histamine receptors, C_s(t) is the concentration function of selectins, k_pmnps is the contraction rate of capillary permeability, I_pmnhr(t) is the input indicating block/un-block histamine receptors, and I_pmns(t) is the input indicating block/un-block selectins. Similarly, the permeability function for MΦ can be modeled as,

$${\stackrel{.}{C}}_{mpp}\left(t\right)=\frac{k_{mpipt}{C}_{hr}\left(t\right)C_s{I}_{mps}\left(t\right)I_{mphr}\left(t\right)}{k_{mpipb}+C_{hr}\left(t\right)C_s{I}_{mps}\left(t\right)I_{mphr}\left(t\right)}-k_{mpps}{C}_{mpp}\left(t\right),$$ (7)

where C_mpp(t) is the capillary permeability function for MΦ to move into peritonea, k_mpipb and k_mpipt are the rates for histamine receptors and selectins to increase permeability for MΦ, and k_mpps is the contraction rate of capillary permeability. Now we can model the recruited PMN as,

$${\stackrel{.}{C}}_{pmn}\left(t\right)=C_{pmnp}\left(t\right)-k_{pmns}{C}_{pmn}\left(t\right),$$ (8)

where C_pmn(t) is the concentration function of PMN, C_pmnp is the permeability for PMN, k_pmns is the rate of self degradation. Now we can model the recruited MΦ as,

$${\stackrel{.}{C}}_{mp}\left(t\right)=C_{mpp}\left(t\right)-k_{mps}{C}_{mp}\left(t\right),$$ (9)

where C_mp(t) is the concentration function of MΦ, C_mpp is the permeability for MΦ, k_mps is the rate of self degradation.

IV. Parameter Estimation

The aforementioned phagocyte transmigration contains numerous parameters whose values indicate characteristics of the system. The estimation of parameter is essential to understanding individual component's behavior and a successful computational modeling. Our proposed DSLM method is motivated by the following observations. The classical Levenberg-Marquardt method converges quickly to the optimum solution [5]. However, it tends to fall into the local optimum. Hence, if it is possible to discretize each dimension of the space with number N to cover possibly every local curves, the Levenberg-Marquardt algorithm can then be extended to a global algorithm searching all local curves in the discrete space. DSLM seeks to search the global optima for each dimension of the input variables iteratively instead of comprehensive dimensions which may lead unforeseeable computational cost. In the following paragraphs, we will show how the searching space is reduced to be linear.

1) Selection

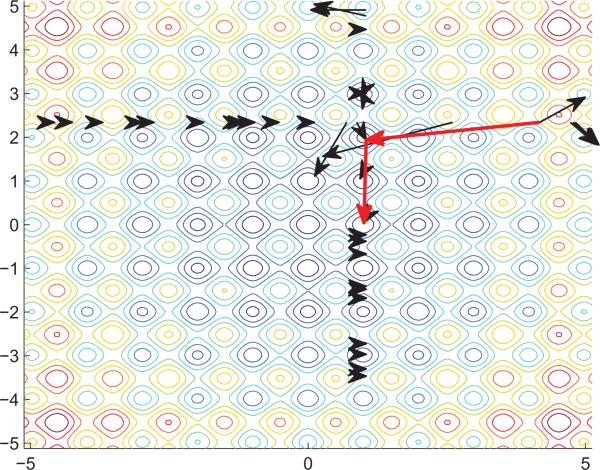
Instead of seeking to converge to the local optima, DSLM attempts to vary the initial guesses within the dimension of each parameter fixing other parameters. Denote P_i as a finite vector to represent the i^th parameter spaces. While the global optimizations search the comprehensive spaces whose complexity is P₁×P₂×···P_p, the complexity of searching space in DSLM becomes P₁+P₂ +···+P_p because it iteratively searches each parameter space. Then, it checks the scores of the function calculated with an updated x by conducting the Levenberg-Marquardt method. In Fig. 3, the arrows show that it checks the scores of the function varying vertical dimension variables under the condition that the horizontal dimension variable is fixed for the 2-dimension space. The score of the function is calculated by the result that the Levenberg-Marquardt algorithm converges to. Once it selects the optimal parameter that has the best function score in the dimension, the parameter is updated to the new parameter that the Levenberg-Marquardt method converges. Then, it seeks the next optimal parameters with fixed parameters previously chosen as the optimum. This process iterates until all parameters’ change falls into a certain range or the number of iteration is greater than a predefined value.

Fig. 3.

Illustration for the flow of DSLM Algorithm

2) Discretization

Discretization of each parameter dimension is the key part for DSLM algorithm which will affect its performance and computational cost. Given N numbers of discrete spaces of a parameter, the discrete dimension can be denoted as a vector, $P_i=(P_i^1,\dots ,P_i^N)$. It is worth mentioning that it is not necessary to calculate the function score from all discrete spaces. This is because the Levenberg-Marquardt method updates the initial parameter x_i to the new parameter $x_i^{\prime }$ which is subject to converging toward its local optimum. DSLM algorithm marks between the discrete spaces where x_i and $x_i^{\prime }$ belong to, respectively. Then, DSLM continues to check unmarked discrete spaces to find the global minimum. Unlike other discretization algorithms, DSLM's discretization does not affect accuracy of the solution but only for preventing re-checking the space.

DSLM function constantly checks the function scores of discrete spaces while updating parameter estimation. The discretization number is a pre-defined constant which may cover local curves of the function. By constantly checking current calculated mean squared error and historical minimum one, it will ensure the current parameter selection as a better candidate which avoids falling to the local minima. After selection of all parameters, LM method is conducted to get the global optimum.

V. EXPERIMENTS AND RESULTS

In the study of phagocyte transmigration, accumulation of PMN and MΦ on the surfaces of Fg-coated PET implants following 16 hours in vivo was measured (number/cm²). Implants were placed in up to six Swiss Webster mice. Estimated numbers of PMN were calculated from myeloperoxidase activities and MΦ were from nonspecific esterase activities. Different biological knock out experiments were carried out by blocking out various components in Fig. 1. Due to the sparseness of the data, we developed data interpolation using an iterative weighted mean algorithm which calculates the arithmetic mean using an adaptive weight. Linear interpolation was carried out for every discrete time period.

A. Parameter Estimation

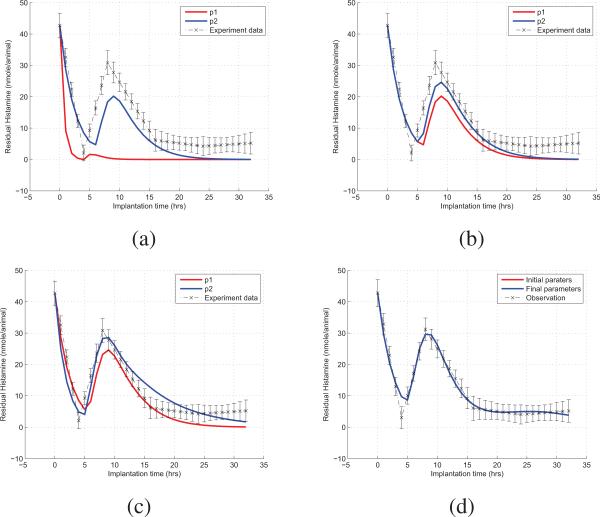
Totally seven unknown parameters - β, t₁, k_e0, k_k1, k_w0, k_k2, k_rhch - are estimated, given a 100 synthetic data set. Figures 4(a) to (c) illustrate the processes that DSLM converges to the optimum for each iteration. In the figure, observation data set is depicted by its mean and standard deviation for convenient comparison between estimation and observation. In conclusion, DSLM estimation converged quickly in the beginning of the iterations. Then, it stopped after meeting the convergence criteria. Figure 4(d) shows the final result of the experiment after 103 iterations.

Fig. 4.

Computation Results for Residual Histamine.(a)-(d) show the results from the first to the third, and the final iteration of DSLM.

For phagocyte simulation, 15 parameters - k_hs, k_hchrb, k_hchrt, k_hrs, k_hcsb, k_hcst, k_ss, k_pmnipb, k_pmnipt, k_pmnps, k_mpipb, k_mpipt, k_mpps, k_pmns, and k_mps - are estimated by DSLM. The result of optimal estimation for parameters for phagocyte transmigration modeling is listed in Table I. According to the result, we can verify the half life of histamine, k_hs, is relatively short as reported in current biological literature [2].

Table I.

Estimated Optimal Parameters

Par.	Est.	Par.	Est.	Par.	Est.
t 1	3.5000	k e0	11.2464	k k1	0.1017
β	0.0134	k w0	1.4037	k k2	0.0937
krhch	0.3704	khs	0.0002	khchrb	0.9997
khchrt	0.0757	khrs	0.7232	khcsb	1.9997
khcst	0.2668	kss	0.1024	kpmnipb	0.2226
kpmnipt	2.0000	kpmnps	0.1003	kmpipb	0.0001
kmpipt	1.0108	kmpps	0.1961	kpmns	0.0582
kmps	0.0307

B. Simulation

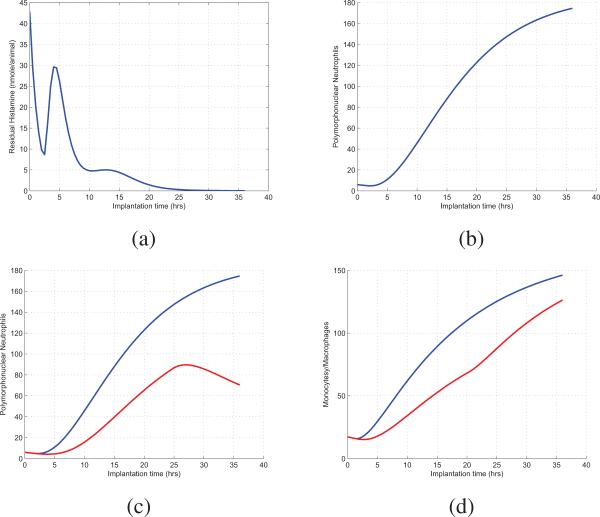
From the modeling equations and estimated parameters, we can use simulation for the prediction of yet-to-be-observed biological experiments. Figures. 5(a) and 5(b)

Fig. 5.

Simulation Results. (a) Prediction of Residual Histamine up to 36 hours; (b) Prediction of PMN up to 36 hours; (c) PMN prediction when blocking mast cells and histamine receptors; and (d) MΦ prediction when blocking selectins. show the prediction of recruited residual histamine and PMN in temporal space up to 36 hours, respectively. For deficiency simulation, Fig. 5(c) illustrates the prediction of dynamic evolution of PMN when mast cells are blocked up to 25 hours and histamine receptors are blocked after 25 hours. Figure 5(d) shows the simulation result of MΦ when selectins are blocked up to 20 hours.

VI. Conclusion

In this study, phagocyte transmigration has been studied to tackle the problem of fibrotic tissue formation surrounding biomaterial implants, which causes implantation failure. System biology concepts and control theory were incorporated in the computational modeling of the transmigration process. For a better estimation of the modeling parameters, we proposed a global heuristic optimization technique, DSLM, which is designed to overcome the limitations of existing algorithms. The computational simulation can be used to predict the future evolution of long term phagocyte transmigration after implantation which eventually can be applied for successful implant surgical procedures.