Rapid Transfer of Abstract Rules to Novel Contexts in Human Lateral Prefrontal Cortex

Abstract

Flexible, adaptive behavior is thought to rely on abstract rule representations within lateral prefrontal cortex (LPFC), yet it remains unclear how these representations provide such flexibility. We recently demonstrated that humans can learn complex novel tasks in seconds. Here we hypothesized that this impressive mental flexibility may be possible due to rapid transfer of practiced rule representations within LPFC to novel task contexts. We tested this hypothesis using functional MRI and multivariate pattern analysis, classifying LPFC activity patterns across 64 tasks. Classifiers trained to identify abstract rules based on practiced task activity patterns successfully generalized to novel tasks. This suggests humans can transfer practiced rule representations within LPFC to rapidly learn new tasks, facilitating cognitive performance in novel circumstances.

Introduction

The ability to flexibly adapt to novel circumstances is a fundamental aspect of human intelligence (McClelland, 2009; Cole et al., 2010b). Its profound importance for daily life is made clear by the substantial debilitation of individuals lacking this capacity (Burgess, 1997; Gottfredson, 2002). For instance, individuals with lesions in lateral prefrontal cortex (LPFC) have difficulty with grocery shopping and other common errands, especially when novel and complex (Shallice and Burgess, 1991). Among the neurologically unimpaired, measures of fluid intelligence – also associated with LPFC (Duncan, 2000; Burgess et al., 2011) – test for the ability to solve complex novel puzzles, and are able to predict important life outcomes such as academic and job performance (Blair, 2006; Gottfredson and Saklofske, 2009).

Despite its considerable importance, it is not understood exactly how the human brain allows for this kind of rapid learning of complex novel tasks (i.e., new multi-rule procedures). One possibility is that this ability relies upon the specific coding scheme used by LPFC. For instance, a compositional scheme of rule representation – in which new task representations can be constructed from different combinations of familiar rule representations – would allow for rapid representation of a wide variety of novel task states within LPFC. Rather than having to learn each complex set of task rules from scratch, a compositional coding scheme could allow LPFC to transfer skills and knowledge tied to constituent familiar rules into new task contexts (i.e., unique combinations of constituent rules) to vastly improve task learning. For example, rather than having to learn the task “If the answer to ‘is it sweet?’ is the same for both words, press your left index finger” all at once, compositional representation could allow recent practice assessing sameness of decision outcomes (the SAME rule) and, separately, practice with judging the sweetness of objects from memory (the SWEET rule) to facilitate learning this novel task.

So far, evidence for compositional representation within LPFC has been limited. Non-human primate studies suggest that LPFC representations are conjunctive – unique to each rule rather than compositionally building upon previously learned rules (Warden and Miller, 2007, 2010). Similarly, a prominent theory of LPFC representation emphasizes the fully adaptive nature of representation within LPFC (Duncan, 2001), based on observations that neurons in non-human primate LPFC alter what they represent depending on task demands (Asaad et al., 2000). Perhaps counter-intuitively, a less flexible LPFC coding scheme – in which rules are represented statically and used to compositionally build complex task representations – might facilitate cognitive flexibility by allowing knowledge and skill developed with the constituent rules to rapidly transfer to complex novel tasks.

A recent study suggests that in contrast to non-human primates, human LPFC may represent complex tasks compositionally (Reverberi et al., 2011). However, Reverberi et al. (2011) used complex tasks composed of rules that were independent of one another (e.g., “If there is a house press left” + “If there is a face press right”), such that the complex task representation did not require any integration of the rules. Task rules can be considered integrated if the outcome of one rule influences implementation of another rule. Without integrated rules, it remains unclear if Reverberi et al. (2011) demonstrated compositional representation within LPFC in a non-trivial way, or rather simply as the consequence of simultaneous independent representation of multiple non-interacting rules.

Here we used complex tasks composed of integrated rules to demonstrate compositional representation within LPFC. Further, we demonstrate a unique benefit of compositional coding: the ability to transfer practice with rules to facilitate rapid learning of complex novel tasks composed of those rules. We show transfer both behaviorally (demonstrating faster novel task learning after rules are practiced) and in the brain (demonstrating practiced LPFC rule activity patterns are present during novel tasks).

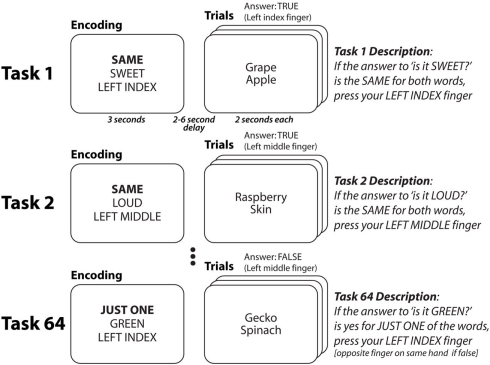
Each trial of our cognitive paradigm (Cole et al., 2010a) involved three distinct rules that had to be successfully integrated with each other to achieve accurate task performance (Figure 1). For instance, in the task “SWEET–SAME–LEFT INDEX” participants must decide if two objects are sweet and press their left index finger if they are (left middle finger otherwise). Thus, for this task, the first (semantic) rule specifies that two words (e.g., “grape” and “apple”) must each be categorized as sweet or not, with the outcome of these semantic categorizations used by the second (decision) rule to decide if the two words have the same semantic categorization or not. Finally, the third (response) rule specifies which finger is used to indicate if the decision rule is satisfied. Importantly, there must be some integration of the rules (i.e., they must be coordinated and influence each other) as each of these rules depends on the others (e.g., the decision rule cannot elicit a response without inputs from the semantic rule and outputs to the response rule). We were most interested in decision rules given that they are likely the most abstract rule type (they do not depend directly on stimuli or directly influence motor responses) and they are the most highly integrated of the rule types (they receive information from semantic rules and send information to response rules).

Figure 1.

Cognitive paradigm to investigate rapid instructed task learning. Participants performed 64 distinct tasks in randomly intermixed short blocks (see Cole et al., 2010a for more details). Tasks were conceptualized as collections of rules. Each word was presented separately, but they are grouped here to facilitate illustration. Each task consisted of a decision rule (highlighted here in bold, though not for participants) and a semantic rule + response rule combination. Thus, each of the four decision rules could appear in any of 16 task contexts (four decision ^* 16 semantic/response = 64 tasks). Four of the tasks (counterbalanced across participants) were practiced for 2 h in a prior session. For all participants there was one practiced task per decision rule, and no overlap between the semantic and response rules across practiced tasks.

Participants learned each of the rules in one of four tasks (counterbalanced across participants) during a 2-h practice session, such that practice for each rule occurred only within a single static task context (i.e., a fixed combination with other rules). Participants were then asked to perform these practiced tasks as well as 60 completely novel tasks (i.e., novel rule combinations) during a functional MRI session. Their impressive accuracy performing the novel tasks (>90%) led us to hypothesize that, consistent with our compositionality hypothesis and despite the static nature of the rule practice, each participant’s practiced rule representations transferred to novel task contexts to facilitate novel task performance.

We investigated this hypothesis using functional MRI with multivariate pattern analysis (MVPA; Norman et al., 2006), a method that can identify distributed activity patterns consistently associated with particular task representations (Woolgar et al., 2011). We began by applying MVPA to test for compositionality of LPFC rule representations, assessing if the same activation patterns differentiate rule representations despite changes over 64 distinct novel rule combinations. Next, we used MVPA to test for transfer of rules from practiced-to-novel tasks, assessing if the same LPFC activation patterns that differentiate practiced task rule representations might also differentiate these same rules when performed in novel task contexts. Successful MVPA classification performance in this analysis would demonstrate the extent to which decision rules exhibit transfer of highly practiced rules to novel task contexts, possibly generalizing the benefits of practice to novel circumstances and helping to explain the extensive adaptability of human intelligence.

Materials and Methods

Participants

We included 14 right-handed participants (seven male, seven female), aged 19–29 (mean age 22) in the study. Participants were recruited from the University of Pittsburgh and surrounding area. Participants were excluded if they had any medical, neurological, or psychiatric illness, any contraindications for MRI scans, were non-native English speakers, or were left-handed. All participants gave informed consent. Theoretically and methodologically distinct analyses of these data were included as part of Cole et al. (2010a).

MRI data collection

Image acquisition was carried out on a 3-T Siemens Trio MRI scanner. Thirty-eight transaxial slices were acquired every 2000 ms (FOV: 210 mm, TE: 30 ms, Flip angle: 90°, voxel dimensions: 3.2 mm³), with a total of 216 echo-planar imaging (EPI) volumes collected per run. Siemens’s implementation of generalized autocalibrating partially parallel acquisition (GRAPPA) was used to double the image acquisition speed (Griswold et al., 2002). Three-dimensional anatomical MP-RAGE images and T2 structural in-plane images were collected for each subject prior to functional MRI data collection.

Task paradigm

The task paradigm combines a set of simple rule components in many different ways, creating dozens of complex task sets that are novel to participants (Figure 1). The paradigm was presented using E-Prime software (Schneider et al., 2002). Novel and practiced task blocks (each consisting of task encoding and three trials of a single task) were randomly intermixed across 10 functional MRI runs (six novel and six practiced blocks per run).

Four semantic rules, four decision rules, and four response rules were used in the paradigm. The semantic rules consisted of sensory semantic decisions (e.g., “is it sweet?”). The decision rules specified (using logical relations) how to respond based on the semantic decision outcome(s) for each trial. The SAME rule required that the semantic answer was the same (“yes” and “yes” or “no” and “no”) for both words, the JUST ONE rule required that the answer was different for the two words, the SECOND rule required that the answer was “yes” for the second word, while the NOT SECOND rule required that the answer was not “yes” for the second word. The motor response rules specified what button to press based on the decision outcome. The task instructions made explicit reference to the motor response for a “true” outcome, while participants knew (from the practice session) to use the other finger on the same-hand for a “false” outcome.

Since the tasks consisted of one rule from each of the three categories, combining the rules in every possible unique combination creates 64 distinct tasks. Of these tasks, four (counterbalanced across participants) were practiced (30 blocks, 90 trials each) during a 2-h behavioral session 1–7 days prior to the neuroimaging session. These “practiced” tasks were chosen for each subject such that each rule was included in exactly one of the four tasks, ensuring that all rules were equally practiced. During the neuroimaging session, half of the blocks consisted of the practiced tasks and half of novel tasks. Novel and practiced blocks were randomly interleaved, with the constraint that exactly six blocks of each type (practiced, novel) occurred within every run. With 10 runs total per participant, each novel task was presented in one block and each practiced task was presented in 15 blocks.

Each task block consisted of two phases: encoding and trial. The encoding phase consisted of an initial cue indicating the upcoming task type: novel (thin border) or practiced (thick border), followed by three rule cues indicating the rules making up the task. The order of these rule cues was consistent for each participant but counterbalanced across participants. Asterisks filled in extra spaces around each rule cue to reduce differences in visual stimulation across task rules. The three rule cues appeared sequentially, with each presented for a duration of 800 ms followed by a 200-ms delay. The encoding period was then followed by a 2- to 6-s delay period to allow the construction of the relevant task representation.

The trial phase began after the encoding phase, and was comprised of a sequence of three task trials (each separated by a randomly jittered 2–6 s inter-trial interval). Each task trial consisted of a pair of target stimuli presented in sequence (again with 800 msec duration, 200 msec inter-stimulus interval). Stimuli were normed by a separate group of participants (21 male, 33 female). Word stimuli were included in the neuroimaging experiment with exactly two category questions; one in which the norming group answered “yes” over 75% of the time and one in which they answered “no” over 75% of the time. Forty-five stimuli were included per semantic category. Each stimulus was presented eight times (50% in a “yes” context, 50% in a “no” context) across both the behavioral practice (50%) and scanning (50%) sessions.

ROI-based analysis: Image processing

Image preprocessing was carried out in AFNI (version 2009-12-31). The images were slice-time corrected, motion-corrected (realigned), and detrended by run (using a first order polynomial to remove linear trends). The voxels were kept at the acquired size of 3.2 mm × 3.2 mm × 3.2 mm. The images were not spatially normalized, nor smoothed.

Temporal compression (Mourão-Miranda et al., 2006) to one summary volume per block was performed by averaging the volumes that were judged, based on a canonical hemodynamic response to contain the most signal. Specifically, we averaged the image volumes corresponding to the time period of 4 s (2 TR) after block onset to 8 s (4 TR) after block offset (i.e., after the final trial of the block). Note that the second TR always corresponded to 4 s after block onset because block onset was time-locked to image acquisition. More images were averaged for some blocks than others due to variable block duration. Repeating the analyses with slightly different choice of volumes to average (e.g., using the same number of volumes from every block) did not appreciably alter the results; nor did using parameter estimates (β values) instead of averaging.

To examine the activity selective to the encoding phase we created a separate summary volume that consisted of the first two volumes included in the whole-block temporal compression (at 4 and 6 s after block onset; i.e., 3–6 s following the first encoding screen) were averaged to summarize activity occurring during the encoding phase. These encoding phase summary volumes likely had lower signal-to-noise than the summary volumes for the whole block, since fewer volumes were averaged.

The summary volumes were subjected to a preprocessing step that normalized activation values. Specifically, each summary volume was z-normalized across the voxels in each ROI, such that every summary volume and ROI had a mean activation level of 0 and an across-voxel variance of 1. This form of normalization ensures that the mean activation level of the voxels in each ROI in each block is equal, so that ROI-level differences in activation between the conditions cannot positively bias the classification. This may help to rule out the effects of mean differences in activity due to differences in difficulty that may be present across decision rules (e.g., between the SAME rule and the other rules).

The LPFC region of interest was defined anatomically for each participant using automated FreeSurfer (version 4.2) gyral-based segmentation (Desikan et al., 2006). LPFC was defined here as the anterior and posterior middle frontal gyrus (i.e., the dorsal and anterior LPFC) along with the pars triangularus and pars opercularis (i.e., the ventral LPFC). These masks were dilated by one voxel (3.2 mm) to help account for any misalignment between the anatomical and function images. The post-central gyrus (postCG; i.e., the somatosensory cortex) was included as a control ROI, given the use of motor responses. The post-central gyrus was chosen instead of the nearby precentral gyrus to reduce the chance that LPFC and the control region would overlap.

All non-zero-variance voxels in each ROI mask were included; no further feature selection was performed. Since the images were not spatially normalized, the number of voxels included in each ROI was different for each participant, as summarized in Table 1. Note that there was no significant correlation between ROI size and classification accuracy (r = 0.15, p = 0.59, N.S.; based on LPFC four-way novel → novel classification accuracies).

Table 1.

Number of voxels in each ROI.

ROI	Mean	SD	Maximum	Minimum
LPFC	1909.8	282	2490	1579
Left LPFC	956.3	144	1245	795
Right LPFC	953.5	143.7	1245	784
Left postCG	278.6	34.6	319	192
Right postCG	261.8	38.6	328	206

Ranges are given since the volumes were not spatially normalized to an atlas, and so the number of voxels in each ROI varied across participants.

ROI-based analysis: classification and statistical tests

Two different types of analyses were performed: (1) determining classification accuracy for the four decision rules, using only novel task blocks for training and testing; (2) determining classification accuracy using practiced task blocks for training and novel task blocks for testing.

The ROI-based classification and statistical analyses were performed in R (version 2.11.1, R Foundation for Statistical Computing) using custom-written scripts. In all cases classification was performed using support vector machines, with a linear kernel and the cost parameter fixed at 1 (implemented in the R e1071 package interface to LIBSVM), which are typical choices for fMRI data. The classifications were performed within-subjects, fitting a classifier to each individual participant and averaging the accuracies across participants. Average classification accuracy across participants (proportion correct) was the outcome measure. Four-way classification was performed (since there were four rules of each type), followed by pair-wise classification performed to identify which individual rules could be distinguished. The four-way classifications used the standard “one-against-one” LIBSVM multi-class approach (Hsu and Lin, 2002).

For the first analysis – training and testing on novel task blocks only – fivefold cross-validation was used (leave-three-out partitioning) when selecting blocks for the testing set. The time between adjacent trials, random trial order, and temporal compression makes it unlikely that temporal dependencies inflated the results (see Etzel et al., 2011 for additional discussion of these issues). There were no missing trials, so 10 unique fivefold cross-validation partitionings were randomly generated and used for all classifications and permutation tests; accuracies for each subject were averaged over these 10 repetitions.

For the second analysis – when training on practiced task blocks and testing on novel blocks – all practiced trials were used as the training data and all novel as the testing. Since this partitioning is unique, no repetitions were needed for cross-validation or permutation testing.

Significance was calculated by permutation testing (Golland and Fischl, 2003; Etzel et al., 2009). Non-parametric statistical testing was chosen to provide a stringent test despite the small number of subjects and the possibility of skewed distributions. The permutation test was performed by repeating each analysis 1000 times, randomly permuting the data labels each time. The significance was calculated as the proportion of permuted data sets classified more accurately than the true data. When the accuracies were calculated by averaging over repetitions (to compensate for the randomness in partitioning for the novel-only classification) the permuted-label data sets were classified using the same examples as the true-label data sets, with the accuracy for each permuted-label set averaged across the repetitions in the same manner as the true data. Since 1000 permutations were used, the lowest p-value possible (if the true-labeled data was classified more accurately than all permuted-label datasets) is 0.001. A significance threshold of p < 0.05 was used. Significance thresholds accounted for multiple comparisons by using the logic of Fisher’s least significant differences, since all LPFC ROIs tests were subtests of the statistically significant block-level four-way decision rule classification in LPFC.

Searchlight-based analyses

Linear support vector machines were used to classify functional MRI activity patterns in 9.6 mm (three voxel) radius “searchlight” spheres surrounding each voxel (Kriegeskorte et al., 2006) in the anatomical LPFC ROI using PyMVPA (version 0.4.4; Hanke et al., 2009). Temporal compression was performed using general linear model parameter estimates from fitting a canonical hemodynamic response function to each block separately. The activation values of the voxels making up each searchlight were z-normalized in order to remove any mean activation effects (such as might originate from subtle differences in difficulty across the task rules). Four-way classification (of the four decision rules) was performed in each searchlight sphere, separately for each participant. Classification was performed by training on all practiced blocks and testing on all novel blocks (similar to one of the analyses performed on the ROI as a whole).

The resulting statistical maps of classification accuracies were then spatially normalized to Talairach atlas space and smoothed at 6 mm FWHM. Each voxel’s accuracy value was then compared to chance (25%) using one-way one-sample t-tests. The resulting group map was then thresholded and cluster thresholded to correct for multiple comparisons within the LPFC ROI. The cluster size was estimated using AFNI’s AlphaSim with 10000 Monte Carlo simulations using p < 0.01 uncorrected as the threshold and smoothing parameter 8.59 mm FWHM. The resulting cluster size correcting to p < 0.05 was 26 voxels (for the whole brain, 34 voxels). The AlphaSim smoothing parameter was estimated empirically using AFNI’s 3dFWHMx for the group searchlight map. Statistical results were mapped to the PALS-B12 surface using Caret software (Van Essen, 2005).

Results

Testing for rule difficulty effects

We first calculated behavioral accuracy for each task rule to determine if differences in rule difficulty might confound potential MVPA effects. Overall accuracy was 92% for novel tasks and 93% for practiced tasks. Mean accuracies for the decision rules were: 89% (SAME), 95% (JUST ONE), 94% (SECOND), and 93% (NOT SECOND). Mean reaction times for the decision rules were: 1331 ms (SAME), 1299 ms (JUST ONE), 1256 ms (SECOND), and 1363 ms (NOT SECOND). There were no statistically significant differences in accuracy or reaction time between the rules (each p > 0.05, Bonferroni corrected for multiple comparisons). Note, however, that the SAME rule showed a trend toward having lower accuracy (p = 0.03 when compared to JUST ONE and p = 0.04 when compared to SECOND, uncorrected for multiple comparisons). The smallest p-value for the reaction time comparisons was SECOND vs. NOT SECOND, but this was not statistically significant (p = 0.28, N.S.).

We further tested the possibility that differential rule difficulty influenced our results by testing for correlations between LPFC decision rule classification accuracy (practiced → novel) and differences in behavioral difficulty. We calculated the correlations using the six pair-wise comparisons between decision rules across the 14 subjects (i.e., six data points per subject), such that 84 data points were included per correlation test. Neither the correlation between reaction times and classification accuracy (r = −0.03, p = 0.78, N.S.) nor between behavioral accuracy and classification accuracy (r = 0.006, p = 0.96, N.S.) were statistically significant. This supports our conclusion that the MVPA classifications are likely driven by rule identity rather than differences in rule difficulty. As a complementary approach, we calculated a correlation for each subject separately (six data points per subject) and used an across-subject t-test with the (Fisher z transformed) correlation values to assess statistical significance. This approach led to the same conclusion (for accuracies: t = 0.23, p = 0.81, N.S.; for reaction times: t = −0.75, p = 0.47, N.S.).

In the other task dimensions there were also only small differences in performance accuracy among the different rules. For the response rules, mean accuracies were: 91% (L INDEX), 94% (L MID), 94% (R MID), and 92% (R INDEX), with no significant differences among the rules. For semantic rules the mean accuracies were: 88% (SOFT), 95% (LOUD), 94% (GREEN), and 92% (SWEET). The only significant difference among the semantic rules was between SOFT and LOUD (t = 3.0, p = 0.04, Bonferroni corrected). There were no significant effects of reaction time for any of the rule types. Together, these results suggest that there were no strong or consistent differences in rule difficulty (e.g., one rule that is more difficult than all others) that could bias or confound MVPA decoding.

Testing for behavioral transfer from practiced-to-novel tasks

Consistent with our hypothesis that novel task performance benefited from practiced task transfer, we found a significant increase in performance between the first “practiced” task trials and the first “novel” task trials [13% increase; t(38) = 2.1, p = 0.046]. Practiced task performance was assessed during each task’s first trial during the practice session, while the novel task performance was assessed during each novel task’s first trial during the test session.

Note that, due to a technical issue, subjects’ performance during the practice sessions was not recorded for the main experiment. We therefore used a separate experiment (N = 28) including identical tasks to test for behavioral transfer from practiced to novel tasks. However, there were several advantages to conducting the analysis using this alternate dataset. First, unlike the primary experiment, the practiced tasks were each learned serially (in 144-trial blocks), allowing us to disentangle the learning of the common task structure (e.g., familiarity with the kinds of stimuli used and the task timing) from the learning of the task rules. We accomplished this by excluding the first practiced task learned for each subject (in which the common task structure is also learned) from the analysis of the first practiced task trials. Second, we limited subjects’ preparation and response windows in this experiment in order to assess if the behavioral transfer effect would be robust to increased difficulty. This decreased novel task accuracy from 92% (in the primary dataset) to 71%, suggesting our finding of a 13% practiced-to-novel transfer effect is highly conservative.

Response and semantic rule classifications

We expected, based on the previous LPFC research described above, that decision rule representations would be consistently decodable by MVPA within LPFC. In contrast, we did not necessarily expect semantic rules to be consistently decodable within LPFC, since the semantic categories were based on distinct perceptual modalities and therefore might each be represented in distinct parts of the brain (Goldberg et al., 2006a,b). Similarly, we did not expect motor response rules to be consistently decodable within LPFC, but rather in specialized motor and somatosensory areas.

Consistent with our expectations, right and left post-central gyrus (postCG) could effectively classify response rules, while LPFC could not (Table 2, training and testing on novel trials only). Only the left LPFC was able to decode the semantic rules better than chance (Table 3), though this appears to have been primarily driven by the SOFT semantic rule rather than the entire set of rules.

Table 2.

Response rule classification test results.

		LPFC	Left LPFC	Right LPFC	Left postCG	Right postCG
Four-way	Mean	0.252	0.264	0.258	0.45	0.449
	p	0.469	0.152	0.289	0.001	0.001
L INDEX vs. R INDEX	Mean	0.489	0.504	0.486	0.844	0.852
	p	0.67	0.451	0.715	0.001	0.001
L INDEX vs. L MID	Mean	0.55	0.548	0.539	0.53	0.528
	p	0.023	0.035	0.064	0.118	0.143
L INDEX vs. R MID	Mean	0.552	0.537	0.55	0.841	0.869
	p	0.022	0.062	0.024	0.001	0.001
R INDEX vs. L MID	Mean	0.496	0.501	0.509	0.79	0.816
	p	0.558	0.462	0.368	0.001	0.001
R INDEX vs. R MID	Mean	0.521	0.514	0.52	0.548	0.538
	p	0.197	0.315	0.214	0.031	0.066
L MID vs. R MID	Mean	0.499	0.504	0.516	0.821	0.863
	p	0.517	0.427	0.25	0.001	0.001

Four-way and pair-wise tests of novel blocks. Only across-hand response comparisons (e.g., L INDEX vs. R INDEX) were expected to classify better than chance since same-hand responses (e.g., R INDEX vs. R MID) were equally likely within each block. Values in italics are statistically significant (p < 0.05).

Table 3.

Semantic rule classification test results.

		LPFC	Left LPFC	Right LPFC	Left postCG	Right postCG
Four-way	Mean	0.262	0.278	0.242	0.252	0.229
	p	0.201	0.026	0.725	0.449	0.949
GREEN vs. LOUD	Mean	0.439	0.461	0.438	0.466	0.473
	p	0.987	0.919	0.986	0.91	0.89
GREEN vs. SOFT	Mean	0.535	0.556	0.51	0.517	0.489
	p	0.087	0.019	0.363	0.262	0.666
GREEN vs. SWEET	Mean	0.498	0.516	0.471	0.51	0.477
	p	0.506	0.252	0.878	0.354	0.826
LOUD vs. SOFT	Mean	0.587	0.584	0.565	0.526	0.495
	p	0.002	0.001	0.004	0.172	0.579
LOUD vs. SWEET	Mean	0.506	0.521	0.472	0.495	0.48
	p	0.374	0.189	0.875	0.574	0.783
SOFT vs. SWEET	Mean	0.543	0.531	0.547	0.525	0.498
	p	0.041	0.095	0.029	0.16	0.543

Four-way and pair-wise tests of novel blocks. Values in italics are statistically significant (p < 0.05).

Decision rule classifications, novel tasks only

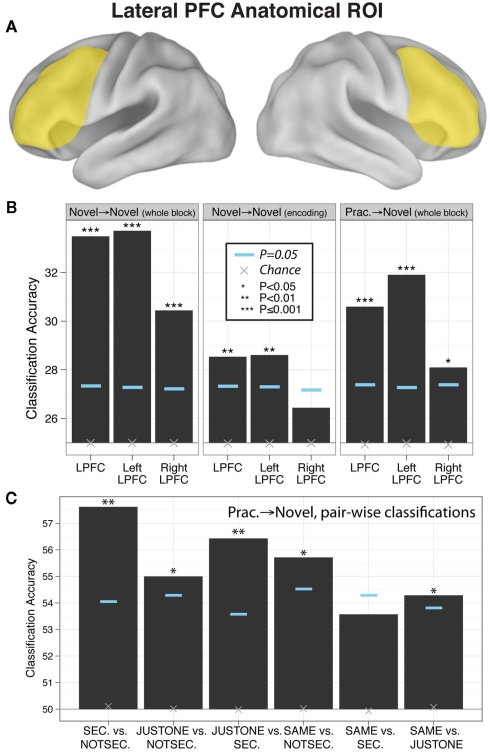
We found that block-averaged LPFC (Figure 2A) activity during the novel tasks (novel → novel analysis) could be used to decode the four decision rules at accuracy significantly better than chance (35% classification accuracy; chance = 25%; p ≤ 0.001; Figure 2B). Most pair-wise decision rule classifications were also significantly above chance (Table 4), suggesting that the four-way classification performance was not driven by a particular subset of rules.

Figure 2.

Evidence of practiced-to-novel transfer of context-independent decision rule representations within LPFC. (A) Location of the anatomical LPFC ROI. (B) Classification accuracies across the four rules using the anatomically defined LPFC ROI for whole novel blocks, novel task encoding periods, and practiced → novel (classifier trained on practiced blocks, tested on novel blocks). Significance was assessed using permutation tests. Left and right LPFC accuracies were significantly different for the novel → novel whole block (p = 0.006) and practiced → novel (p = 0.02) classifications (based on permutation tests). (C) Pair-wise classifications across the six between-rule comparisons (practiced → novel) underlying the four-way classifications.

Table 4.

Lateral prefrontal cortex four-way and pair-wise decision rule classification results.

Four-way	SAME vs. JUST ONE	SAME vs. SEC.	SAME vs. NOT SEC.	JUST ONE vs. SEC.	JUST ONE vs. NOT SEC.	SEC. vs. NOT SEC.
A – DECISION RULE CLASSIFICATION, BILATERAL LPFC, NOVEL BLOCKS
0.34**	0.52	0.58**	0.58**	0.56**	0.59**	0.59**
B – DECISION RULE CLASSIFICATION, LEFT LPFC, NOVEL BLOCK ENCODING PERIODS
0.29**	0.56*	0.55*	0.57**	0.50	0.58**	0.52
C – DECISION RULE CLASSIFICATION, BILATERAL LPFC, TRAINED ON PRACTICED & TESTED ON NOVEL BLOCKS
0.31**	0.54*	0.53	0.56*	0.56**	0.55*	0.58**

(^*p < 0.05, ^**p < 0.01). Values in bold are statistically significant (p < 0.05).

We reasoned that if LPFC activity truly reflects abstract/context-independent rule representations then they should also be present prior to task execution, during the task encoding phase. We thus repeated the previous analysis, but performed the decision rule classification using summary volumes spanning the encoding phase only, rather than both the encoding and trial phases. Classification accuracy was significantly greater than chance in left LPFC (four-way accuracy 29%; chance = 25%; p = 0.008; Figure 2B), with most pair-wise decision rule classifications also better than chance (Table 4). However, right LPFC classification accuracy (26%) was not statistically above chance (p = 0.16). These results support the conclusion that, at least in left LPFC, the activity patterns reflect an abstract (both stimulus-independent and task-independent) encoding of decision rules that is in place prior to task performance.

Testing for a response and decision rule dissociation

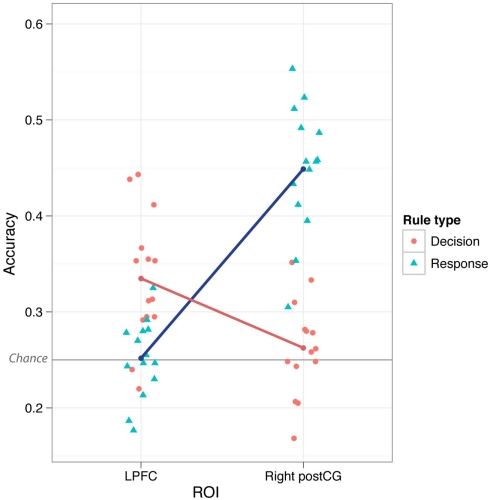
We found that LPFC could be used to decode (novel → novel) decision rules better than response rules (p ≤ 0.001). This could reflect a real difference in rule representation in LPFC, or it could result from noise or inconsistency of response rule representations. However, in contrast to LPFC, we found that both left and right postCG could decode response rules better than decision rules (p ≤ 0.001). This double dissociation between LPFC and postCG (ROI × Rule Type interaction) was highly statistically significant [F(1,13) = 85, p < 0.001 for right postCG, F(1,13) = 54, p < 0.001 for left postCG; tested using parametric ANOVAs; Figure 3]. This result suggests that LPFC activity patterns were relatively selective to decision rule representation. Moreover, it indicates that the lack of response rule decoding within LPFC is unlikely to be due to poor data quality that might be associated with response rules, since this rule dimension is clearly decodable in a different brain region (postCG).

Figure 3.

Lateral prefrontal cortex vs. postCG double dissociation. Mean classification accuracy was significantly higher for decision vs. response rules in LPFC, but was significantly higher for response vs. decision rules in postCG (both right and left). This interaction was highly statistically significant (p = 4.7e-07 for right postCG, p = 5.3e-06 for left postCG). The individual points in the plot are the classification accuracies for each subject separately.

Decision rule classifications, transfer of representations from practiced to novel tasks

In this analysis we trained a pattern classifier to discriminate the decision rules using the practiced tasks only, but then tested the classifier with the novel tasks. This is an especially stringent test for transfer of rule representations, because it requires that the decision rule activation patterns present when performing practiced tasks are also present when performing the novel tasks (i.e., for the first time in a new context). Nevertheless, we found evidence for significant generalization: in the LPFC the classifier trained on practiced tasks showed significant classification accuracy when tested on novel tasks (31% accuracy; chance = 25%; p ≤ 0.001; Figure 2A). We also found that five of the six pair-wise classifications driving this four-way classification result were significant (Figure 2C; Table 4).

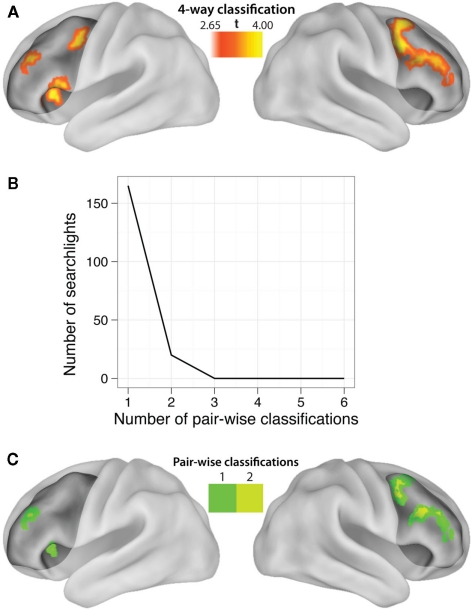
LPFC searchlight pattern analysis

Our hypotheses focused on LPFC as a whole, but abstract decision rule representations could be present in only a subset of voxels within the LPFC ROI. We tested this possibility by performing a searchlight analysis on voxel clusters within the LPFC. Four-way classification analysis revealed clustered regions showing significant practiced → novel generalization effects within all major subdivisions of LPFC (i.e., dorsal, ventral, anterior, and posterior; Table 5). We next performed a conjunction analysis across pair-wise (rather than four-way) decision rule searchlight maps (Figures 4B and 4C). Note that we accounted for the multiple (six) comparisons by only reporting significant pair-wise searchlights that also showed significant four-way searchlight effects. None of the searchlights showed statistically significant results for all or even most of the six rule comparisons (maximum of any searchlight was two), suggesting each searchlight is driven by a subset of rules. This suggests the anatomical LPFC ROI is able to decode most of the pair-wise classifications due to distributed or spatially distant representations within the LPFC ROI. Alternatively, though less likely, this result could be due to inconsistent localization of the pair-wise classifications across subjects, such that only one or two classifications overlap consistently across subjects. In either case, this result demonstrates that there is no single location within LPFC that can be used to consistently decode a majority of the decision rules across subjects.

Table 5.

Statistically significant decision rule searchlight clusters.

	Mean accuracy (%)	Mean T-stat	Number of searchlights	X	Y	Z
Right LPFC	29	3.2	306	35.9	12.4	36.4
Left vPFC/AIC	29	3.2	96	−41.3	15.4	6.9
Left aPFC	28	2.8	42	−36.3	34.1	25.0
Left pPFC	29	3.1	41	−41.4	−3.5	38.5

LPFC four-way classifications (practiced → novel) in 9.6 mm radius searchlights.

PPC, posterior parietal cortex; aPFC, anterior PFC; vPFC, ventral PFC; pPFC, posterior PFC; AIC, anterior insula cortex.

Figure 4.

Localization of LPFC practiced-to-novel decision rule transfer. (A) Searchlight MVPA of decision rule four-way classifications (practiced → novel, whole block) within LPFC. The highlighted locations are clusters of “searchlights” (spheres with 9.6 mm radii) that consistently decoded which decision rule individuals were using. See Table 5 for a list of significant clusters. (B) Most of the searchlights were only able to decode a single pair-wise comparison, with two pair-wise comparisons as the maximum decoded by any single searchlight. This demonstrates an advantage of using MVPA with anatomical ROIs rather than searchlights, and suggests the Figure 2C result is due to spatially variable or distributed coding of rules within LPFC. (C) Localization of the pair-wise results, restricted to the significant four-way classification searchlights to correct for multiple comparisons.

Finally, for completeness we include decision, semantic, and response rule four-way whole brain searchlight classification results (Tables 6–8). It is important to note that – in contrast to what was found with the LPFC ROI – these searchlight results can easily be driven by a small subset of rules (as shown for LPFC searchlights).

Table 6.

Whole brain decision rule searchlight results.

	Mean accuracy (%)	Mean T-stat	Number of searchlights	X	Y	Z
L parietal	29	3.4	1113	−20.7	−65.3	45.5
R lat. & med. PFC	28	3.3	650	18.7	20	49.2
R inf. parietal	28	3.1	305	44.1	−54.5	47.9
L vPFC/AIC	28	3.1	110	−43.9	16.7	6.8
L aPFC	29	3.0	76	−38.2	38.4	23.3
L pPFC	28	3.2	55	−43.7	−1	38.7
Parahippocampus	27	3.4	42	20.6	−35.9	−16.9
R thalamus	28	3.2	39	7.1	−16.1	0.5
R cerebellum	27	3.0	34	33.4	−56.5	−35.4

Four-way classifications (practiced → novel) in 9.6 mm radius searchlights. Note that significant classification in four-way classifications can be driven by a single rule or subset of rules (e.g., the “L parietal” cluster could only classify three of the six comparisons better than chance).

Table 8.

Whole brain response rule searchlight results.

	Mean accuracy (%)	Mean T-stat	Number of searchlights	X	Y	Z
Motor & somatosensory cortex	32	5.2	7798	1.3	−27.1	55.3
Cerebellum	30	4.0	3446	−2.5	−61.4	−16.5
R cuneus	28	3.7	201	25.4	−88.8	26
Mid. temporal	28	3.5	128	−55.8	−4.5	−20.3
Medial frontal	28	3.6	55	12.3	51.1	−11.8
R putamen	28	3.4	51	30.8	−7.5	9.1
R inf. putamen	27	3.7	46	25.8	2.6	−12.1
Inf. ant. cingulate	27	3.6	44	5.2	14.3	−10.5
L mid. occipital	27	3.7	39	−42.7	−78.6	16.2
L vPFC	27	3.5	32	−58.5	9.2	8.2
R pPFC	28	3.7	26	56.4	11.8	24.4

Four-way classifications (practiced → novel) in 9.6 mm radius searchlights. Note that significant classification in four-way classifications can be driven by a single rule or subset of rules. The italicized clusters are significant for within LPFC correction for multiple comparisons, but not for whole brain cluster correction (p < 0.05).

Table 7.

Whole brain semantic rule searchlight results.

	Mean accuracy (%)	Mean T-stat	Number of searchlights	X	Y	Z
Inf. ant. cingulate	28	3.2	181	−18.3	14.4	−22.4
R mid. occipital	27	3.1	107	45.9	−73.6	11.3
L inf. temporal	28	3.2	99	−43.3	−17.6	−26.2
L inf. parietal	28	3.2	74	−53.5	−47.9	28.6
L thalamus	28	3.0	64	−9.7	−10.4	−8.2
L pPFC	28	3.1	59	−39	4.4	38.2
L cerebellum	27	3.3	58	−31.8	−61.8	−45.6
Sup. colliculus	28	3.0	54	−6.6	−28.7	−8.2
R aPFC	27	3.4	44	50.7	36.5	6.5
Med. aPFC	27	3.3	38	4.7	63.5	10.9
L med. parietal	28	3.2	38	−20.1	−73.9	40.4

Four-way classifications (practiced → novel) in 9.6 mm radius searchlights. Note that significant classification in four-way classifications can be driven by a single rule or subset of rules.

Discussion

We began by asking how individuals are able to rapidly learn complex novel tasks from instruction. The present results suggest this is possible because the human brain can retain the benefits of practice even during novel task performance, through the transfer of practiced rule representations within LPFC into novel contexts. Similar benefits likely also arise via transfer between novel task contexts, since this would allow practice effects to accumulate even with frequent task changes. Transfer of decision rules is likely possible because these rule representations are highly abstract and compositional, and are thus usable across a wide variety of contexts.

These results also suggest that individuals use the same abstract decision rule representations within LPFC even after extensive practice with a given complex task. This is an intriguing result given that participants were unlikely to have gained any advantage by using compositional/context-independent (rather than task-specific) rule representations during the practice session. This is because: (1) the four practiced tasks were non-overlapping, such that no rules were shared across tasks and so practice with the rules in one task would not transfer to any other task that participants were aware of, and (2) there was likely adequate time (2 h) to develop optimized task-specific representations for each of the four tasks. These results suggest that humans use abstract and compositional rule representations even when optimized task-specific representations are viable, possibly “just in case” task rules are useful in new contexts in the future. This may help to explain the impressive flexibility of intelligent human behavior. Further, this interpretation suggests that cognitively impaired populations might “over fit” task representations in LPFC to practiced task contexts (by inappropriately using less abstract, task-specific representations), reducing their ability to rapidly learn new tasks. Future research is necessary to test this possibility.

It should be noted that the fMRI experiment included a relatively small group of participants (14 individuals), and that evidence for behavioral transfer was based on a separate group of participants. Nonetheless, it appears likely that the fMRI participants experienced substantial behavioral transfer from practiced to novel tasks, given their high performance (over 90% accuracy) on the novel tasks. In other words, it is unlikely that the fMRI participants performed at the same level during the initial trials of the practice session (when the “practiced” tasks were novel) as during subsequent novel tasks. Supporting this conclusion, the separate group of participants was only 58% accurate on the first trials of the “practiced” tasks, and experienced a large increase in accuracy on novel tasks after the practice session.

We defined LPFC anatomically in order to utilize the advantages of anatomical ROI analysis with MVPA (Etzel et al., 2009). For instance, defining an ROI anatomically allows for statistical independence of the ROI (Kriegeskorte et al., 2009). Further, using an anatomical ROI allows classification of activity patterns that might vary over relatively large distances across subjects and/or be distributed over a considerable area, which searchlight analyses would miss. Indeed, none of the searchlights (Figure 4) showed classification beyond two pair-wise decision rule comparisons, while the LPFC ROI showed classification across five of six possible pair-wise comparisons (Figure 2C). This suggests that the LPFC results are likely based on spatially variable and/or spatially distributed activation patterns within LPFC.

Our primary analyses were restricted to LPFC based on strong evidence from previous studies that LPFC represents task rules. We found that decision rules may be represented in a distributed manner within LPFC. However, it is also possible that LPFC is a component of an even more distributed, brain-wide network involved in rule representation (Cole and Schneider, 2007; Duncan, 2010). Thus, it will be important for future research to explore decision rule representations in other parts of the brain, especially those that are functionally connected with LPFC.

The current results significantly extend the findings of several previous studies that have successfully identified abstract rule representations within LPFC. In particular, nearly all prior work on abstract rule representation has focused on simple tasks that involve the application of only a single, highly practiced rule on each trial (e.g., Asaad et al., 2000; Wallis et al., 2001; Bunge et al., 2003; Wallis and Miller, 2003; Haynes et al., 2007; Bode and Haynes, 2009; Stiers et al., 2010; Woolgar et al., 2011). Several of these studies included more than one rule (Woolgar et al., 2011; Reverberi et al., 2011), but they were not integrated and so only a single rule had to be applied on each trial. In contrast, the present study used somewhat more complex tasks that each involved multiple integrated and interchangeable rules that were frequently performed in novel contexts. These differences provided our study with several advantages. First, using multiple interchangeable rules for each task allowed us to test for abstract rule representations more rigorously than previous studies, given that we could test for generalization of rule representations not only across different stimuli and responses but also across different rule combinations. Second, using complex, rule-integrated tasks (as opposed to tasks involving simple stimulus–response rules, e.g., Bode and Haynes, 2009; Woolgar et al., 2011) made task-independent rule generalization non-trivial, as it was not clear a priori that procedures underlying such rules would be represented in a compositional manner in the brain. Third, the use of complex and novel tasks provided increased ecological validity as an investigation of human mental flexibility, as these kinds of tasks more closely approximate the types of novel problem-solving and task learning situations that individuals tend to encounter outside of the laboratory (Gottfredson, 1997; Gottfredson and Saklofske, 2009; also see Singley and Anderson, 1989, for ecologically valid complex rule-integrated tasks involving text editing). Finally, including both practiced and novel tasks allowed us to test our main hypothesis: that rule representations used in practiced tasks transfer to novel tasks to allow for accurate performance in novel circumstances.

The present results are compatible with, but significantly extend upon, a recent demonstration of compositional coding in LPFC (Reverberi et al., 2011). They used MVPA to show that complex tasks (composed of two rules) could be decoded using brain activity patterns identified from the simple constituent rules. Critically, however, their rules were not integrated during the complex tasks (i.e., they were maintained together but the outcome of one rule did not influence the other), leaving open the possibility that LPFC uses compositional coding only when rules are executed independently. The present results demonstrate compositional coding within LPFC even when rules are highly integrated. These results further extend upon those of Reverberi et al. (2011) by showing compositionality in a much larger task state space [four different rules in 16 tasks vs. two rules in two contexts (simple vs. compound)]. Finally, these results demonstrate a major advantage of compositional coding by showing behavioral and neural practiced → novel transfer of rule representations.

Our investigation of rule representation during novel task performance is also important because novel task performance is a central component of rapid instructed task learning (RITL; pronounced “rittle”), a recently developed domain of inquiry within cognitive neuroscience (Cole et al., 2010a; Ruge and Wolfensteller 2010). RITL focuses on the mechanisms that underlie learning of new tasks on the order of seconds, with little or no practice, with learning occurring primarily via instruction from symbolic cues. Consequently, RITL can be distinguished from studies of task-switching since task-switching studies focus on a small set of repeatedly practiced tasks (i.e., the control condition for RITL studies). RITL can also be distinguished from other studies of incremental task learning, since these typically focus on how learning occurs gradually via trial-and-error or reinforcement-based feedback; in RITL, learning is very rapid (e.g., one trial) and based on explicit instructions.

The growing interest in RITL within cognitive neuroscience stems from the need to understand the neural mechanisms that underlie what has been called “the great mystery of human cognition” (Monsell, 1996) – the ability of the human brain to be rapidly programmed with novel procedures (Cole et al., 2010a; Hartstra et al., 2011; Ruge and Wolfensteller, 2010). This impressive mental flexibility is central to human intelligence, compatible with the observation that individual differences in RITL ability are highly correlated with general fluid intelligence (Dumontheil et al., 2011). Although to our knowledge this is the first study to investigate the rule representations underlying RITL with MVPA, we expect that the increasing recognition of the utility of MVPA will make its use in this domain a growing trend.

One potential alternative interpretation of the present results is that they do not specify a role for LPFC in the coding of rule representations, but rather reflect the coding of visual or linguistic information present in rule cues. This interpretation is unlikely, however, given that information regarding semantic or response rules could not be consistently decoded from LPFC activity. Each of these other two rule dimensions were presented along with the decision rules, and were specified via the same kinds of visual and linguistic cues as used for the decision rules. Thus, a brain region involved in visual or linguistic coding should have shown equal sensitivity to all three rule dimensions. Instead, the current results suggest that LPFC was primarily involved in representing the task-related meanings of the decision rules.

Another possible alternative interpretation of the results is that the apparent decision rule sensitivity in LPFC actually reflects sensitivity to cognitive demands associated with the difficulty of implementing different decision rules. Although it is impossible to strictly rule out such an interpretation, behavioral performance measures suggest no strong difference in difficulty among the four decision rules, with the possible exception of the SAME rule having slightly worse performance. Moreover, if LPFC activity patterns reflected the differential difficulty associated with particular task rules, then a difficulty-related bias in classification performance would be expected – e.g., the classifier was actually discriminating more difficult from less difficult rules. Yet, such effects were not observed in the pair-wise decision rule classifications. Instead, nearly every pair-wise classification was significant, not just those involving the potentially more difficult SAME rule. Further, difficulty-related activation effects would likely show up in terms of mean across-voxel signal differences, such as those typically detected by general linear models (Duncan and Owen, 2000; Cole and Schneider, 2007). However, mean cross-voxel differences in activation level were removed by our use of spatial z-normalization, which adjusted for overall mean differences in signal within the ROIs (and each searchlight in the searchlight analyses). Finally, if rule classification was driven by differential rule difficulty then we would expect differences in classification accuracy to correlate with differences in difficulty (in terms of reaction time or behavioral accuracy), yet neither of these correlations were statistically significant (p > 0.75).

Unlike here, a previous study found that activity patterns in LPFC could distinguish between semantic rule representations (Li et al., 2007). That study used visual categorization of moving dot patterns as the basis for semantic categorization. This is in contrast to the present study’s use of diverse perceptual categories based on word stimuli. These categories were designed to be as semantically distinct from one another as possible (each involving a distinct sensory modality), in order to better test the compositional context-independence of decision rules by covering a wide set of distinct semantic rule contexts. The substantially different semantic representations involved across these semantic rules likely reduced the chances of a single region (such as LPFC) containing all of the relevant representations across the categories (see Goldberg et al., 2006a). Alternatively, functional MRI or the MVPA approach used here may not have been sensitive enough to distinguish subtle differences in activity patterns associated with each semantic rule.

The present study focuses primarily on representation of information within LPFC, while many studies have found evidence of process-specific involvement of LPFC (e.g., Duncan et al., 1995; Chein and Schneider, 2005). This reflects a recent shift in emphasis on representational content, rather than processes, within LPFC (Wood and Grafman, 2003). However, several theories of LPFC function can accommodate both representational and processing functions. For instance, it may be that activation of specific representations within LPFC lead to implementation of processes via top-down “context” biases (Cohen et al., 1996; Miller and Cohen, 2001).

Previously reported results using the same dataset as here emphasized differential activation among LPFC regions rather than spatial patterns of information contained within those regions (Cole et al., 2010a). Importantly, those results are complementary to the results reported here. The current results suggest that the same rule representations are used across task contexts, but they do not indicate the mechanism by which rule representations transfer from practiced to novel tasks. The previous study found evidence for a mechanism involving anterior PFC (aPFC) as a coordinator of rule representations in posterior PFC. This mechanism might allow transfer by providing the appropriate co-activation/coordination of multiple practiced compositional rules in novel task contexts. It may be the case that aPFC uses task-specific coding (in conjunction with the compositional coding identified here) to enable coordinated use of several compositional rule representations that have never been used together before. Future work should investigate the possibility of such conjunctive codes in addition to the compositional codes identified here. See Cole et al. (2010a) for discussion of other alternative explanations of the observed LPFC activity.

In conclusion, the present results demonstrate for the first time that the human brain codes task rules that are compositional (i.e., abstract/independent of task context) and utilized even when such an abstracted, compositional form of coding is unnecessary (i.e., during highly practiced tasks). As such, the findings contrast with theoretical accounts suggesting that PFC representations are fully adaptive, flexibly reconfiguring according to changes in task context (Duncan, 2001). The alternative interpretation warranted by our results is that task rule representation is less flexible, and thus indicative of a seemingly suboptimal control system. However, the transfer effects observed between practiced and novel tasks suggest that the context-independent and compositional coding of task rules actually comes with its own advantage: rules learned during (or prior to) the practice session can be rapidly transferred to new contexts, allowing high performance on the first trials of novel tasks. Thus, the seemingly paradoxical consequence of less flexible task rule representation is that it enables greater cognitive and behavioral flexibility during novel task learning and performance – a key aspect of human intelligence.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.