Synthesis and Characterization of a Hydrogel with Controllable Electroosmosis: A Potential Brain Tissue Surrogate for Electrokinetic Transport

Abstract

Electroosmosis is the bulk fluid flow initiated by application of an electric field to an electrolyte solution in contact with immobile objects with a non-zero ζ-potential such as the surface of a porous medium. Electroosmosis may be used to assist analytical separations. Several gel-based systems with varying electroosmotic mobilities have been made in this context. A method was recently developed to determine the ζ-potential of organotypic hippocampal slice cultures (OHSC) as a representative model for normal brain tissue. The ζ-potential of the tissue is significant. However, determining the role of the ζ-potential in solute transport in tissue in an electric field is difficult because the tissue's ζ-potential cannot be altered. We hypothesized that mass transport properties, namely the ζ-potential and tortuosity, could be modulated by controlling the composition of a set of hydrogels. Thus, poly(acrylamide-co-acrylic acid) gels were prepared with three compositions (by monomer weight percent): acrylamide/acrylic acid 100/0, 90/10, and 75/25. The ζ-potentials of these gels at pH 7.4 are distinctly different, and in fact vary approximately linearly with the weight percent of acrylic acid. We discovered that the 25% acrylic acid gel is a respectable model for brain tissue, as its ζ-potential is comparable to the OHSC. This series of gels permits the experimental determination of the importance of electrokinetic properties in a particular experiment or protocol. Additionally, tortuosities were measured electrokinetically and by evaluating diffusion coefficients. Hydrogels with well-defined ζ-potential and tortuosity may find utility in biomaterials, analytical separations, and as a surrogate model for OHSC and living biological tissues.

Introduction

When an electric field is applied across an electrolyte-filled, porous matrix, electrophoresis and electroosmosis may occur. The electrokinetic transport velocity depends on properties of the matrix and solutes. Electrophoresis is the movement of a charged solute under the influence of an applied electric field, traditionally used for separation and analysis. In contrast, electroosmosis is the bulk fluid flow that is stimulated when an electric field is applied to an electrolyte solution in a porous, charged matrix. The counterions that accumulate in proximity to a charged surface, such as that of a polymeric hydrogel, produce a net charge density in the electrolyte that results in electroosmotic flow upon application of an electric field. Two related approaches may be used to describe this phenomenon. In the first case, the charged matrix is viewed as a surface with a given charge density in contact with an electrolyte solution with a given permittivity that leads to the development of a ζ-potential at a particular electrolyte concentration. The electroosmotic velocity of the electrolyte solution in an electric field is proportional to the ζ-potential. In the second case, the fluid medium is taken as having an effective volumetric charge density resulting from the counterions to the fixed charges on the porous matrix. The volumetric charge density and ζ-potential are proportional when the pore size within the matrix is much larger than the thickness of the electrical double layer.¹ Using the ζ-potential to describe electrokinetic phenomena allows for the correlation of a wide variety of experimental results on both electrophoresis and electroosmosis, e.g: proteins, nanoparticles, macroscopic surfaces, microfluidic device surfaces, as well as gels have all been described in these terms. When the pore size in a matrix is of the same order or smaller than the Debye length, this model also allows for the treatment of electrical double layer effects. The effective charge density framework is desirable to describe mass transport according to the Navier-Stokes-Brinkman equations, as the product of the applied electric field and effective charge density has units of a pressure gradient.¹ Similarly, very detailed formulations of the force balance problem in the electrokinetic transport of nanoparticles through gels can provide insight into the role of factors such as the hydraulic permeability of the hydrogel, frictional coupling between particles and the gel, the gel segment number density as well as the hydrogel charge density.² However, in this paper, we will use the ζ-potential framework.

In the simple case of an open, electrolyte-filled capillary, the electroosmotic velocity of a neutral solute is governed by the ζ-potential at the capillary wall and the magnitude of the applied electric field. This relationship may be simply described by the Helmholtz-Smoluchowski equation as shown in Equation 1, where v_eo,o is the electroosmotic velocity in the open tube, η is the viscosity of the medium, ε is the permittivity of the fluid, ζ is the ζ-potential, μ_eo,o is the corresponding electroosmotic mobility, and E is the applied electric field.

$${\mathit{v}}_{\mathrm{eo},o}={\mu }_{\mathrm{eo},o}\mathit{E}=-\frac{\epsilon \zeta }{\eta }\mathit{E}$$ (1)

In porous media such a gels, several factors act to impede solute transport. Viscous coupling to the gel network,^2–3 the tortuous nature of the medium,⁴ and even the structure of the porous medium^4–5 all contribute to what is commonly termed tortuosity. This concept has been developed in the neuroscience literature through discussion of hindered diffusion.⁶ According to Nicholson et al., the tortuosity of a medium can be determined as a ratio of the diffusion coefficients for a molecule in free solution to a molecule in the tortuous medium (i.e.: the matrix of interest), as given by Equation 2 where λ is the tortuosity, D is the diffusion coefficient in free solution, and D* is the diffusion coefficient in the medium of interest.⁶

$$\lambda =\sqrt{\frac{D}{D^{\ast }}}$$ (2)

With the assumption that the frictional drag force – consisting of hydrodynamic interactions and steric effects – acts to impede transport to the same degree in diffusion and electroosmosis/electrophoresis, eq. 1 can be restated for the porous medium as Equation 3.

$${\mathit{v}}_{\mathit{eo}}=\frac{{\mu }_{\mathit{eo}}}{{\lambda }^2}E=-\frac{\epsilon \zeta }{{\lambda }^2\eta }E$$ (3)

It is worth restating that the use of ζ and λ rather than more detailed mathematical formulations of the electrostatic and frictional problems, is done for convenience. Deriving these lumped parameters from data is straightforward, but their use certainly obscures a certain amount of detail.

Poly(acrylamide)-based hydrogels applied to separations were first developed over fifty years ago, and their utility was explored for separation of proteins, DNA, and other macromolecules.⁷ One reason for the wide acceptance of poly(acrylamide) over other matrices used for electrophoresis is the lack of significant electroosmotic flow, and thus a ζ-potential. Interestingly and in contrast, there has been considerable work in recent years for the development of separations matrices that provide electroomosis to separate both neutral and charged molecules.⁸ For example, Fujimoto et al. introduced negatively charged sulfonate moieties into an acrylamide-based hydrogel to increase separation of neutral molecules under physiological pH.^8e Anionic gellan gels can be crosslinked by Ca²⁺, but the resulting gel is not neutral. The additive poly(ethylene oxide) reduces electroosmotic flow in these gellan gels to aid with electrophoretic separation.^8c Negatively charged polyacrylamide-based matrices have also been synthetically prepared for capillary electrochromatography.^{8e, 9} Acrylates have also been used as the organic component in organic-silica hybrid monolithic capillary columns.^{8f, 10} Multilayered polyelectrolytes incorporating acrylic acid have been developed for control of electroosmotic flow in capillaries and microfluidic channels. By suitable control of the surface modification chemistry, a range of electroosmotic mobilities can be obtained at pH 7.4 (or other values).¹¹ Introducing silica nanoparticles into polyacrylamide hydrogels^8b creates an electroosmotic pumping mechanism to increase solute flux into and out of polyacrylamide hydrogels.¹² These nanoparticle-doped hydrogels have been assessed theoretically to understand how the added nanoparticles alter solute flux in an electric field.¹³ Thus, the development and fine control over electrokinetic transport in polymeric gels, and in channels with walls of multilayered polyelectrolytes, have been of long-standing interest and practical importance.

The translational motion of molecules in the extracellular space of biological tissues is typically viewed as occurring by diffusion and tortuosity.¹⁴ Electroosmotic flow represents an additional transport mechanism that can occur in tissues due to natural processes, such as neuronal depolarization¹⁵ or due to applied electric fields.¹⁶ We have previously measured the ζ-potential and tortuosity of organotypic hippocampal slice cultures (OHSC) as a representative for living brain tissue. The ζ-potential of OHSC is −22.8±0.8 mV and the tortuosity is 2.24±0.10.¹⁷ The ζ-potential of skin pores is also important, as electroosmosis is a fundamental component of transdermal iontophoresis.¹⁸ While electroosmotic transport in skin has been investigated for many years, the understanding that the ζ-potential in brain is significant is recent. We have demonstrated the application of electroosmosis in OHSC for drawing peptides through the OHSC, followed by analysis of the captured sample to infer peptidase activity in the extracellular space.¹⁹ However, in the work just cited, or any related attempt to use electroosmosis in brain, it is necessary to assess the degree to which electroosmosis contributes to solute transport. Unfortunately, it is impossible to control the ζ-potential in the extracellular space of a living tissue, as the ζ-potential is intrinsically tied to the physical composition of the tissue. A model system for tissue is therefore necessary to reproducibly control the ζ-potential and tortuosity to evaluate the transport contribution from electroosmosis.

As such, we developed poly(acrylamide-co-acrylic acid) hydrogels with a range of ζ-potentials and tortuosities. At physiological pH, the acrylic acid exists as the negatively charged acrylate species. These fixed anions create a ζ-potential in the gel polymer matrix. Three hydrogels were prepared with 0, 10, and 25% (w/w) acrylic acid. These three types of hydrogel had distinctly different ζ-potentials and degrees of electroosmosis, with the highest acrylate content hydrogel demonstrating a ζ-potential comparable to the OHSC. This work describes the synthetic preparation of the three hydrogel types as well as the determination of their ζ-potentials and tortuosities. The result is a set of gels with well-known ζ-potentials and tortuosities.

Experimental

Chemicals

All reagents used to make the poly(acrylamide-co-acrylic acid) hydrogels were purchased from Aldrich (St. Louis, MO) and were used without additional purification. Fluorescent dyes –Texas Red dextran conjugate 70 kDa (TR70), fluorescein dextran conjugate 70 kDa (FL70), and Texas Red dextran conjugate 3kDa (TR3) – were purchased from Invitrogen/Molecular Probes (Eugene, OR).

Standard Solution Preparations

HEPES-buffered salt solution (HBSS) containing (mM): 143.4 NaCl, 5 HEPES, 5.4 KCl, 1.2 MgSO₄, 1.2 NaH₂PO₄, and 2.0 CaCl₂, was prepared with 18 MΩ purified water from a Millipore Synthesis A10 system (Millipore, Billerica, MA), filtered, adjusted to pH 7.40, and refrigerated at 2.6 °C. It was warmed to 37 °C before use. TR70 and FL70 were dissolved in HBSS to make 0.34 mM and 0.67 mM solutions, respectively, then filtered with 13 mm, 0.45 μm nylon filter units or equivalents (Millipore) and frozen until use. Before use, dextran conjugates were modestly diluted with HBSS to final concentrations of 0.19 mM for TR70, 0.29 mM for FL70, and 0.40 mM for TR3.

Synthesis of Hydrogels

Poly(acrylamide-co-acrylic acid) hydrogels were prepared by a thermally-initiated radical polymerization reaction. The total weight of reagents was kept constant (279 mg/5 mL) while the component w/w ratios of acrylic acid and acrylamide were varied, as described in Table 1. The gels had an acrylic acid percentage of 25%, 10%, and 0% (weight of acrylic acid/weight of all monomer species). The bisacrylamide cross-linker was maintained at a fixed weight percentage of approximately 1.4%. Early efforts to weigh this small amount of cross-linker with a standard electronic balance (Mettler-Toledo, Columbus, OH, Model AG245; readability 0.1 mg) resulted in somewhat variable gel parameters. In later experiments, the cross linkers was more accurately weighed (Mettler-Toledo, Columbus OH, Model XS105DU; readability 0.01 mg). This is described further in the results and discussion section.

Table 1.

Table of reagents for each synthetic gel type.

	25%		10%		0%
	weight (mg)	mmol	weight (mg)	mmol	weight (mg)	mmol
Acrylamide	206.0	2.90	247.5	3.48	275.0	3.87
Acrylic Acid	69.0	0.96	27.5	0.38	0.0	0.00
Bisacrylamide	4.0	0.03	4.0	0.03	4.0	0.03

The reagents were weighed and dissolved in 4.5 mL of ultrapure water (Cayman Chemical, Ann Arbor, MI) each and stirred vigorously for 5 minutes. The solutions were then titrated to a pH range of 7 to 8 using an aqueous 1 M NaOH solution. The final solution volumes were brought to 5.0 mL with ultrapure water. The three solutions were then deaerated with nitrogen for 20 minutes at room temperature. Immediately after deaerating, 5.0 mg of ammonium persulfate (0.02 mmol) and 5.2 μL of tetramethylethylenediamine (TEMED, 0.03 mmol) were quickly added to each solution, which was vigorously stirred for another 3 minutes at room temperature. Each clear solution was poured in a 50 mm × 16 mm Pyrex glass dishes and placed inside an oven at 100±5 °C for 2 hours. The Pyrex dishes were removed from the oven and allowed to cool for 10 minutes at room temperature. The clear, colorless gels were separated from the Pyrex dish walls and slowly peeled from the dish. Each gel was individually placed in a covered plastic dish filled with approximately 25 mL HBSS solution and shaken lightly at 10 °C overnight. The buffer solution was exchanged the following day with 25 mL of fresh HBSS, placed back in the shaker at 10 °C for another 24 hours. Finally, the HBSS was exchanged once more (25 mL), and the gels were placed in the refrigerator where they were allowed to complete the equilibration. A final pH check was performed to assure the gels were pH 7.40 with full immersion of the probe into the gel before further characterization.

Characterization of the ζ-Potential & Tortuosity

The experimental apparatus was used without modification from our previously reported setup.¹⁷ Briefly, the velocities of the probe solutes FL70 and TR70 were simultaneously observed with an Olympus IX-71 inverted fluorescence microscope with an Olympus UPlan Apo 4× objective lens (Melville, NY), and a charge-coupled device camera (ORCA-285 Hamamatsu, Hamamatsu City, Japan). A DA/Fl/TA-3C-A triple-band “Pinkel” filter set (Semrock, Rochester, NY) with exciter 1 at 387 nm, exciter 2 at 494 nm, exciter 3 at 575 nm, triple-band dichroic mirror: 394–414 nm, 484–504 nm, 566–586 nm, emitter: 457, 530, 628 nm were used according to the fluorescence properties of the molecules.

The gel was injected with a solution of TR70 and FL70 using a FemtoJet® express (Hamburg, Germany). A constant electric field was maintained in the gel using a four-electrode potentiostat coupled with a differential amplifier, while reference Luggin capillary electrodes monitored the electric field through the hydrogel. An electric field between 60 and 250 V/m was applied to each gel. One image was acquired every second. The electric field was monitored at the two Luggin capillaries and at the platinum electrodes in the reservoirs by two multimeters to ensure accurate control of the electric field. Movement of a fluorophore towards the cathode was defined as positive movement. The velocities of the TR70 and FL70 fluorophores were measured post-analysis using Simple PCI 6 software (Cranberry, PA). Specifically, the velocity was measured as the distance that the fluorophore moved over a period of time. The locations of the fluorophores were defined by their maximum peak intensities at time zero and at some other time during the experimental run. Typically, 6 to 9 timepoints (30 to 60 seconds apart) were analyzed per run to arrive at an average velocity.

The ζ-potential and tortuosity for each gel were extracted as follows.¹⁷ The observed mobility, μ_obs, is described by Equation 4, as the sum of the electroosmotic (μ_eo) and electrophoretic (μ_ep) mobilities, where the electroosmotic mobility is provided by Equation 1.

$${\mu }_{\mathit{obs}}=\frac{v_{\mathit{obs}}}{E}=\left(\frac{1}{{\lambda }^2}\right)({\mu }_{\mathit{ep}}+{\mu }_{\mathit{eo}})=\left(\frac{1}{{\lambda }^2}\right)\left({\mu }_{\mathit{ep}}-\frac{\epsilon \zeta }{\eta }\right)$$ (4)

By simultaneously determining μ_obs for two fluorescent dextran conjugates, the ζ-potential and tortuosity (λ) may be determined according to Equations 5 and 6, where the numerical subscripts refer to the two dextran conjugates.

$$\zeta =\frac{{\mu }_{\mathit{obs}1}\frac{({\mu }_{\mathit{ep}1}-{\mu }_{\mathit{ep}2})}{({\mu }_{\mathit{obs}1}-{\mu }_{\mathit{obs}2})}-{\mu }_{\mathit{ep}1}}{\left(\frac{-\epsilon }{\eta }\right)}$$ (5)

$$\lambda =\sqrt{\frac{{\mu }_{\mathit{ep}1}-{\mu }_{\mathit{ep}2}}{{\mu }_{\mathit{obs}1}-{\mu }_{\mathit{obs}2}}}$$ (6)

Measurement of Solute Diffusion Coefficients in the Gels

Nicholson and Tao have shown how to determine whether the optical properties of the objective and microscope will yield a two-dimensional image that accurately represents the three-dimensional, radially symmetrical concentration distribution that is expected following the injection of a small volume of dye into a gel.^{6, 20} Using our parameters (objective lens magnification: 4×; NA: 0.16; microscope tube length: 180 mm), we find that the lateral resolution (2.3 μm) is a very small distance compared to the features of the Gaussian curves (typically 100 to 200 μm in diameter). Thus, TR70 or TR3 solutions were injected (Femtojet, Eppendorf, Hamburg, Germany) into a gel under the fluorescence microscope. An image was taken every 2 to 5 seconds for a total duration of 3 to 6 minutes to record the diffusion of the fluorophore. All experiments were conducted at ambient temperature (24 to 26 °C). Following acquisition, the images at 10 second time intervals were exported as an (x,y)-matrix of fluorescence intensities. Images as (x,y)-matrices of fluorescence intensities were imported into OriginPro 8.1 software (OriginLab, Northampton, MA). A two-dimensional Gaussian surface was fit to the data set in order to find the peak. The image was then cropped three standard deviations from the peak's center in the x- and y-directions. With this reduced data set, a second Gaussian fit was performed. The standard deviations in the x- and y-directions were very similar and consistent with the Gaussian fit. The variance was plotted against time and a linear regression was performed. If a line fit had an R² value less than 0.95, it was not included in the final average. As with work by Nicholson et al., dividing the slope of this line by four afforded the diffusion coefficient.⁶ Averaging the diffusion coefficients from each run (typically 3 to 6 runs per gel) allowed determination of a final diffusion coefficient with standard error.

Photobleaching of the fluorescent dextran conjugates was evaluated using 0% acrylic acid hydrogels doped with either TR3 or TR70 under the most potentially damaging condition – one image per second. The hydrogels were allowed to equilibrate overnight in a solution of the respective fluorophore in HBSS. The hydrogel was removed, and cut to a thickness of 1 mm. The hydrogel fluorescence was imaged with a 0.3 sec or 0.1 sec pulsed exposure time for TR70 and TR3 respectively. (as for diffusion coefficient and □-potential determinations) for TR70 and TR3 respectively. The mean fluorescence intensity within a circular region of interest drawn at the center of the microscopy field was observed for 3.5 min. In no case was there a change in fluorescence intensity greater than 1%.

Free Diffusion Coefficients of Dextran Conjugates

Free diffusion coefficients were determined as described in Beisler et al.²¹ HBSS mobile phase pumped through the system using a Pico Plus syringe pump (Harvard Apparatus, Holliston, MA). The sample solutions were injected using an HP 1050 autosampler (Hewlett-Packard, Palo Alto, CA) into a 1 μL loop in a VICI 6-port Cheminert Injector (Houston, TX). An ISCO 3850 Capillary Electropherograph UV detecctor (Teledyne ISCO, Lincoln, NE) was used for detection (215 nm) of the fluorophores. Signals were collected by Peaksimple 3.29 software (SRI Inc., Torrance, CA) for analysis. The data were imported into OriginPro for differentiation, followed by the determination of the first and second central moments using PeakFit 4.0 software (Systac Software Inc., San Jose, CA). Diffusion coefficients were calculated from the slopes of second moment versus first moment linear plots. In addition, errors for the diffusion coefficients were calculated based on the error of the slope, assuming negligible error in the flow rate, capillary length, and capillary diameter.

Characterization of the Hydrogel Water Content

The water content of each gel was determined by weighing after dehydration. A 10 mm × 10 mm piece of gel was cut and placed inside of a pre-weighed 1.8 mL ROBO autosampler vial (VWR, West Chester, PA). The aggregate weights were recorded for each vial, and they were placed in an oven at 110 °C overnight. The vials were removed from the oven and reweighed. The water content, by weight, was determined by subtracting the post-dehydration weight from the pre-dehydration weight, controlling for the autosampler vial weight and residual salt content within the HBSS buffer. Six runs were completed for each gel type, with the final porosity data provided as an average with standard error.

Statistics

All data are presented as mean ± standard error of the mean (SEM), where N represents the number of experimental runs. Comparisons amongst groups were made by one-way analysis of variance (ANOVA) with p<0.05 considered as significant.

Results

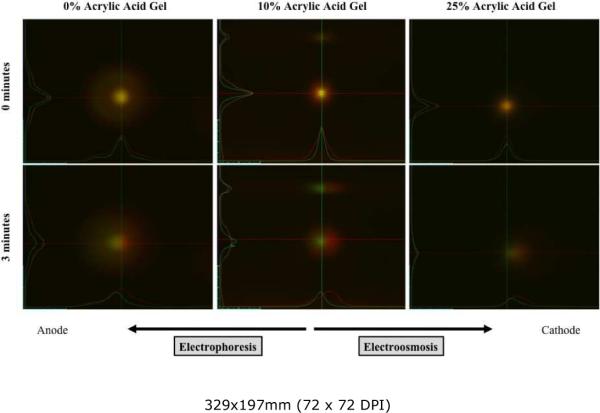
As demonstrated in Figure 1, while under a constant electric field, in the 0% acrylic acid gel composition there is significant movement of the anionic FL70 dextran conjugate (electrophoretic mobility −8.80±0.2 ×10⁻⁹ m²/Vs, N=3)²² towards the anode and negligible movement of the weakly cationic TR70 dextran conjugate (electrophoretic mobility 0.46±0.03 ×10⁻⁹ m²/Vs, N=3, slightly different from published value due to our using TR70 with a different commercial batch number),²² The 10% acrylic acid gel composition showed movement of the TR70 dextran conjugate towards the cathode and negligible movement of the FL70 dextran conjugate, while the 25% acrylic acid gel composition showed movement of both the FL70 and TR70 dextran conjugates towards the cathode. These results indicate qualitatively that as the percentage of acrylic acid increases, the ζ-potential becomes more negative, and there is an increasing contribution of electroosmosis to the observed field-induced velocity.

Figure 1.

Representative example of electrokinetic transport of TR70 (red) and FL70 (green) dextran conjugates under a uniformly applied electric field in poly(acrylamide-co-acrylic acid) gels prepared at 0%, 10%, and 25% w/w acrylic acid.

The magnitudes of the ζ-potential and tortuosity were determined for each hydrogel, as displayed in Table 2. Of note, the ζ-potential is consistent within each set of gels with the same nominal composition, with a linear correlation describing the w/w percentage of acrylic acid and the ζ-potential. One-way ANOVA analysis for the effect of composition (percent acrylic acid) on ζ-potential shows that the effect is significant (p<0.001). Furthermore, as a general trend, for every 1% increase in acrylic acid added to reaction mixture, the ζ-potential changes by −0.9 mV, as shown in Figure 2. Regression of all ζ-potential values versus percentage of acrylic acid yields a correlation that is highly significant (R²=0.91, p<0.001). Moreover, the 25% acrylic acid gel composition demonstrates a ζ-potential similar to the OHSC.

Table 2.

ζ-Potentials and Tortuosities Determined by the Electrokinetic Method.

Gel Type	Gel Code	ζ-Potential (mV)	Tortuosity (λ)	Replicates (N)	Average ζ-Potential (mV)	Average Tortuosity (λ)
0%	0A	−0.3 ± 0.04	1.69 ± 0.16	4	−1.3 ± 0.5§ (N = 16)	2.28 ± 0.13§ (N = 16)
	0B	−1.6 ± 1.1	2.56 ± 0.16	6
	0C	−1.9 ± 0.6	2.39 ± 0.18	6
10%	10A	−13.1 ± 0.3	2.21 ± 0.12	6	−12.8 ± 0.7§ (N = 15)	1.80 ± 0.10§ (N = 15)
	10B	−15.2 ± 0.8	1.46 ± 0.07	5
	10C	−9.5 ± 0.2	1.61 ± 0.08	4
25%	25A	−27.9 ± 0.4	1.39 ± 0.03	6	−24.9 ± 0.9§ (N = 21)	1.44 ± 0.09§ (N = 21)
	25B	−22.1 ± 0.6	1.07 ± 0.03	6
	25C	−24.7 ± 1.7	1.71 ± 0.18	9
25%*	25*	−23.0 ± 0.3	2.36 ± 0.18	4	Not Included

^*Note: the pH for this 25% gel was not adjusted to pH 7–8 before radical polymerization, and is not included in statistical calculations or comparisons.

^§Note: Groups are statistically different by one-way ANOVA (p<0.05).

Figure 2.

Summary of ζ-potential for each hydrogel as a function of the acrylic acid w/w% content. Linear regression fit, R² = 0.91.

To determine the mass of water within the gel, a series of dehydration experiments was performed, the results of which are shown in Table 3. The 25% acrylic acid gel composition had a larger percentage of water than the gels with lower w/w percentages of acrylic acid, with one-way ANOVA revealing a significant difference among the gel types (p<0.001). The fluid content was correlated with the percentage of acrylic acid (R²=0.73, p<0.001). This is consistent with the observation that there is greater swelling in gels containing more acrylate as 291 the negative charges attract counterions with concomitant fluid influx.²³ It is for this reason that careful equilibration of our gels in HBSS was conducted following synthesis and prior to characterization and all experimentation utilized careful control of the pH.

Table 3.

Summary of water content in the various gel types.

Gel Type	Gel Code	Percentage of Water in Gel	Number of Runs (N)
25%	25C	98.3 ± 0.1 %	6
10%	10C	97.5 ± 0.3 %	6
0%	0C	96.6 ± 0.1 %	6

The tortuosities for the 70,000 MW fluorescent dextran conjugates as determined by application of an electric field within each gel type¹⁷ are shown in Table 2. One-way ANOVA demonstrated a significant effect of composition on tortuosity (p<0.001). Additionally, the tortuosity of each gel was significantly correlated with the percentage of acrylic acid added during synthesis (R²=0.24, p<0.0002). Recall that there is also a correlation between gel composition and water content. An increase in the percentage of water results in an increased hydrodynamic volume fraction for the fixed amounts of hydrogel components used in these syntheses. An increase in the hydrodynamic volume fraction will increase the effective pore size in the hydrogel matrix with a concomitant decrease in tortuosity. The tortuosity, as measured according to Equation 2, is to a degree dependent on the hydrodynamic radius of the solute, and by extension its molecular weight.^{22, 25} The hydrodynamic radii of TR3 and TR70 are 1.5 nm and 7 nm respectively.²⁶ We determined D* of the smaller TR3 in the same hydrogels and D by Taylor dispersion measurements, with results also shown in Table 4. As expected, TR3 demonstrated faster diffusion than TR70 in the hydrogels. The tortuosities of the gels as perceived by the solute TR3 in the 25% and 0% acrylic acid gels were 1.02±0.06 and 1.11±0.04 respectively. These values approach unity and reflect that the diffusion of smaller molecules is relatively unhindered compared to larger molecules.

Table 4.

Summary of TR70 and TR3 Diffusion Coefficients and Tortuosities in 25% and 0% Acrylic Acid Gels.

	Observed Diffusion Coefficient (D*) (10−7 cm2/s) 25% Gel (25C)	Observed Diffusion Coefficient (D*) (10−7 cm2/s) 0% Gel (0C)	Free Diffusion Coefficient (D) (10−7 cm2/s) Free D(CE)	Tortuosity (Eq. 2) 25% Gel	Tortuosity (Eq. 2) 0% Gel
Texas Red 70,000 MW	0.94 ± 0.09 (N = 3)	0.62 ± 0.05(N = 3)	3.66 ± 0.16 (N = 32)	1.97 ± 0.20	2.43 ± 0.11
Texas Red 3,000 MW	10.12 ± 1.19 (N = 5)	8.44 ± 0.51 (N = 4)	10.48 ± 0.48 (N = 48)	1.02 ± 0.06	1.11 ± 0.04

Even though there is a significant difference between gel types, there is also a significant range of tortuosity values within each gel type. This range may be due to minor variability in gel synthesis as a result of imprecise weighing of reagents, measurement error in determining the observed velocity of dextran conjugates in the applied electric field, heterogeneity of the gel matrix itself, and to a much lesser extent, affinity of a molecule for the gel matrix and shrinking or swelling of a gel in response to an applied electric field.²⁴ Shrinking and/or swelling may result from local pH changes and the movement of counterions once an external electric field is applied. This local physical distortion may alter the tortuosity from its equilibrium state without an applied electric field. Typically, gels that demonstrate this phenomenon involve higher concentrations of acrylic acid and lower cross-linker concentrations.^24e

To determine whether there is an effect of electric-field-induced shrinking or swelling, we determined the tortuosity in the absence of an electric field in the 25% acrylic acid gel (which is most susceptible to the electric field). From Equation 2, the tortuosity of a system without application of an electric field is obtained by merely observing the diffusion of a fluorescent molecule of interest in the gel, yielding D*. To arrive at a value for D, we performed Taylor dispersion measurements of the fluorescent dextran conjugates. The results for these experiments are shown in Table 4. The resulting diffusion coefficient-based tortuosities for the 70,000 MW TR70 dextran conjugate in the 25% acrylic acid gel (Gel Code 25C) were compared to the tortuosities obtained electrokinetically. The two tortuosities were not significantly different (p=0.39). Unlike the 25% acrylic acid gels, the 0% acrylic acid gel should be immune to electric field effects. Thus, as a test of this assumption, D* for TR70 was also measured in a 0% acrylic acid gel (Gel Code 0C). Again, the resulting diffusion coefficient-based tortuosity was not significantly different from the tortuosity obtained from application of an electric field (ANOVA p=0.87). Each of the high and low ζ-potential gel types has a tortuosity that is independent of the characterization method. If electric-field-induced shrinking/swelling occurred to a large extent, the two tortuosity measurements would be different in the 25% acrylic acid hydrogels, but not the 0% acrylic acid hydrogels. This is not the case, therefore the effect of shrinking or swelling of our gels in an electric field is not appreciable.

Other potential sources of error in tortuosity measurement include affinity-type interactions of the fluorophore with the hydrogel matrix and error in determining the diffusion coefficients themselves. Affinity-type interactions are observed in gel electrophoresis applications between the gel matrix and ligand, including with proteins, DNA, and small molecules.²⁷ An affinity-type interaction would result in a slower observed velocity independent of the presence of an electric field, and thus alter both the tortuosity (as measured by electrokinetic or diffusional characterization methods) and ζ-potential measurements. However, dextran conjugates demonstrate a lack of affinity for the biological matrix. Thus, they have been used for extracellular diffusion measurements by Nicholson and Tao (and references therein),⁶ for intracellular measurements of transport,²⁸ as well as for surface modification of membranes to prevent the adsorption of biomolecules.²⁹ Finally, the method of determining diffusion coefficients described in this work is susceptible to error also. The largest source of error is probably the shape of the initial spot of fluorophore. An extended initial spot will lead to a non-Gaussian profile at short times. This may become almost Gaussian at longer times, of course. It is for this reason that we rejected experiments in which the fit to the two-dimensional Gaussian curve was poor (R²<0.95). Retrospective analysis of these omitted runs demonstrated abnormal fluorophore injections and pressure-induced deformation of the gel matrix.

As mentioned above, there may be gel-to-gel differences among gels of the same nominal composition. For example, differences within a gel type may perhaps arise from the inaccuracy of weighing small amounts of the bisacrylamide cross-linker used in the hydrogel synthesis. Altering the bisacrylamide cross-linker concentration (and also the total acrylamide concentrations) was shown to alter dramatically the apparent gel pore size and relative mobilities of small nucleic acids.³⁰ To determine whether the accuracy of the weight of cross-linker was responsible for some of the variability, the bisacrylamide was more accurately weighed (see Experimental) to prepare a series of three 10% acrylic acid gels (Gel Codes 10D,E,F) for comparison to the other 10% acrylic acid gels presented in Table 2. The diffusion coefficient (D*) of TR70 was then characterized in each of these gels, with data shown in Table 5. The average tortuosity for the three gels is 1.62 ± 0.08 (N=13). This can be compared to the electrokinetically determined value of 1.80 ± 0.10 (N=15) in Table 2. While the two methods yielded statistically indistinguishable tortuosity results (p=0.19), accurate weighing of the bisacrylamide cross-linker reduced the variability of the tortuosity results (variance reduced to 0.07 from 0.16). As such, tortuosity may be better controlled by a using a more consistent bisacrylamide cross-linker concentration. Of note, higher cross-linker concentrations result in brittle and opaque hydrogels.

Table 5.

Summary of TR70 Diffusion Coefficients and Tortuosity in 10% Acrylic Acid Gel with 4.0 ± 0.1 mg bisacrylamide.

10% Gel Code	Observed Diffusion Coefficient (D*) (10−7 cm2/s)	Free Diffusion Coefficient (D) (10−7 cm2/s)	Tortuosity (Eq. 2) vs. Free D
10D	1.07 ± 0.11 (N = 4)	3.66 ± 0.16 (N = 32)	1.85 ± 0.10
10E	2.10 ± 0.10 (N = 5)		1.32 ± 0.04
10F	1.22 ± 0.07 (N = 4)		1.73 ± 0.06

Conclusions

Ultimately, poly(acrylamide-co-acrylic acid) hydrogels are relatively easy to produce and may represent a useful matrix for analytical or preparative separations and a synthetic surrogate for biological tissue to understand tissue-related electrokinetic phenomena in a simpler, more controllable environment than tissue itself. The ζ-potential of these gels in physiological buffer is, remarkably, nearly directly proportional to the percentage of acrylic acid used in the hydrogel synthesis. As a result, we are able to mimic the electrokinetic properties of brain tissue, as well as removing the ζ-potential from the matrix. This capability will allow for quantitative determination of the degree to which the ζ-potential contributes to solute transport in brain tissue in an electric field. Moreover, the tortuosities of the hydrogels were determined by application of an electric field and by measurement of field-free diffusion coefficients, with the two methods yielding statistically indistinguishable results. While the tortuosities were different amongst gel types, there was significant variability within each gel type. This variability is probably due to a slight inconsistency between syntheses. It is noteworthy that there is also considerable difference between the tortuosity of acute rat cortical slices (2.25±0.09)⁶ and the tortuosity of rat cortex in vivo (2.68±0.11)²⁶ by measurement of diffusion coefficients. Clearly, the tortuosity of `soft' matter is highly dependent on conditions.

The ζ-potential, tortuosity, and equilibrium fluid content of the hydrogels are all correlated with the percentage of acrylic acid added during synthesis. This is inconvenient from the perspective of determining the relative importance of ζ-potential and tortuosity on molecular transport because a change in the acrylate percentage changes both ζ-potential and tortuosity. However, this correlation is expected. The higher the acrylic acid content, the more swelling is expected – that is, the equilibrium water content is higher. The higher water content leads to a more dilute gel with a larger spacing between polymer chains and thus a lower tortuosity. This internal consistency suggests that the gels studied were at equilibrium, and thus that the results are equilibrium properties of the gels. Moreover, the tortuosity derived from electrokinetic and two-dimensional diffusion coefficient methods was not significantly different. This is the first report in which tortuosity of a material was determined both electrokinetically and by diffusion. This is also, to our knowledge, the first report of the determination of the ζ-potential and tortuosity of hydrogels with correlation of these electrokinetic transport properties with synthetic procedure. Besides representing a synthetic tissue surrogate, the ability to control the gel's properties may afford further utility in the fields of separations, biomaterials, and polymer science.