Abstract
In a previous report, we calculated the infrared absorption spectrum and both the isotropic and anisotropic pump-probe signals for the OD stretch of isotopically dilute water in dilauroylphosphatidylcholine (DLPC) multi-bilayers as a function of the lipid hydration level. These results were then compared to recent experimental measurements and are in generally good agreement. In this paper, we will further investigate the structure and dynamics of hydration water using molecular dynamics simulations and calculations of the two-dimensional infrared and vibrational echo peak shift observables for hydration water in DLPC membranes. These observables have not yet been measured experimentally, but future comparisons may provide insight into spectral diffusion processes and hydration water heterogeneity. We find that at low hydration levels the motion of water molecules inside the lipid membrane is significantly arrested, resulting in very slow spectral diffusion. At higher hydration levels, spectral diffusion is more rapid, but still slower than in bulk water. We also investigate the effects of several common approximations on the calculation of spectroscopic observables by computing these observables within multiple levels of theory. The impact of these approximations on the resulting spectra affects our interpretation of these measurements and reveals that, for example, the cumulant approximation, which may be valid for certain systems, is not a good approximation for a highly heterogeneous environment such as hydration water in lipid multi-bilayers.
INTRODUCTION
Understanding the structure and dynamics of hydration water around biological molecules is an important problem, as much of the water in a cell is closely associated with proteins, DNA, and lipid membranes.1, 2, 3 Hydration water is known to affect strongly the stability, fluidity, and phase behavior of lipid bilayers, for example, and the dynamics of such “biological water” is typically slowed relative to the bulk.4, 5, 6, 7 Many techniques such as x-ray and neutron diffraction,5, 6, 8, 9 dielectric relaxation,10, 11, 12 fluorescence,13, 14, 15 NMR,16, 17, 18 and infrared spectroscopy19, 20, 21, 22 have been used to study water molecules interacting with lipid systems, and molecular dynamics simulations have allowed for the microscopic investigation of hydration water.23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 For a bilayer composed of phosphatidylcholine (PC) lipids, these techniques suggest that water molecules form strong hydrogen bonds with the lipid phosphate groups, and a smaller fraction of water molecules bind deep within the lipid headgroup region to the lipid carbonyl oxygens.9, 18, 29, 39 Water also is thought to form a clathrate-like cage around the choline headgroup, though for other lipids such as phosphatidylethanolamine, water forms direct hydrogen bonds to the amine group.23, 24, 25
Infrared spectroscopy has the potential to investigate more fully the local structure and dynamics of hydration water, as the OH stretch is sensitive to its local hydrogen-bonding environment, with strong hydrogen bonds resulting in a decrease in the stretching frequency. However, in neat water, the stretching modes are nearly resonant and coupled together, resulting in vibrational modes that can extend over multiple water molecules.40 In order to probe local structure, isotopically dilute HDO in H2O is thus often used, as the OD stretch is off resonance from the other water stretching modes, while the small number of deuterium atoms makes only a minimal perturbation to the water dynamics.41 This technique has been used to study systems including bulk water and ice, water in aqueous salt solutions, and water in reverse micelles.42, 43, 44, 45, 46, 47, 48, 49 Zhao et al.22 have recently measured the Fourier transform infrared (FTIR) spectrum of isotopically dilute hydration water in dilauroylphosphatidylcholine (DLPC) lipid multi-bilayers as a function of hydration level, as well as both the isotropic and anisotropic pump-probe signals. They observed a systematic redshift in the OD absorption peak as the lipid hydration level was decreased from X = 16 to X = 2, where X is defined as the ratio of water to lipid molecules. As the hydration level decreased, Zhao et al. also observed a slow-down in the decay of the anisotropic pump-probe signal, indicating that water molecules undergo slower reorientational motion at low hydration levels. The isotropic pump-probe signal, which provides information on the vibrational lifetime of the OD stretch, decayed with two separate time scales, which Zhao et al. ascribed to two populations of water molecules: “lipid-bound” and “bulk-like” waters. They observed that as hydration is decreased, the vibrational lifetimes for each component increase, and for each hydration level, the lifetime of the bulk-like waters is longer than the lipid-bound lifetime.22
In part one of this series, Ref. 50, we used molecular dynamics simulations and a mixed quantum∕classical model for the water OD stretch to calculate the spectroscopic observables measured experimentally by Zhao et al. Our calculated FTIR absorption spectra qualitatively reproduced the observed redshift as lipid hydration was decreased, and we further analyzed this redshift by calculating the spectral densities for water in various environments. In order to calculate the isotropic pump-probe signal, we divided the OD stretches into two populations: “lipid-associated” and “water-associated” groups. The vibrational lifetime T1 for each population was then treated as an adjustable parameter, and we determined best-fit lifetimes in order to match the experimental isotropic pump-probe spectra. Our fitted lifetimes are systematically longer than those inferred directly from experiment.22, 50 Finally, in Ref. 50 we computed the anisotropic pump-probe decay, while including vibrational lifetime and non-Condon effects in the calculation. These results are in reasonable agreement with the experimental results, while calcuations within the common “P2” approximation51, 52 showed relatively poor agreement.
In this second part of the series, we will now turn to other third-order techniques such as two-dimensional infrared (2DIR) and vibrational echo peak shift spectroscopy. While Volkov et al. used a 2D infrared hole-burning technique to investigate water hydrogen-bonding in a PC lipid bilayer system,21 such measurements have not yet been performed experimentally for lipid multi-bilayers as a function of hydration level, and so we will calculate these observables in hopes of providing a comparison for future experiments. While the peak shift and 2DIR methods are derived from the same third-order processes that generate the pump-probe spectra, there are more time degrees of freedom available, and as such 2DIR and peak shift spectroscopy can provide information unobtainable from the FTIR or pump-probe spectra.53, 54, 55 The peak shift signal and the 2DIR lineshape are sensitive to spectral diffusion processes on the picosecond time scale, and this spectral diffusion is in turn a result of hydration water and lipid dynamics.56, 57 While these fast dynamics are in principle probed with peak shift and 2DIR spectroscopy, the interpretation of the experimental results is often unclear. Thus, comparison of theoretical and experimental spectra is useful for a more complete picture of hydration water dynamics.
The interpretation of vibrational spectra often depends upon key simplifying assumptions. For example, the anisotropic pump-probe signal is typically analyzed purely in terms of reorientational motion through the “P2” approximation.51 However, the environmental dependence of the transition dipole matrix elements (non-Condon effects) is non-negligible for the water stretch, as the magnitude of the transition dipole varies by about a factor of five for water molecules in different hydrogen-bonding environments.53 This means that molecules on the red side of the absorption spectrum interact more strongly with electromagnetic radiation. Similarly, the vibrational lifetime of the water stretch depends on local environment, and thus only molecules with a long lifetime will contribute to the spectroscopy at long times. Therefore, while reorientational motion makes a large contribution to the observed anisotropic pump-probe signal, the importance of these other effects cannot be ignored. Likewise, within the Condon approximation53 to the transition dipole matrix elements and within a further cumulant approximation58 to the dynamics, the lineshapes for the FTIR, 2DIR, and peak shift spectra can all be described through the frequency-fluctuation autocorrelation function Cω(t). The cumulant approximation assumes that the OH stretch frequency fluctuations describe a Gaussian process. Analysis of 2DIR spectra therefore allows for the extraction of Cω(t), but this interpretation of the experimental data is only valid if the Condon and cumulant approximations are reasonable. Hydration water, however, samples a chemically heterogeneous environment, and frequency fluctuations take place on multiple time scales. As such, the frequency fluctuations for the water stretch are likely not Gaussian, and the cumulant approximation may not be reliable. As a result, we will investigate the validity of these and other approximations to the calculation of spectroscopic observables and assess their application to a heterogeneous system such as hydration water in lipid multi-bilayer systems.
In this paper, we will use a mixed quantum∕classical model and molecular dynamics simulations to calculate the 2DIR spectra and vibrational echo peak shift signals for hydration water in DLPC multi-bilayers as a function of the hydration level X. In Sec. 2 we review the theoretical methods and approximations for the calculation of spectroscopic observables. We then discuss the impact of approximations on the FTIR absorption spectrum and the anisotropic pump-probe signal in Sec. 3. In Sec. 4 we calculate the vibrational echo peak shift for hydration water and discuss the time scales of spectral diffusion as a function of hydration. The 2DIR spectra and associated center-line slopes (CLS) are calculated in Sec. 5, and the microscopic origin of spectral diffusion is analyzed. In Secs. 4, 5 we also discuss theoretical approximations to the peak shift and 2DIR spectra, respectively. Finally, we summarize our findings and discuss the implications of our calculations for the structure and dynamics of hydration water in Sec. 6.
COMPUTATIONAL METHODS
In order to calculate spectroscopic observables for isotopically dilute HDO in hydrated lipid multi-bilayers, we shall adopt a mixed quantum∕classical model wherein the OD stretch is treated quantum mechanically, other stretching modes and the water bend are ignored, and all other motions are treated classically, as discussed in Ref. 50. The FTIR spectrum I(ω) for the OD stretch chromophore is then given within linear response theory58 by
| (1) |
| (2) |
where ω10(t) is the 1-0 transition frequency of the OD stretching mode at time t, is the 1-0 matrix element of the transition dipole, T1(t) is the vibrational lifetime, and is the polarization of the incident electric field. As in Ref. 50, the incident laser beams are directed along the lipid-bilayer normal (denoted ), and thus we shall only consider . The brackets in Eq. 2 indicate an ensemble average over all classical bath degrees of freedom.
The dipole matrix elements of the transition dipole are taken to lie along the OD bond vector, and the magnitude of the dipole is given by
| (3) |
where x10 is the 1-0 matrix element of the coordinate operator and μ′ is the dipole derivative. Both x10 and μ′ depend on the bath degrees of freedom (termed a non-Condon effect), and previous work in our group has demonstrated that such non-Condon effects make non-negligible contributions to the vibrational spectroscopy of bulk water and ice systems.53 However in the interpretation of experimental spectra, it is common practice to make the Condon approximation, and replace with a constant value. We shall investigate the effects of making this Condon approximation on both linear and third-order vibrational spectroscopic observables in Secs. 3, 4, 5.
If we neglect the effects of dynamics in Eq. 2, and if we further neglect the vibrational lifetime T1, we can approximate I(ω) by the spectral density,
| (4) |
If we further make the Condon approximation to the transition dipole elements in Eq. 4, the spectral density is simply the frequency distribution,
| (5) |
Rather than neglecting dynamics in Eq. 2, it is common to instead make the Condon approximation and then further assume that the frequency fluctuations are Gaussian. This leads to the cumulant approximation58 to the absorption spectrum,
| (6) |
In Eq. 6, g(t) is the lineshape function given by
| (7) |
| (8) |
and Cω(t) is the frequency-fluctuation autocorrelation function. The frequency fluctuations δω are defined by δω(t) ≡ ω10(t) − 〈ω10〉 where 〈ω10〉 is the mean frequency. The cumulant approximation leads to a straightforward interpretation of the spectroscopic lineshape in terms of frequency fluctuations. However, in heterogeneous systems where the frequency fluctuations are not Gaussian, the cumulant approximation fails. This was previously shown to be the case for bulk water,53 and we shall demonstrate that the cumulant approximation performs poorly for hydration water in lipid multi-bilayers.
Vibrational pump-probe spectroscopy is a third-order technique that provides information on molecular reorientations and vibrational lifetimes that is unobtainable from the linear FTIR spectrum.20, 21, 44, 59, 60 By adjusting the relative polarization of the pump and probe beams, both the isotropic and anisotropic pump-probe signal can be measured. The absorption change, assuming impulsive excitation and frequency-resolved detection, for pump and probe beams of polarizations and respectively is given by
| (9) |
where Riikk is the sum of the components of the third-order vibrational response function given in Eqs. A7, A8. The isotropic pump-probe spectrum is then simply
| (10) |
where S∥ signifies and S⊥ signifies . Within the Condon approximation to the transition dipole matrix elements, and if one assumes that the vibrational lifetime T1 is independent of environment, then the decay of P(t) in Eq. 10 is simply due to this vibrational lifetime. However, if the Condon approximation is not valid, or if the lifetime depends on the environment, then the interpretation of the isotropic pump-probe spectrum is less clear, as we discussed in detail in Ref. 50.
The anisotropic pump-probe signal is similarly given by
| (11) |
The anisotropy r(t) is usually interpreted in terms of molecular reorientations, though this is only strictly true if we again make the Condon approximation and assume the vibrational lifetimes are independent of environment.51 Within these approximations, and if we then integrate over the frequency ω in Eq. 9, we obtain the integrated P2 approximation to the anisotropy,
| (12) |
| (13) |
where P2 indicates the second Legendre polynomial and is a unit vector along the OD bond. In Eq. 12, the anisotropic pump-probe spectrum is determined solely by the reorientational motion of the water OD bond vectors. Alternatively, if we do not integrate over ω but instead consider the inhomogeneous limit,51 we obtain a frequency-resolved P2 approximation to r(t; ω),
| (14) |
Other third-order spectroscopic techniques allow us to probe spectral diffusion in a system and to separate the effects of homogeneous and inhomogeneous broadening. One such technique is the integrated vibrational echo intensity which is calculated from the rephasing component of the third-order response function in Eq. A7,
| (15) |
The signal I(t1; t2) is maximal at time , and this peak time typically decreases towards zero as the waiting time t2 increases. The peak shift signal is then obtained by plotting as a function of the waiting time. The decay of with time yields information on spectral diffusion in a system.61 In some cases, such as for heterogeneous systems, the structure of I(t1; t2) may be more complicated and the peak position can be ambiguous. In this case, the first moment,
| (16) |
is more easily used than the peak shift.62 As with the FTIR and pump-probe measurements, we can again make several approximations to the third-order response functions including the Condon and cumulant approximations. These approximations will alter the calculated peak shift result and are important when analyzing experimental spectra in terms of spectral diffusion. The cumulant approximation to the third-order response function is discussed further in the Appendix.
The 2DIR spectrum is similarly calculated from the Fourier transform of the rephasing and non-rephasing components of the third-order response functions, Eqs. A7, A8,
| (17) |
A number of methods are commonly used to analyze spectral diffusion in 2DIR spectroscopy. The changes in shape of the 2DIR peak are typically quantified through the ellipticity,63 nodal slope,64, 65 or CLS analysis.56, 57 The center line (CL) consists of the set of frequencies ω3 for each ω1 for which I2D is maximal. Within the Condon and cumulant approximations, the slope of the center line for each waiting time t2 yields the non-homogeneous component of the frequency-fluctuation autocorrelation function Cω(t).56, 57 As a result, the time scales for spectral diffusion can be extracted from the decay of the CLS.
In order to calculate the vibrational spectroscopic observables described above, we require the environmental dependence of the OD stretching frequencies, transition dipole moments, and vibrational lifetimes. As in Ref. 50, we will utilize electrostatic maps developed previously in our group46, 51, 53, 55 that relate the i–j transition frequencies ωij and transition dipole matrix elements to the electric field along the OD bond vector at the location of the deuterium atom. These electrostatic maps are given in Table I of Ref. 50 and were determined from electronic structure calculations on water clusters.46, 55 For the vibrational lifetime T1, we previously introduced a two-population model for the OD stretches of hydration water. In this model, each water hydrogen atom was designated as either “water-associated” or “lipid-associated” for each step of the simulation. If the hydrogen atom is closer to any lipid oxygen atom than to a water oxygen on another molecule, then it is “lipid-associated”. If the hydrogen is closer to an oxygen atom on another water molecule, however, then it is “water-associated”. This population index n is defined as
| (18) |
and the mean population at a particular hydration level X is given by 〈n〉. This mean population as well as the average number of waters associated with lipid phosphate and carbonyl groups is presented in Table II of Ref. 50. We also define the population fluctuation autocorrelation function Cn(t),
| (19) |
where the population fluctuations are given by δn(t) ≡ n(t) − 〈n〉. The decay of Cn(t) yields the time scales for the exchange of water molecules between the lipid- and water-associated environments. Based on the two-population model presented in Eq. 18, we previously determined best-fit vibrational lifetimes for lipid- and water-associated molecules by comparing our calculated isotropic pump-probe signal to the experimental results.22 These vibrational lifetimes are tabulated in Table II of Ref. 50, and in general, our values for the vibrational lifetimes are in qualitative agreement with the results of Zhao et al.,22 though our lifetimes are systematically longer.
FTIR AND ANISOTROPIC PUMP-PROBE SPECTROSCOPY
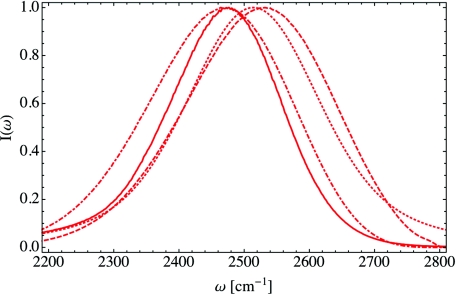
The FTIR spectrum of isotopically dilute HDO in DLPC lipid multi-bilayers was measured by Zhao et al.22 as a function of the hydration level X. They found that as the hydration level decreases, the absorption peak ωpeak redshifts to lower frequencies, and the peak width first broadens and then narrows. In Ref. 50, we calculated FTIR spectra for the same hydration levels measured by Zhao et al. and compared our theoretical results to the experiments. While the shifts in the peak positions and widths were not quantitatively accurate, we qualitatively reproduced the experimental trends. Our previous calculations of the FTIR spectra included both non-Condon and vibrational lifetime effects as in Eq. 2. In order to investigate the changes various common approximations make to the spectrum, we have recalculated the FTIR spectrum for the low hydration, X = 2 case, shown in Figure 1. The full calculation, from Eq. 2, is shown as the solid curve, while the spectral density, Eq. 4, is given by the dotted-dashed curve. Note that the spectral density does not include vibrational lifetime effects, but these effects only have a minor impact on the absorption spectrum. Making the Condon and cumulant approximations, Eq. 6, yields the dotted curve in Figure 1. This cumulant result does include some motional narrowing but neglects molecular rotations. Ignoring non-Condon effects results in a significant blueshift to the FTIR spectrum, and the spectrum within the cumulant approximation is symmetric, unlike the full calculation. Finally, the frequency distribution, Eq. 5, is shown as the dashed curve. The small peak in the frequency distribution at high frequencies is due to water hydrogens that are not hydrogen-bonded in our simulations, though non-Condon effects result in the suppression of this peak.53 This high-frequency shoulder was observed by Zhao et al.22 in the experimental FTIR spectra for low hydration levels.
Figure 1.
The absorption spectrum I(ω) for X = 2 within differing levels of theory. The full absorption spectrum, Eq. 2, is given by the solid line, while the spectral density, Eq. 4, is depicted by the dotted-dashed line. The spectrum within the cumulant approximation, Eq. 6, is given by the dotted curve and the frequency distribution, Eq. 5, is indicated by the dashed line.
Zhao et al. also measured the anisotropic pump-probe signal, r(t), for HDO in DLPC multi-bilayers as a function of hydration. These spectra provide information on the reorientational motions of the OD bond vector in hydration water. As lipid hydration X decreases, r(t) decays on slower time scales, indicating slower rotational motion. Both Zhang and Berkowitz52 and our group50 have calculated the anisotropic pump-probe signal for this system, and both calculations reproduce the experimental qualitative trends. Zhao et al.22 and Zhang and Berkowitz52 proposed that this slow down in rotational dynamics with decreasing hydration could be understood in terms of the molecular jump model66, 67, 68, 69 for water reorientational motion. While Zhang and Berkowitz52 were able to reproduce the qualitative slow-down in rotational dynamics with decreasing hydration, their calculation of the anisotropic pump-probe signal was based on the P2 approximation discussed in Eq. 12. Our calculation in Ref. 50, however, included non-Condon and inhomogeneous vibrational lifetime effects as given in Eq. 11, and r(t) was frequency resolved at the peak frequency ωpeak of the FTIR absorption spectrum, as in the experiment.22
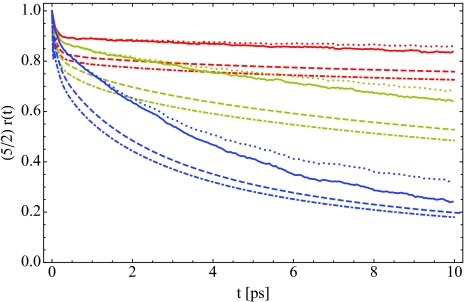
In Figure 2, we have calculated the anisotropic pump-probe signal for hydration levels X = 2 (red), 6 (yellow), and 16 (blue) within several approximations. The full calculation is indicated by the solid curves, while for the dotted curve, we have assumed the vibrational lifetime is a constant and independent of environment. This is equivalent to removing the lifetime entirely from Eq. 11 when calculating r(t). While the solid and dotted curves are identical for short times, after a few picoseconds they begin to diverge. The dashed and dotted-dashed curves in Figure 2 give r(t) within the integrated and frequency-resolved P2 approximations, Eqs. 12, 14, respectively. In each case, the P2 approximation to r(t) results in a rapid initial drop that is significantly larger than the full calculation. Zhang and Berkowitz52 normalized their P2 calculations to match the experimental values at 200 fs, which partially eliminates this rapid initial drop. None of the calculations in Figure 2, however, have been normalized, and the dramatic difference between r(t) within these approximations demonstrates that care must be taken in the analysis of anisotropic pump-probe signals. The interpretation of these measurements in terms of purely reorientational motion is only true within the integrated P2 approximation, and the results shown here demonstrate that this approximation is rather poor for each hydration level studied.
Figure 2.
The anisotropic pump-probe signal r(t) for X = 2 (red), 6 (yellow), and 16 (blue). The solid curve is the full theoretical calculation from Eq. 11, while in the dotted line, we have taken the vibrational lifetime T1 to be an environment-independent constant. The dashed curve is the frequency-resolved P2 approximation to r(t), Eq. 14, while the dotted-dashed line is the integrated P2 approximation, Eq. 12.
VIBRATIONAL ECHO SPECTROSCOPY
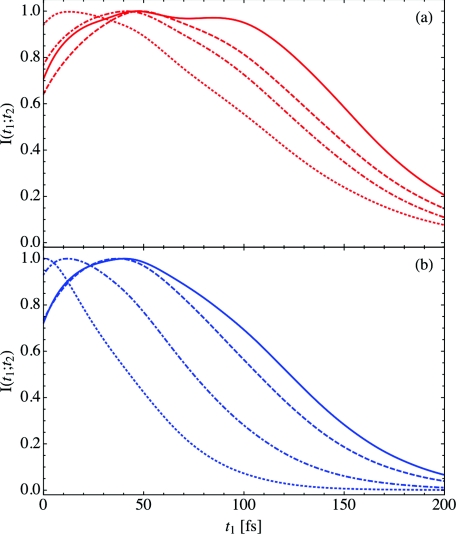
While the FTIR spectrum and the anisotropic pump-probe signal provide insight into water structure and rotational dynamics respectively, vibrational echo peak shift spectroscopy allows us to investigate spectral diffusion on the picosecond time scale. Spectral diffusion in turn gives us a window into picosecond hydration water and lipid dynamics. In Figure 3, we have calculated the vibrational echo intensity I(t1; t2), Eq. 15, for both the low hydration, X = 2 case (panel (a), red), and the high hydration, X = 16 case (panel (b), blue). The solid, dashed, dotted-dashed, and dotted curves indicate the results for increasing waiting times of t2 = 0.0, 0.1, 1.0, and 25 ps, respectively. In each case, the intensity has been normalized to unity at its peak. While the intensity at long waiting times for the X = 16 case has only a single peak, at low hydration levels or for short waiting times at high hydration levels, the intensities exhibit a complicated structure. For example, at t2 = 0 ps, X = 2 (solid, red curve), I(t1; t2) has two peaks of nearly equal magnitude separated by approximately 50 fs. As the waiting time increases beyond a few hundred femtoseconds, the intensity of the second peak decreases, though even at t2 = 25 ps (red, dotted curve), a shoulder can be observed in the spectrum. This complex structure is indicative of the heterogeneity present for hydration water in lipid multi-bilayer systems. Water bound deep in the lipid bilayer will have a very different local environment from water associated with the lipid choline groups or bulk water, and these distinct environments result in the multiple peaks and shoulders observed in Figure 3.
Figure 3.
The vibrational echo intensity I(t1; t2), Eq. 15, as a function of t1 for t2 = 0.0 ps (solid), 0.1 ps (dashed), 1.0 ps (dotted-dashed), and 25 ps (dotted). The low hydration case X = 2 is depicted in panel (a) (red), and the high hydration case X = 16 is shown in panel (b) (blue).
As shown in Figure 3, for each hydration level, the peak position of I(t1; t2) generally decreases as the waiting time is increased. This shift is a result of spectral diffusion, and in the limit of long waiting time t2, the spectrum will be peaked at t1 = 0 fs. For high hydration levels at long waiting times (blue, dotted curve), this is the case, indicating that spectral diffusion is nearly complete. For low hydration levels, the peak of the vibrational echo intensity does not shift to zero for any waiting time we considered. This is consistent with previous calculations and experiments,18, 23, 29, 50, 70 which suggest that the time scale for water molecules to diffuse from the bulk to deep within a lipid bilayer is on the order of 100 ps. Thus for low hydration levels, we do not expect spectral diffusion to be complete for waiting times less than several hundred picoseconds—far beyond the experimentally accessible time scale. As discussed in relation to Eq. 16, the first moment 〈t1〉 of the vibrational echo intensity also shifts as a function of the waiting time. Unlike the peak position, which may be difficult to define accurately when there are multiple peaks present in I(t1; t2), 〈t1〉 is a less ambiguous measure of spectral diffusion.
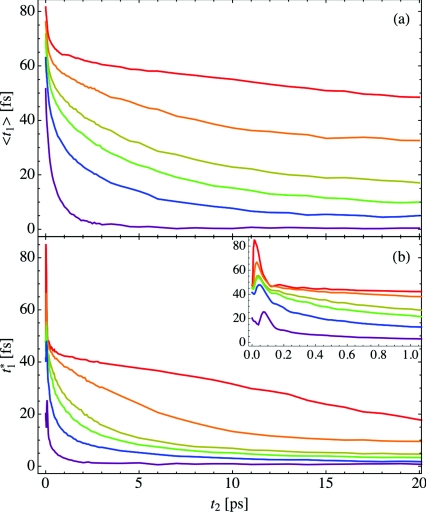
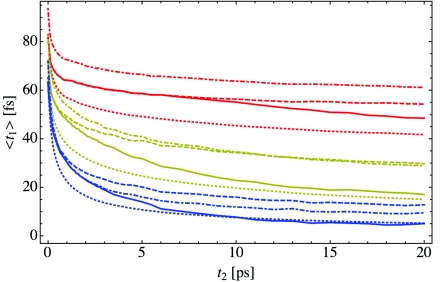
The peak shift is generated by plotting either the peak position or first moment 〈t1〉 as a function of the waiting time t2. In Figure 4 we show the peak shift for both 〈t1〉 (panel (a)) and (panel (b)) as a function of the hydration X. The red, orange, yellow, green, blue, and purple curves represent X = 2, 4, 6, 8, 16, and bulk water, respectively. Generally, as hydration increases, the peak in the vibrational echo intensity shifts to shorter times for fixed t2, and at high hydration levels, the peak position is essentially zero for waiting times greater than 10 ps. For low hydration levels, spectral diffusion is incomplete for the calculated waiting times. Also, for each hydration level and most waiting times, the first moment 〈t1〉 occurs at a larger time than the peak position . This results from the asymmetry in time and complex structure of the vibrational echo intensity I(t1; t2). Note that in order to calculate the first moment spectrum, I(t1; t2) must be calculated for negative times t1.
Figure 4.
The vibrational echo peak shift for hydration levels X = 2 (red), 4 (orange), 6 (yellow), 8 (green), 16 (blue), and bulk water (purple). Panel (a) shows the first moment 〈t1〉, while panel (b) shows the peak shift , and the short-time behavior of the peak shift is shown in the inset to panel (b).
In the inset to panel (b) of Figure 4, the short-time behavior of the peak shift is displayed. Unlike the first moment, the peak position does not monotonically decrease as the waiting time increases, but instead increases beyond its initial value for very short waiting times. In bulk water, this oscillation in the peak shift is a result of the hydrogen-bond stretching frequency53, 71, 72 and occurs at roughly 140 fs. For hydration water in lipid multi-bilayers, this oscillation shifts to shorter times as hydration decreases and results from the multiple peaks that make up the vibrational echo intensity, as shown in Figure 3. The first moment in panel (a) does not contain any observable oscillations, however.
As with the FTIR and pump-probe results discussed in Sec. 2, there are a number of approximations we can make in the calculation of the vibrational echo intensity, and these approximations play a key role in the interpretation of the resulting peak shift signal. In Figure 5 we have computed the first moment spectra for hydration levels X = 2 (red), 6 (yellow), and 16 (blue). The solid curves are the full calculations shown previously in Figure 4, while for the dashed curves, vibrational lifetime effects have been neglected. The peak shift within the Condon approximation to the transition dipole matrix elements is given by the dotted-dashed curve, and the dotted line indicates the result within both the Condon and cumulant approximations. As is the case for bulk water (not shown), the Condon approximation causes 〈t1〉 to increase relative to the full calculation, Eq. 15, for each hydration level and waiting time studied. In bulk water, however, the cumulant approximation only changes the peak shift slightly relative to the result within the Condon approximation. For lipid hydration water, this is not the case, as the cumulant approximation results in a significant decrease in 〈t1〉. This is especially noticeable for the low hydration X = 2 case. The cumulant approximation is only strictly valid for systems where the frequency fluctuations δω are Gaussian, and as lipid hydration water is highly heterogeneous, it is not surprising that the cumulant approximation is quite poor.
Figure 5.
The first moment of the vibrational echo intensity, 〈t1〉, for X = 2 (red), 6 (yellow), and 16 (blue) within various approximations. The solid curve is the full calculation, Eq. 15, while the dashed curve does not include vibrational lifetime effects. The dotted-dashed and dotted curves are the spectra within the Condon and cumulant approximations, respectively.
Vibrational lifetime effects also play a key role in the peak shifts shown in Figure 5. If each OD stretch has the same, constant vibrational lifetime T1, and if we only include such lifetime effects during the population t2 period (as in Eqs. A1, A2, A3, A4, A5, A6, A7, A8), then the vibrational lifetime plays no role in the peak shift. However, as discussed in Ref. 50, the vibrational lifetime for hydration water in lipid membranes depends on the environment. We previously determined that water molecule hydrogens bound to lipid phosphate and carbonyl groups have a shorter vibrational lifetime than water molecules associated more closely with other waters.50 As such, at long waiting times t2, only the population of water OD stretches with a longer lifetime will contribute to the vibrational echo signal. This results in the discrepancy between the solid and dashed curves in Figure 5: as water-associated molecules undergo more rapid spectral diffusion than lipid-associated ones, vibrational lifetime effects result in a more rapid decay of the peak shift signal. The importance of lifetime effects can also be observed in the long-time behavior of the peak shift shown in panel (b) of Figure 4 for X = 2 (red). Even though at low hydration levels most of the waters are bound to the lipids, only the small fraction bound to other waters contribute to the signal at long waiting times. This effect is important in the analysis of experimental peak shift signals and will play a role in Sec. 5 when we discuss 2DIR spectroscopy.
2DIR SPECTROSCOPY AND CENTER-LINE SLOPE ANALYSIS
As with the vibrational echo peak shift, analysis of 2DIR spectra provides information on spectral diffusion processes, as well as the homogeneous and inhomogeneous linewidths of a system. The positive and negative peaks in a 2DIR spectrum are split by the frequency difference between the 0-1 and 1-2 transition frequencies, and the peak shape provides information about system heterogeneity. In the homogeneous limit, the peaks in a 2DIR spectrum will be roughly circular, while in a system with inhomogeneous broadening, the peaks will be stretched along the ω1 = ω3 diagonal for short waiting times t2. As discussed in Sec. 2, we shall utilize the CLS method to analyze our calculated 2DIR spectra. The center line is defined by the curve connecting frequencies ω3 for each ω1 for which the positive peak in the 2DIR spectrum is at a maximum. Around the peak ω1 frequency, this center line will be essentially linear, though non-Gaussian dynamics will result in frequency-dependent curvature of the center line, as discussed in detail by Roy et al.73 The CLS is then given by the slope of the center line for each waiting time t2. As derived by Kwak et al.,56, 57 within the cumulant approximation, the CLS directly yields the non-homogeneous components of Cω(t). The short-time, homogeneous component of Cω(t) cannot be directly obtained through CLS analysis, though it can be inferred from the homogeneous linewidth.
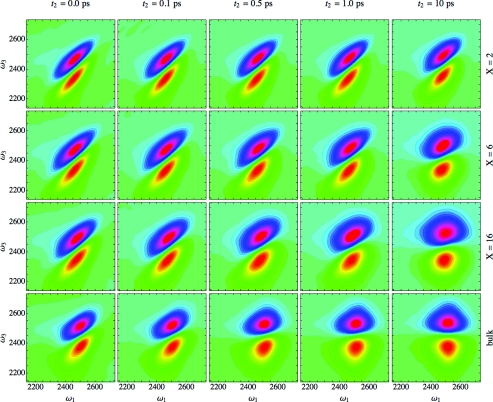
We have calculated 2DIR spectra for HDO in DLPC multi-bilayers as a function of hydration using Eq. 17, as shown in Figure 6. Each row represents the hydration levels X = 2, 6, 16, and bulk water, respectively, from top to bottom. Each column shows a different waiting time, t2 = 0.0, 0.1, 0.5, 1.0, and 10 ps, from left to right. The positive peak is shown in blue and purple, while the negative peak is depicted in yellow and orange. Each spectrum has been normalized such that its maximum value is unity. As seen in the leftmost column, for short waiting times the 2DIR spectra for each hydration level is stretched along the diagonal, indicating that each system has a degree of inhomogeneity. At the lowest hydration level (top row), this stretching is particularly noticeable. For bulk water (bottom row), the peak shape rapidly becomes more circular as the waiting time increases, indicating that spectral diffusion is essentially complete after roughly one picosecond. For the high hydration X = 16 case, the peak shape is only slightly elongated at t2 = 10 ps. At low hydration levels, the peak is still highly stretched even at long waiting times. This is in agreement with the peak shift signal at low hydration discussed in Sec. 4, in which the vibrational echo peak did not shift to zero femtoseconds, even at long waiting times. As noted previously in Ref. 50, this is most likely due to the long, 100+ ps time scale for the exchange of water molecules bound deep within the membrane with molecules located nearer the bilayer surface.
Figure 6.
2DIR spectra from Eq. 17 as a function of ω1 and ω3. The columns represent the waiting times t2 = 0.0, 0.1, 0.5, 1.0, and 10 ps from left to right, while the rows indicate the hydration levels X = 2, 6, 16, and bulk water from top to bottom. Blue and purple regions indicate positive values, while yellow and orange regions are negative.
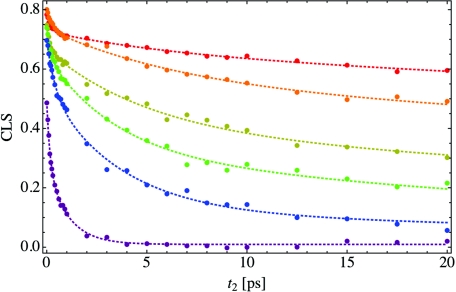
Using the calculated 2DIR spectra, we have determined the center line as a function of hydration, and then computed the CLS. The CLS was calculated by fitting the center line to a linear function of ω1 over a range of 100 cm−1 centered on the 2DIR peak frequency. As the Condon and cumulant approximations are not strictly valid, and due to numerical noise, the center line is not exactly linear, and the range over which the linear fitting is performed makes a small difference to the CLS.73 The nonlinearity of the center line is especially noticeable on the low-frequency side of the 2DIR peak. The resulting CLS is shown in Figure 7, where the colors indicate the hydration level, as in Figure 4. The filled circles indicate the calculated CLS values for each waiting time, while the dotted curves are tri-exponential fits through the data and are meant to guide the eye. For each hydration level, the CLS starts at a positive value less than one and then decays monotonically. In the long-time limit when spectral diffusion is complete, the CLS will decay to zero, as is the case for bulk water (purple curve). For low hydration levels, the CLS decays slightly for waiting times on the scale of a picosecond but then levels off and decays at a much slower rate. For X = 2 (red curve), the CLS only decays to around 0.6 after 20 ps, indicating that the system is highly heterogeneous.
Figure 7.
The center line slope (CLS) as a function of waiting time t2 for the same hydration levels as in Figure 4. The filled circles show the calculated CLS, while the dotted line is a tri-exponential fit to the data and is meant to guide the eye. Each CLS was calculated at the peak frequency of the 2DIR spectrum for the appropriate waiting time, and the slope for the center line was fit over a frequency range of 100 cm−1.
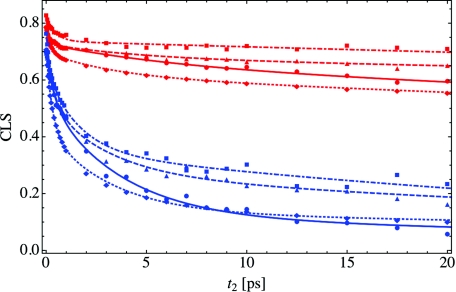
In the calculation of the 2DIR and CLS spectrum, we can perform the same approximations as we did previously for the peak shift. These approximations to the CLS are plotted in Figure 8, where the red and blue curves indicate X = 2 and 16, respectively. As in Figure 5, the solid curve (circles) indicates the full CLS calculation from Eq. 17, while in the dashed curve (triangles) we have again neglected vibrational lifetime effects. The Condon approximation to Eq. 17 is shown as the dotted-dashed curve (squares), and the result within both the Condon and cumulant approximations is given by the dotted line (diamonds). Note that in both the Condon and cumulant calculations, we have in addition neglected vibrational lifetime effects. The filled-in shapes once again give the CLS data points, and the curves are fits through the data. As with the peak shift in Figure 5, making the Condon approximation results in an increase in the CLS relative to the full calculation for all hydration levels studied. The further addition of the cumulant approximation significantly reduces the CLS, indicating once again that the cumulant approximation is not valid for this highly heterogeneous system. As the cumulant approximation is not valid, we should not interpret the decay of the CLS solely in terms of the frequency-fluctuation autocorrelation function Cω(t).
Figure 8.
The CLS for X = 2 (red) and 16 (blue) within the same approximations as in Figure 5. The solid line and filled circles represent the full calculation as shown in Figure 7, the CLS without lifetime effects is given by the dashed lines and triangles, and the dotted line and diamonds and dotted-dashed line and squares represent the CLS within the cumulant and Condon approximations, respectively. As in Figure 7, the lines through the data points are tri-exponential fits and are only meant to guide the eye.
As was the case for the peak shift, the results both with and without vibrational lifetime effects (solid and dashed lines) are essentially equivalent for short waiting times, but for long times the calculation without the vibrational lifetime has a larger CLS. For long waiting times, only the subset of water-associated OD stretches contributes to the signal. As we discussed previously in Ref. 50, these water-associated molecules have more rapid reorientational motion due to a relatively larger number of available hydrogen bonding partners. As such, this subset of molecules undergoes faster spectral diffusion, resulting in a smaller CLS for long waiting times than if all molecules contributed to the signal. The importance of vibrational lifetime effects once again underscores the caution that must be exercised when interpreting the results of 2DIR spectroscopy.
In addition to the CLS, we also calculated the waiting time dependence of other metrics used to extract the frequency-fluctuation correlation function from 2DIR spectra, including the nodal slope, inhomogeneity index, and ellipticity.63 Each of these quantities was calculated within the same set of approximations as the CLS in Figure 8 for the case of intermediate hydration, X = 6. In every case, the qualitative trends upon making each approximation are the same as those observed for the CLS, though the effect of the making the cumulant approximation is larger for metrics such as the nodal slope than for others such as the inhomogeneity index.
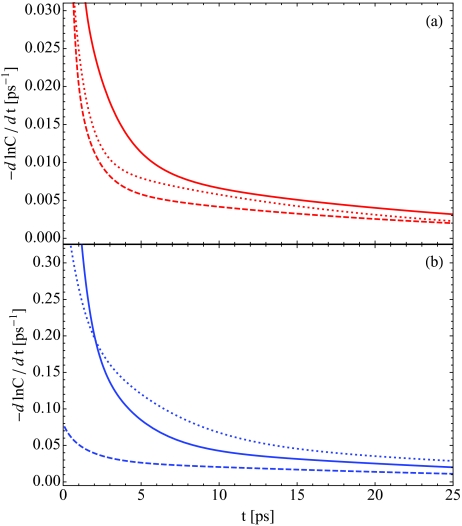
Though peak shift and 2DIR spectroscopy yield information on the time scales for spectral diffusion, these techniques do not directly allow us to investigate the microscopic mechanism behind these spectral changes. Spectral diffusion for hydration water in lipid multi-bilayers is a result of changes in the local environment for a water molecule on the picosecond time scale, either due to water rotations or translations in the membrane, changes in the local hydrogen-bonding environment, or fluctuations in the lipid bilayer. We will compare the relative time scales for these processes through three time-correlation functions: frequency fluctuations Cω(t), Eq. 8, dipole reorientations C2(t), Eq. 13, and population fluctuations Cn(t), Eq. 19. Spectral diffusion is described by the decay of Cω(t), while C2(t) and Cn(t) describe molecular rotations and diffusion within the membrane respectively. In Figure 9, we plot the negative time derivative of the natural logarithm of each normalized correlation function. For exponential decay, this would yield a constant decay rate. Thus Figure 9 can be interpreted as the instantaneous decay rate for each correlation function. Panel (a) shows these decay rates for low hydration, X = 2, while panel (b) shows the result for high hydration, X = 16. The solid, dotted, and dashed curves indicate the time dependence of Cω(t), C2(t), and Cn(t), respectively.
Figure 9.
The negative time derivative of the natural logarithm of the frequency-fluctuation autocorrelation function Cω(t), Eq. 8 (solid), the population fluctuation autocorrelation function Cn(t), Eq. 19 (dashed), and the second Legendre polynomial of molecular rotations C2(t), Eq. 13 (dotted). The low hydration, X = 2, case is shown in red in panel (a), while the X = 16 case is in blue in panel (b).
For all times and for each hydration level, the time scale for population fluctuations is slower than either molecular rotations or spectral diffusion. This indicates that the exchange of water molecules between lipid- and water-associated environments is not the dominant factor in spectral diffusion (up to 25 ps). On time scales of tens to hundreds of picoseconds, however, we do expect such population exchange to be relevant in controlling the decay of Cω(t). From Figure 9, we also observe that for short times, Cω(t) decays more quickly than the time scale of molecular rotations. For intermediate times of several picoseconds, these time derivatives become more similar, and in fact cross for high hydration levels. As the time derivatives of Cω(t) and C2(t) are not the same, we can conclude that spectral diffusion is not solely determined by molecular rotations, but it is probable that the reorientational motion of water is an important factor that influences the spectral changes evident in the peak shift and 2DIR spectra.
CONCLUSIONS
Previously we reported calculations of the FTIR and pump-probe vibrational spectroscopy of hydration water in DLPC lipid multi-bilayers as a function of the hydration level.50 Our results were in qualitative agreement with recent experiments,22 and we reproduced the systematic redshift in the absorption spectrum and slow-down in water reorientational dynamics as the hydration was decreased. Here, we have extended our investigation of this system by calculating the peak shift and 2DIR spectra for hydration water and analyzing the results in terms of spectral diffusion processes in the lipid multi-bilayer system. These observables have not yet been measured experimentally, so we present these calculations to aid future comparisons with experiment. In our calculations, we observed that spectral diffusion for each hydration level occurs on multiple time scales, and as the hydration is decreased, these times become longer. In addition, hydration water occupies a highly heterogeneous environment. Water molecules bound deep in the lipid bilayer reorient and diffuse more slowly than molecules closer to the bilayer surface, and these multiple environments manifest themselves in the spectroscopy through multiple peaks in the vibrational echo intensities and significant inhomogeneous components in the peak shift and CLS results.
We also investigated the effects of various approximations on the calculation of vibrational spectroscopic observables, using hydration water as an example of a heterogeneous system. The environmental dependence of the OD vibrational lifetime, evident from the multi-exponential decay of the isotropic pump-probe signal,22 plays a key role in the calculation of the anisotropic pump-probe signal and both the peak shift and 2DIR spectra. Water molecule OD stretches with a shorter vibrational lifetime (here the lipid-associated stretches) do not contribute to the third-order response for long waiting times t2, and thus only the water-associated stretches with a long lifetime contribute to the observed spectra. As is the case for bulk water, the environmental dependence of the transition dipole elements (non-Condon effects) makes a significant impact on all spectroscopic observables examined. As the magnitude of the transition dipole increases for decreasing OD stretch frequency, making the Condon approximation tends to overestimate the importance of molecules on the blue side of the absorption spectrum. The cumulant approximation to the frequency fluctuations was also discussed and for each hydration level was shown to be a poor approximation to the true dynamics. For the anisotropic pump-probe signal, we in addition analyzed the effects of the “P2” approximation. The disagreement between the full calculation of r(t) and the P2 results imply that the anisotropic pump-probe signal should not be interpreted solely in terms of water reorientational motion for hydration water.
The overall picture developed for hydration water in lipid multi-bilayer systems in both this and our previous paper50 agrees quite well with other experimental and simulation results.22, 52 Water molecules can bind to both the lipid phosphate and carbonyl groups as well as associate with the lipid choline headgroup. Molecules strongly hydrogen-bonded to the lipid phosphate oxygens absorb at lower frequencies than in bulk water, and hydration water in general exhibits slower rotational and diffusive motion, resulting in slow spectral diffusion. Our calculations are subject to many potential errors,50 including problems with the lipid and water force fields, the electrostatic maps for the OD frequencies and transition dipole elements, and the procedure used to determine the environmentally dependent vibrational lifetimes. Even so, these model calculations provide useful comparisons for different levels of theory, and imply that for spectroscopic calculations on water in complex environments, it is important to include non-Condon effects, non-Gaussian frequency fluctuations, and heterogeneous lifetimes. Hopefully future experiments will provide a check on our calculations and yield further information on the structure and dynamics of hydration water in lipid multi-bilayers.
ACKNOWLEDGMENTS
The development of the theoretical spectroscopic methods is supported by the National Science Foundation through Grant No. CHE-1058752, the calculation of the spectroscopic observables is supported by the Department of Energy through Grant No. DE-FG02-09ER16110, and the development and implementation of the lipid bilayer simulations is supported by the National Institute of Health through Grant No. R01-DK088184. The authors wish to thank Professor M. Fayer and Ms. E. Fenn for helpful conversations.
APPENDIX: NONLINEAR RESPONSE FUNCTIONS
The six terms that contribute to the rephasing and non-rephasing components of the third-order response function are given by
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
The rephasing and non-rephasing response functions are then the sum of R1 to R3 and R4 to R6, respectively,
| (A7) |
| (A8) |
In Eqs. A1, A2, A3, A4, A5, A6, we have only included vibrational lifetime effects during the t2 population period. The indices i and k indicate the , , and components of the dipole matrix elements, though in all calculations presented here, we have only considered the and components as discussed previously in Ref. 50.
Within the Condon and cumulant approximations, and if we neglect the vibrational lifetime T1(t), the third-order response functions simplify to
| (A9) |
| (A10) |
| (A11) |
| (A12) |
| (A13) |
| (A14) |
where Gre(t1, t2, t3) and Gnr(t1, t2, t3) are defined by
| (A15) |
| (A16) |
and the lineshape function g(t) is given in Eq. 7. In Eqs. A9, A10, A11, A12, A13, A14, we have in addition neglected molecular rotations, we have assumed that the 1-2 coherence frequency fluctuations δω21(t) are equal to the 1-0 coherence frequency fluctuations δω10(t), and we have made a harmonic approximation and set . The cumulant approximation is only strictly valid if frequency fluctuations δω describe a Gaussian process. Within the cumulant approximation, the waiting time dependence of the CLS yields the frequency-fluctuation autocorrelation function Cω(t), as derived within a short-time approximation by Kwak et al.56, 57
References
- van Meer G., Voelker D. R., and Feigenson G. W., Mol. Cell. Biol. 9, 112 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball P., Chem. Rev. 108, 74 (2008). 10.1021/cr068037a [DOI] [PubMed] [Google Scholar]
- Zhong D., Pal S. K., and Zewail A. H., Chem. Phys. Lett. 1, 1 (2010). 10.1021/jz9001899 [DOI] [Google Scholar]
- Koynova R. and Caffrey M., Biochim. Biophys. Acta 1376, 91 (1998). [DOI] [PubMed] [Google Scholar]
- Nagle J. F. and Tristram-Nagle S., Biochim. Biophys. Acta 1469, 159 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tristram-Nagle S. and Nagle J. F., Chem. Phys. Lipids 127, 3 (2004). 10.1016/j.chemphyslip.2003.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milhaud J., Biochim. Biophys. Acta 1663, 19 (2004). 10.1016/j.bbamem.2004.02.003 [DOI] [PubMed] [Google Scholar]
- Fitter J., Lechner R. E., and Dencher N. A., J. Phys. Chem. B 103, 8036 (1999). 10.1021/jp9912410 [DOI] [Google Scholar]
- Foglia F., Lawrence M. J., Lorenz C. D., and McLain S. E., J. Chem. Phys. 133, 145103 (2010). 10.1063/1.3488998 [DOI] [PubMed] [Google Scholar]
- Klosgen B., Reichle C., Kohlsmann S., and Kramer K. D., Biophys. J. 71, 3251 (1996). 10.1016/S0006-3495(96)79518-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tielrooij K. J., Paparo D., Piatkowski L., Bakker H. J., and Bonn M., Biophys. J. 97, 2484 (2009). 10.1016/j.bpj.2009.08.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berntsen P., Svanberg C., and Swanson J., J. Phys. Chem. B 115, 1825 (2011). 10.1021/jp110899j [DOI] [PubMed] [Google Scholar]
- Pal S. K., Sukul D., Mandal D., and Bhattacharyya K., J. Phys. Chem. B 104, 4529 (2000). 10.1021/jp993348t [DOI] [Google Scholar]
- Sykora J., Kapusta P., Fidler V., and Hof M., Langmuir 18, 571 (2002). 10.1021/la011337x [DOI] [Google Scholar]
- Sykora J., Jurkiewicz P., Epand R. M., Kraayenhof R., Langner M., and Hof M., Chem. Phys. Lipids 135, 213 (2005). 10.1016/j.chemphyslip.2005.03.003 [DOI] [PubMed] [Google Scholar]
- Zhou Z., Sayer B. G., Hughes D. W., Stark R. E., and Epand R. M., Biophys. J. 76, 387 (1999). 10.1016/S0006-3495(99)77205-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurze V., Steinbauer B., Huber T., and Beyer K., Biophys. J. 78, 2441 (2000). 10.1016/S0006-3495(00)76788-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawrisch K., Gaede H. C., Mihailescu M., and White S. H., Eur. Biophys. J. 36, 281 (2007). 10.1007/s00249-007-0142-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hübner W. and Blume A., Chem. Phys. Lipids 96, 99 (1998). 10.1016/S0009-3084(98)00083-8 [DOI] [Google Scholar]
- Volkov V. V., Palmer D. J., and Righini R., J. Phys. Chem. B 111, 1377 (2007). 10.1021/jp065886t [DOI] [PubMed] [Google Scholar]
- Volkov V. V., Palmer D. J., and Righini R., Phys. Rev. Lett. 99, 078302 (2007). 10.1103/PhysRevLett.99.078302 [DOI] [PubMed] [Google Scholar]
- Zhao W., Moilanen D. E., Fenn E. E., and Fayer M. D., J. Am. Chem. Soc. 130, 13927 (2008). 10.1021/ja803252y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alper H. E., Bassolino-Kilmas D., and Stouch T. R., J. Chem. Phys. 99, 5547 (1993). 10.1063/1.465947 [DOI] [Google Scholar]
- Damodaran K. V. and Merz K. M., Langmuir 9, 1179 (1993). 10.1021/la00029a005 [DOI] [Google Scholar]
- Damodaran K. V. and Merz K. M., Biophys. J. 66, 1076 (1994). 10.1016/S0006-3495(94)80889-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieleman D. P. and Berendsen H. J.C., J. Chem. Phys. 105, 4871 (1996). 10.1063/1.472323 [DOI] [Google Scholar]
- Scott H. L., Curr. Opin. Struct. Biol. 12, 495 (2002). 10.1016/S0959-440X(02)00353-6 [DOI] [PubMed] [Google Scholar]
- Rog T., Murzyn K., and Pasenkiewicz-Gierula M., Chem. Phys. Lett. 352, 323 (2002). 10.1016/S0009-2614(02)00002-7 [DOI] [Google Scholar]
- Lopez C. F., Nielsen S. O., and Klein M. L., J. Phys. Chem. B 108, 6603 (2004). 10.1021/jp037618q [DOI] [Google Scholar]
- de Vries A. H., Yefimov S., Mark A. E., and Marrink S. J., Proc. Natl. Acad. Sci. U.S.A. 102, 5392 (2005). 10.1073/pnas.0408249102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murzyn K., Zhao W., Karttunen M., Kurdziel M., and Rog T., Biointerphases 1, 98 (2006). 10.1116/1.2354573 [DOI] [PubMed] [Google Scholar]
- Sapay N., Bennett W. F. D., and Tieleman D. P., Soft Matter 5, 3295 (2009). 10.1039/b902376c [DOI] [Google Scholar]
- Vacha R., Siu S. W. I., Petrov M., Bockmann R. A., Barucha-Kraszewska J., Jurkiewicz P., Hof M., Berkowitz M. L., and Jungwirth P., J. Phys. Chem. A 113, 7235 (2009). 10.1021/jp809974e [DOI] [PubMed] [Google Scholar]
- Berkowitz M. L., Biochim. Biophys. Acta 1788, 86 (2009). 10.1016/j.bbamem.2008.09.009 [DOI] [PubMed] [Google Scholar]
- Vacha R., Berkowitz M. L., and Jungwirth P., Biophys. J. 96, 4493 (2009). 10.1016/j.bpj.2009.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stepniewski M., Bunker A., Pasenkiewicz-Gierula M., Karttunen M., and Rog T., J. Phys. Chem. B 114, 11784 (2010). 10.1021/jp104739a [DOI] [PubMed] [Google Scholar]
- de Meyer F. J.-M., Benjamini A., Rodgers J. M., Misteli Y., and Smit B., J. Phys. Chem. B 114, 10451 (2010). 10.1021/jp103903s [DOI] [PubMed] [Google Scholar]
- Broemstrup T. and Reuter N., Biophys. J. 99, 825 (2010). 10.1016/j.bpj.2010.04.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khandelia H. and Kaznessis Y. N., Biochim. Biophys. Acta 1768, 509 (2007). 10.1016/j.bbamem.2006.11.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auer B. M. and Skinner J. L., J. Chem. Phys. 128, 224511 (2008). 10.1063/1.2925258 [DOI] [PubMed] [Google Scholar]
- Corcelli S. A., Lawrence C. P., and Skinner J. L., J. Chem. Phys. 120, 8107 (2004). 10.1063/1.1683072 [DOI] [PubMed] [Google Scholar]
- Loparo J. J., Roberts S. T., and Tokmakoff A., J. Chem. Phys. 125, 194521 (2006). 10.1063/1.2382895 [DOI] [PubMed] [Google Scholar]
- Loparo J. J., Roberts S. T., and Tokmakoff A., J. Chem. Phys. 125, 194522 (2006). 10.1063/1.2382896 [DOI] [PubMed] [Google Scholar]
- Piletic I. R., Moilanen D. E., Spry D. B., Levinger N. E., and Fayer M. D., J. Phys. Chem. A 110, 4985 (2006). 10.1021/jp061065c [DOI] [PubMed] [Google Scholar]
- Smith J. D., Saykally R. J., and Geissler P. L., J. Am. Chem. Soc. 129, 13847 (2007). 10.1021/ja071933z [DOI] [PubMed] [Google Scholar]
- Lin Y.-S., Auer B. M., and Skinner J. L., J. Chem. Phys. 131, 144511 (2009). 10.1063/1.3242083 [DOI] [PubMed] [Google Scholar]
- Pieniazek P. A., Lin Y.-S., Chowdhary J., Ladanyi B. M., and Skinner J. L., J. Phys. Chem. B 113, 15017 (2009). 10.1021/jp906784t [DOI] [PubMed] [Google Scholar]
- Bakker H. and Skinner J. L., Chem. Rev. 110, 1498 (2010). 10.1021/cr9001879 [DOI] [PubMed] [Google Scholar]
- Li F. and Skinner J. L., J. Chem. Phys. 132, 204505 (2010). 10.1063/1.3430518 [DOI] [PubMed] [Google Scholar]
- Gruenbaum S. M. and Skinner J. L., J. Chem. Phys. 135, 075101 (2011). 10.1063/1.3615717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y.-S., Pieniazek P. A., Yang M., and Skinner J. L., J. Chem. Phys. 132, 174505 (2010). 10.1063/1.3409561 [DOI] [PubMed] [Google Scholar]
- Zhang Z. and Berkowitz M. L., J. Phys. Chem. B 113, 7676 (2009). 10.1021/jp900873d [DOI] [PubMed] [Google Scholar]
- Schmidt J. R., Corcelli S. A., and Skinner J. L., J. Chem. Phys. 123, 044513 (2005). 10.1063/1.1961472 [DOI] [PubMed] [Google Scholar]
- Schmidt J. R., Roberts S. T., Loparo J. J., Tokmakoff A., Fayer M. D., and Skinner J. L., Chem. Phys. 341, 143 (2007). 10.1016/j.chemphys.2007.06.043 [DOI] [Google Scholar]
- Auer B. M., Kumar R., Schmidt J. R., and Skinner J. L., Proc. Natl. Acad. Sci. U.S.A. 104, 14215 (2007). 10.1073/pnas.0701482104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwak K., Park S., Finkelstein I. J., and Fayer M. D., J. Chem. Phys. 127, 124503 (2007). 10.1063/1.2772269 [DOI] [PubMed] [Google Scholar]
- Kwak K., Rosenfeld D. E., and Fayer M. D., J. Chem. Phys. 128, 204505 (2008). 10.1063/1.2927906 [DOI] [PubMed] [Google Scholar]
- Mukamel S., Principles of Nonlinear Optical Spectroscopy (Oxford, New York, 1995). [Google Scholar]
- Moilanen D. E., Piletic I. R., and Fayer M. D., J. Phys. Chem. A 110, 9084 (2006). 10.1021/jp0623084 [DOI] [PubMed] [Google Scholar]
- Moilanen D. E., Piletic I. R., and Fayer M. D., J. Phys. Chem. C 111, 8884 (2007). 10.1021/jp067460k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piryatinski A. and Skinner J. L., J. Phys. Chem. B 106, 8055 (2002). 10.1021/jp0202542 [DOI] [Google Scholar]
- Hamm P., Lim M., and Hochstrasser R. M., Phys. Rev. Lett. 81, 5326 (1998). 10.1103/PhysRevLett.81.5326 [DOI] [Google Scholar]
- Roberts S. T., Loparo J. J., and Tokmakoff A., J. Chem. Phys. 125, 084502 (2006). 10.1063/1.2232271 [DOI] [PubMed] [Google Scholar]
- Kwac K. and Cho M., J. Phys. Chem. A 107, 5903 (2003). 10.1021/jp034727w [DOI] [Google Scholar]
- Kim Y. S., Liu L., Axelsen P. H., and Hochstrasser R. M., Proc. Natl. Acad. Sci. U.S.A. 106, 17751 (2009). 10.1073/pnas.0909888106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laage D. and Hynes J. T., Science 311, 832 (2006). 10.1126/science.1122154 [DOI] [PubMed] [Google Scholar]
- Laage D. and Hynes J. T., Chem. Phys. Lett. 433, 80 (2006). 10.1016/j.cplett.2006.11.035 [DOI] [Google Scholar]
- Laage D. and Hynes J. T., Proc. Natl. Acad. Sci. U.S.A. 104, 11167 (2007). 10.1073/pnas.0701699104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji M., Odelius M., and Gaffney K. J., Science 328, 1003 (2010). 10.1126/science.1187707 [DOI] [PubMed] [Google Scholar]
- Bhide S. Y. and Berkowitz M. L., J. Chem. Phys. 123, 224702 (2005). 10.1063/1.2132277 [DOI] [PubMed] [Google Scholar]
- Rey R., Møller K. B., and Hynes J. T., J. Phys. Chem. A 106, 11993 (2002). 10.1021/jp026419o [DOI] [Google Scholar]
- Møller K. B., Rey R., and Hynes J. T., J. Phys. Chem. A 108, 1275 (2004). 10.1021/jp035935r [DOI] [Google Scholar]
- Roy S., Pshenichnikov M. S., and Jansen T. L. C., J. Phys. Chem. B 115, 5431 (2011). 10.1021/jp109742p [DOI] [PubMed] [Google Scholar]