Abstract
The “three sites per nucleotide” (3SPN) model provides a coarse-grained representation of nucleic acids for simulation of molecular processes. Previously, this model has relied on an implicit representation of the surrounding ionic environment at the level of Debye-Hückel theory. In this work, we eliminate this limitation and present an explicit representation of ions, both monovalent and divalent. The coarse-grain ion-ion and ion-phosphate potential energy functions are inferred from all-atom simulations and parameterized to reproduce key features of the local structure and organization of ions in bulk water and in the presence of DNA. The resulting model, 3SPN.1-I, is capable of reproducing the local structure observed in detailed atomistic simulations, as well as the experimental melting temperature of DNA for a range of DNA oligonucleotide lengths, CG-content, Na+ concentration, and Mg2 + concentration.
INTRODUCTION
The biophysics of nucleic acids are of interest in a wide range of disciplines. In particular, the effect of confinement on nucleic acids has attracted considerable attention in recent years.1, 2, 3, 4, 5, 6, 7, 8 Interesting phenomena arise when double-stranded DNA (dsDNA), a semi-flexible polyelectrolyte with a negatively charged backbone, is confined to high densities in biological systems, such as chromatin, viruses, and other natural entities that must package a genome. The persistence length of double-stranded DNA is on the same order of magnitude as the structures into which it is often confined, and yet nature routinely overcomes the bending rigidity of the molecule, often by manipulating charge.
Computer simulations can provide insight into these confinement phenomena. Simple polyelectrolyte bead-spring models have been used to model large DNA molecules.9, 10, 11, 12, 13, 14, 15, 16 Such models, however, cannot capture important processes such as the dehybridization and subsequent rehybridization of DNA. For problems in which the degree of hybridization is of interest, a finer level of description is required. The “three sites per nucleotide” (3SPN) model of Knotts et al. provides this level of detail while retaining the advantages of a coarse-grain model.17 The 3SPN model represents a top-down approach that seeks to incorporate available experimental information into the development of a coarse-grain description, and should be contrasted with bottom-up strategies that rely solely on atomistic models for the development of effective coarse-grain potentials and parameters.18 In 3SPN, three sites are mapped onto the full atomistic representation of each DNA base and water is treated implicitly through Langevin dynamics, thereby resulting in fewer interacting sites and faster calculations of molecular processes. A subsequent version of this model, 3SPN.1, was published by Sambriski et al. and extends the model through an additional interaction that accounts for the entropic effect of solvation on interacting DNA strands.19 This interaction enables dehybridized DNA to rehybridize spontaneously and is parameterized to correctly capture the melting behavior of arbitrary DNA sequences under various ionic conditions. The 3SPN.1 model for DNA has since been employed to study the mechanism of melting and renaturation via transition path sampling.20, 21
However, both 3SPN and 3SPN.1 address electrostatic interactions implicitly through a Debye-Hückel approximation. While this approximation is appropriate in the limit of monovalent salts at low concentration, it does not hold at high salt concentrations. Furthermore, the Debye-Hückel approximation cannot capture fundamental phenomena associated with multi-valent ions, such as charge inversion, that are involved in the condensation of DNA.22, 23, 24
Coarse-grain simulations of nucleic acids have become increasingly common as fully detailed atomistic simulations are still unable to capture the time and length scales at which important biological processes occur. Attempts to include explicit ionic representations, however, have been limited.25, 26, 27 Prytkova et al. included sodium explicitly in simulations of small-molecule DNA-hybrid dimer structures.25 That work did not include a rigorous parameterizing of the ion-ion model or assess the melting behavior of the construct. Demille and co-workers extended 3SPN to include explicit, coarse-grain representations for water and monovalent ionic species.26 They employed a Stillinger-Weber potential to describe water-water and water-ion interactions with an additional shielded Coulomb (Yukawa) potential acting between cation and anion pairs. That model predicts a local structure of water and ions in the vicinity of the double helix that is consistent with results of detailed atomistic calculations, but is unable to reproduce the melting behavior that is observed experimentally (the predicted melting temperatures are on the order of 200 °C, well above experimental values). Savelyev and Papoian developed a one-site-per-nucleotide model for DNA that includes explicit ionic representations.27 Their coarse-grain ion-ion and ion-DNA models were parameterized to capture the local structure and distribution of ionic species in the vicinity of double-stranded DNA. However, the melting behavior of DNA was not addressed. In all cases, only monovalent cations were considered.
In the spirit of the 3SPN.1 model, we present a coarse-grain representation for DNA with explicit ions that relies on the model proposed by Lenart and co-workers for ionic species.28 This model treats electrostatic interactions as a sum of terms including a Lennard-Jones contribution (induced dipolar interactions and excluded volume), an electrostatic contribution, and an additional term to account for the presence of one or more solvation shells. These solvation shells arise due to the favorable arrangement of water in the vicinity of charged species.29, 30, 31, 32 The premise of the model is that it is difficult for an interacting particle to displace these highly ordered water molecules, thereby resulting in the appearance of regions of depletion in the radial distribution function (RDF) between the interacting charged species. This solvation contribution is described by a simple Gaussian function. The parameters for this coarse-grain representation were chosen such that the correct mean ionic activity coefficient was reproduced in simulations of simple salt solutions such as NaCl in water.
The approach we take here is to choose new parameters for this coarse-grain ion-ion model such that the local molecular structure of the system is consistent with results from detailed atomistic representations. This approach is analogous to the Boltzmann inversion method for automatic coarse-graining,33, 34 in which a numerical potential is iteratively determined such that the coarse-grain RDF converges on some target provided by a more detailed model. In this case, rather than using the difference between the target RDF and the coarse-grain RDF to drive the convergence of the ion-ion potential, the parameters for an analytical pair potential are altered until good agreement exists between a detailed atomistic RDF and that of the coarse-grain system. A similar approach was employed in Refs. 26, 35 wherein a short-range approximation was developed to describe the local structure of sodium-chloride systems.
The present work extends the 3SPN.1 model through the inclusion of explicit ions, both mono- (Na+) and divalent (Mg2 +). In addition to parameterizing new contributions to the model, particular attention is paid to the “sugar-sugar” interaction of the 3SPN.1 model. This inter-strand interaction acts between the sugar sites of each DNA strand and takes the form of a Morse potential (the reader is referred to Ref. 19 and Appendix A1 for complete details). The energy scale of this interaction, εsug, is a function of both salt concentration and sequence length, and combines the effect of solvent entropy and electrostatic fluctuations associated with ion-phosphate interactions as long-range driving forces for hybridization. As this work extends 3SPN.1 by the incorporation of explicit ions, the relationship of εsug to salt concentration and sequence length necessarily changes in order to recover good agreement with experimental DNA melting temperature data.
This work is divided into three sections. Section 2 presents the ion-ion potential implemented to accommodate explicit ions and outlines the simulation methods employed in this work. In particular, a biased parallel tempering scheme is presented and used to determine the melting temperature of DNA oligonucleotides. Section 3 presents the local molecular structure and melting temperatures of representative DNA oligonucleotides predicted by this extended model, hereafter referred to as 3SPN.1-I. Section 4 presents a discussion of these results in the context of previous work.
MODEL AND METHODS
Coarse-grain model for DNA
In the 3SPN model for dsDNA originally proposed by Knotts et al.,17 each nucleotide in a dsDNA molecule is represented by three sites corresponding to each of the chemical moieties of DNA (i.e., sugar, phosphate, adenine (A), cytosine (C), guanine (G), and thymine (T)). Sites constituting a single DNA strand are subject to intramolecular bonding, bending, and torsional constraints that produce an arrangement matching the observed equilibrium canonical geometry (B-form) for DNA under physiological conditions. Readers are referred to the work of Sambriski et al.19 for complete details regarding the 3SPN.1 mesoscale model for DNA. For completeness, a brief summary of the model and its parameters is also given in Appendix A1.
Coarse-grain potential for ionic species
As mentioned above, the 3SPN.1-I model proposed here extends the model for 1:1 electrolyte solutions presented by Lenart et al. to describe ion-ion and ion-DNA interactions.28 The functional form of the potential is the same as that presented by Lenart and co-workers. However, the parameters are modified to better reproduce RDFs observed in detailed atomistic simulations of DNA and ionic species. In addition, new parameters are obtained to capture the interaction between the DNA phosphate moieties (“P”) and Na+ and Mg2 +. An additional modification is the incorporation of a second hydration shell into the functional form of the model for the Na+–Cl−, Mg2 +–Cl−, Na+–P, and Mg2 +–P interactions, consistent with detailed atomistic simulations in which two well-defined hydration shells are observed.
The ion-ion potential of Lenart et al. consists of three contributions: a Lennard-Jones contribution, an electrostatic contribution, and a hydration contribution to capture solvation effects. The electrostatic contribution includes a correction for dielectric saturation at small inter-particle separations. The Lennard-Jones contribution is given by
| (1) |
with energy scale ε and length scale σ. The electrostatic interaction is given by
| (2) |
where qi is the charge associated with particle i, ε0 is the permittivity of free space, r is the interparticle separation, and εD(r) is the distance-dependent dielectric constant given by
| (3) |
Here, εs is the dielectric of the bulk solvent, rmε is the midpoint of the transition, and σε is the width of the transition from the saturated dielectric constant to that of the bulk solvent. This construct captures dielectric saturation as two interacting charged particles approach each other. For the work presented here, εs was taken to be 78.0. The hydration contribution is given by
| (4) |
where rmh is the location of the midpoint of the hydration shell, σh is the width of the hydration shell, and H is the height of the Gaussian describing the hydration shell. The complete ion-ion potential consists of the sum of the individual contributions:
| (5) |
As mentioned previously, all unlike-charged species include a second solvation shell contribution in addition to the three terms shown above. Ions interact with non-charged DNA sites (sugar and base moieties) via a simple excluded volume potential of the form
| (6) |
where σi is the length scale, εexcl is the energy scale of the excluded volume interaction, and the index i represents Na+, Mg2 +, or Cl−. The cutoff radius rcut is taken to be the point at which the potential is 0 kJ∕mol. The energy scale, εexcl, of the excluded volume interaction is not altered from that of 3SPN.1 (εexcl = 0.769856 kJ mol−1). The length scale, σi, is determined by a simple mixing rule,
| (7) |
where σ0 is the general repulsion length scale employed in 3SPN.1 (σ0=6.86Å), and σNa–Na, σMg–Mg, and σCl–Cl are the length scales for the LJ interactions given in Table 1.
Table 1.
Ion-ion parameters for 3SPN.1-I.
| ε | σ | rmε | σε | rmh, 1 | σh, 1 | H1 | rmh, 2 | σh, 2 | H2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pair | kJ mol−1 | Å | Å | Å | Å | Å | kJ mol−1 | Å | Å | kJ mol−1 |
| Na+–Cl− | 0.3509 | 3.1352 | 3.9 | 2.06 | 3.3 | 0.57 | 23.0 | 5.6 | 0.4 | 1.7 |
| Mg2 +–Cl− | 2.081 | 4.74 | 4.48 | 0.57 | 5.48 | 0.44 | 4.6 | 8.16 | 0.35 | 0.25 |
| Na+–Na+ | 0.0469 | 2.43 | 2.7 | 0.57 | 5.8 | 0.57 | 0.75 | ... | ... | ... |
| Mg2 +–Mg2 + | 3.743 | 1.412 | 1.412 | 0.5 | ... | ... | ... | ... | ... | ... |
| Cl−–Cl− | 0.15 | 4.045 | 4.2 | 0.56 | 6.2 | 0.5 | 1.0 | ... | ... | ... |
| Na+–P | 0.105 | 4.14 | 3.44 | 1.25 | 4.1 | 0.57 | 13.2 | 6.5 | 0.4 | 2.00 |
| Mg2 +–P | 0.50 | 4.87 | 3.75 | 1.00 | 6.1 | 0.5 | 5.4 | 8.3 | 1.2 | 4.1 |
| Cl−–P | 0.3398 | 5.5425 | 4.2 | 0.5 | 6.7 | 1.5 | 3.5 | ... | ... | ... |
| P–P | 0.76986 | 6.86 | 6.86 | 0.5 | ... | ... | ... | ... | ... | ... |
| Mg2 +–Na+ | 0.208 | 2.37 | 2.37 | 0.5 | ... | ... | ... | ... | ... | ... |
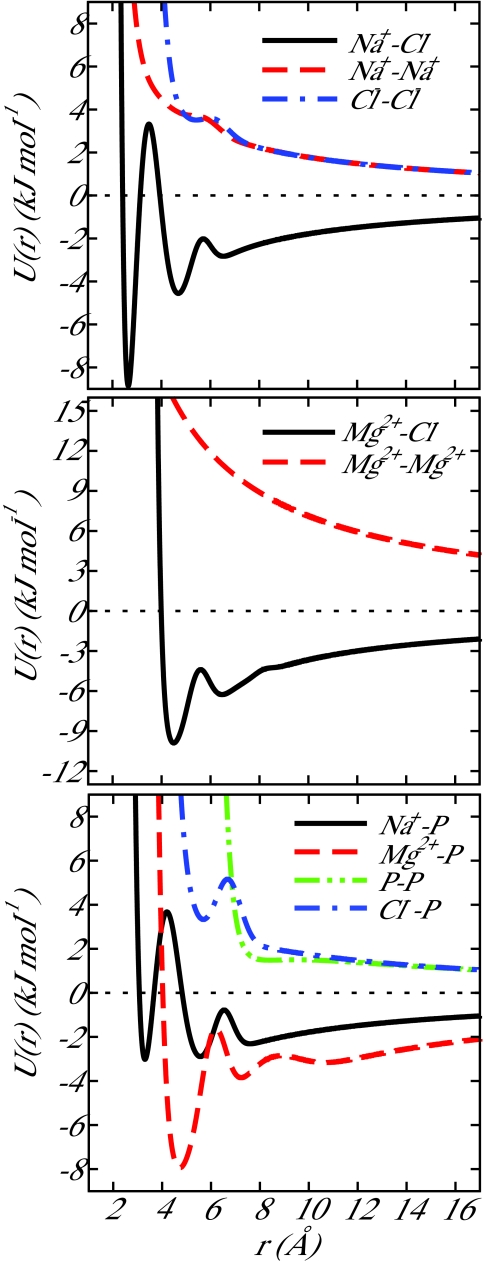
The parameters employed in this work are given in Table 1. All parameters were chosen to reproduce the local molecular structure generated in all-atom simulations (see below). Simulation details are given in Sec. 2C. The resulting ion-ion and ion-DNA potentials are shown in Figure 1.
Figure 1.
Ion-ion potentials for 3SPN.1-I. Parameters for each potential are given in Table 1. The functional form of the ion-ion potential is given by Eqs. 1, 2, 3, 4, 5.
Simulation details
Section 2C outlines the simulations performed to parameterize and evaluate the 3SPN.1-I model. Three systems are employed to parameterize ion-ion and ion-DNA interactions: an aqueous NaCl system, an aqueous MgCl2 system, and an aqueous ion-DNA system. RDFs from atomistic simulations of these systems were used as targets for parameterization of the coarse-grain model. As it is crucial for a coarse-grain model of nucleic acids to quantitatively reproduce dehybridization behavior, parallel tempering36, 37 calculations were employed to parameterize the sugar-sugar interaction and evaluate the performance of the model in this regard.
Coarse-grain Langevin dynamics simulations
All coarse-grain simulations were evolved via the Langevin dynamics (LD) approach described by Bussi and Parrinello.38 This method reproduces the translational diffusivity of simulated species without incorporating explicit solvent through the damping constant in the LD integrator for which the diffusion constant is a parameter. The value taken for dsDNA diffusivity remains unchanged from that described in the literature for 3SPN.1, DDNA = 9.20 × 10−13 m2∕s/bead.17, 19 To describe the diffusion of ionic species in water, published diffusivity data were used with D Na +=1.33×10−9 m2∕s,39D Cl −=2.03×10−9 m2∕s,39 and D Mg 2+=0.71×10−9 m2∕s.40 For all coarse-grain simulations, an integration time-step of 0.01 ps was employed.
For parameterization of Na+–Cl−, the coarse-grain model was used to simulate a 1 M aqueous NaCl system at 298 K. Na+ and Cl− particles were randomly placed in a cubic simulation box with sides of 60 Å. The system was equilibrated and then evolved via LD in the NVT ensemble employing Ewald sums. The real space cutoff was 20 Å with 4 k-space vectors and the damping constant was set to α = 0.175 Å−1. Likewise for Mg2 + and Cl−, particles were randomly inserted in a 60 Å cubic box corresponding to a MgCl2 concentration of 200 mM. The system was evolved via LD in the NVT ensemble at 300 K. The treatment of long-range interactions was the same as that for Na+–Cl−.
For ion-DNA coarse-grain simulations, the sequence TACTAACATTAACTA was placed in a 63 × 63 × 86 Å box with the DNA molecule oriented in the long direction of the box. Weak harmonic springs located at the 5′ terminus of each strand maintained this orientation throughout the simulation. By weakly restraining only the 5′ end of each DNA strand, we ensured that no unrealistic forces were applied to the molecule that caused the DNA to adopt configurations other than B-DNA. This ensured identical box conditions with the all-atom case described in Sec. 2C2. Additional weak harmonic springs constrained the native complimentary base pairs to their minimum energy separation to prevent dehybridization. This was done to permit the use of a smaller cutoff during the simulation (3SPN.1-I cutoff is 50 Å for both electrostatic interactions and the sugar-sugar interaction). Ewald sums were used to treat electrostatics with a real space cutoff of 15 Å, 5 k-space vectors, and α = 0.233 Å−1. The salt concentration corresponded to 100 mM [Na+] and 20 mM [Mg2 +]. Positive ions were randomly placed within the simulation box until the appropriate concentrations were achieved and then sufficient Cl− particles were inserted to achieve electroneutrality. The system was equilibrated and evolved at 300 K in the NVT ensemble.
For subsequent calculations to parameterize the sugar-sugar interaction εsug, a reaction field approach was employed for electrostatic interactions following the method of Tironi et al.41 A cutoff of 50 Å was employed for all electrostatic and sugar-sugar interactions.
Benchmarking simulations were performed for 3SPN.1-I for comparison against 3SPN.1. Three systems were considered, namely, a 15 base pair sequence at 69, 119, and 220 mM [Na+]. For 3SPN.1, all three systems have the same computational cost, as ions are treated implicitly. Table 2 summarizes the run times for a 5 ns trajectory in a 112 Å cubic simulation box. Simulations were performed serially on a 2.67 GHz Intel Xeon central processing unit (CPU). Addition of explicit ions significantly increases simulation time: one should weigh the tradeoff between the higher resolution provided by the explicit ion representation and the additional computational cost.
Table 2.
Comparison of 3SPN.1-I to 3SPN.1 CPU time requirements for three representative systems. The results correspond to 5 ns trajectories of a 15 base pair DNA molecule.
| CPU time | |||
|---|---|---|---|
| System | DNA sites | Ion sites | (min) |
| 3SPN.1 | 88 | ... | 1.1 |
| 3SPN.1-I, 69 mM [Na+] | 88 | 88 | 11.9 |
| 3SPN.1-I, 119 mM [Na+] | 88 | 174 | 27.0 |
| 3SPN.1-I, 220 mM [Na+] | 88 | 346 | 84.7 |
Fully detailed atomistic simulations
Noy and co-workers calculated potentials of mean force and RDFs for ions and DNA in explicit water for a variety of published force fields.42 We rely on their results to parameterize Na+–Cl− interactions. Noy et al. limited their study to monovalent salts; for Mg2 +–Cl− and ion-DNA interactions we therefore use our own atomistic simulations as follows.
To determine the local structure exhibited by Mg2 + and Cl− in aqueous solution an all-atom simulation was performed using the AMBER99 force field43 in GROMACS.44 Mg2 + and Cl− atoms were randomly placed in a box and solvated with TIP3P water molecules. Following energy minimization, the system was equilibrated in the NPT ensemble at 300 K and 1 bar for 4 ns. The system was then evolved in the NVT ensemble at 300 K and the equilibrated box size employing LD for 40 ns. A particle mesh Ewald method was used to address the long-range electrostatic contributions. RDFs for Mg2 +–Cl− and Mg2 +–Mg2 + were determined from this production run.
To examine ion-DNA interactions, the 15-bp sequence TACTAACATTAACTA was placed in an aqueous environment containing 100 mM NaCl and 20 mM MgCl2 and solvated by TIP3P water molecules. The box dimensions were 63 × 63 × 86 Å and the DNA molecule restrained in the direction of the long axis of the box as described previously for the ion-DNA coarse-grain simulation. The same force field and equilibration and production protocol described for the atomistic MgCl2 system were employed in this simulation.
Parallel tempering simulations
Parallel tempering simulations36, 37 were employed to determine the melting temperature of dsDNA oligonucleotides. The temperature range for parallel tempering was selected such that hybridized configurations were predominantly sampled in the lowest temperature replicas and dehybridized configurations were sampled in the highest temperature replicas. This corresponds to a temperature range of approximately 240 K ≲ T ≲ 520 K. Each replica was placed within a simulation box and equilibrated at that temperature for 40 ns. During production (400 ns in length), exchanges between adjacent replicas were proposed every 1000 LD time-steps. The proposed exchanges were accepted or rejected based on a Metropolis criterion given by
| (8) |
where i and j are adjacent replicas and Δ is given by
| (9) |
and where qi are the Cartesian coordinates of the particles in replica i, U is the total potential energy, and βi is the inverse temperature of simulation window i, defined as (kBTi)−1. Upon successful exchange of replicas, the coordinates were swapped between the two adjacent boxes and the velocities rescaled to achieve the appropriate temperature. The temperatures of adjacent boxes were spaced such that the acceptance rate for proposed exchanges between two adjacent boxes was between 0.2 and 0.3, consistent with the optimal replica spacing.45
To quantify the melting temperature, the Weighted Histogram Analysis Method (WHAM) of Kumar et al. was employed to determine the free energy landscape associated with the transition from hybridized to dehybridized DNA.46, 47 The melting temperature for a given sequence was defined as the temperature at which the free energies of the hybridized and dehybridized states are equal.21 Equivalently, the melting temperature is that temperature at which the probability of finding a DNA oligonucleotide in the hybridized and dehybridized states is the same. The WHAM equations as given by Kumar et al. are
| (10) |
with
| (11) |
Here, R is the number of replicas in our parallel tempering simulation, ξ is the order parameter that describes the degree of hybridization, U is the total potential energy of a configuration, Ubias is the contribution to the potential energy due to a bias if we choose to use a bias to enhance sampling, Nk, bias(U, ξ) is a histogram of simulation data for each simulation window k, nk is the total number of snapshots taken in simulation window k, and fk is the Helmholtz free energy of simulation window k. The definition of β is the same as that given previously.
If the phase transition is a rare event, even long simulations may generate insufficient configurations in the region of the phase transition to produce consistent melting temperatures from simulation to simulation. A bias can be imposed between two complimentary single strands of DNA to enhance sampling in the vicinity of the phase transition. For example, a weak harmonic spring placed between the central base of the two strands can aid in forcing the system to sample the phase transition more frequently during the simulation while still permitting sampling of dehybridized configurations. This leads to more consistent melting temperature determination from run to run. The bias is removed systematically to determine an unbiased probability in the manner employed by Reddy et al.,48
| (12) |
Once these unbiased probabilities have been determined, the free energy as a function of order parameter can be determined from
| (13) |
where A is the Helmholtz free energy, consistent with the canonical ensemble. As proposed by Sambriski,19, 21 we chose the fraction of hybridized base pairs as our order parameter,
| (14) |
where ni is the number of hybridized base pairs for configuration i and nt is the total number of possible hybridized base pairs. The dehybridized state is defined as those configurations with ξ = 0, while the hybridized state is defined as some value of ξ close to 1.0 at which a free energy minimum is observed. It should be noted that fraying of the terminal base pairs of the oligonucleotide due to thermal fluctuations results in the free energy minimum corresponding to the hybridized state being slightly less than ξ = 1.0, as originally observed by Sambriski.21
RESULTS AND DISCUSSION
Local structure: g(r)
Due to strong interactions between ionic species and dipolar water molecules, distinct features arise in the RDFs of ion-ion interactions. These features arise primarily due to the organization of water molecules around the charged ionic species. As two ions approach each other, work must be performed to induce the rearrangement of these highly ordered water molecules and allow for continued approach of the ion-pair. The coarse-grain ion-ion model employed here phenomenologically accounts for the presence of such highly ordered hydration shells around bare ions in an aqueous environment by means of the Gaussian hydration contributions described previously. To parameterize this model for the ion-ion pairs of interest in this work, the RDF generated from detailed atomistic calculations was used as a target. We use the standard definition of g(r) between two species, i and j,
| (15) |
where Vbox is the volume of the system, Vr is the volume of a spherical shell at distance r from each particle i, Ni is the number of particles, i, in the system, and rij is the distance between two particles i and j ≠ i.
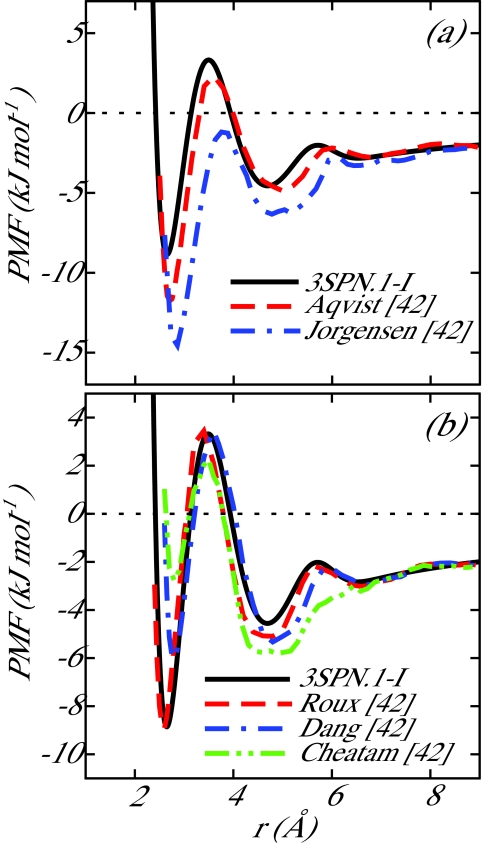
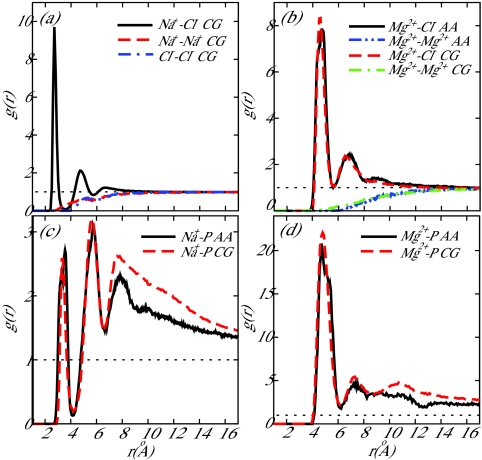
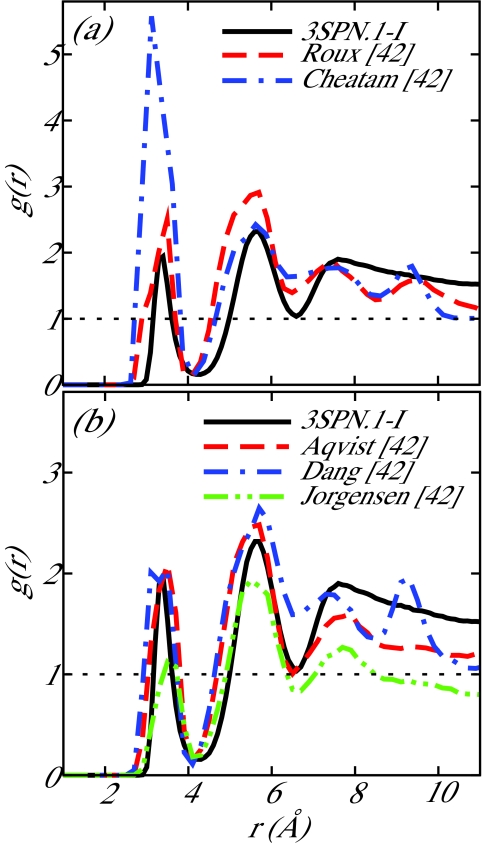
For the Na+–Cl− interaction, the results of Noy et al.42 were used to determine the parameters for the coarse-grain potential. Noy et al. determined the potential of mean force (PMF) between two isolated ions (Na+ and Cl−) in water at 298 K for a number of common force fields. In particular, the Na+–Cl− parameters of Roux et al.49, 50 were suggested by Noy et al. to be well suited for nucleic acid simulations due to a lack of artifacts, such as excessive crystallization of ions in solution. We chose Na+–Cl− parameters to correspond to the Roux PMF. In the limiting case of a Na+ ion and a Cl− ion in a solvent, the ion-ion PMF is equivalent to the effective coarse-grain pairwise potential, thereby providing a convenient means to parameterize our model. The coarse-grain Na+–Cl− potential presented in this work is compared to the Na+–Cl− PMFs resulting from the force fields reviewed in Ref. 42 in Figure 2. The coarse-grain RDFs determined from the production run described earlier for the ion pairs Na+–Cl−, Na+–Na+, and Cl−–Cl− are shown in Figure 4a and the Na+–Cl− RDF is compared to the review of Noy et al. in Figure 3. For the sake of completeness, the RDF predicted by 3SPN.1-I is compared to all force fields investigated in Ref. 42. The local structure exhibited by 3SPN.1-I is well within the range of all force fields presented in that work. Some difficulty was experienced when parameterizing the Na+–Na+ and Cl−–Cl− potentials as ion-water interactions play a crucial role in generating favorable short-range interactions between like-charged ions. The lack of explicit water in the coarse-grain model employed here results in a loss of detail in the local structure of like-charge ion pairs.
Figure 2.
Comparison of potential of mean force, PMF, between 3SPN.1-I and the work of Noy et al.42 for Na+–Cl−. The data are separated into two panels for ease of comparison. 3SPN.1-I produces behavior similar to that obtained by the parameters of Roux.49, 50 In the case of a coarse-grain model with implicit water, the PMF obtained by detailed atomistic simulation is equivalent to the effective ion-ion coarse-grain potential.
Figure 4.
Radial distribution functions, g(r), for (a) Na+–Cl−, (b) Mg2 +–Cl−, (c) Na+–Phosphate, and (d) Mg2 +–Phosphate. In the legends, the notation “CG” denotes results from 3SPN.1-I and “AA” denotes all-atom simulation results described in the text. Na+–Cl− CG interactions are compared to all-atom results in Figures 23.
Figure 3.
Comparison of radial distribution functions, g(r), between 3SPN.1-I and the work of Noy et al.42 for Na+–Cl−. The data are separated into two panels for ease of comparison. 3SPN.1-I produces behavior similar to that obtained with the parameters of Roux.49, 50
As data are not as readily available in the literature for Mg2 +–Cl− interactions, all-atom and coarse-grain simulations of 200 mM aqueous MgCl2 (described in Sec. 2C2) were performed to determine the RDFs. The Mg2 +–Cl− and Mg2 +–Mg2 + RDFs for both the all-atom and coarse-grain cases are shown in Figure 4b. Good agreement is observed in both cases.
All-atom and coarse-grain simulations described previously (Sec. 2C2) were performed to parameterize ion-DNA interactions. RDFs for both Na+–P and Mg2 +–P interactions are shown in Figures 4c, 4d, respectively. Good agreement is observed in both cases, especially in the vicinity of the first and second peaks and the depleted region (hydration shell) separating them. The Cl−–P interaction was parameterized using PMF results from Lyubartsev and Laaksonen.51 The repulsive PMF they reported displays a single hydration barrier at 6.7 Å, consistent with 3SPN.1-I (Figure 1).
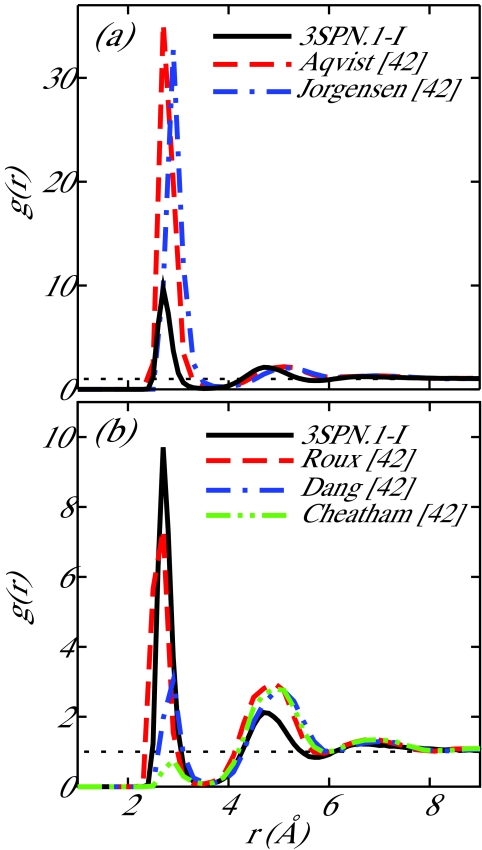
The ion-DNA force field review of Noy and co-workers presented Na+–P RDFs for the five ion force fields compared in their work.42 In addition to the fully detailed atomistic system employed here for parameterization, this prior work enables us to compare our coarse-grain representation to a number of common ion-DNA force fields. Noy et al. considered a 6-bp oligonucleotide in 500 mM [Na+] at 298 K. We performed equivalent coarse-grain simulations of this 6-bp oligonucleotide (CGATCG) in 500 mM [Na+] in a cubic box with sides of 51.61 Å using Ewald sums. Figure 5 provides a comparison of our coarse-grain results and those of the atomistic simulations performed by Noy et al.42 While the 3SPN.1-I RDF for Na+–P does not align exactly with any one representative force field, the values of the RDF fall into the range of values observed in Ref. 42.
Figure 5.
Comparison of radial distribution functions, g(r), between 3SPN.1-I and the work of Noy et al.42 for Na+–P−. The data are separated into two panels for ease of comparison. 3SPN.1-I is consistent with the local structure observed by Noy and co-workers.
In summary, the local structure (RDF) and ion-pair interaction information (PMF) from both the literature and fully detailed atomistic simulations performed here were used as targets for the coarse-grain model parameterization. This combination of previous work and new all-atom molecular dynamics simulation enabled us to parameterize a coarse-grain model that accurately describes ion-ion and ion-DNA interactions.
Melting temperature of DNA
The parallel tempering algorithm outlined in Sec. 2C3 was used to determine the melting temperature of representative DNA sequences. The key parameter driving hybridization in 3SPN.1-I is the sugar-sugar interaction. In addition to providing an entropic driving force for renaturation, this interaction also accounts for the long-range attraction caused by fluctuating dipoles induced by phosphate-cation interactions. With explicit counterions, we directly account for these interactions, requiring a modification of the 3SPN.1 sugar-sugar parameter. In this work we describe εsug as a function of sequence length and the ionic strength of the surrounding medium. A set of DNA sequences of varying length and salt conditions was used to parameterize εsug, hereafter referred to as the “training set.” In addition to developing a new sugar-sugar parameter for 3SPN.1-I, we also demonstrate the predictive capability of the model by calculating the melting temperature of sequences not employed in the model parameterization (the “testing set”). Experimental melting temperatures were taken from Owczarzy and co-workers.52, 53 All sequences employed in the parameterization and evaluation of εsug are given in Table 3. These sequences were chosen to represent a range of conditions in the three relevant variables affecting εsug: sequence length, [Na+], and [Mg2 +]. Additionally, the fractional content of CG, fCG, was varied across the sequences.
Table 3.
Sequences employed for parameterization and evaluation of Eqs. 16, 17, 18, 19. fCG is the fractional content of CG in each sequence.
| Length | |||
|---|---|---|---|
| Index | Sequence | fCG | (bp) |
| 01 | TACTAACATTAACTA | 0.20 | 15 |
| 02 | CTTTCATGTCCGCAT | 0.47 | 15 |
| 03 | CGCCTCATGCTCATC | 0.60 | 15 |
| 04 | ATGCAATGCTACATATTCGC | 0.40 | 20 |
| 05 | TTCTACCTATGTGAT | 0.33 | 15 |
| 06 | CAGCCTCGTCGCAGC | 0.73 | 15 |
| 07 | GCAGTGGATGTGAGA | 0.53 | 15 |
| 08 | ATCGTCTGGA | 0.50 | 10 |
| 09 | TGATTCTACCTATGTGATTT | 0.30 | 20 |
| 10 | ATACTTACTGATTAG | 0.27 | 15 |
| 11 | TGGATGTGTGAACAC | 0.47 | 15 |
| 12 | ACCCCGCAATACATG | 0.53 | 15 |
| 13 | GCGTCGGTCCGGGCT | 0.80 | 15 |
| 14 | CAGTGAGACAGCAATGGTGC | 0.55 | 20 |
| 15 | GTTCTATACTCTTGAAGTTGATTAC | 0.32 | 25 |
| 16 | CGGAATCCATGTTACTTCGGCTATC | 0.48 | 25 |
| 17 | ATAACTTTACGTGTGTGACCTATTA | 0.32 | 25 |
| 18 | AAGGCGAGTCAGGCTCAGTG | 0.60 | 20 |
| 19 | TATGTATATTTTGTAATCAG | 0.20 | 20 |
| 20 | GTCCACGCCCGGTGCGACGG | 0.80 | 20 |
| 21 | ATCAATCATA | 0.20 | 10 |
For parameterization, the melting temperatures of the training set of sequences and conditions (shown in Table 4) were determined. Note that such fitting simulations were performed by calculating the melting temperature of a system over a range of εsug values. A linear regression was then performed for the values of εsug that produced melting temperatures in the immediate vicinity of the experimental melting temperature, resulting in the appropriate εsug for that sequence. The function proposed by Sambriski et al. to describe εsug as a function of sequence length and [Na+] (Ref. 19) was modified in 3SPN.1-I such that the salt-dependent term is a function of the ionic strength to encompass the effect of sodium and magnesium ions in one term. With this change, the function describing εsug becomes
| (16) |
where
| (17) |
| (18) |
| (19) |
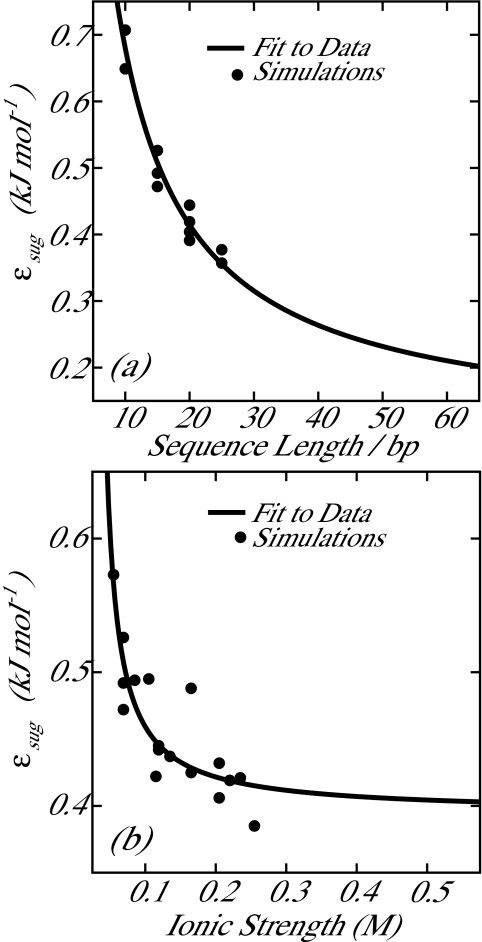
Here, N is the sequence length in base pairs and I is the ionic strength given by , where ci is the concentration (in mol∕L) of ionic species i and zi is the charge associated with ionic species i. Simulations to provide data for fitting Eqs. 16, 17, 18, 19 were performed across a range of sequence lengths and salt conditions. Figure 6a shows data acquired at [Na+] = 0.069 M, [Mg2 +] = 0.0 M (i.e., constant ionic strength), and varying sequence lengths. Figure 6b shows data acquired at a fixed length of 15 base pairs and various [Na+] and [Mg2 +]. Also shown are the resulting predictions of Eqs. 16, 17, 18, 19 for these data with an R2 value of 0.92.
Table 4.
Melting temperatures for training sequences determined by parallel tempering simulations. Experimental melting temperatures were taken from Refs. 52, 53. Parameters given for Eqs. 16, 17, 18, 19 determined by fitting εsug to values determined through fitting simulations performed with these systems. The average absolute deviation for the training data set was 4.2 K with a maximum absolute deviation of 14 K. Data shown visually as black circles in Figure 7.
| Length | [Na+] | [Mg2 +] | Tm,expt. | Tm,sim. | ||
|---|---|---|---|---|---|---|
| Sequence | (bp) | (mM) | (mM) | (K) | (K) | %error |
| SEQ01 | 15 | 69 | 0 | 308.7a | 311 ± 2 | 0.9 |
| SEQ01 | 15 | 119 | 0 | 313.6a | 307 ± 2 | 2.2 |
| SEQ01 | 15 | 220 | 0 | 317.3a | 317 ± 1 | 0.0 |
| SEQ02 | 15 | 69 | 0 | 323.1a | 326 ± 3 | 0.9 |
| SEQ02 | 15 | 119 | 0 | 327.1a | 324 ± 1 | 0.9 |
| SEQ03 | 15 | 69 | 0 | 326.0a | 322 ± 2 | 1.2 |
| SEQ04 | 20 | 69 | 0 | 328.4a | 320 ± 1 | 2.6 |
| SEQ05 | 15 | 105 | 0 | 317.0b | 312 ± 1 | 1.7 |
| SEQ05 | 15 | 55 | 20 | 322.8b | 329 ± 2 | 1.9 |
| SEQ06 | 15 | 55 | 0 | 332.1b | 332 ± 3 | 0.1 |
| SEQ06 | 15 | 55 | 10 | 339.8b | 338 ± 1 | 0.6 |
| SEQ07 | 15 | 55 | 50 | 332.5b | 334 ± 2 | 0.6 |
| SEQ08 | 10 | 69 | 0 | 307.0a | 311 ± 1 | 1.3 |
| SEQ09 | 20 | 55 | 20 | 332.1b | 346 ± 1 | 4.3 |
| SEQ15 | 25 | 55 | 0 | 323.9b | 329 ± 3 | 1.5 |
| SEQ16 | 25 | 69 | 0 | 334.1a | 329 ± 1 | 0.3 |
| SEQ17 | 25 | 69 | 0 | 329.8a | 329 ± 3 | 2.5 |
| SEQ18 | 20 | 69 | 0 | 337.7a | 336 ± 2 | 0.5 |
| SEQ19 | 20 | 69 | 0 | 317.6a | 321 ± 2 | 1.2 |
| SEQ20 | 20 | 69 | 0 | 344.1a | 348 ± 2 | 1.0 |
| SEQ21 | 10 | 69 | 0 | 294.5a | 292 ± 3 | 0.9 |
Figure 6.
Data from fitting simulations (described in text) used to determine parameters for εsug. (a) Simulations at constant ionic strength ([Na+] = 0.069 M, [Mg2 +] = 0.0 M) and various sequence lengths. (b) Simulations at constant sequence length (15 bp) and various ionic strengths. Solid lines are generated by Eq. 16. The R2 value for the entire training data set is 0.92.
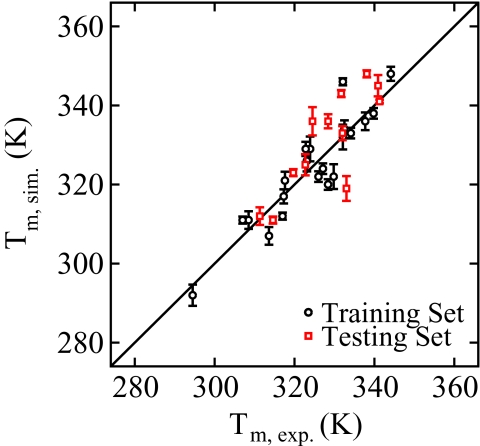
Table 4 gives the simulated melting temperatures for the training set. All results represent an average over six independent simulations, and the uncertainty is taken as the standard error for each set of simulations. Good agreement is observed between the melting temperature predicted by 3SPN.1-I and experimentally determined values. The average absolute deviation of the training set was 4.2 K with a maximum deviation of 14 K. These results are also shown in Figure 7 as black circles.
Figure 7.
Comparison of simulation melting temperatures (y-axis) and experimental melting temperatures (x-axis).52, 53 Shown are both the training and testing data sets.
Table 5 presents melting temperatures for the testing set using 3SPN.1-I (also shown as red squares in Figure 7). In some cases, due to limited experimental data, the sequences employed in the testing set were the same as those used in the training set. In these cases, however, the testing set employed different salt conditions. The agreement observed in the testing set is comparable to that observed in the parameterization set with an average absolute deviation of 5.8 K versus 4.2 K. In addition, the maximum absolute deviation is 14 K in both data sets. Such discrepancies on the order of 10 K can be attributed to the coarseness of the 3SPN topology: regardless of sequence, the excluded volume of each 3SPN interaction site is the same and partial charges are omitted from sugar and base moieties. This leads to similar ion solvation of all bases. In reality, however, the topology of the DNA strand differs according to the sequence with commensurate differences in ion solvation. Without a more refined representation of the base moieties, we view this level of agreement as satisfactory.
Table 5.
Melting temperatures of testing sequences. Experimental melting temperatures were taken from Refs. 52, 53. The absolute average deviation for the testing data set was 5.8 K with a maximum absolute deviation of 14 K. Data shown visually as red squares in Figure 7.
| Length | [Na+] | [Mg2 +] | Tm,expt. | Tm,sim. | ||
|---|---|---|---|---|---|---|
| Sequence | (bp) | (mM) | (mM) | (K) | (K) | %error |
| SEQ06 | 15 | 55 | 50 | 341.3a | 341 ± 2 | 0.1 |
| SEQ07 | 15 | 55 | 0 | 322.7a | 325 ± 3 | 0.8 |
| SEQ07 | 15 | 55 | 20 | 332.0a | 333 ± 2 | 0.3 |
| SEQ10 | 15 | 69 | 0 | 311.3b | 312 ± 2 | 0.3 |
| SEQ10 | 15 | 119 | 0 | 314.6b | 311 ± 1 | 1.1 |
| SEQ11 | 15 | 69 | 0 | 319.7b | 323 ± 1 | 1.2 |
| SEQ12 | 15 | 69 | 0 | 324.5b | 336 ± 4 | 3.5 |
| SEQ12 | 15 | 119 | 0 | 328.4b | 336 ± 2 | 2.4 |
| SEQ12 | 15 | 220 | 0 | 331.7b | 343 ± 1 | 3.3 |
| SEQ13 | 15 | 69 | 0 | 338.1b | 348 ± 1 | 2.9 |
| SEQ13 | 15 | 119 | 0 | 340.9b | 345 ± 3 | 1.1 |
| SEQ14 | 20 | 119 | 0 | 333.0b | 319 ± 3 | 4.1 |
To quantitatively assess the performance of 3SPN.1-I in describing DNA melting temperatures versus the previous generation of the model, 3SPN.1, melting temperatures for both the training and testing sets were determined using the 3SPN.1 parameters. For systems in which [Mg2 +] > 0, εsug was determined using the ionic strength rather than monovalent salt concentration, for which 3SPN.1 was parameterized.19 A detailed comparison of the melting temperatures predicted by 3SPN.1 and 3SPN.1-I is given in Appendix A2. The average absolute deviation across all data sets for 3SPN.1-I is 4.8 K compared to 8.0 K for 3SPN.1. Furthermore, the maximum absolute deviations are 14 K and 20 K, respectively. A closer examination of this comparison shows that 3SPN.1 has an average absolute deviation of 6.5 K when considering systems with monovalent cations and 14.5 K when considering systems with divalent Mg2 +. The average absolute deviations for 3SPN.1-I for these two cases are 4.9 K and 4.3 K, respectively. As this comparison indicates, the performance of 3SPN.1-I is superior to that of 3SPN.1 for the range of sequence lengths and salt conditions examined in this work, particularly in regards to hybridization behavior in the presence of divalent Mg2 +.
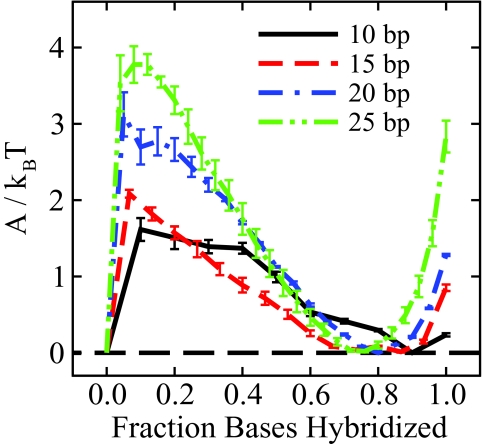
The free energy method employed here to determine melting temperatures can also be used to probe the phase transition and the nature of the barrier separating the hybridized and dehybridized states. Figure 8 shows free energy profiles for four representative sequences of increasing length from 10 to 25 base pairs. We can see that the barrier to the hybridization event increases with increasing length, consistent with experimental observations that show a sharpening of the phase transition with increasing length.52 Figure 8 also demonstrates that, in the vicinity of the phase transition, the molecule is not likely to exist with all complimentary base pairs formed (ξ = 1.0), consistent with behavior first observed in coarse-grain DNA simulations by Sambriski et al.21 Thermal fluctuations cause the ends of the molecule to “fray,” as previously demonstrated by experiment.54 Such behavior was not explicitly parameterized in the 3SPN.1-I model but, rather, arises naturally from the parameters presented in this work.
Figure 8.
Effect of sequence length on the energetic barrier separating the hybridized and dehybridized states. As the sequence length increases, the probability of crossing the phase transition barrier decreases, consistent with a sharpening of the phase transition observed experimentally.52 This figure also demonstrates that the free energy minimum corresponding to hybridized DNA does not coincide with ξ = 1.0. Dynamic fraying of the helix ends results in the free energy minimum shifted below ξ = 1.0.21
CONCLUSION
The 3SPN.1 coarse-grain model for DNA has been extended to incorporate mono- and divalent ions explicitly, resulting in the 3SPN.1-I model for DNA. The ion-ion potential proposed by Lenart et al.28 was adopted, and parameters were chosen in order to capture the local structure observed in detailed atomistic simulations of dsDNA in water. This approach is consistent with previous work in which Boltzmann inversion was used to develop a coarse-grain potential to capture ion-ion interactions. In our case, we developed parameters for an analytical potential with physically significant terms to capture the distance dependence of the dielectric constant and the existence of highly ordered shells of water molecules surrounding ions in aqueous environment. Recovering key local structural detail is possible for unlike-charged ion pairs. However, the local structural detail of like-charged ion pairs was not recovered using the coarse-grain ion-ion model used here due to the absence of water, responsible for forming an attractive bridge between such like-charged pairs.
The modification of 3SPN.1 to include explicit ionic species required the adjustment of the interstrand sugar-sugar potential of Sambriski et al.19 This entropically driven potential has been recast as a function of the ionic strength of the surrounding medium (rather than sodium concentration alone as in 3SPN.1) as well as the sequence length and reparameterized to accurately reproduce the melting temperature behavior of a wide variety of sequences under a number of ionic conditions, including both mono- and divalent species. A biased parallel tempering method was used to efficiently determine the melting temperature of an oligonucleotide as well as characterize the phase transition as a function of an order parameter, namely, the fraction of paired bases. 3SPN.1-I, in conjunction with this method for determining the free energy profile as a function of an order parameter at the melting temperature, is able to qualitatively reproduce the experimentally observed sharpening of the phase transition as sequence length increases as well as dynamic fraying of dsDNA helix ends.
The work presented here improves on previous attempts to incorporate explicit ions in coarse-grain models for DNA25, 26, 27 in that quantitative agreement with experiment is obtained for melting behavior in addition to reproducing local ion structure in the vicinity of DNA observed in detailed atomistic simulations. Properly capturing this behavior is crucial to understanding biological processes involving the helix-coil transition of DNA.
ACKNOWLEDGMENTS
G.S.F. and D.M.H. were supported by a NHCRI training grant to the Genomic Sciences Training Program, T32HC002760. This work was also supported by the National Science Foundation through the University of Wisconsin-Madison Nanoscale Science and Engineering Center, DMR-0832760.
APPENDIX A: 3SPN.1-I FORMALISM
The 3SPN.1-I mesoscale model is described as follows. The reader is also referred to Refs. 17, 19 for additional details. Three bonded interactions enter the force field,
| (A1) |
| (A2) |
| (A3) |
which are typical of two-, three-, and four-body interactions found in molecular models. These interactions describe covalent bonding, bending, and torsion interactions within each single DNA strand. d0i represents equilibrium bond lengths, θ0i represents equilibrium bending angles, and ϕ0i represents equilibrium torsion angles. Instantaneous values of these quantities are denoted by the subscript i. The force constants k1 and k2, kθ, and kϕ control the strength of the bonded interactions and ni is the number of bonded interactions of type i.
Nonbonded interactions are described by four contributions, in addition to electrostatic interactions between charged sites (described at length in the main body of the article),
| (A4) |
| (A5) |
| (A6) |
and
| (A7) |
Ustack is an interaction term that accounts for intrastrand base-stacking through the Gō-like construct described by Hoang and Cieplak.55 This contribution acts uniformly on all native contact pairs, nstack. A native contact is defined as an interaction site and all intrastrand sites within 9 Å in the reference DNA structure (i.e., undeformed B-form DNA). The length scale of this interaction, σij, is interaction-specific, and is determined from the B-form reference structure.
The base pairing contribution, Ubase, acts between all complimentary base sites (i.e., A interacts with T and C with G). A complimentary base pair is considered to be bonded when rij < (σbi + 2.0 Å).
The non-native contribution, Unnat, accounts for excluded volume interactions between all sites that do not participate in either stacking or base pairing interactions. For mismatched base pairs, rcut = 1.00 Å, while for all other pairs of sites not involving ions, rcut = 6.86 Å. Non-native interactions involving ion sites are discussed in Sec. 2B. The length scale at which this purely repulsive interaction vanishes is σ0 = 2−1/6rcut
The solvent-induced contribution, Usolv, also referred to as the “sugar-sugar” interaction, accounts for entropic effects driving the renaturation of single strands to the hybridized state. Taking the form of the Morse potential, this contribution acts on all pairs of sugar moieties on opposite strands (i.e., strictly an interstrand interaction). The spatial scale of the interaction is controlled by α−1 with the energy minimum set by rsug. The energy scale of the sugar-sugar interaction depends on both the sequence length and the ionic conditions of the solvent. Both aspects of the energy scale are discussed in the main body of this work, as is the electrostatic contribution to the force field, Uion-ion.
The equilibrium bond lengths, angles, and torsions can be found in Refs. 17, 19. Summarized in Table 6 are the bonded and non-bonded parameters of 3SPN.1-I. With the exception of εsug, these parameters are unchanged from 3SPN.1.19
Table 6.
3SPN.1-I force field parameters (see also Ref. 19).
| Parameter | Value | Units |
|---|---|---|
| ε | 0.769856 | kJ mol−1 |
| εAT | 2.000ε | kJ mol−1 |
| εGC | 2.532ε | kJ mol−1 |
| εsug | System-dependent | kJ mol−1 |
| k1 | ε | kJ mol−1 Å−2 |
| k2 | 100ε | kJ mol−1 Å−2 |
| kθ | 1400ε | kJ mol−1 rad−2 |
| kϕ | 28ε | kJ mol−1 |
| α−1 | 5.333 | Å |
| rsug | 13.383 | Å |
| σij | Pair-dependent | Å |
| σAT | 2.9002 | Å |
| σGC | 2.8694 | Å |
| σ0 (mismatch) | 1.00 × 2−1/6 | Å |
| σ0 (otherwise) | 6.86 × 2−1/6 | Å |
APPENDIX B: DETAILED COMPARISON OF 3SPN.1 AND 3SPN.1-I: MELTING TEMPERATURE PREDICTIONS
Melting temperature calculations were preformed for all conditions considered in this work using 3SPN.1 for comparison against 3SPN.1-I. Summary statistics of this comparison are given in the main body of this work. Table 7 gives a more detailed comparison for each sequence and condition considered. It should be noted that 3SPN.1 was parameterized using a different definition of melting temperature than 3SPN.1-I. Whereas we consider the melting temperature to be the temperature at which the free energy of the hybridized and dehybridized states are equivalent, 3SPN.1 employed a definition based on the expectation value of ξ for a single DNA duplex, where ξ is the fraction of bound base pairs. The melting temperature was defined as the temperature at which an inflection in this curve occurs (∼ξ = 0.5). Therefore, for the comparison performed here, melting temperatures for 3SPN.1 are computed using this alternative definition of melting temperature, consistent with the parameterization of 3SPN.1. As we carefully followed the parallel tempering procedure outlined by Sambriski et al., simulation details for 3SPN.1 melting temperature calculations can be found in Ref. 19. Each melting temperature represents the average of six independent simulations (each 2000 ns in length) and the uncertainty is taken as the standard error of each set of simulations. Note that 3SPN.1-I results are the same as those shown in Tables 4, 5.
Table 7.
Comparison of 3SPN.1-I and 3SPN.1: Oligonucleotide melting temperatures. Experimental melting temperatures were taken from Refs. 52, 53.
| Length | [Na+] | [Mg2 +] | Tm, expt. | Tm, 3SPN.1-I | Tm, 3SPN.1 | |
|---|---|---|---|---|---|---|
| Sequence | (bp) | (mM) | (mM) | (K) | (K) | (K) |
| SEQ01 | 15 | 69 | 0 | 308.7a | 311 ± 2 | 309 ± 1 |
| SEQ01 | 15 | 119 | 0 | 313.6a | 307 ± 2 | 310 ± 1 |
| SEQ01 | 15 | 220 | 0 | 317.3a | 317 ± 1 | 319 ± 1 |
| SEQ02 | 15 | 69 | 0 | 323.1a | 326 ± 3 | 321 ± 2 |
| SEQ02 | 15 | 119 | 0 | 327.1a | 324 ± 1 | 325 ± 1 |
| SEQ03 | 15 | 69 | 0 | 326.0a | 322 ± 2 | 316 ± 1 |
| SEQ04 | 20 | 69 | 0 | 328.4a | 320 ± 1 | 319 ± 3 |
| SEQ05 | 15 | 105 | 0 | 317.0b | 312 ± 1 | 313 ± 2 |
| SEQ05 | 15 | 55 | 20 | 322.8b | 329 ± 2 | 315 ± 2 |
| SEQ06 | 15 | 55 | 0 | 332.1b | 332 ± 3 | 318 ± 1 |
| SEQ06 | 15 | 55 | 10 | 339.8b | 338 ± 1 | 320 ± 1 |
| SEQ06 | 15 | 55 | 50 | 341.3b | 341 ± 2 | 326 ± 2 |
| SEQ07 | 15 | 55 | 0 | 322.7b | 325 ± 3 | 315 ± 2 |
| SEQ07 | 15 | 55 | 20 | 332.0b | 333 ± 2 | 316 ± 1 |
| SEQ07 | 15 | 55 | 50 | 332.5b | 334 ± 2 | 324 ± 1 |
| SEQ08 | 10 | 69 | 0 | 307.0a | 311 ± 1 | 310 ± 1 |
| SEQ09 | 20 | 55 | 20 | 332.1b | 346 ± 1 | 313 ± 5 |
| SEQ10 | 15 | 69 | 0 | 311.3a | 312 ± 2 | 307 ± 1 |
| SEQ10 | 15 | 119 | 0 | 314.6a | 311 ± 1 | 309 ± 1 |
| SEQ11 | 15 | 69 | 0 | 319.7a | 323 ± 1 | 313 ± 2 |
| SEQ12 | 15 | 69 | 0 | 324.5a | 336 ± 4 | 330 ± 1 |
| SEQ12 | 15 | 119 | 0 | 328.4a | 336 ± 2 | 340 ± 1 |
| SEQ12 | 15 | 220 | 0 | 331.7a | 343 ± 1 | 346 ± 2 |
| SEQ13 | 15 | 69 | 0 | 338.1a | 348 ± 1 | 340 ± 1 |
| SEQ13 | 15 | 119 | 0 | 340.9a | 345 ± 3 | 343 ± 2 |
| SEQ14 | 20 | 119 | 0 | 333.0a | 319 ± 3 | 325 ± 3 |
| SEQ15 | 25 | 55 | 0 | 323.9b | 329 ± 3 | 337 ± 2 |
| SEQ16 | 25 | 69 | 0 | 334.1a | 329 ± 1 | 352 ± 4 |
| SEQ17 | 25 | 69 | 0 | 329.8a | 329 ± 3 | 340 ± 1 |
| SEQ18 | 20 | 69 | 0 | 337.7a | 336 ± 2 | 339 ± 1 |
| SEQ19 | 20 | 69 | 0 | 317.6a | 321 ± 2 | 332 ± 4 |
| SEQ20 | 20 | 69 | 0 | 344.1a | 348 ± 2 | 346 ± 3 |
| SEQ21 | 10 | 69 | 0 | 294.5a | 292 ± 3 | 298 ± 1 |
References
- Minsky A., Ghirlando R., and Reich Z., J. Theor. Biol. 188, 379 (1997). 10.1006/jtbi.1997.0525 [DOI] [PubMed] [Google Scholar]
- Garcia H. G., Grayson P., Han L., Inamdar M., Kondev J., Nelson P. C., Phillips R., Widom J., and Wiggins P. A., Biopolymers 85, 115 (2007). 10.1002/bip.20627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal E., Fondufe-Mittendorf Y., Chen L. Y., Thastrom A., Field Y., Moore I. K., Wang J. P. Z., and Widom J., Nature (London) 442, 772 (2006). 10.1038/nature04979 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rickgauer J. P., Fuller D. N., Grimes S., Jardine P. J., Anderson D. L., and Smith D. E., Biophys. J. 94, 159 (2008). 10.1529/biophysj.107.104612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith D. E., Tans S. J., Smith S. B., Grimes S., Anderson D. L., and Bustamante C., Nature (London) 413, 748 (2001). 10.1038/35099581 [DOI] [PubMed] [Google Scholar]
- Grayson P., Evilevitch A., Inamdar M., Purohit P. K., Gelbart W. M., Knobler C. M., and Phillips R., J. Virol. 348, 430 (2006). 10.1016/j.virol.2006.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evilevitch A., Castelnovo M., Knobler C. M., and Gelbart W. M., J. Phys. Chem. B 108, 6838 (2004). 10.1021/jp0376525 [DOI] [Google Scholar]
- Molineaux I. J., J. Virol. 344, 221 (2006). 10.1016/j.virol.2005.09.014 [DOI] [Google Scholar]
- Petrov A. S., Boz M. B., and Harvey S. C., J. Struct. Biol. 160, 241 (2007). 10.1016/j.jsb.2007.08.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrov A. S. and Harvey S. C., Biophys. J. 95, 497 (2008). 10.1529/biophysj.108.131797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrov A. S., Lim-Hing K., and Harvey S. C., Structure 15, 807 (2007). 10.1016/j.str.2007.05.005 [DOI] [PubMed] [Google Scholar]
- Petrov A. S. and Harvey S. C., Structure 15, 21 (2007). 10.1016/j.str.2006.11.013 [DOI] [PubMed] [Google Scholar]
- Angelescu D. G., Bruinsma R., and Linse P., Phys. Rev. E 73, 041921 (2006). 10.1103/PhysRevE.73.041921 [DOI] [PubMed] [Google Scholar]
- Ali I., Marenduzzo D., and Yeomans J. M., Phys. Rev. Lett. 96, 208102 (2006). 10.1103/PhysRevLett.96.208102 [DOI] [PubMed] [Google Scholar]
- Ali I., Marenduzzo D., and Yeomans J. M., J. Chem. Phys. 121, 8635 (2004). 10.1063/1.1798052 [DOI] [PubMed] [Google Scholar]
- Purohit P. K., Kondev J., and Phillips R., Proc. Natl. Acad. Sci. U.S.A. 100, 3173 (2003). 10.1073/pnas.0737893100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knotts T. A., Rathore N., Schwartz D. C., and de Pablo J. J., J. Chem. Phys. 126, 084901 (2007). 10.1063/1.2431804 [DOI] [PubMed] [Google Scholar]
- de Pablo J. J., Annu. Rev. Phys. Chem. 62, 555 (2011). 10.1146/annurev-physchem-032210-103458 [DOI] [PubMed] [Google Scholar]
- Sambriski E. J., Schwartz D. C., and de Pablo J. J., Biophys. J. 96, 1675 (2009). 10.1016/j.bpj.2008.09.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sambriski E. J., Schwartz D. C., and de Pablo J. J., Proc. Natl. Acad. Sci. U.S.A. 106, 21007 (2009). 10.1073/pnas.0904721106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sambriski E. J., Ortiz V., and de Pablo J. J., J. Phys.: Condens. Matter 21, 034105 (2009). 10.1088/0953-8984/21/3/034105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloomfield V. A., Biopolymers 44, 269 (1997). [DOI] [PubMed] [Google Scholar]
- Gosule L. C. and Schellman J. A., Nature (London) 259, 333 (1976). 10.1038/259333a0 [DOI] [PubMed] [Google Scholar]
- Gelbart W. M., Bruinsma R. F., Pincus P. A., and Parsegian V. A., Phys. Today 53(9), 38 (2000). 10.1063/1.1325230 [DOI] [Google Scholar]
- Prytkova T. R., Eryazici I., Stepp B., Nguyen S. B., and Schatz G. C., J. Phys. Chem. B 114, 2627 (2010). 10.1021/jp910395k [DOI] [PubMed] [Google Scholar]
- Demille R. C., T. E.CheathamIII, and Molinero V., J. Phys. Chem. B 115, 132 (2011). 10.1021/jp107028n [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savelyev A. and Papoian G. A., Proc. Natl. Acad. Sci. U.S.A. 107, 20340 (2010). 10.1073/pnas.1001163107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenart P. J., Jusufi A., and Panagiotopoulos A. Z., J. Chem. Phys. 126, 044509 (2007). 10.1063/1.2431169 [DOI] [PubMed] [Google Scholar]
- Enderby J. E. and Neilson G. W., Rep. Prog. Phys. 44, 593 (1981). 10.1088/0034-4885/44/6/001 [DOI] [Google Scholar]
- Dang L. X., Rice J. E., Caldwell J., and Kollman P. A., J. Am. Chem. Soc. 113, 2481 (1991). 10.1021/ja00007a021 [DOI] [Google Scholar]
- Degreve L., and Silva F. L. B., J. Chem. Phys. 110, 3070 (1999). 10.1063/1.477903 [DOI] [Google Scholar]
- Kovalenko A. and Hirata F., J. Chem. Phys. 112, 10403 (2000). 10.1063/1.481677 [DOI] [Google Scholar]
- Faller R., Polymer 45, 3869 (2004). 10.1016/j.polymer.2003.11.053 [DOI] [Google Scholar]
- Reith L. X., Putz M., and Muller-Plathe F., J. Comput. Chem. 24, 1624 (2003). 10.1002/jcc.10307 [DOI] [PubMed] [Google Scholar]
- Demille R. C. and Molinero V., J. Chem. Phys. 131, 034107 (2009). 10.1063/1.3170982 [DOI] [PubMed] [Google Scholar]
- Sugita Y. and Okamoto Y., Chem. Phys. Lett. 314, 141 (1999). 10.1016/S0009-2614(99)01123-9 [DOI] [Google Scholar]
- Yan Q. L. and de Pablo J. J., J. Chem. Phys. 111, 9509 (1999). 10.1063/1.480282 [DOI] [Google Scholar]
- Bussi G. and Parrinello M., Phys. Rev. E 75, 056707 (2007). 10.1103/PhysRevE.75.056707 [DOI] [PubMed] [Google Scholar]
- Passiniemi P., J. Solution Chem. 12, 801 (1983). 10.1007/BF00653183 [DOI] [Google Scholar]
- Mills R. and Lobo V. M. M., Self-diffusion in Electrolyte Solutions: A Critical Examination of Data Compiled from the Literature (Elsevier, New York, 1989). [Google Scholar]
- Tironi I. G., Sperb R., Smith P. E., and van Gunsteren W. F., J. Chem. Phys. 102, 5451 (1995). 10.1063/1.469273 [DOI] [Google Scholar]
- Noy A., Soteras I., Luque F. J., and Orozco M., Phys. Chem. Chem. Phys. 11, 10596 (2010). 10.1039/b912067j [DOI] [PubMed] [Google Scholar]
- Wang J., Cieplak P., and Kollman P. A., J. Comput. Chem. 21, 1049 (2000). [DOI] [Google Scholar]
- Hess B., Kutzner C., Spoel D. van der, and Lindahl E., J. Chem. Theory Comput. 4, 435 (2008). 10.1021/ct700301q [DOI] [PubMed] [Google Scholar]
- Rathore N., Chopra M., and de Pablo J. J., J. Chem. Phys. 122, 024111 (2005). 10.1063/1.1831273 [DOI] [PubMed] [Google Scholar]
- Kumar S., Bouzida D., Swendsen R. H., Kollman P. A., and Rosenberg J. M., J. Comput. Chem. 13, 1011 (1992). 10.1002/jcc.540130812 [DOI] [Google Scholar]
- Chodera J. D., Swope W. C., Pitera J. W., Seok C., and Dill K. A., J. Chem. Theory Comput. 3, 26 (2007). 10.1021/ct0502864 [DOI] [PubMed] [Google Scholar]
- Reddy A. S., Wang L., Lin Y. S., Ling Y., Chopra M., Zanni M. T., Skinner J. L., and de Pablo J. J., Biophys. J. 98, 443 (2010). 10.1016/j.bpj.2009.10.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beglov D. and Roux B., J. Chem. Phys. 100, 9050 (1994). 10.1063/1.466711 [DOI] [Google Scholar]
- Roux B., Biophys. J. 71, 3177 (1996). 10.1016/S0006-3495(96)79511-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyubartsev A. P. and Laaksonen A., J. Chem. Phys. 111, 11207 (1999). 10.1063/1.480476 [DOI] [Google Scholar]
- Owczarzy R., You Y., Moreira B. G., Manthey J. A., Huang L. Y., Behlke M. A., and Walder J. A., Biochemistry 43, 3537 (2004). 10.1021/bi034621r [DOI] [PubMed] [Google Scholar]
- Owczarzy R., Moreira B. G., You Y., Behlke M. A., and Walder J. A., Biochemistry 47, 5336 (2008). 10.1021/bi702363u [DOI] [PubMed] [Google Scholar]
- Andreatta D., Sen S., Lustres J. L. P., Kovalenko S. A., Ernsting N. P., Murphy C. J., Coleman R. S., and Berg M. A., J. Am. Chem. Soc. 128, 6885 (2006). 10.1021/ja0582105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoang T. X. and Cieplak M., J. Chem. Phys. 112, 6851 (2000). 10.1063/1.481261 [DOI] [Google Scholar]