Model-based dynamical analysis of functional disconnection in schizophrenia

Abstract

Schizophrenia is shown to be associated with impaired interactions in functional macro-networks of the brain. The focus of our study was if there is an impairment of cognitive control of learning during schizophrenia. To investigate this question, we collected fMRI data from a group of stable schizophrenia patients and controls performing an object-location associative learning task in which the learning performance of the patient group was significantly worse. We applied Dynamic Causal Modelling to analyse the fMRI data A set of causal models of BOLD signal generation were defined to evaluate connections between five regions material to the task (Primary Visual Cortex, Superior Parietal and Inferior Temporal Cortex, Hippocampus and Dorsal Prefrontal Cortex). Bayesian model selection was used to investigate hypotheses on differences in model architecture across groups, and indicated fundamental differences in model architecture in patients compared to controls. Models lacking connections related to cognitive control were more probable in the patient group. Hypotheses on differences in effective connectivity between groups were tested by comparing estimates of neural coupling parameters in winning model structures. This analysis indicated reduced fronto-hippocampal and hippocampo-inferior temporal coupling in patients, and reduced excitatory modulation of these pathways by learning. These findings may account for the documented reductions in learning performance of schizophrenia patients.

1. Introduction

Schizophrenia is a complex polygenic disorder with diverse neural correlates. Widely accepted as being biological and developmental in its bases [11], decades of research have identified diverse neurobiological correlates of schizophrenia pathology [17, 28]. Whereas the complete pathology of schizophrenia is diverse, impaired dopamine-related prefrontal function and impaired glutamate related hippocampal function have emerged as a central framework for explaining disordered fronto-hippocampal interactions in the illness [29, 30, 31, 3]. In this framework, abnormal dopamine levels in the prefrontal cortex may directly affect modulation of the excitability of prefrontal neurons. Hyper- or hypo-dopaminergia may underlie working memory impairments which are associated with schizophrenia pathology and in turn impair learning processes that are reliant on these basic domains of cognition [8, 41]. Altered fronto-hippocampal function and interaction may be related to anatomical and/or functional disconnection [21], and altered synaptic plasticity [48], which in turn may result from a complex expression of genes on the brain’s macro-networks [31, 51].

Studies of associative memory and learning assume particular significance. In humans associative learning is heavily dependent on pre-frontal-hippocampal interactions [5] and these interactions during critical stages are hypothesized as central to long term memory consolidation in the neo-cortex [15]. In the absence of, or reduced effective interactions between the prefrontal cortex and the hippocampus, learning is likely to be impaired [52]. Here we investigated impaired macro-network interactions in schizophrenia by applying Dynamic Causal Modelling (DCM) [46] to the analyses of fMRI data collected during a paired-associate learning paradigm [4]. The aim of modelling neuronal interactions using DCM is to characterize: a) the intrinsic connectivity of the network and b) the contextual modulation of the intrinsic connections by psychological aspects of the task. In the present study we were interested in investigating whether or not there is a plausible difference between patients and controls in the intrinsic connectivity of the learning related macro-network, and in the modulatory effects on these connections by learning related variables such as time. This approach allowed us to simultaneously investigate hypotheses of disconnection (intrinsic connections) and reduced plasticity (modulatory effects of learning) in schizophrenia.

1.1. Disconnection hypotheses of schizophrenia

It has been hypothesized that schizophrenia is best understood in terms of pathological interactions between different brain regions. This claim can be formulated on two different levels: on one hand, we can investigate the structural organization of the cortex and look for physical differences between patients and controls, and on the other hand, we can investigate whether there is a difference in the task-dependent functional interaction of cortical areas regardless to the underlying neural structure.

The concept of structural “disconnection syndrome” goes back at least to Wernicke [55], who interpreted psychosis as a result anatomically disrupted connections. It was reintroduced by Geschwind [26, 27], and had a crucial role in behavioural neurology and psychiatry [9]. Newer meta-analysis also supported the hypothesis [17].

The relevance of the concept of functional disconnection for interpreting schizophrenia now also seems to be promising: studies showed impairments in functional macro-networks in schizophrenia [36], and based on brain imaging experiments it was suggested that reduced performance of schizophrenic patients in cognitive tasks requiring working memory is related to abnormal prefronto-hippocampal connectivity [54, 23, 21]. The cellular bases of the two types of disconnectivities have also been studied, and two, somewhat interacting mechanisms, i.e. altered anatomical connections and impairments in synaptic plasticity were identified [20, 48, 49].

Specifically, we are interested in the functional reduction, both the qualitative and quantitative nature of it. Consequently, there are two questions to be answered: (i) what are the differences in the model architectures describing the information processing network of healthy and schizophrenia subjects, and (ii) which connections are significantly impaired during schizophrenia? In technical terms, we analyse effective connectivities, which reflect the causal influence that one brain region exerts over another. Effective connectivity can consist of two components. The first characterizes the intrinsic connectivity of the network, and the second models input-dependent changes in them. (Inputs, however, may have effects for brain dynamics not only by modulating connections, but also via direct or indirect influence on specific regions). Pathological connectivities may appear in both components.

Task-related functional connectivity can be investigated with respect to various functions of the brain, e.g. learning, memory, control, etc. We studied associative learning, since this is a cortical function that requires the integration of multiple sensory, representation and cognitive control pathways, making it a useful approach to grasp disordered functional interaction.

2. Material and methods

2.1. Associative learning: behavioural task and data

Paired-associate learning paradigms that require learning of associations between diverse memoranda over time, have been a cornerstone of the experimental learning literature [5, 6, 56]. These paradigms provide a framework for evaluating the role of the hippocampus in binding as well as in examining the temporal dynamics of neural signals that correlate with changes in performance in learning. [19]. In addition to fronto-hippocampal interactions [44], associative learning is based in part on the hippocampal integration of memory streams as diverse memoranda must be bound into integrated associations [14]. It also relies on the consolidation and retrieval of associations between diverse memoranda, sensory inputs and streams of neural activity, particularly by hippocampal neurons. Yet tasks of paired-associate learning and memory have been infrequently applied in understanding dysfunction in schizophrenia, even though they have provided evidence of particularly strong deficits, relative to other tasks [57].

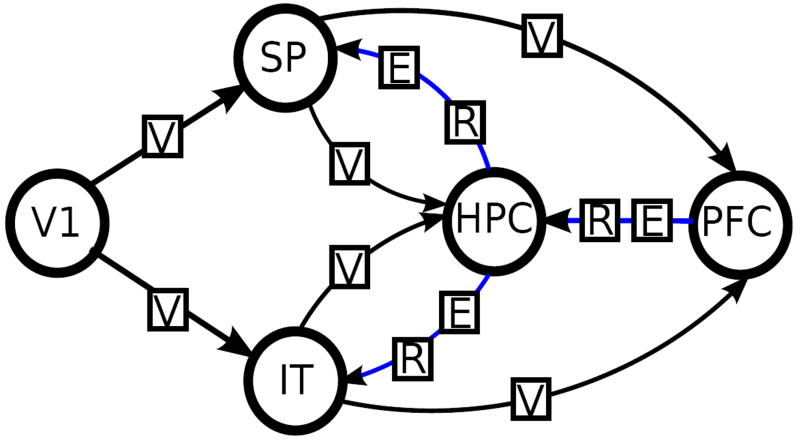
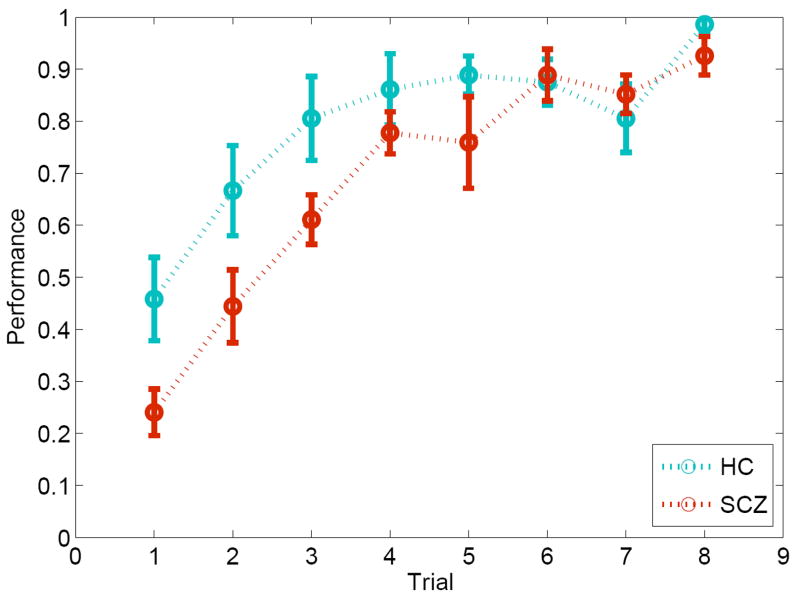
We adopted a paired-associate learning paradigm in which subjects are required to learning arbitrary associations between locations (in space) and objects (with unique identities). The two kinds of memoranda (“where” and “what”) are processed by the two components, i.e. spatial (dorsal) and object (ventral), of the forward visual pathway [4, 32, 42]. It is assumed that these information streams converge in the hippocampus, with potential supervisory inputs from the prefrontal cortex [5]. The result macro-network (depicted in Figure 2) provides a relative rich framework to estimate model architectures using DCM [47]. Through the repeated alternation between learning and retrieval epochs using a block design [1] (see Methods), we were able to capture learning dynamics in controls and patients over time (see Figure 1).

Figure 2.

The model space for varying endogenous connections. Connections marked by blue are varied. The effects of external inputs Visual, Encoding and Retrieval are marked by V, E and R respectively. The effect of Time is applied to all connections.

Figure 1.

Learning dynamics in the associative memory task in controls and schizophrenia patients over time. The data provide evidence of generally asymptotic learning in both groups, with reduced learning rates in patients compared to controls.

For details see Appendix A.

2.2. Functional network models

Dynamic causal modelling (DCM) is an important method for estimating effective connectivity from neuroimaging data [24]. DCM uses an explicit model of neural dynamics to capture causal interactions between regions within the network (intrinsic connections), modulation of intrinsic connections by the experimental context (e.g., the valence of a face) and driving inputs to regions (e.g., visual stimulation driving face processing regions). Using Bayesian methods, DCM selects from among competing models, i.e., hypotheses, that best capture network interactions during the examined task [50]. Parameter estimates of inter-regional interactions derived from the model reflect measures of effective connectivity that can then be compared to assess significant differences between groups.

Macro-network models were evaluated based on a combination of anatomical and functional assumptions governing interactions between the five regions of interest material to the task. The basic architecture included intrinsic connections between primary and secondary visual cortices (from both dorsal and ventral pathways) that form two basic multi-synaptic pathways of the visual system [38, 39]. Connections from each of the inferior temporal cortex and the superior parietal cortex to the hippocampus reflect its unique anatomical place in a “hierarchy of associativity” [34] allowing it to integrate multi-modal inputs from unimodal areas before redistribution of potentiated associations into the neocortex [15]. This basic model structure was expanded in each of the evaluated models with intrinsic connections from the hippocampus to each of the inferior temporal and superior parietal cortices [34] that may enhance learning over time, and from the prefrontal cortex to the hippocampus, to implement supervisory inputs from this executive region [18, 40].

2.3. Elements of the models

DCM assumes a coupled dynamics of the neural activity in the involved brain regions and the external inputs. The connectivity parameters can be obtained by fitting the model to measurement data. The parameters describe effective connectivities, including the intrinsic coupling between brain regions (represented by an n × n matrix, A, where n is the number of brain regions, 5 in our case), and the effects of the external modulations on these connections (represented by an m × n × n tensor, B, where m is the number of inputs, 4 in our case).

The cornerstone of dynamic causal modelling is to define the external factors, determined by the experimental paradigm, that modulate the intrinsic connections between brain areas. For our associative learning task we examined the role of four inputs. The first is called Visual, and refers to the presence of any visual stimulus. The second input is Encoding, which refers if the subject is in the encoding period, when the objects are shown in their location, and the third is Retrieval, which indicates if the subject is in the retrieval period, when a cue is presented in a location, and an answer is requested from the subject. The fourth input is Time, which is indicating that which epoch is the subject in, grasping the pass of time. These modulations allow us to examine the change in effective connectivity with respect to different memory functions and temporal development.

For details of the model definitions, the parameter fitting, model comparison and definition of inputs, see Appendix B.

2.4. Model definitions

To model the information processing in the associative learning task, we assumed the presence of two streams connecting the five brain regions. The “forward” or “data” stream propagates sensory information at different levels of processing from the low-level sensory areas towards high-level areas. The “backward” or “control” stream propagates control signals from the high-level areas towards the lower-level ones. In this paper we examine impairments in cognitive control, so the focus of the investigations is the control stream.

Five regions were used in the modelling studies, specifically Primary Visual Cortex (V1), Superior Parietal (SP), Inferior Temporal Cortex (IT), Hippocampus (HPC) and Dorsal Prefrontal Cortex (PFC). We examined the pattern of endogenous connectivity by defining a base model which included the connections as shown in Figure 2. We then explored whether any combination of three additional putative connections would increase the evidence of the model. This resulted in 8 different models with different numbers and patterns of connections. Based on the hypothetical control stream we defined three allowed connections that may extend the basic model in different combinations. These include the intrinsic connections from HPC to IT and SP, and from PFC to HPC. The eight possible combinations of these connections constitute the first model class. All possible intrinsic connections are visualized in Fig. 2, where the fixed data stream is indicated by black arrows and the varied control stream is indicated by blue arrows. The connection patterns of the models in the first class are summarized in Table 1.

Table 1.

Model probabilities for varying endogenous connections

No.	Additional connections	SCZ	HC
1	none	.099	.079
2	PFC→HPC	.145	.106
3	HPC→IT	.099	.079
4	HPC→IT, PFC→HPC	.172	.101
5	HPC→SP	.158	.081
6	HPC→SP, PFC→HPC	.095	.116
7	HPC→SP, HPC→IT	.136	.081
8	HPC→SP, HPC→IT, PFC→HPC	.095	.357

Connections present in all models: V1→(IT,SP), SP→(HPC,PFC), IT→(HPC,PFC)

A second set of models were evaluated using invariant intrinsic connections (both data and control streams) and varying hypotheses-related contextual modulations(B matrix). Here. the effects of the Visual input on the connections of the data stream and of the Time input on all connections were invariant across models. We defined the allowed contextual modulation to be the effects of Encoding and Retrieval on the endogenous connections of the control stream. This resulted in 16 combinations of the allowed contextual modulations which constitute the second model class. Visualization of the application of contextual modulations on intrinsic connections is given in Fig. 2. The connection patterns of the models in the second class are summarized in Table 2.

Table 2.

Model probabilities for varying modulatory connections

No.	Additional connections		SCZ	HC
	Encoding	Retrieval
9	none	none	.063	.063
10	none	PF→HC	.064	.072
11	PF→HC	none	.060	.066
12	PF→HC	PF→HC	.060	.068
13	none	HC→(SP,IT)	.061	.055
14	none	HC→(SP,IT), PF→HC	.068	.053
15	PF→HC	HC→(SP,IT)	.060	.054
16	PF→HC	HC→(SP,IT), PF→HC	.059	.054
17	HC→(SP,IT)	none	.073	.054
18	HC→(SP,IT)	PF→HC	.061	.053
19	HC→(SP,IT), PF→HC	none	.064	.054
20	HC→(SP,IT), PF→HC	PF→HC	.059	.053
21	HC→(SP,IT)	HC→(SP,IT)	.064	.061
22	HC→(SP,IT)	HC→(SP,IT), PF→HC	.065	.061
23	HC→(SP,IT), PF→HC	HC→(SP,IT)	.060	.059
24	HC→(SP,IT), PF→HC	HC→(SP,IT), PF→HC	.059	.120

Connections present in all models: Time→All, Visual→(V1→(IT,SP), SP→(HC,PF), IT→(HC,PF)

In the first model class all meaningful modulatory connections mentioned above were included, (modulatory effects on nonexistent intrinsic connections were excluded only). The direct effects of the experimental conditions on the cortical areas were included in all models and are not in the focus of this study.

3. Results

All 24 models were fitted to the measurement data from all 14 subjects, obtaining 336 parameter sets, sorted into two groups, schizophrenia patients (SCZ) and healthy control (HC). The computational procedure applied serves two quantities, the maximum a posteriori (MAP) parameter values and model evidences. They were approximated by the Expectation Maximization algorithm implemented in the SPM package [22]. The results can be evaluated on multiple levels of abstraction. First, we made an intra-group model comparison to find out which model structures are more probable than others in the subject groups, then we investigated the differences on the level of the individual parameters.

3.1. Model comparison

The goodness of a model can be quantitatively described by its posterior probability obtained from Bayesian model selection. We applied the variational (free energy) method to approximate the log-evidence of the models. As model goodness, we calculated posterior probabilities of model structures by random effects analysis, which allows the subjects to be described by different models with the highest probability within a single group, and so is able to capture variability in the information processing structure applied by different subjects. The expected posterior probabilities are listed in the Tables 1 and 2. The comparison was done within the first and second model classes separately.

The results show that in the control group there is a clear winner for both the endogenous and modulatory connection patterns, the model that contains the full control stream. In the SCZ group, there is no clear winner, there are several more probable models, and the differences are smaller between model probabilities. It can also be seen that while the winning model in the HC group contains all the connections defined, while the most probable models in the SCZ group lack more or less connections. This result implies that the information processing network of schizophrenia patients is fundamentally different than the one of controls. However, the model selection does not provide the specific pathways being impaired, so the parameter level analysis is also necessary. The result of the model comparison is depicted in Fig 3.

Figure 3.

(A) Intrinsic connections in most probable fitted DCM models. Solid arrows denote causal connections present in both HC and SCZ groups, dashed arrows denote connections present in the HC group only. (B) Some of the modulatory connections in most probable fitted DCM models.

3.2. Effective connectivities

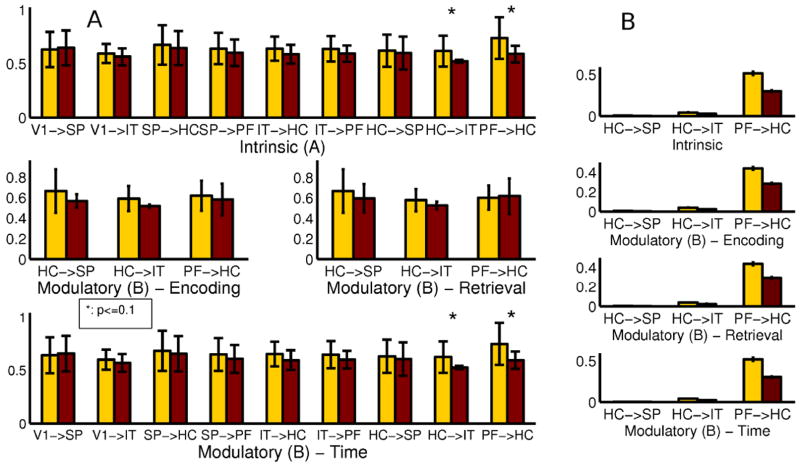
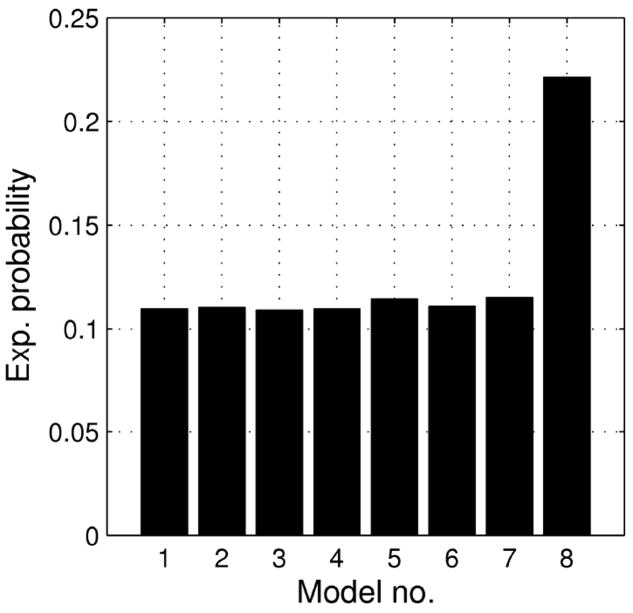
In the next step of the analysis, we give a more detailed quantitative characterization of the results. We look at the parameter space level to see if there are significant differences in the effective connectivity in the models fit to the two subject groups if we assume fixed model structure. To do so, we selected a reference model for comparison by running the model selection for all subjects together with no distinction by group. The results can be seen on Fig. 4, the winning model is the one containing all hypothesized connections. The means and standard deviations of the endogenous coupling and modulatory parameters are depicted in part A of Fig. 5. To obtain the significance of the differences we applied a two-sample t-test on the parameter values in the two groups. For this analysis we used 8 subjects with schizophrenia and 10 healthy controls.

Figure 4.

Model probabilities for all subjects. Model numbers are drawn from Table 1 and 2. Note that models numbered 8 and 24 are identical to each other.

Figure 5.

Average connectivity parameters for HC and SCZ groups. (A) By selecting a reference model, and (B) by Bayesian model averaging. The significant differences are in the prefronto-hippocampal and hippocampo-inferior temporal pathways.

To verify the findings, we also compared the connectivity parameters in the control stream by applying Bayesian averaging of the models of every subject. When a certain connection was not included in a given model, we calculated with delta distributions at zero instead of the Gaussians. We took the grand average of the obtained connection strengths over subjects within groups. The results are depicted in part B of Fig. 5.

The significant differences between the two groups are in the strength of the endogenous connections between prefrontal cortex and hippocampus and between hippocampus and inferior temporal cortex according to the reference model comparison, and also supported by the model averaging comparison. These connections are weakened in the SCZ group, which supports the hypothesis about the impaired effective connectivities in the control stream in schizophrenia. Both these connections are playing important roles in the cognitive control of the associative memory formation. Furthermore, we see the reduced effects of Time on these causal links meaning reduced excitatory contextual modulation of the pathways by learning. This can be seen as a surrogate of reduced task-related plasticity of a pathway in the illness.

3.3. Subject-by-subject analysis

To see a more detailed picture of the effects of the associative learning task on the model parameters, we correlated them with the learning rate of the individual subjects. To obtain this rate, k, for each subject, we fitted a learning curve defined by Eq. 1 to the behavioural data [4].

$$l(t)=1-e^{-\mathit{kt}}$$ (1)

The Spearman rank correlation coefficients between the DCM parameters and the learning rate was calculated. The results averaged over subjects are shown on Fig. 6. The correlations are mostly positive, and high for the hippocampal-superior parietal interaction in the endogenous and also in the modulatory parameter arrays. This result is not in full correspondence with the intergroup comparison of the effective connectivities, suggesting that the learning rate is not necessarily the key element of the differentiation between schizophrenia and other conditions. This is also leading us to the next step of the analysis.

Figure 6.

Correlations between the learning rate of the subjects and the connectivity parameters of the models fit to their BOLD data.

3.4. Illness versus slow learning

A common problem in schizophrenia research is that it is usually hard to separate the effects of the illness on learning skills from the lower performance of naturally slow learners. To address this issue, we selected the subjects from the control group who did not perform better than the SCZ group (there were 3 such subjects in the HC group). We fitted the model space to these subject separately. The resulting posterior model probabilities are shown in Fig. 7. It is apparent that the distribution over the model class is similar to the one obtained for the control group and shares no common features with the one obtained for the SCZ group, as one can see in Table 1. This result suggests that the methods applied by us are independent of the overall learning rate and are able to clearly separate slow learning from schizophrenia by explaining the two phenomena by different model structures.

Figure 7.

Expected posterior probabilities of models from the first class for slow learners. The distribution is similar to the one of the control group and distinctively different from the one of the patient group. Model numbers are drawn from Table 1.

4. Discussion

A widely studied aspect of schizophrenia is the impairment of cognitive control over information processing cortical circuits. The prefrontal cortex is the area that is consensually considered as the center of cognitive control functions, such as attention, memory and executive functions. Numerous functional imaging studies pointed out decreased influence of the prefrontal cortex on areas which are material in tasks effected in schizophrenia. For a review on pathological functional connectivities related to different cognitive functions see [7]. The architecture of cognitive control in schizophrenia is still not well understood, for preliminary ideas see [10, 2, 33], for the normal and pathological neural circuitry of executive functions, see e.g. [16]. Reduced fronto-temporal functional connectivity associated with auditory hallucinations for schizophrenic patients was extensively studied, see e.g. [35, 53]. A focused strategy training was suggested recently [13] to facilitate cognitive task performance in patients with schizophrenia by changing the dynamics of activity within critical control-related brain regions.

Our study targeted the prefrontal control of areas involved in associative learning, primarily the hippocampus. Several model architectures were defined to explain the information processing in the cortex during learning. We compared groups of schizophrenia patients and of healthy controls on two levels, and a fundamental difference between the functional networks implemented in the schizophrenic and healthy brain were found. The parameter level comparison revealed significant impairments in the prefronto-hippocampal and hippocampal-inferior temporal pathways. This finding implies that the lack of cognitive control over the processes of associative learning may underlie the decreased performance of schizophrenia patients in related tasks.

Learning impairments have been considered good markers of hippocampal impairment in schizophrenia [57], and computational models of hippocampal function have been applied to study this cognitive impairment in the disorder [43, 12]. However, the basis of these impairments in terms of network interactions has not been known. Our results (the first based on in vivo fMRI data) provide evidence of impaired frontal inputs to the hippocampus, and reduced learning related plasticity of fronto-hippocampal coupling in the disorder.

Research highlights.

• Associative learning task for fMRI measurements with schizophrenia patients

• We defined several connectivity models and fitted them to data

• Schizophrenia patients implement a different cortical network for memory formation

• Cognitive control is significantly impaired in schizophrenia

• Illness and slow learning is separable by statistical methods

Appendix A. Data Acquisition

Appendix A.1. Subjects

Healthy Controls (n=11; mean age=22 yrs, sd=5; 5 females) and stable early course schizophrenia patients (n=11; mean age=26 yrs; sd=5; 3 females) gave informed consent. Groups did not differ in terms of age (p¿.10). Patients were diagnosed using DSM-IV, SCID and consensus diagnosis. All were on a regimen of atypical anti-psychotics (Risperidone, Olanzapine or Aripiprazole).

Appendix A.2. Behavioural paradigm

Subjects alternated between blocks of encoding, rest/rehearsal and retrieval. During encoding, nine equi-familiar objects with monosyllabic object names [45] were presented in sequential random order (3s/object; 27 s block length) in grid locations for naming (e.g. “bed” and “book”). Following a rest interval (R1; 27 s), memory for object-location pairs was tested using cued recall (3s/cue). The cycle ended with an additional rest interval (R2; 27 s). Subjects were instructed to respond by naming the object (or saying “no”) between the end of the current and the beginning of the subsequent acquisition (1 s; that is when gradients were turned off). Object names were monosyllabic to minimize head motion. Eight blocks (each cycling between consolidation, rest and retrieval) were employed. The paradigm is illustrated in Figure 8.

Figure 8.

Structure of the experimental paradigm is depicted with two examples of associations presented during encoding/consolidation (“bed” and “book”) and examples of those locations cued during recall/retrieval.

Appendix A.3. fMRI Methods

fMRI was conducted on a Bruker MedSpec 4T system with an 8-channel head coil. 288 T2*-weighted gradient-echo echo-planar (EPI) images were acquired (TE=30ms; TR=3s; TA=2s; flip angle = 90°; acquisition matrix = 64 × 64 voxels; FOV = 240 mm; 24 slices; 3.75 × 3.75 × 4mm). During scanning, visual stimuli were presented via a projector system controlled by Presentation (www.neurobs.com).

fMRI data were preprocessed and analysed in SPM2 using a standard processing sequence. Images were manually oriented to the AC-PC line. Following detrending and removal of low frequency components (.008 Hz), images were realigned to correct for head movement, spatially normalized to the MNI (Montreal Neurological Institute) template brain, resliced (2 mm3) and smoothed spatially by a Gaussian filter of 8mm full-width half maximum (FWHM). DCM’s were based on first-level models with eight individual regressors (plus the six motion parameters used as regressors of no interest). Four regressors represented the unique effects of each of the epochs of interest, specifically encoding, R1, retrieval and R2. In addition, time dependent effects on each of these regressors were represented by convolving them with a linear time-ordered component. Time series for DCM analyses were extracted for each subject using a thresholded (p¡.05) effects of interest contrast applied in each of the five regions of interest using stereotactic region-of-interest maps [37].

Appendix B. Modelling techniques

Appendix B.1. Dynamic causal modelling

DCM provides a complete phenomenological model framework for the analysis of BOLD data. For a detailed description see [24]. The model consists of two components: a neural state equation and a hemodynamic model. The neural component describes the time evolution of the neural state variables, x, which refer to the neural activity of the ROIs. This is a bilinear formula of the state variables themselves and the input variables, u, which are the conditions defined by the experiment (Eq. B.1). The parameters of the neural model are the elements of the three matrices, θ_n = {A, B, C}. A contains the endogenous coupling parameters, the causal effects of the ROIs on each other, B contains the modulatory parameters, the effects of the inputs on the endogenous connections, and C contains the direct effects of the inputs on the ROIs.

$$\dot{x}=(A+\sum _{i=1}^N{u}_j{B}^j)x+\mathit{Cu}$$ (B.1)

$$y=\lambda (x,{\theta }_h)$$ (B.2)

The hemodynamic component describes the nonlinear mapping from the neural activity to the BOLD signal, y, actually measured in the ROIs (Eq. B.2). For the details of the hemodynamic model see [25]. The two components define a complete generative forward model of the BOLD signal generation. To estimate the values of the parameter set, θ = { θ_h,θ_n } best fitting to measurement data, the “inverse problem” should be solved. One possible procedure to do so is the Bayesian maximum a posteriori (MAP) estimation technique defined by Eq. B.3, where M denotes the specific connectivity pattern of the model.

$$p(\theta \mid y,M)=\frac{p(y\mid \theta ,M)p(\theta \mid M)}{p(y\mid M)}$$ (B.3)

To exclude specific connections in our model, we can set the prior probabilities of the corresponding parameters to zero. For all probability distributions in B.3, we assume that their form is normal, meaning that both the prior (p(θ | M)) and posterior (p(θ | y,M)) distributions are Gaussians, and the MAP estimation is defined as the mean of the posterior distribution.

Appendix B.2. Comparison of models

We can compare models with different connectivity patterns in a Bayesian fashion by estimating their model evidence:

$$p(y\mid M)=\mathit{\int }p(y\mid \theta ,M)p(\theta \mid M)\mathit{d\theta }$$ (B.4)

The evidence is the probability of obtaining the actual measurement conditioned on the model form, integrated on the whole parameter space of the model. This way we get the overall probability that our actual model explains the measurement data regardless of the choice of parameters, and also punish models with a larger number of parameters. The computation of the evidence is usually not feasible, but there are several methods available to approximate it. One such method is the variational Bayesian approximation. In this method we define a functional that is a lower bound of the log-evidence of the model. We maximize this functional to approximate the log-evidence.

To obtain the expected posterior probabilities of all models in a model class, we assume a hierarchical model of data generation. On the top level, a Dirichlet distribution describes the occurrence probabilities of the individual models in the population. On the next level, we have multinomial variables, parametrized by the occurrence probabilities of the above level, which describe the probability of a certain model generating the data for a certain subject. On the bottom level, the actual data is generated by the dynamic model with parameters defined by the multinomial variable. We can invert this model using a variational Bayesian method that requires only the estimates of the log-evidences for each subject-model pair. In this way we can obtain the parameters of the Dirichlet distribution. If we normalize these parameters, we get the expected posterior probability of each model regarding to the subject group. For a complete description of the comparison method see [50].

Appendix B.3. Coding of external modulations

The numerical values of external modulations as functions of time are constructed as follows. For Visual, the value is 1 in encoding and retrieval periods of the task and 0 in resting periods. The second input, Encoding, is 1 in encoding periods and 0 otherwise. The third, Retrieval, is constructed in a similar fashion. The fourth input, Time, is an integer, starting from 1 and increasing by one in the end of each epoch. The direct effects of all four inputs on the neural activity of all brain areas (C matrix) are present in every model we defined.