Ribulose-1,5-Bisphosphate Carboxylase/Oxygenase Content, Assimilatory Charge, and Mesophyll Conductance in Leaves

Abstract

The content of ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco) (E_t; EC 4.1.1.39) measured in different-aged leaves of sunflower (Helianthus annuus) and other plants grown under different light intensities, varied from 2 to 75 μmol active sites m⁻². Mesophyll conductance (μ) was measured under 1.5% O₂, as well as postillumination CO₂ uptake (assimilatory charge, a gas-exchange measure of the ribulose-1,5-bisphosphate pool). The dependence of μ on E_t saturated at E_t = 30 μmol active sites m⁻² and μ = 11 mm s⁻¹ in high-light-grown leaves. In low-light-grown leaves the dependence tended toward saturation at similar E_t but reached a μ of only 6 to 8 mm s⁻¹. μ was proportional to the assimilatory charge, with the proportionality constant (specific carboxylation efficiency) between 0.04 and 0.075 μm⁻¹ s⁻¹. Our data show that the saturation of the relationship between E_t and μ is caused by three limiting components: (a) the physical diffusion resistance (a minor limitation), (b) less than full activation of Rubisco (related to Rubisco activase and the slower diffusibility of Rubisco at high protein concentrations in the stroma), and (c) chloroplast metabolites, especially 3-phosphoglyceric acid and free inorganic phosphate, which control the reaction kinetics of ribulose-1,5-bisphosphate carboxylation by competitive binding to active sites.

Rubisco (EC 4.1.1.39) catalyzes the irreversible carboxylation of RuBP to form two PGA molecules (in this work the oxygenase reaction was not active since a low O₂ concentration was used). RuBP carboxylation is the major rate-determining reaction in photosynthetic CO₂ assimilation. All factors that influence the photosynthetic rate do so by influencing the activity of Rubisco and the concentration of its substrates, CO₂ and RuBP. E_t in leaves may be as high as 75 μmol m⁻², and for the extracted enzyme K_m(CO₂) = 9.4 μm (Makino et al., 1985a) and K_m(RuBP) = 30 to 40 μm (Yeoh et al., 1981). In leaves photosynthesizing under atmospheric conditions, the concentration of RuBP may increase to 10 to 15 mm (Badger et al., 1984; Sharkey et al., 1986), but the concentration of CO₂ is usually about 4 to 8 μm in leaf intercellular spaces, depending on stomatal conductance. This CO₂ concentration is well below the K_m(CO₂) of the enzyme, and it is the initial slope of the kinetic curve V_M/K_m(CO₂), termed carboxylation conductance, that becomes important.

r_c limits the CO₂-fixation rate in series with the other resistances, r_g and r_md. The carboxylation rates are usually expressed in relation to C_i or C_w. C_c is usually about 20% to 30% lower than C_w because of concentration decrease generated by the carboxylation flux on r_md. Considering the above, the carboxylation conductance in intact leaves in vivo may be found as the initial slope of the A versus C_c graph at low C_c values. If C_c cannot be calculated because r_md is unknown, the closest approximation is a plot of A versus C_w or A versus C_i. The true parameters of the carboxylase can be found only from experiments carried out in nonphotorespiratory conditions (1%–2% O₂); otherwise the competing oxygenase reaction consumes a part of RuBP and partially inhibits carboxylase activity.

Because of technical problems with the measurement of A versus C_w relationships, in many studies only the net photosynthetic rate under atmospheric conditions (21% O₂) was related to Rubisco activity or content. Nevertheless, good correlation has been found (Makino et al., 1983; Hudson et al., 1992; Jacob and Lawlor, 1992; Jiang and Rodermel, 1995; Nakano et al., 1997). These results indicated that the level of Rubisco protein could be a limiting factor in photosynthesis throughout the life span of the leaf under natural environmental conditions. On the other hand, when Rubisco levels in leaves exceeded 4 g m⁻² (60 μmol m⁻²), the in vivo Rubisco activity (measured as photosynthesis under pC_i = 20 to 30 Pa and 21% O₂) became curvilinearly correlated with E_t (Makino et al., 1994, 1997). When measurements were made over the whole life span of wheat leaves, the measured rates of photosynthesis were lower in young leaves, which had high protein content, than would have been expected from the amount and activity of Rubisco (Lawlor et al., 1989).

During senescence the decrease in Rubisco activity was initially greater than the decrease in net photosynthesis (Hall et al., 1978). In a willow canopy, Rubisco-specific activity was higher when the apparent E_t (N content in leaves) was smaller (Vapaavuori and Vuorinen, 1989). A similar nonlinearity was found in our previous experiments (Eichelmann and Laisk, 1990), in which we obtained a saturating relationship when E_t exceeded 30 μmol m⁻². In the latter work the initial slope of the A versus C_w curves under nonphotorespiratory conditions (1.5% O₂) was assumed to represent the Rubisco activity in vivo and was compared with the E_t. We discovered that growth light had the strongest influence on the saturation of the relationship between μ and E_t. In the present work we present insight into this relationship, using not only plants grown under different light intensities but also leaves adapted to different light intensities.

MATERIALS AND METHODS

Plant Material

Sunflower (Helianthus annuus L.), cotton (Gossypium hirsutum L.), bean (Phaseolus vulgaris L.), and English spinach (Rumex patientia L.) were grown in growth boxes in 3-L pots filled with a commercial fertilized peat-soil mixture in a 16-h/8-h 28°C/18°C day/night cycle at a PAD of 250 to 300 μmol m⁻² s⁻¹ (high light) or 40 to 60 μmol m⁻² s⁻¹ (low light). In increased-N experiments plants were watered every 3 d with 200 mL of a solution of 0.5 g carbamide L⁻¹. For different phosphate treatments, plants were grown in a greenhouse under natural sunlight in June, and a nonfertilized peat-soil mixture was supplemented with fertilizers as described below. Leaves of different ages were used in experiments, as specified below.

Gas-Exchange Measurements

A rapid-response leaf gas-exchange measurement system (Fast-Est, Tartu, Estonia; Oja, 1983) was used (leaf chamber, 4.4 × 4.4 × 0.3 cm³; gas flow rate, 20 cm³ s⁻¹). The system consisted of two similar, open gas channels, channels 1 and 2, which allowed independent gas preconditioning. The channels were equipped with laboratory-made psychrometers for water vapor measurements and IR CO₂ analyzers (Infralyt 3, Junkalor, Jena, Germany [channel 1] and LI 6262, Li-Cor, Lincoln, NE [channel 2]). The leaf chamber could be rapidly switched from one channel to the other, which made it possible to produce rapid changes in CO₂ concentration and to start gas-exchange recording 3 s after switching. The abaxial side of the leaf was sealed with starch paste to the chamber window, the temperature of which was controlled with a thermostat water at 22.3°C. This increased the heat-exchange coefficient between the leaf and the water to 30 mW cm⁻² °C⁻¹, which stabilized the leaf temperature within 1°C of the circulated water, even when the maximum PAD was applied. This procedure prevented gas exchange through the upper epidermis, but C_w was calculated for all measurements on the basis of leaf temperature, transpiration, CO₂-exchange rate, and CO₂ solubility (Laisk, 1977; Laisk and Oja, 1998). Since C_w is calculated on a micromolar basis (as dissolved in water), we also present C_w0 in micromolar units considering the concentration that would exist in water in equilibrium with the ambient gas.

AC

AC was measured in 1.5% O₂ and C_w0 = 3.25 μm (C_w from 1.1 to 3.3 μm) independently of the previous conditions of steady-state photosynthesis. The low C_w0 was used to suppress additional postillumination PEP carboxylation, which increases considerably with CO₂ concentration (Laisk, 1985). For the AC measurements, the light was switched off and the leaf chamber was simultaneously switched to channel 2, where CO₂ and O₂ concentrations were as specified above. Alternatively, in some experiments light was switched off but the leaf chamber was left in the same channel as previously. For the measurements of AC_M, an additional 10- to 20-s exposure in CO₂-free N₂ with 1.5% O₂ was added to the routine before the leaf chamber was darkened and switched to channel 2. We assumed that during this exposure most of the Calvin cycle metabolites were converted into RuBP, according to the thermodynamic free energy gradient. The degree of error of the CO₂ concentration and exchange-rate measurements was less than 1%, the degree of error of the calculated C_w was about 5%, and the margin of error of the calculated μ was about 5% (Oja, 1983). Thus, the scattering of data was caused mainly by biological and temporal variation of leaf parameters during and between experiments rather than by measurement errors.

μ

μ was taken as the closest measure of Rubisco activity in vivo. The reciprocal (1/μ) is r_m. The parameter μ is close to the carboxylation conductance, except that there is an additional diffusion component in 1/μ caused by transport of the dissolved CO₂. Experimentally, μ was calculated as the initial slope of an A versus C_w graph using two measurements, one carried out at a C_w0 of 0 and the other at a C_w0 of 3.25 μm. Nonlinearity of the response was corrected according to:

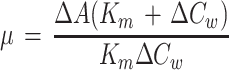1

where K_m is for CO₂ and Δ indicates the difference. K_m(CO₂) = 11 μm, as previously estimated from gas-exchange measurements (Eichelmann and Laisk, 1990), in agreement with the K_m(CO₂) of 9 to 10 μm measured in vitro correcting the pK(HCO₃) for the ionic strength in the chloroplast (Yokota and Kitaoka, 1985). If we consider that

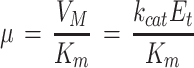2

we see that

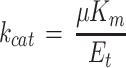3

Equation 2 relates the measured μ to enzyme characteristics.

A_M

A_M was measured as the CO₂ uptake rate at a C_w0 of 70 μm and a PAD of 1200 to 1400 μmol m⁻²s⁻¹, after photosynthesis stabilized under the high CO₂ concentration (about 15 min).

E_t

A sample (6–8 cm²) was cut from an intact leaf, frozen in liquid N₂, ground, and extracted in 3 mL of buffer (80 mm Tris-HCl, pH 6.8, 2% SDS, 100 mm DTT, and 850 mm glycerol). The extract was dissolved (1:2 or 1:4) for 10% SDS gel electrophoresis. The E_t was determined on the basis of the large subunit band, stained with Coomassie blue, and measured photometrically (Eichelmann and Laisk, 1990). Purified Rubisco from sunflower was used as a standard (the concentration was determined gravimetrically) for calibration of the gels. The remaining part of the sampled leaf was left attached to the plant so that another sample could be taken later from the other half of the leaf symmetrically with respect to the midrib.

RESULTS

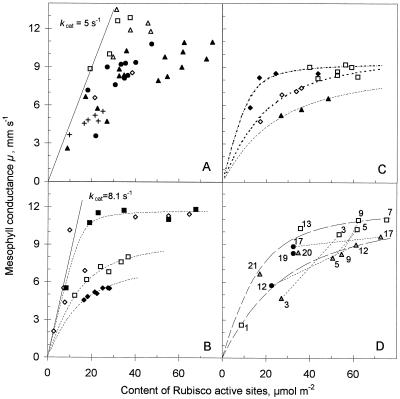
In leaves used in these experiments, E_t varied between 2 and 75 μmol active sites m⁻² (0.14–5 g Rubisco protein m⁻²). At high N nutrition (0.5 g carbamide L⁻¹ in watering solution), E_t varied from 10 to 75 μmol m⁻² in leaves of different ages. In different soil phosphate treatments the maximum E_t was 50 μmol m⁻²; in low-light-grown sunflower the range was from 10 to 30 μmol m⁻² (Fig. 1; Table I). A linear relationship between E_t and μ would be expected if all sites were equally active. However, the measured μ versus E_t relationships were linear only at low E_t, but they were saturated beyond an E_t of approximately 30 μmol m⁻² (2 g Rubisco protein m⁻²; Fig. 1, A and C). The k_cat calculated from Equation 2 using the initial slope of the relationship in Figure 1A was 5 s⁻¹, assuming a M_r of 550,000 and eight active sites per molecule. In low-light-grown sunflower the maximum μ was only about 5 mm s⁻¹ compared with 9 to 13 mm s⁻¹ in high-light-grown plants, but it still showed a tendency toward saturation. Such a saturating relationship between μ and E_t is typical not only for sunflower but also for other C₃-type plants such as cotton, bean, potato, and English spinach (Fig. 1C; Eichelmann and Laisk, 1990).

Figure 1.

Relationships between E_t and μ in leaves. A, Influence of growth conditions. •, High-light-grown, commercially fertilized sunflower, different-aged leaves; ▴, high-light-grown sunflower, increased-N treatment, different-aged leaves; ⋄, 25 mg g⁻¹ KH₂PO₄ kg⁻¹ soil; ▵, 140 mg g⁻¹ KH₂PO₄ kg⁻¹ soil; □, 250 mg g⁻¹ KH₂PO₄ kg⁻¹ soil (plants grown in a greenhouse in May–June); ×, low-light-grown sunflower. Line corresponds to k_cat of 5 s⁻¹ per Rubisco active site. B, Adaptation to different light intensities. ♦, 2.5-week-old, low-light-grown plants; ⋄, low-light-grown plants adapted at high-light intensity for 2 weeks; ▪, 2-week-old, high-light-grown plants; □, high-light-grown plants adapted 2 weeks at low-light intensity. Line corresponds to k_cat 8.1 s⁻¹ per Rubisco active site. C, Different-aged leaves of different species. ♦, Cotton; ⋄, bean; □, potato; ▴, English spinach. D, Changes over the life span of single leaves. □, Different leaves of a 2-week-old plant; , 3.5-week-old plant; •, 5.5-week-old plant. Numbers at the points correspond to the plant leaf, numbered upward, not counting cotyledons and juvenile leaves. Dotted lines indicate changes in the same leaf. C and D, Data from Eichelmann and Laisk (1990).

Table I.

E_t, μ, and AC in leaves

	Growth Condition	Et	μ	AC	SCE
		μmol m−2	mm s−1	μmol m−2	μm−1 s−1
1	LLa	7.4	5.5	123	0.044
2	LL	17.3	5.7	143	0.040
3	HLb	66.0	10.0	255	0.040
4	LL_HLc	7.0	11.1	277	0.040
5	LL	17.9	4.9	123	0.039
6	LL	9.0	4.9	125	0.039
7	LL_HL	42.5	13.5	241	0.056
8	LL_HL	22.5	11.4	200	0.057
9	LL	22.5	8.9	118	0.076
10	HL	22.4	4.7	118	0.040
11	LL	7.4	5.5	124	0.044
12	LL_HL	7.0	11.1	277	0.040
13	LL	27.1	5.5	85	0.065
14	LL_HL	27.0	8.9	135	0.066
15	HL	66.0	10.0	255	0.040
16	HL	66.0	13.5	304	0.043
17	HL	25.0	6.6	145	0.046
18	HL	25.0	9.3	201	0.046

^aLL, Low-light-grown plant. 

^bHL, High-light-grown plant. 

^cLL_HL, Low-light-grown plant adapted to high light. 

In the next experiment a low-light-grown plant was transferred to high light with the aim of inducing Rubisco adaptation (Fig. 1B). Low-light-grown plants are characterized by a low maximum μ of 4.5 to 5 mm s⁻¹ and with a comparatively small range of Rubisco active sites in leaves of different ages (from 18 to 28 μmol m⁻²). Because of this narrow range, no data points were obtained on the initial slope of the relationship, and we can state only that the calculated k_cat was ≥4.5 s⁻¹. When the low-light-grown plants were transferred to high light, the E_t in existing leaves decreased drastically during the 2-week adaptation time to the extent that the E_t came to limit the μ (Fig. 1B). The calculated k_cat was 8 s⁻¹ for these leaves. New leaves grown under high light behaved like typical high-light-grown leaves, having a high μ and the ability to synthesize large amounts of Rubisco, up to 65 μmol m⁻² (Fig. 1B).

In a reverse experiment, high-light-grown plants were readapted under low light. Leaves initially having high μ (11 mm s⁻¹) and large E_t (up to 68 μmol m⁻² in fully expanded leaves) were converted into typical low-light-grown leaves, with a low maximum μ (6–7.5 mm s⁻¹) and a limited range of E_t (15–40 μmol active sites m⁻²).

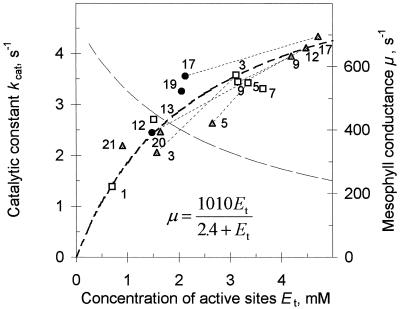
Figure 1D demonstrates changes in μ and E_t during the life span of one plant grown under a light intensity of 180 to 200 μmol m⁻² s⁻¹. To eliminate the effect of the leaf mesostructure (cell and chloroplast anatomy) on the data, E_t from this experiment was transformed into the molar concentration of active sites (Fig. 2). Chloroplast volume per meter squared was assumed to be proportional to chlorophyll concentration using the conversion factor 50 μL stroma mg⁻¹ chlorophyll (Eichelmann and Laisk, 1990). Three measurement series were carried out at plant ages of 2, 3.5, and 5.5 weeks. The leaves were numbered upward and did not include cotyledons and juvenile leaves. Data points connected with dashed lines correspond to the same leaf at different plant ages. In the molar presentation of Figure 2 the scattering of data is smaller than in the area presentation of Figure 1D, but the curvilinear relationship clearly remains. The data show that when a leaf is young its E_t is low (0.8–1.5 mm active sites, leaf no. 13 in the 2-week-old plant and leaf nos. 20 and 21 in the 3.5-week-old plant).

Figure 2.

μ and k_cat presented as functions of E_t (data from Fig. 1D). Thick, dashed line was calculated from the equation; the thin, dashed line corresponds to k_cat calculated from the thick line.

In fully expanded leaves E_t reached a maximum (3–4 mm in leaf nos. 3–9 in the 2-week-old plants or 4–5 mm in leaf nos. 9–17 in the 3.5-week-old plant). During the senescing of leaves E_t and μ both decreased and followed the same relationship as during leaf expansion (senesced leaf no. 1 in the 2-week-old plant, leaf nos. 3 and 5 in the 3.5-week-old plant, and leaf no. 12 in the 5.5-week-old plant). For example, in leaf nos. 12 and 17, during aging from 3.5 to 5.5 weeks, E_t decreased 3-fold, whereas μ decreased only 30%. In the 5.5-week-old plant the relatively young leaf no. 19 did not accumulate as much Rubisco as leaf nos. 3 to 9 from the 2-week-old plant or leaf nos. 9 to 17 in the 3.5-week-old plants, probably because of whole-plant senescence, limitations in mineral nutrition under the pot-bound conditions, and outflow of N to regenerative organs. The saturating relationship between E_t and μ is characterized with the value of k_cat, which decreased from 4.5 to 1.5 s⁻¹ in the range of E_t from 0.5 to 5 mm (Fig. 2).

μ and AC

μ of a leaf depends on E_t and also on the pool of RuBP. The latter can be estimated from AC in intact leaves. AC was measured in different leaves by darkening the leaf during steady-state photosynthesis at C_w0 of 3.25 μm and 1.2% O₂. μ was calculated from the CO₂-fixation rate just before the darkening. In different leaves chosen at different ages from different growth treatments, E_t differed considerably, whereas μ values differed very little in the same leaves (Table I). On the other hand, it was also possible to find pairs with very close E_t values but different μ values (nos. 9–18). Usually, close AC values corresponded to close μ values. The last column in Table I presents the SCE, which is the slope of the μ versus AC curve (Laisk et al., 1984). This parameter is close to 0.045 mm s⁻¹ μmol⁻¹ m² (μm⁻¹ s⁻¹ expressed as a second-order rate constant), being similar in leaves of different ages and from different growth treatments. However, this parameter does not seem to be a basic constant of Rubisco, because in some leaves (mostly in low-light-grown leaves with a small AC) the SCE was significantly higher (0.066–0.076 μm⁻¹ s⁻¹).

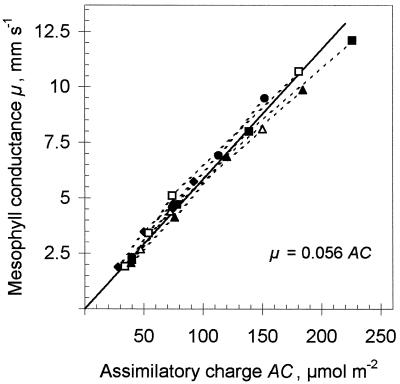
As long as SCE remains constant, μ proportionally depends on AC. This dependence was checked in the next experiment as AC changed under varying light intensity. In a leaf of a high-light-grown plant, AC and μ were measured at a C_w0 of 3.25 μm and O₂ of 1.5% by darkening the leaf during steady-state photosynthesis. After the postillumination CO₂ uptake ceased, the light was turned on again and the steady-state photosynthetic rate was recovered. Then PAD was decreased and after 15 s the light was switched off to measure AC from the low-light state. Fifteen seconds under decreased PAD was sufficient to establish a lower equilibrium RuBP and a higher PGA concentration but too short to change Rubisco activity. Different AC values were obtained by jumping from the maximum PAD to different, lower PADs. From Equation 1 the corresponding μ was calculated for every AC, whether light saturated or light limited, and the calculated μ was plotted against AC (Fig. 3). Data for five different-aged leaves of the same plant all present a proportional dependence, with a SCE of 0.056 mm s⁻¹ μmol⁻¹ m².

Figure 3.

Relationship between μ and AC for five different-aged leaves of one plant. Different assimilatory charges were generated by decreasing light intensity from 1300 μmol m⁻² s⁻¹ to different levels for 10 s, and then μ and AC were measured at a C_w0 of 3.25 μm. SCE was 0.056 mm s⁻¹ μmol⁻¹ m² (the slope of the solid line).

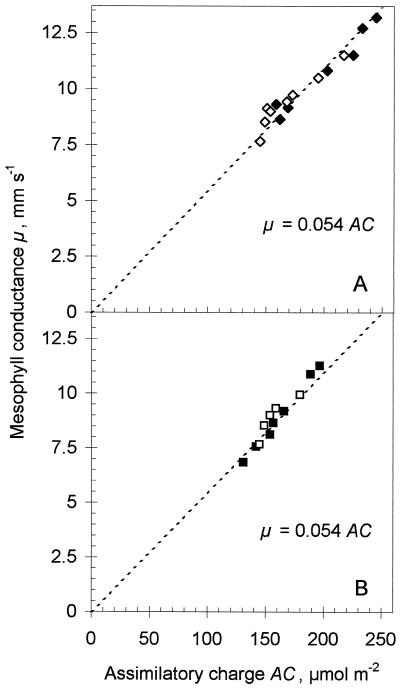
In another experiment, Pi or Man was fed to excised leaves through the petiole. Increasing the Pi concentration in the cytosol is expected to drain triose phosphates out of the chloroplast stroma as a result of the activity of the Pi translocator. Man binds Pi in the cytosol and thus decreases the drainage of triose phosphates from chloroplasts, increasing the concentration of Pi esters in the stroma. Both of these treatments result in decreasing AC, either because the pools of the carbon reduction cycle generally decrease (Pi feeding) or, more likely, because they accumulate in hexose phosphates because of active starch synthesis in Man-fed leaves (Eichelmann and Laisk, 1994). Most remarkably, μ varied proportionally with AC, with an SCE of 0.054 mm s⁻¹ μmol⁻¹ m² (Fig. 4). After Pi or Man was removed, the μ and AC values tended to recover, maintaining the SCE value constant. Although in the above-described experiments we could only decrease AC, a temperature treatment resulted in an increase in AC and μ. After a leaf was exposed at 27°C for 10 min, both AC and μ, measured after a 30-min stabilization following transfer to 23°C, increased by 40%, but μ remained proportional to AC and SCE remained constant (Table I, nos. 17 and 18).

Figure 4.

Relationships between μ and AC obtained by varying the Pi concentration in the cytosol by feeding Pi or Man through the petiole. A, Feeding 10 mm Man for 110 min (♦) and reversing the experiment in distilled water for 125 min (⋄). B, Feeding 33 mm Pi for 190 min (▪) and reversing the experiment in distilled water for 120 min (□). The slope of the dashed lines corresponds to a SCE of 0.054 mm s⁻¹ μmol⁻¹ m².

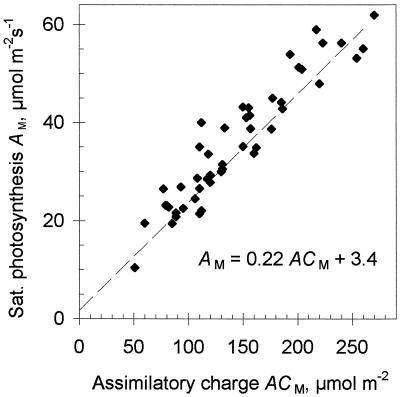
Although A_M is not determined by Rubisco, but in most cases by the end-product synthesis rate and/or the capacity of the RuBP-regeneration chain, a good correlation was still found between A_M and AC_M (maximum AC measured after an exposure to CO₂-free gas) in different-aged leaves from differently treated plants (Fig. 5). To the extent that AC_M reflects the carbon reduction cycle pool of Pi esters, A_M is proportional to that pool. In experiments including high- and low-light-grown and readapted plants, the correlation between A_M and AC_M was high and the slope of the dependence was the same.

Figure 5.

Relationship between A_M and AC_M. Different data points were obtained from different leaves grown at high or low light, re-adapted to different PADs or by feeding Man and Pi. Sat., Saturated.

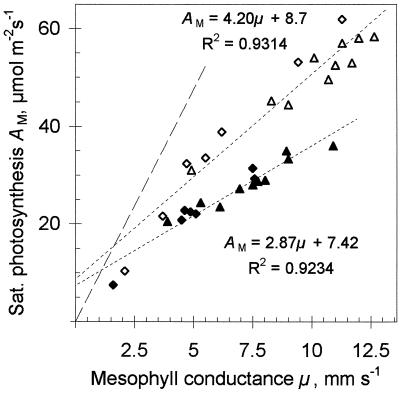
Since proportionality exists in the AC versus μ and the AC versus A_M relationships, proportionality between μ and A_M is also expected. The slope of this regression depends on light conditions during leaf growth (Fig. 6). It is remarkable that adapting plants from one light intensity to another moves the data points precisely from one regression line to another. Feeding Pi concentration changers (Man, Pi, and vanadate) to a leaf through the petiole decreases μ and A_M simultaneously, moving data points along the same lines of proportionality.

Figure 6.

A_M as a function of μ in sunflower leaves adapted to different light intensities. ♦, 2.5-week-old low-light-grown plant; ⋄, low-light-grown plant adapted 2 weeks at high light intensity; ▵, 2-week-old high-light-grown plant; ▴, high-light-grown plants adapted for 2 weeks at low light intensity. Dotted lines are regression lines; dashed line corresponds to V_M of Rubisco calculated from the μ assuming the Michaelis-Menten kinetics.

DISCUSSION

By varying growth conditions and leaf age we obtained leaves that had a wide range of E_t (0.14–5 g protein m⁻², 2–75 μmol active sites m⁻², or 0.5–5 mm active sites in the chloroplast stroma) to find relationships between E_t and photosynthetic parameters of the leaf. In contrast to most previous researchers, we did not compare the E_t with the photosynthetic rate at atmospheric CO₂ and O₂ concentrations but, instead, with μ under nonphotorespiratory conditions, which is the closest parameter to the carboxylation conductance measurable from leaf gas exchange. μ underestimates the carboxylation conductance by the proportion of r_md (since the total r_m = r_md + r_c). r_md usually makes up 20% to 30% of the total r_m (Laisk and Loreto, 1996), and the rest of the resistance is due to the limited speed of carboxylation.

Carboxylation conductance is proportional to the E_t or V_M provided that K_m(CO₂) is constant. We found that μ was linearly related to E_t at low E_t values but was saturated at higher E_t values. This saturation phenomenon caused a 2- to 3-fold decrease in the apparent k_cat calculated from μ and E_t (Fig. 2). This saturation is at variance with what was found in other studies, in which the photosynthetic rate at atmospheric levels of CO₂ and O₂ was linearly correlated with E_t (Makino et al., 1983; Jacob and Lawlor, 1992; Jiang and Rodermel, 1995). A linear relationship between E_t and V_M of Rubisco, calculated from measured μ, was also obtained by von Caemmerer et al. (1994). However, in these investigations the E_t did not exceed 35 μmol m⁻², whereas the calculated k_cat was 3.5 s⁻¹. With this average k_cat, the data in Figure 1 would also approximately satisfy a linear regression below 35 μmol active sites m⁻². Saturating relationships between E_t and photosynthesis have been found in other studies. For example, when E_t exceeded 4 g m⁻² in rice (Makino et al., 1994, 1997), wheat (Lawlor et al., 1989), or leaves of a willow canopy (Vapaavuori and Vuorinen, 1989), the dependence between the rate of CO₂ assimilation and E_t declined from linearity. In Chlorella pyrenoidosa cultures grown under high CO₂, E_t was higher but specific activity was lower than in cultures grown under low CO₂ (Yokota and Canvin, 1986). These results agree with those in Figure 1, which shows a decrease of k_cat with increasing E_t. In our experiments the linearity between μ and E_t broke down above 2 g protein m⁻² or 25 μmol active sites m⁻².

The saturating dependence between the E_t and μ may be caused by physical and/or chemical properties. Physically, as r_cdecreases, the r_md eventually begins to determine μ. Calculations based on leaf anatomy have shown that an r_md of 0.01 s mm⁻¹ corresponds to a diffusion distance of 1 μm in chloroplasts (Laisk et al., 1970). r_md for CO₂ has been estimated to be sufficient to cause depletion of CO₂ at the carboxylation sites and to introduce curvilinearity into the relationship between photosynthesis and E_t (Evans, 1983). Other calculations have shown that a decrease in C_i cannot be large enough to cause curvilinearity in the relationship (Makino et al., 1985a; Lawlor et al., 1989). Calculations from fluorescence-based measurements of the electron-transport rate and the net CO₂-exchange rate (Laisk and Loreto, 1996) showed that r_md was usually between 0.02 and 0.04 s mm⁻¹ in herbaceous plants and did not exceed 20% to 30% of the total r_m. Measurements of sunflower in our laboratory have given similar results, estimating r_md from 0.02 to 0.06 s mm⁻¹ for full-grown leaves (Laisk and Sumberg, 1994; V. Oja and E. Eichelmann, unpublished results). In this work the minimum values of r_m were about 0.1 s mm⁻¹, which means that diffusionally limited μ is about 2 to 5 times greater than the actual maximum μ. This estimate shows that μ could still be carboxylase limited, even at the maximum E_t. This was clear in low-light-grown plants.

r_c is determined by the content and activity of Rubisco on one hand and by inhibiting stroma metabolites, e.g. PGA and free Pi, on the other (Badger and Lorimer, 1981; Foyer et al., 1987). Because our measurements of μ were carried out at limiting CO₂ and low O₂ concentrations, it is likely that Pi and PGA accumulated at very low levels and RuBP was at a maximum (Badger et al., 1984; Dietz and Heber, 1986; Seemann and Sharkey, 1986). Therefore, we initially ignore the metabolite effects and discuss the μ as a function of the content and activity of Rubisco. The data in Figure 1B most clearly show that, in high-light-grown leaves at low E_t, μ increases proportionally with E_t. The calculated k_cat was 8.1 s⁻¹, slightly higher than the highest values obtained in Rubisco assays in vitro (5–6 s⁻¹; Evans and Seemann, 1984; Flachmann et al., 1997), whereas the modeled k_cat values in mature leaves are 3 to 3.6 s⁻¹ (von Caemmerer et al., 1994; Mate et al., 1996).

In leaves that had the highest k_cat values we assume that all of the Rubisco was completely active. When the E_t exceeded 20 μmol active sites m⁻² and μ approached 11 mm s⁻¹, the relationship was saturated, although E_t further increased to 65 μmol m⁻². The abrupt saturation of the relationship (Fig. 1, B and C) supports the case of chemical limitation, because the limitation by r_d would have resulted in a slowly saturating rectangular hyperbola. However, the abrupt saturation might be induced by changes in leaf mesostructure that took place in parallel with the changes in E_t, because the relationship shown in Figure 2 is close to a rectangular hyperbola. Proceeding from the model of chemical limitation, we see that there was a ceiling that limited the amount of active Rubisco to about 20 μmol reaction sites m⁻² in high-light-grown leaves. In low-light-grown leaves the relationship tended toward saturation at slightly higher E_t than in the high-light-grown leaves, but the maximum μ was considerably lower.

It appears that in low-light-grown leaves the same or only a slightly greater maximum number of reaction sites could be activated as in high-light leaves, but each site apparently had a slower k_cat. Proceeding from this, a corresponding model would involve two processes that determine the Rubisco activity in vivo: one that determines the specific activity (turnover rate) of each active site and another that limits the maximum number of active sites. The first process is sensitively regulated by growth light, whereas the second is relatively insensitive to this parameter. For example, there may be a dynamic equilibrium between activation by the Rubisco activase system and nonenzymatic deactivation of Rubisco by a large molar excess of RuBP and other metabolites (Portis et al., 1986; Zhu and Jensen, 1991).

In leaf extracts containing a constant concentration and specific activity of Rubisco activase (about 0.45 μmol min⁻¹ mg⁻¹), the specific activity of Rubisco declined as the amount of Rubisco increased (Portis et al., 1986). This result is similar to what we found in intact leaves: an increase in the E_t resulted in a decrease of k_cat (Fig. 1). In experiments by Portis et al. (1986) the optimum concentration was 100 μg mL⁻¹ Rubisco and 300 μg mL⁻¹ Rubisco activase. In intact leaves this ratio seems to be shifted toward a higher E_t. In transgenic leaves with limited expression of Rubisco activase, photosynthesis was not influenced before activase content decreased more than 10 times (Mate et al., 1996). This result seemingly contradicts our above-described model, which emphasizes the limiting role of activase; however, several cofactors are needed to activate the activase itself.

ATP is an important cofactor of Rubisco activase in isolated chloroplasts (Robinson and Portis, 1988) but not in intact leaves (Brooks et al., 1988). In leaves light-induced electron transport through the PSI region of the electron-transport chain and the establishment of a transthylakoid pH gradient are obligatory for full activation of Rubisco (Campbell and Ogren, 1990, 1992). A good correlation between the dark-light pH difference in chloroplast stroma and μ has been observed (Eichelmann and Laisk, 1990). These results suggest that its binding sites at the PSI region of thylakoids may govern the activation process of Rubisco, not the content and activity of the Rubisco activase. Another important factor limiting the activation process may be the limited diffusibility of activase and Rubisco proteins, which could limit the protein-to-protein interaction required for activation. In our experiments E_t increased to 350 mg mL⁻¹ in the chloroplast stroma, or to about 700 mg mL⁻¹ of total soluble protein. At such a concentration the state of the protein is close to crystalline, strongly limiting the movement of the activase and the carboxylation substrates. In crystalline Rubisco, the water content is 200 mg g⁻¹ protein (Paulsen and Lane, 1966). In protein-bound water, diffusion of small molecules is from 2 to 5 times slower than in free water (Lawlor et al., 1989), and the Michaelis-Menten kinetics of Rubisco catalysis may no longer apply because of limited diffusibility of RuBP and PGA.

Whatever the mechanistic reasons, our results confirm the notion that a part of Rubisco is not available for carboxylation and plays the role of storage protein. This idea was suggested as early as the 1960s, when Rubisco was discovered and found to make up as much as 60% of soluble protein in the chloroplast (Paulsen and Lane, 1966). Alteration of the source-to-sink ratio by removing the fruit in soybean resulted in the formation of an insoluble form of Rubisco in leaf extracts, with a specific activity 5 times less than that of the soluble form (Crafts-Brandner et al., 1991).

In transgenic rice leaves it was necessary to reduce Rubisco levels by about 55% to achieve 100% Rubisco activation (Makino et al., 1997). Using radioactive label Mae et al. (1983) demonstrated that Rubisco is a major N depot to support the growth of young tissues. This is in good accordance with our measurements of E_t during the life span of sunflower leaves (Figs. 1D and 2). During leaf expansion E_t increased, and during senescence it decreased again (e.g. leaf nos. 3 and 9 in Fig. 2). In a 2-week-old plant, the two leaves had similar E_t (3.2 mm) and μ (570 s⁻¹) values. Later (1.5 weeks), leaf no. 9 was fully expanded and E_t increased to 4.2 mm, whereas μ (620 s⁻¹) increased only 8%. Leaf no. 3 had begun to senesce and the E_t (1.6 mm) had decreased by 50%, whereas μ (330 s⁻¹) had decreased by 40%. The process of remobilizing the N depot from old leaves to support the growth of new leaves explains why, during the adaptation of high-light-grown leaves to low light, the data points of the μ versus E_t graph are above the data points for normal low-light-grown leaves (Fig. 1B): the readapted leaf still has a larger N content than the low-light-grown leaf.

As defined above, the second component of carboxylation resistance is related to inhibiting stroma metabolites. μ correlated surprisingly well with assimilatory charge (Figs. 3 and 4), which is a gas-exchange measure of the RuBP pool (Laisk et al., 1984, 1987; Eichelmann and Laisk, 1990; Ruuska et al., 1998). It is not easy to explain why the μ versus AC relationships were so linear up to RuBP concentrations of 10 to 20 mm, considering that K_m(RuBP) for Rubisco is about 40 μm in vitro (Servaites et al., 1991). Farquhar (1979) and von Caemmerer and Farquhar (1985) attempted to resolve this problem by assuming that not all RuBP is available for carboxylation, only its nonchelated part, whereas the RuBP-Mg²⁺ complex cannot be a substrate for carboxylation. In the presence of ample Mg²⁺ only a minor fraction of RuBP remains free to be the carboxylation substrate. When the RuBP concentration is less than the concentration of active sites (2 mm in the activated state in our experiment) the reaction kinetics remain proportional to the RuBP concentration (Farquhar, 1979). This is a plausible explanation, except that it does not explain why the concentration of substrate RuBP, a small residual of the budget, is so constant and well reproducible from experiment to experiment, as is the measured maximum μ.

According to Michaelis-Menten kinetics, the reaction rate is expected to have little dependence on the RuBP concentration until it decreases to the concentration of active sites. The measured proportionality between the RuBP pool (AC) and reaction rate (μ) suggests that Rubisco must become progressively inhibited while the RuBP concentration decreases. In experiments with extracted Rubisco having a concentration up to 1.6 mm active sites, Paech (1986) found that an initial, fast PGA formation soon faded, indicating decreasing Rubisco activity in time. Eichelmann (1985) measured kinetic curves of RuBP utilization in extracts from sunflower leaves and in solutions of partially purified enzyme with E_t values from 5 to 30 mg mL⁻¹ protein (0.07–0.4 mm active sites). No RuBP saturation plateau was observed, and the kinetic curves of RuBP utilization were very similar to postillumination uptake curves in leaves (Laisk et al., 1987).

The continuous decrease in Rubisco activity during the RuBP utilization reaction was explained by competitive inhibition of the enzyme by the product, PGA. The K_I(PGA) calculated from the in vitro curves was 0.54 mm. However, when external PGA was added or when RuBP was repeatedly injected, leaving previously generated PGA in the reaction mixture, its K_I(PGA) was much higher (3.7 mm). It was concluded that enzyme-bound, freshly generated PGA has a higher efficiency for inhibition than the free PGA. A similar result was reported later (Fong and Butcher, 1988), confirming that enzyme-bound PGA molecules formed by RuBP carboxylation are not equivalent to free PGA. The explanation is that PGA formed from C-3, C-4, and C-5 of the six-carbon intermediate (2-carboxy-3-keto-arabinitol-1,5-bisphosphate) is rapidly released, but PGA formed from C-1, C-2, and C-2′ is tightly bound to the Mg²⁺ of the enzyme and occupies the active site for a relatively long time.

Reversible binding of external PGA to Mg²⁺ of the active site is less likely. PGA and free Pi are both known to be competitive inhibitors for Rubisco: K_I(PGA) is 0.85 mm (Badger and Lorimer, 1981) and K_I(Pi) is 0.65 mm (Jordan et al., 1983). It is a general rule that the RuBP pool is complementary to PGA and Pi pools (Badger et al., 1984), because the total Pi pool is a constant and other carbon reduction cycle pools (except hexose phosphates under some conditions) are smaller than those directly involved in RuBP carboxylation. In the initial state of our postillumination experiments, under saturating light and limiting CO₂ concentrations, most of the Pi was probably bound in RuBP, leaving little of it in PGA or in a free state. Beginning from this state, decreases of AC were created by decreasing the light intensity for 10 s. This time was sufficient to convert a part of the RuBP into PGA, increasing the PGA-to-RuBP ratio. The relationship between μ and the RuBP pool (measured as AC) in the presence of a varying PGA-to-RuBP ratio was strictly linear, with the same proportionality constant for different leaves grown under similar conditions (Table I; Fig. 3) but also when Pi and Man were fed to influence the cytosolic and chloroplast Pi pools (Fig. 4). Linear kinetics have been modeled to describe the postillumination CO₂-fixation process, during which the RuBP pool decreases and the PGA pool increases, using the above inhibition coefficient by PGA (Laisk et al., 1987), showing that product inhibition can explain the close-to-linear kinetics of Rubisco.

The proportionality constant relating μ to AC, SCE, was 0.04 to 0.065 mm s⁻¹ μmol⁻¹ m². SCE varies when external conditions lead to variations in Rubisco activation state (e.g. waiting until Rubisco activity stabilizes at each limiting PAD; Laisk et al., 1984), but its maximum value is usually relatively constant in similarly grown leaves. It is a rule of thumb that SCE is higher in leaves that have lower maximum AC pools (Laisk et al., 1984, 1987) and decreases with senescence (Eichelmann and Laisk, 1990). This is consistent with the above product-inhibition model, which predicts that the true uninhibited μ can be measured only under conditions in which PGA and Pi pools are minimal, i.e. under saturating light and limiting CO₂ concentrations and low O₂ concentrations.

Under low light and in the presence of saturating CO₂ or high O₂ concentrations, the PGA pool is not minimized and it has an inhibitory effect on Rubisco. Evidently, this is one reason why μ decreases with increasing O₂ concentration (Laisk and Loreto, 1996), despite the fact that RuBP pool may still be large enough to saturate the enzyme. During postillumination CO₂ fixation, the initially maximum μ decreases continuously during the whole period of RuBP consumption, which lasts longer the greater the RuBP pool. However, the larger the chloroplast Pi pool, the larger the RuBP pool. Thus, SCE is steeper the lower the initial RuBP concentration, i.e. the lower the chloroplast Pi content. An important conclusion is that SCE is not a true characteristic of Rubisco but is influenced by the chloroplast Pi pool. To the extent the latter stays constant, relative changes in SCE may be interpreted to indicate changes in Rubisco-specific activity, but one should be cautious when comparing SCEs from different species or leaves. It is also important that only μ measured under conditions in which PGA and Pi are minimized can be safely interpreted as Rubisco activity and related to its content.

We also made some observations that are more complicated to explain by the competitive inhibition model. Incubation of a leaf for 10 min at only a 4°C higher temperature (27°C) caused a 40% increase in AC, whereas the μ versus AC relationship remained constant. Staying with the model, we conclude that a part of the Pi was converted from an inhibitory state (PGA, Pi) into the substrate state (RuBP). Thus, one must be careful in interpreting the maximum AC_M pool and the corresponding μ obtained under the light-saturating and CO₂-limiting conditions as a true maximum. Some Pi may still reside in an inhibitory form, e.g. as hexose phosphate.

Another way to change μ and AC while maintaining SCE constant was to feed compounds through the phloem (Fig. 4). Our treatments were expected to increase (feeding Pi) or decrease (feeding Man) Pi concentration in the cytosol and to influence the Pi concentration and Pi distribution in stroma sugar phosphates via the Pi translocator. Since these treatments were not expected to change the total Pi in the stroma but only its distribution between free and organic forms, the correlated changes between μ and AC were expected. Either increasing or decreasing cytosolic Pi resulted in a decrease in the RuBP pool. It is possible that the formation of hexose phosphates traps Pi and thereby decreases the amount available for RuBP formation, as suggested previously (Eichelmann and Laisk, 1994).

Aside from the proportionality between μ and AC, A_M was also proportional to μ (Fig. 6). This proportionality was noted earlier when photosynthesis was influenced by salinity (Seemann and Sharkey, 1986), in ozonation of bean (Moldau et al., 1991; Moldau and Kull, 1993) and aspen (Kull et al., 1996), by varying growth light in sunflower (Eichelmann and Laisk, 1990), and in a Cyt b₆/f-deficient antisense mutant of tobacco (H. Eichelmann, unpublished data). The clearest demonstration so far of the proportionality between μ and the rate of CO₂ assimilation at 500 μbar CO₂ in spinach leaves grown at different nitrate levels was given by Evans and Terashima (1988). The novelty of our present work is that the slope of μ versus A_M was dependent on the growth light (Fig. 6).

The relationship between μ and A_M deserves to be discussed because it was theoretically unexpected. A_M is usually determined by end product (Suc and starch) synthesis rate and Pi turnover, which limits RuBP regeneration (Laisk and Laarin, 1983), whereas μ is determined by Rubisco and carbon reduction cycle pools. Such good correlative relationships between different photosynthetic parameters show that genes controlling different subsystems of leaf photosynthetic metabolism are proportionally expressed and controlled during development and adaptation.

It is possible that the total pool of Pi in chloroplasts is an important parameter controlling the development of the photosynthetic apparatus, or at least proportionally related to its amount. Presently we know very little about factors that determine the total Pi pool in chloroplasts. The good proportionality between different photosynthetic parameters may be a result of spatial compartmentation of the photosynthetic machinery into small units that can perform almost completely independently, or of association of enzymes into supercomplexes that channel intermediates (Gontero et al., 1988; Süss et al., 1995; Echeverria et al., 1997).

We suggest that saturation of the relationship between E_t and μ is caused by three limiting components. Physical diffusion resistance in the liquid phase would limit the μ at about 2 to 5 times higher values than measured. An essential limitation of μ is caused by factors that allow only partial activation of Rubisco. We suggest that these are related to Rubisco activase, which itself is activated by thylakoid membrane-bound complexes such as PSI, ATPase, and the transthylakoid pH gradient. The slower diffusibility of Rubisco at high protein concentrations in stroma is a factor that may limit the activation process of Rubisco, breaking the balance between activation and deactivation processes. Finally, chloroplast metabolites, especially PGA and free Pi, control the reaction kinetics of RuBP carboxylation by competitively binding to active sites.

Abbreviations:

A

net CO₂ uptake rate

A_M

light- and CO₂-saturated CO₂ uptake rate

AC

assimilatory charge

AC_M

maximal assimilatory charge measured after exposure to CO₂-free gas

C_c

CO₂ concentration at carboxylation sites

C_i

CO₂ concentration in the intercellular space

C_w

dissolved cell wall CO₂ concentration

C_w0

external CO₂ concentration

E_t

content of Rubisco sites

k_cat

catalytic constant

K_I

inhibition constant

μ

mesophyll conductance (initial slope of the response curve of CO₂ uptake versus dissolved cell wall CO₂ concentration)

PAD

absorbed photon flux density

PGA

3-phosphoglyceric acid

r_c

carboxylation resistance

r_g

gas-phase resistance

r_m

mesophyll resistance

r_md

liquid-phase diffusion resistance

RuBP

ribulose-1,5-bisphosphate

SCE

specific carboxylation efficiency

V_M

maximum rate of the enzyme