Nucleotide modifications and tRNA anticodon–mRNA codon interactions on the ribosome

To study the effect of the common tRNA modifications cmo⁵U34 and m⁶A37, the authors have carried out molecular dynamics simulations of the tRNA anticodon and mRNA codon, inside the ribosome. In tRNA^Val, these modifications allow all four nucleotides to be successfully read at the wobble position in a codon. No prestructuring effect on the tRNA anticodon stem–loop from the two modifications could be observed, but two mechanisms that may contribute to the expanded decoding capability by the modifications were identified: The further reach of the cmo⁵U34 allows an alternative outer conformation to be formed for the noncognate base pairs, and the modification results in increased contacts between tRNA, mRNA, and the ribosome.

Abstract

We have carried out molecular dynamics simulations of the tRNA anticodon and mRNA codon, inside the ribosome, to study the effect of the common tRNA modifications cmo⁵U34 and m⁶A37. In tRNA^Val, these modifications allow all four nucleotides to be successfully read at the wobble position in a codon. Previous data suggest that entropic effects are mainly responsible for the extended reading capabilities, but detailed mechanisms have remained unknown. We have performed a wide range of simulations to elucidate the details of these mechanisms at the atomic level and quantify their effects: extensive free energy perturbation coupled with umbrella sampling, entropy calculations of tRNA (free and bound to the ribosome), and thorough structural analysis of the ribosomal decoding center. No prestructuring effect on the tRNA anticodon stem–loop from the two modifications could be observed, but we identified two mechanisms that may contribute to the expanded decoding capability by the modifications: The further reach of the cmo⁵U34 allows an alternative outer conformation to be formed for the noncognate base pairs, and the modification results in increased contacts between tRNA, mRNA, and the ribosome.

INTRODUCTION

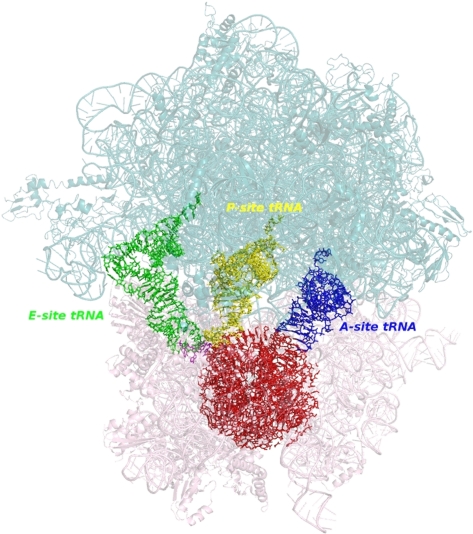
The ribosome plays a central role in protein synthesis by decoding mRNA and catalyzing peptide bond formation during assembly of a new protein. The two ribosome subunits contain roughly equal amounts of protein and RNA; the small subunit contains only one ribosomal RNA (16S-like rRNA), the large subunit contains one (two in eukaryotes) small rRNA(s), referred to as 5S rRNA (5S and 5.8S in eukaryotes) and a large 23S-like rRNA (Fig. 1).

FIGURE 1.

The two prokaryotic ribosomal subunits, 5S (pale pink) and 23S (pale blue) together with three tRNAs bound to the A-, P-, and E-sites. The studied system is colored red.

Although the basic functions of the ribosome are conserved among all known living organisms, ribosomes from prokaryotic and eukaryotic organisms show several differences. The prokaryotic ribosome contains fewer protein species, and the major rRNAs are considerably shorter than in eukaryotes.

Due to its central role in protein synthesis, ribosomal activity is intimately linked to cellular growth. As expected, inhibition of ribosomal activity and, hence, of de novo synthesis of proteins will automatically slow down cell growth. This makes the ribosome a highly suitable target for development of drugs that aim at reducing the growth rate of bacterial cells as well as of human tumor cells (Knowles et al. 2002; Tenson and Mankin 2006). Approximately 50% of the antibiotics currently used in clinical medicine for treatment of bacterial infections target the ribosome. In most cases, these drugs interfere with functionally important sites in the ribosomal RNA. These sites are basically conserved in humans and bacteria, but subtle differences between ribosomes from different domains of life allow these drugs to distinguish between bacterial and human ribosomes, thereby specifically inhibiting bacterial protein synthesis and bacterial growth. In particular, there are several antibiotics that work by interfering with the fidelity of the anticodon:codon recognition at the so-called decoding center on the small subunit.

Recognition of a correctly matched codon:anticodon occurs in several steps, where GTP hydrolysis allows the free energy difference between correct and incorrect pairing to be utilized twice (proofreading). One important aspect of this scheme is that discrimination is, to a large extent, kinetically controlled, since the rates of EF-Tu GTPase activation differ significantly for cognate and noncognate complexes. The elongation cycle of protein synthesis moves through three fundamental steps at a rate of 10 sec⁻¹, with an estimated error rate of about 10⁻⁴. This error rate, mainly due to incorrect translation on the ribosome, is significantly smaller than what would be anticipated from the Boltzmann-distribution of the differences in binding energy between a match and mismatch, thanks to the proofreading step (Daviter et al. 2006). The primary codon:anticodon interaction event is accompanied by a conformational change from an “open” to a “closed” form of the decoding center (Ogle et al. 2003); this somehow influences activities several nm away on the EF-Tu.

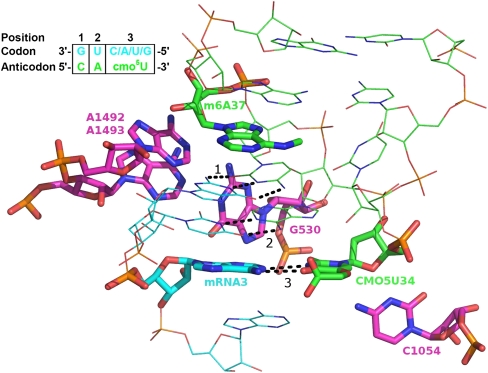
However, it has been shown that the process of GTP hydrolysis and aminoacyl-tRNA accommodation (peptide bond formation) is accelerated more for cognate base-pairing compared to near-cognate (e.g., G-U and A-C base pairs) than the relatively small difference in binding energy would account for (Pape et al. 1998, 1999). This implies that the energy derived from the binding of a cognate aa-tRNA anticodon induces conformational changes in the ribosomal A-site (Fig. 2) that near-cognate binding does not trigger. The nucleotides involved in these conformational changes are G530 from the ribosomal shoulder domain and A1492 and A1493 in helix H44 which are positioned in the minor groove of the first two codon-anticodon base pairs. The close interactions of these three bases to the first and second codon-anticodon positions sense the characteristic shape of a cognate Watson-Crick pair and form hydrogen bonds not possible for non- or near-cognate pairs. For example, when there is a U-G mismatch in codon position 1, the U is displaced into the minor groove, preventing it from forming hydrogen bonds with A1493, without providing enough space for solvation of its polar groups (Ogle et al. 2002). Effects like these enhance the specificity far beyond that of the base-pairing alone by contributing additional interacting energy between the ribosome and matching mRNA and tRNA.

FIGURE 2.

The ribosomal decoding center. tRNA^Val ASL in green, mRNA valine codon in blue, and ribosomal RNA in magenta. The wobble base pair and surrounding residues, participating in hydrogen bonds, are highlighted in sticks. The three codon-anticodon base pairs are numbered and specified with dashed bonds.

In contrast, in the third (wobble) position of the codon, near-cognate base pairs are usually still accepted by the ribosome. This is allowed since this position is monitored less stringently than the first and second positions. In spite of this, the wobble position is observed to have contacts to ribosomal nucleotides. G530 lies within hydrogen bond distance, and the H34 nucleotide C1054 has been observed to pack against the third codon-anticodon base pair, but the details of its function are not known. In addition to this, pairing at the wobble position is heavily influenced by nucleoside modifications on the tRNA (Agris et al. 2007).

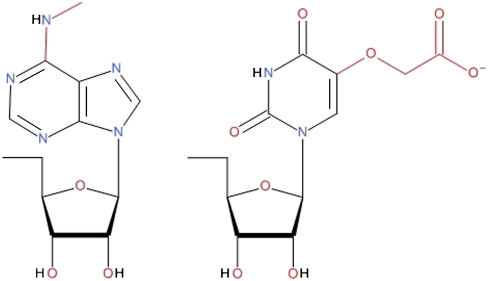
Although modification of nucleosides comes at a considerable genetic and energetic cost, more than 70 distinct modifications have been identified on the ∼40 known tRNAs (Agris 1996). The modifications can be situated in all domains of the tRNA and are conserved in many organisms, but the wobble position 34 and the purine 37 on the 3′ side of the anticodon stand out as being almost universally modified. The modifications in these places vary greatly in size, ranging from simple methyl groups, like the m⁶A37, to complex structures, like the ms²t⁶A37 (Durant et al. 2005) but are all, with little doubt, involved in codon recognition (Nishimura and Watanabe 2006). The main effects of the modifications in these two positions are believed to be to open up the anticodon loop by negating intra-loop hydrogen bonds (Olejniczak and Uhlenbeck 2006) and to constrain the dynamics of the loop by increasing the stacking of its bases (Agris 2008). Of the common modifications present on U34 (s²U34, mcm⁵U34, mnm⁵U34, and cmo⁵U34), cmo⁵U and its derivatives stand out for their ability to decode all four nucleotides at the wobble position (Näsvall et al. 2004). This is the case in, e.g., tRNA^Val which, with the anticodon 5′-UAC-3′, can read all four redundant codons [5′-GU(A/G/U/C)-3′] for valine. The main structural difference between cmo⁵U34 and similar modifications, like mcm⁵U34 and mnm⁵U34, which only enable the decoding of two nucleotides (Agris 2008), lies in the highly polar carboxyl group at the end of the arm (Fig. 3); however, little is known of the atomistic function of the modification.

FIGURE 3.

(Left) N⁶-methyladenosine (m⁶A) and (right) uridine 5-oxyacetic acid (cmo⁵U).

Molecular modeling/simulation has emerged over the last three decades as a very powerful tool to analyze features of biomolecular structures that are difficult or impossible to capture experimentally, ranging from ranking of interaction strengths and affinity calculations to the mapping of transition states and pathways involved in conformational changes. The detailed structural and dynamic description provided in molecular dynamics (MD) simulations thus is very valuable for an in-depth understanding of the subtle balance between competing interactions involved in molecular recognition processes. The effects of slight structural changes interplay with solvent and ions, and entropic effects are very difficult to guess; more precise methods, such as free energy perturbation (FEP) or potential of mean force calculations, therefore, are necessary.

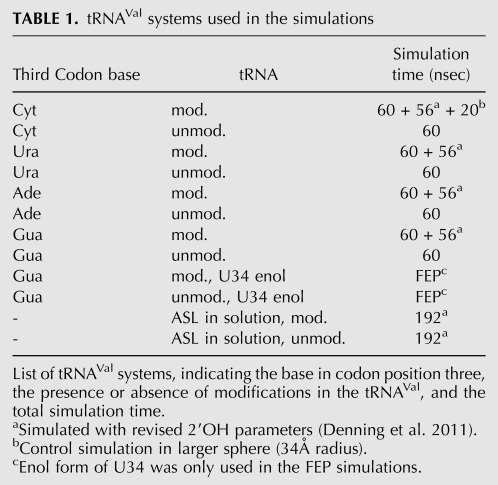
Ribosome movement along the mRNA was simulated as a stochastic process (treating the ribosome as a single particle) (von Heijne et al. 1978) already at the same time as MD simulations were beginning to be applied to proteins (McCammon et al. 1977). Since most of the decoding activity in the A-site involves helix 44 of the 16S rRNA, several simulation studies on A-site containing 16S rRNA fragments in the presence and absence of antibiotics have been performed. (Reblova et al. 2006; Vaiana et al. 2006; Meroueh and Mobashery 2007; Romanowska et al. 2008) These include classical MD as well as enhanced sampling simulations using replica exchange or targeted MD protocols. These studies have revealed changes in mobility of residues 1492 and 1493 when antibiotics are bound or when the nearby residue 1408 is changed from the prokaryotic adenine to the eukaryotic guanine. Furthermore, the hydration pattern around the RNA and antibiotic binding affinities were evaluated. The recent availability of high quality ribosome structures has resulted in a small number of atomistic simulation studies of the peptidyl transfer reaction (Trobro and Aqvist 2005) and of some aspects of codon:anticodon interactions in the decoding center (Sanbonmatsu and Joseph 2003; Sanbonmatsu 2006b; Almlöf et al. 2007; Vaiana and Sanbonmatsu 2009), which has also been studied free in solution (Lahiri and Nilsson 2000). Despite the wealth of structural and biochemical/biophysical information available for ribosomes in many states (Ogle and Ramakrishnan 2005; Noller 2006; Agris et al. 2007), there are still a number of unresolved issues. For the recognition process in the decoding center, these range from questions concerning the importance of particular hydrogen bonds, the role of commonly found nucleotide modifications, or the pathways of local structural rearrangements to the alignment of catalytic elements on EF-Tu in response to codon:anticodon recognition (Daviter et al. 2006). We have analyzed some of these problems using more than 300 individual molecular dynamics simulations of 12 systems (Table 1), comprising a total of 1.3 μsec (∼100,000 CPU hours), primarily focusing on a small region around the decoding center on the 30S subunit.

TABLE 1.

tRNA^Val systems used in the simulations

We investigate the initial step in the tRNA anticodon:mRNA codon recognition by calculating the relative affinities of a select set of cognate, near-cognate, and noncognate complexes in the presence as well as in the absence of the ribosome. We use the most exact computational method, free energy perturbation, to achieve this to the accuracy of the interaction model (i.e., the force field). Linear interaction energy calculations on tRNA^Phe binding to different codons in the ribosomal decoding center (Almlöf et al. 2007) and free energy calculations on the formation (Scheunemann et al. 2010) of modified base pairs in RNA double helices in solution (Scheunemann et al. 2010) have shown that current force fields and simulation protocols are capable of providing accurate results for this kind of system.

Following this, we investigate the role of two commonly occurring modifications of the tRNA (modification of the base in the first anticodon position and of the base on the 3′ side of the anticodon). It has been suggested that the geometric parameters of the base pair, which apparently are critical for proper recognition, are adjusted toward being more acceptable in the presence of some of these modifications. Another possibility that has also been put forward is that the modifications reduce the entropic cost of binding to the ribosome by prestructuring (Agris et al. 2007) the anticodon stem–loop (ASL) before binding. Rigidity of tRNA has also been proposed to be important for transmitting a signal from the decoding center to the GTPase function on EF-Tu after the formation of a correct codon:anticodon pair (Sanbonmatsu 2006a).

RESULTS AND DISCUSSION

General stability

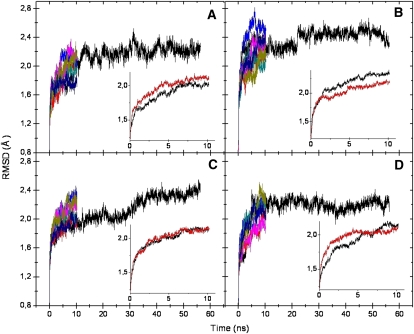
The root mean square deviation (RMSD) from the initial X-ray structures (Fig. 4) shows that all systems are generally well-behaved, with none of the systems having an RMSD exceeding 2.5 Å. The longer simulations do not reach any higher RMSD than the shorter ones, indicating that equilibration is reached within 10 nsec. Only small differences between the modified and unmodified systems exist (Fig. 4, inset), suggesting that the absence of modifications causes no large structural changes. The relatively high RMSD for the modified tRNA bound to adenine in one of the simulations is due to a few residues, e.g., the fourth (end) residue of mRNA, which undergo large structural changes. The simulations of tRNA free in solution are also well-behaved, stabilizing after just a few nsec and reaching a maximum RMSD of just over 3 Å. No significant differences can be seen between modified and unmodified systems.

FIGURE 4.

Root mean square deviations of all solute atoms (modified systems, seven replica simulations) for the ASL bound to cytosine (A), adenine (B), uracil (C), and guanine (D) at the third codon position. The insets show the average of the first 10 nsec for modified (black) and unmodified (red) systems.

Throughout all simulations, the first (GC) and second (UA) codon-anticodon base pairs remain bound and stable, and they will not be discussed any further. The ribosomal residues A1492 and A1493 which are believed to monitor these two base pairs also lie stably in the minor/major groove of the codon-anticodon mini helix. Over all simulations, the average number of hydrogen bonds to tRNA and mRNA are 0.52 and 1.6 for A1492 and A1493, respectively, with small deviations between simulations.

The randomly placed potassium ions do not participate in any binding or bridging around the codons but instead mostly find pockets of negative electrostatic potential where they reside until replaced by another ion (data not shown). The mobility of the remaining ions around the codons is high, with residence times in the range of tens of picoseconds.

When included, magnesium ions from the X-ray structure display only minor translations. Mg²⁺ ions directly coordinated to at least one RNA atom remain bound on our 20-nsec timescale and do not move at all relative to the surrounding RNA. Magnesium ions completely complexed with water, Mg²⁺(H₂O)₆, and only bound to RNA through second shell interactions display considerably more freedom from the RNA but are limited to translations below a few Å due to the size of the binding pocket in which they reside.

A tendency for local opening of Watson-Crick (WC) base pairs in simulations using the CHARMM27 force field has been observed and found to be due to oversampling of the O3′ orientation of the 2′-OH group of RNA (Denning et al. 2011). This results in opening of ∼20% of the WC base pairs in a range of double helical RNA model systems, which is not consistent with the experiment. A modification of the parameters for the 2′-OH group (parameter set CHARMM27d) resolves the problem (Denning et al. 2011). In Supplemental Fig. S1, we compare the N1-N3 distance distribution of WC pairs in the stem of the tRNA anticodon arm for our simulations of the ASL free in solution and in the ribosome, using parameter sets CHARMM27 and CHARMM27d. Some base pair opening can be seen with CHARMM27, but it is significantly less common (≪1%) than for the systems studied by Denning et al. (2011), most likely because bases in the ribosomal environment are more confined than they are in free helices. Root mean square fluctuation (RMSF) data obtained with CHARMM27d (Supplemental Fig. S2) also generally lie within the error margin of several replica simulations with CHARMM27.

Since our data obtained with CHARMM27 and the updated CHARMM27d are very similar, the 2′-OH artifact present in CHARMM27, which is used in the majority of our simulations, should have no significant effect on the results.

To check the influence of system size, we ran one of the systems (with cytosine in position 3 of the codon) using a sphere with 34-Å radius for 20 nsec with the CHARMM27d parameters. The RMSD lies ∼0.3 Å higher than in the smaller system (radius 25 Å) and is stable for the entire trajectory after initial equilibration. To compare the dynamics of the two system sizes, the RMSF of atoms around their average positions was calculated for RNA residues in the ASL. In Supplemental Figure S1, the RMSF is shown for the two system sizes as columns, and as a solid line for the average of the six simulations with the original CHARMM27 force field. The differences stemming from system size are small and mostly lie within the error margin from replica simulations, supporting that the smaller system size is sufficient.

Prestructuring of the anticodon stem–loop

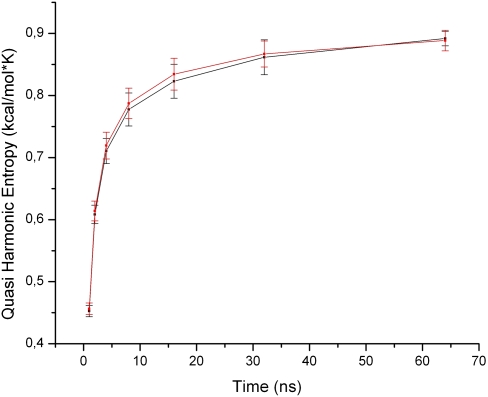
The quasiharmonical configurational entropy (Andricioaei and Karplus 2001) was calculated for the ASL in solution with and without the two modifications present. Convergence was tested by plotting the entropy against the amount of time used for its calculation, and, as can be seen in Figure 5, the simulations are very close to convergence at 64 nsec. However, no statistically significant differences between the modified and unmodified ASLs can be seen. For ASLs bound to the ribosome, there were also no entropy differences between the unmodified and modified systems (data not shown). This, together with structural analysis showing negligible differences, prompts the conclusion that these modifications do not contribute to any prestructuring within our models.

FIGURE 5.

Quasiharmonic entropy as a function of time for the ASL free in solution (modified in black, unmodified in red).

Free energy of binding

Free energy perturbation

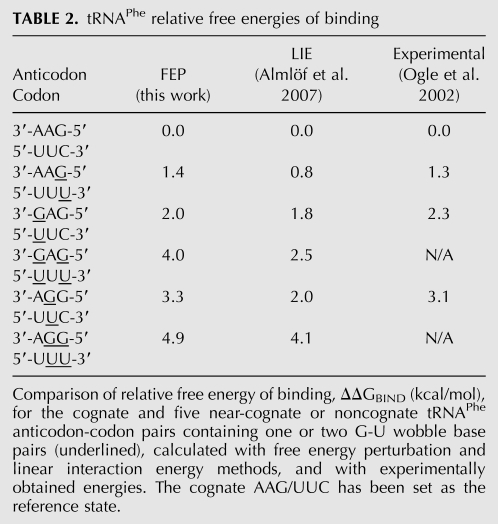
To validate our approach for determining the ΔΔG_BIND of codon-anticodon base pairs in the ribosomal A-site with free energy perturbation, we first performed six calculations on a tRNA^Phe anticodon-codon system with the cognate (3′-AAG-5′:5′-UUC-3′) and five near-cognate (with a G-U base pair in one or two of the three codon positions) anticodon-codon pairs. This is a very well characterized system, for which binding free energies have been previously calculated using the linear interaction energy method (LIE) (Aqvist et al. 1994; Almlöf et al. 2007) and obtained experimentally (Ogle et al. 2002). The largest deviation from experiment in our test calculations was only 0.3 kcal/mol (Table 2), and the rank order of the relative free energy differences agrees with the existing experimental values. As expected, the cost for the near-cognate case of a G-U wobble base pair in the third codon position (1.3 kcal/mol) is less than for the noncognate cases with a G-U base pair in the first or second positions (2–3 kcal/mol), and the presence of two G-U wobble pairs leads to a decrease in the affinity by 4–5 kcal/mol.

TABLE 2.

tRNA^Phe relative free energies of binding

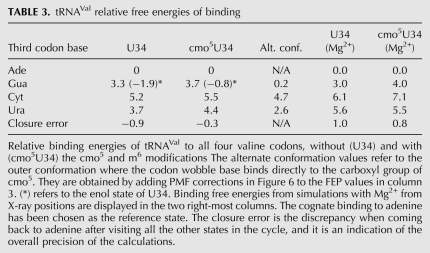
We then used free energy perturbation to study the effect of the cmo⁵U34 and m⁶A37 modifications in tRNA^Val on ΔG_BIND for all three mismatches (G-U, C-U, U-U) in the third codon-anticodon base pair relative to the cognate A-U (Table 3). For the U34-G3 base pair, we include both the keto and enol forms of the uracil included since it has been suggested that the cmo⁵ modification promotes the enol form of uracil when base-pairing to guanine (Weixlbaumer et al. 2007). The ribosome depends on Mg²⁺ ions for proper structure and function (Agris 1996), but the ions are believed to mainly affect the folding and stabilization of tertiary structures (Draper 2004). To find out if Mg²⁺ ions have any effect in the short timescales studied here, the FEPs were also performed (Table 3) with the Mg²⁺ included in the X-ray structure (Weixlbaumer et al. 2007).

TABLE 3.

tRNA^Val relative free energies of binding

The cognate adenine was used as the reference point for both the modified and unmodified systems. An indication of the error margin is given by the closure error (Table 3, last row) obtained from the full transformational cycle, when the base (originally adenine), after several transformations, is once again an adenine. Generally, the effect of the modifications on ΔG_BIND is within this error margin, and if any trend can be seen, it is that the modifications enhance the difference between the codon bases, contrary to the hypothesis that the modification would diminish the difference between codons. The inclusion of Mg²⁺ ions does not seem to affect the effect of the modifications on the binding energies, but the energies are generally higher with Mg²⁺ present. Other observations are that the base pair between guanine and the enol form of U34 would be very stable if the unusual enol form was attainable (this issue is not addressed in our calculations), even more so than the cognate adenine and that, in accordance with previous observations (Weixlbaumer et al. 2007; Vendeix et al. 2009), uracil binds better than cytosine to U34.

Potential of mean force

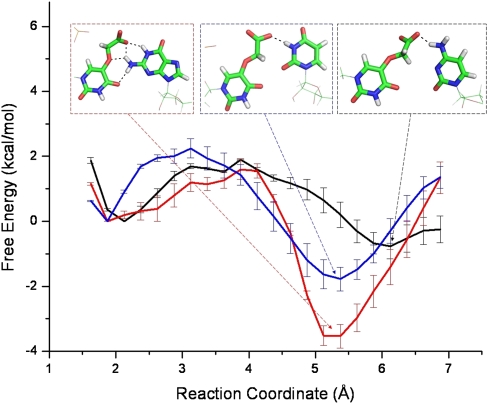
The sampling in each FEP 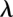window proved insufficient to sample an outer conformation where the wobble codon base binds directly to the carboxyl group of cmo⁵, which was observed in the standard simulations (see section “General structure and hydrogen bonds” below). To shed more light on this part of the energy landscape, potential of mean force (PMF) profiles between the standard mismatch and outer conformations were calculated (Fig. 6). Standard errors were calculated from three parts of the last 0.6 nsec (1 nsec total) of each trajectory, and no specific trend could be seen among them, indicative of convergence. All three profiles have a global minimum at the outer conformation, 5–6 Å away from O4 of cmo⁵U34, offering an energy stabilization of −0.8 to −3.5 kcal/mol compared to the standard, inner conformation. The 2 kcal/mol barriers between the conformations explain the absence of the outer conformations in the short FEP simulations.

FIGURE 6.

Relative free energy between the inner and outer (insets) conformations obtained by PMF calculations. The standard mismatch (inner) conformation has been chosen as the reference state. The reaction coordinate is the distance between O4 of cmo⁵U34 and H1, H42, and H3 for guanine (red), cytosine (black), and uracil (blue), respectively. Error bars are standard errors calculated by comparing three parts of the trajectories.

General structure and hydrogen bonds

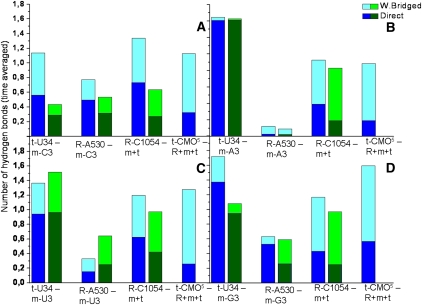
Hydrogen bonds have been studied in detail (Fig. 7) for four sets of residues: (1) within the wobble base pair; (2) between the third codon residue and the ribosomal G530 which are mostly positioned close to each other; (3) between the ribosomal C1054 and the mRNA and tRNA chains. The role of C1054 in translation is not well-understood, but the residue is flipped out from a hairpin just beneath residue 34 in the anticodon and is within direct hydrogen bonding distance to U34 and residues 3 and 4 of the mRNA; and (4) between the cmo⁵ modification and all surrounding nucleotides and amino acids.

FIGURE 7.

Hydrogen bond interactions between some selected residues around the wobble base pair for the ASL (modified in blue, unmodified in green) bound to cytosine (A), adenine (B), uracil (C), and guanine (D). Direct interactions are shown in dark colors and the water-bridged are added on top with light colors. (R) Ribosomal residues, (m) mRNA, (t) tRNA.

For the contacts within the third codon base pair, the modifications have the most prominent effect when uracil is paired with cytosine or guanine. With cytosine, the direct contacts are nearly doubled and nearly tripled when put together with the water-bridged contacts. An explanation of these large differences is that, without the modifications, the cytosine was observed to flip out on several occasions and lose contact completely with U34 for prolonged periods. When paired to a guanine, a >50% increase in contacts is observed within the third codon-anticodon base pair. The reason for this is largely the formation of a hydrogen bond network (Fig. 8A). For uracil paired to the cognate adenine, the effect of the modifications on the hydrogen bonds within this base pair is insignificant since the U-A pair is tightly bound as it is. The U-U pair has a very stable hydrogen bond between O4 of U34 and H3 of U3. However, when the modification is present, this bond is, on occasion, broken when H3 of U3 flips out a bit and binds to the carboxyl group of cmo⁵, forming an alternative “outer” conformation (Fig. 8B). This behavior is also observed when cmo⁵U34 is paired with cytosine and guanine, although less often, and not at all in the cognate, very stable, base pair with adenine. Doing this, the cmo⁵ modification extends the reach of uracil when paired with a near- or noncognate base. This trapping of the codon base provides additional stability to the normally unstable (Agris et al. 2007) pyrimidine-pyrimidine base pairs.

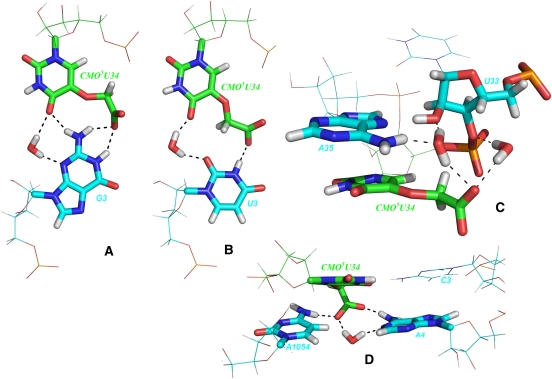
FIGURE 8.

Observed interactions of cmo⁵U34. (A) A network of hydrogen bonds between G3 and U34 is possible with the cmo⁵-modification. (B) cmo⁵ extends the reach to help binding with U3. (C) When free in solution, the cmo⁵-modification forms several water-bridged contacts to the backbone. (D) The carboxylic oxygens of cmo⁵ bridge the gap between the ribosomal C1054 and A4 of mRNA.

Ribosomal G530 makes frequent contacts with the third residue of the codon and is again favorably affected by the modifications in the case of cytosine and guanine. For cytosine, the interactions are increased by ∼50%, and for guanine, a large part of the water-bridged contacts are replaced by stronger direct hydrogen bonds. The cognate adenine has, due to being so tightly bound to U34, very few interactions with G530 and the modifications seem to have no effect on them. For uracil, the modifications seem to have a negative effect on G530 interactions, especially water-bridged. This is due to the stabilization by the cmo⁵ modification of the uracil in the outer conformation where it is further away from G530.

Ribosomal C1054 interactions with tRNA and mRNA are enhanced by the modifications for all four codons. The effect is most prominent for the direct hydrogen bonds with water-bridged contacts more or less unaffected in all cases but for cytosine, where they, similarly to the direct, are nearly doubled. The explanation for this increase can be found in Figure 8D, where the cmo⁵ modification can be seen to be bridging between C1054 and A4 of mRNA. This behavior is, to some degree, observed for all four codons and is the main reason for the increased interactions of C1054 toward tRNA and mRNA in the presence of the cmo⁵U34 modification.

The contacts of the cmo⁵ modification with its surroundings consist in large part of water-bridged interactions for all four codons. Guanine enables the largest number of direct hydrogen bonds, due to the network described above. The water-bridged contacts go to various surrounding residues in other chains but also to a large extent toward the neighboring residues in the ASL. When free in solution, the cmo⁵ modification forms a weak and transient network of water bridges with neighboring residues. (Fig. 8D).

The hydrogen bond between the 2′-OH of U33 and the ether oxygen (O5) of cmo⁵U34 (Weixlbaumer et al. 2007) is not observed here, neither with the CHARMM27 parameters or the updated CHARMM27d parameters. Instead, 2′-OH of U33 forms a hydrogen bond with N7 of A35, which is also within hydrogen-bonding distance in the X-ray structure.

CONCLUSIONS

We have studied the atomistic mechanism responsible for the unique ability of tRNA^Val with the modified bases cmo⁵U34 and m⁶A37 to accept all four bases at the codon wobble position in the mRNA decoding process. The cmo⁵-modification consists of a highly polar carboxyl group attached with a flexible ether linker to uracil, giving it a wealth of possible interactions. We have, indeed, found that there is a combination of several mechanisms involved in the expanded acceptance of base pairs of cmo⁵U34:

• Alternate binding conformations. The extended reach of cmo⁵U34 allows an alternative conformation to be formed for the noncognate base pairs. These conformations are lower in free energy than the standard mismatch binding by ∼1–3 kcal/mol.

• Increased contact with the ribosome. Additional contacts between the ribosome and anticodon enhance the “catalyzing” effect of the ribosome. One of these contacts is the bridging between ribosomal C1054 and the first base of the next mRNA codon which could pre-order the codon.

• No significant differences in ASL entropy or structure could be observed within our models on the 0.1-μsec timescale, suggesting that cmo⁵U34 and m⁶A37 have a limited prestructuring effect.

MATERIALS AND METHODS

Standard simulations

All MD simulations were carried out using the program CHARMM (Brooks et al. 1983, 2009) applying the fast lookup routines for nonbonded interactions (Nilsson 2009) where applicable. The CHARMM27 all-hydrogen force field (MacKerell et al. 1998; Foloppe and MacKerell 2000; MacKerell and Banavali 2000) was used in most simulations, and some test simulations were also run with the updated 2′-hydroxyl parameters “CHARMM27d” (Denning et al. 2011) in the CHARMM27 force field. The initial coordinates of the ribosome in complex with modified tRNA^Val bound to mRNA with adenine, cytosine, uracil, and guanine in the third codon position were taken from X-ray structures with PDB ID 2UU9, 2UUA, 2UUB, and 2UUC, respectively (Weixlbaumer et al. 2007).

In all of these structures, data for large parts of the tRNA bound to the A-site is missing, making the ASL incomplete. To remedy this, the ASL of the A-site tRNA was extended to its full size (Supplemental Fig. S3) by aligning backbone atoms to a fragment of yeast tRNA^Phe (PDB ID 1EHZ) (Shi and Moore 2000). The residue numbering from the X-ray structure is kept, and the chains are denoted r for ribosomal RNA, m for mRNA, and t for tRNA.

The parameters for cmo⁵U34 and m⁶A37 were determined by analogy with similar, already parameterized atom groups in the CHARMM force field and are presented in Supplemental Material.

Hydrogen atoms were added using a standard CHARMM procedure (Brünger and Karplus 1988).

A spherical system with radius 25 Å, centered on t-U34-O4, was cut out from the original X-ray structures. The system includes the mRNA, tRNA, and the surrounding ribosomal helices and proteins. This size of the system has been shown to model the ribosomal A-site well (Almlöf et al. 2007), but we also simulated a larger system in a 34-Å-radius sphere using the 2′OH updated CHARMM27d parameters for testing purposes. The spherical systems were solvated with TIP3P water (Jorgensen et al. 1983). Overlapping water molecules, with the oxygen atom within 2.8 Å of any solute heavy atom, were removed. The paromomycin antibiotic molecule which was included during crystallization and present in all X-ray structures was deleted together with all ions. In all systems, the remaining negative charge of the nucleic acids was counteracted by randomly placed K⁺ ions to obtain a neutral system.

Mg²⁺ and other divalent ions present particular challenges for MD simulations. They have a very strong polarization effect on their surroundings and may influence neighboring residues in a way that is not accounted for by current classical force fields (Ditzler et al. 2009), and, in addition, the positions of Mg²⁺ ions in X-ray structures are often ambiguous. The effect of Mg²⁺ ions on our results was tested by also running a subset of the simulations with Mg²⁺ included.

Water molecules and ions were subjected to a spherical boundary potential (Brooks and Karplus 1983) to prevent them from leaving the sphere. Solute atoms outside the sphere were restrained with a force constant of 2 kcal/mol/Ų throughout all simulations and minimizations.

An energy minimization was made on the systems: first, 150 steepest descent (SD) and 150 adopted-basis Newton-Raphson (ABNR) steps with the solute atoms restrained with a force constant of 15 kcal/mol/Ų, followed by 300 SD and 300 ABNR steps with no restraints.

SHAKE (Ryckaert et al. 1977) was used to constrain all bonds involving hydrogens. Newton's equations of motion were integrated using the leap-frog algorithm with a 2 fsec time step. Electrostatic and van der Waals interaction energies and forces were smoothly shifted to zero at 12 Å, a method that has been shown to work well for nucleic acids (Norberg and Nilsson 2000). The nonbonded list was constructed using a 16-Å cutoff and was updated every time an atom moved >2 Å since the last update.

All simulations were started with a 200 psec equilibration phase in which the systems were heated from 50 to 298 K. During this phase, a restraining harmonic potential was assigned to keep the hydrogen bond distance between atom pairs: m-G1-O2′–r-A1493-H2′, m-U2-H2′–r-A1492-N3, t-C36-H2–r-A1493-N1, t-A35-H2′–r-G530-N3, and r-A1492-N1–r-G530-H1. The two first pairs were restrained to make up for the increased flexibility caused by the abrupt end of the A-site mRNA included in the crystal structures, and these two restraints were also kept throughout the following production runs. The remaining atom pairs were restrained to balance out initial stress on the system from removing the paromomycin and the ions present in the crystal structure and were kept only during the equilibration phase.

For the standard ribosomal simulations in this work, we constructed eight different systems (Table 1): Each of the four codons bound either to tRNA modified with cmo⁵U34 and m⁶A37, or to unmodified tRNA. These eight systems were simulated for 10 nsec with six independent replicates, starting with different initial velocities, for a total of 60 nsec each. Running independent replicates is a very cost-effective way to sample conformational space (Elofsson and Nilsson 1993). Computer resources continue to grow, and with standard GNU/Linux PC clusters, we achieve 40–50 nsec/day for one of our typical systems with 8000 atoms when running eight jobs on eight cores each with CHARMM. In addition to these, one 56-nsec-long test simulation was run for each of the modified systems with the CHARMM27d parameters (Denning et al. 2011).

We also performed simulations of the tRNA ASL alone, not bound to the ribosome, to examine if the cmo⁵U34 and m⁶A37 modifications induce any structural or dynamic changes compared to an unmodified ASL. The coordinates of tRNA free in solution were taken from the structure of tRNA in complex with the cognate adenine codon from Weixlbaumer et al. (2007) with the extension of the ASL as described above.

Two systems of the ASL in solution, with and without the two modifications, were set up as described above but with a water sphere of radius 34 Å centered on G24-O4. In addition to the ASL, these larger systems also include the D-loop and variable loop of the tRNA for a total of about 30 residues. Three independent replicates were simulated for 64 nsec each, giving a total of 192 nsec for each system. These simulations were run with the new 2′-hydroxyl parameters (Denning et al. 2011).

Free energy calculations

FEP simulations

Free energy calculations using the free energy perturbation protocol have been thoroughly described elsewhere (Jorgensen et al. 1983; Beveridge and Dicapua 1989; Straatsma and McCammon 1992; Kollman 1993; Simonson et al. 2002; Hart and Nilsson 2008), and here we will only present a brief introduction and information specific to our systems. We have used the dual-topology implementation of the FEP method in CHARMM by Fleischman and Brooks (1987) to determine the difference in free energy of binding (i.e., the relative affinity) of different codons to the tRNA^Val anticodon, with or without the modifications of cmo⁵U34 and m⁶A37 present. The structures from Weixlbaumer et al. (2007) were used.

The free energy perturbation method can be used to efficiently calculate differences in free energy by utilizing a thermodynamic cycle, here exemplified with the pairing of adenine or cytosine to uracil:

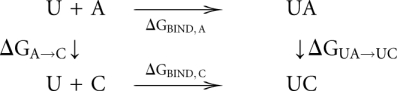The horizontal reactions, which are the experimentally relevant reactions, would be computationally very demanding using a physics-based potential energy since they involve moving the reactants through the solvent, possibly also requiring large conformational changes to allow access to the binding site. Since the free energy difference is a thermodynamic state function and, thus, independent of the path taken in the scheme above, we can more easily obtain the difference between 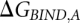and 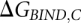(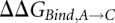) by instead calculating the vertical reactions. The difference in free energy of binding is then given by .

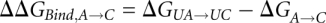To be able to perform the transformation of one residue to another in the 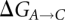and 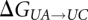reactions, a hybrid residue consisting of both the reactant and product residues is created. The energy of the transformation is described by 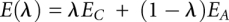, where λ is a coupling parameter ranging from 0 (product state) to 1 (reactant state) in small steps. The free energy difference is calculated by summing the contributions from the simulations at all intermediate λ-values: 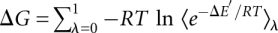, where the angular brackets denote averaging over a simulation performed at a given value of λ, and .

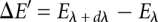The effect of the base modifications is finally obtained by comparing the 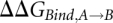with and without modifications: 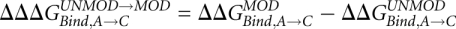. Different sizes of the unbound reference system, ranging from a single nucleoside to pentamers, have been used in FEP studies of base transformations (Sarzynska et al. 2003) with virtually identical results, and we, therefore, used a reference system containing triplets, with the nucleotide being transformed in the middle, free in solution.

To validate the method for our system, we also performed a set of simulations for a 30S:mRNA:tRNA^Phe system (PDB id 2J00) (Selmer et al. 2006) and compared to binding energies calculated by Almlöf et al. (2007) and experimentally obtained by Ogle et al (2002). The systems for the FEP calculations were set up similarly to the standard simulations described above but with a sphere of radius of 34 Å.

In the hybrid residues containing atoms from both states (see Supplemental Material), all interactions between atoms belonging to different states are disabled allowing only the surroundings to interact with both states simultaneously. The purine-purine and pyrimidine-pyrimidine hybrids, A/G and C/U, share all atoms but the ones that actually differ between them. The mixed purine-pyrimidine hybrids, G/C and U/A, however, only share the backbone and sugar atoms; the base parts are represented by both nucleotide bases individually. The simulated transitions of mRNA codon residues in the tRNA^Val system [A→G(k), G(k)→G(e), G(e)→C(e), C(e)→C(k), C(k)→U, U→A; here (k) and (e) denote the keto and enol tautomers of t-U34] form a closed loop with an ideal net 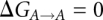. The overall calculated 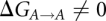and is an estimate of the error of the method.

Starting structures for the FEP calculations were obtained by taking a snapshot from the end of a 1 nsec of equilibrium simulation for each system. The residue at position three in the codon was then replaced with one of the hybrid residues. The reference system consisted of the hybrid residue with one adjacent residue on each side, solvated in a 17 Å radius sphere of water and three K⁺ ions.

Simulations with magnesium were prepared by using the Mg²⁺ coordinates in the X-ray structure (Weixlbaumer et al. 2007); K⁺ ions were added until zero net charge. Preliminary simulations with Mg²⁺ ions included resulted in severe local structural distortions (data not shown), in particular, around Mg²⁺ ions that were not properly six-coordinated after the initial solvation of the X-ray structure. To obtain six-coordination of the Mg²⁺ ions without distorting the structure, we prepared the system in several steps, with energy minimization with initial restraints on both solute and ions, followed by a new minimization with restraints only on the solute. This scheme was repeated for 0.5 nsec of dynamics before the restraints on the solute were removed.

The FEP calculation was divided into 15 windows ranging from 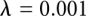to 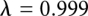with nonlinear spacing at the boundaries. Each window was individually minimized, similarly to the procedure described above, and after a 100-psec equilibrium simulation, 300 psec of data collection was run. To avoid possible problems due to the creation of atoms when going from a small to a larger residue, soft-core methods, in which the Lennard-Jones r⁻¹² repulsive term is replaced with a term that is finite for r = 0, have been successfully used (Beutler et al. 1994). We opted for the simpler scheme of performing the perturbations in a direction that avoids the sudden appearance of atoms in locations accessible to the surroundings. The mixed purine-pyrimidine hybrids were thus calculated in the purine → pyrimidine direction which avoids this end-point catastrophe, since the appearing pyrimidine is protected by the disappearing purine at small values of λ.

The net 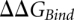was computed from the difference between 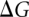values obtained using doublewide sampling at each 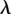-value for the ribosome complex and the reference system.

Potential of mean force calculations

Potential of mean force profiles were calculated using umbrella sampling with the harmonic bias potential 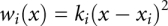along a reaction coordinate, x, defined as the distance between O4 of cmo⁵U34 and H1, H42, and H3 for adenine, cytosine, and uracil, respectively. Initial conformations for the 23 windows (with x_i ranging from 1.5 to 7.0 Å, in 0.25Å increments) were generated by running 20 psec of MD, with k_i = 25 kcal/mol/Ų, starting from a snapshot taken from the standard simulations and with the last structure in each window as the starting structure in the next window.

The production phase for each window was run for 1.0 nsec (of which 0.4 nsec was equilibration time) with k_i = 10 kcal/mol/Ų, and the PMF was constructed from the last resulting distance distribution using the Weighted Histogram Analysis Method (Kumar et al. 1992; Boczko and Brooks 1993). Standard error bars were obtained by dividing the trajectory into three parts.

Analyses

To monitor the structural change from the initial X-ray structure, the RMSD was calculated for all unrestrained solute atoms.

The hydrogen bond contacts were calculated using a 2.4-Å distance cutoff (De Loof et al. 1992) and 5-psec time cutoff. The same distance and time cutoffs were used when calculating contacts bridged by water molecules. Contacts between RNA and ions were calculated with a 2.8-Å distance cutoff and 5-psec time cutoff.

The configurational entropy was determined for the ASL loop (residues 32–38) with quasiharmonic vibration analysis (Andricioaei and Karplus 2001). The cmo⁵ and m⁶ groups were excluded in the case of the modified systems to get the effect on the actual ASL. The trajectories were divided into time windows ranging from 1 nsec up to the total 64 nsec, and the entropy was calculated and averaged over all available windows, and standard deviations were calculated for the three replica simulations.

The rotational and translational entropy are not considered here since it has been found to account for <1% of the total entropy (Wrabl et al. 2000); in addition, the very small structural change resulting from the addition of the cmo⁵ and m⁶ groups (M_w = 75g/mol) to the ASL (M_w = 2360g/mol) will have a negligible effect on rotational/translational entropy.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.