Skip to main content
PMC home page
Frontiers in Computational Neuroscience logoLink to Frontiers in Computational Neuroscience
. 2011 Nov 22;5:53. doi: 10.3389/fncom.2011.00053

A Biologically Plausible Transform for Visual Recognition that is Invariant to Translation, Scale, and Rotation

Pavel Sountsov 1, David M Santucci 1, John E Lisman 1,*
PMCID: PMC3222220  PMID: 22125522

Abstract

Visual object recognition occurs easily despite differences in position, size, and rotation of the object, but the neural mechanisms responsible for this invariance are not known. We have found a set of transforms that achieve invariance in a neurally plausible way. We find that a transform based on local spatial frequency analysis of oriented segments and on logarithmic mapping, when applied twice in an iterative fashion, produces an output image that is unique to the object and that remains constant as the input image is shifted, scaled, or rotated.

Keywords: biological classifier, cortico-striatal, hybrid model, reinforcement, unsupervised, hierarchical

Introduction

Objects are easily recognized by our visual system despite variation in the size of the object, its position in the environment, or even its rotation (as in television viewing while lying on the couch). Physiological analysis of regions high in the cortical hierarchy show cells having substantial invariance (Gross et al., 1969; Perrett et al., 1982; Logothetis et al., 1994; Tanaka, 1996; Hung et al., 2005). Prominent models (Olshausen et al., 1993; Salinas and Abbott, 1997; Riesenhuber and Poggio, 2000; Elliffe et al., 2002; Shams and von der Malsburg, 2002; Wiskott and Sejnowski, 2002; Serre et al., 2007; Li et al., 2009; Rodrigues and Hans du Buf, 2009) show how some aspects of invariance could be achieved.

Existing models fall into several classes (reviewed in Wiskott and Sejnowski, 2002). One class of solutions routes information between regions in a way that changes the position and magnification of the image. The particular routing is selected by a controller and results in the image reaching a canonical form in some unspecified higher visual region (Olshausen et al., 1993). In this way, position and scale invariance can be achieved. A second class of solutions involves combining outputs of sets of identically oriented filters that vary in scale and position using a MAX function to create complex cells (Riesenhuber and Poggio, 1999). The output of these cells has some invariance to position and scale while still being selective to features. The output of differently oriented complex cells can be combined to create composite feature detectors (e.g., angle detectors). Such cells can again be generalized using a MAX function, leading eventually to high-level networks that detect a pattern in a way that shows scale and position invariance. Two-D rotation invariance refers to rotation of the object in the plane of the object. Neither of the solutions provides a basis for achieving such invariance. Thus, for the system to recognize different rotated versions of the same object, each rotation must be separately learned. However, several lines of experiments show that a component of the visual system achieves complete rotation invariance (Guyonneau et al., 2006; Knowlton et al., 2009) and does so without learning. Another class of solutions (SIFT) does achieve complete invariance (Lowe, 1999, 2004). Input pattern features that are likely to be resistant to changes in scale are isolated and given invariant descriptors. The combined set of features of the input pattern, however, is not invariant to the same transformations. Recognition, therefore, needs to be a multi-step process where individual features are first matched without regard to object identity and are then polled to see if they give consistent values for input pattern identity, as well as its rotation, scale, and position.

Work in machine vision has shown that general solutions to translation, scaling, and rotation invariance exist. These can function without learning (Casasent and Psaltis, 1976a,b; Yatagai et al., 1981). These, however, use Fourier analysis of the full field, an operation that is not biologically plausible. Here, building on ideas developed by (Cavanagh, 1984, 1985), we show how sequential application of a biologically plausible transform can produce an output pattern that remains constant as the input pattern is shifted, scaled, and rotated. This is achieved without learning. Importantly, the proposed mechanism utilizes a form of local spatial frequency analysis, a process for which there is both psychophysical and physiological evidence (see Discussion).

Material and Methods

First stage

Formally, the output map of the first stage of the transformation T can be reduced to a chained application of an edge detector E and an interval detector S to an input image M:

Tθ,IM=Sθ,I;E(θ,I;M) (1)

where θ is the orientation of the edge detector and I is the interval of the interval detector. For most of the data shown, the input image was 1000 × 1000 pixels, and the output image was 100 × 100 [i.e., 10,000 distinct (I, θ) pairs]. For these images, the range of I was 100–700 pixels. The range of θ was 0–180°. This 7-fold range of spatial frequency is realistic, given the greater than 10-fold range in visual cortex (Issa et al., 2000).

Edge detector

We constructed a collection of filters at different orientations (θ) and scales. The filter F was a 1 × 3 pixel white bar and an adjacent 1 × 3 black bar, rotated by angle θ and scaled by convolution with a box filter. Bilinear interpolation was used for both operations. The width of the filter (w) was related to the width of the interval detector in the second step by w = 0.1·I. The orientation selectivity of this filter was quite broad (FWHM = 120°); similar results were obtained with a narrower filter (data not shown), but its execution time was prohibitively slow in our implementation. The edge detector output was then produced by convolving the filter with the entire input image to yield a map:

Eθ,I;M=M*Fθ,I (2)

Interval detector

The interval detector S was designed to give an output if the edge detector output map E for a given θ had two edges separated by an interval, I. This was computed as follows:

S(θ,I;E)=H(∑i,jEi,jEi−Icos⁡(θ+90),j−Isin⁡(θ+90)/(∑i,jEi,j)2) (3)

For a given interval I and angle θ, the edge detector output image was shifted by I at angle þeta + 90 and multiplied pixelwise by the unshifted image. Bilinear interpolation was used when generating the shifted image. This multiplication insured that there was no output if only a single edge was present. All pixels in the filtered image were then summed. The sum was normalized by the squared sum of the input and then rectified using the Heaviside function H. A plot was made of these sums for all I and θ.

Second stage

The second stage of the transformation was carried out identically to the first, except that the output of the first stage was given periodic boundary conditions on the θ axis by duplicating the right-hand portion of the image to the left of the image (and similarly for the left-hand portion). The input images were now 100 × 100, and the range of I was typically 15–85 pixels.

Image classification

Rotated and scaled versions of the letters were classified by the Euclidian nearest neighbor method (Cover and Hart, 1967). In this method, the 10,000-dimensional output for rotated and scaled letters was compared to the 26 unrotated and unscaled parent letters. Images were classified as the closest parent letter.

Multidimensional scaling

For visualization purposes, all 33,670 of the 10,000-dimensional pairwise distances between the 26 parent and the 234 rotated and scaled letters were plotted in two dimensions using non-classical multidimensional scaling (MDS), as implemented in the Matlab Statistics Toolbox. Non-classical MDS iteratively attempts to find the best arrangement of points by minimizing a goodness-of-fit criterion (in this case, Kruskal’s normalized stress1 criterion).

Results

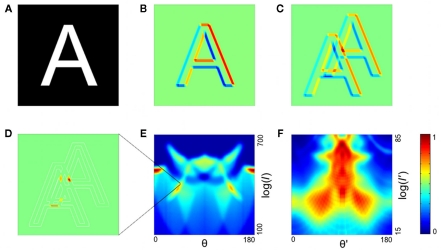
What we term the transform is itself composed of several steps. In the first step, oriented edges are detected by a family of edge detectors. Each detector has a given scale and orientation, defined by angle θ. These detectors tile a subregion of the visual scene (an attentional window; see Discussion) that is large enough to include the object to be detected (e.g., a letter; Figure 1A). The output of the edge detection process for a given orientation and scale is shown in Figure 1B. The second step of the transform is related to standard spatial frequency analysis but is simpler; rather than looking for highly repeated periodicities, our interval detector looks for pairs of oriented edges that have a given distance between them (Figure 1C,D). The interval detector is applied to all positions in the subregion, and the outputs over this subregion are summed. Such sums, for a range of orientations and intervals, are plotted as a function of orientation and log interval (Figure 1E). The summing over space is noteworthy because the sum is invariant to the position of the object within the window.

Figure 1.

Figure 1

Open in a new tab

The two-stage transformation. (A,B) In the first step of the first stage, edge detection is performed, illustrated for an orientation of 45° in (B) (red, positive values; blue, negative). (C,D) The second step of the transform is a spatial interval detector looking for edges separated by interval I at the same angle as the interval detector. To achieve this, the image is shifted (C), and the pixel values are multiplied, with negative values set to zero (D). (E) The image in (D) is summed over all positions to yield a single point in the log interval vs. orientation map (and similarly for other orientations and intervals; orientation range 0–180; interval range 100–700 pixels). Color code is at far right; this is linear with dark blue as zero. (F) In the second stage, the same transform is applied again, yielding a map whose coordinates are log I′ and θ′ (defined relative to the axes of the stage 1 output; interval range 15–85 pixels). Color code is at right; this is linear with dark blue as zero.

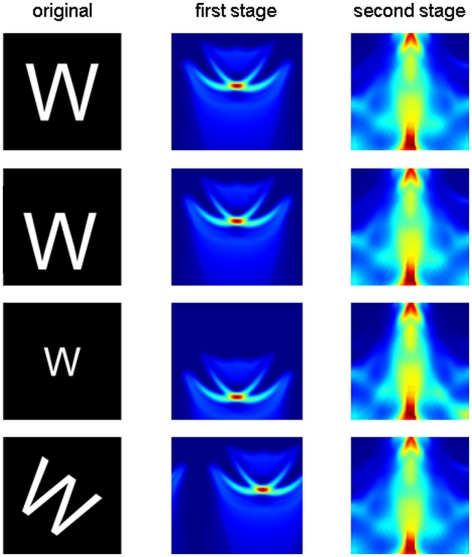
Examination of how such plots change as the image is rotated and scaled (Figure 2, first and second columns) reveals a strategy for obtaining complete invariance: as the object is rotated, the output image of the first stage moves along the orientation axis (θ) but does not change its shape. Similarly, as the object is scaled, the output image moves along the log interval axis but does not change its shape. Thus, total invariance would be achieved if the output image was processed by a second stage that was invariant to the position of the first-stage output. As we noted above, the summing operation in our transform makes the output invariant to position. Therefore, total invariance can be achieved by taking the output of the first transform and applying the same transform again (Figure 1F). As can be seen in Figure 2 (third column), the output of the second stage is insensitive to position, scale, and rotation of the original input.

Figure 2.

Figure 2

Open in a new tab

The two-stage transform produces an output invariant to translation, scale, and rotation. First column: the letter W is translated (second row), scaled (third row), or rotated (fourth row). Second column: first-stage output. Third column: second-stage output. Axes and color code are as in Figure 1E,F respectively.

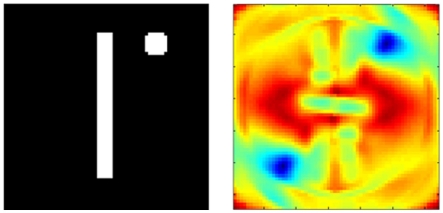
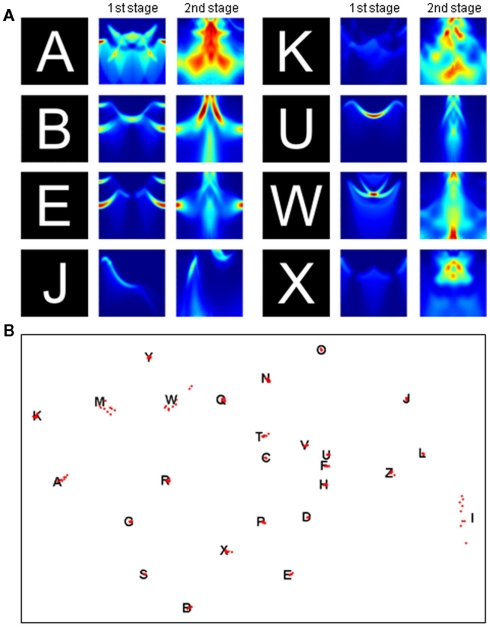
This two-stage transform has elegant invariance properties, but perhaps so much information is thrown away (e.g., by the summing operation) that more than one object could have the same output. To examine this possibility, we conducted two tests. First, we picked a very simple object consisting of a line and a dot. We then asked whether moving the dot to any other position could produce an output transform confusable with that of the original image. Figure 3 shows that the only confusable position is a rotation of the original image. In a second test, we applied the two-stage transform to the complete set of capital letters (examples shown in Figure 4A) and to rotated and scaled versions of the “parent” letters. The outputs of the rotated and scaled versions were then classified according to which parent letter they were closest. Figure 4B shows that these letters produced outputs that, as judged by the pattern classifier, were closer to the corresponding parent letter than to any other letter (i.e., 100% were classified correctly). Thus, the two-stage transform retains sufficient information to differentiate all of these letters.

Figure 3.

Figure 3

Open in a new tab

The two-stage transform provides a unique description of the object. The object in the left panel (line and dot) was varied by moving the dot exhaustively to all positions in the panel. For each position, the two-stage transform was applied. The difference in output from the pattern at left was computed as a Euclidian distance and color coded (red, most different; blue, most similar). The only similar output (blue region at bottom left) is produced by a rotation of the original image.

Figure 4.

Figure 4

Open in a new tab

Output of the two-stage transform is sufficient for object recognition. (A) First- and second-stage transforms for various letters. Axes and color code as in Figure 1E,F. (B) To test recognition, the transform of nine rotated and scaled versions of each letter was compared to the transform of the parent letter. The distances between the 26 parent letters (black letters) and 234 rotated and scaled versions (red dots) are approximately rendered in two dimensions by multidimensional scaling (see Materials and Methods).

We next analyzed the robustness of our algorithm. Real-world vision involves difficulties posed by occlusion, distortion, crowding by other objects, and figure/ground separation. There are likely to be multiple mechanisms that aid recognition in the presence of such difficulties, including attractor properties and top-down contextual information, neither of which is incorporated into our model. Nevertheless, one would want an initial transform that was not brittle. If brittle, minor variations in the letter appearance, including the addition of a non-uniform background, would produce large differences in the output of the first- and second-stage transforms due to non-linear effects of interval detection, and this would lead to misclassification of the affected letter. We therefore examined whether the letter was correctly identfied as various graded perturbations of the image were made. We graded the perturbation until misidentification occurred. This, then, allowed determination of the maximum perturbation that still allowed correct identification. The result is shown in Figure 5A for letter distortions, in Figure 5B for superposition of an additional spatial frequency, and in Figure 5C for the addition of noise or a natural scene background. It can be seen that our transform does not catastrophically amplify variations in the input images, allowing a significant range of perturbation over which correct identification still occurs.

Figure 5.

Figure 5

Open in a new tab

Letter identification is resistant to perturbations of the image. Different perturbations were gradually applied to the letter A until the resulting image was not correctly recognized by the linear classifier. Panels depict the maximum amount of perturbation before misidentification occurred. (A) Distortion of the letter shape. Insets illustrate the effect of the distortion on an outlined square. Top: horizontal shear. Bottom: foreshortening due to perspective. (B) Texture superposition. The images were generated by linearly mixing the source image and an image composed of horizontal (top) or randomly oriented (bottom) bars. (C) Whole image manipulation. Top: White noise was added to every pixel of the source image, followed by normalization of the image pixel intensity to span the range 0–1. The blending of the source image and the noise was varied. Bottom: The black background of the source image was replaced by an image of a natural scene with different levels of mean intensity.

Discussion

We describe a set of biologically plausible transforms that achieves position, size, and rotation invariance. The mechanisms involved are simple to understand. In an early step, a spatial interval detector is applied over the entire region and the results summed, producing position invariance. The resulting sums (for all spatial frequencies and edges) are plotted as a function of angle and log spatial frequency. In this coordinate system, rotation shifts the image along the angle axis, whereas scaling shifts the image along the log frequency axis. Thus, invariance to position, scale, and rotation could be achieved by an additional transform that was insensitive to these shifts. The early step discussed above meets this requirement. We show that although information is lost by applying this set of transforms (e.g., spatial information is lost by summing), enough information is retained by the set of spatial frequency analyzers to enable letter recognition. While it is not yet possible to directly map the operations of our model onto particular parts of the visual system, each of the operations that we have utilized in our transforms is biologically plausible.

Unlike previous models in which spatial frequency either had no function or served only for edge detection (e.g., Riesenhuber and Poggio, 1999), our model depends on spatial frequency analysis (our interval detector) in a way that is fundamental to the recognition process. This makes the model consistent with the spatial frequency tuning of cells in V1 and higher-order visual areas (Andrews and Pollen, 1979; De Valois et al., 1982; De Valois and Tootell, 1983; Shapley and Lennie, 1985; Issa et al., 2000; Pollen et al., 2002). Our spatial frequency detector involves two bars, separated by a given interval. There are families of such detectors at different orientation and spatial frequency. This corresponds to the property of V1 cells that have orientation preference and that have either linear or non-linear dependence on the number of repeating bars (Movshon et al., 1978; von der Heydt et al., 1992). Hubel and Wiesel (1962) reported that a substantial fraction of V1 simple cells is strongly excited by two parallel bars (but only weakly by one bar), consistent with the multiplication step of our interval detector. There are several neural mechanisms that can produce multiplication (Gabbiani et al., 2004; Kepecs and Raghavachari, 2007). In our case, exact multiplication is not required; a strong non-linearity will suffice (data not shown). The importance of spatial frequency in vision is strongly supported by psychophysical experiments demonstrating independent spatial frequency channels: notably, the adaptation of detection produced by presenting one spatial frequency does not affect the detectability of other spatial frequencies (Sachs et al., 1971; Arditi et al., 1981).

Additional elements of the model are also biologically plausible. We assume that cortical mapping can be logarithmic, and there is precedent for such mapping (Tootell et al., 1982; Adams and Horton, 2003). Also, we have used the same transform serially to obtain invariance. This is consistent with the observation that different levels of the cortical hierarchy have similar cellular structure and network properties (Mountcastle, 1997; Buxhoeveden and Casanova, 2002), as if they perform similar computations.

There are several limitations of the model that warrant discussion. One objection is that the model is too good: after all, one can recognize that a letter is upside down. Thus, recognition cannot depend solely on a system that has complete rotation invariance. However, many lines of evidence indicate that the visual system is not unitary but is rather composed of many visual processing streams that operate either serially or in parallel (Felleman and Van Essen, 1991). It thus seems reasonable to suppose that some cortical regions encode invariant representations produced by the mechanism that we propose, while others retain information about position, scale, and rotation.

A further objection is that some psychophysical measurements (Copper, 1975; Hamm and McMullen, 1998) show that invariance occurs only over a limited range of rotation. Our model achieves complete invariance by using a wrap-around map of orientation (zero is next to 360, as in cortical pinwheels Bonhoeffer and Grinvald, 1993). Abandonment of this assumption would reduce the rotation invariance of our system. However, other psychophysical experiments show that under some conditions, vision is completely rotation invariant (Guyonneau et al., 2006; Knowlton et al., 2009). Our model shows how such complete rotation invariance could be achieved. It should be emphasized that some models promote rotation invariance by training at all rotations. In contrast, our model achieves complete rotation invariance after training at only a single rotation. We stress that the rotation invariance in our model is for rotation in the plane. The most explicit model for rotation out of the plane (3D) posits that the system learns several views and interpolates between views (Riesenhuber and Poggio, 2000). Our model could be similarly adapted to solve the 3D problem.

A final difficulty has to do with how the size of the computational subregion affects recognition. We adopted the concept of a subregion so that spatial frequency analysis would not be global, there being no evidence for the kind of global spatial frequency processes that underlie Fourier analysis. We envision that the size of the subregion is controlled by selective attention. Such a process, for which there is psychophysical evidence, creates a window around an object, minimizing interference from nearby objects (Sagi and Julesz, 1986; Sperling and Weichselgartner, 1995). The covert movement of an attentional window (not involving saccades) as objects are serially searched has recently been observed electrophysiologically (Buschman and Miller, 2009). Indeed, the reason for an attentional window may be to allow recognition of objects without interference from nearby objects. It remains possible, however, that subregions might be hard-wired and that attention is not required; in this case, the problem of interference has be dealt with by brute force, i.e., by having subregions of different size so that, by chance, a given subregion would frame the object to be recognized.

An important issue in any recognition process is tolerance to noise and distortion. Attractor networks (Hopfield, 1982) are generally seen as a solution to this problem but suffer from a limitation: scaled and rotated inputs produce different patterns for which there must be separate attractors. Given the limited memory capacity of such networks, treating each variant as a different pattern is problematic. Thus, the capability of attractor networks will be greatly enhanced if they work upon the invariant output of our two-stage transform. Additional processes that are important for recognition use top-down contextual processes. A theoretical model has been formulated that shows how the interactions of top-down and bottom-up processes can account for fundamental properties of recognition: the logarithmic dependence of recognition time of set size and the speeding of recognition by contextual cues (Graboi and Lisman, 2003). However, that model assumes that letters are in a canonical form and thus requires a front end to make them so. The model proposed here (modified to include attractors) could serve as such a front end.

Our model leads to a testable prediction. Consider the simple case of an input pattern with two spatial frequencies. The first-stage transform will produce output at these frequencies. Because the output pattern is logarithmic, the distance between the regions of high output will be proportional to the ratio of the frequencies. In the brain region that encodes the second-stage transform, cells will be excited that represent this distance. These cells will thus be tuned to the ratio of spatial frequencies in the input pattern and will be unaffected by changing the input frequencies, so long as they are changed proportionally. The discovery of such cells would directly link the computations that produce invariance to spatial frequency analysis.

Conclusion

The algorithm we describe provides a principled solution to the invariance problem based on spatial frequency analysis, log-polar mapping, and sequential use of the same transform. In spirit, the algorithm is similar to the Fourier-Mellin transform used in machine vision, but unlike that transform does not require a biologically unrealistic 2-D Fourier transform of the entire image. This is replaced in our algorithm by orientation-sensitive cells similar to those in V1 that produce a form of local spatial frequency analysis (interval detection). Unlike the Fourier transform, which is based on analysis in only x and y, our algorithm makes use of information at all orientations. The existence of a simple, biologically plausible solution to the invariance problem will, we hope, inspire efforts to test this class of models. Give the multitude of visual areas in the visual system and the different requirements for vision, it seems unlikely that any one analysis strategy will be used on a system-wide basis. Thus an important step would be to identify those parts of the visual system that compute and/or utilize invariant representations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dan Pollen for comments on the manuscript. We thank Antonella DeLillo for development of an earlier model of invariant recognition, the limitations of which inspired the current version. This work was supported by NIH/NIDA CRCNS Grant R01DA027807, IGERT Grant 0549390, NIH Computational Neuroscience Training Grant (CNTG) T90 DA032432, and NIH grant T32 NS07292.

References

  1. Adams D. L., Horton J. C. (2003). A precise retinotopic map of primate striate cortex generated from the representation of angioscotomas. J. Neurosci. 23, 3771–3789 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Andrews B. W., Pollen D. A. (1979). Relationship between spatial frequency selectivity and receptive field profile of simple cells. J. Physiol. 287, 163–176 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Arditi A. R., Anderson P. A., Movshon J. A. (1981). Monocular and binocular detection of moving sinusoidal gratings. Vision Res. 21, 329–336 10.1016/0042-6989(81)90160-7 [DOI] [PubMed] [Google Scholar]
  4. Bonhoeffer T., Grinvald A. (1993). The layout of iso-orientation domains in area 18 of cat visual cortex: optical imaging reveals a pinwheel-like organization. J. Neurosci. 13, 4157–4180 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Buschman T. J., Miller E. K. (2009). Serial, covert shifts of attention during visual search are reflected by the frontal eye fields and correlated with population oscillations. Neuron 63, 386–396 10.1016/j.neuron.2009.06.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buxhoeveden D. P., Casanova M. F. (2002). The minicolumn hypothesis in neuroscience. Brain 125, 935–951 10.1093/brain/awf110 [DOI] [PubMed] [Google Scholar]
  7. Casasent D., Psaltis D. (1976a). Position, rotation, and scale invariant optical correlation. Appl. Opt. 15, 1795–1799 10.1364/AO.15.002631 [DOI] [PubMed] [Google Scholar]
  8. Casasent D., Psaltis D. (1976b). Scale invariant optical correlation using Mellin transforms. Opt. Commun. 17, 59–63 10.1016/0030-4018(76)90249-2 [DOI] [PubMed] [Google Scholar]
  9. Cavanagh P. (1984). “Image transforms in the visual system,” in Figural Synthesis, eds Dodwell P. C., Caelli T. (Hillsdale, NJ: Lawrence Erlbaum Associates; ), 185–218 [Google Scholar]
  10. Cavanagh P. (1985). “Local log polar frequency analysis in the striate cortex as a basis for size and orientation invariance,” in Models of the Visual Cortex, eds Rose D., Dobson V. G. (London: John Wiley & Sons; ), 85–95 [Google Scholar]
  11. Copper L. A. (1975). Mental rotation of random two-dimensional shapes. Cogn. Psychol. 7, 20–43 10.1016/0010-0285(75)90003-1 [DOI] [Google Scholar]
  12. Cover T., Hart P. (1967). Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 13, 21–27 10.1109/TIT.1967.1053964 [DOI] [Google Scholar]
  13. De Valois K. K., Tootell R. B. (1983). Spatial-frequency-specific inhibition in cat striate cortex cells. J. Physiol. 336, 359–376 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. De Valois R. L., Albrecht D. G., Thorell L. G. (1982). Spatial frequency selectivity of cells in macaque visual cortex. Vision Res. 22, 545–559 10.1016/0042-6989(82)90112-2 [DOI] [PubMed] [Google Scholar]
  15. Elliffe M. C., Rolls E. T., Stringer S. M. (2002). Invariant recognition of feature combinations in the visual system. Biol. Cybern. 86, 59–71 10.1007/s004220100284 [DOI] [PubMed] [Google Scholar]
  16. Felleman D. J., Van Essen D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47 10.1093/cercor/1.1.1 [DOI] [PubMed] [Google Scholar]
  17. Gabbiani F., Krapp H. G., Hatsopoulos N., Mo C.-H., Koch C., Laurent G. (2004). Multiplication and stimulus invariance in a looming-sensitive neuron. J. Physiol. Paris 98, 19–34 10.1016/j.jphysparis.2004.03.001 [DOI] [PubMed] [Google Scholar]
  18. Graboi D., Lisman J. (2003). Recognition by top-down and bottom-up processing in cortex: the control of selective attention. J. Neurophysiol. 90, 798–810 10.1152/jn.00777.2002 [DOI] [PubMed] [Google Scholar]
  19. Gross C. G., Bender D. B., Rocha-Miranda C. E. (1969). Visual receptive fields of neurons in inferotemporal cortex of the monkey. Science 166, 1303–1306 10.1126/science.166.3910.1303 [DOI] [PubMed] [Google Scholar]
  20. Guyonneau R., Kirchner H., Thorpe S. J. (2006). Animals roll around the clock: the rotation invariance of ultrarapid visual processing. J. Vis. 6, 1008–1017 10.1167/6.10.1 [DOI] [PubMed] [Google Scholar]
  21. Hamm J. P., McMullen P. A. (1998). Effects of orientation on the identification of rotated objects depend on the level of identity. J. Exp. Psychol. Hum. Percept. Perform. 24, 413–426 10.1037/0096-1523.24.2.413 [DOI] [PubMed] [Google Scholar]
  22. Hopfield J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558 10.1073/pnas.79.8.2554 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hubel D. H., Wiesel T. N. (1962). Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. (Lond.) 160, 106–154 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hung C. P., Kreiman G., Poggio T., DiCarlo J. J. (2005). Fast readout of object identity from macaque inferior temporal cortex. Science 310, 863–866 10.1126/science.1116739 [DOI] [PubMed] [Google Scholar]
  25. Issa N. P., Trepel C., Stryker M. P. (2000). Spatial frequency maps in cat visual cortex. J. Neurosci. 20, 8504–8514 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kepecs A., Raghavachari S. (2007). Gating information by two-state membrane potential fluctuations. J. Neurophysiol. 97, 3015–3023 10.1152/jn.01242.2006 [DOI] [PubMed] [Google Scholar]
  27. Knowlton B. J., McAuliffe S. P., Coelho C. J., Hummel J. E. (2009). Visual priming of inverted and rotated objects. J. Exp. Psychol. Learn. Mem. Cogn. 4, 837–848 [DOI] [PubMed] [Google Scholar]
  28. Li N., Cox D. D., Zoccolan D., DiCarlo J. J. (2009). What response properties do individual neurons need to underlie position and clutter “invariant” object recognition? J. Neurophysiol. 102, 360–376 10.1152/jn.91342.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Logothetis N. K., Pauls J., Bulthoff H. H., Poggio T. (1994). View-dependent object recognition by monkeys. Curr. Biol. 4, 401–414 10.1016/S0960-9822(00)00089-0 [DOI] [PubMed] [Google Scholar]
  30. Lowe D. G. (1999). “Object recognition from local scale-invariant features,” in Proceedings of the Seventh IEEE International Conference on Computer Vision, Vol. 2, Corfu, 1150–1157 10.1109/ICCV.1999.790410 [DOI] [Google Scholar]
  31. Lowe D. G. (2004). Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 60, 91–110 10.1023/B:VISI.0000029664.99615.94 [DOI] [Google Scholar]
  32. Mountcastle V. B. (1997). The columnar organization of the neocortex. Brain 120(Pt 4), 701–722 10.1093/brain/120.4.701 [DOI] [PubMed] [Google Scholar]
  33. Movshon J. A., Thompson I. D., Tolhurst D. J. (1978). Spatial and temporal contrast sensitivity of neurones in areas 17 and 18 of the cat’s visual cortex. J. Physiol. 283, 101–120 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Olshausen B. A., Anderson C. H., Van Essen D. C. (1993). A neurobiological model of visual attention and invariant pattern recognition based on dynamic routing of information. J. Neurosci. 13, 4700–4719 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Perrett D. I., Rolls E. T., Caan W. (1982). Visual neurones responsive to faces in the monkey temporal cortex. Exp. Brain Res. 47, 329–342 10.1007/BF00239352 [DOI] [PubMed] [Google Scholar]
  36. Pollen D. A., Przybyszewski A. W., Rubin M. A., Foote W. (2002). Spatial receptive field organization of macaque V4 neurons. Cereb. Cortex 12, 601–616 10.1093/cercor/12.6.601 [DOI] [PubMed] [Google Scholar]
  37. Riesenhuber M., Poggio T. (1999). Hierarchical models of object recognition in cortex. Nat. Neurosci. 11, 1019–1025 [DOI] [PubMed] [Google Scholar]
  38. Riesenhuber M., Poggio T. (2000). Models of object recognition. Nat. Neurosci. 3(Suppl.), 1199–1204 10.1038/81479 [DOI] [PubMed] [Google Scholar]
  39. Rodrigues J., Hans du Buf J. M. (2009). A cortical framework for invariant object categorization and recognition. Cogn. Process. 10, 243–261 10.1007/s10339-009-0262-2 [DOI] [PubMed] [Google Scholar]
  40. Sachs M. B., Nachmias J., Robson J. G. (1971). Spatial-frequency channels in human vision. J. Opt. Soc. Am. 61, 1176–1186 10.1364/JOSA.61.001176 [DOI] [PubMed] [Google Scholar]
  41. Sagi D., Julesz B. (1986). Enhanced detection in the aperture of focal attention during simple discrimination tasks. Nature 321, 693–695 10.1038/321693a0 [DOI] [PubMed] [Google Scholar]
  42. Salinas E., Abbott L. F. (1997). Invariant visual responses from attentional gain fields. J. Neurophysiol. 77, 3267–3272 [DOI] [PubMed] [Google Scholar]
  43. Serre T., Wolf L., Bileschi S., Riesenhuber M., Poggio T. (2007). Robust object recognition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 29, 411–426 10.1109/TPAMI.2007.56 [DOI] [PubMed] [Google Scholar]
  44. Shams L., von der Malsburg C. (2002). The role of complex cells in object recognition. Vision Res. 42, 2547–2554 10.1016/S0042-6989(02)00130-X [DOI] [PubMed] [Google Scholar]
  45. Shapley R., Lennie P. (1985). Spatial frequency analysis in the visual system. Annu. Rev. Neurosci. 8, 547–583 10.1146/annurev.ne.08.030185.002555 [DOI] [PubMed] [Google Scholar]
  46. Sperling G., Weichselgartner E. (1995). Episodic theory of the dynamics of spatial attention. Psychol. Rev. 102, 503–532 10.1037/0033-295X.102.3.503 [DOI] [Google Scholar]
  47. Tanaka K. (1996). Inferotemporal cortex and object vision. Annu. Rev. Neurosci. 19, 109–139 10.1146/annurev.ne.19.030196.000545 [DOI] [PubMed] [Google Scholar]
  48. Tootell R. B., Silverman M. S., Switkes E., De Valois R. L. (1982). Deoxyglucose analysis of retinotopic organization in primate striate cortex. Science 218, 902–904 10.1126/science.7134981 [DOI] [PubMed] [Google Scholar]
  49. von der Heydt R., Peterhans E., Dursteler M. R. (1992). Periodic-pattern-selective cells in monkey visual cortex. J. Neurosci. 12, 1416–1434 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wiskott L., Sejnowski T. J. (2002). Slow feature analysis: unsupervised learning of invariances. Neural. Comput. 14, 715–770 10.1162/089976602317318938 [DOI] [PubMed] [Google Scholar]
  51. Yatagai T., Choji K., Saito H. (1981). Pattern classification using optical Mellin transform and circular photodiode array. Opt. Commun. 38, 162–165 10.1016/0030-4018(81)90314-X [DOI] [Google Scholar]

Articles from Frontiers in Computational Neuroscience are provided here courtesy of Frontiers Media SA

RESOURCES