Nanochannel Confinement: DNA Stretch Approaching Full Contour Length

Abstract

Fully stretched DNA molecules are becoming a fundamental component of new systems for comprehensive genome analysis. Among a number of approaches for elongating DNA molecules, nanofluidic molecular confinement has received enormous attentions from physical and biological communities for the last several years. Here we demonstrate a well-optimized condition that a DNA molecule can stretch almost its full contour length: the average stretch is 19.1 μm ± 1.1 μm for YOYO-1 stained λ DNA (21.8 μm contour length) in 250 nm × 400 nm channel, which is the longest stretch value ever reported in any nanochannels or nanoslits. In addition, based on Odijk’s polymer physics theory, we interpret our experimental findings as a function of channel dimensions and ionic strengths. Furthermore, we develop a Monte Carlo simulation approach using a primitive model for the rigorous understandings of DNA confinement effects. Collectively, we present more complete understanding of nanochannel confined DNA stretching via the comparisons to computer simulation results and Odijk’s polymer physics theory.

Introduction

Many of the recent advances in the genomic sciences are directly linked with new molecular insights and tools that manipulate and analyze DNA molecules in new ways.^{1, 2} This is evidenced by the explosion of new platforms for DNA sequencing,^{3, 4} analyzing molecular libraries comprising single DNA molecules, which are promising the commodization of sequence information.⁵ Even newer sequencing approaches are leveraging the direct analysis of individual DNA molecules for engendering “third generation sequencing”.^6–9 A critical advantage of sequencing systems using single molecule analytes is that they obviate the need for template amplification, a feature that not only saves time and reduces reagent costs, but more importantly, points the way for the development of new approaches offering significantly longer read lengths. Such advantages potentiate comprehensive genome analysis that elucidates all parts of a genome for careful analysis. Unfortunately, most contemporary single DNA molecule sequencing approaches are limited to the analysis of short DNA fragments usually with less than hundreds of base pairs.¹

On the other hand, stretched genomic DNA molecules from tens of kilobases to megabases (μm ~ mm in length) are promising analytes because they intrinsically reveal the location of each sequence read along the same, long DNA molecule.^9–12 These advantages for mapping, though not sequencing, entire genomes were originally pioneered through development of the Optical Mapping System.^13–17 Briefly, Optical mapping generated physical genomic maps have been utilized for guiding sequence assembly for numerous genome projects,¹⁸ and detecting large scale genomic variations,^{19, 20} and DNA methylation.²¹ In addition to physical genomic maps, elongated DNA molecules on the surface have also been utilized as platforms for biochemical studies such as RNA polymerase on DNA backbones,²² and also extended to a novel sequencing technology like optical sequencing.⁹ Even though elongated DNA molecules deposited on the surface have been versatile analytes for many different biochemical applications, they have intrinsic limitations due to the surface fixation and difficulties in controlling surface properties. In order to overcome these limitations caused by DNA fixation on surface, we have recently developed nano-/microfluidic approaches for dynamic elongation of single DNA molecules.^{10, 23} Over the surface fixation, these fluidic components for DNA elongation offer the advantage of facile integration into more sophisticated microfluidic devices as a micro total analytical system (μTAS).

Nanochannel confined DNA elongation is now being actively investigated to the direction of high-throughput DNA analysis with high resolution.^{10, 24–26} Toward high resolution DNA analysis, the first goal of DNA elongation in nanochannels is to attain fully stretched DNA molecules without knots or hairpins. Simultaneously, to achieve a high-throughput analytical system, nanochannels should be large enough for efficient DNA loading using a conventional nanofabrication technology instead of superb nanotechnology difficult to follow. In addition, for practical biological applications, disposable and flexible polydimethyl siloxane (PDMS) material is more promising than any other solid materials.²⁷ Accordingly, here we have pursued to design an optimum system for long stretch of DNA molecules in reasonable nanochannel dimensions by using practical materials.

For a system design, it is naturally expected that DNA elongation can be accomplished by reducing dimensions of nanoconfinement.²⁸ Nanochannels would be ideal if they are slightly larger than the diameter of double helical DNA molecules, which would result in the stretching up to their full contour length. However, there are limitations in reducing channel dimensions: First, the fabrication of very small nanochannels with long length is extremely challenging.²⁹ In general, smaller nanochannels require more advanced and more expensive nanofabrication technologies. Second, the DNA loading efficiency into very small nanochannels is dramatically reduced.³⁰ As an alternative way of reducing the channel dimension, the DNA stretch can be enhanced by increasing the persistence length of DNA or by increasing polymer’s stiffness, which was previously demonstrated by lowering ionic strengths.¹⁰ However, the optimum condition for channel dimension and ionic strength has yet to be found. Accordingly, our overarching goal in this study here is to achieve fully stretched DNA molecules by adjusting channel dimensions and ionic strengths with the aid of theory and computer simulation.

RESULTS

DNA stretching mediated by nanoconfinement geometry and ionic strength

Our scheme for increasing DNA stretch was to both minimize nanochannel dimensions using PDMS replica molding techniques and buffer ionic strength conditions. We first fabricated a series of PDMS nanoslit devices using interference lithography and replica molding with the following dimensions (nm; width × height): 250 × 100, 250 × 150, 250 × 250, 400 × 250, 600 × 250, 800 × 250, 900 × 250; the length of each channel is about 140 μm. Among them, the 250 nm × 250 nm (Fig. 1A) is the smallest dimension of nanochannels into which we have successfully and reproducibly loaded λ DNA molecules (see Experimental).

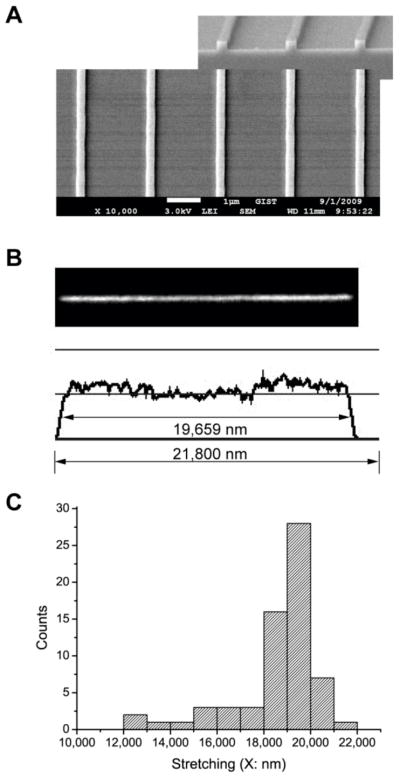
Fig. 1.

(A) Scanning electron micrograph of 250 nm × 250 nm channel’s template on silicon wafer fabricated by interference lithography. The nanochannel template is utilized for replica molding of PDMS nanochannels into which DNA molecules are loaded. (B) Fluorescence micrograph and fluorescence intensity profile of an individual λ DNA molecule (48.5 kb, contour length is 21.8 μm; YOYO-1 stained) in a nanochannel (250 nm × 250 nm). Molecule length is 19.7 μm, which is 90% of its contour length of 21.8 μm. (C) Histogram of DNA stretches in 250 nm × 250 nm channels. The average length is 18.7 μm ± 1.9 μm but the most abundant range is 19 μm to 20 μm.

Very low ionic strength conditions were established by careful illumination conditions instead of using anti-photobleaching agents which increase ionic strength. In our previous report,¹⁰ we boosted DNA stretch (X/L) to 0.60 (X is defined as the average apparent length and L is the dye adjusted polymer contour length, L, 21.8 μm for λ DNA; a stretch of 1.0 indicates complete elongation) in nanoslits (1000 nm × 100 nm) by decreasing ionic strength of loading buffer. However, there were limitations of stretching because we didn’t use high resolution lithography technology. In addition, we also found that we could not further increase DNA stretching because β-mercaptoethanol, an anti-photobleaching agent, affects ionic strength via protonic dissociation from a thiol group (pKa of 9.6).³¹ Unfortunately, anti-bleaching agents are an essential part of fluorescence imaging for preventing photobleaching and photolysis, but generally, they perturb ionic strength: e.g., dithiothreitol (DTT; pKa=9.2), ascorbic acid (vitamin C; pKa=4.2), and the oxygen scavenger system using glucose oxidase and catalase.³¹ Accordingly, we developed an imaging approach obviating the need for anti-photobleaching agents through judicious illumination conditions (see Experimental).

Fig. 1B presents an image of the λ DNA molecule in 1/40xTE solution (1xTE: 10 mM Tris and 1mM EDTA titrated with HCl to pH 8.0). The molecule is 19.7 μm long (X/L= 0.90 for YOYO-1 stained λ DNA), examined with an intensity profile (Fig. 1B). The intensity profile analysis not only gives the estimation of molecular length, but also allows identifying DNA’s conformational details, which facilitates easy differentiation of fully elongated molecules from folded ones. For example, the intensity profile in Fig. 1B depicts a little higher intensity at the ends of molecule, which can be interpreted as the ends of the DNA molecule are more relaxed compared to the well-stretched central portions, which may be due to polymer ends having more entropic freedom than internal segments.^{23, 32} Using this method, we examined a total 66 stretched λ DNA molecules in the 250 × 250 nm nanochannels as the histogram presented in Fig. 1C. The most abundant range is from 19 μm to 20 μm, whereas the average stretch is 18.7 μm with the standard deviation of 1.9 μm.

For a highly stretched polymer chain, as what we studied here, Odijk developed a model to explain the deflection-dominant polymer elongation in nanochannels using a scaling relationship in 1983,³³ and recently refined his model to an analytical equation as given by^{10, 34}

$$X/L=1-0.085\left({\left(\frac{A}{P}\right)}^{2/3}+{\left(\frac{B}{P}\right)}^{2/3}\right)$$ (1)

where X is the observed elongated length, L is the polymer contour length, A and B are, respectively, channel width and height, and P is polymer persistence length. Polymer persistence length (P) can be calculated from ionic strength by an equation developed by Odijk,³⁵ Skolnick and Fixman (OSF).³⁶ This OSF equation is given by

$$P=P_o+P_{el}=p_o+\frac{1}{4{\kappa }^2{l}_B}=P_o+0.0324I^{-1}\text{nm}$$ (2)

where P_o is the non-electrostatic intrinsic persistence length due to base stacking, P_el is the electrostatic persistence length due to intrachain repulsion, κ is the inverse of the Debye-Hückel screening length, l_B is the Bjerrum length (0.7 nm in water) and I is ionic strength of the solution.³⁷ Odijk’s equation (Eq. 1) combined with the OSF equation (Eq. 2) can predicts the DNA stretching in nanochannels at a specific ionic strength for various channel dimensions.

Although the OSF equation (Eq. 2) uses a term for ionic strength, to the best of our knowledge, it has never been experimentally validated for multivalent ions. Please note that Skolnick and Fixman, and Bauman et. al. used only monovalent ions (e.g. NaCl) to validate the OSF equation.^{36, 37} Furthermore, Bauman et. al. proved that the OSF equation is not applicable to multivalent cations,³⁷ since multiple charges can collapse DNA structure.³⁸ Accordingly, we have concluded that it may not be appropriate to use calculated ionic strength from the buffer components. Instead, we measured the conductivity of diluted TE buffer and compared its conductivity value with equivalent sodium chloride (NaCl) solution. In the case of 1/40xTE, the conductivity corresponds to 0.12 mM NaCl solution, which roughly agrees with positive Tris ion concentration (0.13 mM) in 1/40xTE solution. Hence, in this paper we use 0.12 mM as the ionic strength for 1/40xTE solution.

Before calculating persistence length from the ionic strength, we have to determine another term in the OSF equation (Eq. 2), non-electrostatic intrinsic persistence length (P_o). For native DNA, P_o is known to be 50 nm,³⁷ but there are three different opinions for P_o of DNA stained with bis-intercalator YOYO-1 (e.g. 66 nm,³⁹ 12 nm,⁴⁰ and 44 nm⁴¹). The idea of 66 nm originated from the assumption that P_o may increase in the same ratio as DNA contour length increases.³⁹ It is well-known that the staining of YOYO-1 increases the contour length of DNA by about 30% because dyes intercalate into stacks of base pairs; for example, native λ DNA has the contour length of 16.5 μm (0.34 nm × 48502 base pairs), but YOYO-1 intercalated λ DNA has the contour length of 21.8 μm. On the other hand, an optical trapping experiment reported that P_o could be 12 nm,⁴⁰ but this value seems too small to explain other experimental observations. Recently, Zhang et. al. reported that P_o should be 44 nm according to their calculation which takes the effect of positive charges in YOYO-1 molecules into account.⁴¹ They claimed that P_o of 44 nm agreed well with their experimental observations. At the ionic strength of 0.12 mM, the OSF equation predicts the DNA persistence length (P) would be 320 nm, 336 nm, 282 nm, 314 nm for P_o=50 nm, 66 nm, 12 nm, and 44 nm, respectively. Interestingly, whatever value used for P_o except 12 nm, the calculated stretch of the λ DNA by Odijk’s theory (Eq. 1) is about 18.7 μm (X/L = 0.86), which agrees well with our experimental finding (18.7 μm ±1.9 μm in the 250 nm × 250 nm nanochannel). Therefore, we use 50 nm as a primary P_o, with additional graphs drawn by using 44 nm and 66 nm P_o values (see Fig 2 and Fig 3).

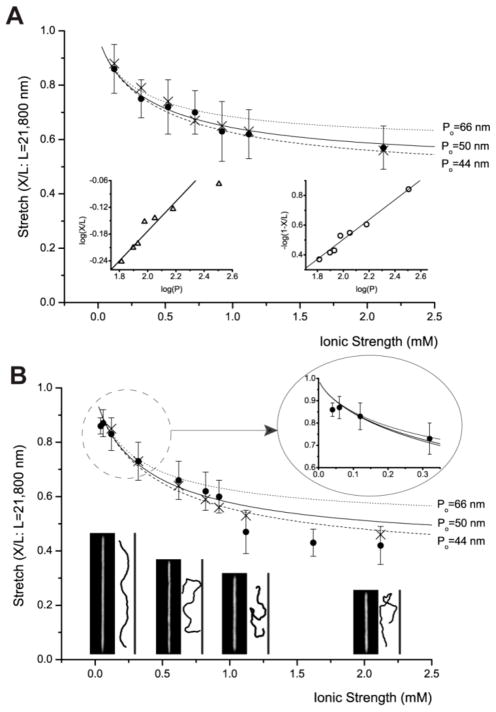
Fig. 2.

Ionic strength dependence of DNA stretching. These graphs include experiment (●: closed circle) and simulation (×: cross) with graphs of Odijk’s equation (Eq. 1), in which persistence length P is determined by OSF equation (Eq. 2). However, this equation is drawn in three different graphs using different non-electrostatic intrinsic persistence length (P_o) values such as 50 nm, 66 nm,³⁹ and 44 nm.⁴¹ Each experimental data point represents measurement from 30 to 200 molecules; error bars show standard deviations of measured lengths. (A) DNA stretching in 250 nm × 250 nm channels: The left inset depicts a log-log plot of de Gennes relationship of X/L≈ (wP/D²)^1/3, and the right inset depicts a log-log plot of Odijk’s equation for square channels 1- X/L=0.085×2× (A/P)^2/3. This linear relationship shows R²=0.98. (B) DNA stretching in 250 nm × 400 nm channels: magnified plot describes the details of low ionic strengths (1/80xTE and 1/120xTE). Representative fluorescence images of DNA molecules are compared with simulation snapshots at four ionic strengths: 0.12 mM, 0.62 mM, 1.12 mM, and 2.12 mM. Simulation snapshots are magnified for better comparison.

Fig. 3.

Width dependence of DNA stretches with the same height of 250 nm at the fixed ionic strength (1/40xTE and 0.2 mM NaCl). (A) The graph shows experiment (●: closed circle) and simulation (×: cross) with three graphs of Odijk’s equation (Eq. 1) using three different nonelectrostatic intrinsic persistence length (P_o) values such as 50 nm, 66 nm,³⁹ and 44 nm.⁴¹ Each experimental data point represents measurement from 40 to 90 molecules; error bars show standard deviations of measured lengths. Molecular length is determined by intensity profile analysis illustrated in Fig. 1. We do not include error bars of simulation result because their standard deviation is very small (≤ 1%) (B) Scanning electron micrographs of 250 nm × 400, 600, 800, 900 nm channels’ template on silicon wafer fabricated by interference lithography. The nanochannel templates were utilized for replica molding of PDMS nanochannels for DNA loading.

Given a specific ionic strength, we demonstrate that Odijk’s equation (Eq. 1) with the OSF equation (Eq. 2) can predict DNA stretch in a nanochannel with good agreement to experiments. This theory also predicts that the DNA stretch would decrease as ionic strength increase in a nanochannel, which should be validated by experiments. In our previous report,¹⁰ we controlled the ionic strengths by the degree of dilution of 1xTE, but the multivalent ionic state of EDTA makes the interpretation more complicated as mentioned in a previous paragraph. Hence, here we controlled ionic strengths by adding NaCl (0.2 mM~ 2.0 mM) into the DNA solution of 1/40xTE. In addition, we did not use anti-bleaching agents to avoid the complication of calculating ionic strengths. As shown in Fig. 2A, we clearly demonstrate that the DNA stretch decreases with the increase of ionic strength as predicted by the Odijk’s theory despite the fact that its validity has been disputed.^{34, 41–43} For this analysis, we used 50 nm as a primary P_o, but, we also present predictions with different P_o such as 66 nm, and 44 nm for comparison. Since all the graphs using three P_o stay in our experimental error ranges, we cannot tell which value of P_o is correct for YOYO-1 stained DNA from these data.

In addition, we compared our experimental results with de Gennes’ scaling blob theory: X/L≈ (wP/D²)^1/3; w: molecular width, D: diameter of channel.^{28, 44} As shown in the left inset of Fig. 2A, the log-log plot (X/L vs. P) suggests that three data points of short persistence lengths seem to follow 1/3 scaling relation, but the other four points of long persistence lengths obviously deviate from the scaling relation. For direct comparison, Odijk’s equation (Eq. 1) for rectangular channels has been rewritten to a form for square channels like 1-X/L=0.085×2×(A/P)^2/3.

This rewritten expression is equivalent to Odijk’s original scaling relationship:^{33, 34}

$$X/L=cos\theta \cong 1-\frac{{\theta }^2}{2}\mathit{where}{\theta }^2\approx {\left(\frac{A}{P}\right)}^{2/3}$$ (3)

As shown in the right inset of Fig 2A, the log-log plot (1-XL vs. P) shows better linearity (R² = 0.98). These analyses indicate that Odijk’s analytical equation describes highly-stretched DNA molecules in nanochannels in a more appropriate manner than de Gennes scaling relationship.

We extended the theory validation from a square channel (250 nm × 250 nm) to a rectangular channel (250 nm × 400 nm). Interestingly, Odijk’s equation (Eq. 1) is only valid below 1 mM, and three points above 1 mM show distinct deviations. Notice that all deviated stretches are less than 50% of its contour length (Fig. 2B). This deviation may suggest the existence of a theoretical regime boundary where polymer’s deflection is not dominant anymore.

As opposed to adding more salts, we added more water to dilute 1/40xTE to 1/80xTE (see magnified graph in Fig. 2B). In this condition, we observed that the average stretch of λ DNA is 19.1 μm ± 1.1 μm in 250 nm × 400 nm channels that is the longest average length ever reported in any nanochannels, though it is little lower than Odijk’s prediction of 19.3 μm. To get a longer DNA stretch, we attempted loading 1/80xTE DNA solution into 250 nm × 250 nm channels, but we could not succeed in DNA loading. From these results, it seems that DNA elongates more in the condition of 1/80xTE in 250 nm × 400 nm channels comparing to 1/40xTE in 250 nm × 250 nm channels shown in Fig. 1. However, histogram analysis reveals that although the dominant peaks are located in the range from 19 μm to 20 μm in both conditions, the number of short stretched molecules is fewer in the condition of 1/80xTE in 250 nm × 400 nm nanochannels (data not shown): i.e., the reduction in number of short stretching molecules is the actual cause of the longest average stretching in 250 nm × 400 nm channels.

To increase DNA stretch, we dropped the TE concentration to 1/120xTE; we measured conductivity to confirm its ionic strength. As opposed to our expectation, the average stretch actually decreased to 18.7 μm ± 0.7 μm whereas Odijk’s theory predicts 19.9 μm at 1/120xTE in 250 nm × 400 nm channels. In addition, we also attempted more diluted conditions like 1/240xTE and others, but we haven’t got any success in loading DNA into nanochannels. Now we haven’t fully understood why stretches does not reach Odijk’s prediction at 1/120x TE and why DNA molecules do not enter nanochannels at very low ionic strength conditions. However, we suspect that the deviation of Odijk’s prediction and unsuccessful loadings at very low ionic strengths in 250 nm × 400 nm channels may be related to unsuccessful loading of smaller channels previously mentioned in this paper (e.g. 250 nm × 100 nm with 1/40x TE). Consequently, these observations imply that more elaborate theoretical models are necessary for the complete understanding.

Monte Carlo Simulation

Computer simulations provide a useful means of investigating the structure of nanochannel-confined DNA at low ionic strengths. Past simulations of confined DNA have been largely focused on high ionic strength systems.^{45, 46} Some of our observations for low ionic strengths, however, remain to be explained.^{41, 47} In this work we use Monte-Carlo simulations of a “primitive” model of DNA molecule in a nanochannel. In this model, the DNA molecule is represented as a linear chain of N charged spherical monomers, with diameter σ and charge −Ze (Z and e are the charge valence and the elementary charge). The rectangular nanochannel is represented by hard walls having the same dimensions as those employed in our experiments. In this study N and σ are set to 256 and 10 nm, respectively. The contour length of our model DNA is approximately 2.56 μm, consistent with our experiments. The monomer charge valence Z is set to 20 because it is known that the bare charge density of YOYO-1 stained DNA is around −2 e/nm.⁴¹

The interaction between monomers is the sum of hard-sphere (U_hs) and electrostatic (U_elec) interactions, which are respectively defined as

$$U_{hs}(r)=\{\begin{array}{ll}\hfill \infty \hfill & \hfill \text{if}r\le \sigma \hfill \\ \hfill 0\hfill & \hfill \text{otherwise}\hfill \end{array}\text{and}\frac{U_{\mathit{elec}}(r)}{k_{B}T}=\frac{I_B{Z}^{2}exp(-\kappa r)}{r}$$ (4)

where k_B, T, l_B, and κ are, respectively, the Boltzmann constant, the absolute temperature, the Bjerrum length and the inverse of the Debye length. The Bjerrum length, defined as l_B ≡ e²/(4πε₀ εk_BT) (ε₀ and ε are vacuum permittivity and the dielectric constant of a solution), is the separation at which the electrostatic interaction between two elementary charges is comparable in magnitude to the thermal energy scale, k_BT, (= 0.6 kcal/mol at T=298K), and is approximately 0.7 nm in water at T = 298 K. The Debye length, κ⁻¹, controls the range of the electrostatic interaction in ionic solutions and is given by ${\kappa }^{-1}=1/\sqrt{8\pi l_B{N}_{A}I}$, where N_A and I are Avogadro’s constant and the ionic strength of the solution, respectively. The electrostatic interaction is calculated for all pairs of charged monomers without cutoff radius. In addition to these interactions, each monomer experiences a hard-core interaction with the rectangular nanochannel, i. e., it is not allowed to approach the channel surface closer than σ/2.

An additional angle potential (U_angle) is used to impart the stiffness to the chains. That potential is given by

$$U_{\mathit{angle}}(\theta )=k_{\mathit{angle}}{\left(cos\theta +1\right)}^2$$ (5)

where θ is the angle between three successive bonds in the DNA molecule and k_angle is the force constant of the angle potential. The force constant of the angle potential, k_angle, is, in fact, the only parameter in our primitive DNA model and was fitted using experimental data in Fig. 2A to give 90 k_BT (= 54 kcal/mol).

Using this primitive model, we performed canonical ensemble Monte Carlo (MC) simulations to sample equilibrium configurations of the DNA molecule in a nanochannel. Trial moves included reptation, crank-shaft, continuum configurational bias, and rotations.^48–51 Once a single DNA molecule was randomly inserted into the nanochannel, each system was equilibrated until both the system potential energy and the DNA stretch attained a steady-state value. Production runs consisted of a total of 10⁹ MC steps, and were sampled every 10⁵ steps to generate 10⁴ equilibrium configurations. The results given in this study therefore represent averages of at least 10⁴ configurations; the error bars, obtained from block averaging, correspond to one standard deviation from the average. More information about model parameterization and simulation methods can be found elsewhere.⁵²

Simulation results are compared with experimental findings and Odijk’s theory in Fig. 2. For the case of the DNA stretch in the 250 nm × 250 nm nanochannel (Fig. 2A), the simulation results exhibit good agreement with both experiments and Odijk’s theory. Some deviations are seen at low ionic strengths (< 0.5 mM). This agreement is expected in that parameter k_angle in the primitive model was fitted to these data. For the 250 nm × 400 nm nanochannel (Fig. 2B), our simulation results with a primitive model provide better agreement with experiment than Odijk’s theory, which significantly overestimates the DNA stretch at high ionic strengths. However, our simulations do not reproduce the transition behavior near I = 1.0 mM that is seen in experiments.

Fig. 2B provides a comparison of the results of simulations with fluorescent images of DNA molecules. Note that simulation snapshots are magnified for better comparison to experiment. As expected, at very low ionic strength (I = 0.12 mM), the DNA molecule is extended in the channel direction and exhibits a smooth sinusoidal shape. At I = 0.62 mM, it starts to exhibit hairpin-like structures, but the curvature of the loop is still smooth, which indicates that the electrostatic repulsion between monomers persists and prevents sharp turns. Note that the Debye length (about 13 nm) at this ionic strength is slightly longer than the monomer diameter. At higher ionic strengths (> 1 mM), the electrostatic repulsion is significantly screened, and the DNA molecule shows several hairpin structures that include sharp turns.

At this point it is important to emphasize some of the limitations of our primitive model. First, it does not consider any specific interaction between monomers or between monomers and the nanochannel other than mean-field type electrostatic interactions and excluded volume interactions (hard-sphere potential). Second, our model does not include explicit water molecules or explicit salt ions. The delicate interplay of multivalent ions in the DNA moiety or the hydrophobic behavior of the DNA molecule in a nanochannel cannot be properly treated in our model. Third, the DNA length in this study is about 10 times shorter than that employed in experiments. It is possible that wavelength modes such as multi-stacking longer than the DNA length in our model may play an important role in the real system. We will present the effect of the DNA length on the structural behavior of DNA in a nanochannel elsewhere.⁵²

So far, we have validated Odijk’s equation with our experimental observations and our computer simulation results by using two different nanochannels: a square channel 250 nm × 250 nm and a rectangular channel 250 nm × 400 nm. We extended this validation to high aspect ratio channels such as the widths of 600 nm, 800 nm, and 900 nm with the same height of 250 nm (Fig. 3). We used a fixed ionic strength of 0.32 mM (0.2 mM NaCl added to 1/40xTE). The reason to choose this ionic strength is that 0.32 mM is low enough to generate highly stretched DNA molecules in relatively wide nanochannel, but ionic strength should be stable or less susceptible to pH change due to major component of NaCl. Given the same ionic strength, DNA stretch decreases with increasing channel widths as shown in Fig. 3, which also presents a comparison among our experiment, our simulation and Odijk’s theory. Interestingly, the primitive model gives an excellent agreement with experiments in wider channels (> 400 nm), which is even better than Odijk theory. This implies that although it has been quite successful in describing the structure of polymers including DNA in a nanochannel, Odijk theory still has room for more sophistication such as considering more structural motifs in addition to hairpins.

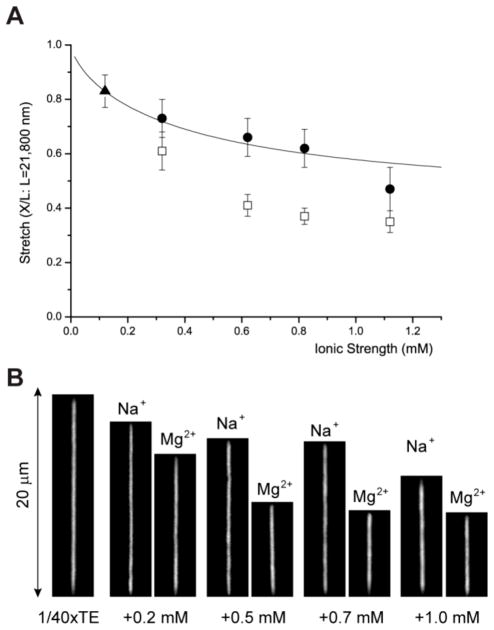
Also, Odijk’s theory with OSF equation has a critical shortcoming in applying to biological experiment since OSF equation does not work with multivalent ions.^{37, 38, 53, 54} Fig. 4 demonstrates an example of the effect of Mg²⁺ ions, which dramatically reduce DNA’s persistence length resulting in shorter stretches in nanochannels compared with Na⁺ ions. The previous other studies have reported that the addition of multivalent cation reduces not only electrostatic persistence length (P_e) but also intrinsic non-electrostatic persistence length (P_o), (e.g. P_o from 50 nm to 25 nm).^{37, 53} Although the understanding of DNA’s persistence length with multivalent ions is known as a very challenging theoretical topic,^{53, 54} the development of more sophisticated theories is essentially necessary to understand and predict nanochannel confined DNA stretching in complex ionic environments most biological buffers usually have.

Fig. 4.

Divalent ion effect on DNA stretches in 250 nm × 400 nm channels. (A) The graph shows four points of MgCl₂ (□: open square) of equivalent ionic strength of NaCl (●: closed circle) and a reference point of 1/40xTE (▲: closed triangle); these five points are already shown in Fig. 2B. The graph (solid line) of Odijk’s equation (Eq. 1) uses 50 nm as P_o. Each experimental data point represents measurement from 30 to 80 molecules; error bars show standard deviations of measured lengths. Molecular length is determined by intensity profile analysis as illustrated in Fig. 1. (B) Representative fluorescence images of DNA molecules at the same ionic strength for visual comparison between the effects of monovalent sodium ions and divalent magnesium ions on DNA stretches.

EXPERIMENTAL

Fabrication

Here we utilized PDMS nanochannels fabricated by replica molding on silicon wafer mold. Fabrication steps of the silicon wafer mold include interference lithography (IL), lift-off, reactive ion etching, and microchannel overlay. First, the wafer was cleaned in a 1:1 mixture of hydrochloric acid and hydrogen peroxide with consecutive sonication in acetone, isopropyl alcohol and deionized water for ten minutes each, and then dried with nitrogen gas. HMDS (Hexamethyldisilane, Fluka) was spin-coated on the substrate to improve the adhesion of photoresist. A negative photoresist (AZ nLOF 2020, Clariant) was diluted with thinner (AZ1512, Clariant) and spin-coated on the silicon substrate with 150 nm thickness. Interference lithography with a light source of He-Cd laser at 325 nm was used to make a periodic structure. One-beam, some portion of the light, irradiates the photoresist directly, and the other beam projects to the substrate after being reflected from the Lloyd mirror. These two beams projected to the photoresist with a certain angle interfere together and result in a sinusoidal exposure. The spatial period can be modulated by changing the incident angle, wavelength of a laser source and developing time. After exposure and the following post exposure bake, the substrate was dipped into a MIF 500 developer solution for 2 min at room temperature. After these IL processes, 15 nm thick chromium (Cr) layer was deposited on the patterned photoresist and subsequent lift-off process was performed to define Cr mask in the following etching process with an EKC-830 (Dupont Electronic Technologies) for 30 min at 80 °C. To generate 100, 150, and 250 nm relief patterns, reactive ion etching (RIE) with a gas mixture of CHF₃ and O₂ was used at a power of 100 W and 5 mTorr and finally the Cr mask was removed with Cr etchant (CR-7, Cyantek).

After fabrication of the nanochannel template, we followed the procedure as described previously.¹⁰ Briefly, a microchannel (5 μm high, 100 μm wide) pattern was overlaid on the nanopatterned wafer using the negative photoresist SU-8 2005 for convenient loading DNA into nanochannels. A monolayer of tridecafluoro- 1,1,2,2- tetrahydro octyl-trichloro silane was deposited on the surface of the silicon master mold to promote PDMS releasing in the following replica molding step. The 10:1 mixture of PDMS monomer and curing agent was poured onto the patterned silicon wafer master and allowed to cure at 65 °C for 4 h or longer. PDMS devices were treated in an air plasma generator for 30 s (Femto Science Cute Basic) to make the surface hydrophilic. These plasma-treated PDMS devices were stored in high-purity water for 24 hours because PDMS surfaces are reactive immediately following plasma treatment. Afterward, the PDMS devices were washed with 30 mL of 0.5 M EDTA (pH 8.0) for 15 minute with sonication, then washed with high-purity water by sonicating three times for 15 minutes each and stored in high-purity water before use. Finally, a PDMS device was mounted on a glass previously cleaned in the piranha solution. The DNA samples were loaded into the microchannels via capillary action and then lead into the nanochannels by using an applied electrical field (30–50 V across 25 mm) with platinum electrodes inserted into the reservoirs. DNA samples used in this paper have 0.125 μg/μL λ DNA in 0.25 mM Tris and 25 μM EDTA with various NaCl from 0 mM to 2 mM.

Imaging

Instead of using anti-bleaching agents, in this study we adjusted the power of a solid-state laser (Coherent Sapphire 488) with an additional optical density filter (NDQ-100-1.00, Korea Electro Optics). The optimum light intensity we used was 0.12 mW measured at a 63x objective lens in a microscope (Zeiss Observer A1). In addition, we removed an emission filter to enhance transmittance of fluorescent light to CCD camera (Roper Scientific CoolSNAP EZ). Instead, a holographic notch filter was used to filter out 488 nm laser source light. Using this microscopic set-up without anti-bleaching agent, we were able to watch and take images of DNA without significant photo-damage such as photolysis or severe photo-bleaching as shown in Fig. 1B. Here we determined the molecular length by the distance between two points where the intensity profiles is equal to the half of the unit intensity: the unit intensity represent the expected intensity if a molecule fully stretches, which value is calculated from a molecule’s integrated intensity divided by its contour length (e.g. 21,800 nm for λ DNA).

Conclusions

DNA elongation via nanoconfinement is informed by new physical insights, which are readily translated into new molecular analysis approaches in the genomic sciences. Accordingly, we have comprehensively addressed both challenges, through the fabrication of nanochannels for effective presentation of well-stretched DNA molecules, while understanding stretching effects mediated by ionic strengths and channel dimensions guided by using Odijk’s theory. For more rigorous understanding, we have also developed a primitive DNA model in a nanochannel and performed Monte Carlo simulations to evaluate our experimental findings as well as to validate Odijk’s analytical equation. Here we demonstrate reasonable agreements among experiment, computer simulation, and theory with some limitations. We believe that our systematic analysis will provide a firm basis for the design of nanochannel platforms offering high-resolution and high-throughput DNA analysis.