Studies With Staggered Starts: Multiple Baseline Designs and Group-Randomized Trials

Abstract

Objectives. Multiple baseline designs (MBDs) have been suggested as alternatives to group-randomized trials (GRT). We reviewed structural features of MBDs and considered their potential effectiveness in public health research. We also reviewed the effect of staggered starts on statistical power.

Methods. We reviewed the MBD literature to identify key structural features, recent suggestions that MBDs be adopted in public health research, and the literature on power in GRTs with staggered starts. We also computed power for MBDs and GRTs.

Results. The features that have contributed to the success of small MBDs in some fields are not likely to translate well to public health research. MBDs can be more powerful than GRTs under some conditions, but those conditions involve assumptions that require careful evaluation in practice.

Conclusions. MBDs will often serve better as a complement of rather than as an alternative to GRTs. GRTs may employ staggered starts for logistical or ethical reasons, but this will always increase their duration and will often increase their cost.

The randomized controlled trial (RCT) is the gold standard for causal inference for individual-level interventions.¹ When interventions are applied at the group level and outcomes are measured at the individual level, the cluster- or group-randomized trial (GRT) is the gold standard for causal inference.^2,3 However, GRTs are often costly and time-consuming, prompting researchers to look for alternatives. One alternative that has been suggested is the multiple baseline design (MBD), which has a venerable history in education and applied behavior research with individual-level interventions but is relatively new in public health research with group-level interventions.^4–6 The MBD makes repeated measurements over a period of time and introduces a sustained intervention on a staggered schedule; intervention effects synchronized with the staggered start times provide evidence for causal inference. Hawkins et al. described the MBD as “a viable alternative to the RCT” and suggested that it will be lower cost, use smaller sample sizes, and still be statistically rigorous.⁵ Biglan et al. suggested complementary roles, with MBDs used to “develop and sort through potentially effective intervention methods, followed by evaluation in RCTs both to test efficacy and to determine the extent of generalizability.”⁴ We review the structural features that have made MBDs useful in other fields and consider whether similar success is likely in public health. We also compare the statistical power of MBDs and GRTs.

METHODS

We reviewed the MBD literature to identify key structural features. We reviewed recent suggestions that the MBD be adopted in public health research. Finally, we reviewed the literature on GRTs with staggered starts and compared the power of that design with the more traditional parallel design.

RESULTS AND DISCUSSION

We used the Murray convention, in which “condition” refers to the study arm, “group” refers to a collection of participants assigned together to a condition, and “member” refers to an individual participant.³ Experiments involve a single intervention, so at any particular time a group will be in either the control condition or the intervention condition.

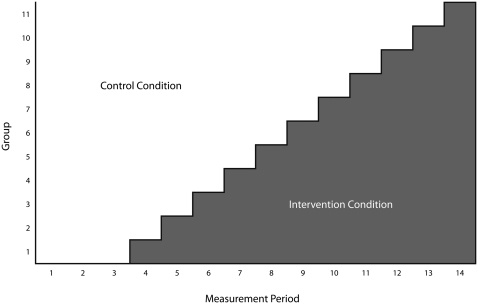
The MBD has several variations with and without randomization; we focused on MBDs that introduce the intervention to groups on a staggered schedule and in a random order. Before any intervention occurs, the outcome is measured in each group. Then the intervention is initiated in 1 or more groups while the others continue in the control condition. After sufficient time has passed for the intervention to affect the outcome in the first group(s), outcome measurements are conducted in all groups and the intervention is introduced in 1 or more additional groups. This proceeds until all groups receive the intervention. Once a group starts the intervention, it remains in that condition until the end of the study. Figure 1 illustrates an MBD involving 14 measurement periods and 11 groups with 1 group crossing to intervention at each start time.

FIGURE 1.

Conceptual diagram of the multiple baseline or stepped wedge design.

Note. The intervention commences on a staggered schedule across groups with the idea that a measureable effect in the outcome variable(s) will follow a similar pattern.

If every group shows a similar change after crossing to the intervention condition and does not change at other times, the experiment provides compelling evidence that the changes resulted from the intervention. Even with a limited number of groups, consistently replicated effects can be persuasive, and that is why some researchers have been drawn to the MBD.

The term group-randomized trial covers a broad array of designs in which groups are randomized to conditions and measurements are taken from the members of those groups. In a parallel GRT, baseline measurements are conducted in every group and then the intervention commences simultaneously in half of the groups; the remainder serves as controls and does not receive the intervention during the study. One or more additional measurements occur in all groups.

MBDs for public health interventions always have multiple members per group, and randomization is used to select the order in which groups start the intervention. Because these 2 conditions define a GRT, the MBDs we considered are GRTs as well. These MBDs are also called stepped wedge designs (SWDs). The name stepped wedge originated with the Gambia Hepatitis Study and refers to the wedge shape of the intervention timeline across groups, as depicted in Figure 1.⁷ Brown and Lilford reviewed a dozen stepped wedge studies; the stated reasons for using staggered starts included easier implementation of the intervention, ethical requirements to give the intervention to all participants, a desire to estimate trends over time, and a desire to use participants as their own controls.⁸

Structural Features of Multiple Baseline Designs

The following features of the MBD have contributed to its success in fields such as applied behavior research and education.^9–19 It is important to consider whether they are likely to be as effective in public health research.

• Designs with staggered start times can be persuasive if the timing of the effects is synchronized with the timing of the introduction of the intervention. Furthermore, they guard the internal validity of the study by ruling out the possibility that a single external event (e.g., a celebrity cancer diagnosis or a change in legislation) could explain the results. In some cases it would be prohibitively expensive or impossible to start the intervention in half of the groups simultaneously. This is especially true when a single team trains all the intervention personnel or when groups are separated by large geographical distances. With staggered start times, each group can start the intervention shortly after being trained.

• Many measurements may be required to reliably estimate baseline trends and intervention effects within each group. In some situations, data collection and reporting will be standardized processes that occur with fortunate frequency. Otherwise, the cost of many measurements may make MBDs prohibitively expensive.

• Randomization of the order in which the groups start the intervention protects against bias associated with readiness or eagerness to participate.

• Each group experiences a single transition from the baseline condition to the intervention condition. MBDs are typically used in settings in which it would not be ethical, healthy, or practical to withdraw the intervention or in which it is unrealistic to expect participants to revert to their pretreatment condition quickly after the withdrawal.

• The time between intervention onsets in different groups is long enough for the intervention to show its full effect in the most recently treated group. Treatments with a long latency are not good candidates for the MBD.

Analysis Methods for Multiple Baseline Designs

Matyas and Greenwood reported that 75% of the experiments they examined in the Journal of Applied Behavior Analysis looked for effects that shifted the mean outcome by more than 5 standard deviations; 50% looked for effects larger than 10 standard deviations.²⁰ Thus it is no surprise that MBDs in applied behavior research have traditionally been analyzed by simple visual inspection for a substantial change in within-unit outcomes shortly after the intervention starts.^10,12 This method works best if the intervention effects are large. More recent work has explored formal hypothesis testing both within and between groups to detect more modest effects. The methods described include Box-Jenkins time series analysis, interrupted time series analysis, randomization tests, and multilevel modeling.^11,21–24 Approaches to the analysis of stepped wedge GRTs are complex and are described in Brown and Lilford,⁸ Brown et al.,²⁵ Hayes and Moulton,²⁶ and Hussey and Hughes.²⁷

Optimistic Claims for Multiple Baseline Designs in Public Health Research

Hawkins et al. suggested,

Conceptually a multiple baseline design may use as few as two groups to test an intervention, reducing costs and alleviating some of the difficulties in obtaining a sufficient sample size required in RCTs.^5(p163)

Success in 2 staggered groups may dispel the counterfactual suggestion that success resulted from a single external event, and it may provide justification for testing in a broader set of groups. But numerous examples in the MBD literature demonstrate intervention success in some, but not all, groups.^4,11 Given the small effect sizes that are typical in public health interventions, mixed results will be difficult to interpret.

Biglan et al. observed that

in addition to knowing whether the intervention was successful or not, data on the differential effects of alternative forms of the intervention implemented in individual communities and implemented at different times will help advance knowledge on which components influence [the study outcome].^4(p39)

With individual-level interventions, MBD researchers may be able to guess at the reasons for their intervention failures if they interact with the study participants frequently.²⁸ In public health studies, it will be impractical for any single investigator to have contact with all study participants, and those participants will not be observed often. In addition, community-based investigators will have a multitude of confounding factors to consider. Data on differential effects will be confounded with the community effects, the times of implementation, different baseline trends, and possibly different implementation teams. Investigators will have difficulty attributing differential effects to specific features of the intervention.

Finally, Hawkins observed that “[the MBD] is a viable alternative to the RCT.”^5(p167) We believe that an MBD would need to have many of the features of an RCT to provide compelling evidence in public health studies. Modest effects require many groups, and simple visual inspection of the time series of results will usually not suffice. There are conditions under which SWDs (MBDs for groups) can be more powerful than parallel GRTs with the same number of groups. However, the SWD design will often require more measurements and more time than the parallel GRT, sometimes substantially more, so study designers must carefully consider the tradeoffs involved. Unless the intervention's effect sizes are large, we do not share Hawkins's optimism that the SWD or MBD can provide substantially faster or less expensive evidence than the parallel GRT for causal inference for group-level interventions.

Stepped Wedge Versus Parallel Design

There may be situations in which the study designer is able to choose between an SWD and parallel GRT. We compare the statistical power of those designs and highlight some considerations that might influence the choice. Several questions interest us: Which design is more statistically powerful given the same number of groups and measurement periods? What are the design parameters that influence the answer? In cases in which the SWD is more powerful than the parallel design, how many fewer groups or measurements can be used without sacrificing statistical power?

Brown et al. provided an illustrative Poisson event example in which the SWD intervention effect was estimated using a weighted average of between-groups differences at each measurement time point.²⁵ Those authors acknowledged the point raised by Hayes and Moulton: the number of groups in intervention and control conditions are markedly unbalanced near the beginning and end of the stepped wedge study, and that leads to loss of efficiency for this analytic model.²⁶ Hussey and Hughes described the orthogonal complement to that approach: analyzing an SWD with an estimator that is a weighted average of within-groups differences when it is reasonable to assume that there is no time effect.²⁷ The same problem applies in that case: some groups spend most of the study in the control condition and some spend most of the study in the intervention condition, and that leads to loss of efficiency for this analytic model.

Hussey and Hughes proposed an alternative weighted least squares estimator for SWDs that combines information from within and between groups.²⁷ This estimator is more complicated but usually more efficient than either the purely between-groups or purely within-groups estimators, and we used it to make observations about conditions under which the SWD can be more powerful than a parallel GRT. They assumed a mixed effects model that describes the individual-level response Y_ijk for member k in group i and measurement period j (i in 1, …, I; j in 1, …, T ),

where μ_ij is the average response in group i during measurement period j, α_i ∼ N(0, τ²) is a random effect for group i, β_j is a fixed effect for time period j, θ is the intervention effect, X_ij takes the value 1 if group i is in the intervention condition during period j and 0 otherwise, and 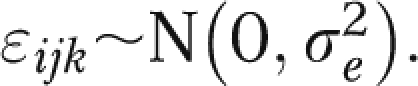. Under this model, 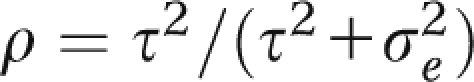is the intraclass correlation coefficient (ICC), describing the correlation between 2 individuals in the same group, either at the same point in time or across 2 different measurement occasions.

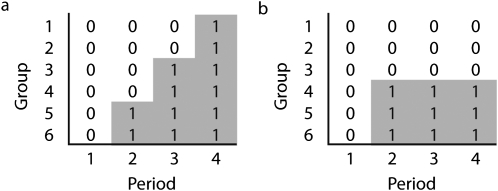
This model can be used to describe parallel GRTs, SWDs, and traditional crossover designs by varying the pattern of X_ij values. Figure 2 shows the pattern of Xs for a parallel GRT design with a single baseline and 3 follow-up measurements and for a SWD with 4 measurements; both designs involve 6 groups. Hussey and Hughes observed that if τ² and 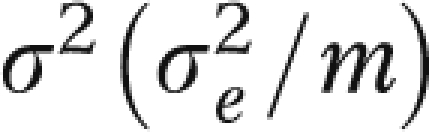are known, where m is the number of members per group, then estimates of the fixed effects can be obtained with a weighted least squares analysis of the cluster means.²⁷ If Z is the IT × (T + 1) design matrix corresponding to the parameter η = (μ, β₁, β₂, …, β_T−1, θ) for the SWD, then 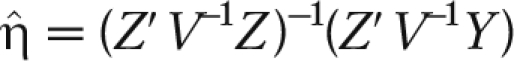and the covariance matrix of 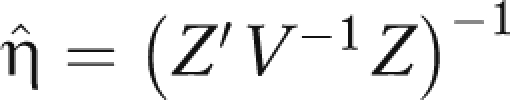, where V is an IT × IT block diagonal matrix. The estimate of the intervention effect, 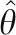, is the T + first element of 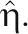. Each T × T block within V describes the correlation structure between the repeated (in time) cluster means and has σ² + τ² in every element along the diagonal and τ² in the off-diagonal elements.²⁷

FIGURE 2.

Conceptual comparison of (a) stepped wedge and (b) parallel group-randomized trial designs.

Note. Intervention and control conditions are represented with both shading and the 0/1 X_ij nomenclature of Hussey and Hughes.²⁷ A 0 means the group is in the control condition, and a 1 means the group is in the intervention condition.

Hussey and Hughes suggested that power can be computed for the weighted least squares analysis using

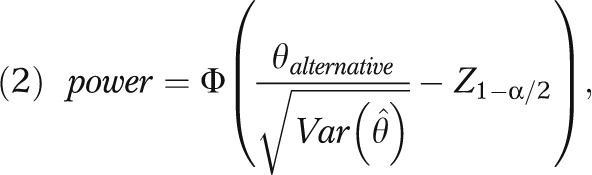where Φ is the cumulative standard normal distribution function, Z_1−α/2 is the (1−α/2)th quantile of the standard normal distribution function, and θ_alternative is the hypothesized treatment effect.²⁷

They gave a closed form expression for :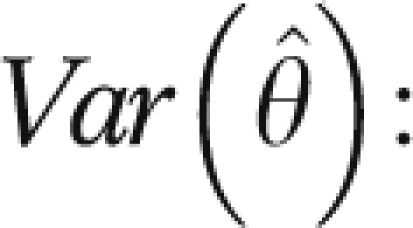

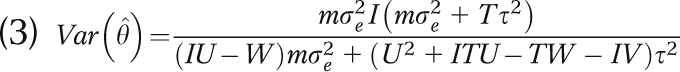where 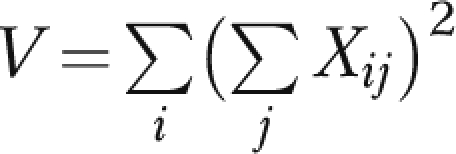, 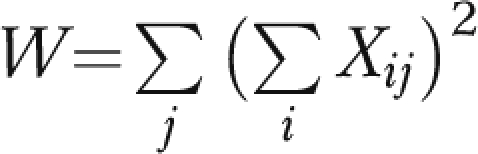. Equation 3 is general and may be solved for any pattern of 0 and 1 X_ij values. They also used values of X that increase from 0 to 1 gradually to indicate that the intervention effect sometimes takes more than 1 measurement period to be fully realized. Although we have not done so here, it is possible to use the same approach to model problems with intervention adherence in long studies. Note that although the weighted least squares estimator works with values of X between 0 and 1, Equation 3 is only valid when X takes the value 0 or 1.

For the remainder of this section we define a balanced SWD to be a study of T periods with I groups, each of which has m members, where all groups are in the control condition in Period 1 and then the same number of groups, k = I/(T − 1), crosses over from control to intervention in each remaining period. In that case, Equation 3 may be rewritten as

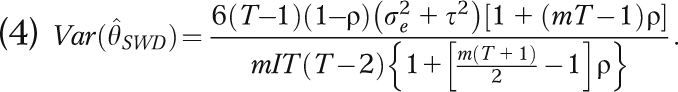Similarly, we constrain a parallel GRT to be a study with T measurement periods in which all I groups are in the control condition in Period 1 and half the groups (I/2) transition to intervention in Period 2. For this design, Equation 3 may be rewritten in a form that is valid for parallel GRTs with T > 2:

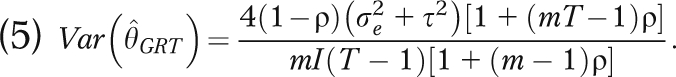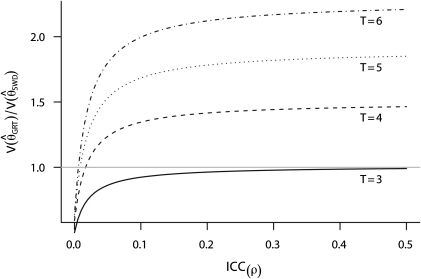
Using Equations 4 and 5, we can compare the power of the parallel GRT with the SWD under the Hussey and Hughes mixed effects model. Figure 3 plots 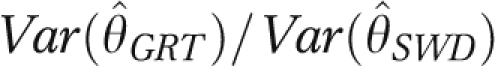as a function of the ICC (ρ) and number of time periods (T ) with m = 50 individuals per group. This result holds for any number of groups entering the intervention in each time period in the SWD. For T = 3 the parallel GRT has a smaller variance for all values of the ICC. For T > 3 the SWD yields a smaller variance than the parallel GRT for all but the very lowest values of the ICC.

FIGURE 3.

The variance of the estimator using a parallel group-randomized trial design from Equation 5 divided by the variance of the estimator using a stepped wedge design from Equation 4, assuming equal numbers of groups and measurement occasions, and 50 persons per group for various numbers of measurement occasions and ICCs from 0.0 to 0.5.

Note. GRT = parallel group-randomized trial; ICC = intraclass correlation coefficient; SWD = stepped wedge design; T = number of measurement occasions.

We can also use Equations 4 and 5 to investigate the extent to which the SWD can employ fewer or smaller groups, measure on fewer occasions, or look for a smaller effect size than that of the parallel GRT without compromising power. Hussey and Hughes described a cross-sectional SWD to evaluate an intervention to reduce the prevalence of chlamydia infections in 24 counties of Washington State.²⁷ We expanded on that example to explore the relative sizes of parallel GRTs and SWDs that have comparable power. We start with a parallel GRT with 3 measurement periods and 24 counties. In Period 1, all counties are in the control condition. In Period 2, 12 randomly selected counties receive the intervention and continue to do so through Period 3. The remaining 12 counties stay in the control condition. Equations 5 and 2 indicate that a parallel GRT with 3 measurement occasions and 24 groups would have 81% power to detect a 50% reduction in prevalence, assuming prevalence = μ = 0.05, m = 100, T = 3, I = 24,ρ = 0.01, 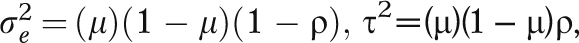θ_alternative = −0.025, and α = 0.05. Again, the parallel GRT has a smaller variance than a SWD with the same number of groups when T = 3; Equations 4 and 2 indicate that a balanced SWD where T = 3 and I = 24 would have only 69% power to detect the same 50% reduction in prevalence.

Table 1 shows the total number of groups necessary for the SWD to reach or exceed the power of the parallel GRT under various values of ICC. The ICC = 0.010 row shows that a SWD using as few as 8 counties could be used in the Washington chlamydia project and achieve the same power as the parallel GRT with 24 counties. Note, however, that the ICC = 0.010 SWD where I_SW = 8 would require 9 measurement periods, which is 3 times as many as the parallel GRT. Both would require 72 group-level measurement efforts: 8 counties on 9 occasions for the SWD and 24 counties on 3 occasions for the parallel GRT. Table 1 uses a superscript to identify cells in which SWDs would require fewer total measurements than would the parallel GRT.

TABLE 1.

Total Groups as a Function of Measurement Periods Required in Stepped Wedge Designs to Provide Power at Least as Great as That in the Parallel Group-Randomized Trial With 24 Counties and 3 Measurement Periods

	TGRT = 3a	TSW = 3	TSW = 4	TSW = 5	TSW = 6	TSW = 7	TSW = 8	TSW = 9	TSW = 10	TSW = 11	TSW = 12	TSW = 13
ICC	IGRTP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %	ISWP, %
0.0001	24 98	48 98	27 98	20 98	20 99	18 >99	14 99	16 >99	9 98	10 >99	11 >99	12 >99
0.001	24 96	44 96	27 96	20 97	20 99	18 99	14 98	16 >99	9 96	10 98	11 99	12 >99
0.005	24 87	36 87	24 90	20 93	15 91	12 89	14 96	16 99	9 91	10 96	11 98	12 99
0.01	24 81	32 81	21 84	16 85	15 89	12 88	14 95	8 82	9 90	10 95	11 97	12 99
0.05	24 70	28 73	18 76	12b71b	10b73b	12 87	7b71b	8 82	9 89	10 94	11 97	12 99
0.1	24 70	26 72	18 78	12b73b	10b75b	12 88	7b73b	8 83	9 91	10 95	11 98	12 99
0.2	24 74	26 76	15b 75b	12b78b	10b79b	12 91	7b78b	8 87	9 94	10 97	11 99	12 >99

Note. GRT = group-randomized trial; I = number of groups; ICC = intraclass correlation coefficient (ρ); P = power to detect a drop in prevalence from 0.050 to 0.025 with cross-sectional measurements made on m = 100 persons per group per measurement period, assuming α = 0.05; SW = step wedge; T = number of measurement periods. Stepped wedge table entries are rounded up to be integer multiples of T_SW − 1, so the same number of groups start the intervention in each measurement period.

^aThe T_GRT = 3 column shows the power for the parallel GRT with 24 groups and 3 measurement periods at various values of ICC. Each of the remaining T_SW columns to the right lists the number of groups necessary to achieve at least as much power as the 3-group GRT using an SWD with T_SW measurement periods.

^bDesigns with fewer total measurements (I_SW × T_SW) than the 24 × 3 = 72 measurements required by the group-randomized trial.

Time is often as important a consideration as cost. The parallel GRT in the T_GRT column of Table 1 would require 3 measurement periods. To achieve the same level of power, the SWDs would always require additional measurement periods. ICC values < 0.050 are common in public health; with such ICCs, appreciably more measurement periods may be required for the SWD to achieve the same power as the parallel GRT. Thus when choosing between the parallel GRT and SWD, investigators would need to consider the time required to complete each design in addition to the other factors.

Table 1 also lists the power of those study designs to detect a 50% reduction in prevalence (from 0.050 to 0.025). By design, the power of the SWDs is at least as high as that of the parallel GRT. In some cases the SWD is substantially higher in power than the parallel GRT because the number of SWD groups was rounded up to be an integer multiple of T_SW − 1 so the same number of groups would start the intervention in each of T_SW − 1 measurement periods.

Limitations

We benefited greatly from Hussey and Hughes's weighted least squares formulation to write closed form expressions for the variance of the intervention effect estimator. Even so, our approach has several limitations. The intervention effect, θ, is assumed to be constant across groups and to persist throughout the study. The correlation between earlier and later measurements within a group is assumed to be constant no matter how much time elapses. And we rounded the number of groups in the SWD up to ensure a balanced number of groups starting the intervention in each time period. Note that the Hussey and Hughes model assumes repeated cross-sectional measurements, so we do not have to worry about loss to follow-up of individual group participants; this would be an important consideration in a stepped wedge cohort design. Further work is needed to develop results that are free of these limitations.

Conclusions

The MBD is a good design when interventions are applied to individuals and result in rapid, large changes in the outcome variable. The design is especially compelling when the change is large enough to be obvious just from looking at the time series of measured outcome data. These conditions are not likely to hold in most public health interventions in which effect sizes are often on the order of 0.25–0.50 standard deviations.^29–31 There may be a place for small, quick MBDs in the early stages of protocol development, when interventions that will eventually be applied at the group level are tested out at the individual level. But to draw causal inferences, we do not share the enthusiasm expressed by Hawkins et al. that small MBDs might be a “viable alternative” to RCTs.

To support strong conclusions and to estimate a generalizable treatment effect in group-level public health interventions, investigators who have reason to use a staggered start design should use a stepped wedge GRT. Before doing so, they should recognize the limitations of the SWD and the available evidence on its power. The SWD will take longer than the parallel GRT and may require as many measurements even if there are fewer groups involved. With fewer groups, adjustment for group-level confounding factors will be important because randomization will be less likely to balance differences, and it will be challenging because there will be fewer degrees of freedom. Investigators will want to consider all these factors as they choose between the parallel GRT and the SWD.