Characterizing Phase-Only fMRI Data with an Angular Regression Model

Abstract

FMRI voxel time series are complex-valued with real and imaginary parts that are usually converted to magnitude-phase polar coordinates. Magnitude-only data models that discard the phase portion of the data have dominated fMRI analysis. However, when such analyses are performed, the data that is discarded may contain valuable biologic information that is not in the magnitude data. This biologic information from BOLD fMRI data may be vascular (Menon, R.S., 2002. Postacquisition suppression of large-vessel BOLD signals in high-resolution fMRI. Magn. Reson. Med. 47(1), 1–9) or neuronal (Bodurka, J., Jesmanowicz, A., Hyde, J.S., Xu, H., Estowski, L., Li, S.-J. 1999. Current-induced magnetic resonance phase imaging. J. Magn. Reson. 137(1), 265-271) in origin.

When phase-only time series that discard the magnitude portion of the data have been analyzed, ordinary least squares (OLS) regression has been the technique of choice. However, OLS models may fit poorly when phase-wrap or low signal-to-noise ratio (SNR) is present. We have explored alternatives to the OLS model which will account for the angular response of the phase while also allowing us the flexibility to develop similar hypothesis tests.

We adopt an angular regression model by Fisher and Lee (Fisher, N.I., Lee, A.J. 1992. Regression models for an angular response. Biometrics 48, 665–677) for our analysis and show its improvement over the OLS model at low SNR in terms of both parameter estimation and inferences. We found an improvement in parameter estimation along with modeling for the Fisher and Lee method in simulated data while detailing potential benefits when used with experimentally acquired data. Finally, we look at a map of the statistics testing the association of the observed voxel phase time course and the reference function in our acquired data. This shows the possible detection of biological information in the generally discarded phase.

1 Introduction

Functional magnetic resonance imaging (fMRI) is an invaluable tool used to investigate biological phenomena in both animals and humans. However, the results derived from fMRI depend on the model used to analyze the data. Although voxel time courses are complex-valued (Haacke et al., 1999), traditionally the real-imaginary voxel measurements are converted to magnitude-phase measurements and only the magnitude portion of the data is analyzed for experimental or task related changes (Bandettini et al., 1993; Rowe and Logan, 2005). This discards potentially important information. Recently, models that determine task related magnitude changes within the complex-valued data have shown improvements over those that examine magnitude-only data (Rowe and Logan, 2004; Rowe and Nencka, 2006).

In addition, there is evidence that the phase portion of the data also contains biological information not wholy contained in the magnitude portion, namely, data indicative of vascularization (Menon, 2002; Nencka and Rowe, 2005; Nencka and Rowe, 2006) or of possible direct detection of neuronal firing (Borduka et al., 1999). Thus is is also important to analyze the phase portion of the fMRI data.

Historically, when phase-only data has even been analyzed, an ordinary least squares (OLS) regression model is used. But this method neglects the problem of the phase angle wrapping back over itself after it has crossed the ±π value. Fisher and Lee (1992) developed an angular regression model which has never been applied to fMRI data. We aim to improve the modeling of the generally discarded phase portion of the data by using the Fisher and Lee model compared to OLS without unwrapping and an intermediate approach of OLS which attempts to (artificially) unwrap the data.

2 Background

As previously mentioned, the model for brain function and distributional specifications are essential for fMRI analysis results. It is well established that the real and imaginary parts of the complex-valued voxel observations are normally distributed (Gudbjartsson and Patz, 1995; Haacke et al., 1999) provided the dominant noise is scanner related. When viewed from the magnitude and phase angle, ρ and θ point of view, the phase lies in a plane taking on values only between and including −π to +π. The angle −π is the same as +π.

2.1 Real-Imaginary Data

The real and imaginary components (y_R, y_I) of the complex-valued data in a voxel at a particular time point have been described as

$$\begin{array}{ccc}{y}_R& =& \rho \cos \theta +{\eta }_R\\ y_I& =& \rho \sin \theta +{\eta }_I\end{array}$$ (2.1)

where (ρ θ) are the magnitude and phase from a conversion to polar coordinates and (η_R, η_I) are the real and imaginary noise components (Nan and Nowak, 1999; Rowe and Logan, 2004). Additionally, the real and imaginary noise has been well characterized as independent normally distributed with mean zero and variance σ². The joint distribution of (y_R, y_I)′ is bivariate normal with phase coupled mean (ρ cos θ, ρ sin θ)′ and covariance matrix σ²I₂. The above description is for a single time point and a t subscript for temporally ordered observations will be omitted until specifically noted.

2.2 Magnitude-Phase Data

The above mentioned complex-valued data is commonly transformed into magnitude and phase polar coordinates $r=\sqrt{y_R^2+y_I^2}$ and ϕ = tan⁻¹(y_I/y_R) with Jacobian r. It is important to understand that the previous distributional specifications were on the observed real and imaginary parts of the data and not on the magnitude or phase that to which the data are transformed. The derivation of the joint distribution of r and ϕ is presented in and Logan (2004) and has the form

$$p(r,\varphi )=\frac{r}{2\pi {\sigma }^2}{e}^{-\frac{1}{2{\sigma }^2}[r^2+{\rho }^2-2\rho r\cos (\varphi -\theta )]}$$ (2.2)

where r, ρ, σ > 0 and −π < ϕ, θ ≤ π. Note that r and ϕ are not statistically independent.

2.3 Phase-Only Data

The magnitude information in equation 2.2 can be integrated out and the resulting marginal distribution for the phase is (Rowe and Logan, 2004)

$$p(\varphi )=\frac{e^{-\frac{{\rho }^2}{2{\sigma }^2}}}{2\pi }\left[1+\frac{\rho \cos (\varphi -\theta )}{2\pi \sigma }{e}^{\frac{{\rho }^2{\cos }^2(\varphi -\theta )}{2{\sigma }^2}}\mathrm{\Phi }\left(\frac{\rho \cos (\varphi -\theta )}{\sigma }\right)\right]$$ (2.3)

where −π < ϕ, θ ≤ π, ρ, σ > 0, and Φ (·) is defined to be the cumulative distribution function (CDF) for the standard normal distribution. The marginal distribution of the phase approaches the normal distribution

$$p(\varphi )={[2\pi {(\sigma /\rho )}^2]}^{-1/2}{e}^{-\frac{{(\varphi -\theta )}^2}{2{(\sigma /\rho )}^2}}$$ (2.4)

with mean θ and variance (σ/ρ)² for large signal-to-noise (SNR) as described in Gudbjartsson and Patz (1995). We define SNR to be ρ/σ.

However, phase data lies within an interval of (−π, π] which leaves it vulnerable to phase-wrap and can cause the OLS model fit to be questionable. We define phase-wrap to be the event of successive temporal phase measurement points crossing a |π| value. Phase-wrap is detected by differencing pairs of temporally adjacent phase values and defining a phase-wrap when the difference is greater than |π|.

Introducing the subscript t for each time point combined with the limiting distribution, we are able to model the phase

$${\varphi }_t={\tan }_4^{-1}\left[\frac{{\rho }_t\sin ({\theta }_t)+{\eta }_{\mathit{It}}}{{\rho }_t\cos ({\theta }_t)+{\eta }_{\mathit{Rt}}}\right],t=1,\dots ,n,$$ (2.5)

with a normal distribution and an OLS model. One can see that the argument of the four quadrant inverse tangent is the ratio of noncentral normal variates. The ratio of noncentral normal variates has been studied by Marsaglia (1965) who showed that it can be symmetric, asymmetric, unimodal or bimodal.

3 Models for Phase Data Analysis

As previously noted, phase-only time series data is not generally analyzed in fMRI, because it is sensitive to physiologic noise. It has been argued that respiration causes movement of internal organs which in turn alters the B-field and thus the phase (Pfeuffer et al., 2002). Pfeuffer et al. (2002) used the common phase data across a whole slice to correct for this respiration caused movement.

When fMRI phase time series data is analyzed, the OLS model is utilized (Borduka et al., 1999). Before an OLS model can be fit, the time series is generally artificially unwrapped. The process of artificially unwrapping the data and then fitting an OLS model to it will be described shortly. Menon (2002) looked at phase time series after unwrapping and noticed an approximate linear association with the magnitude data which he believed was attributed to large blood vessels and thus biological information in the phase. The OLS model will be briefly summarized, then an alternative model will be introduced along with its advantages and disadvantages.

3.1 Ordinary Least Squares Regression Models for Phase

The OLS model (Rowe, 2003; Rowe and Hoffmann, 2006) for the phase assumes that the phase varies linearly with the task related reference function. The phase-only data model at time t for an arbitrary voxel can be written as

$${\varphi }_t=u_t^{\prime }\gamma +{\delta }_t,$$ (3.1)

where ϕ_t is the observed phase angle measurements, $u_t^{\prime }$ is a specific row of a design matrix U, an example of which is presented in equation 3.2, the γ are the fixed but unknown phase regression coefficients, and δ_t is the measurement error. This measurement error is assumed to originate from the normal distribution $N(0,{\tau }_t^2)$ where ${\tau }_t^2={\sigma }^2/{\rho }_t^2$. Estimation of the linear regression model parameters by OLS does not require any distributional assumption. A distributional assumption is necessary in order to draw inferences. The OLS model and the OLS model plus a normal distribution specification on the errors produce identical model parameter estimates.

For our examples in the following sections, U = (u₁, …, u_n)′ is constructed to have three covariates,

$$U^{\prime }=\left(\begin{array}{cccccc}1& 1& \dots & 1& \dots & 1\\ 1& 2& \dots & 17& \dots & 256\\ 1& 1& \dots & -1& \dots & -1\end{array}\right).$$ (3.2)

The above design matrix includes a column of 1’s to model the intercept, a column of counting numbers to account for a possible linear trend over time (Smith et al., 1999), and a third column with alternating sets of sixteen 1’s and −1’s to characterize a task related reference function. Sets of 16 are used in our matrix to coincide with both our simulated and acquired experimental data which have stimulus lengths of 16 observations. Clearly, this can easily correspond to more complicated sets of tasks (or even event-related data).

The SNR at time t is defined to be ρ_t/σ = (β₀ + β₁t + β₂x_2t)/σ but β₁t + β₂x_2t is generally very small when compared to β₀ within the brain and should be zero outside the brain. The approximation ρ_t/σ ≈ β₀/σ is utilized and the phase variance in a given voxel becomes constant over time. For a large SNR, the OLS model corresponds to a phase angle that is concentrated over a small range of values. When the phase-only data is described with the large SNR OLS model, phase hypotheses can be tested using a d × (q+1) contrast matrix D where d is the number of orthogonal constraints in the rows of D and q is the number of non baseline regressors. Inferences can be drawn using standard regression analysis tests – Likelihood Ratio tests or OLS Wald type z-tests.

However, there are three conditions that can lead to difficulties with the OLS model: the first is when the baseline angle is located near the ±π value where the phase angle (within the OLS models) becomes discontinuous; the second is when a linear trend pushes the data past the ±π value and the third is the case where the amplitude of the magnitude is low (a low SNR). In these three cases, the angular response of the phase-only OLS model can cause modeling problems at the phase-wrap junction if not accounted for properly. These conditions result in poor parameter estimation and incorrect inferences.

Conversely, when the three following conditions are valid we can describe the phase data with little concern using our standard OLS regression model. These conditions are 1) a large SNR, 2) a baseline angle, γ₀, that is not near the ±π value, and 3) the linear trend is small enough that the data does not rise or fall beyond the ±π value. The large SNR assumption makes the probability of a large difference between successive measurements very small; the other conditions bound the phase angle away from the problematic value of ±π.

3.2 Unwrapped OLS Model for Phase

In real acquired experimental fMRI data the SNR and mean phase in voxels varies greatly over space. The above stringent conditions are, in general, not met across an image. Often within an fMRI data set phase angles are observed close to ±π. As previously mentioned, the method generally used to deal with this issue is “unwrapping.” Time series unwrapping is the process of beginning with the first observation, proceeding through the time series and flagging an observation in which the next point in the time series has an absolute difference greater than or equal to a predefined value, generally π, then shifting the rest of the time series by ±2π. This process is repeated to the end of the time series. However, when the assumption of high SNR becomes suspect, the model fails and the investigator needs another model.

In many instances there is no phase-wrap and simply fitting an OLS regression line to the data is sufficient. This situation will be defined as the “control” case. However, when there is phase-wrap and low SNR, unwrapping may not be the proper procedure. We will define this as a “test” case. This implies the need for another model that can account for the angular response even with low SNR. Instead, we explore angular models and look at fitting the data under an angular regression model along with OLS and OLS after unwrapping. Implementing an angular regression model procedure to deal with the angular nature of the response will allow us to relax the large SNR requirement.

3.3 Linear-Circular Regression Models for Phase

As previously described, fitting an OLS regression model to artificially unwrapped data may not be an ideal method and is especially poor for low and moderate SNR data. There are models in the statistical literature that deal with angular responses and linear predictors (Gould, 1969, Johnson and Wehrly, 1978 and Fisher and Lee, 1992). This type of model with linear explanatory variables and an angular response is referred to as linear-circular regression (Jammalamadaka and SenGupta, 2001).

The key concept in these angular regression models is the von Mises distribution, also known as the circular normal distribution. This distribution specifically deals with random variables on the interval of (−π, π]. The general von Mises distribution is the conditional distribution of the phase given the magnitude.

The von Mises distribution has the following form

$$p(\varphi \mid r)=\frac{e^{\kappa \cos (\varphi -\theta )}}{2\pi I_0(\kappa )}$$ (3.3)

where κ = r ρ/σ², −π ≤ ϕ, θ < π, and 0 ≤ κ < ∞. In the von Mises distribution, I₀(·) is the zeroth order modified Bessel function of the first kind. This conditional distribution is referred to as a von Mises with mean θ and concentration κ (Jammalamadaka and SenGupta, 2001). The von Mises distribution has a limiting normal distribution with mean θ and variance 1/κ when κ is large. The linear-circular regression models utilize the von Mises distribution conditional upon the population and sample magnitudes being unity. If κ is small, the von Mises distribution tends to the the uniform distribution. If κ is large, the distribution tends to look like a normal distribution with its two tails tied together at θ − π for positive θ and θ + π for negative θ through the ±π value.

Gould (1969) introduced a model for the phase angle which estimated the overall mean direction of each data point in terms of the the number of time points and the covariates modulus 2π. The modulus 2π is chosen because in a circular distribution the angle continues around 360 degrees or 2π just like a barber pole in complex variable space through time. Estimates for the coefficients of the covariates are obtained via an iterative process. However, in fMRI data the phase angle rarely wraps around more than once in time unless the SNR is extremely low as would be seen outside the brain. In addition the MLE estimates (Johnson and Wehrly, 1978) are non-unique in this model because the likelihood function has infinitely many equally high peaks. Thus this model by Gould (1969) will not be used.

Johnson and Wehrly (1978) introduced an alternative model to be used for angular response data with linear predictors. Their model assumed that the predictor variable u_1t was random with a known distribution rather than the fixed covariates that are usually assumed in fMRI. They also restricted the phase angle not to wrap around more than once. Using a von Mises distribution for the random covariates allowed them to derive the joint distribution for p(ϕ∣U). They also show that the maximum likelihood estimates for the mean angle γ₀ and the concentration κ are well defined for this model. However, this model has the drawback of needing to know the distribution of each u_1t. We often do not know the PDF or CDF of our predictor variables and tend to view them as fixed numbers that don’t originate from a known distribution. Also, their model only allowed for a single predictor u_1t. Thus this model by Johnson and Wherly (1978) will not be used.

Fisher and Lee (1992) generalized the Johnson and Wehrly model to allow for multiple predictor variables and eliminated the need for distributional assumptions on the design matrix. Their model assumes the angular observations ϕ₁, …, ϕ_n are temporally independent von Mises distributed with constant concentration parameter κ. In other words, each ϕ_t originates from a von Mises distribution with mean θ_t and concentration κ. We will use this model by Fisher and Lee (1992).

The fixed effect model for the mean of the phase angle over time is

$$E({\varphi }_t)={\theta }_t={\gamma }_0+g(w_t^{\prime }\gamma )$$ (3.4)

where γ₀ is the intercept and g(·) is a link function to ensure that the linear regression function of the design matrix $w_t^{\prime }\gamma$ is mapped to the interval −π to π. The link function that we will use (see Appendix A)

$$g(w_t^{\prime }\gamma )=2{\tan }_2^{-1}(\mathrm{sgn}(w_t^{\prime }\gamma )\left|w_t^{\prime }\gamma \right|)$$ (3.5)

includes any covariates. Since γ₀ includes the intercept, w_t doesn’t need to include it. In addition, the use of this link function scales the γ coefficients by 1/2 compared to the corresponding coefficients from the OLS and unwrapped OLS. This link function also scales the variances by 1/4; thus the Wald tests are the same for all three models. We will adjust the estimates for these scale factors in subsequent sections.

Fisher and Lee give us equations to obtain parameter estimates and draw inferences using the model in equation A.1 with the link function given in equation A.2, where ν = 1. Fisher and Lee also give us a solution for the large sample asymptotic variance of the estimated coefficient vector, var(γ̂), (see Appendix A) which will allow us to draw inferences on our covariates within γ, and for γ̂₀ using asymptotic Wald tests.

This now provides us with an estimate for the phase regression coefficients, γ, and their variances. The fitted phase time course can then be plotted to compare to the observed time course utilizing

$${\widehat{\varphi }}_t={\tan }_4^{-1}\left[\frac{\sin ({\widehat{\gamma }}_0+g(w_t^{\prime }\widehat{\gamma }))}{\cos ({\widehat{\gamma }}_0+g(w_t^{\prime }\widehat{\gamma }))}\right]$$

because, although g(·) is within −π to π, the addition of γ̂₀ may shift it out of this interval. We can then use a large sample normal approximation to test the hypothesis, H₀: γ_m = 0 verses H₁: γ_m ≠ 0 for the m^th element of γ using the constructed test statistics, ${\widehat{\gamma }}_m/\sqrt{\mathrm{var}({\widehat{\gamma }}_m)}$. Alternatively, one could set up linear contrast hypothesis tests and obtain the likelihood ratio statistic −2 log λ, then use the large sample asymptotic ${\chi }_d^2$ distribution or when d = 1 a signed likelihood ratio statistic $\mathrm{sign}({\widehat{\gamma }}_m)\sqrt{-2\log \lambda }$ that has a large sample asymptotic normal distribution to draw inferences.

4 Results with Simulated fMRI Phase-Only Data

In order to compare the three phase-only models: (1) OLS without unwrapping, (2) OLS with manual unwrapping and (3) the FL model with automatic unwrapping via angular regression, we use data simulated data from two separate cases.

Case one is where the baseline magnitude is large relative to the standard deviation (high SNR = β₀/σ) and the mean phase is not near the ±π boundary. For this case the three models should agree. Case two has a small baseline magnitude relative to the standard deviation (low SNR) and the mean phase is near the ±π boundary. In this case unwrapping is necessary to properly track the data and the models should differ in their interpretation of the data. This also represents the case that is usually encountered through space in real fMRI phase data.

We generated data to simulate activation in a voxel which is similar to that observed from a bilateral finger tapping fMRI block design experiment as described in the Section 5. The simulated time series consisted of n = 256 points where the true values for the data are known before random noise is added according to a pre-specified normal distribution. The simulated fMRI data was constructed according to a general non-linear model as described by Rowe and Logan (2005) which for the magnitude consists of an intercept β₀; a time trend coefficient β₁; and a coefficient β₂ for a reference function, related to a block experimental design. We also included regression coefficients for our phase change which consists of γ₀, γ₁, and γ₂, as before. This allows the complex-valued data to have the following form,

$$y_t=[({\beta }_0+{\beta }_1{x}_{1t}+{\beta }_2{x}_{2t})\cos ({\theta }_t)+{\eta }_{\mathit{Rt}}]+i[({\beta }_0+{\beta }_1{x}_{1t}+{\beta }_2{x}_{2t})\sin ({\theta }_t)+{\eta }_{\mathit{It}}]$$ (4.1)

where

$${\theta }_t={\gamma }_0+{\gamma }_1{u}_{1t}+{\gamma }_2{u}_{2t}$$ (4.2)

for t = 1, …, n, and (η_Rt, η_It) ~ N (0, σ² I₂).

After creating the data we obtained the corresponding phase time series by taking the four-quadrant inverse tangent of the imaginary component over the real component which we have previously shown to have the complicated distribution given in equation 2.3, which is normal for large SNR. For the current simulations we looked at two basic cases for the fMRI phase time series and fit both the standard OLS model along with the Fisher and Lee angular model to the data. We looked at the two fits graphically and examined the parameter estimates along with the variances of the parameter estimates for regression coefficients γ with each model. The two cases include a “control” case where there is no phase-wrap present and a “test” case where the issue of phase-wrap is present.

4.1 Case I: No Phase Wrap Present in the Data

We used the first time series which is our “control” case to compare the two models when OLS could be used with little concern and verify the Fisher and Lee model is working properly.

The first time series had an SNR= 10 with the true values being (β₀, β₁, β₂) = (0.5, 0.00001, 0.25), (γ₀, γ₁, γ₂) = (π/6, 1/255, π/36), and σ = 0.05. These three values are have been used before (Rowe, 2005). We obtained coefficients, coefficient standard errors, and model variance estimates for the OLS model without unwrapping (OLS), the OLS model with unwrapping (UNW) and the FL model to be as in Table 1. In Table 1 the FL model variance estimate is 1/κ̂ and all coefficient variances were multiplied by 10³ .

Table 1.

Control case estimated values. Coefficient variances were multiplied by 10³. FL non baseline coefficients were also multiplied by 2 and variances by 4 respectively.

	γ̂0	γ̂1	γ̂2	var(γ̂0)	var(γ̂1)	var(γ̂2)	σ̂2	z(γ̂2)
OLS	0.5198	0.0100	0.0788	0.0389	0.1160	0.0390	0.0100	12.6268
UNW	0.5198	0.0100	0.0788	0.0389	0.1160	0.0390	0.0100	12.6268
FL	0.5198	0.0099	0.0789	0.0392	0.1163	0.0391	0.0099	12.6161

As mentioned in Section 3.3, the effect of the link function is to scale the FL estimates of the nonbaseline phase coefficients, the γ’s by a factor of two smaller than those of the OLS model and a corresponding factor of four difference in coefficient variances although the model fits are identical. The decisions based on test statistics for H₀: γ₂ = 0 vs H₁: γ₂ ≠ 0 also agreed when using the large sample asymptotic 5% two sided critical value of 1.96. Repeating these simulations 10, 000 times confirmed the results.

In Fig. 1a the true phase signal is shown with the black line, the observed time series (with noise) is plotted with cyan and the Fisher and Lee fitted model is plotted as red. Since that the OLS and FL models give us identical curves when no phase-wrap is present we omitted the overlapping plot of the OLS curve.

Figure 1.

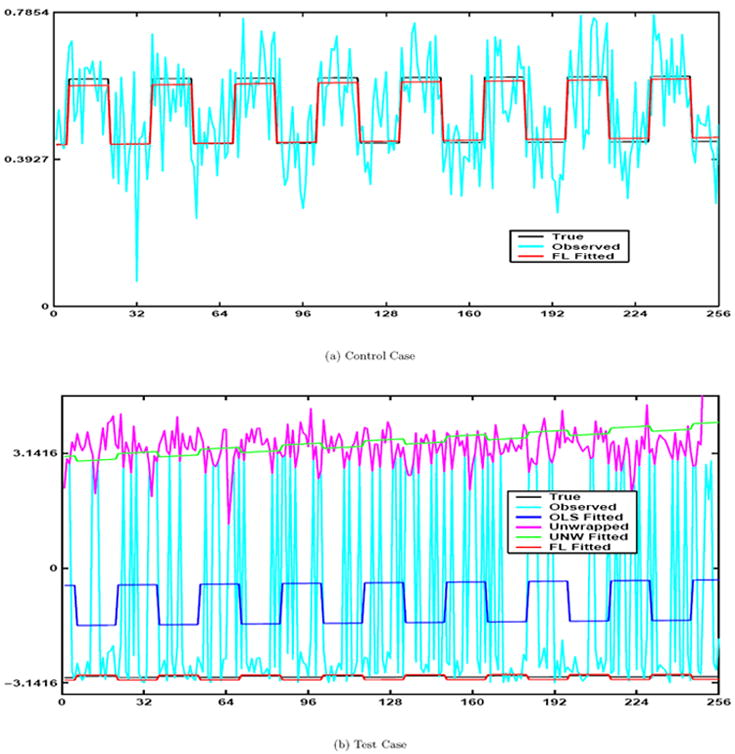
Part a: True signal (Black), observed signal (Cyan), and FL fitted line (Red). Part b: True signal (Black), observed signal (Cyan), OLS fitted line (Blue), unwrapped signal (Magenta), unwrapped OLS fitted (Green), and FL fitted line (Red)

4.2 Case II: Phase Wrap Present in the Data

The latter phase time series which is our “test” case will demonstrate to the reader that the OLS model poorly fits the data when the stringent conditions are not met. We will denote estimates of the phase regression coefficients under the unconstrained alternative hypothesis for the OLS model to be γ̂_OLS and those from the FL model with γ̂_FL The second time series has an SNR= 2.5 with identical β and σ² values (except for β₀ = σSNR) as the previous simulation but now with true values of (γ₀, γ₁, γ₂) = (−π + π/18, π/255, π/180). We obtain coefficient, coefficient standard errors, and model variance estimates for the OLS model without unwrapping (OLS), the OLS model with unwrapping (UNW) and the FL model to be as in Table 2. In Table 2 the FL model variance estimate is 1/κ̂ and all coefficient variances were multiplied by 10².

Table 2.

Test case estimated values. Coefficient variances were multiplied by 10². FL non baseline coefficients were also multiplied by 2 and variances by 4 respectively.

	γ̂0	γ̂1	γ̂2	var(γ̂0)	var(γ̂1)	var(γ̂2)	σ̂2	z(γ̂2)
OLS	-0.9467	0.0762	-0.5495	2.5239	7.5252	2.5281	6.4612	-3.4560
UNW	3.4466	0.4662	-0.0740	0.4053	1.2083	0.4059	1.0375	-1.1613
FL	-2.9858	0.0104	0.0678	0.0880	0.2609	0.0877	0.2001	2.2910

Note that the estimated mean angle γ̂₀ is different for the three methods and that only the FL angular model was consistent with the true value of −2.9671. Further, note that the decisions based on the test statistic z(γ̂₂) for H₀: γ₂ = 0 vs H₁: γ₂ ≠ 0 do not agree for the three methods when using a large sample asymptotic two sided 5 % critical value of 1.96.

By looking at Fig. 1b we can see that the red fitted FL angular regression model has a strong association with the phase time series values and we would agree with the FL decision in Table 1 that it is statistically significant. In Fig. 1b the true noiseless phase signal is shown with the black line, the simulated observed time series (with noise) is plotted with cyan, the OLS fitted model is signified with blue, the unwrapped data in magenta, the unwrapped OLS fitted values in green, and the FL fitted model is plotted as red. We see that the OLS and FL models no longer give us similar results. The OLS model does not fit the data well and is situated between most of the observations. We also see that the unwrapped OLS model does not fit the data well either. Also note that the OLS and UNW fitted time series are out of phase with the true time series unlike the fitted FL time series. The estimated values for the γ’s were much closer to the true values for the FL model compared with the OLS or OLS unwrapped model. Also, the variances for the FL estimates are much smaller especially for γ̂_2FL which is the coefficient of primary interest.

Repeating these simulations 10, 000 times confirmed that the mean baseline angle is very close to the true value for the FL model but far from the true value for the two other methods. The mean sample variance for the non-baseline coefficients and model variance from these 10, 000 estimates was also much smaller for the FL model.

5 Experimental Data

We now will compare the two models using actual experimental data. A bilateral sequential finger tapping experiment was performed in a block design with 16s off followed by eight epochs of 16s on and 16s off. Scanning was performed using a 1.5T GE Signa in which 5 axial slices of size 96 × 96 were acquired with a full k-space single shot gradient echo pulse sequence having a FA= 90° and a TE = 47ms. In image reconstruction, the acquired data was zero filled to 128 × 128. After Fourier image reconstruction, each voxel has dimensions in mm of 1.5625 × 1.5625 × 5. Observations were taken every TR= 1000 ms so that there are 272 in each voxel. Data from a single axial slice through the sensorimotor cortex was selected for analysis. Pre-processing included the removal of the first three points to omit magnetic field equalization effects followed by the use of an ideal 0/1 frequency filter (Gonzales and Woods, 1992; Press et al., 1992) for frequencies .1992 – .3398 Hz and .0078 – .0273 Hz to remove respiration, scanner drift, and low frequency physiological noise.

If the phase-only data contains no information regarding possible biological phenomena in the brain we would anticipate seemingly random activations above the threshold. If the phase-only data is to contain information regarding possible biological phenomena in the brain we would anticipate seeing phase activations with some sort of pattern. One possible pattern is to be in similar locations as the magnitude-only activations. The association between magnitude-only and phase-only time series observed by Menon for areas with large blood vessels would suggest phase activations can be found in similar places as magnitude activations, given that such blood vessels are present (Menon, 2002; Nencka and Rowe, 2005; Nencka and Rowe, 2006). Any similarities between the statistics for the magnitude-only and phase-only models would strengthen the idea that valuable temporal phase information is discarded when magnitude-only data is analyzed.

Even though the three phase-only models produce similar activation maps (as seen in Figure 3b-d), the parameter estimates are radically different. As seen in Fig. 2a-c, the estimated baseline phase angles, the γ₀’s are similar within the brain for the OLS model in Fig. 2a, the unwrapped OLS model in Fig. 2b, and the FL model in Fig. 2c, except for about a dozen voxels with the OLS model along two vertical wavy lines bordering a baseline ±π transition, but are all very different outside the brain. The same trends may be observed for γ₁ in Fig. 2d-f, γ₂ in Fig. 2g-i, and σ in Fig. 2j-l. Further note that the variance estimate for many voxels is lower with the FL model as compared to the other two models.

Figure 3.

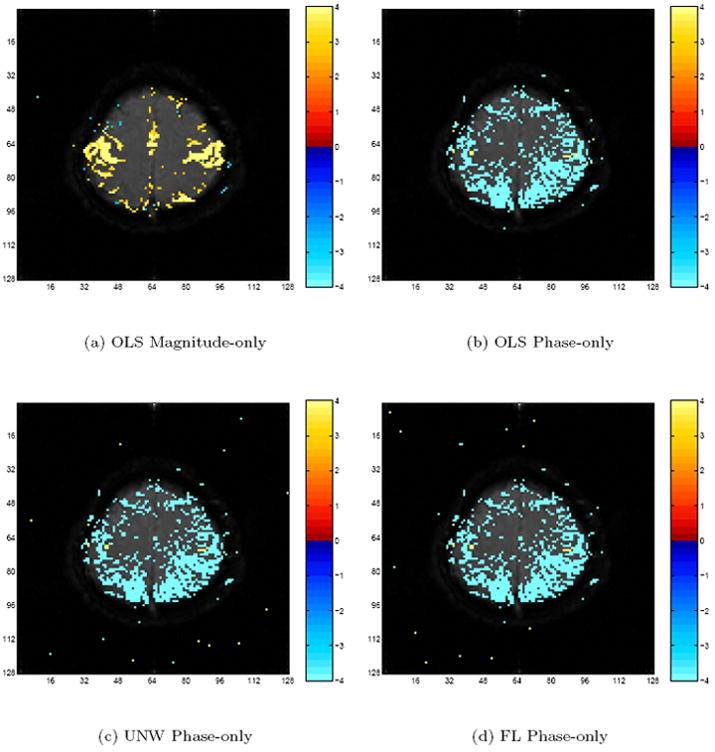
Magnitude-only and Phase-only data test statistics with 5% Bonferroni threshold.

Figure 2.

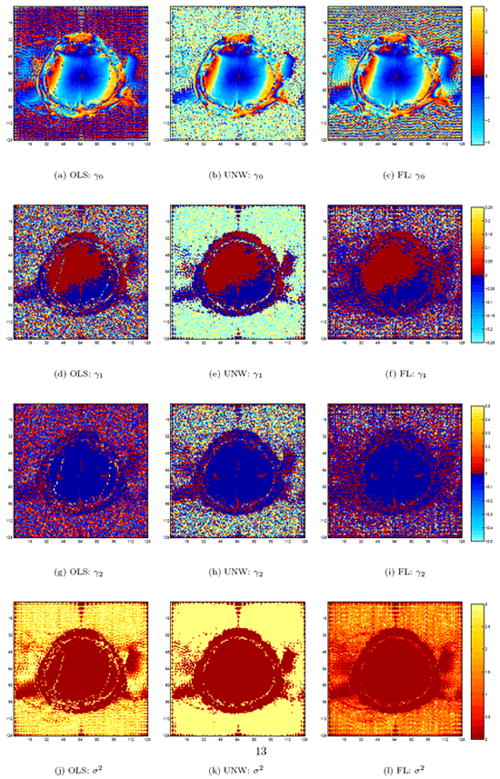
Estimated parameters for the three models.

5.1 Comparison of Phase-Only and Magnitude Model

Finally after examining the phase-only data, we looked at the magnitude-only data to compare the information added by the phase only model. An OLS model is fit to the magnitude-only time series in each voxel with design matrix X = U as previously described and magnitude-only regression coefficients β = (β₀, β₁, β₂)′. We computed activation t-statistics in each voxel testing the hypothesis of the coefficient corresponding to the reference function in the last column of X being zero.

The bilateral activation in the motor cortex regions for the magnitude-only OLS model can be seen in Fig. 3a along with the activation along the midline in the supplemental motor area. In Fig. 3a are t-statistics with a threshold that was Bonferroni corrected for multiple comparisons, as described in Logan and Rowe (2004), at a 5% family wise error (FWE) rate.

If the phase-only data contains no information regarding possible biological phenomena in the brain we would anticipate seemingly random activations above the threshold. If the phase-only data is to contain information regarding possible biological phenomena in the brain we would anticipate seeing phase activations with some sort of pattern. One possible pattern is to be in similar locations as the magnitude-only activations. The association between magnitude-only and phase-only time series observed by Menon for areas with large blood vessels would suggest phase activations can be found in similar places as magnitude activations, given that such blood vessels are present (Menon, 2002; Nencka and Rowe, 2005; Nencka and Rowe, 2006). Any similarities between the statistics for the magnitude-only and phase-only models would strengthen the idea that valuable temporal phase information is discarded when magnitude-only data is analyzed.

Although as seen in Fig. 3 b-d the three models produce similar thresholded phase-only activation maps with focal positivity associated voxel time series within the primary motor cortex which is where the diffuse magnitude-only activations were found. Even though the three phase-only models produce similar activation maps, the parameter estimates are radically different. This difference is especially prominent in low SNR areas such as outside the brain. Further note that the variance estimate for many voxels is lower with the FL model as compared to the other two models.

6 Conclusion

Modeling fMRI phase time series with OLS regression may result in some troublesome phenomena, which may include poor fit, incorrect parameter estimation, and potentially inaccurate test statistics, even after being unwrappped. Most of these problem arise from the issue of phase-wrap in the time series. We discussed using the linear-circular regression model proposed by Fisher and Lee (1992) to solve these problems. It allowed us to define a design matrix which could account for several regressors including a linear trend and a reference function from which to make and test hypothesis using a large sample asymptotic z statistic. We were able to implement a numeric algorithm given by Fisher and Lee to obtain our coefficient estimates, along with the variances of the coefficient estimates, and thus test hypotheses.

Simulations were performed for both a control case with no phase-wrap and a test case with phase-wrap present. In the case of no phase-wrap we found that the fitted line for the Fisher-Lee model was nearly identical to that of the OLS model, either with or without having been unwrapped. The test statistics also were very similar and the conclusion for each agreed. This would imply the models are equivalent under these conditions. In the generated time series where phase-wrap was present, we noted that the estimates for the Fisher-Lee model were much closer to the true values compared with the OLS model.

Also, the test statistics for the Fisher-Lee model differed from those for the OLS model and led to different conclusions with respect to γ₂, the coefficient of the reference function for the task, for the case with wrap-around. We also showed during our second set of simulations that the γ₂ estimates were more accurate and precise when we compared the Fisher-Lee model to the OLS models for the 10, 000 simulated phase-only data sets created with the same parameters.

The actual phase time series we presented support our findings that the Fisher-Lee model is an excellent choice for fitting with fMRI phase-only data. We showed a specific simulated voxel example where OLS was unable to match the modeling accuracy of the Fisher-Lee model and actually contained fitted values not consistent with the simulated fMRI phase angular property. Fisher and Lee’s model does not appear to be susceptible to low SNR problems, and if applied to other real data examples with more noise, we would expect it to perform at least as well as OLS. In real fMRI data that is of a higher resolution with smaller voxels and lower SNR, we expect there to be a larger difference between the two models. This newly implemented angular model does detect temporal correlations between the phase time course and a reference function in many of the same places as the OLS models. We suggest using the Fisher-Lee angular model as both a comparative tool along with an exploratory method for fMRI phase data. It may be more beneficial for the investigator to implement this new angular method on a voxel-wise basis where the fitted values can be compared to both the observed data and the OLS fits allowing the appropriate modeling decision to be made.

Finally, as we have shown with simulated data, the Fisher-Lee model has fewer assumptions that need to be met and often describes the data better compared with OLS regression.

A Appendix

Linear-circular regression models currently in the statistical literature that deal with angular responses and linear predictors were given by Gould (1969), Johnson and Wehrly (1978) along with Fisher and Lee (1992). Gould (1969) introduced a model which estimated the overall mean direction of each data point which assumes the phase angle continuously wraps around for every multiple of [-π, π]. Consequently, the MLEs are non-unique in this model because the likelihood function has infinitely many equally high peaks on successive intervals. Johnson and Wehrly (1978) introduced an alternative model assuming that the predictor variable u_1t was random with a known distribution, but this model has the drawback of requiring the specification of the distribution of the predictor variable u_1t. We rarely think of our predictor variables as being from a random distribution and usually treat them as fixed.

Subsequently, Fisher and Lee (1992) generalize the Johnson and Wehrly model to relax the need for distributional assumptions on the design matrix and allow for multiple predictor variables. Their model assumes the angular observations ϕ₁, …, ϕ_n are temporally independent von Mises distributed with constant concentration parameter κ. Each ϕ_t originates from a von Mises distribution with mean θ_t and concentration κ. The overall mean of the direction of each datapoint is

$${\theta }_t={\gamma }_0+g(w_t^{\prime }\gamma )$$ (A.1)

where the t^th row $w_t^{\prime }=(w_{1t},\dots ,w_{(q+1)t})$ of the design matrix W is comprised of all columns except the first in the design matrix U. There is no need to include the baseline column in W, because the intercept is already estimated within the model. The link function g(·) has the purpose of mapping its argument to be in −π to π. The use of a link function eliminates the non-identifiability problem of MLEs that is present in the Gould model. One of the possible link functions given by Fisher and Lee is

$$g(·)=2{\tan }_2^{-1}(\mathrm{sgn}(·){|·|}^{\nu })$$ (A.2)

where sgn(·) is the operator that returns the sign of its argument, ${\tan }_2^{-1}(·)$ is a two quadrant inverse tangent, and the transformation parameter ν can be estimated from the data similar to the Box-Cox transformation (Box and Cox, 1964; Fisher and Lee, 1992).

Fisher and Lee give equations to obtain parameter estimates and draw inferences using the model in equation A.1 with the link function given in equation A.2, where ν = 1. For this choice of the link function, first define the natural log likelihood, denoted log L to be

$$\log L=-n\log 2\pi -n\log I_0(\kappa )+\kappa \sum _{t=1}^n\cos ({\varphi }_t-{\gamma }_0-g(w_t^{\prime }\gamma )).$$ (A.3)

Then Fisher and Lee define the following

$$\begin{array}{lll}{\upsilon }_t& =& \sin ({\varphi }_t-{\gamma }_0-g(w_t^{\prime }\gamma )),\\ \upsilon & =& {({\upsilon }_1,\dots ,{\upsilon }_n)}^{\prime },\\ W& =& {(w_1,\dots ,w_n)}^{\prime }\\ G& =& \mathrm{diag}(g^{\prime }(w_t^{\prime }\gamma ),\dots ,g^{\prime }(w_n^{\prime }\gamma ))\\ S& =& \frac{1}{n}\sum _{t=1}^n\sin ({\varphi }_t-g(w_t^{\prime }\gamma ))\\ C& =& \frac{1}{n}\sum _{t=1}^n\cos ({\varphi }_t-g(w_t^{\prime }\gamma ))\\ R& =& {(S^2+C^2)}^{1/2}.\end{array}$$

In the above ν is an n × 1 vector and G is a n × n matrix while S, C, and R are scalars. The function g′(·) is defined to be the derivative of the link function which in our example is $g^{\prime }(w_t^{\prime }\gamma )=2/[1+{(w_t^{\prime }\gamma )}^2]$. The MLEs are found by solving the following equations

$$\begin{array}{ccc}\hfill W\text{'}G\upsilon & =& 0,\hfill \\ \hfill {\tan }_4({\widehat{\gamma }}_0)& =& S/C,\hfill \\ \hfill A(\widehat{\kappa })& =& R\hfill \end{array}$$

where A(κ̂) = I₁(κ̂)/I₀(κ̂). The second equation above involving the four quadrant tangent of γ̂₀ is found by utilizing the trigonometric addition formula for ${\gamma }_0-({\varphi }_t-g(w_t^{\prime }\gamma ))$ in the log likelihood before differentiation. Fisher and Lee describe an iterative procedure for finding a solution to these equations. They suggest centering the individual columns of W around their means will optimize the numeric calculations. Starting with an initial value for γ̂ and calculating values for S, C, and R from the above equations. An updated value of γ̂, denoted by γ̂^* is then found by solving the following equation for γ̂^*,

$$(W\prime G^{2}W)({\widehat{\gamma }}^{\ast }-\widehat{\gamma })=W\prime G^{2}y$$ (A.4)

where y = (y₁, … , y_n)′ and $y_t={\upsilon }_t/[A(\widehat{\kappa })g^{\prime }(w_t^{\prime }\widehat{\gamma })]$. We also find an updated estimate for γ₀ at each iteration by computing γ̂₀ from the four quadrant inverse tangent ${\tan }_4^{-1}(S/C)$ and κ from A(κ). The updated estimate of γ̂^* is used recursively. When it is a priori known that κ is “large” then the approximation

$$A(\kappa )=\left(1-\frac{1}{2\kappa }-\frac{1}{8\kappa }-\cdots \right)$$

can be utilized while if it is a priori known that κ is “small” then the approximation

$$A(\kappa )=\frac{\kappa }{2}\left(1-\frac{{\kappa }^2}{8}+\frac{{\kappa }^4}{48}-\cdots \right)$$

can be utilized (Jammalamadaka and SenGupta, 2001). When κ is above 1.25, the large κ approximation works well and one can simply approximate κ̂ by

$$\widehat{\kappa }=\frac{1+\sqrt{3-2R}}{4(1-R)}$$ (A.5)

while if κ is below .75, then one can simply approximate κ̂ by

$$\widehat{\kappa }=2R.$$ (A.6)

for intermediate values, a simple average works well.

Fisher and Lee solved for the large sample asymptotic variance of the estimated coefficient vector,

$$\mathit{var}(\widehat{\gamma })=\frac{1}{\widehat{\kappa }A(\widehat{\kappa })}\left\{{(W^{\prime }{G}^{2}W)}^{-1}+\frac{{(W^{\prime }{G}^{2}W)}^{-1}{W}^{\prime }g{g}^{\prime }W{(W^{\prime }{G}^{2}W)}^{-1}}{\left(n-g^{\prime }W{(W^{\prime }{G}^{2}W)}^{-1}{W}^{\prime }g\right)}\right\},$$

which allows us to draw inferences on our γ’s where g is a vector whose elements are the diagonal elements of G. They also describe the large sample asymptotic variance for γ̂₀ and κ̂ to be equal to ${[(n-q)\widehat{\kappa }A(\widehat{\kappa })]}^{\frac{1}{2}}$ and 1/(nA′(k̂)), respectively, where A′(κ) = 1 − A(κ)/κ − A²(κ) is the derivative of the ratio of the Bessel functions with respect to κ. The variance of the large sample asymptotic normal limiting distribution of the von Mises is 1/κ (Jammalamadaka and SenGupta, 2001).