Abstract
It is difficult for radiologists to classify pneumoconiosis with small nodules on chest radiographs. Therefore, we have developed a computer-aided diagnosis (CAD) system based on the rule-based plus artificial neural network (ANN) method for distinction between normal and abnormal regions of interest (ROIs) selected from chest radiographs with and without pneumoconiosis. The image database consists of 11 normal and 12 abnormal chest radiographs. These abnormal cases included five silicoses, four asbestoses, and three other pneumoconioses. ROIs (matrix size, 32 × 32) were selected from normal and abnormal lungs. We obtained power spectra (PS) by Fourier transform for the frequency analysis. A rule-based method using PS values at 0.179 and 0.357 cycles per millimeter, corresponding to the spatial frequencies of nodular patterns, were employed for identification of obviously normal or obviously abnormal ROIs. Then, ANN was applied for classification of the remaining normal and abnormal ROIs, which were not classified as obviously abnormal or normal by the rule-based method. The classification performance was evaluated by the area under the receiver operating characteristic curve (Az value). The Az value was 0.972 ± 0.012 for the rule-based plus ANN method, which was larger than that of 0.961 ± 0.016 for the ANN method alone (P ≤ 0.15) and that of 0.873 for the rule-based method alone. We have developed a rule-based plus pattern recognition technique based on the ANN for classification of pneumoconiosis on chest radiography. Our CAD system based on PS would be useful to assist radiologists in the classification of pneumoconiosis.
Keywords: Computer-aided diagnosis (CAD), Pneumoconiosis, Chest radiography, Power spectra, Artificial neural network
Introduction
Pneumoconiosis is classified as either fibrotic or non-fibrotic [1]. Silicosis, coal worker’s pneumoconiosis, and asbestosis are types of fibrotic pneumoconiosis [1]. In an individual with a history of exposure to silica or coal dust, nodular and/or reticulonodular patterns are suggestive of silicosis or coal worker’s pneumoconiosis on chest radiography [1]. The International Labour Organization has established a standardized system for classifying radiographic abnormalities of pneumoconiosis. On chest radiographs, silicosis appears as small and round irregular opacities while asbestosis appears as small irregular opacities [2]. Thus, it is difficult for radiologists to classify pneumoconiosis with small nodular and irregular opacities on chest radiographs. Therefore, a computer-aided diagnosis (CAD) system for detection of pneumoconiosis on chest radiographs has been developed to improve detection performance by radiologists [3–6]. Turner et al. investigated the use of texture analysis and hybrid optical–digital methods with Fourier transform for the detection of pneumoconiosis in coal workers [4]. In addition, to assist radiologists in interpreting interstitial lung disease on chest radiographs, a number of researchers have developed a texture analysis method [7–12] based on the Fourier transform and a geometric pattern feature analysis method [13–15]. In the texture analysis method with root mean square variation and first moment of the power spectrum (PS), abnormal lungs with various interstitial diseases can clearly be distinguished from the normal lung [7]. Using a combined rule-based method with texture analysis and the geometric pattern feature analysis plus artificial neural network (ANN) method, a high specificity of 96.1% was obtained at a sensitivity of 95.0% [14]. Monnier-Cholley et al. showed that radiologists’ performance in detecting interstitial lung disease was improved by these CAD schemes [12].
The ANN was used in many fields as a powerful classification tool. Specifically, ANNs have been applied for distinction between lesions and non-lesions [16–21] and for distinction between malignant and benign lesions [22–24] in CAD schemes. A multi-massive training artificial neural network (multi-MTANN) reduced the false positive rate of CAD schemes from 4.5 to 1.4 false positives per image at an overall sensitivity of 81.3% [20]. The training of each MTANN in the multi-MTANN was performed 500,000 times. Training took a central processing unit (CPU) time of 29.8 h on a PC-based workstation [20] because the training region in input images was divided on a pixel-by-pixel basis into a large number of overlapping subregions [20]. In addition, it was found that the ANN could distinguish clustered microcalcifications from normal non-clustered areas based on the PS values. However, there have been no studies regarding the distinction between normal and abnormal patterns in pneumoconiosis using the ANN trained with the PS values. Therefore, we have developed a CAD system based on the rule-based plus ANN method for distinction between normal and abnormal regions of interest (ROIs) selected from chest radiographs with and without pneumoconiosis. To investigate the basic characteristic of the trained ANN, we also investigated the effects on overall performance with simulated lesions using various parameters.
Materials and Methods
Materials
We used an image database that consisted of 11 normal and 12 abnormal posteroanterior chest radiographs. Eleven normal chest radiographs were selected randomly from the publicly available digital image database collected by the Japanese Society of Radiological Technology. The absence or presence of nodules on the chest radiographs was confirmed by computed tomography. These chest radiographs were confirmed to be from normal cases by three chest radiologists. Twelve abnormal chest radiographs were selected randomly from the digital image database developed by the Ministry of Labor. These abnormal cases include five cases of silicosis, four of asbestosis, and three of other pneumoconioses. These images were digitized with a pixel size of 0.175 mm; matrix sizes of 2,034 × 2,034 and 2,048 × 2,048; and 12-bit grayscale.
Preprocessing of ROI Images
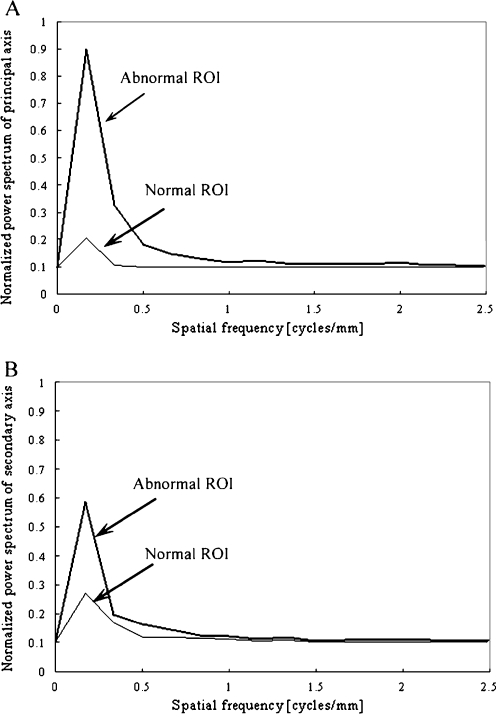
ROIs (matrix size, 32 × 32) were selected from normal and abnormal lungs between ribs and over rib spaces [7]. We obtained a background trend correction in selected ROIs using a two-dimensional surface-fitting technique based on the least-squares method because pixel values were different between perihilar and peripheral regions on chest radiographs [7]. We obtained 112 ROIs from both abnormal and normal lungs. We obtained the background trend correction with second-order polynomial surfaces. We then determined the PS values in these ROIs by fast Fourier transform. We used only PS values on the principal and secondary axes, which have the maximum and the second maximum PS values on the radial line from the central point, respectively. We used the PS values of the plus side on spatial frequency because they were symmetrical to the central point [24]. The PS values were linearly normalized from 0.1 to 0.9 such that they ranged from 0 to 10 [7]. Compared with the PS values of the normal ROIs, the PS values of the abnormal ROIs were higher at low spatial frequency of the principal and secondary axes regardless of where the abnormal patterns were placed within the ROI (Fig. 1).
Fig. 1.
Comparison of PS values for abnormal and normal ROIs on a the principal axis and b the secondary axis
Rule-Based Method
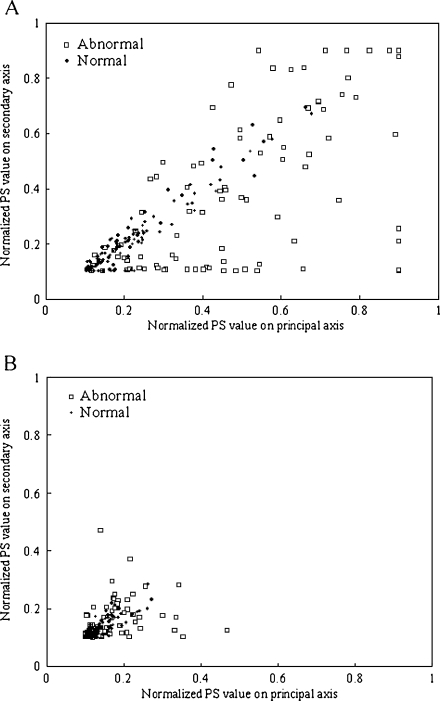
A rule-based method using PS values at 0.179 and 0.357 cycles per millimeter, corresponding to the spatial frequencies of nodular patterns, was used for identification of obviously normal or obviously abnormal ROIs. Figure 2a, b shows the relationship between the normalized PS values of 0.179 and 0.357 cycles per millimeter of the principal and secondary axes. The distribution for the normal ROIs was shifted to the lower left, whereas that for the abnormal ROIs was shifted to the upper right. There was a considerable overlap between the two distributions because lung textures in the abnormal ROIs can consist of complicated texture patterns (nodular, reticular, and reticulonodular patterns), and some normal areas were spread throughout the entire lung. If the values for the abnormal ROIs were higher than that of the maximum normal ROI, these abnormal ROIs were classified as “obviously” abnormal. If the values for the normal ROIs were lower than that of the minimum abnormal ROI, these were classified as “obviously” normal.
Fig. 2.
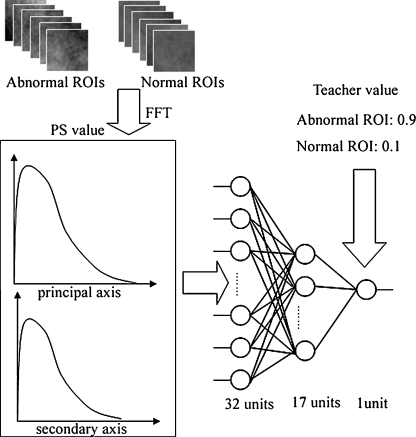
Architecture and training of the ANN for distinction between abnormal and normal ROIs. In this procedure, the normalized PS values in abnormal and normal ROIs were entered as input to ANN. The ANN was trained such that the output value was 0.9 on the abnormal ROIs and the output value was 0.1 on the normal ROIs
Artificial Neural Network Method
ANN has been used in many fields as a powerful classification tool. We used the ANN with a back propagation algorithm. The ANN was composed of three units consisting of input, hidden, and output layers, and the ANN was composed of 32 input units, 17 hidden units, and one output unit (Fig. 3). The ANN is trained with input values and a corresponding training value for the enhancement of specific patterns and suppression of other patterns [18–20, 23]. It is important to note that training with “0.1” for normal patterns and “0.9” for abnormal patterns is intended to distinguish between the abnormal and normal ROIs using the ANN. The input data consisted of a total of 32 pieces (16 normalized PS values for each of the principal and secondary axes). Comparing the input data with the total of 1,024 pieces (ROI with matrix size 32 × 32), training time of the ANN can be shortened in this study. To evaluate the classification performance by the ANN method, we randomly divided the data into 112 abnormal ROIs and 112 normal ROIs, and obtained training data (56 abnormal ROIs and 56 normal ROIs) and non-training data (56 abnormal ROIs and 56 normal ROIs). Finally, the average classification performance for the ANN method alone was determined using ten different training data and non-training data sets. The statistical significance of differences between receiver operating characteristic (ROC) curves was determined by the application of a two-tailed paired t test to the Az values of the non-training data sets.
Fig. 3.
Relationship between normalized PS values on the principal and secondary axes obtained from a 0.179 and b 0.357 cycles per millimeter from the origin of the coordinates in the normal and abnormal ROIs
Rule-Based Plus ANN Method
The rule-based method was employed for the identification of obviously normal and abnormal ROIs. The rule-based method was applied to the total number of abnormal and normal ROIs (112 abnormal ROIs and 112 normal ROIs). The ANN method was applied for the classification of the remaining ROIs, which were not classified as obvious cases by the rule-based method [15]. Thus, the rule-based plus ANN method was applied to the remaining abnormal and normal ROIs (54 abnormal ROIs and 89 normal ROIs). We randomly divided the data into 54 abnormal ROIs and 89 normal ROIs, and obtained the training data (27 abnormal ROIs and 44 normal ROIs) and the non-training data (27 abnormal ROIs and 45 normal ROIs). Finally, the average classification performance for the rule-based plus ANN method was determined using five different training data and non-training data sets. The statistical significance of differences between ROC curves was determined by the application of a two-tailed paired t test to the Az values of the non-training data sets.
Effects of Various Parameters with Simulated Lesions on ANN Method Alone
To investigate the basic characteristics of the ANN method alone, we created simulated abnormal patterns. Twenty-two spherical polyurethane resins (2 mm in diameter; Kyotokagaku Co., Ltd., Kyoto, Japan) were set on the imaging plate in a random manner. We obtained ten images (five images with and without the polyurethane resin) with the same parameters (60 kV, 100 mA, 0.16 s). These images were digitized with a Fuji Computed Radiography system (Fuji Medical Systems Co., Ltd., Tokyo, Japan). These images were digitized with a pixel size of 0.1 mm; matrix size of 1,770 × 2,370; and 12-bit grayscale. The ROI was selected manually at the center of the simulated abnormal pattern. In the same manner as described above, we obtained the training data (55 simulated abnormal ROIs and 55 non-simulated abnormal ROIs) and non-training data (55 simulated abnormal ROIs and 55 non-simulated abnormal ROIs). The ANN was trained such that the output value was 0.9 on the simulated abnormal ROIs and 0.1 on the non-simulated abnormal ROIs. For the classification performance on the non-training data, we investigated the effects of the alignment of simulated abnormal patterns, noise, number of training samples, and pixel size.
Results and Discussion
Simulation Experiments
Alignment of Simulated Abnormal Patterns
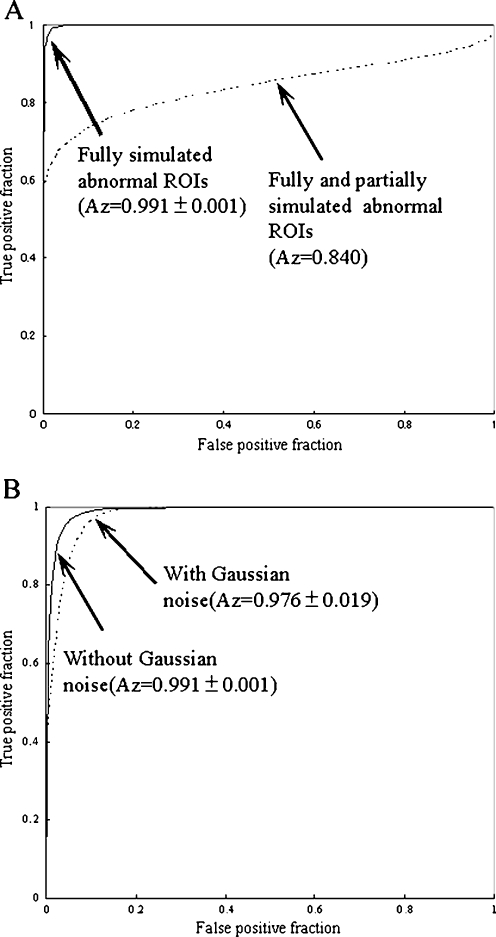
We obtained 49 ROIs with a fully simulated abnormal pattern, 73 ROIs with a partially simulated abnormal pattern, and 142 ROIs with a non-simulated abnormal pattern in the non-training data. Figure 4a shows ROC curves for the distinction between the fully simulated abnormal ROIs and fully and partially abnormal ROIs and the non-simulated abnormal ROIs with the non-training data. The Az value (0.991 ± 0.001) for the fully simulated abnormal ROIs was larger than this value (0.8398) for the fully and partially simulated abnormal ROIs. In addition, comparing the Az value for the fully simulated abnormal ROIs with those for the fully and partially simulated abnormal ROIs, the classification performance on the fully and partially simulated abnormal ROIs was decreased by 0.158. However, using only the training data with and without the fully simulated abnormal patterns, the ANN method distinguished between the fully and partially simulated abnormal ROIs and the non-simulated abnormal ROIs. Thus, the ANN method showed high classification performance regardless of where the partially abnormal patterns (nodular patterns, reticular patterns, etc.) were placed in the ROIs.
Fig. 4.
Effects of a the alignment in the simulated abnormal ROIs and b Gaussian noise on the classification performance for the non-training data
Effects of Gaussian Noise
To evaluate the effects of noise, we obtained training and non-training data with Gaussian noise (S.D. = 3) because the contrast was 6 pixels between the simulated abnormal pattern and background, as the ratio of contrast and S.D. was 2:1. Figure 4b shows the effects of Gaussian noise on the ROC curves for the fully simulated abnormal ROIs with the non-training data. The Az value (0.991 ± 0.001) for the fully simulated abnormal ROIs without Gaussian noise was larger than the value (0.976 ± 0.019) for fully simulated abnormal ROIs with Gaussian noise (P = 0.09). System noise can be considered as a combination of several noise sources, including (1) increased electronic noise of the laser scanner due to low signal-to-noise ratio at high pixel values, (2) increased quantum mottle at low pixel values, (3) increased quantization noise of laser scanner at low pixel values, and (4) interference artifacts caused by the laser beam [11]. Therefore, we believe that the ANN method is required to distinguish between the simulated abnormal patterns and the simulated normal patterns because the differences in classification performance with and without this noise were relatively small.
Effects of Pixel Size
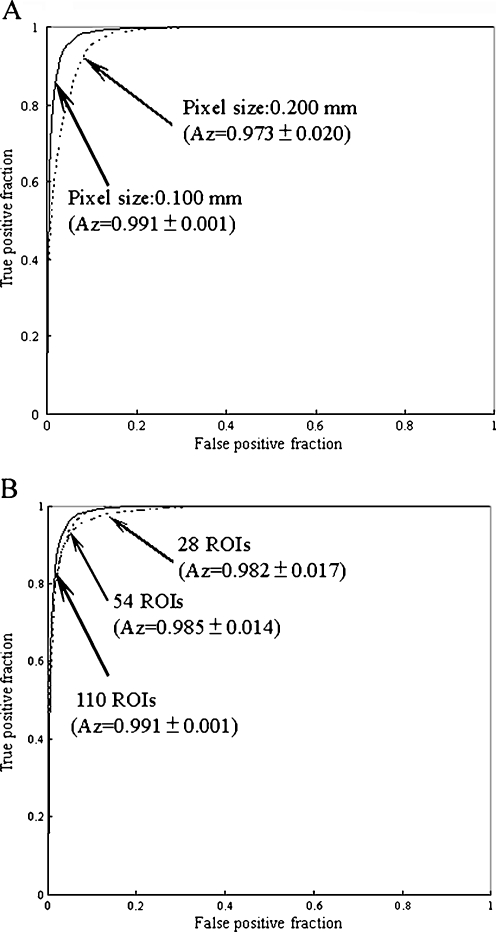
To evaluate the effects of pixel size, we obtained training and non-training data with pixel sizes between 0.10 and 0.20 mm. Figure 5a shows the effects of pixel size on ROC curves for the fully simulated abnormal ROIs with the non-training data. The Az value (0.991 ± 0.001) for the fully simulated abnormal ROIs with a pixel size of 0.10 mm was larger than the value (0.973 ± 0.020) for the fully simulated abnormal ROIs with a pixel size of 0.20 mm (P = 0.03). The area under the ROC curve increased as the pixel size decreased. These results indicated that classification performance of this computerized method improved at smaller pixel sizes [8]. However, a small pixel size resulted in a long image processing time. Thus, it may be reasonable to employ a pixel size of 0.10 mm, as the difference in ROC curves between pixel sizes of 0.10 and 0.20 mm was relatively large.
Fig. 5.
Effects of a pixel size and b the number of training samples on the classification performance for the non-training data
Effects of Number of Training Samples
To evaluate the effects of the number of training samples, we changed the numbers of training and non-training data. Figure 5b shows the effects of the number of training samples on the classification performance for the non-training data. Note that a set with a large number of training samples included a set with a small number of training samples. The Az value (0.991 ± 0.001) for 110 training samples (55 simulated abnormal ROIs and 55 non-simulated abnormal ROIs) was larger than the value (0.985 ± 0.014) for 54 training samples (27 simulated abnormal ROIs and 27 non-simulated abnormal ROIs) (P = 0.19). With a larger number of training samples, the ANN was trained for distinction between the simulated abnormal ROIs and the non-simulated abnormal ROIs in various cases.
Classification Performance by Overall Scheme
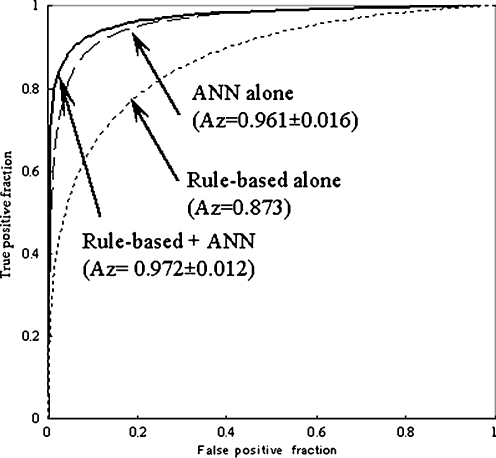
Figure 6 shows the ROC curve obtained for classification with the rule-based method alone, the ANN method alone, and the rule-based plus ANN method. The Az value was 0.972 ± 0.012 for the rule-based plus ANN method, which was larger than the value of 0.961 ± 0.016 for the ANN method alone (P = 0.15) and that of 0.873 for the rule-based method alone. It should be noted that the rule-based plus ANN method showed a higher classification performance than either method alone. The classification performance obtained with the ANN method alone was superior to that with the rule-based method. These results indicated that the overall classification performance was improved if the easy ROIs were eliminated initially by the rule-based method and only the remaining difficult ROIs were classified by the ANN method [15]. This is probably because the ANN showed improved classification performance using various patterns of abnormal and normal ROIs included in training data.
Fig. 6.
ROC curves obtained from various classification methods with the rule-based method alone, the ANN method alone, and the rule-based plus ANN method
At a sensitivity of 95%, the specificity was 83.7 ± 7.9% for the rule-based plus ANN method which was larger than the value of 79.2 ± 10.3% for the ANN method alone. The classification performance in the present study was slightly lower than those in previous studies of CAD for the classification with interstitial lung disease [14, 15]. This is because the overall classification performance was affected by false negatives, which may be classified incorrectly as obvious ROIs in the rule-based method. Therefore, to improve classification performance, further advances in CAD systems are required. For example, each ANN is trained independently for typical texture patterns and different types of normal lung (small round opacities and soft tissue opacity, etc.) [18, 19]. A multi-ANN may show the highest classification performance.
For the highest classification performance on ANN, the training took a CPU time of approximately 180 s. In comparison with MTANN using chest radiographs [19], the training times here were short, as the number of input data (32 units) in this study was smaller than that of the input data (81 units) in MTANN. However, it was necessary to obtain large training samples (112 ROIs) in this study. Therefore, by obtaining a large number of overlapping subregion ROIs with smaller matrix size, it may be possible for ANN to obtain high classification performance to distinguish between abnormal and normal lung with fewer cases.
Conclusion
We have developed a rule-based plus pattern recognition technique based on the ANN for classification of pneumoconiosis on chest radiography. Our CAD system based on PS would be useful to assist radiologists in the diagnosis of pneumoconiosis.
References
- 1.Chong S, Lee KS, Chung MJ, Han J, Kwon OJ, Kim TS. Pneumoconiosis: comparison of imaging and pathologic finding. Radiographics. 2006;26(1):59–77. doi: 10.1148/rg.261055070. [DOI] [PubMed] [Google Scholar]
- 2.Guidelines for the use ILO international classification of radiographs of pneumoconiosis. Genva: ILO; 1980. [DOI] [PubMed] [Google Scholar]
- 3.Muir DC, Bernholz CD, Morgan WK, Roos JO, Chan J, Maehle W, Julian JA, Sebestyen A. Classification of chest radiographs for pneumoconiosis: a comparison of two methods of reading. Br J Ind Med. 1992;49:869–871. doi: 10.1136/oem.49.12.869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Turner AF, Kruger RP, Thompson WB. Automated computer screening of chest radiographs for pneumoconiosis. Invest Radiol. 1976;11(4):258–66. doi: 10.1097/00004424-197607000-00002. [DOI] [PubMed] [Google Scholar]
- 5.Ledley RS, Huang HK, Rotolo LS. A texture analysis method in classification of coal workers’ pneumoconiosis. Comput Biol Med. 1975;5(1–2):53–67. doi: 10.1016/0010-4825(75)90018-9. [DOI] [PubMed] [Google Scholar]
- 6.Hall EL, Crawford WO, Jr, Roberts FE. Computer classification of pneumoconiosis from radiographs of coal workers. IEEE Trans Biomed Eng. 1975;22(6):518–527. doi: 10.1109/TBME.1975.324475. [DOI] [PubMed] [Google Scholar]
- 7.Katsuragawa S, Doi K, MacMahon H. Image feature analysis and computer-aided diagnosis in digital radiography: detection and characterization of interstitial lung disease in digital chest radiographs. Med Phys. 1988;15(3):311–319. doi: 10.1118/1.596224. [DOI] [PubMed] [Google Scholar]
- 8.Katsuragawa S, Doi K, Nakamori N, MacMahon H. Image feature analysis and computer-aided diagnosis in digital radiography: effect of digital parameters on the accuracy of computerized analysis of interstitial disease in digital chest radiographs. Med Phys. 1990;17(1):72–78. doi: 10.1118/1.596530. [DOI] [PubMed] [Google Scholar]
- 9.Katsuragawa S, Doi K, MacMahon H, Nakamori N, Sasaki Y, Fennessy JJ. Quantitative computer-aided analysis of lung texture in chest radiographs. Radiographics. 1990;10(2):257–269. doi: 10.1148/radiographics.10.2.2326513. [DOI] [PubMed] [Google Scholar]
- 10.Chen X, Doi K, Katsuragawa S, MacMahon H. Automated selection of regions of interest for quantitative analysis of lung textures in digital chest radiographs. Med Phys. 1993;20(4):975–982. doi: 10.1118/1.596979. [DOI] [PubMed] [Google Scholar]
- 11.Morishita J, Doi K, Katsuragawa S, Monnier-Cholley L, MacMahon H. Computer-aided diagnosis for interstitial infiltrates in chest radiographs: optical-density dependence of texture measures. Med Phys. 1995;22(9):1515–1522. doi: 10.1118/1.597419. [DOI] [PubMed] [Google Scholar]
- 12.Monnier-Cholley L, MacMahon H, Katsuragawa S, Morishita J, Ishida T, Doi K. Computer-aided diagnosis for detection of interstitial opacities on chest radiographs: Evaluation by means of ROC analysis. AJR Am J Roentgenol. 1998;171(6):1651–1656. doi: 10.2214/ajr.171.6.9843307. [DOI] [PubMed] [Google Scholar]
- 13.Katsuragawa S, Doi K, MacMahon H, Monnier-Cholley L, Morishita J, Ishida T. Quantitative analysis of geometric-pattern features of interstitial infiltrates in digital chest radiographs: preliminary results. J Digit Imaging. 1996;9(3):137–144. doi: 10.1007/BF03168609. [DOI] [PubMed] [Google Scholar]
- 14.Ishida T, Katsuragawa S, Kobayashi T, MacMahon H, Doi K. Computerized analysis of interstitial disease in chest radiographs: Improvement of geometric-pattern feature analysis. Med Phys. 1997;24:915–924. doi: 10.1118/1.598012. [DOI] [PubMed] [Google Scholar]
- 15.Katsuragawa S, Doi K, MacMahon M, Monnier-Cholley L, Ishida T, Kobayashi T. Classification of normal and abnormal lung with interstitial disease by rule-based method and artificial neural networks. J Digit Imaging. 1997;10(3):108–114. doi: 10.1007/BF03168597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shiraishi J, Li F, Doi K. Computer-aided diagnosis for improved detection of lung nodules by use of posterior-anterior and lateral chest radiographs. Acad Radiol. 2007;14:28–37. doi: 10.1016/j.acra.2006.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shiraishi J, Li Q, Suzuki K, Engelmann R, Doi K. Computer-aided diagnostic scheme for the detection of lung nodules on chest radiographs: localized search method based on anatomical classification. Med Phys. 2006;33:2642–2653. doi: 10.1118/1.2208739. [DOI] [PubMed] [Google Scholar]
- 18.Suzuki K, Armato SG, Li F, Sone S, Doi K. Massive training artificial neural network (MTANN) for reduction of false positive in computerized detection of lung nodules in low-dose computed tomography. Med Phys. 2003;30:1602–1617. doi: 10.1118/1.1580485. [DOI] [PubMed] [Google Scholar]
- 19.Suzuki K, Shiraishi J, Abe H, MacMahon H, Doi K. False-positive reduction in computer-aided diagnostic scheme for detecting nodules in chest radiographs by means of massive training artificial neural network. Acad Radiol. 2005;12:191–201. doi: 10.1016/j.acra.2004.11.017. [DOI] [PubMed] [Google Scholar]
- 20.Suzuki K, Doi K. How can a massive training artificial neural network (MTANN) be trained with a small number of cases in the distinction between nodules and vessels in thoracic CT? Acad Radiol. 2005;12:1333–1341. doi: 10.1016/j.acra.2005.06.017. [DOI] [PubMed] [Google Scholar]
- 21.Nakamura K, Yoshida H, Engelmann R, MacMahon H, Katsuragawa S, Ishida T, Ashizawa K, Doi K. Computerized analysis of the likelihood of malignancy in solitary pulmonary nodules with use of artificial neural networks. Radiology. 2000;214:823–830. doi: 10.1148/radiology.214.3.r00mr22823. [DOI] [PubMed] [Google Scholar]
- 22.Aoyama M, Li Q, Katsuragawa S, MacMahon H, Doi K. Automated computerized scheme for distinction between benign and malignant solitary pulmonary nodules on chest images. Med Phys. 2002;29(5):701–708. doi: 10.1118/1.1469630. [DOI] [PubMed] [Google Scholar]
- 23.Suzuki K, Li F, Sone S, Doi K. Computer-aided diagnostic scheme for distinction between benign and malignant nodules in thoracic low-dose CT by use of massive training artificial neural network. IEEE Trans Med Imaging. 2005;24:1138–1150. doi: 10.1109/TMI.2005.852048. [DOI] [PubMed] [Google Scholar]
- 24.Wu Y, Doi K, Giger ML, Hikawa RM. Computerized detection of clustered microcalcifications in digital mammograms: Applications of artificial neural networks. Med Phys. 1992;19(3):555–560. doi: 10.1118/1.596845. [DOI] [PubMed] [Google Scholar]