Regional Context-Sensitive Support Vector Machine Classifier to Improve Automated Identification of Regional Patterns of Diffuse Interstitial Lung Disease

Abstract

We propose the use of a context-sensitive support vector machine (csSVM) to enhance the performance of a conventional support vector machine (SVM) for identifying diffuse interstitial lung disease (DILD) in high-resolution computerized tomography (HRCT) images. Nine hundred rectangular regions of interest (ROIs), each 20 × 20 pixels in size and consisting of 150 ROIs representing six regional disease patterns (normal, ground-glass opacity, reticular opacity, honeycombing, emphysema, and consolidation), were marked by two experienced radiologists using consensus HRCT images of various DILD. Twenty-one textual and shape features were evaluated to characterize the ROIs. The csSVM classified an ROI by simultaneously using the decision value of each class and information from the neighboring ROIs, such as neighboring region feature distances and class differences. Sequential forward-selection was used to select the relevant features. To validate our results, we used 900 ROIs with fivefold cross-validation and 84 whole lung images categorized by a radiologist. The accuracy of the proposed method for ROI and whole lung classification (89.88 ± 0.02%, and 60.30 ± 13.95%, respectively) was significantly higher than that provided by the conventional SVM classifier (87.39 ± 0.02%, and 57.69 ± 13.31%, respectively; paired t test, p < 0.01, and p < 0.01, respectively). We conclude that our csSVM provides better overall quantification of DILD.

Introduction

The use of automated classification systems for the detection of diseased or abnormal tissues is becoming an important aspect of computer-aided diagnosis. Several automatic classification systems have been proposed for classifying lung disease images. Uppaluri et al. developed systems for classifying emphysema and diffuse interstitial lung disease (DILD) using 2-D textural analysis [1, 2]. Xu et al. developed a system that used 3-D textural analysis to solve the same problem [3, 4]. Prasad et al. proposed a multi-level classification method for emphysema classification [5], and Chabat et al. proposed a textural system for identifying obstructive lung disease [6]. Support vector machines (SVMs) are often used for image classification and have been shown to outperform other classifiers, such as Bayesian classifiers, artificial neural networks (ANNs), and generalized linear models [7–9]. SVM classifiers have been used to identify emphysema [10–12] and classify five regional disease patterns and normal tissues in DILD patients [13, 14].

In clinical practice, application of SVMs in selected region of interest (ROI)-based data with unambiguously classified regions is needed to extend this approach to whole lung data. Whole lung quantification allows for the evaluation and quantification of disease patterns over the entire lung, thereby allowing assessment of pathogenesis and response to therapy. Previous research has attempted to classify whole lung tissue, but these systems have been limited because they could not identify small areas of initial disease pattern due to the relatively large size of the classification pixels (i.e., 15 × 15) [3, 4] or because they had poor accuracy [14].

Furthermore, most traditional classifiers assume that regions in the image data may be independently classified into several classes. Thus, these classifiers label an ROI based on its feature properties and do not consider spatial correlations between neighboring ROIs. In the specific case of high-resolution computerized tomography (HRCT) of the lung, neighboring ROIs are highly correlated because regional disease patterns typically contain more than one ROI. Traditional classifiers do not consider the rich information that can be gleaned by considering the regions neighboring each ROI.

In the context of remote sensing image classification, researchers have proposed the use of context-sensitive classifiers that consider neighboring information in the appropriate classification of ROIs [15]. In general, context-sensitive classification methods yield excellent classification results for high-resolution images because high-resolution images contain more ROIs. For this reason, incorporation of spatial correlations and relationships provides contextual knowledge to the classifier and improves classification accuracy.

Previous image analysis approaches have addressed this issue. Remote sensing problems, such as land cover classification at the rural–urban fringe, have been analyzed by assuming a probabilistic relaxation of spatial information [16–19]. More recent research has incorporated context information by using a Markov random field (MRF), which models the spatial correlations between neighboring ROIs by modeling the joint probability of observation and the corresponding class for processing of remote sensing images [20, 21]. In the MRF framework, however, efforts have been devoted to modeling the joint probability, which incorporates modeling of intrinsic classes. The conditional random field (CRF), another random field approach, was developed to model the distribution P(Y|X) directly, where Y is the joint label and X is the observation [22]. This model is less computationally demanding than the MRF [23].

Several CRF framework methods, such as the discriminative random field and the support vector random field, have been applied to the segmentation of man-made structures [24] and brain tumors [8]. Although these approaches performed better than the MRF, they were developed for binary image segmentation and could not be applied if more than two classes were present. In the present study, we hypothesized that, in the case of diffuse lung disease, neighboring ROIs will be correlated, and hence that consideration of local contextual information for a ROI under consideration will improve the classification accuracy. To test this hypothesis, we developed a context-sensitive support vector machine (csSVM) and compared the accuracy of the csSVM with that of an existing multiclass SVM [25] by incorporating local context information into the classification of normal and regional disease patterns across whole lung images. In addition, we improved previous random field approaches using the heuristic modification to extend the binary classification problem to multiclass problems.

Materials and Methods

Automatic Quantification System

HRCT images of the whole chest were selected from a collection of images from 106 patients in the department of radiology, Asan Medical Center (Seoul, South Korea). All images were acquired with 220 mA and 140 kVp, with the patients at full inspiration. Images were reconstructed (1 mm slice thickness, 10 mm slice intervals) using an enhancing (B70f) reconstruction kernel with a 16-detector row CT (Sensation 16, Siemens Medical Solutions, Forchheim, Germany).

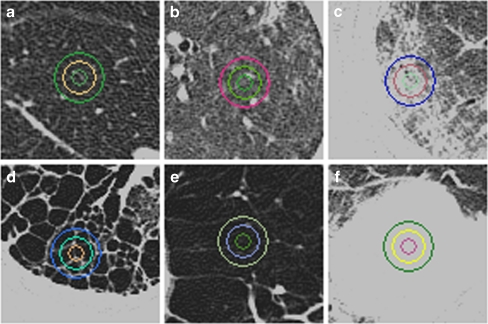
For the training set, a thoracic radiologist with 10 years of clinical experience assessed a total of 900 ROIs (20 × 20 pixels) and marked them as normal (n = 150), ground-glass opacity (n = 150), reticular opacity (n = 150), honeycombing (n = 150), emphysema (n = 150), or consolidation (n = 150; Fig. 1). The size of each ROI (20 × 20) was assessed according to previous methods [13] and expert knowledge for considering subtleties associated with the size of diffuse lung disease patterns. Only one ROI was selected in each image to minimize clustering effects. If several ROIs were selected in one patient, the ROIs were chosen from different lobes.

Fig. 1.

HRCT scans of the chest (window level, −850 HU; width, 400 HU). On each image, note the three different sizes of circular (16-, 32-, and 64-pixel diameters) highlighted regions of interest (ROI) typical of any particular condition. a Normal, b ground-glass opacity, c reticular opacity, d honeycombing, e emphysema, f consolidation

A total of 13 textural and 8 shape features were computed to characterize each ROI. The textural features were histogram features (mean, SD, skewness, and kurtosis), gradient features (mean and SD), run-length matrices (short- and long primitive emphasis), and gray-scale level co-occurrence (contrast, correlation, energy, and homogeneity) [6]. The bin size (Q) of the run-length encoding and co-occurrence were optimized to 196 and 32, respectively [26]. The shape features were from three types of white top-hat transforms (mean and SD), black top-hat transforms (mean and SD), and cluster analysis (number of clusters, cluster area mean and SD, circularity mean and SD, and aspect ratio mean and SD). Thus, each ROI was represented as a 21-dimensional feature vector with the values given in Table 1.

Table 1.

Summary of 13 textural features and 8 shape features that represent each ROI

Category	Descriptor	Dimension
Textual feature	Histogram	Mean
		S.D.
		Skewness
		Kurtosis
	Gradient	Mean
		S.D.
	Run-length matrix	Short primitive emphasis
		Long primitive emphasis
	Co-occurrence matrix	Angular second moment
		Contrast
		Correlation
		Inverse difference moment
		Entropy
Shape feature	Top-hat transform	White top-hat mean
		White top-hat S.D.
		Black top-hat mean
		Black top-hat S.D.
	Cluster	LAA Area
		Number of cluster
		Mean
		S.D.

The validity of these descriptors for characterizing the textural and shape information during classification of lung parenchyma has been demonstrated previously [7, 10–12, 14]. Applying all 21 features listed in Table 1, we conducted sequential forward feature selection (SFS), which showed superior performance in previous studies [6, 10, 12], to remove irrelevant features that might have led to misclassification.

A near-optimal feature set of 900 ROIs, calculated from SFS, was employed to build the classifier. Subsequently, 84 whole lung images were quantified by the previously trained classifier. In addition, a radiologist was asked to draw an area map of 84 whole lung images, using dedicated in-house software, to validate the accuracy of the classification by the ROI comparison. The basic diagram for the automatic quantification system is shown in Fig. 2.

Fig. 2.

Automatic quantification system procedure diagram used for the detection of diffuse interstitial lung disease

Proposed Method

Overview

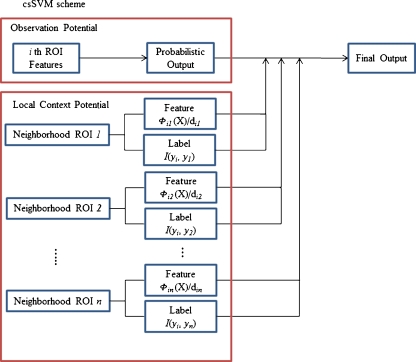
Our method employs a multiclass SVM [25]. The two components, observation potential and local context potential, capture the relationship between observation and labeling using multiclass SVM, and between a classified ROI and its neighboring ROIs.

Let the observed data from an input image be given as X = {x_i} _i ∈ S and the corresponding labels as Y = {y_i} _i ∈ S, where x_i is the data from ith ROI, and S is the total set of ROIs. In this work, y_i can have n classes, i.e., y_i ∈ {1, 2,…, n}. Thus, the joint distribution over the labels y_i, given the observation X_i, can be written as:

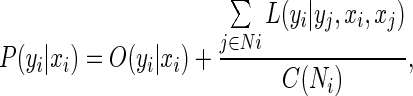1

where O(.) and L(.) are the observation and local context potential, respectively, and N_i is a neighboring ROI, the ith ROI, and C(N_i) is the number of ith neighborhoods. A schematic diagram of this process is illustrated in Fig. 3.

Fig. 3.

Schematic diagram of the csSVM, consisting of the observation potential and the local context potential, for classifying a current ROI using the current ROI’s features along with the neighborhood ROIs’ features and labels

Observation Potential

The observation potential measures the likelihood that the ith ROI will have the label y_i ∈ {1, 2,…, n} in a given image x_i, ignoring information about other ROIs. In this paper, we used a multiclass SVM to calculate the observation potential. Multiclass probability outputs were required to calculate the observation potential. We used the method of Wu et al. [27], who introduced methods that transfer the support vector into multiclass probability estimates, to obtain multiclass probability estimates for the observation potential.

Local Context Potential

The local context potential measures how neighboring ROIs i and j are affected by each other and compensates for the error derived from the observation potential. In the MRF framework, the Ising model is a commonly used local context potential [28]. This method penalizes discontinuities in the labeling of neighboring ROIs i and j by a cost β [29]. However, it captures the dissimilarities only in the labels of adjacent ROIs and does not consider neighborhood-to-neighborhood discontinuities in the feature vectors. In the present study, we treated label and feature vector dissimilarities, to model the local context potential. Thus, the local context potential is modeled as:

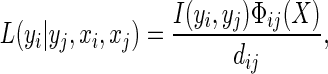2

where the function I(y_i, y_j) is the interaction vector, d_ij is the Euclidean distance between the ith and jth ROI, Ф_ij(X) is a function of the computed feature vector distance between the ith and jth ROI based on observation X. The function I(y_i, y_j) is a 1 × k vector that contains 1 in the y_jth column, −1 in the y_ith column, and 0 in the other columns when y_i = y_j; if y_i ≠ y_j, I(y_i, y_j) contains 0 on all columns. Thus, it may be represented as:

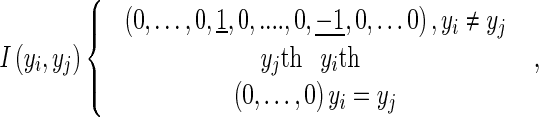3

Since the y_i have categorical values, {1, 2, …., n}, the interaction vector adjusts the observation potential’s posterior probability by the amount Ф_ij(X)/d_ijC(N_i). The function Ф_ij(X) can be modeled as:

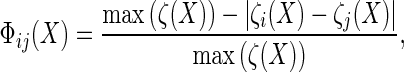4

where the function ζ_k maps the kth ROI into a feature vector. This function yields larger values because neighboring elements are more similar. Thus, a neighboring ROI that has a feature vector similar to that of the currently classified ROI has more of an influence on classification of the current ROI than an ROI with a dissimilar feature vector.

Experimental Setting

Previous kernel function tests for the SVM indicated that a radial basis function performed better than other kernel functions [12]. Thus, we applied a kernel function of the radial basis function against a polynomial, and the associated parameters (e.g., cost C and gamma value) were optimized by a grid search. The purpose of inference is to identify an optimal joint label, given an image X. Inference was performed iteratively unless the improvement in the probability of a joint label dropped below the predetermined threshold. The conventional SVM and observation potential in our proposed method employed a classifier that used the LIBSVM [30]. Computation time and accuracy were measured by running the MATLAB (The MathWorks, Natick, MA, USA) routine on a PC with an i5 Core, 2.67 GHz, and 2 GB RAM.

Statistical Analysis

The conventional SVM and our csSVM were initially tested on 900 ROIs using 20 applications of fivefold cross-validation. The fivefold cross-validation was performed as follows: the 900 ROIs of each class were divided uniformly and randomly into five exclusive stratified subsets. Each fold was in turn held aside as a test set, and the other exclusive four subsets were used to train the classifiers. The average of the fivefold cross-validation results yielded the overall result. Eighty-four whole lung images were tested by the conventional SVM and our csSVM to evaluate image classification accuracy and computational time. Computational times were compared by measuring the testing time (the time required to classify each whole lung image) as calculated by the conventional SVM or our csSVM. All testing results were compared with a t test, and an α-value of 0.01 was considered statistically significant.

Experiment Results

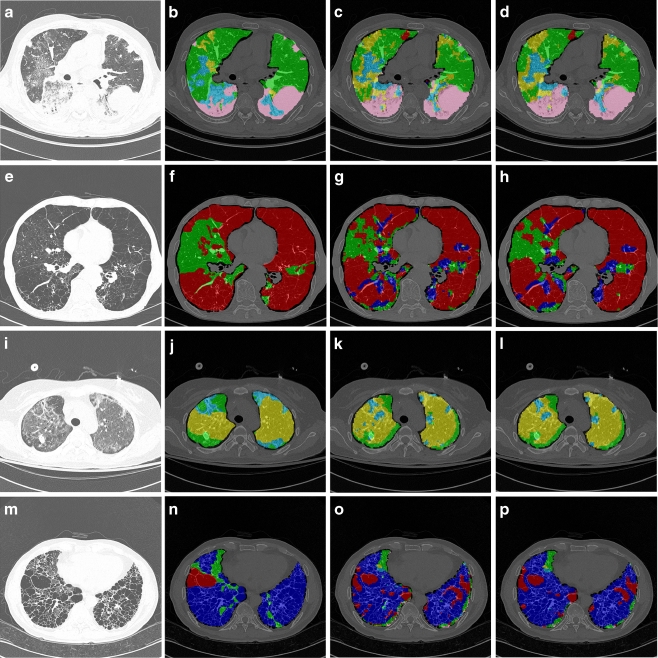
Table 2 shows the accuracy of our proposed method and the conventional multiclass SVM for whole lung images and ROI-based data (paired t test, p < 0.01). We also measured computational times required for whole lung quantification using either classifier. In this task, we used features that had been extracted prior to conducting the actual quantification. Thus, the times in Table 2 indicate the time elapsed during quantification by each classifier. Figure 4 illustrates an example of regional lung disease pattern classification by conventional SVM and by our proposed csSVM.

Table 2.

Overall accuracy and computational time for whole lung images and ROI-based data for the conventional SVM method and the proposed method

Classifier	Accuracy (%)		Time (s)
	Whole lung (p < 0.01)	ROI (p < 0.01)	Whole lung (p < 0.01)
Conventional SVM	57.69 ± 13.31	87.39 ± 0.02	2.25 ± 0.41
Proposed method	60.30 ± 13.95	89.88 ± 0.02	3.05 ± 0.91

Fig. 4.

Whole lung quantification results for comparing the conventional SVM to the proposed method. Each pixel was coded by the classification result, indicated by a semi-transparent color (normal, green; ground-glass opacity, yellow; reticular opacity, cyan; honeycombing, blue; emphysema, red; and consolidation, pink). a Original HRCT image (case 1), b drawing by an expert (case 1), c quantification results from the conventional SVM (case 1), d quantification results from the csSVM (case 1), e original HRCT image (case 2), f drawing by an expert (case 2), g quantification results from the conventional SVM (case 2), h quantification results from the csSVM (case 2), i original HRCT image (case 3), j drawing by an expert (case 3), k quantification results from the conventional SVM (case 3), l quantification results from the csSVM (case 3), m original HRCT image (case 4), n drawing by an expert (case 4), o quantification results from the conventional SVM (case 4), p quantification results from the csSVM (case 4)

Discussion and Conclusion

In this study, we developed a csSVM that incorporates neighborhood information, including neighboring ROI features and labels. Our method can be applied to multiclass classification problems that cannot be addressed by previously proposed methods employing conditional random fields [9, 24]. Although the overall computational time of our csSVM was 35% greater than that of the conventional SVM, the overall accuracy of our csSVM was significantly better, by 2.61% for the whole lung and by 2.49% for ROI-based data.

In medical imaging analysis, our multiclass csSVM may be applied to classification-based image quantification to estimate texture-based emphysema indices in patients with chronic obstructive pulmonary disease and to assess the pathogenesis of DILD. Furthermore, our proposed csSVM may be applicable to other areas, such as remote sensing and computer vision, in which spatial relationships are important. Other classifiers, such as ANNs and Bayesian classifiers, could be extended to context-sensitive classifiers to obtain more accurate results.

The present study has several limitations. First, application of the proposed method to the whole lung yielded lower accuracy classification results (60.30 ± 13.95%) than did the ROI-based classification system (89.88 ± 0.02%). ROIs in the ROI-based data were selected in regions that were representative of the disease, whereas the ROIs classified throughout an entire lung would include transitional regions, which could contribute to disagreements in disease pattern. This problem may be overcome by using adaptive ROIs on borderlines. Another possible explanation is that different quantification methods were used by the expert radiologist and the classifier. The expert radiologist divided the whole lung into six classes using in-house software (a line-based drawing program), whereas the classifier quantified the whole lung using a pixel-based method. This discrepancy in quantification should be further studied in experiments in which experts classify whole images using a pixel-based rather than a line-based program.

Second, our proposed method was applied to 2D images, which prevented us from removing systematic errors, such as those introduced by an airway or vessel [3]. Use of 3D images would provide better results for whole lung quantification, although the computational cost would be significantly greater. Finally, csSVM was only applied to the quantification of DILD patient lungs. To examine the general effectiveness of the model, further evaluations should be performed using datasets from different organs or tissues.

In our proposed csSVM method, the accuracy of DILD quantification was greater than that provided by traditional SVM, with only a slight increase in computational load. We propose that csSVM be considered for the quantification of DILD.