CAUDLES-EF: Carotid Automated Ultrasound Double Line Extraction System Using Edge Flow

Abstract

The evaluation of the carotid artery wall is essential for the diagnosis of cardiovascular pathologies or for the assessment of a patient’s cardiovascular risk. This paper presents a completely user-independent algorithm, which automatically extracts the far double line (lumen–intima and media–adventitia) in the carotid artery using an Edge Flow technique based on directional probability maps using the attributes of intensity and texture. Specifically, the algorithm traces the boundaries between the lumen and intima layer (line one) and between the media and adventitia layer (line two). The Carotid Automated Ultrasound Double Line Extraction System based on Edge-Flow (CAUDLES-EF) is characterized and validated by comparing the output of the algorithm with the manual tracing boundaries carried out by three experts. We also benchmark our new technique with the two other completely automatic techniques (CALEXia and CULEXsa) we previously published. Our multi-institutional database consisted of 300 longitudinal B-mode carotid images with normal and pathologic arteries. We compared our current new method with previous methods, and showed the mean and standard deviation for the three methods: CALEXia, CULEXsa, and CAUDLES-EF as 0.134 ± 0.088, 0.074 ± 0.092, and 0.043 ± 0.097 mm, respectively. Our IMT was slightly underestimated with respect to the ground truth IMT, but showed a uniform behavior over the entire database. Regarding the Figure of Merit (FoM), CALEXia and CULEXsa showed the values of 84.7% and 91.5%, respectively, while our new approach, CAUDLES-EF, performed the best at 94.8%, showing a good improvement compared to previous methods.

Background

Numerous studies from around the world have demonstrated that there is a strong correlation between the risk of cerebrovascular diseases and the characteristics of the carotid artery wall [1–3]. Ultrasound examination is a widely used diagnostic tool for assessing and monitoring the plaque buildup via the carotid window. Ultrasounds offer several advantages in clinical practice:

1. They only propagate mechanical (i.e., non-ionizing) radiation;

2. No short-term or long-term adverse biological effects have been demonstrated in the power and intensity range commonly used in clinical scans;

3. The examination is quick and safe;

4. The ultrasound equipment is among the more inexpensive equipment when compared to other imaging devices.

However, ultrasound examinations are operator-dependent, and the ultrasound images can tend to be quite noisy and require training to be correctly interpreted.

The intima–media thickness (IMT) is the most used and validated marker of progression of carotid artery diseases [4, 5] and can be measured using image processing strategies and ad hoc computer techniques. The goal is to first segment the carotid artery distal wall, so as to then find the lumen–intima (LI) and media–adventitia (MA) boundaries. The distance calculated between these two interfaces is taken as an estimate of the IMT.

The segmentation process can conceptually be thought of as two cascading stages:

• Stage I

  Recognition of the carotid artery (CA) and delineation of the far adventitia layer (AD_F) in the two-dimensional B-mode ultrasound image;

• Stage II

  Tracing of the LI/MA wall boundaries in the ROI of the recognized CA.

In Stage I, the carotid artery must be correctly located within the ultrasound image frame. This stage is generally better performed by human experts, who can mark the position of the CA by either tracing rectangular regions-of-interest (ROI) or by placing markers. In Stage II, the guidance zone is created in which the LI and MA borders are estimated. The IMT can be subsequently measured once the LI and MA borders are determined during the segmentation process. These two stages cannot be independent from each other. In fact, Stage I is of fundamental importance since the found AD_F profile is used as a starting point for Stage II, which is also automated. The performance of Stage I directly affects the initialization of Stage II, and therefore also affects the final results. This fact emphasizes the importance of the need of an accurate yet versatile technique to perform Stage I.

In order to achieve complete automation, both of these stages must be designed to be independent of the user. To do so, first of all appropriate detection strategies are required to automatically locate the carotid artery in the image. These strategies must be robust with respect to noise and must be able to process carotids with different geometrical appearance.

The majority of the algorithms proposed in literature for the automated segmentation of the CA in ultrasound images require a certain degree of user-interaction, which precludes real complete automation. Any user-interaction also slows down the analysis process and introduces a dependence on the operator if gain settings are not optimal, bringing subjectivity into the process. Complete automation, instead, can be an asset for multi-center large studies since it enables the processing of large image databases.

This paper presents a completely user-independent Carotid Automated Ultrasound Double Line Extraction System using Edge Flow (CAUDLES-EF) algorithm, which performs both Stages I and II. Starting from the ultrasound image, the algorithm first segments the distal border of the CA and then performs the automatic detection of the LI and MA interfaces. Neither of these processes require any user interaction. The first part of our new algorithm is based on scale-space multi-resolution analysis while the second part is based on flow field propagation. CAUDLES-EF was specifically designed for the IMT measurement of the far (distal) wall of the common carotid artery. In this paper, we also show the characterization of this algorithm in terms of automatic versus human traced segmentation, and we also benchmarked the results with two other completely automatic techniques that we previously developed [6–10]. Our image database consisted of 300 images coming from two different institutions consisting of both normal and pathological arteries. Two different technicians acquired the images, using two different ultrasound scanners. We used the Hausdorff distance as a performance metric for Stage I and we measured the distance between the computed far adventitial wall and the LI/MA profiles that were manually traced by experts, the so-called ground truth. For assessing the performance of Stage II, we used the polyline distance and calculated the error between the IMT estimated using our algorithm and ground truth IMT.

Materials and Methods

Image Database and Preprocessing Steps

We tested an image database consisting of 300 images coming from two different Institutions. Two hundred images were acquired using an ATL HDI 5000 ultrasound scanner equipped by a 10–12 MHz probe at the Neurology Division of Gradenigo Hospital (Torino, Italy), from one hundred fifty asymptomatic patients who referred to the Neurology Division for carotid assessment (age 69 ± 16 years old; range 50–83 years old). Ninety-three subjects were male. Eighty of these subjects had hypertension history, forty had hypercholesterolemia, and thirty had both. Ten patients were diabetic. Resampling was set to 16 pixels/mm, leading to an axial resolution equal to 62.5 μm/pixel. The remaining one hundred images were acquired at The Cyprus Institute of Neurology and Genetics (Nicosia, Cyprus) from asymptomatic individuals (age 54 ± 24; range 25–95 years) using a Philips ATL HDI 3000 ultrasound scanner equipped with a linear 7–10 MHz probe. These images were resampled at a density of 16.67 pixels/mm, therefore obtaining an axial spatial resolution equal to 60 μm/pixel. Both of the Institutions made sure to obtain written informed consent from the patients prior to enrolling them in the study and approval by the respective IRBs. Both the experimental protocol and the data acquisition procedure were approved by the respective local Ethical Committees. Three different expert sonographers (a cardiologist, a vascular surgeon, and a neurologist—all with more than 20 years of experience in their field) independently manually segmented the images by tracing the boundaries of the lumen–intima (LI) and media–adventitia (MA) interfaces, and the average tracings were considered as ground truth (GT).

In order to discard the surrounding black frame containing device headers and image/patient test data, the raw ultrasound image is automatically cropped in one of two ways. The first method is for DICOM images with fully formatted DICOM tags: we used the data contained in the specific field named SequenceOfUltrasoundRegions, which contains four subfields that mark the location of the image which contains the ultrasound representation. These fields are named RegionLocation (with their specific labels being: x_min, x_max, y_min, and y_max), and they mark the horizontal and vertical extensions of the image. The raw B-Mode DICOM image is then cropped in order to extract only the portion which contains the carotid morphology. If, however, the image was not in a DICOM format or if the DICOM tags were not fully formatted, the second method was applied: adopting a gradient-based procedure, we computed the horizontal and vertical Sobel gradients of the image. When computed outside of the region of the image containing the ultrasound data, gradients are equal to zero. Hence, the beginning of the image region containing the ultrasound data can be found as the first row/column with a gradient different from zero. Similarly, the last nonzero row/column of the gradient marks the end of the ultrasound region.

Architecture of CAUDLES-EF

Stage I: Far Adventitia Estimation

Since the CAUDLES-EF algorithm was developed to help remedy the human operator dependence and therefore be totally user-independent, the first stage of the algorithm is the completely automatic recognition of the CA. This is done through a novel and low-complexity procedure, which detects the far adventitia border using a method based on scale-space multi-resolution analysis. Starting from the automatically cropped image (Fig. 1a), the automated Stage I is divided into different steps described in detail here:

• Step 1: Fine to coarse downsampling. The image is first downsampled by a factor of two (i.e., the number of rows and columns of the image is halved; Fig. 1b) implementing the downsampling method discussed by Ye et al. [11] adopting a bicubic interpolation. This method was tested on ultrasound images and showed a good accuracy and a low computational cost [11].

• Step 2: Speckle reduction. Speckle noise is attenuated using a first-order local statistics filter (called lsmv by the authors [12, 13]), which has given the best performance in the specific case of carotid imaging. This filter is defined by the following equation:

  1

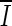  where I_x,y is the intensity of the noisy pixel, is the mean intensity of a NxM pixel neighborhood and k_x,y is a local statistic measure. The noise-free central pixel in the moving window is indicated by J_x,y. Louizou et al. [12, 13] mathematically defined 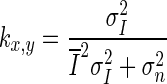, where 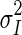represents the variance of the pixels in the neighborhood, and 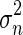the variance of the noise in the cropped image. An optimal neighborhood size was demonstrated to be 7 × 7. Fig. 1c shows the despeckled image.

• Step 3: Higher-order Gaussian derivative filter. The despeckled image is then filtered using a 35 × 35 pixels first-order derivative of a Gaussian kernel. The scale parameter of the Gaussian derivative kernel is taken equal to 8 pixels. This value is chosen because it is equal to half the expected dimension of the IMT value in an original fine resolution image, since an average IMT value equal to 1 mm corresponds roughly to about 16 pixels in the original image scale and therefore 8 pixels in the downsampled image. The white horizontal stripes in Fig. 1d show the proximal (near) and distal (far) adventitia layers.

• Step 4: Automated far adventitia (AD_F) tracing. Figure 1e shows the intensity profile of one column (from the upper edge of the image to the lower edge of the image) of the Gaussian filtered image. The proximal (near) and distal (far) walls are clearly identifiable as intensity maxima saturated to the maximum value of 255. A heuristic search is then applied to the intensity profile of each column to automatically trace the profile of the distal (far) wall. The image convention uses (0,0) as the top left-hand corner of the image, and so this search is done starting from the bottom of the image (i.e., from the pixel with the highest row index) and searching for the first white region consisting of at least 6 pixels (computed empirically). The deepest point of this region (i.e., the pixel with the highest row index) marks the position of the far adventitia AD_F layer on that column. The overall automated AD_F tracing is found as the sequence of points resulting from the heuristic search for all of the image columns.

• Step 5: Upsampling of the far adventitia (AD_F) boundary locator. The AD_F profile that is found is then subsequently upsampled to the original fine scale and superimposed over the original cropped image (Fig. 1f) for both visualization and performance evaluation.

Fig. 1.

CAUDLES-EF procedure for AD_F tracing. a Original cropped image. b Downsampled image. c Despeckled image. d Image after convolution with first-order Gaussian derivative (sigma = 8). e Intensity profile of the column indicated by the vertical dashed line in d. (AD_F indicates the position of the far adventitia wall). f Cropped image with far adventitia profile overlaid

This Stage I consists essentially of an architecture based on fine-to-coarse sampling for vessel wall scale reduction, speckle noise removal, higher-order Gaussian convolution, and automated recognition of the far adventitia border. This multi-resolution method prepares the vessel wall’s edge boundary so that the thickness of the vessel wall is roughly equivalent to the scale of the Gaussian kernels. This allows an optimal detection of the CA walls since when the kernel is located close to a near gray level change, it enhances the transition. Consequently, the most echoic image interfaces are enhanced to white in the filtered image. This fact, as clearly shown in Fig. 1d, e, is what allows this procedure to detect the far adventitia layer.

Stage II: Double Line (LI/MA) Border Estimation

The whole idea of double line extraction for IMT measurement in Stage II is to first extract the strong LI/MA edges which lie between the lumen region and the ADF border. There are two kind of strong edges: LI strong edges and MA strong edges. The search for the double line (LI/MA borders) strong edges is performed in the grayscale guidance zone. This grayscale guidance zone is computed empirically from the knowledge database. The strong edge estimation in this guidance zone is implemented using our Edge Flow algorithm. Since the intensity of the strong edges is not uniform, some edges are weak along the carotid arterial wall. The weak edges in the guidance zone are estimated using a labeling process, which then joins strong edges. The strong and weak edges are then combined to form the raw LI/MA borders or double lines. These extracted double lines are finally smoothed using a spike reduction method leading to smooth LI/MA borders. The layout of this section is the following: first we show the guidance zone estimation, then we present the Edge-Flow algorithm, and finally, we show the MA and LI weak borders estimation.

Guidance Zone Mask Estimation

Stage II consists of an automatic extraction of a Guidance Zone Mask, which is estimated from the AD_F profile by extending it toward the upper edge of the image by 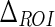. We set the 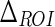value equal to 50 pixels. The choice of this mask height was obtained after empirically computing the distances from AD_F profile w.r.t. ground truth LI/MA borders. The original image is then cropped with the smallest rectangle possible that includes the entire Guidance Zone Mask. Consequently, the Edge Flow algorithm is run on the cropped grayscale guidance mask image to obtain the initial edges.

Stage II (a): Edge Flow Magnitude and Edge Flow Direction

The Edge Flow algorithm, originally proposed by Ma and Manjunath [14], facilitates the integration of different image attributes into a single framework for boundary detection and is based on the construction of an Edge Flow vector 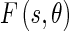defined as

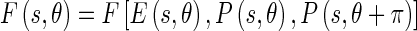2

where:

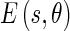• is the edge energy at location s along the orientation θ;

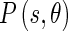• represents the probability of finding the image edge boundary if the corresponding Edge Flow “flows” in the direction θ;

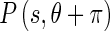• represents the probability of finding the image edge boundary if the Edge Flow “flows” backward, i.e., in the direction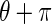

The final single Edge Flow vector can be thought of as the combination of Edge Flows obtained from different types of image attributes. Since ultrasound images near the walls have higher intensities and texture like distribution, the image attributes we chose were: intensity and texture. In order to calculate the edge energy 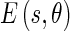and the probabilities of forward and backward Edge Flow direction, a few definitions must first be clarified, specifically the first derivative of Gaussian (GD) and the difference of offset Gaussian (DOOG). Considering the Gaussian kernel 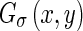, where σ represents the standard deviation, the first derivative of the Gaussian along the x-axis is given by

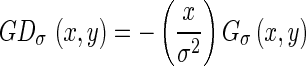3

and the difference of offset Gaussian (DOOG) along the x-axis is defined as:

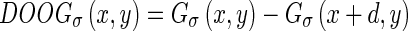4

where d is the offset between the centers of two Gaussian kernels and is chosen proportional to σ. This parameter is significant in the calculation of the probabilities of forward and backward Edge Flow, as it is used to estimate the probability of finding the nearest boundary edge in each of these directions. This is the only parameter that is required for running the Edge Flow algorithm. As suggested in previous studies [14], we selected a σ equal to 2 pixels. Higher values would cause the deletion of any image boundary smaller than σ itself, therefore precluding the recognition of thin boundaries. We found that 2 pixels is an optimal value for the detection of LI/MA borders in ultrasound carotid images. Table 1 reports the list of parameters we used in this algorithm.

Table 1.

List of the parameters used in the Edge Flow algorithm and refinement functions

Parameter	Value	Description
ΔROI	50 pixels	Vertical size of the Guidance Zone Mask.
σ	2 pixels	Sigma value of the Gaussian kernels used by Edge Flow (eq. (3)).
ϕ	0.1	Area ratio in MA border detection (eq. (18)).
φ	7 pixels	Threshold for detecting connectable edge objects (eq. (20)).
IMratio	0.4	Threshold value used for LI segmentation (eq. (23)).
λ	5 pixels	Threshold value for determining if an edge object can be classified as belonging to the LI segment (eq. (24)). This is the average distance of an edge object from the MA boundary.

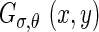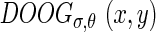By rotating these two functions, we can generate a family of previous functions along different orientations θ and they can be denoted as and , respectively:

5

6

where: 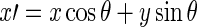, and

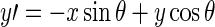Intensity Edge Flow

Considering the original image I(x,y) at a certain scale σ, 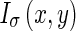is obtained by smoothing the original image with a Gaussian kernel 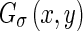. The Edge Flow energy 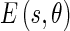at scale σ, defined to be the magnitude of the gradient of the smoothed image 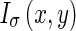along the orientation θ, can be computed as

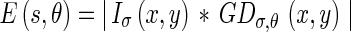7

where s is the location (x,y). This energy indicates the strength of the intensity changes. The scale parameter is very important in that it controls both the edge energy computation and the local flow direction estimation so that only edges larger than the specified scale are detected.

To compute 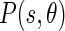, two possible flow directions (θ and θ + π) are considered for each of the edge energies along the orientation θ at location s. The prediction error toward the surrounding neighbors in these two directions can be computed as:

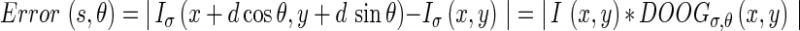8

where d is the distance of the prediction and it should be proportional to the scale at which the image is being analyzed. The probabilities of Edge Flow direction are then assigned in proportion to their corresponding prediction errors, due to the fact that a large prediction error in a certain direction implies a higher probability of locating a boundary edge in that direction:

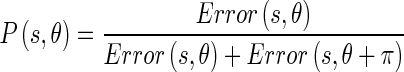9

Texture Edge Flow

Texture features are extracted from the image based on Gabor decomposition. This is done basically by decomposing the image into multiple oriented spatial frequency channels, and then the channel envelopes (amplitude and phase) are used to form the feature maps.

Given the scale σ, two center frequencies of the Gabor filters (the lowest and the highest) are defined. The range of these center frequencies generates an appropriate number of Gabor filters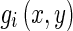. The complex Gabor filtered images are defined as:

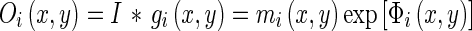10

where 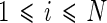, N is the total number of filters, i is the sub band, 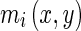is the magnitude, and 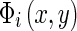is the phase. A texture feature vector 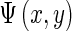can then be formed by taking the amplitude of the filtered output across different filters at the same location (x,y):

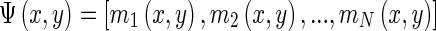11

The change in local texture information can be found using the texture features, thus defining the texture edge energy:

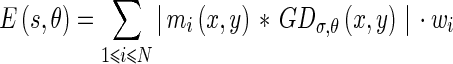12

where 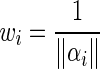and 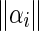is the total energy of the sub band i.

The direction of the texture Edge Flow can be estimated similarly to the intensity Edge Flow, using the prediction error:

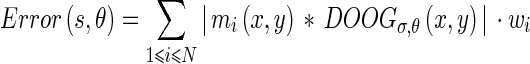13

and the probabilities 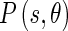of the flow direction can be estimated using the same method as was used for the intensity Edge Flow.

Texture and Intensity Edge Flow Integration

For general-purpose boundary detection, the Edge Flows obtained from the two different types of image attributes can be combined:

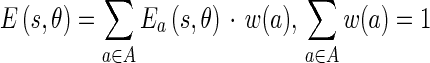14

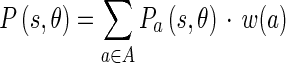15

where 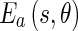and 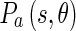represent the energy and probability of the Edge Flow computed from the image attributes a (in our case, intensity and texture). w(a) is the weighting coefficient among various types of image attributes. To search for the nearest boundary, we identify the best direction. We therefore consider the Edge Flows 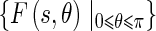and identify a continuous range of flow directions that maximizes the sum of probabilities in that half plane:

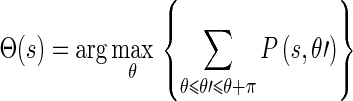16

The vector sum of the Edge Flows with their directions in the identified range is what defines the final resulting Edge Flow and is given by:

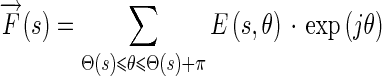17

where 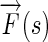is a complex number whose magnitude represents the resulting edge energy and whose angle represents the flow direction.

Flow Propagation and Boundary Detection

Once the Edge Flow 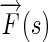of an image is computed, boundary detection can be performed by iteratively propagating the Edge Flow and identifying the locations where two opposite flow directions encounter each other. The local Edge Flow is then transmitted to its neighbor in the direction of flow if the neighbor also has a similar flow direction. The steps which describe this iterative process are as follows:

• Step 1Set n = 0 and
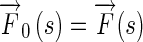
• Step 2Set the initial Edge Flow 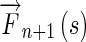at time n + 1 to zero
• Step 3At each image location s = (x,y), identify the neighbor s′ = (x′,y′) which is in the direction of Edge Flow
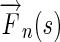
• Step 4
  Propagate the Edge Flow if

  

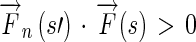
  Otherwise,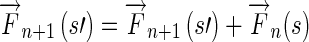

  
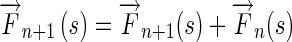
• Step 5If nothing has been changed, stop the iteration. Otherwise, set n = n + 1 and go to step 2.

The image boundaries can then be detected once the Edge Flow propagation reaches a stable set by identifying the locations which have nonzero Edge Flow coming from two opposing directions. For all of the images, we considered 8 different orientations, starting from 0° and going to 315° with equal degree intervals in between. Figure 2a shows the total energy of the Edge Flow 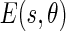obtained for the various orientations, while Fig. 2b shows the total probabilities of the Edge Flow .

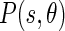Fig. 2.

Example of the total Edge Flow computed in eight orientations. a Total Edge Flow energy. b Total Edge Flow probability. On top of the columns, the grayscale Guidance Zone is showed

Once the image boundaries are detected, the final image is generated by performing region closing (i.e., morphological closing operation). This operation helps in limiting the number of disjoint boundaries. The basic idea is to search for the nearest boundary element within the specified search neighborhood at the unconnected ends of the contour. If a boundary element is found, a smooth boundary segment is generated to connect the open contour to another boundary element. The neighborhood search size is taken to be proportional to the length of the contour itself.

This approach of edge detection has the following characteristic features: (i) the usage of a predictive coding model for identifying and integrating the different types of image boundaries; (ii) the use of flow field propagation for boundary detection; and (iii) the need for a single parameter controlling the whole segmentation process.

Figure 3a shows an example of an output image from the Edge Flow algorithm while Fig. 3b shows this output binary image overlaid on the original image in white.

Fig. 3.

a Binary edge output from the Edge Flow algorithm. b Superposition of the binary edges on the corresponding grayscale carotid region of interest image

As Fig. 3b clearly shows, the Edge Flow algorithm over-segments in many different points, due partly to the fact that the image was cropped to contain the entire Guidance Zone Mask and therefore may contain sections of the image that are found below the AD_F profile. This problem could be even more serious in presence of a curved or inclined artery, because more tissue structures below the AD_F would be enclosed into the Guidance Zone. Figure 3b also shows a disconnected edge object. Also, while part of the MA and LI edge estimation may be done using the Edge Flow algorithm, the segmentation cannot yet be considered complete as there are still some missing weak MA and weak LI edges and the edges found must be classified as either belonging to the MA profile or the LI profile. This refinement and classification process is done using a strong dependency on the edges found by the Edge Flow algorithm and via labeling and connectivity, which will be explained in further detail in the next two sections.

Stage II (b): Weak MA or Missing MA Edge Estimation Using Strong MA Edge Dependency via Labeling/Connectivity and Complete MA Estimation

Before we discuss the challenges, we first define the concept of an edge object. It is defined as a connected component in the binary image.

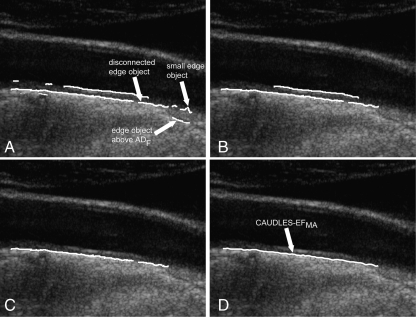
As said in the previous subsection, Edge Flow causes discontinuities in the edge objects. Three types of problems are connected to discontinuity edges: the first is the presence of edge objects that are not overlaid on the correct interface (i.e., edge objects located below the far carotid wall and, thence, the AD_F profile), the second is the presence of many small segments, and the third is the breaking of the LI/MA profile into disconnected edge objects. For the sake of clarity, we will call incorrect edge objects the edge objects that were traced below the AD_F profile; small edge objects those who are very short compared to the length of the image, and disconnected edge objects those which are possibly part of the correct MA profile, but which are disconnected from it. Therefore, overall our system handles these three main challenges:

1. Removing the incorrect edge objects outside the region of interest;

2. Removing the small edge objects in the region of interest;

3. Connecting disconnected edge objects.

The solution to challenge (a) is simply the deletion of all the edge objects in the output image that are not included in the Guidance Zone. Figure 4a shows the effect of the deletion of the incorrect edge objects from the initial segmentation shown in Fig. 3b.

Fig. 4.

Steps showing the refinement of weak MA or missing MA edges. a Results of the Edge Flow segmentation showing edge objects located above the AD_F, isolated small edge object, and disconnected edge objects. b Removal of small isolated edge objects. c Edge objects that are classified as being part of the MA segment overlaid on the original grayscale image. d Final MA profile on the original image

The solution to challenge (b) requires the definition of a small edge object. Small edge objects around the ROI are defined as those that have an area ratio below a limit ϕ when compared to the totality of the edge objects of the image. The area ratio is defined by the following equation:

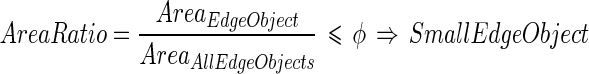18

Our experimental data showed that ϕ = 0.1 is an optimal value to guarantee the rejection of the small edge objects. Such small edge objects are discarded and therefore removed from the image; an example is shown in Fig. 4b.

The solution to challenge (c) is based on the identification of those disconnected edge objects, which can be linked to form the final MA edge object. The MA segment is first initialized as being the edge object with the highest pixel row index (i.e., the lowest edge object in the image) and its right top (RT) and left top (LT) end points are called as RT_MA and LT_MA, respectively. These end points are characterized by the two coordinates, so that, for example, RT_MA(x) refers to the column index of the edge point RT_MA and RT_MA(y) to its row index. The remaining (disconnected) edge objects are then sorted by their mean pixel row index value so as to examine the edge objects starting from those which are lowest in the image and working upward. The edge objects are then classified by following these steps:

1. Find the unconnected end points of the ith edge object as the right top and left top pixels of the examined edge object (RT_i and LT_i, respectively)

1. Determine the correct unconnected end point pair (either LT_MA and RT_i or LT_i and RT_MA) as the pair which yields a lesser column difference in absolute value. Hence, we check the following condition:

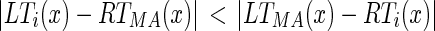19

and if it is true, then the edge points to be connected are LT_i and RT_MA (i.e., the edge object is located on the right of the MA edge object), otherwise the connectable edge points are LT_MA and RT_i (i.e., the edge object is located to the left of the MA edge object). From now on, let us call the unconnected edge points as LT and RT.

1. Calculate the respective row distance in absolute value () and column distance () between the correct unconnected end points. The examined (disconnected) edge object can be classified as being part of the MA segment if:

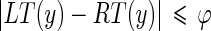20

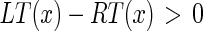21

where φ is the maximum acceptable row distance. The condition eq. (21) on the column distance is needed to ensure that the edge object considered does not overlap the already existing MA segment, while the condition eq. (20) on the row distance is necessary so as to avoid including edges that are too far above the existing MA edge object. Pilot studies we performed on our image dataset showed that φ = 7 is a suitable threshold for detecting connectability between MA and disconnected edge objects. In fact, 7 pixels approximately correspond to 0.45 mm, which is half of the value of the IMT. With this φ value we can link disconnected edge objects even if they are not perfectly aligned with the MA edge object, and this ensures the possibility of correctly linking disconnected edge objects when in presence of curved vessels or of arteries that are not horizontally placed in the image. Lower values of φ would cause the deletion of a large amount of disconnected edge objects, resulting in a reduced and incomplete MA edge object, whereas higher values would allow the linking of disconnected edge objects too far from MA and, therefore, possibly incorrect.

1. Repeat steps 1–3 until all edge objects have been examined. Figure 4c shows the edge objects that were classified as being part of the MA segment overlaid in white on the original image

Once all of the weak edge objects have been examined, those which are classified as being part of the MA segment are then connected together and B-spline fitted to produce the final MA profile (Fig. 4d).

This post-processing and refinement algorithm has the advantage of linking disconnected edge objects and removing small edge objects on the basis of thresholds that are relative (i.e., like ϕ in eq. (18)) or linked to the calibration factor of the image (i.e., like φ in eq. (20)). The threshold value φ should therefore be adjusted if the calibration factor is very different from the value of 0.06–0.0625 mm/pixel as we have in our images. Table 1 summarizes the parameters we used in our procedure, whereas we clarify the rationale for their selection in the discussion section.

Stage II (c): Weak LI and LI Missing Edge Estimation Using Strong LI Edge and MA borders

The post-processing of the LI edge is more complicated with respect to that of MA. Beside the problem of discontinuous edges (i.e., of the LI profile broken into disconnected edge objects), there is the problem of false edge objects located in the vessel lumen (i.e., above LI) and in the media layer (i.e., in between MA and LI).

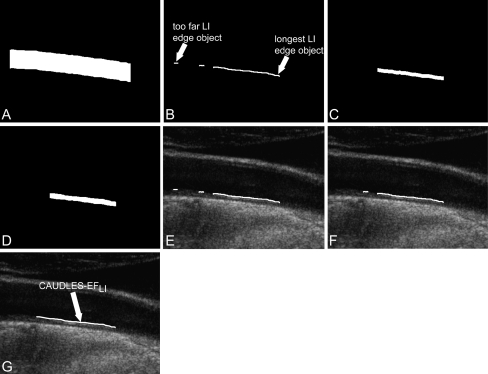
We developed a technique for the LI missing edge estimation that is completely dependent on the MA profile (determined in Stage II (b)). In fact, the guidance zone is created starting from the MA profile and extending it upward 50 pixels (Fig. 5a). This is used so as to find solely the edge objects above the MA profile and that have at least some common support with it (Fig. 5b). The common support between two profiles was defined as the range of column coordinates that was common to both the profiles. The remaining i edge objects are processed by this sequence of steps:

1. Find the common support between the MA profile and the ith edge object and cut the MA profile to the common support (call it - MAcut_i).

2. Create a mask starting from MAcut_i and extending it upward 10 pixels and calculate the mean (call it Image Mask mean - 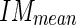) and standard deviation (call it Image Mask standard deviation - 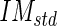) of the pixel values found in the mask (Fig. 5c). We chose a value of 10 pixels in order to include, in this mask, only pixels belonging to the media layer. Thus, we expect relatively low 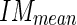and 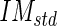values (in our sample dataset, the average 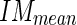± 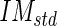value was equal to about 63 ± 19 in a scale range 0–255).

3. Create a second mask starting from MAcut_i and extending it up to the ith edge object (Fig. 5d). For each pixel found in this mask, determine if it can be defined as an acceptable pixel based on the following relation:

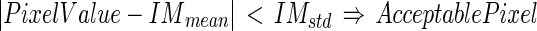22

This check rejects too bright and too dark pixels, thus avoiding incorrect edge objects located into the vessel lumen and in the media layer. Also, we determined an 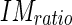as the ratio between the number of acceptable pixels found and the total number of pixels considered.

1. Calculate the row distance between the left unconnected end point of the ith edge object and the first point of MAcut_i (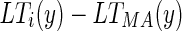) and the row distance between the right unconnected end point of the ith edge object and the last point of MAcut_i ().

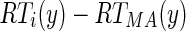2. Determine that the edge object can be classified as being part of the LI segment if the following two conditions are met:

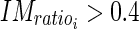23

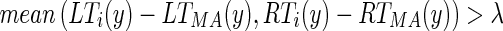24

The first condition is important in that it avoids classifying an edge object which is found in the lumen since the pixel values in the lumen are considerably lower than 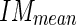and those pixels would therefore not be classified as an acceptable pixel, lowering by a good deal the calculated 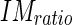. The second condition is necessary so as to not include discontinuous edge objects which are located too close to the MA profile (i.e., in between the MA and LI profiles.). We selected a value λ = 5 (further discussion is reported by Table 1).

1. Repeat steps 1–5 until all edge objects are examined.

Fig. 5.

Process of weak LI edge or missing LI edge estimation. a Guidance zone obtained using the MA profile and extending it upward. b Objects which are above the MA profile and have a common support with it. c Example of a mask obtained for one edge object starting from the cut MA profile and extending it upward 10 pixels. d Example of a mask obtained for one edge object starting from the cut MA profile and extending it up to the examined edge object. e Edge objects that were classified as being part of the LI segment overlaid on the original grayscale image (all three edge objects are part of the LI profile). f Edge objects that are part of the longest LI segment found overlaid on the original grayscale image (the far edge object has been removed). g Final LI profile on the original grayscale image, where the two edge objects belonging to LI have been linked and the third one has been removed because too far

Figure 5e shows the edge objects that were classified as being part of the LI segment overlaid in white on the original image.

Once all of the edge objects are examined, those found to be part of the LI segment (good edge objects) must be tested to see if the distance between two adjacent edge objects is too high. This is to avoid connecting two edge objects which are too far from each other, which could have a negative affect on the outcome of the final LI profile. To do this, the good edge objects are considered by adjacent pairs. Once all good edge objects have been examined, the final LI segment is determined by those that are part of the longest LI segment found (Fig. 5f).

The edge objects that are part of the final LI segment are then connected together and B-spline fitted to produce the final LI profile (Fig. 5g).

Design of the Performance Metric

Our algorithm was tested on a multi-institutional database consisting of 300 longitudinal B-mode ultrasound images of the common CA. We then had three expert operators independently and manually trace the LI and MA profiles in all of the images. The operators manually segmented the images by using a MATLAB interface we previously developed. The manual profiles were interpolated by a B-spline and averaged. The averaged profile was considered as ground-truth (GT).

Our performance evaluation method consisted in two different strategies:

1. Assessment of the performance of the automated tracing of the far adventitial border;

2. Overall system distance of the LI/MA traced profiles from GT and of the IMT measurement bias.

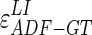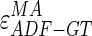Concerning (i), we calculated the Hausdorff distance (HD) between the AD_F profile and the LI_GT profile and then between the AD_F profile and the MA_GT profile for each image, to find the LI and MA distances between ADF and GT ( and , respectively). The HD between two boundaries is a measure of the farthest distance that must be covered moving from a given point on one boundary and traveling to the other boundary. So first of all, given two boundaries B₁ and B₂, the Euclidean distances of each vertex of B₁ from the vertices of B₂ must be calculated. For every vertex of B₁, the minimum Euclidean distance is kept. Then once all B₁ vertexes have been examined, the maximum distance between all of these minimum distances is kept and we can indicate it with d₁₂. Likewise, we can calculate the Euclidean distances of each vertex of B₂ from the vertices of B₁ and find d₂₁. The HD can then be mathematically defined as:

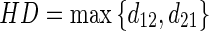25

This assessment helps give a general idea of how far the AD_F tracing is from the actual distal wall LI and MA borders. Since this distance measure is sensitive to the longest distance from the points of one boundary to the points of the other, we cut the computed profiles to the same support of GT, rendering the HD unbiased by points that could perhaps be located out of the GT support.

Regarding the second point (ii), to assess the performance of the automatic tracings of the LI and MA profiles, we calculated the polyline distance (PD) as proposed by Suri et al. in 2000[15].

Considering two boundaries B₁ and B₂, we can define the distance d(v,s) between a vertex v and a segment s. Let’s consider the vertex 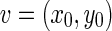on the boundary B₁ and the segment s formed by the endpoints 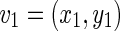and 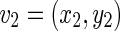of B₂. The PD d(v,s) can then be defined as:

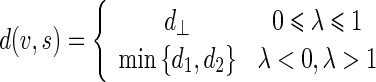26

where

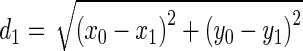27

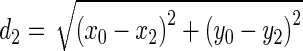28

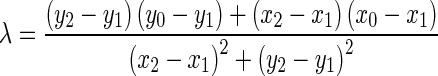29

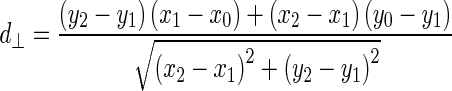30

Being 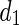and 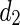the Euclidean distances between the vertex v and the endpoints of segment s, λ the distance along the vector of the segment s, and 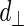the perpendicular distance between v and s. The polyline distance from vertex v to the boundary B₂ can be defined as 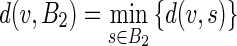. The distance between the vertexes of B₁ to the segments of B₂ is defined as the sum of the distances from the vertexes of B₁ to the closest segment of B₂:

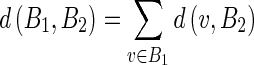31

Similarly, the distance between the vertices of B₂ to the closest segment of B₁ (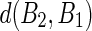) can be calculated by simply swapping the two boundaries. Finally, the polyline distance between two boundaries is defined as:

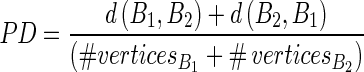32

Using the polyline distance metric, one can then compute the IMT using Edge Flow method and compare that with the IMT using the GT LIMA borders:

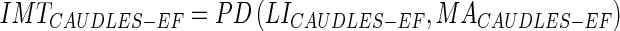33

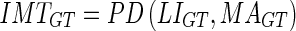34

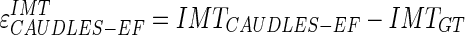35

The PD measures the distance between each vertex of a boundary and the segments of the other boundary.

This assessment helps evaluate the performance of the IMT using CAUDLES and the error is purposefully calculated without an absolute value so as to see how much the algorithm under estimates and/or over estimates the IMT measure. The units of the calculated HD and PD are initially in pixels, but for our performance evaluation we converted the calculated pixel distances into millimeters, using a calibration factor, which is equal to the axial spatial resolution of the images. In our database, the 200 images acquired at the Neurology Division of Torino had a calibration factor equal to 0.0625 mm/pixel while the 100 images acquired at the Cyprus Institute of Neurology had a calibration factor equal to 0.0600 mm/pixel.

Third, for an overall assessment of the algorithm performance, we calculated the Figure of Merit (FoM) which is defined by the following formula:

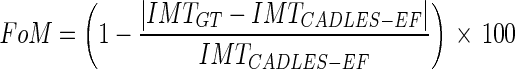36

Results: Performance Evaluation and Benchmarking

Segmentation Results on Healthy and Diseased Carotids

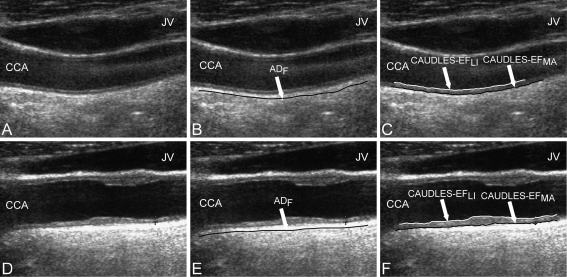
Figure 6 demonstrates the performance of CAUDLES-EF on two different kinds of images. The first column represents the original B-mode images; the middle column shows the tracings of the far adventitial wall with the ultrasound image in the background; the last column depicts the tracings of the LI and MA borders with the ultrasound image in the background. Figure 6a shows a normal CA that is not horizontally oriented in the frame and in which the central portion of the image is corrupted by high blood backscattering. Figure 6b shows the capability of CAUDLES-EF to follow the curved vessel while avoiding the noise due to backscattering, and Fig. 6c finally shows how the LI and MA borders were properly segmented, in spite of these potential challenges. Figure 6d instead depicts an image in which the jugular vein is clearly present and whose artery wall is thicker due to deposition. Figure 6e shows how CAUDLES-EF was able to correctly identify the CA and Fig. 6f finally shows how the algorithm can effectively segment the image avoiding problems due to the presence of a thicker artery wall and jugular vein.

Fig. 6.

Examples of CAUDLES-EF performance on normal but nonhorizontal carotid artery and carotid artery in the presence of jugular vein. First column the original cropped images; middle column AD_F profile (Stage I output) overlaid on the original cropped grayscale images; last column LI and MA borders estimated using CAUDLES-EF algorithm overlaid on the original grayscale images. Top row normal CA that is not horizontal and that is corrupted by blood backscattering. Bottom row vessel with a thicker artery wall and presence of the jugular vein in the image. CCA common carotid artery, JV jugular vein

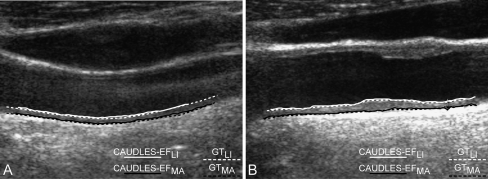
Figure 7 shows the comparison between CAUDLES-EF and GT tracings of the LI and MA profiles in the same two cases as depicted in Fig. 6. The GT tracings were obtained as the average of the three experts’ tracings. The continuous solid lines represent the CAUDLES-EF tracings, while the dotted lines represent the GT tracings.

Fig. 7.

Comparison between CAUDLES-EF and expert tracings (GT) of the LI and MA borders. The CAUDLES-EF tracings are depicted by continuous solid lines, whereas dotted lines indicate the GT tracings. Left image nonhorizontal geometry; right image carotid artery in the presence of jugular vein

Performance Evaluation of CAUDLES-EF

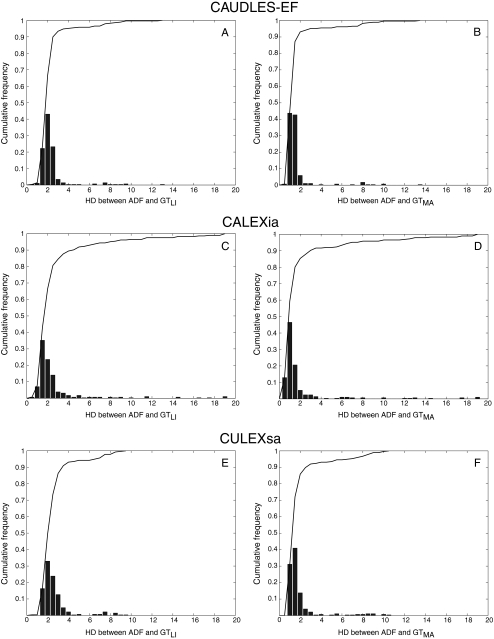
CAUDLES-EF correctly identified the carotid artery by tracing of the AD_F profile in all 300 images (100% success rate). The first row of Fig. 8 shows the CAUDLES-EF distribution of 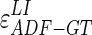and 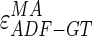(i.e., the LI and MA errors between AD_F and GT, respectively) on the 300 tested images. This error data was interpreted using the cumulative distribution plots. The horizontal axis of the histogram represents the class center values, while the vertical axis represents the cumulative frequency. Figure 8a is relative to the LI border, Fig. 8b is relative to the MA border. The black lines represent the cumulative functions of the error distributions. We considered the maximum height of a guidance zone one can support to efficiently compute accurate LI and MA borders to be equal to 60 pixels (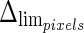). To convert this to millimeters, we considered the worst cases of a calibration factor equal to 0.06 mm/pixel, that yielded a maximum height of a guidance zone equal to 3.6 mm (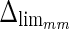). The histogram in Fig. 8a shows that 94% of the errors between AD_F and GT_LI are below 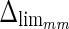. However, as the histogram clearly shows, some of the remaining 6% of the LI errors can reach some very high values, in one case almost 4 times more than 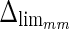. This distribution evidences that CAUDLES-EF tracings are overall accurate and can be used for the definition of a guidance zone for IMT computation, even though in a few cases the error can reach higher values.

Fig. 8.

Distribution of 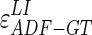and 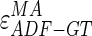for CAUDLES-EF, CALEXia, and CULEXsa. a, b LI and MA distances for CAUDLES-EF, respectively. c, d LI and MA distances for CALEXia, respectively. e, f LI and MA distances for CULEXsa, respectively. The horizontal axis represents the distance classes in millimeters, and the vertical axis represents the cumulative frequency. The black lines represent the cumulative function of the distance distributions

Analogous results can be observed in Fig. 8b, which shows the MA errors between AD_F and GT_MA: 95% of the MA errors are below , while the remaining 5% still can reach slightly higher values.

Considering all of the images, the AD_F profiles using CAUDLES-EF had a mean error between AD_F and GT_LI equal to 2.327 mm with a standard deviation equal to 1.394 mm; the MA error had a mean of 1.632 mm with a standard deviation equal to 1.584 mm. Table 2 summarizes these results.

Table 2.

Performance evaluation of CAUDLES-EF, CALEXia, and CULEXsa

	ADF w.r.t. GT-LI	ADF w.r.t. GT-MA	Automated LI w.r.t. GT-LI	Automated MA w.r.t. GT-MA
CAUDLES-EF	2.327 ± 1.394 mm	1.632 ± 1.584 mm	0.475 ± 1.660 mm	0.176 ± 0.202 mm
CALEXia	2.733 ± 2.895 mm	2.036 ± 3.024 mm	0.406 ± 0.835 mm	0.313 ± 0.850 mm
CULEXsa	2.651 ± 1.436 mm	1.965 ± 1.733 mm	0.124 ± 0.142 mm	0.118 ± 0.126 mm

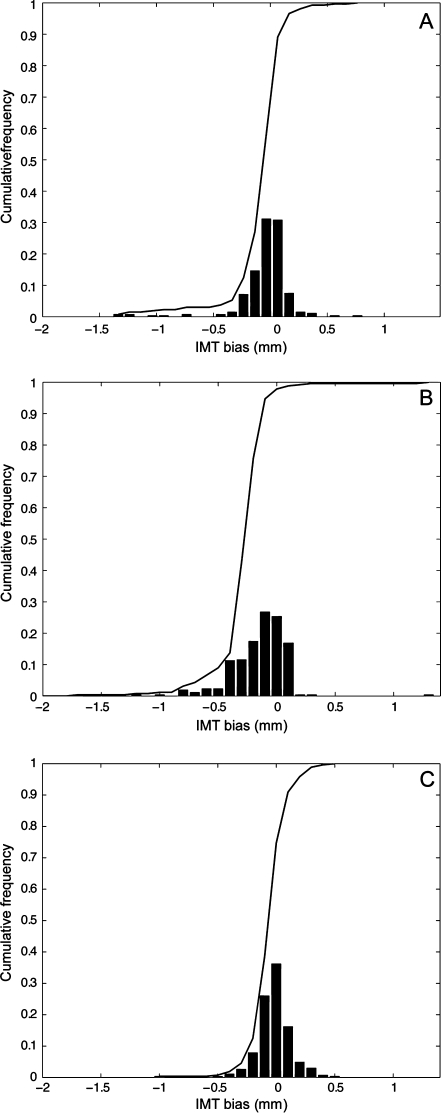
Figure 9a shows the CAUDLES-EF distribution of 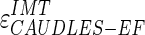without 5 images that were found problematic (a detailed description of the possible CAUDLES-EF error sources is reported in the discussion section). We then calculated the PD in millimeters between the two computed boundaries and binned the error values in intervals having an extension of 0.1 millimeters. The horizontal axis of the histogram represents the class center values, while the vertical axis represents the cumulative frequency. The black lines represent the cumulative functions of the error distributions. The histogram in Fig. 9a reveals that 97.3% of the images processed have an absolute value of 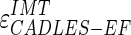that is equal to or less than 0.5 mm. The mean 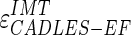is equal to –0.043 mm while the standard deviation is equal to 0.222 mm. Table 3 summarizes the results about IMT measurement. In Table 3, the Ground Truth IMT average value shows the slight different for the three techniques. This is due to the exclusion of images on which the technique did not satisfactorily perform. This distribution suggests that the CAUDLES-EF LI and MA tracings can be clinically used for IMT computation. The overall FoM was found to be equal to 94.8%, and we found that CAUDLES-EF under estimates and over estimates the true IMT value in a similar manner, with a slight tendency toward under estimation, which is observable in Fig. 9a.

Fig. 9.

Distribution of 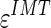for CAUDLES-EF, CALEXia, and CULEXsa once removing the images with an unacceptable AD_F profile. a Distribution for CAUDLES-EF. b Distribution for CALEXia. c Distribution for CULEXsa. The horizontal axis represents the error classes in millimeters, and the vertical axis represents the cumulative frequency. The black lines represent the cumulative function of the error distributions

Table 3.

Overall automated IMT measurement performances of the CAUDLES-EF, CALEXia, and CULEXsa algorithms compared to ground truth

	Computer-estimated IMT	GT IMT	IMT bias	FoM
CAUDLES-EF	0.861 ± 0.276 mm	0.818 ± 0.246 mm	−0.043 ± 0.093 mm	94.8%
CALEXia	0.746 ± 0.156 mm	0.880 ± 0.164 mm	0.134 ± 0.088 mm	84.7%
CULEXsa	0.805 ± 0.248 mm	0.879 ± 0.237 mm	0.074 ± 0.092 mm	91.5%

Benchmarking CAUDLES-EF with Existing Automated Techniques

To better evaluate the performance of our new algorithm, we benchmarked the results with two other completely automatic techniques for IMT measurement previously developed by our research group, CALEXia (Carotid Artery Layer EXtraction using an integrated approach) and CULEXsa (Completely User-independent Layer EXtraction based on signal analysis). Complete and more detailed explanations of these two algorithms can be found in our previous papers [6–10]. This comparison can be quite meaningful because the three main characteristics of the techniques are the same: i.e., (1) there is no need for human interaction, (2) they are designed to work in normal as well as pathologic images, and (3) they trace all three profiles of interest: the far adventitial layer, the LI border and the MA interface. All three of these algorithms were tested on the same database.

Figure 8c, d shows the LI and MA errors, respectively, between ADF and GT for CALEXia while Fig. 8e, f shows these errors for CULEXsa. Figure 9b, c shows the distribution of 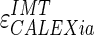and 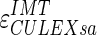, respectively. Tables 2 and 3 reports the segmentation errors and the IMT measurement bias for the three techniques. The overall FoM for CALEXia was found to be equal to 84.7%, while for CULEXsa it was equal to 91.5%. We found that CALEXia underestimates the IMT, while CULEXsa tends to underestimate the IMT value in a manner more similar to CAUDLES-EF (even though with slightly more marked tendency toward underestimation).

Discussion

We have developed a novel technique for automatic computer-based measure of IMT in longitudinal B-mode ultrasound images. This new technique consists of two stages: (1) an automatic tracing of the AD_F profile based on scale-space multi-resolution analysis and (2) an automatic tracing of the LI and MA profiles based on a flow field propagation and the subsequent IMT measure which is obtained calculating the polyline distance between the computed LI and MA boundaries. We tested our method on a database of 300 images coming from two different institutions acquired with two different ultrasound scanners and compared it with expert human tracings. We validated our new method by benchmarking the results with two other completely automatic techniques we previously developed.

Rationale for Using the Hausdorff and Polyline Distances

The Hausdorff distance measures how far two different subsets are from each other. In a nutshell, these two sets can be considered close based on the HD measure if every point of either set is close to at least one other point in the other set. The far adventitia boundary that is automatically detected is a guiding boundary, which represents the region of coarse identification of the carotid artery. It is quite likely that this boundary is not a smooth boundary, with the possibility of having sharp curvature changes. As a result, we are interested in finding the farthest possible distance between the computed AD_F and the GT borders. HD is an ideal choice for evaluating the performance of the AD_F boundary since this measure reveals the worst limit of the boundary.

The polyline distance, on the other hand, seems to be a more robust and reliable indicator of the distance between two given boundaries, and is very robust since it does not depend on the number of points in either boundary. This last property is very crucial when calculating the error between an IMT measure that is obtained with boundaries that have one point for every column (i.e., our automatically computed LI and MA profiles) and an IMT measure that is obtained with a much more limited number of points (i.e., the GT_LI and GT_MA profiles).

Overall Performance of CAUDLES-EF and Its Interpretation

The first row of Table 2 summarizes the overall performance of the CAUDLES-EF method. Comparing the CAUDLES-EF performance with the other two automatic techniques that we examined, we can see that our new algorithm presents very promising results.

First, CAUDLES-EF outperformed both CALEXia and CULEXsa in the automatic Stage I (Table 2), by providing AD_F tracings closer to the ground truth LI/MA boundaries of the far wall.

Second, it also outperformed CALEXia in the automatic Stage II and showed an average comparable performance with CULEXsa (the performance was, however, not statistically different from that of CULEXsa when tested by a Student’s t-test, resulting in a p value higher than 0.3), with a slightly higher standard deviation.

The major advantage of this new technique is versatility of the Edge Flow, which always reached convergence. The convergence of CAUDLES-EF was superior to that of CULEXsa. Being based on snakes, CULEXsa showed convergence issues when in presence of small plaques or of deformed vessels. In fact, it is very difficult to fine-tune the snake tension and elasticity parameters in order to cope with possible different carotid wall morphologies. As a result, CULEXsa could not process 14 images out of 300.

The computational time was comparable. Using MATLAB on a dual 2.5 GHz PC equipped by 8 MB of RAM, CAUDLES-EF took 60 s compared to 50 s for CULEX. CALEXia was fastest and its MATLAB implementation took 3 s.

Possible Error Sources

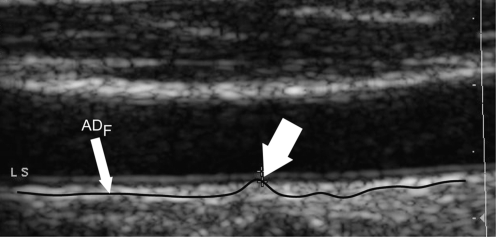
Presence of Hyperechoic Structures The automated technique for the AD_F profile we presented still could not reach 100% satisfactory performance. We observed inaccurate AD_F tracings in 4 images. Figure 10 reports a sample of inaccurate AD_F tracing. The white arrow indicates a section of the profile, which overlaps the MA profile. This is an error condition, since the AD_F profile should always be below the MA boundary so as to be able to correctly define a guidance zone. This problem is given by image markers that are present in the image, which attract the AD_F profile. We never experienced such error if markers were not present on the image. We adopted a spike-rejection algorithm to correct such possible problem. This algorithm identifies spikes by detecting the zero crossings of the AD_F derivative. Spikes are removed by interpolation between previous and following AD_F values. This technique allowed for correcting 3 images out of 4.

Fig. 10.

Sample of inaccurate AD_F tracing due to the presence of image markers. The continuous black line represents the AD_F profile. The thick white arrow indicates the inaccurate adventitia tracing showing the bump

Edge Flow Algorithm and Refinement Process There are two error conditions originated by the Edge Flow operator. The first one is depicted by Fig. 11: the Edge Flow algorithm outputs one single profile, which is partly overlaid to the LI border and part to the MA. The white arrows in Fig. 11 show the transitions of the edge object between the LI and the MA border. In such condition, no refinement is possible. Two images gave this error.

Fig. 11.

Sample of Edge Flow inaccurate segmentation. The LI and MA boundaries are merged together in a single profile. The white arrows indicate some points where the edge object bumps between LI and MA (or vice versa). This is an error condition, which showed in only two images out of 300

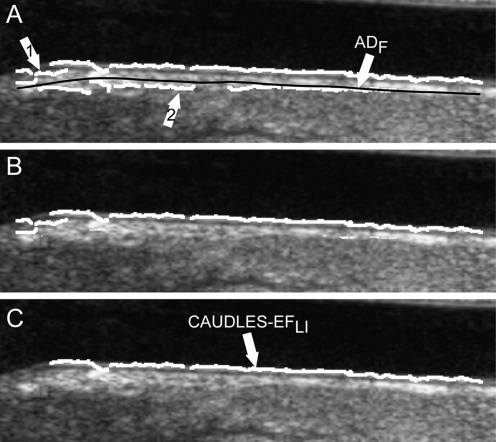
The second error condition caused by Edge Flow is represented by Fig. 12: the MA profile is inaccurate, it is traced too close to the AD_F and not to the actual MA interface, and it is broken into many small edge objects. The arrow 1 of Fig. 12a indicates small edge objects, whereas arrow 2 the MA edge objects that are below the AD_F (black line). In such condition, all the edge objects below AD_F profile and the small edge objects are removed by the refinement procedure (Fig. 12b). The subsequent step of deletion of the small edge objects removes the remaining MA edge objects (Fig. 12c). As a consequence, the MA boundary can be totally erased. Two images gave this error.

Fig. 12.

Sample of inaccurate segmentation of the LI and MA border. The initial MA edge estimation is weak and therefore leads to an incorrect classification of the MA border. a Output image from the Edge Flow algorithm overlaid on the original image. The white arrow indicates edge objects located below the black line that indicates the AD_F. The arrow 1 indicates the discontinuity of the edge objects of Edge Flow producing many small edge objects. The arrow 2 indicates the edge objects of the MA profile that are incorrectly traced below AD_F.b Binary image containing only the edge objects above the AD_F profile overlaid in white on the original image. c Binary image obtained after removing the small edge objects. The MA border has been removed

Sensitivity of the Parameters

Table 1 summarizes the parameters of the CAUDLES system. In the second column of Table 1 we reported the parameter values we used in our work. Such values were selected after a careful testing and tuning of our system.

The first parameter we introduced was 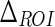, which is the size of the Guidance Zone Mask. This value is used as vertical size: the AD_F profile is repeated 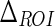pixels above. We set 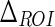to be 50 pixels (approximately corresponding to 3 mm, which is three times the maximum value of IMT). This value ensures we comprised into the Guidance Zone the entire distal wall in every condition: straight and curved artery. Also, this value ensured a correct segmentation of small atherosclerotic plaques (see Fig. 6f). Lower values of 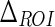caused the LI border to partially fall out of the Guidance Zone, whereas higher values increase computational time.

The parameter σ is value of the derivative Gaussian kernels used by Edge Flow for DOOG computation. We took σ equal to 2 pixels. The size of the Gaussian derivative kernel must be comparable to the size of the interfaces that one wants to detect in the image. We found that higher values of σ caused the deletion of the LI/MA borders.

The parameter ϕ represents the area ratio used for detecting small edge objects in MA border refinement. Higher values caused the deletion of edge objects of significant length, thus shortening the final MA profile length to few pixels.

The parameter φ, which we took equal to 7 pixels, is the threshold for detecting connectable edge objects. This value was established on the basis of the calibration factor of the images: 7 pixels correspond to about 0.45 mm, which is half the expected value of the IMT. Therefore, such limit avoids connecting edge objects belonging to different boundaries (i.e., LI edge objects cannot be connected with MA, and vice versa).

By 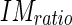we indicated the threshold value for determining if an edge object can be classified as belonging to the LI segment. Lower values of this parameter caused the incorrect assignment of edge objects located into the vessel lumen (and detected by Edge Flow because of blood rouleaux) to the LI segment.

Finally, λ is the threshold value for determining if an edge object can be classified as belonging to the LI segment. This is the average distance of an edge object from the MA boundary. This value avoids the assignment to the LI segment of edge objects too close to the MA profile. Lower values would be too selective and not suited to curved or not horizontal vessels. Higher values would have caused the deletion of too many edge objects.

Overall, we found that the selection of these parameters is not very specific and strict. Our database was multi-ethnic, multi-institutional, multi-scanner, and multi-operator, and overall, the parameters values were suitable for all the images.

Relationship Among the Three Paradigms

There are still many challenges in developing fully automated techniques for the carotid wall IMT measurement. These can be grouped in Stage I and Stage II. The major challenges in Stage I are: (i) the presence of the jugular vein (JV), (ii) the presence of hyperechoic structures located in-between the LI and MA profiles; (iii) resolution and gain setting challenges. The major challenges in Stage II are: (i) the presence of noise backscattering in the vessel lumen, (ii) the hypoechoic representation of the LI layer, (iii) the presence of a plaque on the distal wall, and (iv) the presence of image artifacts (such as, shadow cones originated by calcium deposits and reverberations of the ultrasound waves). These factors increase the dataset variability (especially when the dataset is multi-institutional) and, consequently, limit the performance of the fully automated techniques. CULEXsa, being based on parametric models, needed an accurate tuning in order to reach optimal performance. When the image characteristics changed, the snake model needed re-tuning. Moreover, the presence of blood backscattering in the vessel lumen was a potential limit to lumen detection that was based on statistical classification. This was the bottleneck in Stage I of CULEXsa [7]. CALEXia showed an improved accuracy in the segmentation of the MA border, but a lower accuracy in the LI. Also, the robustness of CALEXia in Stage I was higher than that of CULEXsa [10]. Though fully automated, the overall performance in terms of IMT measurement did not completely reach the best reproducibility standards. CAUDLES is a step ahead in both Stage I and Stage II architectures. The scale-space multi-resolution edge-based Stage I brought 100% carotid identification. Stage II, which was intensity and texture-based on the Edge Flow method offered satisfactory LI/MA segmentation performance and proved effective in following any vessel morphology. The major advantage of CAUDLES with respect to CULEXsa was the possibility of tracing LI/MA profiles in any morphological condition without changing the system parameters. With respect to CALEXia, the Stage II of CAUDLES is more robust with respect to image noise. Therefore, even thought the three methodologies can be seen as technically very different, they have a common aim of developing a versatile and effective technique coupling 100% identification accuracy in Stage I and noise robustness and optimal LI/MA segmentation in Stage II.

Conclusions

The CAUDLES-EF algorithm we developed can be proficiently used for the segmentation of B-mode longitudinal ultrasound images of the common CA wall. It is completely user-independent: the raw US image can be completely processed without any interaction with the operator. It is based on a scale-space multi-resolution analysis to determine initial location of the CA in the image and is then based on a flow field propagation based on intensity and texture to determine edges, which are then classified and refined to provide the final contours of the LI and MA interfaces.

We tested this algorithm on a set of 300 images from two different institutes, which were acquired by two different operators using two different scanners. The image database contained images of both normal and diseased arteries. The performances of our new technique were validated against human tracings and benchmarked with two other completely user-independent algorithms. The average segmentation errors were found to be comparable or better than the other techniques and provided acceptable results, both in cases of normal CAs and those with plaques. We find that the results are very encouraging and we are porting the system for clinical usage.

From a clinical point of view, the algorithm traces the boundaries of both the intima and media layers, which can be used for measurements and also in algorithms of image co-registration and image fusion and for the accurate analysis of the carotid wall texture.