Distributed vs. Focused Attention (count vs. estimate)

Abstract

Quantity or numerosity is one of the basic properties of our environment. Humans and animals both have the neural representation of quantity or “number sense”. The ability to extract and to manipulate numbers is closely related to our various cognitive functions such as the capacity of working memory, mathematical achievement, and texture perception. Evidence shows that the sense of number is not a unitary mechanism but rather a composition of two distinct processes; enumeration and estimation. The review examines how numerosity is represented in the visual domain and its relation to different modes of attention. Enumeration or counting permits an exact representation of a distinct number of objects, with an awareness of each object achieved through focal deployment of attention to each object serially. On the other hand, estimation involves an approximation of the number of different items or a sense of ensemble statistics, achieved through fast deployment of distributed attention over a set of objects as a whole. In this overview we suggest that a focused attention mode is more suitable for enumeration, whereas a distributed attention mode is better for estimation.

Numbers are very important in our daily lives. They define virtually every aspect of our lives: our age and health, the size and nature of our communities, and our economy. They are universally used in science as well. Sense of number, either represented in our ability to count or our ability to estimate, is deeply embedded in many aspects of our everyday life. Some would even argue it has a very clear ecological relevance, allowing for appropriate social interactions, for efficient foraging and even for optimizing reproductive strategies¹. Sometimes we need to know an exact number and sometimes we just have to estimate an approximate number. We cannot pay 112.54 dollars in cash without counting. However, we are able to prepare a correct amount of food to serve tonight’s party of 8 or 10.

Counting and estimating are also very important in visual processing. Both abilities are present early on in infancy with cortical substrates reliably found and are available to all humans regardless of language and education. Our abilities to track multiple objects² and to store visual items temporally³ are both constrained by the number of objects. There is evidence that perceived numerosity is susceptible to adaptation like primary visual features⁴, arguing for perceived numerosity as an independent primary visual property. Estimation of statistical properties has been shown to be important for texture perception^{5, 6} and number estimation acuity is correlated with mathematical achievements in children⁷. Moreover, it is proposed that common cortical metrics are used for time, space, and quantity perception^{8, 9, 10} and that they are represented in parietal cortex¹¹. For instance, recent studies have demonstrated the existence of neurons that are broadly tuned for numerosity in macaque parietal cortex^{12, 13, 14} while fMRI studies in humans point to symbolic and non-symbolic representation of number in the intraparietal sulcus^{15, 16} (however see references 17 and 18). There is evidence that shows that the sense of number is important throughout human and animal development. The abilities to count and estimate emerge as early as 6 months of age^{19, 20, 21}. Comparable counting ability observed in infants has also been found in monkeys²², while a comparable ability to estimate is observed in both rats²³ and monkeys²⁴.

The sense of number has two components that differ significantly from one another. One component is called counting or enumeration which involves individuation and localization of each item, the summation of the items and the maintenance of the running total. It may require serial shifts of spatial attention and is effortful. The other component is called magnitude estimation. Estimation involves an approximation of the number of different items or a sense of statistics such as mean and variance; all achieved in a fast fashion often with no conscious access to individual items. It is because of these differences that counting and magnitude estimation are thought to involve two different mechanisms.

In 2004, Feigenson, Dehaene, and Spelke²⁵ put forth a general number apprehension theory, in which they propose two core systems for representing numerosity. The first is the counting system where precise representations of up to three distinct objects are possible. The second is the magnitude system where approximate representations of larger number of objects are possible. The first system differs from the second system in that the former can represent the exact number of objects whereas the latter can only represent the inter-relations between different numerosities (i.e. the ratio between different numerosities).

In this review we will concentrate more specifically on counting and estimation in the visual domain with respect to the relationship between two modes of numerosity judgments and two modes of attention. If an object is found within an uncrowded scene²⁶, one may identify, locate, and count each of the objects, while having conscious access to all aspects of the process. However, if objects are within a crowded scene, one can access only their overall magnitude without access to all of their individual features²⁷. Objects within a crowded scene cannot be counted item per item and thus their absolute number is unknown to us. One can only estimate the overall magnitude of the features of those objects (i.e. size, orientation). We are fully aware of each item when we count item by item, whereas we estimate overall magnitude without awareness of how we achieve it. Consequently, we have conscious access to the exact number of counted objects, while we only have relative sense of overall magnitude of uncounted objects.

Since the process and function of the two numerosity judgments is different, the type of attention deployed during two judgments may differ. There is growing evidence that when numerosity is represented visually, counting and estimation rely on different modes of attention. Therefore we propose enumeration and estimation are related to two separate modes of attention: focused and distributed attention.

To count more than 5 items, we need to individualize each item. To individualize, we need focused attention. If one reflects upon one’s experience of counting large numbers over 5 or 6, the necessity of focused attention is evident because item-by-item counting is necessary. The visual system uses focused attention to sequentially select each object in a scene that needs to be counted. For example, although we know objects occupy distinct positions, we cannot count the exact number of them if the spacing between them is narrow²⁸. Since the resolution of attention is lower than the perceptual resolution, we cannot count the exact number of objects even though we know they are distinct objects. Thus, improving distinction of objects by tagging different colors to objects can even help a patient with severe counting deficits²⁹. It is only when we can focus our attention on each one individually that we are able to count them.

More recently it has been shown, in contrast to previous evidence, that even for counting a small number of objects (less than five) under subitizing range³⁰ the visual system needs attentional resources^{31, 32}. Vetter and colleagues³² showed that one cannot count a small number of objects when performing a concurrent high-load task. Furthermore, Burr et al.³¹ reported that the just noticeable number difference (Weber fraction of counting) increased in the dual-task condition as compared to the single-task condition, suggesting that subitizing is not an attention free mechanism. Superior performance in the subitizing range previously observed^{30, 33} may be explained by high perceptual discriminability between items in subitizing range. For example, distinguishing 1 from 2 items has higher discriminability (Weber fraction is 0.5) than distinguishing 6 from 7 items (Weber fraction is 0.86)³⁴. Consistent with this interpretation, Mandler and Shebo³⁵ found reaction time increase (50 ms per item) even in the subitizing range. Therefore, counting even small numbers may require focused attention when the task is rendered difficult with increased perceptual load.

However, as long as the display is perceived as a whole, the visual system is able to estimate the overall magnitude of presented items without serially focusing on each item. We are able to estimate overall orientation although we do not have conscious access to individual orientations²⁷. One can also track centroids of multiple objects quite accurately without knowing exact locations of each object outside the focus of attention³⁶ and detect global changes of orientations with reduced attention³⁷. As long as distributed attention is deployed, performing an additional task does not interfere with mean size estimation^{38, 39}. For example, participants’ thresholds of mean size estimation were lower after searching for a C among Os (distributed attention), even though the duration of a search display was 2 times longer for searching for an O among Cs (focused attention)³⁸. When participants search for a C among O’s, C pops out allowing the participants to identify the C without focusing on each element and consequently perceive the display as a whole. However, they have to make sure that each item is not a target when they search for an O among C’s, which requires focused attention to each item in turn. Therefore, distributed attention facilitates the process of estimation as compared to focused attention considering the sizable search time differences. Consistent with these findings, focused attention did not influence just noticeable number differences in estimation, whereas it increased them in counting³¹.

Attention can be spread similarly across time as is evident from studies using the attentional blink⁴⁰. The attentional blink occurs during rapid serial visual presentation of items during which the observer is required to report two target items which are presented consecutively with a variable interval. Vul et al. ⁴⁰ found that the probability of reporting items presented around the second target item was increased during the attentional blink period. This trend was not found for the first target item. These results suggest that attentional selection spreads around the second target in time, thus increasing the probability of reporting items neighboring the second target item. In this situation, while the ability to identify the second target is impaired, the ability to estimate the mean size of multiple items presented around the second letter (e.g. seven different sized circles surrounding seven letters before and after the second letter) could be accurate because of distributed attention across time. Indeed, mean size estimation was accurate even during the attentional blink³⁹ while attention was temporally distributed. Furthermore, the ability to estimate numbers was greatly improved for patients with simultanagnosia (i.e. patients with bilateral parietal lesion) when multiple objects were grouped easily or were presented in a regular formation because it allowed for all similar items to be coded as one²⁹. Demeyere andHumphreys²⁹ found that grouping elements by smaller spacing, color or regular configuration benefited the patients’ estimating performance greatly, while it had no effect on their counting ability.

Note that both counting and estimation require attention, even though they rely on different types of attention. Focused attention facilitates counting by helping the visual system to individualize objects, whereas distributed attention helps estimation by perceiving the scene as a whole. One good example of how the two modes of attentional deployment allow for different coding of numbers is a study reported by Treisman⁴¹. Participants were briefly presented with displays composed of colored shapes (letters O, X, and T in red, green and blue respectively). They were asked to estimate either the proportion of shapes that were green or the proportion of green T’s. The participants did very well reporting the proportion of the display with items containing a single attribute (e.g. one feature, all green items) but did very poorly on reporting the proportion of items that were a combination of two attributes (e.g. a conjunction, all green T’s). The participants were unable to estimate the proportion of conjunction items within the short display exposure time, indicating that focused attention is needed for perception of items defined by feature conjunctions. In order to answer the question about the proportion of the display occupied by green T’s, it would have involved focusing attention of each element and then counting them. However, participants had no trouble giving an estimate of the proportion of items defined by a single feature, which was accessible through deployment of distributed attention.

While focused attention can explain the mechanism of counting, distributed attention can provide the framework for understanding the process of estimation. Distributed attention is different from focused attention in that it covers a larger spatial area, encompasses a large number of objects, and processes objects as a whole⁴¹ (see Figure 1 for graphic comparison of the two modes). Since in a distributed attention mode the visual system can pay attention to a larger area containing many objects, it can extract statistical properties of a scene more easily than focused attention^{38, 41}. A specific mechanism of magnitude estimation proposed by Allik and colleagues is consistent with the distributed attention mode^{42, 43}. Allik and his colleagues assumed that an object occupies a fixed subjective amount of area (an occupancy index). They showed that the total area occupied by objects predicted people’s number estimations very accurately. Although the occupancy model has only one parameter, it can explain human performance very well. Note that in this model the total area formed by objects is calculated by summing up all occupancy indices. In order to compute this total area, the visual system most likely distributes its resources over a large area without the need to access each item. Durgin⁴⁴ extended this model by suggesting that numerosity estimation should consider the density and grouping pattern of a display, especially for larger number of objects. He showed that the occupancy model could simulate human estimation performance for up to 100 objects, but it should take density into account in explaining human performance for over 100 objects. In addition, recent studies show that there are additional structural factors that can affect estimation^{45, 46}. He et al.⁴⁵ found that apparent numerosity of a field of dots can be reduced by the addition of connecting lines between a portion of the dots. Once connected the paired dots contribute to estimation as a single entity and no longer as two separate dots. In addition, the authors report that underestimation of numerosity happens even after very brief exposure duration of only 50 milliseconds, providing a strong argument against serial deployment of attention to access the exact number.

Figure 1.

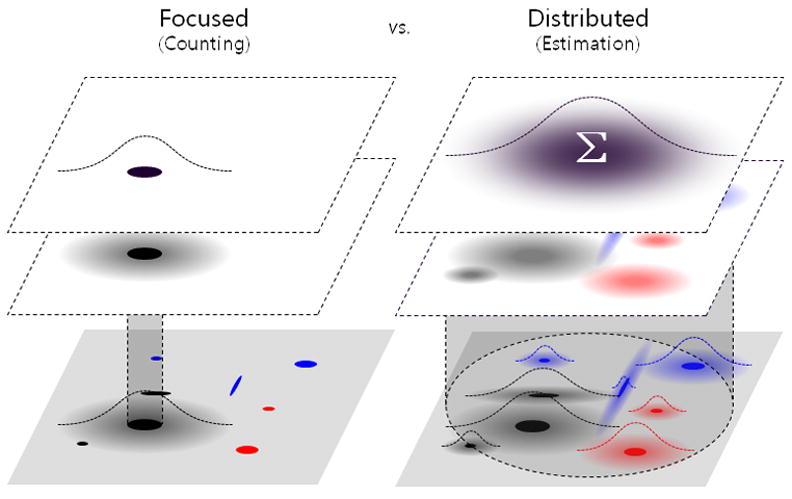
Schematic diagram of focused and distributed attention modes. In the focused attention mode (the left side), the visual system can individualize, identify, and count each object. In the distributed attention mode (the right side), one can estimate statistical properties of multiple objects without conscious access to each object. Note that attention can be distributed over time as well.

In summary, counting and estimation, the two components of numerosity, rely on different types of attention in the visual modality (focused and distributed attention respectively). Although conscious access to the end results of each system is possible, the process of estimation is unconscious. Element-by-element scrutiny is necessary for counting, whereas seeing the display as a whole is enough for estimation without relying much on attentional resource. Perhaps, through the process of counting we may have access to the bound objects with distinct location information, while estimation may allow us to have only the overall magnitude of unbound features.