Learning an Atlas of a Cognitive Process in Its Functional Geometry

Abstract

In this paper we construct an atlas that captures functional characteristics of a cognitive process from a population of individuals. The functional connectivity is encoded in a low-dimensional embedding space derived from a diffusion process on a graph that represents correlations of fMRI time courses. The atlas is represented by a common prior distribution for the embedded fMRI signals of all subjects. The atlas is not directly coupled to the anatomical space, and can represent functional networks that are variable in their spatial distribution. We derive an algorithm for fitting this generative model to the observed data in a population. Our results in a language fMRI study demonstrate that the method identifies coherent and functionally equivalent regions across subjects.

1 Introduction

The functional architecture of the cerebral cortex consists of regions and networks of regions that become active during specific tasks or at rest when the brain is suspected to engage in activities such as memory encoding [1]. The functional networks vary spatially across individuals due to natural variability [15], developmental processes in early childhood [9] or adulthood [4], or pathology [5]. Reorganization can appear over remarkably short periods of even few days [4]. The relationship between the structure of functional networks and their spatial distribution is not well understood.

The traditional brain imaging paradigm in most functional MRI (fMRI) studies treats functional activity as a feature of a position within the anatomical coordinate frame. The anatomical variability in a population is typically mitigated by smoothing and non-rigid registration of the anatomical data, and the corresponding normalization of functional signals into a stereotactic space. The remaining spatial variability of functional regions is ignored. An alternative approach is to localize functional regions of interest (fROIs) in individuals or groups [15] as a precursor to analysis, and subsequently study the responses in the resulting small number of fROIs.

Both approaches limit the range of questions that can be formulated on the fMRI observations. For example, the spatial normalization framework cannot express or account for spatial variability within the population since it assumes perfect spatial correspondences when detecting networks by averaging over multiple subjects. In contrast, the fROI approach is based on detection results for each subject, which can be infeasible if the activation is weak and cannot be distinguished from noise in individual subjects without averaging over the group.

We propose a different approach to characterize functional networks in a population of individuals. We do not assume a tight coupling between anatomical location and function, but view functional signals as the basis of a descriptive map that represents the global connectivity pattern during a specific cognitive process. We develop a representation of those networks based on manifold learning techniques and show how we can learn an atlas from a population of subjects performing the same task. Our main assumption is that the connectivity pattern associated with a functional process is consistent across individuals. Accordingly, we construct a generative model (the atlas) for these connectivity patterns that describes the common structures within the population.

The clinical goal of this work is to provide additional evidence for localization of functional areas. A robust localization approach is important for neurosurgical planning if individual activations are weak or reorganization has happened due to pathologies such as tumor growth. Furthermore the method provides a basis for understanding the mechanisms underlying formation and reorganization in the cerebral system.

Related work

A spectral embedding [18] represents data points in a map that reflects a large set of pair-wise affnity values in the Euclidean space. Diffusion maps establish a metric based on the concept of diffusion processes on a graph [2]. A probabilistic interpretation of diffusion maps has recently been proposed [13]. Previously demonstrated spectral methods in application to fMRI analysis mapped voxels into a space that captured joint functional characteristics of brain regions [10]. This approach represents the magnitude of co-activation by the density in the embedding. Functionally homogeneous units have been shown to form clusters in the embedding in a study of parceled resting-state fMRI data [17]. In [7] multidimensional scaling was employed to retrieve a low dimensional representation of positron emission tomography (PET) signals in a set of activated regions. In an approach closely related to the method proposed in this paper [11], an embedding of fMRI signals was used to match corresponding functional regions across different subjects. Recently a probabilistic generative model that connects the embedding coordinates with a similarity matrix has been demonstrated in [14].

2 Generative Model of Functional Connectivity

We start by reviewing the original diffusion maps formulation. We then derive a probabilistic likelihood model for the data based on this mapping and use the model to link diffusion maps of functional connectivity across subjects.

2.1 Diffusion Distances, Diffusion Maps, and fMRI Time Courses

Given an fMRI sequence $\mathbf{I}\in {\mathbb{R}}^{T\times N}$ that contains N voxels, each characterized by an fMRI signal over T time points, we calculate matrix $\mathbf{W}\in {\mathbb{R}}^{N\times N}$ that assigns a non-negative symmetric weight to each pair of voxels (i, j)

$$\mathbf{W}(i,j)=e^{\frac{\langle {\mathbf{I}}_i,{\mathbf{I}}_j\rangle }{∊}},$$ (1)

where 〈·, ·〉 is the correlation coeffcient of the time courses I_i and I_j, and is ε the weight decay. We define a graph whose vertices correspond to voxels and whose edge weights are determined by W [2,10]. In practice, we discard all edges that have a weight below a chosen threshold. This construction yields a sparse graph which is then transformed into a Markov chain. We define the Markov transition matrix P = D⁻¹W, where D is a diagonal matrix such that d_i = D(i, i) = ∑_j w(i, j) is the degree of node i. By interpreting the entries P(i, j) as transition probabilities, we can define the diffusion distance

$$D_t(i,j)=\sum _{i^{\prime }=1,\dots ,N}\frac{{({\mathbf{P}}^t(i,i^{\prime })-{\mathbf{P}}^t(j,i^{\prime }))}^2}{\varphi \left(i^{\prime }\right)}\text{where}\varphi \left(i\right)=\frac{d_i}{\sum _{i^{\prime }}{d}_{i^{\prime }}}.$$ (2)

The distance is determined by the probability of traveling between vertices i andj by taking all paths of at most t steps. The transition probabilities are based on the functional connectivity of node pairs; the diffusion distance integrates the connectivity values over possible paths that connect two points and defines a geometry that captures the entirety of the connectivity structure. This distance is characterized by the operator P^t, the t^th power of the transition matrix. The value of the distance D_t(i, j) is low if there is a large number of paths of at most length t steps with high transition probabilities between the nodes i and j.

The diffusion map coordinates Γ = [γ₁, γ₂, · · · , γ_N]^T yield a low dimensional embedding of the signal such that the resulting pairwise distances approximate diffusion distances, i.e., ∥γ_i−γ_j∥² ≈ D_t(i, j) [13]. They are derived from the right eigenvectors of the transition matrix. In Appendix A we show that a diffusion map can be viewed as a solution to a least-squares problem. Specifically, we define a symmetric matrix A = D^−1/2WD^−1/2, and let L be the normalized graph Laplacian

$$\mathbf{L}={\mathbf{D}}^{-1∕2}{\mathbf{A}}^{2t}{\mathbf{D}}^{-1∕2}.$$ (3)

The embedding coordinates are then found as follows:

$${\Gamma }^{\ast }=\underset{\Gamma \in {\mathbb{R}}^{N\times L}}{\text{argmin}}\sum _{i,j}{d}_i{d}_j{(\mathbf{L}(i,j)-{\gamma }_i^T{\gamma }_j)}^2,$$ (4)

where L is the dimensionality of the embedding. To simplify notation, we omit t for L and Γ in the derivations, assuming that all the results are derived for a fixed, known diffusion time.

2.2 A Generative Model for Diffusion Maps across Subjects

The goal of the generative model is to explain jointly the distribution of pairwise functional affnities of voxels across all subjects. We use latent variables $\Gamma ={\left\{{\Gamma }_s\right\}}_{s=1}^S$ to represent the diffusion map coordinates for S subjects indexed by s ∈ {1, . . . , S}. We can interpret Eq. (4) as maximization of a Gaussian likelihood model. We let γ_si denote the embedding coordinates of voxel i in subject s and let L_s be the normalized graph Laplacian for subject s. We further assume that elements of L_s are conditionally independent given the embedding coordinates:

$$p({\mathbf{L}}_s(i,j)\mid {\gamma }_{si},{\gamma }_{sj})=\mathcal{N}\left({\mathbf{L}}_s(i,j);{\gamma }_{si}^T{\gamma }_{sj},\frac{{\sigma }_s^2}{d_{si}{d}_{sj}}\right),$$ (5)

where N (·; μ, σ²) is a Gaussian distribution with mean μ and variance σ².

Note that the variance depends on the degrees d_i, d_j, which is technically a problem since these quantities depend on the data W. We find that in practice, the method works well and leave the development of rigorous probability models for diffusion maps as an interesting future direction.

In the absence of a prior distribution on Γ_s, fitting this model to the data yields results similar to the conventional diffusion maps for each subject independently from the rest of the population.

The goal of this paper is to define an atlas that represents a population-wide structure of functional connectivities in the space of diffusion maps. To capture this common structure, we define a shared prior distribution on the embedding coordinates Γ_s for all subjects, and expect the embedded vectors to be in correspondence across subjects [11]. Here, we assume that the common distribution in the embedding space is a mixture of K Gaussian components. We let z_si ∈ {1, · · · , K} be the component assignment for voxel i in subject s and obtain the prior on the embedding coordinates of voxel i in subject s:

$$p({\gamma }_{si}\mid z_{si}=k;\mu ,ϴ)=\mathcal{N}({\gamma }_{si};{\mu }_k,{ϴ}_k),$$ (6)

where μ_k and Θ_k are the center and covariance matrices for component k. We let the component assignments be independently distributed according to the weights of different components, i.e.,

$$p(z_{si}=k)={\pi }_k.$$ (7)

Together, Eqs. 5 to Eqs. 7 the joint distribution of the embeddings Γ , the component assignments z, and the observed affnities $\mathit{L}={\left\{{\mathbf{L}}_s\right\}}_{s=1}^S$. The distribution is parameterized by component centers {μ_k}, covariance matrices {Θ_k}, and weights {π_k}.

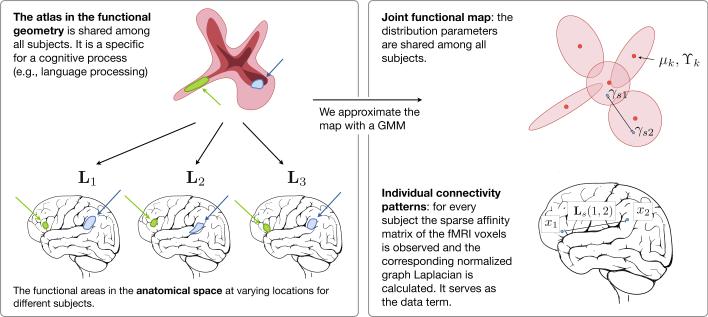
By adding the group prior over diffusion maps, we constrain the resulting subject maps to be aligned across subjects and further encourage them to resemble the population-wide structures characterized by the mixture model (Fig. 1). The mixture model acts as a population atlas in the embedding space.

Fig. 1.

Joint functional geometry scheme

3 Atlas Learning and Inference

We employ the variational EM algorithm [8] to estimate the parameters of our model from the observed data. We approximate the posterior distribution of latent variables p(Γ , z|L) with a product distribution of the form

$$q(\Gamma ,\mathit{z})=\prod _{s,i}q\left({\gamma }_{si}\right)q\left(z_{si}\right).$$ (8)

The problem is then formulated as the minimization of the Gibbs free energy

$$\mathcal{F}={\mathbb{E}}_q[\ln q(\Gamma ,\mathit{z})-\ln p(\Gamma ,\mathit{z},\mathit{L};\mu ,ϴ,\pi )],$$ (9)

where ${\mathbb{E}}_q$ indicates the expected value operator with respect to distribution q(·). We derive coordinate descent update rules that, given an initialization of all latent variables and parameters, find a local minimum of the cost function in Eq. (9). Appendix B presents the derivation of the update rules.

3.1 Initialization

The algorithm requires initial estimates of the latent variables and model parameters. Initialization affects convergence and the quality of the final solution. Here, we describe a simple initialization scheme that matches closely the structure of our model and enhances the performance of the algorithm.

In general, the relationship between the diffusion map coordinates Γ and the corresponding symmetric matrix L is defined up to an arbitrary orthonormal matrix Q since (ΓQ)(ΓQ)^T = ΓQQ^TΓ^T = ΓΓ^T = L. In order to define an atlas of the functional connectivity across all subjects, we seek matrix Q_s for each subject s such that the maps ${\left\{{\Gamma }_s{\mathbf{Q}}_s\right\}}_{s=1}^S$ are aligned in a common coordinate frame. Consider aligning the diffusion map Γ_s of subject s to the diffusion map Γ_r of reference subject r. Similar to the construction of the diffusion map, we compute the inter-subject affnities between the fMRI signals of subjects s and r using Eq. (1) and only keep those with a correlation above the threshold. This step produces a set of M node pairs ${\left\{(i_m,j_m)\right\}}_{m=1}^M$, characterized by affnities ${\left\{w_m\right\}}_{m=1}^M$. The initialization should ensure that nodes with similar fMRI signals are close in the common embedding space. Therefore, we choose matrix Q that minimizes the weighted Euclidean distance between pairs of corresponding embedding coordinates

$${\mathbf{Q}}_{sr}^{\ast }=\underset{\mathbf{Q}}{\text{argmin}}\left[\sum _{m=1}^M{w}_m{\Vert \mathbf{Q}{\gamma }_{s{i}_m}-{\gamma }_{r{j}_m}\Vert }_{L_2}^2\right].$$ (10)

We define matrices Γ_sm = [γ_si1 , . . . , γ_siM]^T and Γ_rm = [γ_rj1, . . . , γ_rjM]^T . It can be shown that ${\mathbf{Q}}_{sr}^{\ast }={\mathbf{VU}}^{\mathrm{T}}$, where we use the singular value decomposition $\mathbf{U}\Sigma {\mathbf{V}}^T={\Gamma }_{s_m}^{\mathrm{T}}$ diag(w_m)Γ_rm [16].

We find initial estimates of ${\{{\mu }_k,{ϴ}_k,{\pi }_k\}}_{k=1}^K$ by fitting a K component Gaussian mixture model to the initial estimates of the atlas embedding coordinates ${\left\{{\Gamma }_s{\mathbf{Q}}_{sr}^{\ast }\right\}}_{s=1}^S$ for a randomly chosen reference subject r.

4 Experiments and Results

Data

We demonstrate the method on a set of six healthy control subjects. The fMRI data was acquired using a 3T GE Signa system (TR=2s, TE=40ms, flip angle=90°, slice gap=0mm, FOV=25.6cm, volume size of 128 × 128 × 27 voxels, voxel size of 2 × 2 × 4 mm³). The language task (antonym generation) block design was 5min 10s long, starting with a 10s pre-stimulus period. Eight task and seven rest blocks, 20s each, alternated in the design. For each subject, an anatomical T1 MRI scan was acquired and registered to the functional data. Grey matter was segmented with FSL [19] on the T1 data. The grey matter labels were transferred to the co-registered fMRI volumes, and computation was restricted to grey matter.

Evaluation

We construct a joint functional diffusion map for all six subjects. For the results presented in this paper, we set the dimensionality of the diffusion map to be L = 20 and choose a diffusion time t = 2 that satisfies (λ_L/λ₁)^t < 0.2 for all subjects. To facilitate computation we only keep nodes for which the degree is above a certain threshold. In the experiments reported here we choose a threshold of 100. For the EM algorithm, we fix a value of ${\sigma }_s={10}^2{N}_s^{-1}{\sum }_i{d}_{si}$ for the first 10 iterations, then allow this parameter to update for the remaining iterations according to the rule defined in Appendix B. In our experiments, an initial value of σ_s specifically proportional to 10² allows the algorithm to achieve the lowest Gibbs free energy.

We hypothesize that working in the embedding space should allow us to more robustly capture the functional structure common to all subjects. In order to validate this, we compare the consistency of clustering structures found in the space of fMRI time courses (Signal), a low-dimensional (L=20) PCA embedding of these time courses (PCA-Signal), and the low-dimensional (L=20) embedding proposed in this paper. We report results for the initial alignment (Linear-Atlas) and the result of learning the joint atlas (Atlas).

We first apply clustering to signals from individual subjects separately to find subject-specific cluster assignments. We then apply clustering to signals combined from all subjects to construct the corresponding group-wise cluster assignments. Since our group atlas for the lower-dimensional space is based on a mixture model, we also choose a mixture-model for clustering in the Signal and PCA-Signal spaces. In both cases, each component in the mixture is an isotropic von Mises-Fisher distribution, defined on a hyper-sphere after centering and normalization of the fMRI signals to unit variance [12].

Likewise, we cluster the diffusion map coordinates Γ_s separately in each subject to obtain subject-specific assignments. We cluster the diffusion map coordinates of all subjects aligned to the first subject, {Γ_sQ_(s,1)}_s for the Linear-Atlas and in ${\left\{{\Gamma }_s^{\ast }\right\}}_s$ for Atlas to obtain group-wise clustering assignments. Analyzing the consistency of clustering labels across methods evaluates how the population structure captures the individual embeddings. For the diffusion maps, Euclidean distance is a meaningful metric; we therefore use a mixture model with Gaussian components that share the same isotropic variance.

Since clusters are labeled arbitrarily in each result, we match group and subject-specific cluster labels by solving a bipartite graph matching problem. Here, we find a one-to-one label correspondence that maximizes voxel overlap between pairs of clusters, similar to the method used in [12]. After matching the labels, we use the Dice score [3] to measure the consistency between group and subject-specific assignments for each cluster.

4.1 Results

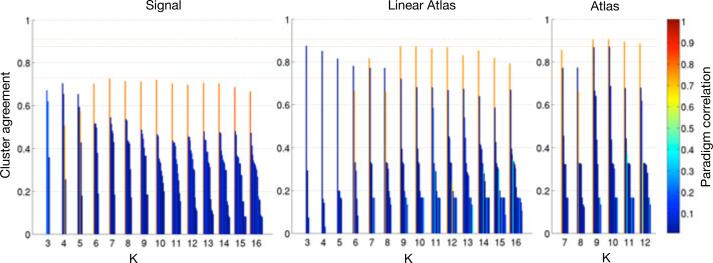
Fig. 2 reports the consistency of clusters between group-level and subject-specific assignments, measured in terms of Dice score averaged across subjects. To illustrate the temporal nature of the clusters, the colors of the bars indicate the correlation of the average fMRI signal in the cluster with the fMRI language paradigm convolved with the hemodynamic response function. Note that the paradigm was not used at any point during the generation of the maps or clusters. The cluster with the highest paradigm correlation is the most consistent cluster over a large range of cluster numbers. The highest Dice score (0.725) for Signal clustering is achieved, with similar values for larger numbers of clusters. Although the plot is not shown here, clustering in the PCA-Signal space exhibits no noticeable improvement. Initial alignment of the diffusion maps into the Linear-Atlas substantially increases the Dice score of the highest ranked clusters for all K, with a maximum value of 0.876. The variational EM algorithm performed using a range of reasonable cluster numbers and further improves the cluster agreement for the top ranked clusters (0.905).

Fig. 2.

Mean cluster Dice scores for clustering in Signal, Linear Atlas, and Atlas. For each number of clusters K, we report the mean Dice score across subjects for each cluster. Color illustrates correlation of the cluster average fMRI signal with the paradigm signal.

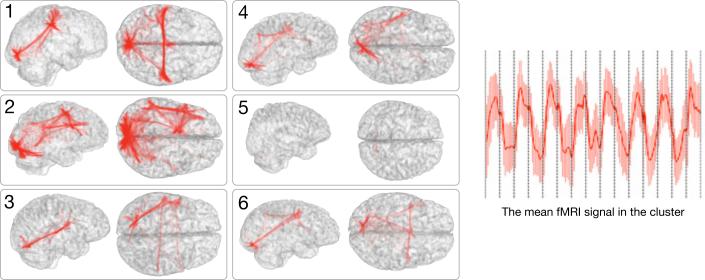
Fig. 3 shows the networks of the subjects that correspond to the top ranked atlas cluster (K=10), together with the corresponding average fMRI signal. The paradigm is recovered very well, and for most subjects the cluster network plausibly spans visual, motor, and language areas.

Fig. 3.

A cluster in the joint map corresponds to a network in each subject. Here we illustrate a network in 6 subjects that corresponds to one cluster in the atlas, and the mean fMRI signal of this cluster. The 8 block stimulus in this language study was not used by the analysis, but was recovered by the algorithm and corresponding networks were identified across all subjects. They typically span the visual cortex, the language areas (Wernicke and Broca), and the motor areas in some cases.

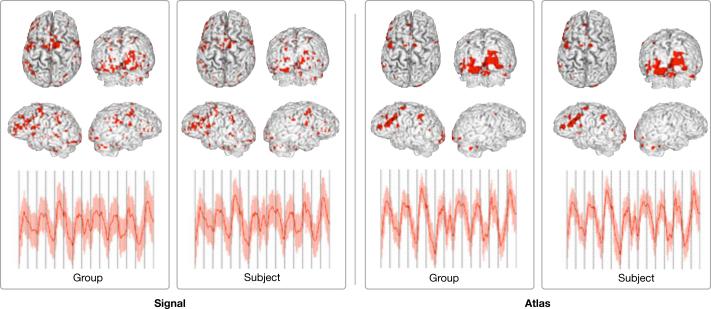
Fig. 4 compares the location and average signal of the top ranked of 10 clusters for Signal and Atlas clustering in a single subject. While both recover parts of the paradigm, the clustering in the diffusion map atlas exhibits more consistency between the group and the subject levels. Additionally, the Signal clusters suffer from a relatively high dispersion across the entire cortex. This is not the case for the diffusion map atlas. In summary, these results demonstrate that the representation of fMRI time courses in the low dimensional space of diffusion maps better captures the functional connectivity structure across subjects. Not only are clustering assignments more consistent, but the anatomical characteristics of these clusters also are also more plausible. Furthermore, our results using the variational EM algorithm suggest that the probabilistic population model further improves the consistency across the population, and consolidates the distribution in the embedding space.

Fig. 4.

Most consistent cluster in the Signal space and the Atlas shown in the anatomical space. For each method, we show the group-wise (left) and subject-specific (right) assignment. Also shown is the average and standard deviation of the cluster fMRI signal. Results for subject 2.

5 Conclusion

We propose a method to learn an atlas of the functional connectivity structure that emerges during a cognitive process from a group of individuals. The atlas is a group-wise generative model that describes the fMRI responses of all subjects in the embedding space. The embedding space is a low dimensional representation of fMRI time courses that encodes the functional connectivity patterns within each subject. Results from a fMRI language experiment indicate that the diffusion map framework captures the connectivity structure reliably, and leads to valid correspondences across subjects. Future work will focus on the application of the framework to the study of reorganization processes.

A Diffusion Map Coordinates

In the standard diffusion map analysis, the embedding coordinates Γ for a L-dimensional space are obtained via the first L eigenvectors of matrix A = D^−1/2WD^−1/2 [13]. Here we show that we can represent the embedding as a solution of a least-squares problem formulated directly on the similarity matrix W.

Formally, $\Gamma ={\mathbf{D}}^{-1∕2}{\mathbf{V}}_{1:L}{\Lambda }_L^t$, where A = VΛV^T is the eigenvector decomposition of matrix A, t s the diffusion time, and subscripts indicate that we select the first L eigenvectors. Matrix $\tilde{\mathbf{A}}={\mathbf{V}}_{1:L}{\Lambda }_L{\mathbf{V}}_{1:L}^T$ is a low-rank approximation of matrix A that is quite accurate if the remaining eigenvalues are much smaller than the sum of the first L eigenvalues. We define

$$\mathbf{L}={\mathbf{D}}^{-1∕2}{\mathbf{A}}^{2t}{\mathbf{D}}^{-1∕2}\approx {\mathbf{D}}^{-1∕2}{\tilde{\mathbf{A}}}^{2t}{\mathbf{D}}^{-1∕2}={\mathbf{D}}^{-1∕2}{\left({\mathbf{V}}_{1:L}{\Lambda }_L{\mathbf{V}}_{1:L}^T\right)}^{2t}{\mathbf{D}}^{-1∕2}={\mathbf{D}}^{-1∕2}{\mathbf{V}}_{1:L}{\Lambda }_L^t{\Lambda }_L^t{\mathbf{V}}_{1:L}^T{\mathbf{D}}^{-1∕2}=\Gamma {\Gamma }^T$$ (11)

and use a generalization of the Eckart-Young theorem [6] to formulate the eigen decomposition as an optimization problem:

$${\Gamma }^{\ast }=\underset{\Gamma \in {\mathbb{R}}^{N\times L}}{\text{argmin}}{\Vert {\mathbf{A}}^2-{\mathbf{D}}^{1∕2}\Gamma {\Gamma }^T{\mathbf{D}}^{1∕2}\Vert }_F^2=\underset{\Gamma \in {\mathbb{R}}^{N\times L}}{\text{argmin}}\sum _{i,j}{d}_i{d}_j{({\mathbf{L}}_t(i,j)-{\gamma }_i^T{\gamma }_j)}^2,$$ (12)

where ∥·∥_F denotes the Frobenius norm.

B Variational EM Update Rules

We use a natural choice of a multinomial distribution for cluster membership q(z_si = k) for s ∈ {1, . . . , S}, i ∈ {1, . . . , N_s}, and a Gaussian distribution for the embedding coordinates $q\left({\gamma }_{si}\right)=\mathcal{N}({\gamma }_{si};\mathbb{E}\left[{\gamma }_{si}\right],\text{diag}\left(\mathbb{V}\left[{\gamma }_{si}\right]\right))$, parameterized by its mean $\mathbb{E}\left[{\gamma }_{si}\right]$ and component-wise variance $\mathbb{V}\left[{\gamma }_{si}\right]$.

E-Step

We determine the parameter values of the approximating probability distribution q(·) that minimize the Gibbs free energy in Eq. (9) by evaluating the expectation, differentiating with respect to each parameter and setting the derivatives to zero. This yields

$$q(z_{si}=k)\propto \frac{{\pi }_k}{{\mid {ϴ}_k\mid }^{1∕2}}\text{exp}\left\{-\frac{1}{2}\left({(\mathbb{E}\left[{\gamma }_{si}\right]-{\mu }_k)}^T{ϴ}_k^{-1}(\mathbb{E}\left[{\gamma }_{si}\right]-{\mu }_k)+\text{trace}\left(\text{diag}\left(\mathbb{V}\left[{\gamma }_{si}\right]\right){ϴ}_k^{-1}\right)\right)\right\},\mathrm{s}.\mathrm{t}.\sum _{k}q(z_{si}=k)=1,$$

$$\mathbb{V}\left[{\gamma }_{si}\left(l\right)\right]={\left(\sum _{k}q(z_{si}=k){ϴ}_k^{-1}(l,l)+\frac{d_{si}}{{\sigma }_s^2}\sum _{j\ne i}{d}_{sj}(\mathbb{E}{\left[{\gamma }_{sj}\left(l\right)\right]}^2+\mathbb{V}\left[{\gamma }_{sj}\left(l\right)\right])\right)}^{-1},$$

$$\mathbb{E}\left[{\gamma }_{si}\left(l\right)\right]=\mathbb{V}\left[{\gamma }_{si}\left(l\right)\right]\left[\sum _{k}q(z_{si}=k)\left[{ϴ}_k^{-1}(l,l){\mu }_k\left(l\right)-\sum _{l^{\prime }\ne l}{ϴ}_k^{-1}(l,l^{\prime })\left(\mathbb{E}[{\gamma }_{si}\left(l^{\prime }\right)-{\mu }_k\left(l^{\prime }\right)]\right)\right]+\frac{d_{si}}{{\sigma }_s^2}\sum _{j\ne i}{d}_{sj}\left[{\mathbf{L}}_s(i,j)\mathbb{E}\left[{\gamma }_{sj}\left(l\right)\right]-\mathbb{E}\left[{\gamma }_{sj}\left(l\right)\right]\sum _{l^{\prime }\ne l}\mathbb{E}\left[{\gamma }_{si}\left(l^{\prime }\right)\right]\mathbb{E}\left[{\gamma }_{sj}\left(l^{\prime }\right)\right]\right]\right].$$

Rather than solve the coupled system of equations above, we iteratively update each parameter of the distribution q(·) while fixing all the other parameters.

M-Step

We now find the parameter values similar to the standard EM algorithm, but using the approximating distribution q(·) to evaluate the expectation. Specifically, we find

$${\pi }_k=\frac{1}{\sum _s{N}_s}\sum _{s,i}q(z_i=k),{\mu }_k=\sum _{s,i}\frac{q(z_{si}=k)}{\sum _{s^{\prime },i^{\prime }}q(z_{s^{\prime }{i}^{\prime }}=k)}\mathbb{E}\left[{\gamma }_{si}\right],$$ (13)

$${ϴ}_k=\sum _{s,i}\frac{q(z_{si}=k)}{\sum _{s{,}^{\prime }{i}^{\prime }}q(z_{s^{\prime }{i}^{\prime }}=k)}[(\mathbb{E}\left[{\gamma }_{si}\right]-{\mu }_k){(\mathbb{E}\left[{\gamma }_{si}\right]-{\mu }_k)}^T+\text{diag}\left(\mathbb{V}\left[{\gamma }_{si}\right]\right)],$$ (14)

$${\sigma }_s^2=\frac{2}{N_s(N_s-1)}\sum _{i,j\ne i}{d}_{si}{d}_{sj}\mathbb{E}\left[{({\mathbf{L}}_s(i,j)-{\gamma }_{si}^T{\gamma }_{sj})}^2\right].$$ (15)