Belief Propagation Based Segmentation of White Matter Tracts in DTI

Abstract

This paper presents a belief propagation approach to the segmentation of the major white matter tracts in diffusion tensor images of the human brain. Unlike tractography methods that sample multiple fibers to be bundled together, we define a Markov field directly on the diffusion tensors to separate the main fiber tracts at the voxel level. A prior model of shape and direction guides a full segmentation of the brain into known fiber tracts; additional, unspecified fibers; and isotropic regions. The method is evaluated on various data sets from an atlasing project, healthy subjects, and multiple sclerosis patients.

1 Introduction

Diffusion-weighted imaging (DWI) has become a major tool for the study of connectivity in the living human brain in health and disease [1,2]. Although DWI tractography methods provide useful information about the connectivity between remote regions of the brain [3], the segmentation of fiber bundles or tracts that correspond to known anatomical atlases requires additional grouping, trimming, and labeling, which usually requires manual assistance [4,5]. The development of automatic solutions for white matter tract segmentation is a challenging problem for several reasons. For example, since the reliability of fiber tracking varies with imaging resolution, noise, and patient orientation [6], it is difficult to consistently recover the same fiber tracts in repeated observations of the same individual. As well, lesions in the white matter caused by disease or aging can impair fiber tracking, resulting in poor definition of the tracts.

As an alternative to the reconstruction of fiber samples, level set [7] and non-parametric fuzzy classification methods [8] have been investigated for the segmentation of a given bundle from a set of initial regions of interest (ROIs). These methods focus on a single tract, and often require a careful initialization in order to succeed. Deformable atlas registration techniques segment the white matter into homogeneous regions rather than tracts [9,10], but the relationship between these regions and the tracts is unclear. Probabilistic connectivity methods evaluate the connection strength between regions or voxels [11,12,13], but do not explicitly recover fiber tracts.

In this work, we propose a Markov Random Field (MRF) to model the diffusion properties and a belief propagation (BP) technique to estimate the most likely tracts at every voxel. Shape and direction priors are used to identify the tracts, and the MRF connects regions along their diffusion direction. With this approach, we can automatically and simultaneously segment multiple tracts with known anatomical and functional meaning, reduce the variability of the estimated tracts without manual initialization or post-processing, and handle robustly the presence of white matter lesions.

2 Methods

2.1 Problem Description and Notations

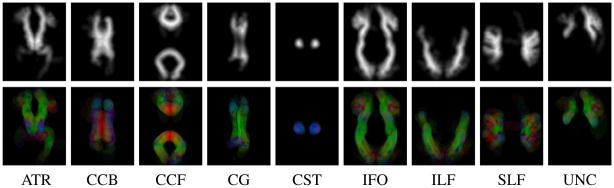
The goal of this work is to extract from this data set several of the major fiber tracts of the human brain: anterior thalamic radiation (ATR), cortico-spinal tract (CST), body of the corpus callosum (CCB), forceps of the corpus callosum (CCF), cingulum (CG), inferior longitudinal fasciculus (ILF), superior longitudinal fasciculus (SLF), inferior fronto-occipital fasciculus (IFO), uncinate fasciculus (UNC). These tracts are first defined using a probabilistic atlas of shape and direction co-registered to the studied images, and then refined by estimating the most likely diffusion pathways from the FA and diffusion directions by belief propagation.

Starting from a series of diffusion-weighted images, we first obtain a set of diffusion eigenvectors and associated eigenvalues ${\{{\mathit{v}}_j^n,{\lambda }_j^n\}}_{1,N}$ with the standard linear reconstruction method [2], as well as a fractional anisotropy (FA) map a_j for each voxel j of the image. Extra-cranial tissues are removed with a semi-automatic method [14] applied to the mean diffusivity image.

When manipulating direction vectors v_j, we denote v̄_j the unsigned orientation axis without direction, i.e., +v_j and −v_j correspond to the same orientation v̄_j. We use the following definitions for the inner product and addition of these orientations:

$${\overline{v}}_i·{\overline{v}}_j=\mid {\mathit{v}}_i·{\mathit{v}}_j\mid ,{\overline{v}}_i+{\overline{v}}_j={\mathit{v}}_i+\text{sign}({\mathit{v}}_i·{\mathit{v}}_j){\mathit{v}}_j.$$ (1)

Finally, the eigenvalues are ranked and normalized so that the largest eigenvalue ${\lambda }_j^1=1$.

2.2 Diffusion Based Tract Gain Functions

The central question for this approach is how to adequately translate our knowledge of fiber tracts observed in DTI into a MRF model of the tracts, represented by gain functions L_ij(x_i, x_j), which we define to be a large positive value if there is evidence that the state x_i is likely conditioned on the state x_j, a large negative value if the data goes against this hypothesis, and close to zero if there is no information for or against it.

Several well-known fiber tracts like the optic radiation or even the corpus callosum were not included in the original, tractography-based atlas because it is difficult to define them consistently based on tractography and ROIs [6]. In addition, many smaller tracts between neighboring regions are present and distinct from these tracts. To provide a complete parcellation, we add two labels to the nine fiber tracts from the atlas: isotropic regions or background (BG), and other fiber tracts (OFT).

Background Model

We assume the background is composed of regions of very low FA, with the following gain function:

$$L_i^B=2exp(-\frac{a_i}{a_0})-1$$ (2)

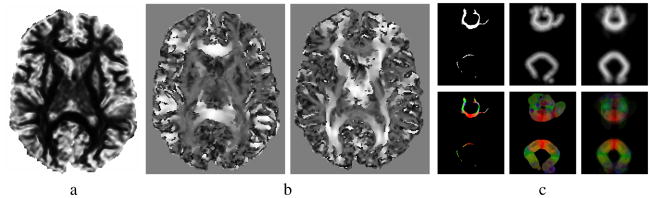
with a₀ a parameter representing the expected transition value for FA (a₀ = 0.1 in our experiments, see Fig. 1a).

Fig. 1.

Gain and atlas functions: a) background gain $L_i^B$, b) diffusion gains L^P for the X and Y directions, c) shape and direction atlas building steps for CCF (left: original delineation, middle: extrapolated image, right: average of seven images)

Diffusion Model

The evidence for fiber tracts comes from the diffusion tensors: if two tensors are aligned they likely correspond to the same tract. Note that we cannot differentiate between the type of tracts based on the diffusion direction alone, without considering some global models of the tracts. However, we can model the similarity between tensors as follows:

$$L_{j\mid i}^P={\text{maxabs}}_{n,m}{\lambda }_i^n{\lambda }_j^{m}exp(-\frac{1-max({\overline{v}}_i^n·{\overline{d}}_{ij},{\overline{v}}_j^m·{\overline{d}}_{ij})}{v_1})\left(2exp(-\frac{1-{\overline{v}}_i^n·{\overline{v}}_j^m}{v_1})-1\right)$$ (3)

with d̄_ij the direction between voxels i and j, and v₁ a constant representing the average expected deviation in angle between similar directions. maxabs_ng(n) selects for the function g(n) with maximum absolute value.

This gain function is positive when the diffusion directions from i to j and from j to i are aligned with the path from i to j. If both diffusion directions are orthogonal to that path, we cannot assume that they are related even if they are aligned: many fiber tracts have “kissing” fibers that follow the same direction before diverging. In such case, the gain goes to zero in order to model the uncertainty. When the diffusion directions are orthogonal and one of them is aligned with the path, then it is clear that both points cannot be part of the same tract, which translates into a large negative gain value (see Fig. 1b).

Shape and Direction Prior

To provide a labeling for the tracts, we use an atlas of shape and direction that gives for each voxel i and tract label l a probability $p_i^l$ of existence, and a probable diffusion orientation ${\overline{d}}_i^l$, with $\mid {\overline{d}}_i^l\mid$ a function of the orientation variability in the atlas.

Our atlas is based on the fiber tract atlas of Mori and Wakana [4,6]. We obtained the individual tensor images and fiber tract delineations used in building this atlas, so we could complement the atlas with tracts that were not originally delineated because of their lower reproducibility [6]. For this work, we added our delineation of the body of the corpus callosum in seven atlas images (see Fig. 2). The remaining, unspecified fibers were segmented as the regions of FA above a₀ = 0.1.

Fig. 2.

Shape and direction atlas for the delineated fiber tracts on selected axial slices: shape prior p^l (top) and direction prior d̄^l (bottom) for each tract

To build the shape and direction atlas, each of the delineated fibers is smoothed over neighborhood of 10mm and its principal orientation is extrapolated as follows:

$${\overline{v}}_i^t=\frac{{\sum }_j{s}_j^t{\overline{v}}_j^t}{{\sum }_j{s}_j^t}\forall j\in N_i\text{s}.\text{t}.s_j^t>s_i^t,$$ (4)

where ${\overline{v}}_i^t$ is the principal direction at voxel i in image t and $s_i^t$ the smoothed delineation on image t for the considered fiber. The shape and orientation are then averaged from the seven images as shown in Fig. 1-c. The 10mm neighborhood was chosen empirically to ensure that tracts from the image to segment are fully included in the neighborhood, making the atlas more generic, even with low numbers of atlas images. As the segmentation is driven simultaneously by the atlas and the diffusion data, it is not necessary that the atlas matches accurately the images to segment.

From the atlas, we define the shape prior gain as follows:

$$L_i^S(x_i=l)=p_i^l-\underset{m\ne l}{max}{p}_i^m$$ (5)

giving positive values where the prior for l is higher than any other, negative values where is it dominated by another prior, and zero where two or more tracts compete. The direction prior gain is similar to the diffusion gain:

$$L_i^D(x_i=l)=p_i^l\mid {\overline{d}}_i^l\mid {\text{maxabs}}_n{\lambda }_i^n\left(exp(-\frac{\mid {\overline{d}}_i^l\mid -{\overline{d}}_i^l·{\overline{v}}_i^n}{\mid {\overline{d}}_i^l\mid v_1})-exp(-\frac{{\overline{d}}_i^l·{\overline{v}}_i^n}{\mid {\overline{d}}_i^l\mid v_0})\right)$$ (6)

with v₀ an angular constant. The gain is positive when the data is well aligned with the prior, negative when it is orthogonal, and goes toward zero in the uncertain area between v₀ and v₁ or when the shape prior is low, i.e., where the orientation is likely to be unknown. For the unspecified fibers, we set $L_i^D(\text{OFT})=0$.

Gain Function

The complete gain function is built from these separate terms for all the different cases as follows:

$$\begin{array}{l}{L}_{i\mid j}(\text{BG}\mid \text{BG})=L_i^B+\alpha L_i^S(\text{BG})+\beta \\ L_{i\mid j}(\text{BG}\mid l)=L_i^B+\alpha L_i^S(\text{BG})\\ L_{i\mid j}(l\mid \text{BG})=-L_i^B+\alpha L_i^S(l)+\gamma L_i^D(l)\\ L_{i\mid j}(l\mid l)=L_{i\mid j}^P{p}_{bj}(l)+\alpha L_i^S(l)+\beta +\gamma L_i^D(l)\\ L_{i\mid j}(l\mid m)=-max(L_{i\mid j}^P,0)p_{bj}(l)+\alpha L_i^S(l)+\gamma L_i^D(l)\end{array}$$ (7)

where $p_{bj}(l)=\frac{exp{b}_j(l)}{{\sum }_{m}exp{b}_j(m)}$ is the current estimate of the posterior probability for label l, and α, β, γ three parameters that modulate the importance of shape priors (α), smoothing (β), and direction priors (γ). Because isotropic regions do not include a direction prior, the relative value of γ with regard to α, β influences the global amount of recovered tracts. In all our experiments, we set α = 0.1, β = 0.2 and γ = 0.5.

2.3 Belief Propagation Algorithm

Belief propagation [15] is the method of choice for maximizing functions that can be decomposed into a sum or product of pairwise interactions E = Σ_i,j L_i|j(l|m) as above. In this work, we use the tree-reweighted belief propagation (TRBP) variant of Kolmogorov, which offers convergence guarantees not present in the original max-product algorithm [16].

First we register the atlas to the image to segment with a multi-scale gradient descent method maximizing $E_{R0}={\sum }_j{\sum }_l{\left|\right|a_j{p}_{T(j)}^l\left|\right|}^2$, where a_j is the computed FA, and T a rigid transform. The direction atlas is rotated accordingly. Then, the algorithm alternates belief propagation with a refinement of the atlas registration:

1. compute the beliefs: b_i(x_i) ← Σ_j∈Nim_ji(x_i),

2. estimate the gain function L_i|j for all labels,

3. update the messages: $m_{ij}(x_j)\leftarrow {max}_{x_i}\left(\frac{\mid N_i\mid }{2}{L}_{ij}(x_i,x_j)+\frac{2}{\mid N_i\mid }{b}_i(x_i)-m_{ji}(x_i)\right)$

4. refine the registration by maximizing $E_R={\sum }_j{\sum }_l{\left|\right|p_{bj}(l)p_{T(j)}^l\left|\right|}^2$

These steps are repeated until the computed beliefs are stable, only about 10–20 iterations in practice thanks to the efficient TRBP propagation method. A 181x217x181 voxel image (1mm cubic resolution) is processed in less than two hours, and a more classical 256x256x60 voxel image takes between 45 minutes and an hour on a modern workstation with 6GB of available memory.

3 Experiments

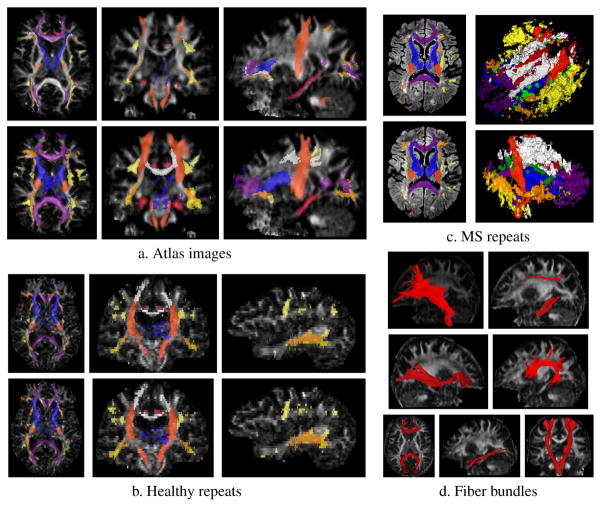
The algorithm is evaluated in several experiments that test its accuracy and reproducibility in real DTI images of the human brain in health and disease, as well as its use in complement to more classical tractography methods. First, we evaluate the algorithm on a set of ten images from the original atlas [4], distinct from the seven images used in building the shape and direction priors (“atlas images” experiment). In clinical practice, two or more DWI acquisitions are often used to reconstruct the DTI tensors in order to mitigate the noise. We reconstructed two separate tensor images from the DWI acquisitions for a set of five healthy subjects. These images have low SNR but describe the exact same anatomy in the same orientation (“healthy repeats” experiment). We also tested the method on a set of seven pairs of DTI acquisitions from multiple sclerosis (MS) patients with extensive white matter lesions, imaged twice at an interval of about six month (“MS repeats” experiment). Finally, we investigate the use of this voxel-based method in conjunction with fiber tractography. Tractography does provide a much finer, sub-voxel representation of connectivity, but automatically labeling regions and bundles of fibers is challenging [17,18]. Our method provides a probabilistic labeling of the entire space, thus we can classify each fiber by its mean belief value.

In DTI segmentation, validation is a challenging issue as there is no accepted gold standard or ground truth beyond simplistic simulations. Even the carefully edited fiber tracts of [4] have limitations, and often portions of the tracts are missing if the underlying fibers are interrupted or stray into a neighboring bundle. Furthermore, the typically elongated shape and small volume of fibers make the classical measures of overlap very sensitive to differences.

For the atlas images, we measured the amount of the original delineation (D) included in the segmentation (S): $I=\frac{D\cap S}{D}$, while we used the Dice overlap $D=\frac{2S_1\cup S_2}{S_1+S_2}$ in the repeats. Average surface distances were computed in all cases, see Table 1. In this context, our experiments still demonstrate that our segmentations correlate well with fiber delineations, and more importantly that they are reproducible in successive acquisitions of clinical quality.

Table 1.

Overlap and distance results for the experiments: average values (standard deviation)

		Structures
		ATR	CCB	CCF	CG	CST	IFO	ILF	SLF	UNC
Atlas images	Inclusion ratio	0.60	n/a	0.67	0.45	0.73	0.50	0.36	0.49	0.32
		(0.10)	n/a	(0.06)	(0.09)	(0.08)	(0.08)	(0.09)	(0.07)	(0.10)
Atlas images	Surface distance	3.90	n/a	2.40	3.99	3.49	4.26	3.31	3.70	4.12
		(1.25)	n/a	(0.25)	(2.00)	(1.09)	(3.53)	(0.48)	(0.89)	(1.31)
Healthy repeats	Dice overlap	0.64	0.70	0.61	0.48	0.73	0.48	0.39	0.54	0.26
		(0.10)	(0.17)	(0.11)	(0.13)	(0.09)	(0.19)	(0.20)	(0.12)	(0.19)
Healthy repeats	Surface distance	0.87	0.83	0.88	1.38	0.92	1.24	1.27	1.03	2.30
		(0.29)	(0.78)	(0.37)	(0.94)	(0.42)	(0.76)	(0.64)	(0.49)	(1.42)
MS repeats	Dice overlap	0.57	0.55	0.56	0.35	0.65	0.42	0.33	0.39	0.22
		(0.11)	(0.15)	(0.07)	(0.18)	(0.12)	(0.13)	(0.10)	(0.12)	(0.13)
MS repeats	Surface distance	1.50	1.51	1.47	3.01	1.51	1.84	2.32	2.03	2.66
		(0.62)	(0.91)	(0.47)	(1.87)	(0.84)	(0.95)	(1.15)	(1.10)	(1.36)

As can be seen on Fig. 3-a, the tractography-based delineations of the atlas were very conservative, and our proposed segmentation is overall more inclusive. For the largest, most distinct tracts (ATR, CC, CST) the segmentation includes most of the original delineations, but the smaller (CG, UNC) and heavily overlapping tracts (IFO, ILF, SLF) are more variable, due to the small number of voxels in the delineation. The repeat experiments show fairly high overlap and very low surface distance for most tracts, and the differences in the resulting segmentations appear mostly to be related to noise, see Fig. 3-b. The method succeeds in the presence of lesions, however with slightly worse overlap than in the healthy cases. This is likely reflecting the added variability due to different head position, different geometric distortions and registration errors. The presence of lesions only impairs the segmentation locally, leading to thinner or missing tracts in some of the diseased regions, but the healthy parts of the tracts remain unaffected, see Fig. 3-c. When tractography is reliable, our method offers an efficient way to cluster the fibers into compact bundles, mostly free of straying fibers as shown in Fig. 3-d.

Fig. 3.

Experiments: a) Atlas images: automatic segmentation (top) compared to tractography-based delineation (bottom), b) Healthy repeats: segmentation for two successive acquisitions, c) MS repeats: segmentations of two separate acquisitions, after coregistration (left) and 3D rendering of the reconstructed fibers intersecting estimated lesions (in green) in the same subject, d) fibers clustered by our segmentation in an atlas image

4 Conclusion

In this paper, we propose a new approach to the segmentation of white matter tracts in DTI. By combining shape and direction priors with a belief propagation method, the algorithm recovers nine of the major fiber tracts in the human brain automatically and simultaneously. Several real data experiments indicate that the method is consistent with manual delineations based on tractography, and can handle clinical quality images with noise and even lesions in a reproducible way. These properties are important for clinical applications, where the interaction of white matter lesions or tumors with the main fiber tracts can inform the diagnosis and treatment for individual patients and provide more insight on the systems targeted by the disease.