Abstract
Imaging of meniscal tissue reveals an extracellular matrix comprised of collagen fibrils arranged in circumferential bundles and radially aligned tie fibers, implicating structural material anisotropy. Biochemical analyses demonstrate regional disparities of proteoglycan content throughout the meniscal body, a constituent known to affect the shearing response of fibrocartilagenous tissue. Despite this phenomenological evidence and previous mechanical testing implicating otherwise, the meniscus if often modeled as a homogenous, transversely isotropic material with little regard for regional specificity and material properties. The aim of this investigation was to determine if shear stress response homogeneity and directionality exists in and between bovine menisci with respect to anatomical location (medial and lateral), region (anterior, central, and posterior) and fiber orientation (parallel and perpendicular). Meniscus explants were subjected to lap shear strain at 0.002 sec−1 with the circumferential collagen fibers oriented parallel or perpendicular to the loading axis. Comparisons were made using a piecewise linear elastic analysis. The toe region shear modulus was calculated from the first observed linear region, between 3%-13% strain and the extended shear modulus was established after 80% of the maximum shear strain. The posterior region was significantly different than the central for the extended shear modulus, correlating with known proteoglycan distribution. Observed shearing anisotropy led to the use of an anisoptropic hyperelastic model based on a two-fiber family composite, previously used for arterial walls. The chosen model provided an excellent fit to the sample population for each region. These data can be utilized in the advancement of finite element modeling as well as biomimetic tissue engineered constructs.
Keywords: Mechanical properties, hyperelastic, anisotropic, glycosaminoglycans, radial tie fibers
1. Introduction
The diarthrodial knee joint contains two fibrocartilagenous c-shaped menisci, separating the articulating tibiofemoral surfaces (Messner and Gao, 1998). Both the medial and lateral menisci function dynamically to aid in force distribution, stability and as a lubricating surface (Ahmed and Burke, 1983, Chevrier, et al., 2009, Fithian, et al., 1990, Shoemaker and Markolf, 1986, Walker and Erkman, 1975). Their proficiency in attenuating complex loading pathways and arresting articular cartilage degradation stems from an intricate structure and mechano-responsive biochemistry (Fithian, et al., 1990, McDevitt and Webber, 1990, Messner and Gao, 1998). Joint trauma can compromise the function of the meniscus leading to attrition of the articulating joint surfaces resulting in osteoarthritis, a degenerative disease that is fast approaching epidemic levels (Ratzlaff and Liang, 2010). Proposed mechanisms to impede degradation include the development of tissue engineered replacements which seek to recreate the native biomaterial (Buma, et al., 2004). The advancement and implementation of these constructs hinges on the ability to accurately mimic the native meniscus (Setton, et al., 1999).
The meniscus is a multiphasic material composed of interstitial water, collagen, proteoglycans, and fibrochondrocytes (AufderHeide and Athanasiou, 2004, McDevitt and Webber, 1990). Meniscal ultrastructure consists of three distinct fibrous layers. The superficial layer, which contacts the articulating joint surfaces, is comprised of randomly orientated fibers providing a smooth lubricating surface. Past the superficial layer is the lamellar layer, with randomly orientated fibers as well as distinct radially aligned fibers at the periphery. Lastly, the deep layer contains circumferentially oriented fibers intermixed with radially aligned tie fibers (McDevitt and Webber, 1990, Peterson and Tillman, 1997, Rattner, et al., 2010, Skaggs, et al., 1994). Previous work reveals that the two identified fiber families are unique in both biochemistry and structural organization (Kambic and McDevitt, 2005, Melrose, et al., 2005, Naumann, et al., 2002, Rattner, et al., 2010). Electron microscopy analysis of various menisci across a wide variety of vertebrate species reveals that the circumferential fibers are primarily collagen I arranged in ~5 μm bundles which are grouped together in organized arrays with a distinct crimping pattern, characteristic of tensile-load bearing structures (Fithian, et al., 1990, Rattner, et al., 2010). In contrast, the radial fibers are a co-localization of type I and II collagens arranged in ~10 μm parallel bundles (Rattner, et al., 2010, Skaggs, et al., 1994). This morphology evokes an anisotropic material response relative to collagen fibril orientations (Anderson, et al., 1991, Bursac, et al., 2009, Fithian, et al., 1990, Leslie, et al., 2000, Proctor, et al., 1989, Zhu, et al., 1994).
In addition to intrinsic fiber orientation, collagen fiber and proteoglycan interactions are believed to influence shear properties of the meniscus (Anderson, et al., 1991, Sweigart and Athanasiou, 2001, Zhu, et al., 1994). Heterogenic proteoglycan distribution throughout the meniscus is a presumed adaptation to joint stress (Mow, et al., 1992). For example, glycosaminoglycans, a proteoglycan side-chain responsible for water retention, have been shown to be greater in percent dry weight in the medial meniscus over the lateral as well as anterior over the central and posterior regions (Bursac, et al., 2009). Analysis of canine menisci showed significantly less glycosaminoglycans in the central region of the medial meniscus, compared to the lateral (Stephan, et al., 1998). These findings encourage evaluating shear performance as a function of anatomical location. Though previous torsional shear testing of bovine meniscus has elucidated material anisotropy no distinction between anatomical site was made (Zhu, et al., 1994). To further understand how meniscal tissue responds to loading, this study seeks to conclude if anatomical and regional dependencies dictate shear performance in accordance with structural and biochemical cues.
Lastly, although previous work has shown bovine meniscus to exhibit material anisotropy, constitutive modeling of the meniscus has often been relegated to transverse isotropy (Donahue, et al., 2003, Spilker, et al., 1992). Recent work correlating histological and mechanical data of arterial walls, which possess a similar multiple fiber family structure as the deep zone of the meniscus, has resulted in novel material formulations. These models superimpose transversely isotropic contributions of each fiber family and the isotropic matrix in order to coincide with observations and satisfy the polyconvexity condition within the framework of invariant theory (Balzani, et al., 2006, Holzapfel, et al., 2000, Schroder and Neff, 2003). Thus, in this study the feasibility for applying this anisotropic constitutive model to meniscal tissue will be examined.
Augmented comprehension of stress distributions within knee soft-tissues will incalculably aid in knee biomechanics and etiopathology; potentially leading to novel joint trauma and osteoarthritis preventative measures (Mow, et al., 1992).
2. Methods
2.1. Specimen Preparation
Pairs of menisci were harvested from nine skeletally mature bovine, obtained from a local abattoir. Bovine menisci were chosen for the present study due to availability and tissue size, as the larger menisci facilitates generating multiple tissue explants from specific regions. Previous studies of the aggregate and shear modulus have found similarity between human and bovine tissue (Sweigart, et al., 2004). No distinction was made between left or right hind limbs for this study. Whole stifle joints were stored at −20°C then dissected at room temperature, while continuously hydrating the exposed tissue surfaces with 0.9% saline solution.
The menisci were sectioned into six regions; medial anterior (MA), medial central (MC), medial posterior (MP), lateral anterior (LA), lateral central (LC), and lateral posterior (LP) (Figure 1). A 6.35 mm diameter cylindrical punch was used to extract meniscal explants from the fibrous tissue body. The explants were then trimmed until only the deep layer of the tissue remained so that fiber orientations were primarily circumferential and radial; resulting in an average specimen length of 3.5 mm. An ink line was applied on the longitudinal axis of each explant as a visual aid to ensure uniform shearing of the tissue. Previous studies have directly applied cyanoacrylate to soft-tissue; however, cite special care being taken to minimize adhesive penetration using a multi-axis loading device (Dokos, et al., 2000, Dokos, et al., 2002). Here, dyed nitrocellulose applied to the traction surfaces was found to effectively block pores and inhibit penetration of cyanoacrylate fixative. Serial sectioning of these surfaces showed total penetration less than 10% of specimen length. Lastly, the meniscal explants were adhered to glass slide covers and hydrated for 10 minutes in a saline bath. Cyanoacrylate fixative was used to adhere the glass slide covers to the parallel platens of a lap shear fixture with collagen fibers orientated perpendicular (Pe) or parallel (Pa) to the direction of the shear load. The removal of the superficial and lamellar layers allows for distinction of the circumferential fiber direction with the naked eye (see Figure 2) (Mow, et al., 1992).
Figure 1.
Anatomical location and regional identification for left leg of a test specimen. Regions were defined by measuring the circumference of each meniscus and marking three equidistant points determined by the arc length, thus accounting for differences in meniscal sizes. Two explants were extracted from each region, one for each of the two fiber orientation deformation cases. Superficial and lamellar surfaces were removed in order to minimize the presence of randomly oriented collagen fibers.
Figure 2.
A) Surface of meniscus appears homogenous to the naked eye due to the small randomly oriented fibrils. B) Removal of superficial and lamellar layer reveals circumferentially aligned collagen fiber bundles. C) Transverse sectioning of the meniscus shows radially aligned tie fibers (white arrows).
2.2. Test setup
A servo-hydraulic uniaxial testing system was utilized to apply simple shear to the explants (Model 8872, Instron Corp, Canton, MA). For our test fixture the top shear platen was mounted to a 44.5N load cell (±0.445N) (Futek, LSB303) and displacement between the shear platens was tracked via a linear variable differential transformer (LVDT) (±0.001mm) (Omega, LD320-2.5) mounted directly adjacent to the test specimen. To ensure specimens underwent simple shear, the shearing platens are allowed free rotation relative to one another (see Figure 3). Additionally, images were captured during testing to monitor changes in the ink lines with respect to load, however only the LVDT was used to record deformation. Meniscal explants were strained at a very low rate of 0.002 sec−1, so as to minimize fluid effects (Proctor, et al., 1989), until material or fixative failure.
Figure 3.
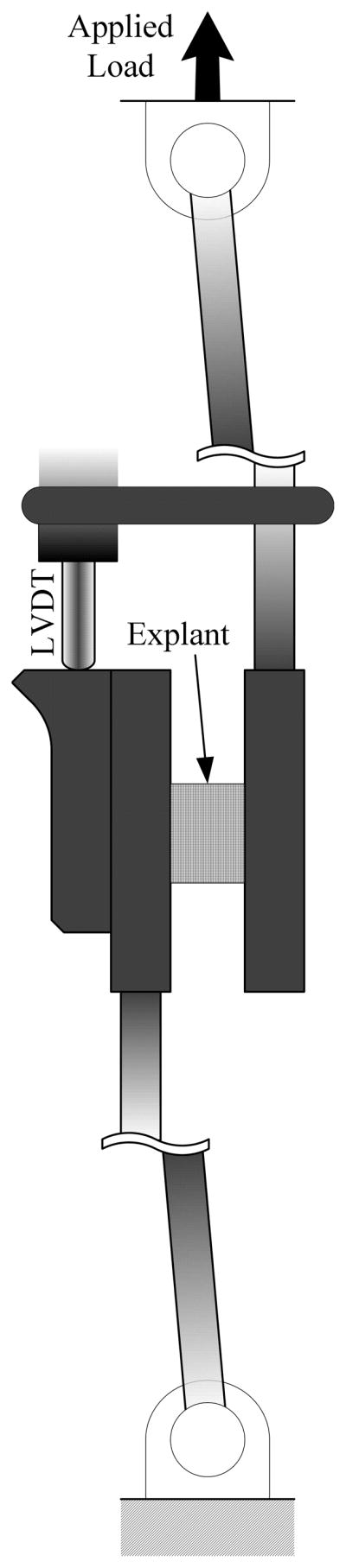
Schematic of lap shearing fixture. Both platens are allowed to freely rotate about the single same dimension. An adjacent LVDT is used to measure relative displacement of the platens.
2.3. Deformation homogeneity
Others have examined simple shearing of fiber-reinforced bio-composites and have utilized various methods to either ensure homogenous deformation or circumvent this concern using inverse FE methods to obtain material parameters (Dokos, et al., 2002, Gardiner and Weiss, 2001, Weiss, et al., 2002). In reviewing of simple shearing of rubbers and biological tissues by Horgan and Murphy the aspect ratio of 1:4, with the sample height between shearing platens being smaller, is recommended in order to ensure homogeneity of shear stresses up to the shearing modulus. Though it is admitted that based on differing and well-qualified assumptions the interpretation of the stress field remains a bit ambiguous (Horgan and Murphy, 2011). Here an experimental ratio closer to 1:2 was utilized due to tissue size constraints and consideration for a small amount of fixative surface penetration. Pilot work using digital image correlation examined the shear deformation homogeneity of the meniscal explants. A random speckle pattern of India ink was applied to the surface of the test specimen using a gravity-fed spray gun backed by 10 psi of air pressure. Inked specimens were sheared and a charge coupled device camera (MicroPix Ltd, West Sussex, UK) recorded images at 7.5 fps. Digital image correlation software (Opticist 0.948, www.opticist.org) was used to process and visualize shear deformation. The 6 parameter zero-normalized sum of squared differences algorithm was utilized to process 21 pixel2 subset displacements as per recommendation of Pan et al. as it has proven to be robust and reliable (Pan, et al., 2009).
2.4. Piecewise linear elastic analysis
All data sampled were processed using a second order Savitzky-Golay smoothing function to aid in regional identification. Experimentally measured force, V, was converted to shear stress, τ, using specimen diameter, d, Eq. (1). The shear strain was calculated using the specimen length, L, and change in displacement, δx, recorded from the LVDT, Eq. (2). The toe region shear modulus was calculated from the first observed linear region, Eq. (3), between 3%–13% shear strain and the 2nd, extended shear modulus, was established after 80% of the maximum shear strain until material or fixative failure. All data processing was performed using custom MATLAB scripts (version 7.6 (R2008a), Natick, MA).
| (1) |
| (2) |
| (3) |
2.5. Anisotropic Hyperelastic Modeling
The meniscus was considered a hyperelastic material (See Appendix 1). To account for both the circumferential and radial tie fibers the material is considered an isotropic matrix reinforced with 2 orthogonal unique collagen fiber families (Rattner, et al., 2010, Skaggs, et al., 1994) represented by the direction vectors ai, i = 1,2 with |ai| = 1. These vectors result in the fiber family structure tensors Mi = ai ⊗ ai, depicting the material anisotropy (Balzani, et al., 2006, Holzapfel, et al., 2000). Due to the presence of hydrophilic glycosaminoglycans the material is considered incompressible thus, similar to Balzani et al. (Balzani, et al., 2006), a decoupled strain-energy potential can be written as
| (4) |
where ψiso and represent the isochoric matrix and fiber contributions, respectively, and ψvol is a purely volumetric contribution. Particularized forms of ψ are such that the isotropic matrix is modeled using the classic neo-Hookean model, Eq. (5), and a polynomial function, Eqs. (6, 7), is leveraged to encapsulate the observed stiffening effect such that
| (5) |
| (6,7) |
| (8) |
where and are so-called mixed invariants which control the square of the stretch in the fiber direction and deformation of an area element with a normal perpendicular to the fiber direction, respectively, with , and p is an indeterminate Lagrange multiplier due to the aforementioned incompressibility (Schroder and Neff, 2003). The implementation of these explicit invariants satisfies the polyconvexity condition in the sense of Ball (Balzani, et al., 2006), thus ensuring a physically reasonable and numerically stable material model. The parameters c > 0 and αai > 0 |i=1, 3 are stress-like material parameters for the matrix and fiber families, respectively, and αaj > 0 |j=2, 4 are dimensionless parameters. Material parameters were determined using all test points for a given group aggregated into a single sorted dataset and fit simultaneously, yielding a single set of parameters (Morrow, et al., 2010). The parameters αa1 & αa2 are not identified as they do not influence the shear responses examined in the present study. Curve-fitting was performed using a nonlinear least squares optimization routine implemented in a custom MATLAB script.
2.6. Statistical analysis
A three-way blocked ANOVA was performed for each group of moduli to make anatomical location, region, and fiber orientation comparisons. Identified significant differences between regions for the extended shear modulus were further investigated using a post-hoc t-test. P-value less than 0.05 was considered significant.
3. Results
Digital image correlation revealed a largely homogenous deformation pattern with slight warping primarily near the edges of the traction surfaces (Figure 4). This warping appeared to penetrate ~10% into the specimen’s surface; however this did not result in any apparent discrepancy between the relative platen displacement and DIC computed deformation.
Figure 4.
Digital texture correlation deformation mesh of parallel and perpendicular specimens. Gaps in parallel mesh are due to indistinguishable speckling in that region. Shear deformation appears more homogenous within the specimen midsubstance. Inhomogeneous deformation is observed closer to the applied traction surfaces, presumably due to adhesive penetration.
There were significant differences between the fiber orientation groups for the toe region modulus with the perpendicular group being more compliant (Figure 5). While the extended shear modulus did not show significant differences between the two different fiber orientation groups, significant regional differences were noted. Post-hoc t-tests revealed an explicit distinction between the central and posterior regions for the extended shear modulus (Figure 5). These findings dictated grouping the data by region and orientation in preparation for hyperelastic curve-fitting, yielding a total of six datasets.
Figure 5.
The parallel and perpendicular fiber orientations are significantly different from one another for small strains (Toe Modulus). The central and posterior regions are significantly different from one another for large strains (Extended Shear Modulus). * = p < 0.05
The utilized strain-energy density function qualitatively fit the trend of the experimental data (Figure 6) for each of the regions. Additionally, the root mean square error for each group was relatively low with an upper bound of 0.018 MPa (Table 1), indicative of the ability of the function selected to characterize the sample population.
Figure 6.
Cauchy stress vs. shear strain for anterior parallel samples. Open symbols represent experimental data and solid line is the fit using the anisotropic hyperelastic constitutive equation (Eq. 4). The chosen model accurately describes the trending behavior for all datasets considered. Root mean square error = 0.001.
Table 1.
Material parameters from the hyperelastic anisotropic analysis for specimens subjected to simple shear. The strain-energy density function utilized accurately describes the material behavior across all groups as demonstrated by low RMSE values. Superscript a defines the fiber family (a=1:Circumferential, a=2:Radial) which the according parameter belongs to.
| Region | Orientation | Parameters [MPa] | RMSE | ||
|---|---|---|---|---|---|
| c | αa3 | αa4 | |||
| Anterior | Parallela=1 | 0.609 | 0.282 | 1.586 | 0.001 |
| Perpendiculara=2 | 0.299 | 1.603 | 0.018 | ||
|
| |||||
| Central | Parallela=1 | 0.543 | 0.236 | 1.577 | 0.013 |
| Perpendiculara=2 | 0.214 | 1.540 | 0.012 | ||
|
| |||||
| Posterior | Parallela=1 | 0.544 | 0.171 | 1.501 | 0.012 |
| Perpendiculara=2 | 0.247 | 1.573 | 0.010 | ||
4. Discussion
The results of this study reinforced that, for small strains, the meniscus exhibits anisotropic behavior (Anderson, et al., 1991, Zhu, et al., 1994). Similar to the theory of others, the lower observed toe modulus for the perpendicular specimens may be due to the sheaths of radial tie fibers (RTF) facilitating slip between circumferential fiber layers, analogous to boundary slip along shear surfaces in composite materials (Mow, et al., 1992, Rattner, et al., 2010). RTF’s in bovine medial menisci have previously been shown to be more abundant and thicker in the posterior region, resulting in higher tensile stiffness when compared to anterior and central (Skaggs, et al., 1994). This trend was repeated for large shear strains as the posterior region was significantly stiffer than the central region. This could be in part due to take up of the shear load by the larger RTF’s as the meniscus is subjected to large shear deformations.
Biochemical analyses have shown that proteoglycan presence and quality has a dramatic effect on shear properties in articular cartilage (Zhu, et al., 1994). Despite the meniscus possessing an eight-fold lower concentration of proteoglycans than articular cartilage (Adams and Muir, 1981) their presence may still have a significant contribution to the observed shear properties. Examination of regional differences in bovine menisci has shown that proteoglycan presence is greatest in the posterior region (Eyre and Wu, 1983) and total GAG presence in canine tissue is lower in the central region (Adams and Muir, 1981), correlating with mechanical findings here. Others have postulated that molecular cross-linking of proteoglycans and the collagen fibrils could be inducing a stiffening behavior, hence resulting in the observed regional differences (Weiss, et al., 2002). Clearly, the mechanisms dictating shear performance appear reliant on both the meniscus ultrastructure and interaction between the extracellular matrix constituents, facilitating the aforementioned layer sliding (Mow, et al., 1992).
Expanding on the observed material anisotropy from the small strain region a modified decoupled strain-energy density function was utilized to describe the material response for the sampled population. The chosen model, based on prior work with anisotropic vascular tissue, readily expedites investigation of complex loading mechanisms and microstructure by means of coupling deformation and structure tensors in the strain-energy density function. An additional advantage is the recent incorporation of anisotropic hyperelastic modeling in commercially available FE software (ABAQUS, Simulia, Providence, RI), which includes the model this analysis is derived from (Holzapfel, et al., 2000). The groundwork performed here should act as a compass for those seeking a material model to emulate the anisotropy and inhomogeneity of the meniscus, both of which are crucial aspects in understanding how this structure functions (Mow, et al., 1992, Setton, et al., 1999).
Experimental techniques utilized in this study pose several limitations. The noted ideal aspect ratio was not adhered to, thus true homogeneity cannot be assured throughout. Digital texture correlation techniques revealed a fairly homogenous distribution in the specimen midsubstance; however, there is evident inhomogeneous warping of the pixel subsets (Figure 4). This effect is observed more often near the traction surfaces, presumably due to adhesive penetration and not a direct effect of tissue ultrastructure. As the primary aim of this study was to assess if regional structure and biochemistry disparities exhibit similar trends in practice, the piecewise linear metrics chosen are employed comparatively rather than definitively. Additionally, the purposefully simplistic loading scenario of explants examined here was exploited to simplify the continuum analysis; however, physiologically and pathologically relevant loading could also be introduced via modification of the deformation tensor. Also, special care was taken to remove the majority of randomly oriented fibers to aid in parameter determination; however, the structure tensors could easily be adapted to incorporate imaging data that assesses the relative fiber angles for a given spatial location throughout the meniscus. Lastly, it is acknowledged that sparse oblique tie fibers do branch from the main radial fibers; however, their influence was not considered in this analysis as it is presumed that the primary axes of interest are explicitly circumferential and radial, which have been rigorously explored in the literature.
Novel to this work is regard for regional and anatomical location of meniscus material response due to shear loading, borne from supporting biochemical analyses linking proteoglycan distribution and mechanical performance. The findings indicate region specific shearing properties should be taken into consideration when attempting to model meniscus material behavior. Additionally, conventional modeling has often regarded the meniscus as a transversely isotropic material; however, the observed shearing anisotropy violates this presumed material symmetry. A structurally driven mechanical model was shown to encapsulate this behavior and is proposed as a viable candidate for those seeking to model knee joint behavior. Continued study of experimental meniscus biomechanics coupled with advanced modeling techniques will undoubtedly forge novel understanding of joint etiopathology and reparative techniques.
Acknowledgments
This publication was made possible by Grant Number R15AR051906-02 from the National Institute of Arthritis and Musculoskeletal and Skin Diseases.
Appendix 1
Kinematics and hyperelasticity
The deformation tensors for the experimental loading scenarios as a function of shear strain γij are
Additionally, the important strain-like right Cauchy-Green tensor, C, is introduced where
The meniscus is considered a hyperelastic material which implies that the Cauchy stress σ is defined as
where ψ is the Helmholtz free-energy function and J = det(F) > 0 is the local volume ratio (Holzapfel, 2001).
Footnotes
5. Conflict of interest statement
The authors recognize no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams ME, Muir H. The glycosaminoglycans of canine menisci. Biochemical Journal. 1981;197:385–389. doi: 10.1042/bj1970385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmed AM, Burke DL. In-vitro measurement of static pressure distribution in synovial joints--Part 1: Tibial surface of the knee. Journal of Biomechanical Engineering. 1983;105 (3):216–25. doi: 10.1115/1.3138409. [DOI] [PubMed] [Google Scholar]
- Anderson DR, et al. Viscoelastic shear properties of the equine medial meniscus. Journal of Orthopaedic Research. 1991;9 (4):550–8. doi: 10.1002/jor.1100090411. [DOI] [PubMed] [Google Scholar]
- AufderHeide AC, Athanasiou KA. Mechanical stimulation toward tissue engineering of the knee meniscus. Annals of Biomedical Engineering. 2004;32 (8):1161–74. doi: 10.1114/b:abme.0000036652.31658.f3. [DOI] [PubMed] [Google Scholar]
- Balzani D, et al. A polyconvex framework for soft biological tissues. Adjustment to experimental data. International Journal of Solids and Structures. 2006;43:6052–6070. [Google Scholar]
- Buma P, et al. Tissue engineering of the meniscus. Biomaterials. 2004;25 (9):1523–32. doi: 10.1016/s0142-9612(03)00499-x. [DOI] [PubMed] [Google Scholar]
- Bursac P, et al. Dynamic compressive behavior of human meniscus correlates with its extra-cellular matrix composition. Biorheology. 2009;46 (3):227–37. doi: 10.3233/BIR-2009-0537. [DOI] [PubMed] [Google Scholar]
- Chevrier A, et al. Meniscus structure in human, sheep, and rabbit for animal models. Journal of Orthopaedic Research. 2009;27 (9):1197–203. doi: 10.1002/jor.20869. [DOI] [PubMed] [Google Scholar]
- Dokos S, et al. A triaxial-measurement shear-test device for soft biological tissues. J Biomech Eng. 2000;122 (5):471–8. doi: 10.1115/1.1289624. [DOI] [PubMed] [Google Scholar]
- Dokos S, et al. Shear properties of passive ventricular myocardium. Am J Physiol Heart Circ Physiol. 2002;283 (6):H2650–9. doi: 10.1152/ajpheart.00111.2002. [DOI] [PubMed] [Google Scholar]
- Donahue TLH, et al. How the stiffness of meniscal attachments and meniscal material properties affect tibio-femoral contact pressure computed using a validated finite element model of the human knee joint. Journal of Biomechanics. 2003;36 (1):19–34. doi: 10.1016/s0021-9290(02)00305-6. [DOI] [PubMed] [Google Scholar]
- Eyre DR, Wu JJ. Biochemistry of the meniscus: unique profile of collagen types and site-dependent variations in composition. Transactions of the Orthopaedic Research Society. 1983;8:56. [Google Scholar]
- Fithian DC, et al. Material properties and structure-function relationships in the menisci. Clinical Orthopaedics and Related Research. 1990;(252):19–31. [PubMed] [Google Scholar]
- Gardiner JC, Weiss JA. Simple shear testing of parallel-fibered planar soft tissues. J Biomech Eng. 2001;123 (2):170–5. doi: 10.1115/1.1351891. [DOI] [PubMed] [Google Scholar]
- Holzapfel GA, et al. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
- Horgan CO, Murphy JG. Simple shearing of soft biological tissues. Proceedings of the Royal Society A. 2011;467:760–777. [Google Scholar]
- Kambic HE, McDevitt CA. Spatial organization of types I and II collagen in the canine meniscus. Journal of Orrthopaedic Research. 2005;23:142–149. doi: 10.1016/j.orthres.2004.06.016. [DOI] [PubMed] [Google Scholar]
- Leslie BW, et al. Anisotropic response of the human knee joint meniscus to unconfined compression. Proceedings of the Institution of Mechanical Engineers. 2000;214 (6):631–5. doi: 10.1243/0954411001535651. [DOI] [PubMed] [Google Scholar]
- McDevitt CA, Webber RJ. The ultrastructure and biochemistry of meniscal cartilage. Clinical Orthopaedics and Related Research. 1990;282:8–18. [PubMed] [Google Scholar]
- Melrose J, et al. Comparative spatial and temporal localisation of perlecan, aggrecan and type I, II and IV collagen in the ovine meniscus: an ageing study. Histochem Cell Biol. 2005;124 (3–4):225–35. doi: 10.1007/s00418-005-0005-0. [DOI] [PubMed] [Google Scholar]
- Messner K, Gao JZ. The meniscus of the knee joint. Anatomical and functional characteristics, and a rationale for clinical treatment. Journal of Anatomy. 1998;193:161–78. doi: 10.1046/j.1469-7580.1998.19320161.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow DA, et al. A method for assessing the fit of a constitutive material model to experimental stress-strain data. Computer Methods in Biomechanics and Biomedical Engineering. 2010;13 (2):247–256. doi: 10.1080/10255840903170686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mow VC, et al. Knee Meniscus: Basic and Clinical Foundations. 1992. Structure and Function Relationships of the Menisci of the Knee; pp. 37–57. [Google Scholar]
- Naumann A, et al. Immunochemical and mechanical characterization of cartilage subtypes in rabbit. J Histochem Cytochem. 2002;50 (8):1049–58. doi: 10.1177/002215540205000807. [DOI] [PubMed] [Google Scholar]
- Pan B, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review. Measurement Science and Technology. 2009;20 (6):062001. [Google Scholar]
- Peterson W, Tillman B. Collagenous fibril texture of the human knee joint menisci. Anatomy and Embryology. 1997;197 (4):317–324. doi: 10.1007/s004290050141. [DOI] [PubMed] [Google Scholar]
- Proctor CS, et al. Material properies of the normal medial bovine meniscus. Journal of Orthopaedic Research. 1989;7 (6):771–82. doi: 10.1002/jor.1100070602. [DOI] [PubMed] [Google Scholar]
- Rattner JB, et al. New understanding of the complex structure of knee menisci: implications for injury risk and repair potential for athletes. Scandinavian Journal of Medicine & Science in Sports. 2010 doi: 10.1111/j.1600-0838.2009.01073.x. Epub ahead of print. [DOI] [PubMed] [Google Scholar]
- Ratzlaff CR, Liang MH. New developments in osteoarthritis. Prevention of injury-related knee osteoarthritis: opportunities for the primary and secondary prevention of knee osteoarthritis. Arthritis Research & Therapy. 2010;12 (4):215. doi: 10.1186/ar3113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroder J, Neff P. Invariant formulation of hyperelastic transverse isotropy based on polyconvex free energy function. International Journal of Solids and Structures. 2003;40:401–445. [Google Scholar]
- Setton LA, et al. Biomechanical factors in tissue engineered meniscal repair. Clin Orthop Relat Res. 1999;367(Suppl):S254–72. doi: 10.1097/00003086-199910001-00025. [DOI] [PubMed] [Google Scholar]
- Shoemaker SC, Markolf KL. The role of the meniscus in the anterior-posterior stability of the loaded anterior cruciate-deficient knee. Effects of partial versus total excision. The Journal of Bone and Joint Surgery. 1986;68 (1):71–9. [PubMed] [Google Scholar]
- Skaggs DL, et al. Radial tie fibers influence the tensile properties of the bovine medial meniscus. Journal of Orthopaedic Research. 1994;12 (2):176–85. doi: 10.1002/jor.1100120205. [DOI] [PubMed] [Google Scholar]
- Spilker RL, et al. A transversely isotropic biphasic finite element model of the meniscus. Journal of Biomechanics. 1992;25 (9):1027–45. doi: 10.1016/0021-9290(92)90038-3. [DOI] [PubMed] [Google Scholar]
- Stephan JS, et al. Water content and glycosaminoglycan disaccharide concentration of the canine meniscus. American Journal of Veterinary Research. 1998;59 (2):213–6. [PubMed] [Google Scholar]
- Sweigart MA, Athanasiou KA. Toward tissue engineering of the knee meniscus. Tissue Eng. 2001;7 (2):111–29. doi: 10.1089/107632701300062697. [DOI] [PubMed] [Google Scholar]
- Sweigart MA, et al. Instraspecies and interspecies comparison of the compressive properties of the medial meniscus. Annals of Biomedical Engineering. 2004;32 (11):1569–79. doi: 10.1114/b:abme.0000049040.70767.5c. [DOI] [PubMed] [Google Scholar]
- Walker PS, Erkman MJ. The role of the menisci in force transmission across the knee. Clinical Orthopaedics and Related Research. 1975;109:184–92. doi: 10.1097/00003086-197506000-00027. [DOI] [PubMed] [Google Scholar]
- Weiss JA, et al. Ligament material behavior is nonlinear, viscoelastic and rate-independent under shear loading. Journal of Biomechanics. 2002;35:943–950. doi: 10.1016/s0021-9290(02)00041-6. [DOI] [PubMed] [Google Scholar]
- Zhu W, et al. Anisotropic viscoelastic shear properties of bovine meniscus. Clinical Orthopaedics and Related Research. 1994;306:34–45. [PubMed] [Google Scholar]
- Zhu W, et al. Viscoelastic shear properties of articular cartilage and the effects of glycosidase treatments. Journal of Orthopaedic Research. 1994;11 (6):771–81. doi: 10.1002/jor.1100110602. [DOI] [PubMed] [Google Scholar]







