Abstract
A number of practical issues must be addressed when using thin carbon films as quarter-wave plates for Zernike phase-contrast electron microscopy. We describe, for example, how we meet the more stringent requirements that must be satisfied for beam alignment in this imaging mode. In addition we address the concern that one might have regarding the loss of some of the scattered electrons as they pass through such a phase plate. We show that two easily measured parameters, (1) the low-resolution image contrast produced in cryo-EM images of tobacco mosaic virus particles and (2) the fall-off of the envelope function at high resolution, can be used to quantitatively compare the data quality for Zernike phase-contrast images and for defocused bright-field images. We describe how we prepare carbon-film phase plates that are initially free of charging or other effects that degrade image quality. We emphasize, however, that even though the buildup of hydrocarbon contamination can be avoided by heating the phase plates during use, their performance nevertheless deteriorates over the time scale of days to weeks, thus requiring their frequent replacement in order to maintain optimal performance.
Keywords: Phase contrast, Electron microscopy, Carbon film, Phase plate
1. Introduction
A number of different technologies have been considered for realizing in-focus phase contrast in electron microscopy, analogous to that which is produced in the Zernike phase-contrast light microscope. Two rather different approaches, both of which were originally proposed by Boersch [1], are (1) to use the inner potential of a thin film as a quarter-wave plate for the scattered electrons or (2) to use a localized electrostatic field, confined by miniature electrodes, to selectively apply a 90° phase shift to the unscattered electrons. The electrostatic-type phase-contrast aperture is difficult to implement because of the very small device size that is required. Nevertheless, there recently has been considerable effort to use modern microfabrication techniques to manufacture devices with suitably small features [2–4]. A thin-film type of phase plate also requires the fabrication of a very small hole in the center of the thin film, and this challenge was first overcome by Danev and Nagayama [5], who used a focused ion beam to drill the hole for the unscattered beam.
An alternative idea is to use the inner potential of a thin film as a half-plane phase plate, thus generating “Hilbert differential contrast” images [6,7], which can be converted into “Zerniketype” phase-contrast images, if desired, by a very simple computation. A thin-film phase plate generates some loss of incident electrons in one sideband but not the other, through both elastic and inelastic scattering. It is thus more ideal to implement a lossless version of a Hilbert differential contrast phase plate, such as the one envisioned by Nagayama [8] that is based upon the Aharonov–Bohm effect. Finally, one can mention that an electrostatic phase-contrast device has been proposed that takes advantage of the anamorphotic images of the electron diffraction pattern that naturally occur at specific planes within an aberration corrector [9].
Use of a thin-film phase plate for Zernike-type (or Hilbert-type) phase contrast is currently the only approach that is sufficiently well developed to be used for cryo-electron microscopy of large biological macromolecules. The development of carbon-film phase-plate technology has, in fact, advanced to the point that a large data set has recently been collected of cryo-EM images of GroEL, an 800 kDa protein complex [10]. The three-dimensional reconstruction obtained with those images compares very favorably with that obtained for a companion data set of “conventional”, i.e. defocus-based phase-contrast images. Both reconstructions were limited to a resolution of ~1.2 nm corresponding to the half-Nyquist frequency of the CCD camera used for data collection. Images would thus have to be recorded at higher magnification in order to take the results to higher resolution. Alternatively, one could record images on photographic film in order to avoid the limitations in pixel size and image area of CCD cameras, especially when such detectors are used with 300 keV electrons.
We describe here a variety of practical issues that had to be addressed in the course of developing the carbon-film phase plate to a point that it is now practical to use it for routine data collection. One must clearly avoid electrostatic charging of the phase plate when it is placed in the electron beam. Unwanted charging is certain to occur if the surface of the phase plate is contaminated by non-conducting material, either during its manufacture or after insertion into the column of the electron microscope. The thickness of the phase plate must be properly controlled in order to provide the desired phase shift and to avoid excessive loss of electrons due to unavoidable scattering. Indeed, in some cases the optimal thickness may be considerably less than that which produces exactly a 90° phase shift [11]. The size of the central hole must be scaled to the focal length of the objective lens in a way that allows even those electrons that are scattered at very small angles to experience the ~90° phase shift. The use of a phase plate with a very small central hole requires, in turn, greater attention than otherwise to setting the illumination conditions in the proper way, and to maintaining the proper beam-tilt alignment of the illumination. The way in which each of these issues is currently being addressed is now described in this paper.
2. Materials and methods
2.1. Preparation of thin carbon-film phase plates
The phase plates were prepared in several steps. First, a core carbon film with thickness ~15 nm was evaporated on a freshly cleaved mica surface by a JEE-420T (JEOL, Tokyo) carbon arc vacuum evaporator at a vacuum level of ~1.5 × 10−4 Pa or by a BAF-060 (BAL-TEC AG, Balzers) electron beam evaporator at a vacuum level of ~1.0 × 10−6 Pa. Both evaporation systems are equipped with turbo-molecular pumps. In the case of arc evaporation the carbon rods had a diameter of 5mm, specific resistance of 4 mΩ/cm, purity of 99.9999% (Nisshin EM Co. Ltd., Tokyo), and the thickness of the film was judged by observing the darkening of a partially shadowed filter paper. In the case of electron beam evaporation the carbon rods had a diameter of 3mm (LZ 02217 KN, BAL-TEC AG, Balzers) and the thickness of the film was monitored by a quartz crystal thickness monitor.
The carbon-coated mica was cut by scissors into ~5 × 5mm square pieces. A mica piece was gradually lowered into a thoroughly cleaned glass Petri dish filled with commercially purchased distilled water (049–16787, Wako Pure Chemical Industries Ltd., Osaka), thus floating the carbon film on the water surface. The film was then picked up by a platinum wire loop and lowered onto specially ordered molybdenum grids resting on top of two to three layers of Whatman Grade No. 1 filter paper. The film was left to dry on the grids for at least 12 h. These grids, which we refer to below as “aperture discs”, are 2mm in diameter and contain a 7 × 7 array of 100 µm diameter holes with a 100 µm spacing between the edges of adjacent holes (Daiwa Techno Systems, Tokyo).
The hole in the center of the phase plates was drilled by a JFIB-2300 (JEOL, Tokyo) focused ion beam machine. In addition, four fiducial markers, in the form of holes similar in size to the central hole, were drilled close to the edge of the apertures. Each marker points to a specific direction of the aperture grid (+X, −X, +Y, −Y) looking from the central hole. The fiducial markers simplify finding the central hole during the initial alignment of a phase plate. First, a marker is found by following the aperture edge. Then, by using the aperture drive that moves in a direction perpendicular to the edge, the central hole is brought into the TV-rate camera’s field of view.
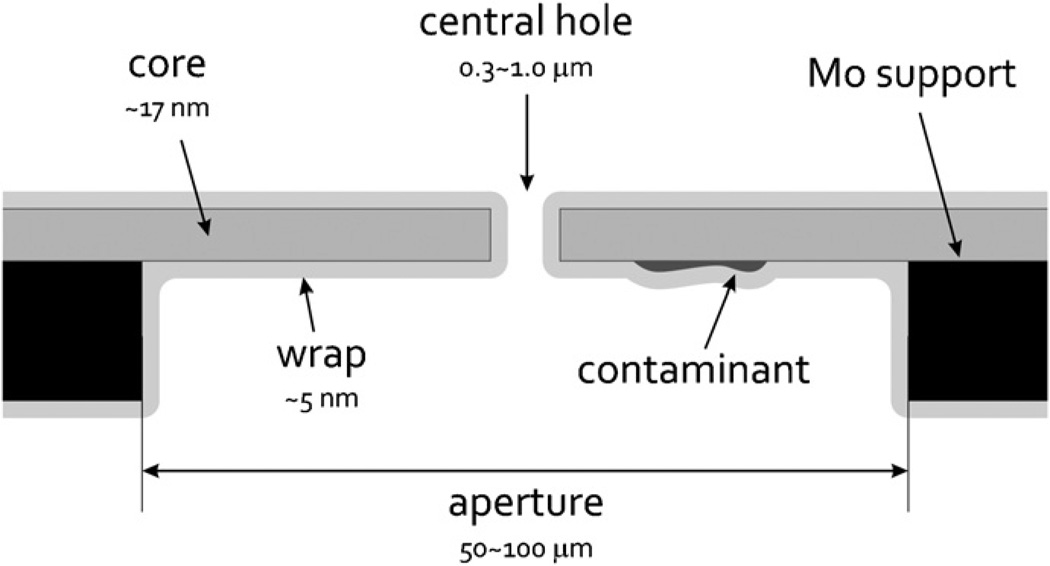
The final step in the phase-plate manufacturing process is to evaporate ~5–7 nm of amorphous carbon onto both sides of the “core” of the phase plate, a process that we describe as “wrapping” the core with an additional layer of evaporated carbon. Fig. 1 shows a schematic of a finished phase plate. The role of the final wrapping is to cover any contaminants on the surface of the core film that may have been accumulated during the manufacturing process. In particular, the water surface transfer process can deposit inorganic salts or other impurities present in the water or dissolved from the filter paper supporting the grid. Such contaminants, unlike vacuum system fluids, cannot be desorbed by heating. Wrapping by a fresh layer of carbon traps the impurities and prevents the formation of surface charges by the electron beam.
Fig. 1.
Schematic diagram of a cross-section through the central hole in a thin carbon-film phase plate. The various features included in this diagram are not shown to scale, but the crucial dimensions are indicated in the figure. The dark rectangles represent the edges of the aperture, and a hypothetical patch of contamination, of unknown origin, is indicated on the under side of the phase plate. The initial, ~17-nm-thick core of evaporated carbon is shown in dark gray, and the thinner ~5-nm-thick finishing layer, or “wrap” of evaporated carbon, is shown in light gray.
2.2. Electron microscopy
All cryo-EM images of biological samples were recorded on a JEOL JEM-3100FFC electron microscope, fitted with a top-entry, liquid-helium cold stage [12]. The cold stage was normally used at a temperature of ~55 K. Our recent tests (unpublished) showed that at that temperature specimen stability and contrast of cryo-specimens were both improved. Maintaining the stage temperature at ~55 K is achieved by initially cooling the inner pot of the Dewar with helium, waiting for it to evaporate, and then topping up the level of liquid nitrogen in the outer shield tank at ~5 h intervals to ensure long-term stability of the temperature.
This instrument was fitted with a modified objective lens, which has a larger than usual gap, and modified specimen cartridges were used to lower the position of the specimen within the lens. The design of this lens allows highly parallel incident illumination to be focused at the plane of the phase-contrast aperture with a focal length (for the equivalent thin lens) of 5 mm. The larger gap also allowed the standard, 60 µm diameter objective aperture to be inserted as usual, but through a port different from that used for the phase-plate aperture rod. The standard objective aperture was thus used to provide a room-temperature, thermal shield between the cryo-specimen and the heated phase-contrast aperture.
A custom-built holder was designed by JEOL to allow heating of the phase-contrast apertures. Fig. 2 shows a photograph of the tip of the aperture rod. A total of four aperture discs, described above, are mounted at one time. The principal features of this aperture rod are that it is fitted with vacuum feed-throughs for the current that is supplied to the micro-ceramic heater (Sakaguchi E.H VOC Corp., Tokyo), and a ceramic thermal insulator is inserted between the heated tip and the main section of the rod. The temperature of the tip is estimated from the known temperature dependence of the resistivity of the heating element. The heated tip is electrically grounded to the main part of the aperture rod with a thin wire, and a metal plate encloses the cavity housing the ceramic heater. A metal enclosure also surrounds the end of the ceramic thermal insulator, as can be seen in Fig. 2. Current for the heater was provided by a model PAR36-3H regulated power supply (Kenwood, Melrose, MA).
Fig. 2.
Photograph of the tip of the aperture rod used for the heated phase plate. A 7 × 7 array of thin-film phase plates, supported on specially manufactured, multihole molybdenum disks (Daiwa Techno Systems, Tokyo), are clamped into the end of the aperture rod. The ceramic heater is mounted below a metal shielding plate, and the “near” end of the thermal insulator is also enclosed by a metal shield.
Movements from one phase-plate position to another within a given aperture disc, and approximate centering of the hole of the phase-contrast aperture, are performed with the mechanical drives provided for the custom-built JEOL aperture rod. These alignment steps, and in particular keeping track of which particular phase plate is being used, are facilitated by initially aligning rows of individual phase plates parallel to the long axis of the aperture rod when the aperture disc is placed into the tip of the rod. Centering of a selected phase plate with a precision of ~0.5 µm is monitored in the defocused diffraction (“Search”) mode, and the hole in the phase plate is placed close to a predetermined fiducial mark that is spotted onto the viewing monitor for the Gatan TV camera. The final, precise centering of the unscattered beam into the hole of the phase plate is carried out by making small adjustments to the beam-tilt angle. In this case the condenser-lens values are set to those used in the “Focus” mode, which produces both a more intense and a more convergent beam than is used in the Photo mode. As a result, the unscattered beam then has a radius larger than that of the hole in the phase plate, and tilting the illumination to make the unscattered beam concentric with the hole is monitored by eye, looking directly at the viewing screen.
The Minimum Dose System (MDS) software provided with the microscope was used to switch between pre-set values for the Search, Focus, and Photo modes mentioned above. A 50 µm diameter second-condenser-lens aperture was used for all modes. The available in-column energy filter was normally operated with an energy slit of 20 eV, placed symmetrically about the zero-loss beam.
Images were recorded with a retractable Gatan (Pleasanton, CA) MegaScan 795 2K × 2K CCD camera, which had previously been fitted with a scintillator that was optimized by Gatan for use with 400 keV electrons. The pixel size of this camera is 30 µm. The microscope magnification was set to 60,000, unless stated otherwise, which resulted in an actual magnification of about 100,000 at the plane of the CCD camera, which was mounted below the film camera. Cryo-EM images were recorded with an electron exposure of 2500 electrons/nm2, using an exposure time of 2 s. The microscope was also fitted with a stationary Gatan 622 SC TV camera, mounted below the housing for the CCD camera. The TV camera was used for video-rate observation of images produced in Search mode.
2.3. Sample preparation
A Vitribot (FEI, Hillsboro, Oregon) was used to prepare cryo-EM samples of all specimens on Quantifoil grids, using a fairly standardized protocol. The sample chamber was equilibrated at 4 °C and the relative humidity was generally set to 95% or 100%. Two-microliter volumes of sample were applied to glow-discharge treated Quantifoil® R 1.2/1.3 (Quantifoil Micro Tools GmbH, Jena) EM grids, and the grids were immediately blotted and plunged into liquid ethane to freeze the sample. The blotting time was typically set to 5–15 s. There was no “drain-time” allowed between blotting and plunging. It should be noted that the applied sample was not initially at a temperature of 4 °C. Although some evaporation of sample buffer is expected to occur under these conditions, it was found empirically that this standard protocol produced a good density of particles for sample concentrations in the range of 1–10 mg/ml, depending upon the sample material.
2.4. Simulation of image contrast for “strong” phase objects
Simulations of phase-contrast TEM imaging were performed using custom scripts for the DigitalMicrograph® software platform provided by Gatan. The simulations consisted of a few steps. A complex object wave was prepared that corresponded to a pure phase object, for example a uniform sphere with π/256 phase shift per nm of thickness. The diffracted wave was calculated as the Fourier transform of the object wave. A complex form of the wave aberration (due to defocus and spherical aberration) and phase-plate functions were applied (by multiplication) to the diffracted wave. The modified diffracted wave was then inverse-Fourier transformed, producing the image wave. The image intensity was calculated as the square of the image wave.
3. Results
3.1. The approximate thickness of carbon that produces a π/2 phase shift was estimated by electron interferometry
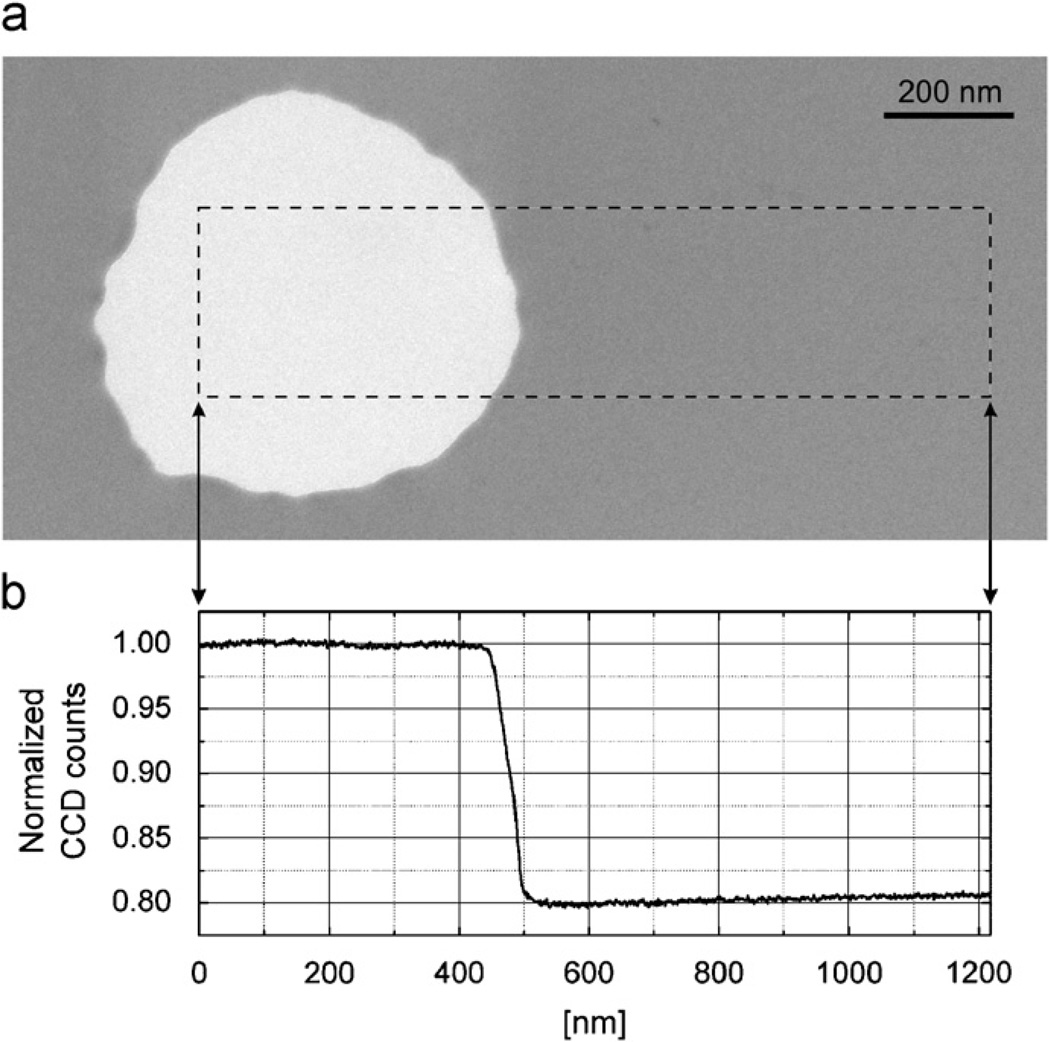
The carbon-film thickness that produces a 90° phase shift for 300 keV electrons is estimated to be ~31 nm, assuming a frequently quoted value of 7.8V for the inner potential of amorphous carbon [13]. The values of the inner potential that have been estimated by different authors vary from 7.8 to 10.7V [13,14], and theoretical calculations are subject to uncertainty due to the model of the structure of amorphous carbon that must be adopted as input for the computations. We thus made our own measurements of the phase shifts for electrons transmitted through actual phase plates by using an electron biprism [14]. The thickness of each phase plate was measured from images recorded at the edges of accidentally torn and folded carbon films. The accuracy of this thickness measurement is between 5% and 10%, as can be judged from the uncertainty with which the positions of arrows can be placed in images such as the one shown in Fig. 3. Samples that are suitable for interferometry were prepared by cutting out a small rectangle from the phase-plate film with a focused ion beam, so as to create an open section for the reference wave.
Fig. 3.
Example of a measurement of the thickness of a carbon-film phase plate. The thickness measurement is made in areas of an aperture disc where one or another phase plate was damaged during handling, and the “wrapped” carbon film is thus folded upon itself. Such folds are measured at the point where the image shows the narrowest profile, as is indicated by the annotations placed on this image. The error in measuring the total thickness is estimated to be less than 1–2 nm.
Our experimental estimates of the inner potential, shown in Table 1, proved to be as variable as those in the literature. The value of 15.9V for the core of the phase plate, which is particularly high, may indicate that charging of that specimen had a greater influence on the measurement than what normally occurs. Even the range of values obtained for “wrapped” phase plates is much greater than can be explained by experimental errors in estimating the fringe positions or by errors in measuring the thicknesses of the carbon film. The value of the inner potential in Table 1 that agrees best with Reimer’s estimate of 7.8V [13] was obtained on a phase plate that was prepared using an electron beam evaporated core film and was wrapped using carbon arc evaporation shortly before the biprism experiment was performed. We note that the variability in the apparent inner potential may be due to the variability in the extent to which carbon films are susceptible to electrostatic charging. As we discuss further below, charging of carbon films seems to be sensitive to the age of the carbon film, although aging does not appear to be the only parameter.
Table 1.
Measured phase shifts and estimated inner potentials for experimentally fabricated thin-carbon phase plates.
| Film type | Total thickness (nm) | Phase shift at 200 kV (π) | Inner potential (V) | Phase shift at 300 kV (π) |
|---|---|---|---|---|
| Core (16 nm arc core) | 16 | 0.59 | 15.9 | 0.53 |
| Sandwich 1 (16 nm arc core+2 × 6.5 nm arc wrap) | 29 | 0.66 | 9.7 | 0.58 |
| Sandwich 2 (14 nm arc core+2 × 7 nm arc wrap) | 28 | 0.71 | 10.9 | 0.63 |
| Sandwich 3 (15 nm EB core+2 × 6 nm arc wrap) | 27 | 0.50 | 8.0 | 0.45 |
As is indicated in the table, one measurement was made for the core of a phase plate, before wrapping with a final layer of evaporated carbon (see Materials and Methods for details), and three measurements were made for wrapped phase plates that were prepared on separate occasions. The error in estimating the thicknesses of the phase plates is between 1 and 2 nm, and the error in estimating the phase shift is less than 0.07π.
In practice we now use phase plates with thickness values close to 27 nm, which we believe provide a phase shift that is only slightly less than 90° for freshly “wrapped” phase plates. In any event, the CTF for Zernike phase plates (including the effect of electron loss) changes only slightly with phase-plate thickness, as we explain below.
3.2. The CTF is insensitive to the exact thickness when near to the optimal value
When using a thin film as a phase plate, it is unavoidable that some of the scattered electrons are lost as they pass through the thin film. Since the contrast in an image of a weak-phase object is proportional to the amplitude of the scattered wave, the image contrast that is obtained with a thin-film phase plate must be reduced—relative to that of a lossless phase plate—by a factor equal to the square root of the electron-transmittance of the phase plate. The contrast transfer function (CTF) of an otherwise perfect thin-film phase plate will thus be uniformly less than one at all spatial frequencies.
We estimate the total mean free path for electron loss (due to both elastic and inelastic scattering) of 300 kV electrons in evaporated carbon films to be ~115 nm. This estimate is based on measuring the decrease in image intensity across the edge of a hole in a phase-plate film, as is illustrated in Fig. 4. In this case the energy filter was used to remove electrons that were scattered with an energy loss greater than ~2.5 eV, and a 5 µm diameter objective aperture (cutoff angle equal to 0.5 mrad) was used to remove a significant fraction of the elastically scattered electrons. The (apparent) transmittance measured for 10 different, 25-nm-thick phase plates, all fabricated from the same carbon film, was 80.2 ± 0.6%.
Fig. 4.
Measurement of the intensity transmittance of a representative carbon-film phase plate. (a) Image of a 25-nm-thick carbon-film phase plate. This image was recorded at a magnification of ~33,000 on the CCD camera. The slit width of the energy filter that was used when recording this image corresponded to an energy loss of 5 eV, and the slit was centered on the position of the zero-loss peak. The image was recorded in a close-to-focus condition, and a 5 µm aperture was used in the objective lens. (b) Intensity trace across the edge of the hole in the phase plate. The correspondence between positions in the image and positions in the line-trace is indicated by the arrows that are shown between panels (a) and (b). Note the very slight decrease in intensity close to the edge of the hole, which may reflect as much as a ~1.5-nm-thick layer of contamination that has built up in this area during use.
The CTF for an ideal thin-film phase plate is almost perfectly flat, beginning from the first spatial frequency at which a phase shift is applied, which we refer to as the “cut-on frequency”, and continuing up to the point that lens aberrations and imperfect adjustment of the defocus become important. Taking into account the loss of electrons due to scattering by the phase plate, and allowing the thickness of the phase plate to be different from that which produces a phase shift of exactly 90°, the value of the flat part of the phase-plate CTF is given by
| (1) |
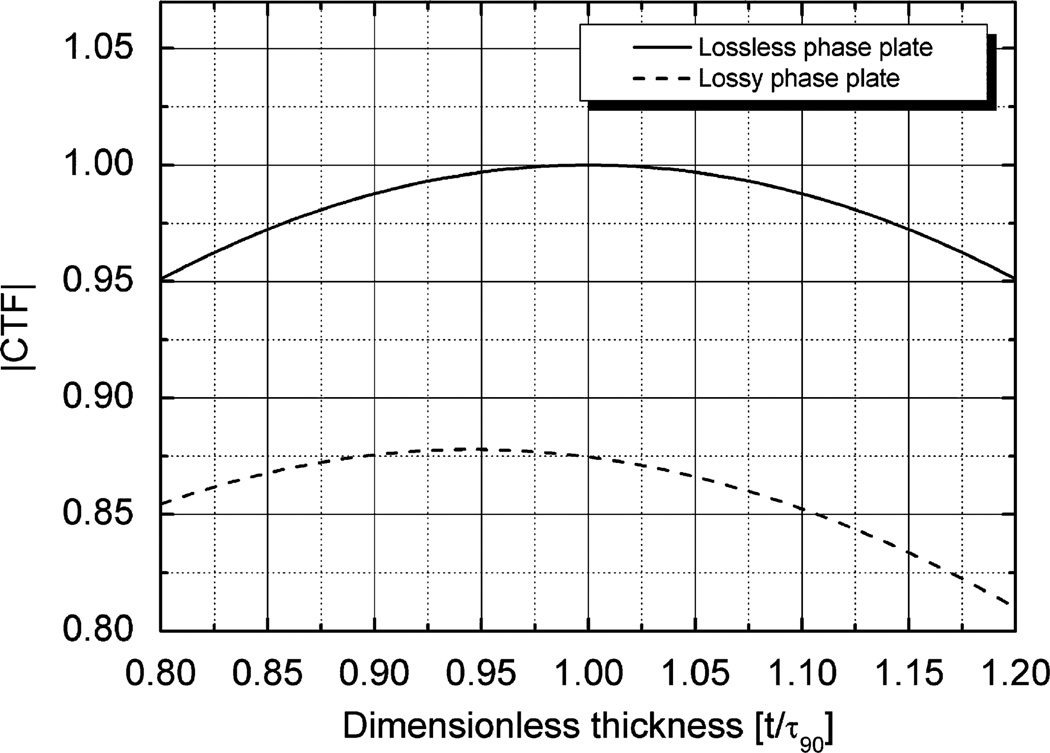
where ΔZ is the defocus, t is the phase-plate thickness, Λ is the mean free path for electron loss, and τ90 is the film thickness that produces a phase shift of exactly 90°. Fig. 5 shows how CTFΔZ = 0(t) varies with thickness for values that are close to τ90. The optimum thickness is (τ90/(π/2)) arctan(πΛ/τ90), which is, in fact, not significantly less than τ90. As can be seen from Fig. 5, the values of the CTF in the neighborhood of the optimum are rather insensitive to the film thickness. As a result, one does not have to be too precise about the thickness when fabricating a phase plate.
Fig. 5.
Dependence of the initially “constant” value of the CTF on the thickness of a thin-film phase plate, shown only for thickness values within ±20% of the thickness for which the phase shift is 90°, τ90. The initially constant value of the CTF (see Eq. (1) and also Fig. 6) is shown as a function of the dimensionless thickness, expressed in units of τ90. The calculation for a lossy phase plate assumed that the mean free path for electron loss is 115 nm, corresponding to the value we measured for 300 kV electrons. The corresponding calculation for a lossless phase plate is shown in order to aid a comparison of the relative contributions made by electron loss and by failure to produce exactly a 90° phase shift. The calculated values assume that the initial cut-on frequency is low enough to not reduce the value of the CTF.
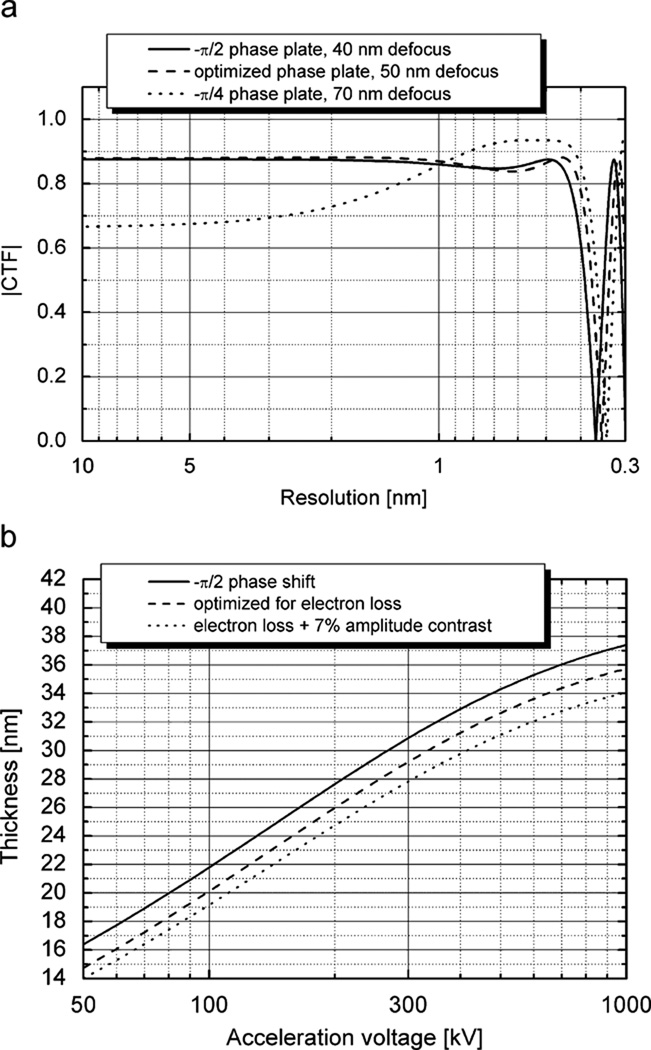
Although the effect of the loss of electrons is already quite small, it is likely that even thinner phase plates can be used for many specimens. The concept here is to accept a certain loss of phase contrast at low resolution and to use the phase shift due to defocus to increase the value of the CTF at higher resolution. For example, as is illustrated by the theoretical curve shown in Fig. 6a, use of a π/4 phase plate can still provide about 2/3 of the full contrast that is, in principle, available at low resolution, and well over 90% of the full contrast at high resolution. In addition, the first zero of the CTF is pushed to slightly higher resolution by use of a π/4 phase plate.
Fig. 6.
Optimization of the thickness of a carbon-film phase plate according to different assumptions. (a) Theoretical CTF curves for a 300 kV microscope with Cs = 5mm. The solid line is the CTF for a phase plate that produces a 90° phase shift. The dotted line is the CTF calculated for the case in which one is willing to accept reduced contrast at the lowest frequencies by using a phase plate that is only thick enough to produce a 45° phase shift. An optimal amount of defocus is then used to obtain a larger phase shift at higher resolution. The dashed line is the CTF for a phase plate that is “optimized” for use with a mixed phase and amplitude object in which the amplitude contrast is ~7% of the phase contrast. (b) Thickness values for carbon-film phase plates that are optimized for three conditions: 90° phase shift (lossless phase plate)—solid line; lossy phase plate—dashed line; and a lossy phase plate used to image an object in which the amplitude contrast is ~7% of the phase-contrast—dotted line.
One might imagine that an even further reduction in the thickness of the phase plate is possible for specimens, like cryo-EM samples, that exhibit a small amount of amplitude contrast. In reality, there is very little difference between the CTF that is optimized for an object with 7% amplitude contrast and that for the phase plate that provides a 90° phase shift, as is shown in Fig. 6a. Fig. 6b shows the values of phase-plate thicknesses that are needed at different acceleration voltages to produce (1) a 90° phase shift, (2) the highest possible value of the CTF at low resolution, and (3) a CTF that is optimized for a mixed, weak object with 7% amplitude contrast.
3.3. The phase-plate parameters can be optimized for the particle size of a given biological specimen
While a phase-plate shift of 90° is the ideal value for a weak-phase object, a 90° phase shift may not always be optimal, a point that has been made previously by Beleggia [11]. Many of the biological objects that are currently of interest in single-particle cryo-EM can produce rather large phase modulations in the transmitted electron wave, i.e. they are not always well approximated as being weak-phase objects. Tobacco mosaic virus (TMV), for example, might already produce a phase shift as large as 0.2 rad (i.e. ~0.064π) relative to the phase of the wave transmitted through an adjacent area of vitreous ice. This estimate is based on (1) the phase shift of 36 mrad/nm calculated for ice by Wang et al. [15], (2) the assumption that the phase shift at the exit face below the protein is about 4/3 (i.e. the mass–density ratio between protein and ice) times that below the same thickness of vitreous ice, and (3) the assumption that the maximum path length through the protein is slightly less than 18 nm.
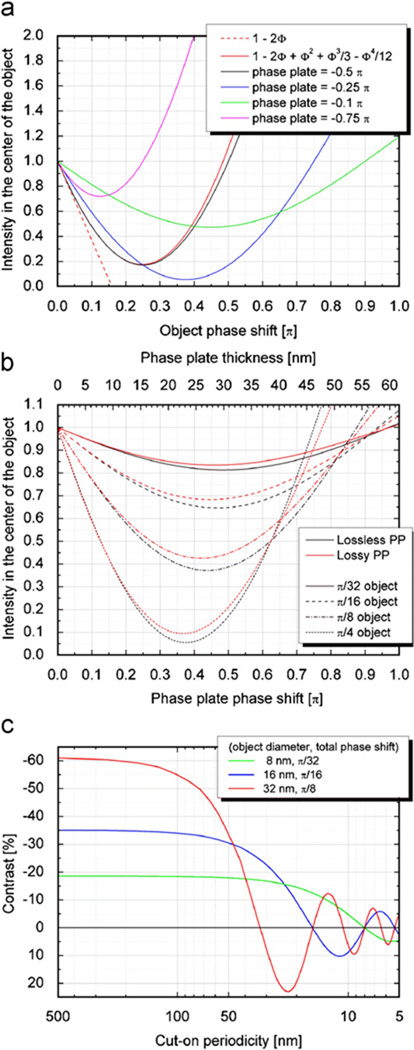
Fig. 7a shows the results of a numerical calculation of how the image intensity depends upon the magnitude of the exit-wave phase modulation. An overall description of simulation methods is given in Section 2.4, and additional details regarding each of the simulations for which results are presented in Fig. 7 are described in the legend. All curves in this panel make the “ideal” assumption that there is no initial, low-frequency “gap” over which the phase plate fails to apply a phase shift. Separate curves are shown for a few different values of the phase shift that is applied by such an “ideal” Zernike phase plate. These calculations also assumed that there is no wave aberration due to defocus or spherical aberration, assumptions that can be satisfied quite accurately at low resolution.
Fig. 7.
Examples of how various parameters can be optimized to best suit the particle size of a given biological specimen. (a) The image intensity obtained in the simulation of a phase disk, calculated as a function of the object phase, i.e. the phase modulation in the exit wave below the disk. Curves are shown for four examples of the phase shift applied by an ideal Zernike phase plate (infinitely small hole). Two analytical approximations for the image intensity are also shown, both of which assume that the phase shift applied by the Zernike phase plate is π/2. The dotted straight line shows the intensity expected for a weak-phase object, while the red curve shows the analytical approximation when the image intensity is expanded to fourth order in the object phase. (b) The image intensity obtained in the simulations for a phase disk, shown in this case as a function of the phase shift applied by an ideal Zernike phase plate. In this case there are four pairs of curves, each pair representing a different value of the phase modulation of the exit wave. The member of each pair of curves that is shown in black assumes that there is no loss of electrons as they pass through the phase plate, while the second member, shown in red, assumes that the mean free path for loss of electrons is 115 nm. (c) The contrast calculated for simulated images of uniform spheres is shown as a function of the cut-on periodicity (reciprocal of the cut-on frequency) of a Zernike phase plate. The contrast in this case is defined as the difference in intensity between the center of the object and the background, divided by the intensity of the background. The phase plate is assumed to apply a phase shift of 90°. The contrast at the center of the particle falls to zero when the cut-on period approaches the diameter of the sphere, and the contrast then oscillates in sign as the cut-on period decreases further.
Two analytical approximations are also shown in Fig. 7a. The first is the weak-phase object approximation, which predicts that the image intensity is proportional to the phase modulation of the exit wave, with a slope of −2. The second analytical approximation is the series-expansion expression given in Eq. (2), which is carried to fourth order in the phase modulation. The image intensity in the case of an ideal, 90° Zernike phase plate is approximated by this expression as being
| (2) |
where ϕ(x) is the local deviation of the phase of the exit wave from the average value. The first-order correction to the linear (weak-phase object) approximation, i.e. ϕ2(x), reduces the expected image contrast for TMV from 40% to 36%, which is a small enough effect to be of little practical importance. Corrections to the weak-phase object approximation rapidly increase in importance as the particle size, and thus the phase modulation, increases. As can be seen in Fig. 7a, the weak-phase object approximation is quite poor when the phase modulation is twice that expected for TMV, but the series expansion in Eq. (2) remains accurate to values of the phase modulation that are more than five times those expected for TMV.
A phase plate that provides less than a 90° phase shift, for example, only a 45° phase shift, can be useful for objects that are considerably thicker than the TMV virus. As is shown in Fig. 7a, the contrast is linear over a wider range of particle thicknesses for a weaker phase plate (one that is thinner than a quarter-wave plate). This improved linearity is realized with only a modest reduction in the amount of contrast at low resolution. A phase shift of 90° (due to the phase plate) is thus not necessarily optimal for strong phase objects [11]. At higher resolution, as was discussed in the previous section, one can then employ an optimal combination of defocus and spherical aberration to actually increase the value of the CTF for such a phase plate.
The phase shift (provided by a phase plate) that results in maximum contrast depends upon the strength of the phase modulation in the object wave. Fig. 7b shows how the intensity at the center of a simulated object depends upon the phase shift applied by the phase plate, for four different values of the phase modulation in the exit wave. Two curves are shown for each “object”, the first (in black) assuming a lossless type of phase plate and the second (in red) assuming that the mean free path for loss of electrons is 115 nm. The amount of contrast is not highly sensitive to the thickness of the phase plate, as one can already infer from the fact, shown in Fig. 5, that the value of the “flat” part of the CTF is relatively insensitive to the thickness of the phase plate.
An ideal Zernike phase plate, in which there is no gap at low frequency before a phase shift is applied, cannot be realized in practice. Instead, there will be an initial “cut-on” frequency at which the phase shift is first applied. In the case of a thin-film phase plate, for example, the cut-on frequency corresponds to the radius of the hole that is created for the unscattered beam. The effect of the value of the cut-on frequency on image contrast can be quite large, depending upon the ratio of the reciprocal of that frequency (the cut-on periodicity) and the size of the particle. As is illustrated in Fig. 7c, it is important that the cut-on periodicity should be at least twice the particle size. Even greater contrast (for weaker phase objects), comparable to that of an “ideal” phase plate, is expected when the cut-on period is four times the particle size. As is shown by the curves in Fig. 7c, it is expected that the contrast will actually be reversed in sign if the radius of the hole is too large for a particle of a given size, for example, if the cut-on periodicity is equal to the particle diameter. In practice, we fabricate phase-contrast apertures that have different hole sizes in a single disc, so that an appropriate phase plate can be selected for any given specimen. While one might think that it is always best, for weak-phase objects, to use phase plates with the smallest possible hole, in practice the alignment becomes more forgiving, the larger the hole size. In addition, as the hole size increases, the images become less sensitive to small beam deflections, for example, deflections that might be produced by local specimen charging.
3.4. Use of a phase-contrast aperture requires strict attention to beam alignment
In order to obtain phase-contrast images such as those shown below, care must be taken to align the illumination and the central hole of the phase plate, and the beam divergence must be much smaller than the angular acceptance angle of the hole in the phase plate. The protocol that we use for low-dose imaging employs standardized values of the condenser-lens currents and the second-condenser aperture size, which result in an illuminated area that is slightly greater than 1 µm at the specimen, and an angular spread of the illumination of ~1.65 × 10−5 rad (full width at half height) for the central area, ~0.7 µm on edge, that corresponds to the image captured on the CCD camera. The acceptance angle of a 0.5 µm hole is 5 × 10−5 rad, and that of a 0.3 µm hole is 3 × 10−5. The mean beam-tilt angle, θ, must be small enough to ensure negligible axial coma [16] out to the resolution of interest, as is true for normal bright-field imaging. The divergence angle denoted by α is characterized by the size of the crossover when the second-condenser lens is overfocused [17], and the angular sweep of beam tilt across the illuminated area denoted by β is determined by the aperture size in the second-condenser lens (C2 lens), and the distance between the C2 lens crossover and the specimen [17] should be as small as the gun brightness and the length of exposure times will allow.
The image at the edges of particles becomes asymmetric when the unscattered beam does not go precisely through the center of the hole in the phase plate. This asymmetry is due to the fact that some rays scattered at small angles pass through the carbon film but their Friedel mates do not. This asymmetry in Fourier space produces a “shadow-contrast” or “first-derivative” type of contrast in real space, similar to that seen in single sideband (schlieren) or Hilbert differential contrast [6,7] images. If asymmetric contrast becomes apparent in predominantly one direction, over the whole field of view, it is likely that an adjustment in the alignment of the phase plate is required. If asymmetric particle-edge contrast is present but not in a systematic pattern over the entire image, then it is likely that local charging of the specimen is responsible for local deflections in the transmitted electrons.
A number of different strategies can be used to focus the image when using a Zernike phase plate. In the current work we adjust the condenser-lens settings to produce an illuminated area with a diameter of ~500 nm at the specimen and a current density of ~6 × 104 electrons/s nm2. These settings produce a spot in the back focal plane that slightly overfills the hole of the quarter-wave plate, and thus a projection of the phase plate hole is visible on the screen. The CTF of such an image is position dependent. The part inside the hole projection exhibits a Zernike-type CTF consisting of a relatively flat region at low spatial frequencies and defocus-dependent oscillations at higher frequencies. This part of the image is imaged using the central 1/4 portion of the CCD camera producing alive display (~1 frame/s) of the Fourier transform. The astigmatism can be accurately corrected in this focusing mode, after which the defocus is adjusted such that the first zero of the CTF is at or above the Nyquist frequency of the CCD camera.
3.5. Charging effects can be avoided in newly fabricated phase plates
As was mentioned above, it has been our experience that freshly prepared carbon-film phase plates are likely to show unacceptable charging effects unless a final coating of evaporated carbon is applied as a finishing step in the fabrication. While the main source of non-conducting material has not been identified, one possibility is that it is deposited during the water transfer process of the “core” carbon film to the aperture grids. Another source of surface or volume-implanted contamination may be the focused ion beam apparatus used to drill a small hole at the center of the phase plate. The key effect observed if a final coating of evaporated carbon is not applied is a beam-induced positive charging of the phase plate, which deforms the CTF in a way similar to overfocusing. Evaporation of a final layer of ~5–7 nm of carbon onto all surfaces, a step that we referred to in Section 2.1 as “wrapping”, removes effectively all evidence of charging. Indeed, even the extreme charging shown by a thin film of sputtered SiO2 is masked after wrapping it with evaporated carbon (unpublished data).
In addition to applying a final coating of evaporated carbon to newly fabricated phase plates, we have taken the precaution to heat the finished phase plate to a temperature of at least 150 °C during use. The intention is to keep the phase plate clean of hydrocarbon material, and thus avoid the buildup of contamination in areas that are hit by the intense unscattered beam. From a practical point of view, this level of heating has been sufficient to prevent a progressive increase in thickness in an area where the unscattered beam is allowed to hit the carbon film over a prolonged period of time. In current practice the aperture is also maintained at a temperature of ~170 °C when the microscope is not in use. However, as we discuss later, the development of methods to avoid deterioration of phase-plate performance over time remains a topic that still requires further research.
3.6. Thin-film phase plates produce a significant improvement in the visibility of single particles
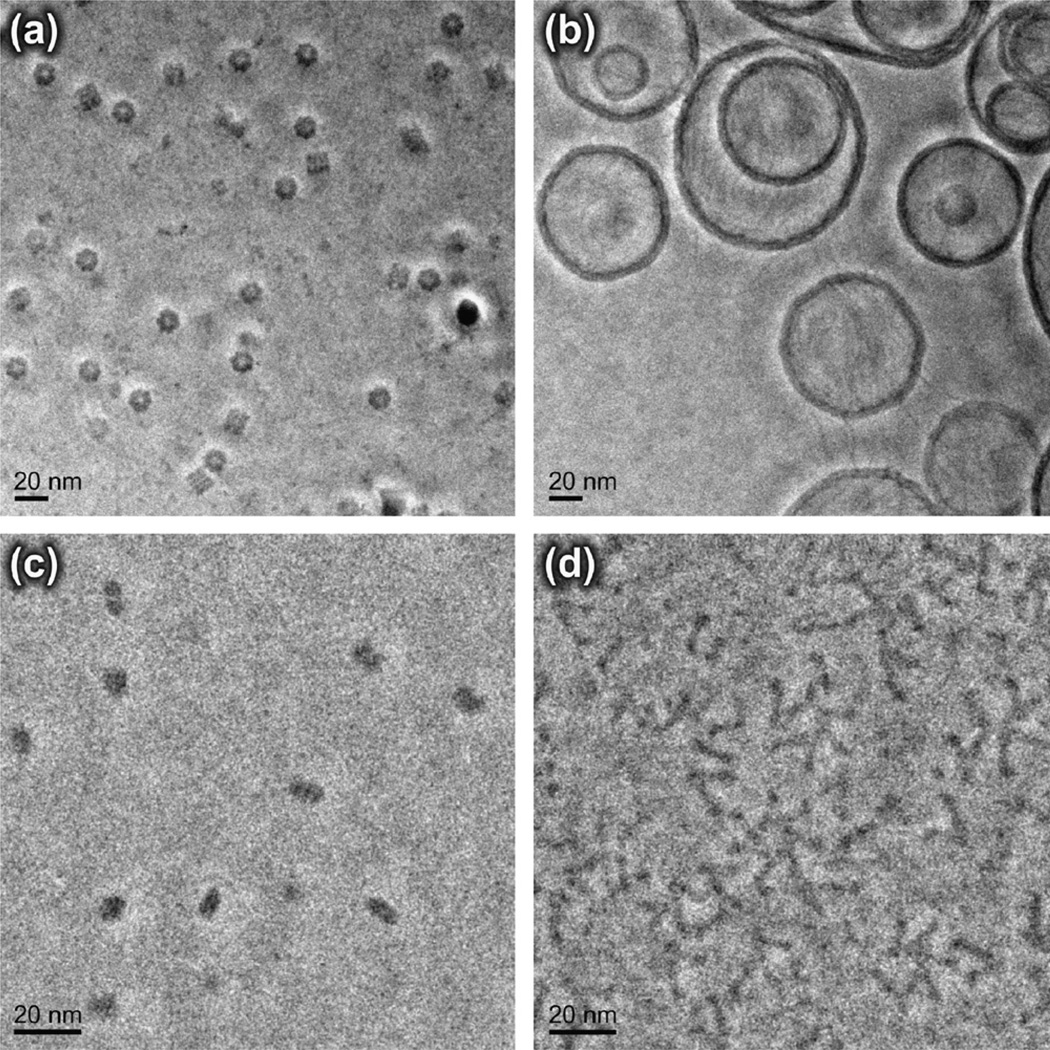
As has been shown previously [10,18], images of cryo-EM specimens that are recorded with an optimally performing carbon-film phase plate show much more contrast than those that are recorded with defocus-based phase contrast. Examples of images obtained for four different cryo-EM specimens are shown in Fig. 8. It should be emphasized that the phase-contrast images shown here were all recorded in a near-to-focus condition, with the first zero of the CTF lying outside the Nyquist limit of the CCD camera. As a result, there are no oscillations in the CTF that need to be corrected (at spatial frequencies below the Nyquist limit) in these examples, nor are some of the image data before the Nyquist limit lost in regions near to what would have been the zeros of such oscillations had the images been recorded with defocus-based phase contrast. In addition, there is no defocus-dependent delocalization of Fourier components of these images [19]. At the same time, oscillations in the CTF, and delocalization as well, still occur at resolutions beyond the Nyquist limit of the images shown in Fig. 8, due to the effect of spherical aberration. In order to avoid these unwanted effects, which would become detectable in images recorded at a higher magnification on the CCD camera, a phase plate can be used in conjunction with a Cs corrector.
Fig. 8.
Phase-contrast images of four representative cryo-EM specimens. Note that the magnification in (c) and (d) is twice that in (a) and (b). (a) E.coli GroEL, a ~800 kDa homo-oligomer consisting of 14 subunits arranged in two stacked rings, with each ring containing seven copies of the protein. Similar micrographs, and a three-dimensional reconstruction obtained from such images, have been published previously [10]. (b) Liposomes prepared from egg-yolk phosphatidylcholine that were mixed with lambda phage DNA. Many of the DNA molecules are adsorbed to the surfaces of the liposomes, while others form numerous bridges between adjacent liposomes. A more extensive description of phase-contrast imaging of this sample is given in [28]. (c) Desulfovibrio vulgaris dissimilatory sulfite reductase (Dsr), a 200 kDa dimer of heterotrimers. (d) Helicobacter pylori VacA toxin, an 88 kDa protein that assembles into pinwheel-shaped rings (both complete and incomplete forms are seen here), and non-chiral double-layered rings [29]. These four examples are representative of the diverse range of macromolecular particles that can be studied by phase-contrast electron microscopy.
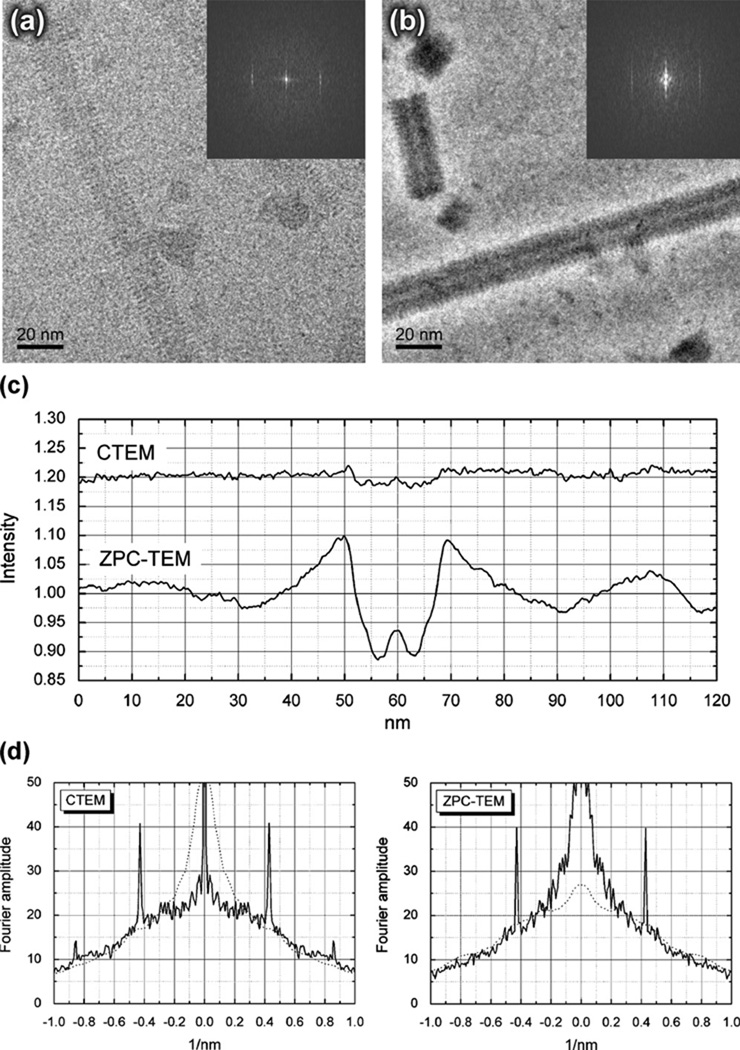
A quantitative measurement has been made of the increase in particle contrast that is observed for cryo-EM specimens of tobacco mosaic virus particles using images recorded from the same grid-square of the same specimen. Fig. 9 shows both a bright-field image of TMV, recorded with a defocus of ~1 µm in order to place the second maximum of the CTF close to the position of the 1.15-nm-resolution layer line, and a Zernike phase-contrast image, recorded close to focus. Fig. 9c then shows intensity profiles calculated across the width of the respective TMV particles. By comparing the intensity below the particle to that in the background, far from the particle, the particle-contrast for the bright-field image is estimated to be about 2%, while that for the phase-contrast image is estimated to be about 10%. The computed Fourier transforms of the respective images both show strong diffraction on the 2.3 nm layer line. The quantitative comparison in Fig. 9d shows that the signal levels on the respective 2.3 nm layer lines are more similar than they appear to be in the gray-scale representations, i.e. the insets in Figs. 9a and b. The difference in signal level, and the absence of detectable signal on the 1.15 nm-resolution layer line for the phase-contrast image, is well within the particle-to-particle variation that is typically seen with cryo-EM specimens. Nevertheless, we believe that the phase plate used for this measurement probably had already begun to deteriorate with age (see below) at the time these images were recorded.
Fig. 9.
Quantitative measurement of the increased visibility (contrast) achieved in cryo-EM images of tobacco mosaic virus (TMV) when using a thin-film phase plate with a cut-on periodicity of about 40 nm. (a) Bright-field image of TMV particles recorded at a defocus of ~1 µm. A gray-scale representation of the modulus of the Fourier transform of a narrowly boxed section of virus, 157 nm in length, is shown in the inset. (b) Phase-contrast image recorded in a close-to-focus condition. A gray-scale representation of the modulus of the Fourier transform of an identically boxed section of virus is again shown in the inset. (c) Intensity profiles across the images of virus particles shown in panels (a) and (b), respectively. The intensity profiles for the virus particles are averaged along a length of 85 nm in a direction parallel to the axis of the virus. For clarity, the averaged profile for the bright-field image of the virus is off set vertically from that for the phase-contrast image by 0.2 units. In the case of the phase-contrast image, the intensity within the virus decreases to about ~0.90 of that in the surrounding ice, whereas in the case of the defocused bright-field image the intensity within the virus decreases to only about 0.98 of that in the surrounding ice. (d) One-dimensional representations of the Fourier-amplitude spectra shown as insets in panels (a) and (b), obtained by projecting the amplitude spectra in a direction parallel to the layer lines. A smoothed version of the curve (with the diffraction peak removed) for the CTEM image is shown as a dotted curve in the panel for the ZPC-TEM image, and similarly a smoothed version of the curve for the ZPC-TEM image is shown as a dotted line in the panel for the CTEM image. The peak heights of the averaged Fourier amplitudes on the 2.3 nm layer line are seen to be much more similar than might have been estimated from the gray-scale representations shown in (a) and (b). The strong Fourier amplitudes that are retained at a resolution below ~1/(5 nm) in the Zernike phase-contrast image make it difficult to compare the gray-scale representations of the two spectra. The slight reduction of the envelope of the phase-contrast image relative to that of the bright-field image is thought to be due to loss of some electrons that pass through the phase plate—see Fig. 10 for additional information on this point.
Although phase-contrast imaging produces excellent contrast for weak-phase objects, it is worthwhile to mention that strong-phase objects show additional contrast effects (“artifacts”) that are generally considered to be undesirable. Images of larger contaminating particles, for example, are surrounded by strong Fourier ripples (data not shown) that look similar to the Fresnel fringes seen in highly defocused images, even though the image in this case is taken in a near-to-focus condition. We attribute such ripples to Fourier-series termination effects, which are due to the low-frequency cutoff of the hole in the phase plate. The result is the same as would be produced in a numerical Fourier synthesis in which those low-frequency Fourier components were not included. Similar edge-ripples are commonly seen when looking at strong phase objects in the Zernike phase-contrast light microscope.
3.7. The increased visibility (contrast) of single particles nevertheless deteriorates with the age of the film
Although one might expect the amount of in-focus phase contrast to depend only on the thickness of a carbon-film phase plate and not on how old it is, in practice we have found that the phase plates show an unexplained “aging” effect. It should be pointed out that our observation of this aging effect is limited to phase-plate films that are inserted into the microscope as soon as possible after fabrication, and which then are heated continuously after they have been inserted into the microscope. We have not undertaken additional experiments to determine whether similar “aging” effects occur when phase plates are stored under ambient conditions. As a result, we do not yet know whether heating accelerates the aging effect. In practice, of course, heating is required in order to prevent contamination and charging, and thus heating is required whether or not it accelerates the aging effect.
The first point to mention is that images recorded with phase plates show significantly greater contrast when the apertures are used shortly after fabrication than 3 to 4 weeks after fabrication. In the early stages of aging, the first few images recorded with a given phase plate may have high contrast, but after ~5 or more images have been recorded the contrast and resolution of the image can degrade considerably. Once such a phase plate is removed from the electron beam, it can happen that its performance will recover by the following day, but of course with the same sensitivity to electron exposure as it showed the previous day.
We have consistently observed that aging of a phase plate ultimately produces more than just a decrease in the particle contrast. Rather complicated changes also occur in the appearance of a particle, and these are associated—as they must be—with deviations in the CTF from the flat (constant) value that is intended at low resolution. In the worst examples, the CTF at the lowest spatial frequencies starts off at a high value but drops very steeply, passes close to or even through zero at a low spatial frequency, and then continues to show an apparently normal progression of Thon rings at higher resolution. Images produced with such a CTF may, in the worst case, show reversed contrast, as if they were over focused, or they may simply be more blurred in appearance.
The change in performance of the phase plates with time is likely to be due to electrostatic charging. What is not yet clear is why the susceptibility of a given phase plate to charging should increase as it ages. In addition we have observed significant variability in both the initial evidence of “charging” of the phase plate, if any, and the rate of “aging”. What has nevertheless been quite clear is that a phase plate, which initially does not appear to suffer from charging, will last much longer before its performance deteriorates than is the case for a phase plate that already starts off with a relatively poor level of performance. Neither the physical cause of the “aging effect” nor the cause(s) of the variability in useful lifetime that we have observed are known at this point.
3.8. The high-resolution envelope is not degraded by the carbon-film phase plate
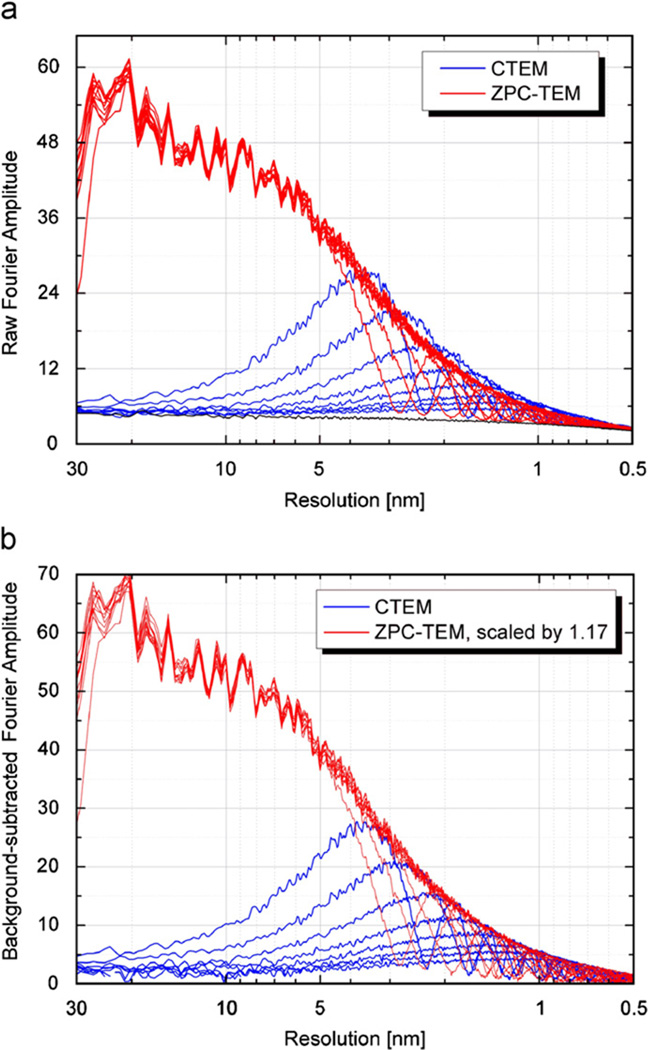
We have used a protocol similar to that employed by Cambie et al. [4] to determine whether the envelope function is degraded by the phase plate at higher resolution. An image of the uniformly illuminated detector (in practice, an image of a large hole in the sample) is used to obtain the mean value (i.e. the mean background) for the amplitude spectrum of shot noise, using the same electron exposure as that which is used to record images of a carbon film. This mean value of the background provides an estimate of the residual amplitude (i.e. additive noise) expected at the zeros of the CTF. We then compared the modulus of the Fourier spectra of images of a ~10-nm-thick carbon film that were taken with and without a phase plate. All images were recorded at a microscope magnification of 200K on the CCD camera and with an electron exposure of ~5700 e/nm2 at the specimen. Although the Nyquist limit for the CCD camera corresponds in this case to a resolution of 0.3 nm, the Fourier-amplitude spectra shown in Fig. 10 are cut off at a resolution of 0.5 nm.
Fig. 10.
Comparison of the circularly averaged Fourier-amplitude spectra of images of a 10-nm-thick carbon film recorded over a range of defocus values when using the “conventional” bright-field mode (blue curves), and when using the Zernike phase-contrast aperture (red curves). All images were recorded with identical illumination conditions and exposure times, and all Fourier transforms were computed for images of the same area of the specimen. Irregular oscillations in the low-resolution part of the amplitude spectra of the phase-contrast images reflect statistical variations in the circular average of the structure factors within the chosen area of the specimen, and should not be confused with noise in the measurement. The cut-on periodicity for the phase plate used in this experiment was ~28 nm, corresponding to a hole diameter of ~700 nm. The base-line spectrum (lowest curve in panel a) is that of an image of a hole in the specimen, i.e. it represents the modulus of the Fourier transform when the input image is a uniform field of randomly distributed electrons. (a) Representative Fourier-amplitude spectra obtained with a phase-contrast aperture (red curves) are compared to those obtained without an aperture (dark blue curves). (b) Background-subtracted versions of the same Fourier-amplitude spectra that are shown in (a). The background was subtracted in quadrature, i.e. the power spectrum of an “image” with no specimen was subtracted from the power spectra of the images of carbon film. The Fourier-amplitude spectra shown in this panel were then obtained by taking the square root of the background-subtracted power spectra. The respective CTF envelopes for phase-contrast and bright-field images are well superimposed when the background-subtracted amplitude spectra of phase-contrast images are multiplied by a factor of 1.17.
As the examples in Fig. 10a show, oscillations in the modulus of the Fourier transforms of images recorded at different defocus values are well-confined between a common “upper envelope” and the background due to shot noise (i.e. the noise transfer function (NTF)) [20]. As is shown in Fig. 10b, the envelope for the modulus of the background-subtracted Fourier transforms of images recorded with a 27-nm-thick phase plate is about 0.86 times that for defocused bright-field images recorded without a phase plate. The fall-off of the envelope function with increasing resolution that is observed for the Zernike phase-contrast images is essentially the same as that for the defocused bright-field images over the band pass that is accessible for this comparison. The lowest frequency for the comparison is determined by the position of the first maximum in the CTF for the most highly defocused bright-field image, while the highest frequency for the comparison is determined by the fall-off in the MTF of the CCD camera. The scale-factor of 0.86 that is needed to superimpose the two envelopes is in good agreement with the uniform decrease of 0.89 that is expected due to loss of about 21% of the electrons that pass through the phase plate, discussed above.
The steep fall-off of the upper envelope shown in Fig. 10a is an undesirable feature of the modulation transfer function (MTF) of the CCD camera that was used in this work. That the performance of the CCD camera, rather than the microscope itself, dominated the fall-off was confirmed by comparing Fourier-amplitude spectra for two series of defocused bright-field images, one taken at an image magnification of 100,000 at the CCD camera and the other taken at twice that magnification.
Although the fall-off of the MTF of CCD cameras is known to be severe at high voltages [21], that fall-off does not prevent a comparison of the envelope functions for the Zernike mode and the bright-field mode out to a resolution of about 0.5 nm. In fact, the bright-field envelope could even be used to correct the camera-MTF for the Zernike mode without amplifying the electron shot noise. The camera noise, on the other hand, would still be amplified by this operation, as would the noise that is attributable to the pulse-height spectrum for single-electron events.
4. Discussion
4.1. In-focus phase contrast has significant advantages for cryo-EM of smaller structures
The visibility of macromolecular particles in cryo-EM is greatly increased when a quarter-wave plate is used to apply a 90° phase shift between the scattered and unscattered electrons. As is well known, unstained biological macromolecules are primarily weak-phase objects, and the contribution that amplitude modulations make to the structure factor at low resolution is only about 7% of the contribution due to phase modulations [22]. The contrast transfer function for “conventional“ (i.e. bright-field) imaging is thus very low at low spatial frequencies, even when the microscope is highly defocused. Fig. 8, on the other hand, demonstrates the high contrast that is produced for four representative examples of macromolecular structures when a thin carbon film is used to produce in-focus phase contrast.
The quantitative estimate of contrast shown in Fig. 9 demonstrates that the contrast produced with a phase plate can be as much as five times that of bright-field images that are recorded with a defocus of 1 µm. Tobacco mosaic virus was chosen as a specimen to use for making a quantitative comparison because (1) the low-resolution contrast is expected to be very consistent from one particle to the next and (2) identical test-specimen particles can be obtained in different laboratories without great difficulty. TMV also has the further property that measurements of the low-resolution contrast can be computed in the form of one-dimensional projections parallel to the long axis of the virus [22,23], thereby improving the signal-to-noise ratio of the measurement.
The increase in particle contrast that is generated with a phase plate may seem to be surprisingly large in view of the relatively small size of the additional angular interval over which the phase plate, but not the usual wave aberration due to defocus, introduces a phase shift of ~90°. It is therefore important to emphasize that the structure factors (Fourier amplitudes) of macromolecular particles are much stronger at low resolution than they are at high resolution. More specifically, the scattering intensity at small angle scales as the square of the particle weight. The total scattering intensity (i.e. the total scattering cross section), on the other hand, scales linearly with the number of atoms in a particle, weighted by their respective atomic scattering cross sections, i.e. essentially as the particle weight [24]. As a result, one might say that the low-frequency Fourier components carry a “disproportionately large” fraction of the total scattered wave. It is to be fully expected, therefore, that images show a steep increase in visibility (contrast) as lower and lower frequencies are included with a 90° phase shift. At the same time, as is shown in Fig. 7c, the increase in contrast becomes rather shallow once the cut-on periodicity is larger than twice the particle size.
The 10% intensity dip shown experimentally for phase-contrast images of TMV, although much greater than one is familiar with for defocused bright-field images, is nevertheless at least three times less than that expected from theoretical estimates. As was indicated above, the phase modulation below a TMV particle embedded in vitreous ice may be as large as 0.2 rad, and thus the dip in image contrast that is estimated by the use of Eq. (2) would be about 36%. A more accurate estimate could be made by computing the phase modulations from the known atomic model of TMV embedded in vitreous ice, and then calculating the intensity profile for a one-dimensional projection of the corresponding phase-contrast image.
A number of factors are expected to cause the experimental value of the contrast to be less than that calculated for the image model of an ideal Zernike phase plate. The phase-plate cut-on periodicity of 40 nm used for these images is expected to be responsible for only ~7% loss of particle contrast (from Fig. 7c). Other factors to consider are the finite electron-source size, and, perhaps more importantly, some jitter in beam-tilt angle due to specimen charging, which will cause a fraction of the small-angle scattered electrons to go through the hole rather than the phase plate while their Friedel mates will do the opposite. The considerable thickness of ice in cryo-EM specimens may also result in effects that are not accounted for in the theoretical image model.
The increase in particle visibility provided by Zernike phase contrast is due primarily to the large value of its CTF at low spatial frequencies, of course. Indeed, the sole purpose of using a large defocus in bright-field cryo-EM is also to increase the CTF at low frequencies. The importance of low-resolution features in determining the visibility of a particle is demonstrated by the simulations that are summarized in Fig. 7c. Such computations show that one should include spatial frequencies in a Fourier synthesis (i.e. a phase-contrast image) that extend down to approximately 1/(2L), where L is the particle width. A “cut-on” frequency this low is needed in order to realize nearly the full amount of particle visibility and to minimize low-frequency “ringing” due to termination of the Fourier synthesis. As a corollary, one can point out that it is worthwhile to match the hole size of the phase plate to the particle size of the object that one is studying. The use of a larger hole size, whenever it is safe to do so, makes the centering of the unscattered beam within the hole less critical than it is for a smaller hole.
The increased visibility (contrast) produced by in-focus phase contrast is expected to lead to major improvements in the use of cryo-EM in biochemistry and cell biology. As is demonstrated by the images of Dsr and VacA shown in Fig. 8, the use of phase contrast makes it very easy to recognize particles at least as small as 200 kDa, and it is clear that even particles well below 90 kDa could be easily “boxed” for single-particle data analysis. The increased visibility also makes it easier to recognize—and thus reject—damaged particles, something that cannot be done with confidence for particles as small as Dsr when they are imaged in bright field, even with a high degree of defocus. It seems likely that computational tools for recognizing structural heterogeneity will also work much more effectively when applied to images recorded with in-focus phase contrast. This benefit is likely to apply equally well to large particles as it does to smaller particles, even though increased contrast provided by a phase plate may not be needed just to box the (larger) particles.
A further advantage of Zernike phase-contrast imaging is that high particle visibility is achieved without generating oscillations in the CTF, and thus no CTF correction is required. In addition, images recorded with in-focus phase contrast do not lose up to half of their signal at high resolution due to defocus-dependent delocalization, an effect that remains even after CTF correction [19]. Both CTF oscillations and delocalization become especially troublesome during bright-field imaging of smaller structures, due to the larger amount of defocus that one must use to visualize such particles. On the other hand, provided that the defocus is not greater than ~2000 nm and one uses the same illumination conditions that are required for Zernike phase-contrast imaging, the spatial-coherence envelope should not be a serious limitation in bright-field imaging at 300 kV, even for a resolution of 0.3–0.4 nm. The temporal coherence envelope, which depends upon fluctuations in focus but not on the absolute value of defocus, is also not a limitation at the resolutions attainable in cryo-EM of single molecules, provided that one again uses an accelerating voltage of 300 kV and that the energy spread of the FEG is less than 2 eV.
4.2. The small hole sizes needed for biological applications impose strict requirements on alignment of the electron beam
The ideal concept of a phase-contrast microscope imagines that the unscattered electrons are focused to a point on the optical axis; that this point lies within the plane of the phase plate; and that the hole of the phase plate is centered perfectly about the axis. Each scattered electron beam and its Friedel mate then passes symmetrically through the quarter-wave plate. In reality, the finite size of the electron source prevents the illumination from being focused to a single point, and in addition the condenser-lens system often does not have the required flexibility to simultaneously adjust the beam intensity, the size of the irradiated area, and the point along the optical axis where the beam is brought to a focus. A condenser-lens system with three adjustable lenses, on the other hand, does provide the three degrees of freedom needed to keep the beam as parallel as is required and at the same time to independently adjust the size of the illuminated area and the beam intensity (within the limitations of the source brightness, of course.)
While some deviation from the ideal concept stated above can be tolerated, the in-focus phase-contrast microscope is much less forgiving about the angular spread of the illumination (i.e. the spatial coherence) and the degree of misalignment that can be tolerated than is the “conventional” bright-field microscope. To illustrate the stringency of illumination conditions that should be met, we note that the acceptance angle (half-angle) of an 0.5 µm diameter hole, located at the back focal plane of a lens with a 5mm focal length, is 5 × 10−5 rad. In order that all unscattered electrons should go through the hole, and the majority of electrons scattered at angles corresponding, for example, to a spatial frequency of 1/(40 nm) should experience a 90° phase shift, the divergence angle of the incident beam should not be greater than ~2 × 10−5 rad, which is about an order of magnitude more parallel than is normally done for bright-field imaging.
As for conventional bright-field imaging, the incident beam should also be sufficiently parallel to the optical axis that one can ignore the effects of axial coma. For a target resolution of 0.8 nm, this angle can be as large as 5 mrad (for 300 keV electrons), but for a target resolution of 0.4 nm it should be nearly an order of magnitude smaller than that. In any case, this angle is much larger than the acceptance angle of the hole in the phase plate, and thus a small change in beam tilt can be used rather than a mechanical centering of the objective aperture in order to keep the hole centered about the focused beam.
The exceptionally small size of the hole in the phase plate and the requirement that the hole must be well centered together raise novel concerns about the stability of the beam-tilt angle. One might like this angle to be stable to an order of magnitude smaller than the acceptance angle of the hole, for example, i.e. to something like 5 × 10−6 rad. Some of the concerns about achieving such high stability include the fact that changes in beam-tilt angle, θ, might occur due to (1) flux leakage whenever the current is changed in one of the other lenses, (2) hysteresis in the condenser-lens system, (3) inadequate stability of currents in the beam-tilt coils, (4) the limited accuracy with which the pivot point can be set such that x, y deflection can be adjusted without changing the beam-tilt angle, (5) deflection of the beam as the stage is moved, due to inclusion of magnetic materials anywhere in the stage or the stage drives, and (6) the risk that something in the condenser-lens portion of the column might become charged, thereby causing small changes in beam-tilt angle. In practice, none of these issues have caused a noticeable problem.
Specimen charging can also cause a locally varying amount of angular deflection of the unscattered beam. Rather large beam deflections are easily seen when attempting to focus the central beam in an electron diffraction pattern of a non-conducting, thin specimen such as an uncoated formvar film or an uncoated plastic section. Even much smaller specimen-charging effects, which may vary in magnitude from one part of the specimen to another, might still be large enough to deflect some of the unscattered electrons to positions that are close to or even outside the edge of the hole in the phase plate. The low-resolution Fourier components at the corresponding locations in the image will then showa “first-derivative” type of contrast, similar to what is produced when a half-plane phase plate is used [6]. It thus is possible that the spatial and azimutal variations in the amounts of contrast that are seen at the edges of different GroEL particles in Fig. 8a are due to local variations in specimen charging. There is, nevertheless, a predominant trend for the white halo to be at the top of each particle. The bias in the particle-edge contrast-effect suggests that there was a systematic off-set of the unscattered beam from the center of the hole in the phase plate, which might or might not be due to specimen charging, for example, in the adjacent area used for focusing. It may be possible that optical effects due to specimen charging can be minimized by preparing samples on continuous carbon films, or by evaporating a thin carbon film onto specimens prepared over open holes [25].
4.3. The partial loss of electrons transmitted through thin carbon films is not a significant limitation for such phase plates
It is a common misconception that the loss of a certain fraction of electrons, due to the elastic and inelastic scattering that occurs when the scattered wave passes though a thin foil, would severely limit the usefulness of a thin-film phase plate. Theoretical estimates of the loss of electrons for a quarter-wave plate, and our own experimental measurements of the fraction of electrons that are lost, agree that approximately 79% of the electrons incident on a 27-nm-thick phase plate are transmitted without being scattered. Since the signal in the image of a weakly scattering object is proportional to the wave amplitude, i.e. the square root of the transmitted intensity, the CTF of a quarter-wave plate is expected theoretically to be about 0.89, i.e. only 11% less than that of a perfect, loss-free phase plate. Our experimental result is closer to 0.86, however.
A CTF with a “flat” value >0.8 is, in fact, far superior to the CTF of a “conventional” bright-field microscope at low spatial frequencies, and it is not significantly worse than that of a “conventional” bright-field microscope at intermediate and high spatial frequencies. The attenuation of the phase-contrast signal in the image of a weak-phase object can be further improved, at frequencies higher than 1/(1 nm), by sacrificing the low-frequency signal somewhat, as is illustrated by the example shown in Fig. 6a.
4.4. Aging of carbon-film phase plates is currently the biggest issue that limits the convenience of their use
As we have described in the results, thin carbon-film phase plates begin to exhibit substantial image artifacts as they age. In the mildest form, these artifacts may consist of little more than a reduced visibility (reduced contrast) for macromolecular specimens. In a more severe form, however, the artifacts may cause the low-resolution features of the image to appear as if the microscope were highly defocused, while at the same time features at intermediate and high resolution remain imaged in the intended way.
It is likely that changes in the CTF of carbon-film phase-contrast apertures are due to electrostatic charging, and that the susceptibility of the phase plate to charging increases with the age of the carbon film. Briefly, we have observed the formation of a saturable, erasable footprint over an irradiated area of the carbon film, a phenomenon commonly referred to as the “Berriman effect” [26,27]. In addition, we have observed progressive, frame after frame changes in the CTF for images recorded after the phase plate had been intentionally shifted to one side, so that the unscattered beam passes through the carbon film rather than through the hole. The fact that these effects are more pronounced in older phase plates suggests that the susceptibility to charging increases with time. A number of other potential causes for changes in the CTF of a thin-film phase plate can be ruled out on the basis of our experience to date. Provided that the phase plate is heated above 150 °C during use, for example, we have not observed a measurable change with time in the thickness of the irradiated area of the phase plates, i.e. neither a clearly visible increase due to contamination nor a thinning due to etching in the electron beam.
We have varied several parameters in our fabrication and use of carbon-film phase plates over the course of routine work, in an attempt to find a way to overcome the aging problem. The parameters that we have explored include (1) the temperature at which the phase plates are heated during use; (2) the temperature at which they are maintained when the microscope is not in use; and (3) whether the final coating (“wrapping”) is applied in an electron-gun system, or in a system in which carbon is evaporated by a carbon arc. None of these parameters seem to have a major influence on the lifetime of the phase plates. Since phase-contrast apertures of the type described here have only a limited useful lifetime, there currently is no alternative but to replace them as soon as the particle visibility begins to fall below an acceptable level, and especially when artifacts of the type described above begin to be noticed.
Since the benefit of in-focus phase contrast is so clear, it would be of great value if there were commercial support for the use of phase plates of the type described here. To begin with, manufacturers should offer microscopes that have a field-emission gun, a condenser-lens system with three independently adjustable lenses, and an objective focal length of at least 5 mm. A heated objective aperture should be provided, along with a room-temperature aperture that can be inserted as a heat shield between the specimen and the heated phase plate. Provision should be made to exchange apertures through an airlock, so that the column does not have to be vented when it is necessary to replace an aperture strip. It would also be helpful if core phase plates were made commercially available with different hole sizes, so that individual laboratories would not have to purchase and maintain their own FIB instrument to drill the central hole. The final carbon coating (wrapping) of such core phase plates, on the other hand, could easily be applied by the customer, shortly before use.
5. Conclusions
Thin carbon films can be used to fabricate quarter-wave phase plates that provide a highly effective realization of Zernike phase-contrast in electron microscopy. In-focus images of tobacco mosaic virus particles obtained with these phase plates, at an electron energy of 300 keV, show about five times higher contrast than what is seen in the defocused bright-field imaging mode at a defocus value of ~1 µm. In addition, the high-resolution envelope function shows only a small, constant reduction in signal relative to that of the bright-field imaging mode. The ~15% reduction in signal observed for 300 keV electrons is close to the value expected due to the loss of electrons that are scattered as they pass through the phase plate. The large increase in particle visibility, with only a minor cost in terms of the high-resolution signal, is expected to be of greatest value for single-particle cryo-EM of protein complexes as small as 100 kDa, and for sorting images of larger protein complexes into subsets according to differences in conformation. The main inconvenience of using thin-carbon phase plates currently is the fact that their performance deteriorates on the time scale of days or weeks, thus requiring that they be replaced at frequent intervals.
Acknowledgements
We wish to thank several individuals for providing the sample materials for which representative results are shown in this paper: Liposomes with adsorbed DNA were provided by Dr. Vasiliy Kuvichkin; Desulfovibrio vulgaris Hildenborough dissimilatory sulfite reductase (Dsr) complex was provided by Dr.Ming Dong; Helicobacter pyroli VacA toxin was provided by Dr. Akihiro Fujikawa; and tobacco mosaic virus (TMV) was provided by Professor Andy Jackson and Dr. Bong-Gyoon Han. The phase plates were prepared by Hiroshi Okawara. We thank Dr. Tsukasa Hirayama for providing use of the electron microscope at the Japan Fine Ceramics Center, Nagoya, and Dr. Kazuo Yamamoto for helping to make electron holography measurements of the inner potential of representative phase plates. We also thank Dr. Hideki Shigematsu for numerous discussions about his experience with the use of Zernike phase-contrast electron microscopy. This work was supported in part by CREST (Core Research for Evolutional Science and Technology), Japan Science and Technology Agency, and by NIH grant GM083039.
Footnotes
PACS:
43.25.–p
42.30.–d
References
- 1.Boersch H. Zeitschrift Fur Naturforschung Section a—a Journal of Physical Sciences. 1947;2:615. [Google Scholar]
- 2.Schultheiss K, Perez-Willard F, Barton B, Gerthsen D, Schroder RR. Review of Scientific Instruments. 2006:77. [Google Scholar]
- 3.Majorovits E, Barton B, Schultheiss K, Perez-Willard F, Gerthsen D, Schroder RR. Ultramicroscopy. 2007;107:213. doi: 10.1016/j.ultramic.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 4.Cambie R, Downing KH, Typke D, Glaeser RM, Jin J. Ultramicroscopy. 2007;107:329. doi: 10.1016/j.ultramic.2006.09.001. [DOI] [PubMed] [Google Scholar]
- 5.Danev R, Nagayama K. Ultramicroscopy. 2001;88:243. doi: 10.1016/s0304-3991(01)00088-2. [DOI] [PubMed] [Google Scholar]
- 6.Danev R, Okawara H, Usuda N, Kametani K, Nagayama K. Journal of Biological Physics. 2002;28:627. doi: 10.1023/A:1021234621466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Danev R, Nagayama K. Journal of the Physical Society of Japan. 2004;73:2718. [Google Scholar]
- 8.Nagayama K. European Biophysics Journal with Biophysics Letters. 2008;37:345. doi: 10.1007/s00249-008-0264-5. [DOI] [PubMed] [Google Scholar]
- 9.Schroeder RR, Barton B, Rose H, Brenner G. Microscopy and Microanalysis. Ft. Lauderdale Florida: 2007. Contrast enhancement by anamorphotic phase plates in an aberration-corrected TEM. [Google Scholar]
- 10.Danev R, Nagayama K. Journal of Structural Biology. 2008;161:211. doi: 10.1016/j.jsb.2007.10.015. [DOI] [PubMed] [Google Scholar]
- 11.Beleggia M. Ultramicroscopy. 2008;108:953. doi: 10.1016/j.ultramic.2008.03.003. [DOI] [PubMed] [Google Scholar]
- 12.Fujiyoshi Y, Mizusaki T, Morikawa K, Yamagishi H, Aoki Y, Kihara H, Harada Y. Ultramicroscopy. 1991;38:241. [Google Scholar]
- 13.Reimer L. Transmission Electron Microscopy: Physics of Image Formation and Microanalysis. four ed. vol. 36. Springer, Berlin, Heidelberg, New York: Springer Series in Optical Sciences; 1997. [Google Scholar]
- 14.Wanner M, Bach D, Gerthsen D, Werner R, Tesche B. Ultramicroscopy. 2006;106:341. doi: 10.1016/j.ultramic.2005.10.004. [DOI] [PubMed] [Google Scholar]
- 15.Wang LG, Bose PS, Sigworth FJ. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:18528. doi: 10.1073/pnas.0608714103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zemlin F, Weiss K, Schiske P, Kunath W, Herrmann KH. Ultramicroscopy. 1978;3:49. [Google Scholar]
- 17.Christenson KK, Eades JA. Ultramicroscopy. 1988;26:113. [Google Scholar]
- 18.Yamaguchi M, Danev R, Nishiyama K, Sugawara K, Nagayama K. Journal of Structural Biology. 2008;162:271. doi: 10.1016/j.jsb.2008.01.009. [DOI] [PubMed] [Google Scholar]
- 19.Downing KH, Glaeser RM. Ultramicroscopy. 2008;108:921. doi: 10.1016/j.ultramic.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Meyer RR, Kirkland A. Ultramicroscopy. 1998;75:23. [Google Scholar]
- 21.Meyer RR, Kirkland AI, Dunin-Borkowski RE, Hutchison JL. Ultramicroscopy. 2000;85:9. doi: 10.1016/s0304-3991(00)00046-2. [DOI] [PubMed] [Google Scholar]
- 22.Yonekura K, Braunfeld MB, Maki-Yonekura S, Agard DA. Journal of Structural Biology. 2006;156:524. doi: 10.1016/j.jsb.2006.07.016. [DOI] [PubMed] [Google Scholar]
- 23.Langmore JP, Smith MF. Ultramicroscopy. 1992;46:349. doi: 10.1016/0304-3991(92)90024-e. [DOI] [PubMed] [Google Scholar]
- 24.Putnam CD, Hammel M, Hura GL, Tainer JA. Quarterly Reviews of Biophysics. 2007;40:191. doi: 10.1017/S0033583507004635. [DOI] [PubMed] [Google Scholar]
- 25.Jakubowski U, Baumeister W, Glaeser RM. Ultramicroscopy. 1989;31:351. [Google Scholar]
- 26.Glaeser RM, Downing KH. Microscopy and Microanalysis. 2004;10:790. doi: 10.1017/s1431927604040668. [DOI] [PubMed] [Google Scholar]
- 27.Downing KH, McCartney MR, Glaeser RM. Microscopy and Microanalysis. 2004;10:783. doi: 10.1017/s143192760404067x. [DOI] [PubMed] [Google Scholar]
- 28.Kuvichkin V, Danev R, Shigematsu H, Nagayama K. Molecular Membrane Biology. doi: 10.1007/s00232-008-9146-0. in press. [DOI] [PubMed] [Google Scholar]
- 29.El-Bez C, Adrian M, Dubochet J, Cover TL. Journal of Structural Biology. 2005;151:215. doi: 10.1016/j.jsb.2005.07.001. [DOI] [PubMed] [Google Scholar]