Improving the Statistics of Quantitative Ultrasound Techniques with Deformation Compounding: An Experimental Study

Abstract

Many quantitative ultrasound (QUS) techniques are based on estimates of the radio frequency (RF) echo signal power spectrum. Historically reliable spectral estimates required spatial averaging over large regions of interest (ROIs). Spatial compounding techniques have been used to obtain robust spectral estimates for data acquired over small regions of interest. A new technique referred to as “deformation compounding” is another method for providing robust spectral estimates over smaller regions of interest. Motion tracking software is used to follow an ROI while the tissue is deformed (typically by pressing with the transducer). The deformation spatially reorganizes the scatterers so that the resulting echo signal is decorrelated. The RF echo signal power spectrum for the ROI is then averaged over several frames of RF echo data as the tissue is deformed, thus undergoing deformation compounding. More specifically, averaging spectral estimates among the uncorrelated RF data acquired following small deformations allows reduction in the variance of the power spectral density estimates and thereby improves accuracy of spectrum-based tissue property estimation. The viability of deformation compounding has been studied using phantoms with known attenuation and backscatter coefficients. Data from these phantoms demonstrates that a deformation of about 2% frame-to-frame average strain is sufficient to obtain statistically-independent echo signals (with correlations of less than 0.2). Averaging 5 such frames where local scatterer reorganization has taken place due to mechanical deformations reduces the average percent standard deviation among power spectra by 26% and averaging 10 frames reduces the average percent standard deviation by 49%. Deformation compounding is used in this study to improve measurements of backscatter coefficients. These tests show deformation compounding is a promising method to improve the accuracy of spectrum-based quantitative ultrasound for tissue characterization.

Introduction

Quantitative ultrasound can provide substantially more information than that contained in traditional B-Mode images, which display only the amplitudes of envelope detected and log-compressed echo signals. Different tissues exhibit different ultrasonic wave propagation phenomena, and these can be characterized by ultrasound attenuation and by properties of the scatterers such as shape, size and number density. Information related to the sources of scattering in tissue can be derived from the echo-signal spectrum as shown by Lizzi, et al (1983; 1997b; 2006), and Insana, et al., (1990; 1991). The measured frequency dependence of scattering has been used to estimate the effective scatterer diameter (Wagner et al, 1987; Insana et al, 1990; Lizzi et al, 1997a; Lu et al, 1999; Oelze and O’Brien, 2002; Romijn et al, 1989a), scatterer spacing (Fellingham and Sommer, 1984; Wear et al, 1993; Varghese and Donohue, 1993, 1994), and scatterer number density (Wagner et al, 1983; Sleefe and Lele, 1988). In many cases these scattering properties have been useful for monitoring and diagnosing disease. For example, it has been demonstrated that estimates of effective scatterer diameter can track changes in the size of glomeruli and afferent and efferent arterioles (Insana et al, 1991, 1992, 1995), and can potentially be used to detect kidney disease (Garra et al, 1994; Hall et al, 1996). Another study (Oelze et al, 2002, 2004) observed significant differences in the effective scatterer diameter found from echo data from a breast-tumor model compared to sizes from non-malignant breast tissues. Similarly other studies suggest that the effective scatterer diameter in liver hemangiomas are somewhat larger than scatterer sizes in the surrounding liver parenchyma (Liu, 2007). Effective scatterer diameter estimation can also be applied to cancellous bone (Padilla et al, 2006). Other studies have also used backscatter estimation in tumor diagnosis in animals (Romijn et al, 1989b).

A common difficulty encountered in imaging an effective scatter diameter, or other parameters derived from spectral data, is the large variance caused by statistical fluctuations in echo signals from random media. Elevational and angular compounding (Gerig et al, 2004b) have been shown to improve signal to noise ratios and to reduce spectral variance in effective scatter diameter imaging, but this approach is most applicable in isotropic media. Here we introduce a new method to reduce statistical uncertainties when determining tissue properties. This method is called “deformation compounding” because multiple statistically-independent realizations of the local RF echo signals, and thereby the average local power spectra from these echo signals, are achieved by applying varying degrees of applied tissue deformations. Deformation compounding can be combined with other methods of compounding but is of particular interest for small regions of interest (ROI’s) that are isolated from a heterogeneous background or otherwise can not support other methods of spatial compounding.

Methods and Materials

Deformation compounding is a method to reduce the variance in power spectral density (PSD) estimates. Often, PSD estimates are then used in the process of estimating another parameter. As an example, PSD estimates are applied in this manuscript to measurements of the ultrasonic backscatter coefficient of samples. However, the deformation compounding approach is applicable for many quantitative ultrasound measurements using pulse-echo data where power spectral estimation is needed.

Overview of Deformation Compounding

The echo signals in this study are assumed to arise from ultrasonic scattering due to a large number of small (relative to the insonification wavelength) inhomogeneities within a resolution cell. The specific realization of a (noise free) echo signal depends on the spatial distribution of these scatterers and their individual scattering amplitudes.

We model the echo signal, r(t), as a component, r̃(t), that depends on a specific realization of scatterers and their spatial locations plus additive electronic noise n(t) :

$$r(t)=\tilde{r}(t)+n(t)$$ (1)

where

$$\tilde{r}(t)=h(t)*z(x,t)$$ (2)

is the noise-free echo signal, h(t) is the system impulse-response function, z(x, t) is the spatial distribution of scattering sources encompassed by the acoustic pulse at time t and * is the convolution operator. The electronic noise is typically modeled as white (amplifier) noise with zero mean. We assume, for this analysis, that the electronic signal to noise ratio (SNR) is reasonably high (e.g., above 20dB) so that electronic noise is a relatively small component of the total signal.

With any given medium, as the position, x, varies, z(x, t) can be mathematically treated as a stochastic function to account for the randomness in the spatial distribution of scatterers and their individual scattering amplitudes.

One realization of the periodogram of r(t) for any given angular frequency ω can be written as follows:

$$\begin{array}{cc}|R(\omega ){|}^2\hfill & ={\left|\tilde{R}(\omega )+N(\omega )\right|}^2\hfill \\ \hfill & ={|H(\omega )Z(x,\omega )+N(\omega )|}^2\hfill \end{array}$$ (3)

where |·| stands for the magnitude of a complex number, and R(ω), R̃(ω), H(ω), Z(ω, x) and N(ω) are Fourier Transforms of r(t), r̃(t), h(t), z(x, t) and n(t) at the angular frequency ω, respectively.

As Eqn. (3) shows, the spectral density provides a measure of the frequency content of a single realization of the RF echo signal. Any spectral-based analysis of the echo signal properties, such as the acoustic backscatter coefficient for the medium (Madsen et al, 1984), requires averaging a large number of realizations of the spectral density function to generate the expectation value of the echo signal power spectral density (PSD) from the medium. The statistical nature of the scatterer locations results in the probability density function of the echo amplitude following a Rayleigh distribution and the PSD of the echo intensity obeying an exponential distribution (Wagner et al, 1987; Lizzi et al, 1997b). It is common to assume that, over a limited spatial extent, the random scattering process is stationary and that sampling the process (windowing the data) in time or in space are equivalent. Therefore, a common approach to improve the accuracy of PSD estimation is to average periodogram estimates using several statistically equivalent, but uncorrelated, echo signals. Although Bartlett’s method or Welch’s method are commonly used to obtain the average of several periodogram estimates, these methods require spectral estimation over larger regions of interest if the objective is to maintain spectral resolution of the single periodogram. Eqn. (3) shows that there are two random components in the signal — the impedance distribution, z(x, t), and the electronic noise, n(t). The random nature of the scatterer positions and amplitudes results in fluctuations in the power spectral density when interrogating the same medium at slightly different locations or from different source-to-scatterer orientations. Thus, the PSD can be estimated by obtaining several uncorrelated observations of the echo signal with new realizations of z(x, t).

The methods proposed here are conceptually similar to those used in the ultrasound spatial compounding literature (Trahey et al, 1986; O’Donnell and Silverstein, 1988; Li and O’Donnell, 1994; Gerig et al, 2004a) where spatial translations or rotations of an object being imaged have been used to change the scatterer distribution, z(x, t), as viewed by the interrogating pulse, in an effort to sufficiently decorrelate the signal allowing independent realizations of echo signal data to be averaged. However, as an alternative approach in this study, we attempted to slightly deform the tissue to spatially redistribute these scatterers in order to obtain more independent realizations of the echo signal from a medium containing randomly positioned scatterers. Besides redistribution of scatterers, when soft scatterers deform, as their surrounding media are deformed, changes may occur in the scattering function, as implied by Insana et al (Insana et al, 2001). We avoid this by limiting deformations to less than 20%

In this study, we used the correlation between two time domain echo signals, r₁ and r₂, before and after deformation of the sample to evaluate the degree of change in the signal from a region. The correlation coefficient is given by

$${\rho }_{r_1,r_2}=\frac{{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^{\ell }}[r_1(i,j)r_2(i,j)]}{\sqrt{{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^{\ell }}{[r_1(i,j)]}^2}\sqrt{{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^{\ell }}{[r_2(i,j)]}^2}}$$ (4)

where ρ is the normalized correlation coefficient and i and j are indices for the two-dimensional region of windowed RF echo data (which includes M temporal samples along a line of echo data and ℓ lines of data in the windowed data). The correlation coefficient is a standard metric to determine, for example, the degree of change in a speckle pattern to assess the effectiveness of spatial compounding in B-mode ultrasound (Trahey et al, 1986; O’Donnell and Silverstein, 1988). More specifically, low normalized correlation values (e.g. ρ <0.2) are an indicator for “significant” signal decorrelation from changes in the underlying scatterer distribution. In this study, a correlation value of 0.2 in the echo signal from a deformed region was empirically chosen to determine that sufficiently independent realizations of r₁ and r₂ have been achieved.

Once the power spectra of decorrelated echo data from the same type of scatterer are averaged, there is a reduction in the variance of the average power spectrum. The larger the number of uncorrelated echo signals used to estimate the power spectrum, the lower the variance in the power spectral estimates (Bendat and Piersol, 2000; Liu and Zagzebski, 2010).

Backscatter Coefficient Determinations

In this study, backscatter coefficients are measured using a reference phantom method (Yao et al, 1990). Ratios of the echo signal power spectrum from a region of interest (ROI) in a sample to the power spectrum acquired from the same depth in a well-characterized reference phantom are used to account for system dependencies of the echo data. The general equation for backscatter coefficient estimations in a sample when using the reference phantom method were reported by Yao et al (1990):

$$\frac{R_s(\omega )}{R_{\mathit{\text{ref}}}(\omega )}=\frac{{\sigma }_s(\omega )}{{\sigma }_{\mathit{\text{ref}}}(\omega )}{e}^{-4d({\alpha }_s(\omega )-{\alpha }_{\mathit{\text{ref}}}(\omega ))}$$ (5)

where R(ω) is the echo signal power spectrum, σ is the backscatter coefficient, d is the depth at the ROI center, α is the attenuation coefficient, ω is the angular frequency, and the subscripts s and ref refer to the sample and the reference phantom, respectively. The speed of sound is assumed to be the same in both the sample and the reference phantom.

Using the known values of backscatter and attenuation in the reference phantom, depth dependent changes in the power spectra ratio can be estimated to obtain the sample’s attenuation coefficient. Then Eq. 5 can be solved directly for the backscatter coefficient of the sample by using the ratio of the echo signal power spectrum within the ROI to that from the reference phantom.

Phantoms

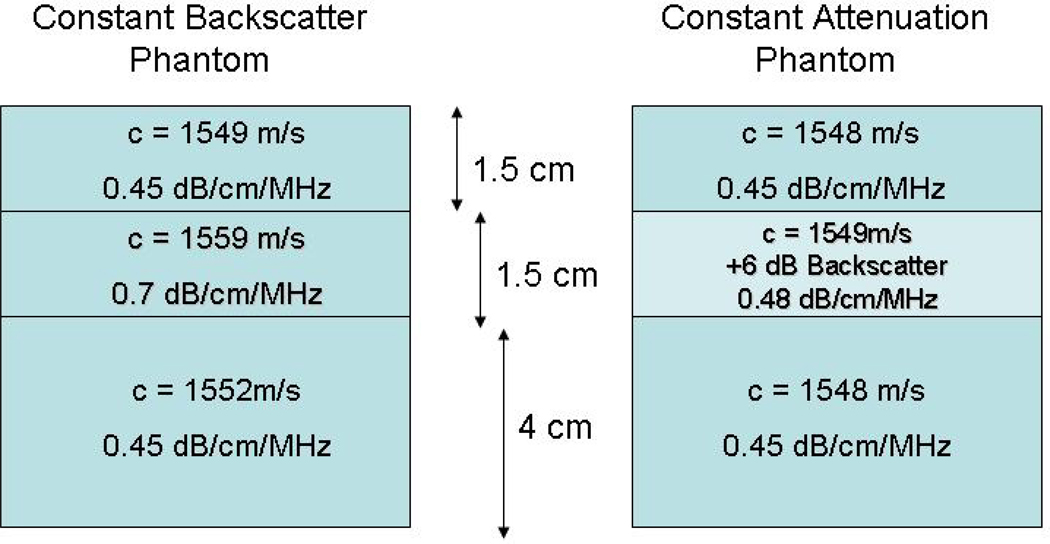
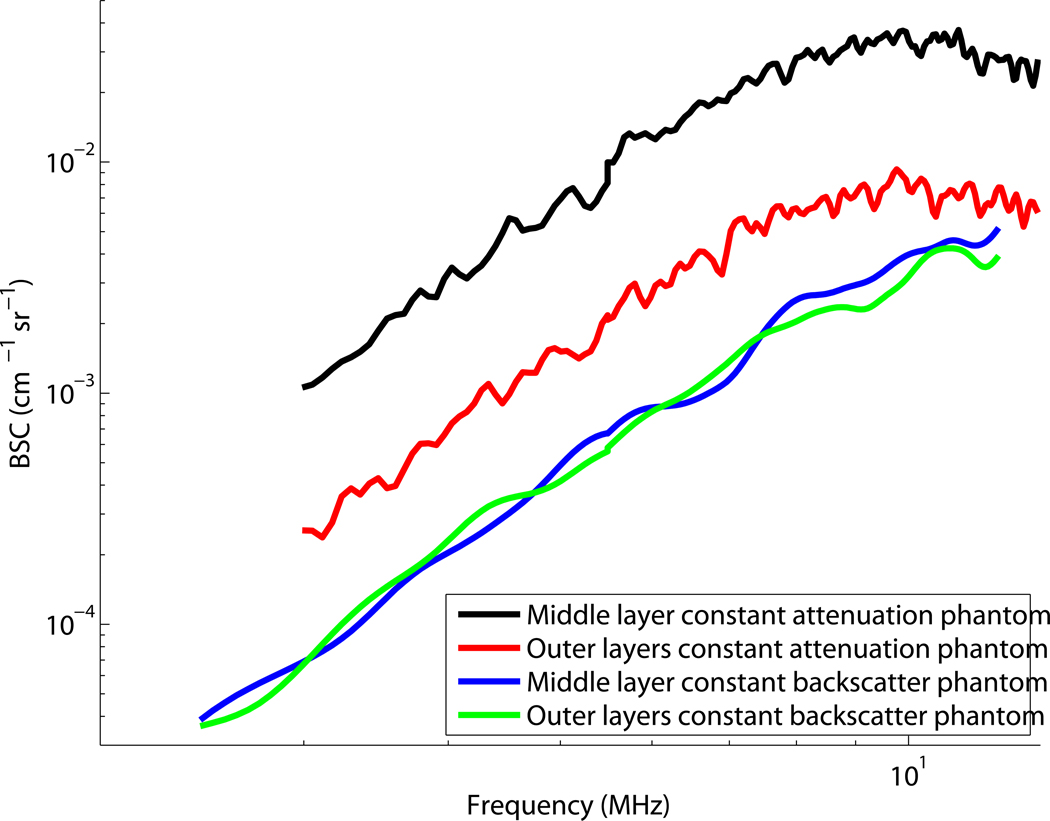
Three phantoms (two “layered” phantoms diagrammed in Fig. 1 and a homogeneous phantom) were used to test deformation compounding. All three phantoms have glass bead scatterers and were made in the University of Wisconsin phantom lab. Speed of sound, attenuation, and backscatter were measured using techniques described by Madsen et al (1986) and Chen et al (1990). The first layered phantom, the “constant backscatter phantom”, contains a broad distribution of glass bead diameters (5–30 µm) in gelatin and consists of three layers with equivalent backscatter and speed of sound (1552 m/s). The attenuation of the upper and lower layers is 0.45 dB/cm/MHz. The inner layer has a higher attenuation (0.67 dB/cm/MHz) than the outer layers. The second layered phantom, the “constant attenuation phantom”, contains a narrower distribution of larger (45–53 µm) glass beads in gelatin and consists of three layers with equivalent attenuation (0.45 dB/cm/MHz) and speed of sound (1549 m/s). The inner layer has a backscatter level 6 dB higher than that of the outer layers. The backscatter coefficients as a function of frequency are plotted in Fig. 2 for both phantoms. Each curve in this figure represents the backscatter measurements for the specific layers of the constant backscatter and constant attenuation phantoms. The BSC was measured using a rigorous method (Chen et al, 1990) that provides system-independent backscatter measurements on an absolute scale. The homogeneous phantom is an oil-in-gelatin dispersion that has approximately 0.5 dB/cm/MHz attenuation and 1540 m/s speed of sound.

Figure 1.

Diagram of the 3 layer phantoms made in the UW phantom lab.

Figure 2.

Backscatter coefficients for the layered phantoms sketched in Fig. 1.

Data Acquisition and Processing

Data were acquired from tissue mimicking phantoms described above using a Siemens SONOLINE Antares (Siemens Medical Solutions USA, Inc, Malvern,PA) clinical ultrasound system with two linear array transducers pulsed at 6MHz (Siemens VFX9-4) and 9MHz (Siemens VFX13-5), respectively. Frames of RF echo data were acquired both in the Axius Direct Ultrasound Research Interface (URI) mode and EI (elasticity imaging; eSie Touch, Siemens Medical Solution USA, Inc) mode. Details of the URI and the Siemens Antares system are given by Brunke et al (2007). Varying amounts of external strain were applied to the phantoms for each data set by pressing with the transducer (mounted in a mechanical stage).

For each set of data, an ROI was chosen for an initial frame. The ROI was tracked between frames using motion tracking software (Jiang and Hall, 2007). As the phantom (or tissue) is deformed the position of specific scatterers changes from one frame to the next. This change in position is the displacement of the scatterers due to phantom (or tissue) deformation. “Motion tracking” software can track where the scatterers move to (estimating their displacement vector) from the previous frame. The displacement estimates for the ROI were not used to compensate for motion (warp the RF echo data back to its original coordinates) but only to determine where that ROI had moved for cross correlation with the appropriate data. The correlation between a “pre-deformation” RF echo signal and a sequence of post-deformation RF echo signals in an ROI was calculated between data frames. When the correlation was small (we chose ρ < 0.2) the power spectrum of the echo signals from the post-deformation ROI was calculated. As discussed above, low correlation values merely demonstrate that statistically-indepedent echo signals were achieved due to scatterer reorganizations under mechanical deformations. Then, that post-deformation echo signal became the new “pre-deformation” signal and the process was repeated through the entire sequence of deformed RF echo signal data. When that process was complete, the resulting power spectra were averaged.

In most cases, unless specifically stated otherwise, the window size was 3.85mm by 2.89mm (containing approximately 15 uncorrelated A-lines). Power spectra were computed using a Hann window and the “periodogram” function in MATLAB (The MathWorks, Inc., Natick, Massachusetts).

Experiments and Results

Three experiments and their results are described in this section to validate the proposed deformation compounding method. The first test was to verify that correlation coefficient values between the pre- and post-deformation echo signals is indeed a good indicator of local scatterer reorganizations due to mechanical deformations. The second test aimed at comparing standard deviations of PSD estimates before and after the deformation compounding method was being applied. The third experiment compared the performance of the proposed deformation compounding method to the well-established reference phantom method (Yao et al, 1990) for backscatterer coefficient (BSC) measurements. In all three experiments, RF echo data from the tissue-mimicking phantoms described above were used.

Strain induced decorrelation

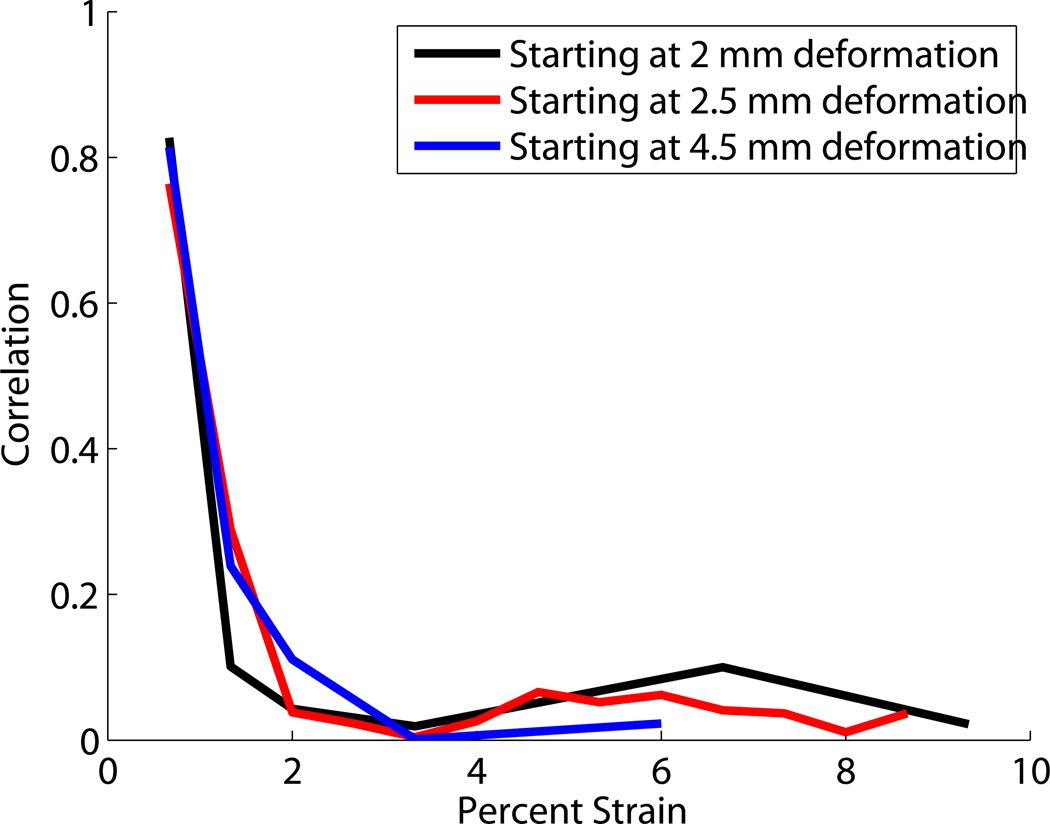
The amount of strain needed for RF echo data in a single ROI to decorrelate was tested using the Antares VFX9-4 transducer. The transducer was attached to a vertical translation stage and brought into contact with a soft homogeneous phantom. Single frames of RF echo data were taken, each after a vertical translation of 0.5mm, for a total of 10mm of deformation on an initially 70mm tall phantom. A window size of 3.85mm by 2.89mm (approximately 15 uncorrelated A-lines) was chosen. Motion tracking software was used to follow a single ROI from one data frame to the following deformed frames. The correlation between the RF echo signals for a single ROI was calculated between an initial frame and one of the following frames with increasing deformation using Eqn. 4. Figure 3 shows the correlation between frames as a function of axial strain for a centrally located ROI. The plot shows the results for initial “reference” frames at a variety of initial deformations. The percent strain in the plot is that relative to the starting frame not the total applied strain. Zero strain, in this case, is based on the difference in strain between the chosen “reference” frame, which is not necessarily in an undeformed state, and the more deformed (“target”) frame. The RF echo signals are decorrelated (ρ <0.2) when the axial deformation exceeds about 2% strain.

Figure 3.

A plot of the correlation coefficient between an initial RF echo ROI and successive observations of the ROI having undergone deformation. Note that the RF echo signals from the same “piece of phantom” are cross correlated (the motion of the ROI during deformation is tracked).

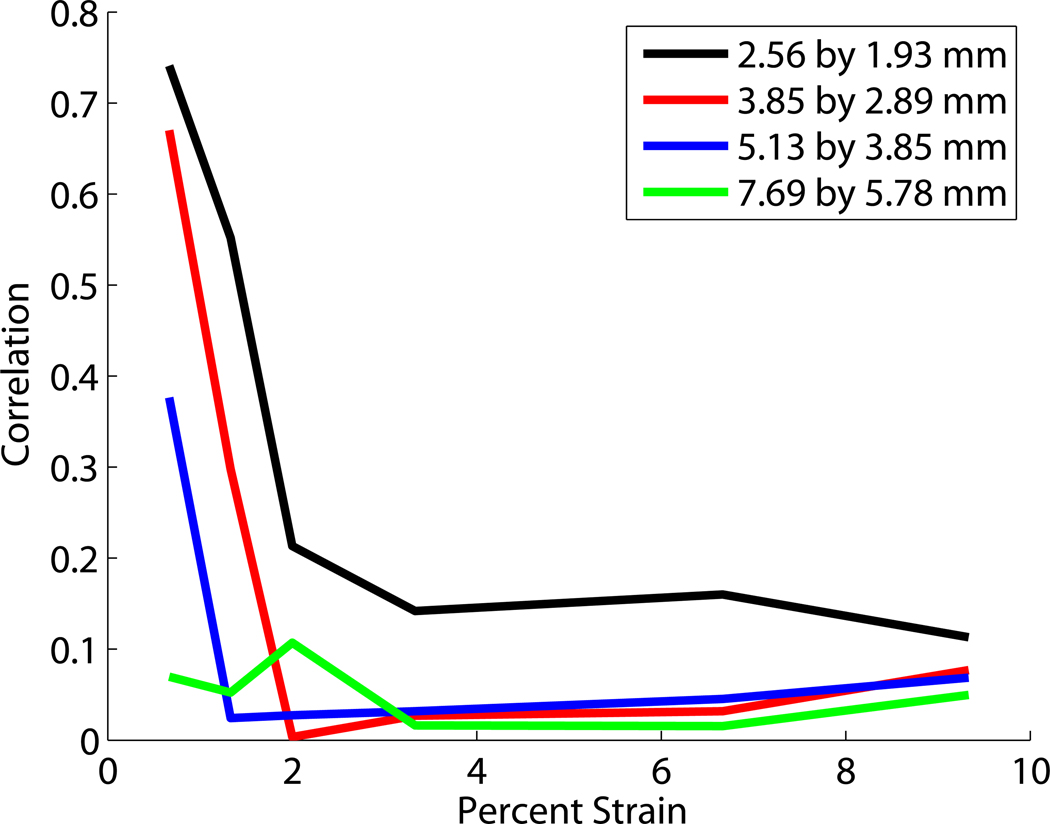
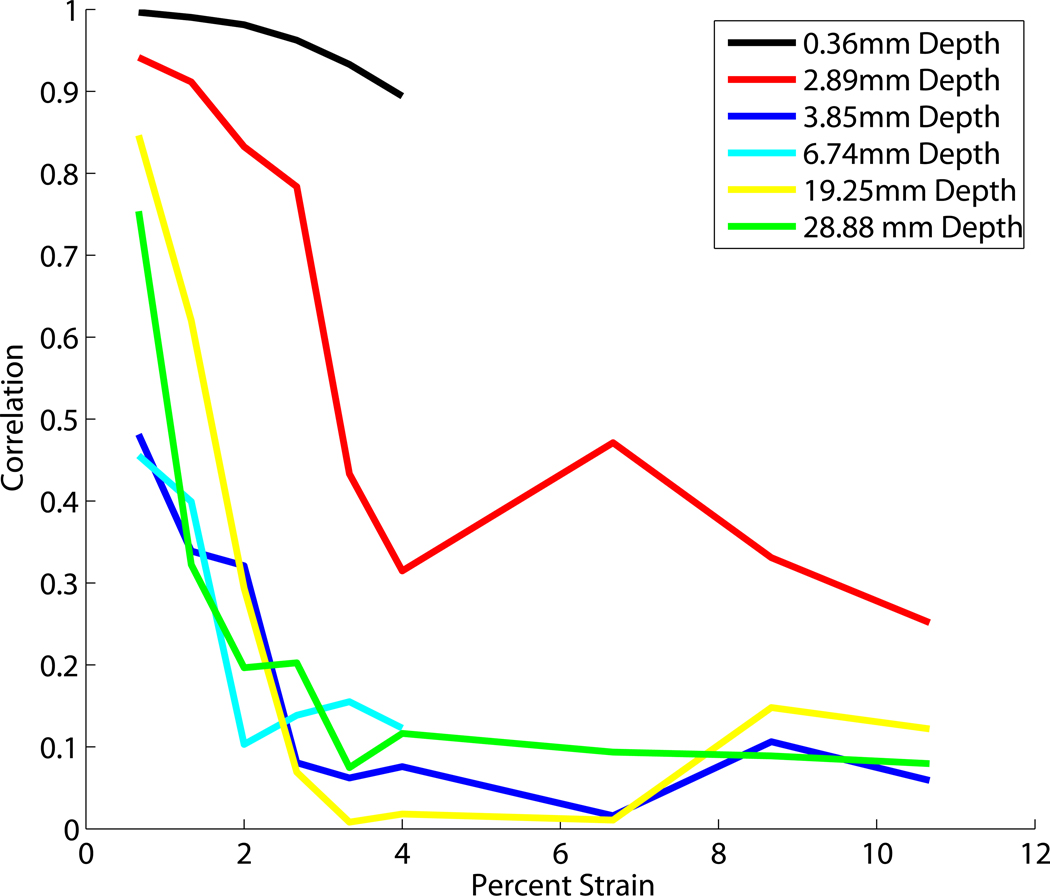
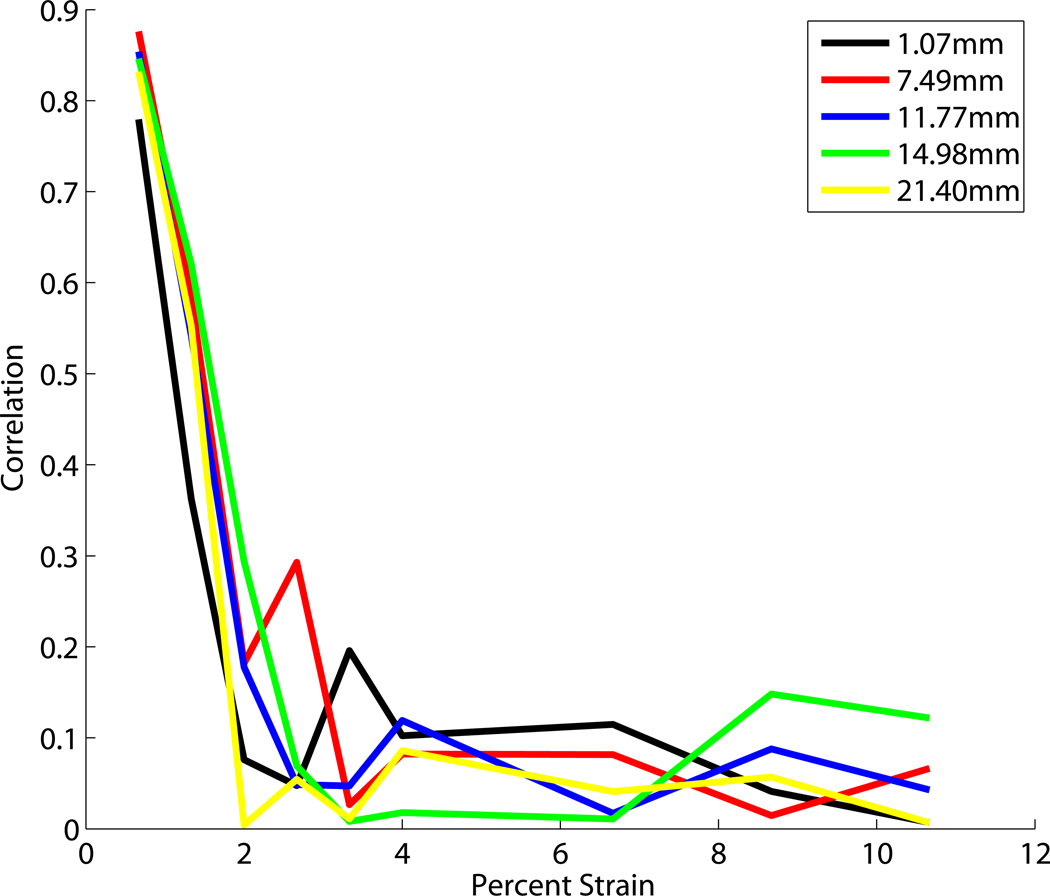
Figure 4 shows correlation verses strain for a variety of ROI sizes and positions. Figure 4a shows the RF echo signal correlation as a function of deformation for varying ROI sizes. The larger ROI’s have lower correlations even for small strains. The echo signal decorrelation that occurs when scatterer positions are redistributed depends on their change in position (δd) relative to the wavelength (λ) of the probing ultrasound pulse. Strain in the medium is a measure of relative displacement. Consider uniform strain (in the direction of the acoustic beam) occurring in a medium represented by an echo signal data segment selected with a rectangular (temporal) window. For window length T corresponding to a spatial length D, the strain is ε = 2 δd/D and the maximum displacement within the window is δd_max. If the gate duration is half as long, the strain remains the same but the maximum displacement within the window becomes δd_max/2 (fewer wavelengths or a smaller fraction of a wavelength). Here the 7.9mm × 5.78mm ROI decorrelated to less than 0.1 when the strain was less than 1%. For very small ROIs the RF does not decorrelate as rapidly.

Figure 4.

Correlation compared to percent strain for a variety of (a) window sizes, (b) window depth, (c) window lateral position from the left.

Figure 4b shows the RF echo signal correlation as a function of deformation for varying ROI depths. The signal does not decorrelate rapidly close to the transducer (within the first few millimeters). This is partially due to the friction between the transducer and phantom surface preventing the scatterers from rearranging as the phantom is deformed. Aside from this, depth does not affect the strain-echo signal correlation relationship.

Figure 4c shows the RF echo signal correlation as a function of deformation for varying lateral position of the ROI. For the linear array transducers used in this work, the lateral position in the RF echo field does not affect the rate of signal decorrelation. These data also indicate that deformation compounding can be accomplished with relatively little applied strain. For a total change in strain of 10% there are 6 frames with correlations below 0.2. For these low correlations the data is sufficiently decorrelated to improve the signal to noise ratio in the power spectrum estimates, as shown in the next section.

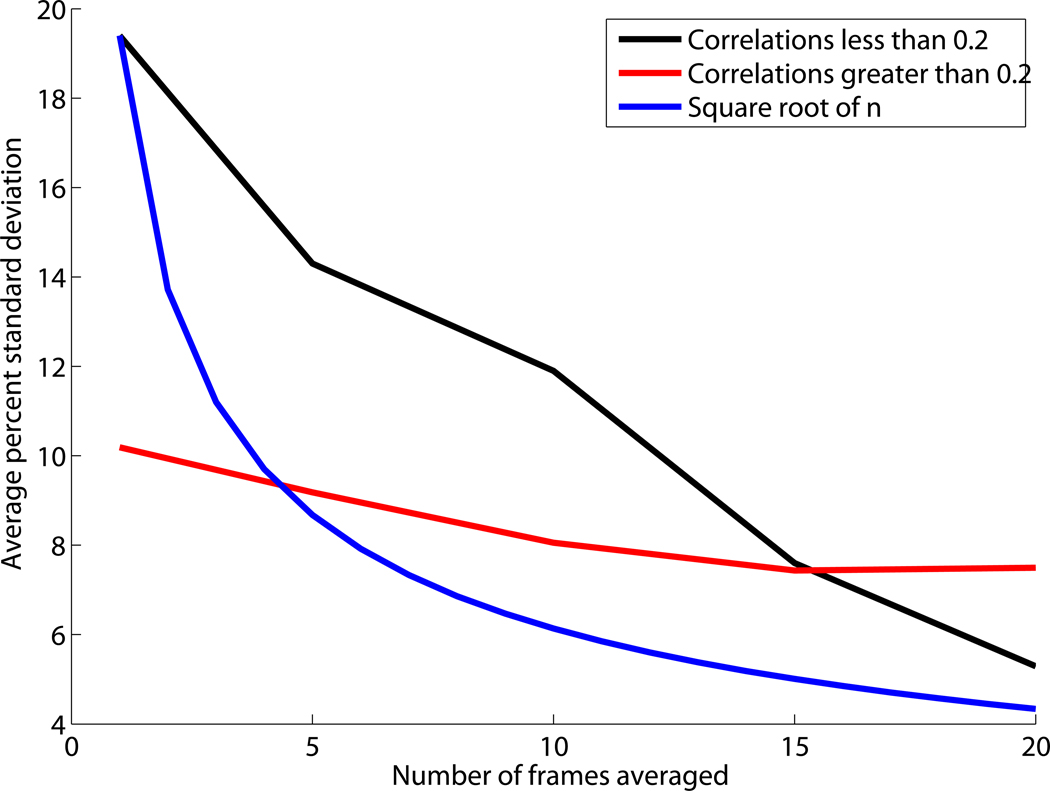
Deformation compounding can significantly reduce the standard deviation of echo signal power spectrum estimates for regions containing randomly positioned scatterers. The reduction in standard deviation by averaging multiple observations is proportional to the one over the square root of the number, n, of statistically independent measurements. In our results the reduction is less than $1/\sqrt{n}$ because the data frames are not completely statistically independent. Although the frames from which the data are averaged are nearly decorrelated (i.e., correlation < 0.2), they still have some residual correlation. (This residual correlation between frames is essential for our motion tracking of the ROI between frames.) Because there is some small correlation between the frames in deformation compounding the reduction in the standard deviation of the power spectrum estimates is less than the ideal $1/\sqrt{n}$. The deviation from $1/\sqrt{n}$, where n is the number of frames, depends on the level of correlation between frames.

When averaging spectral data under large values of n the residual correlation will not impact the result as much, and improvement due to deformation compounding will approach the ideal. As can be seen in figure 6 when the correlation between frames is larger (ρ > 0.5) the deviation from the ideal $1/\sqrt{n}$ is greater. Both combinations of data (with correlations > 0.5 and < 0.2) have variance reduction approaching $1/\sqrt{n}$ as the number of frames averaged becomes large (20). Despite the slower than ideal rate of improvement in spectral estimation there is still a significant reduction in the standard deviation of power spectral estimates using deformation compounding, dropping nearly a factor of 4 when comparing data for a single frame to data from 20 averaged frames.

Figure 6.

Average percent standard deviation verses the number of frames averaged using correlations of less than 0.2, usually near 0.1, average percent standard deviation verses number of frames averaged using correlations of greater than 0.2, usually near 0.5, and the initial average percent standard deviation divided by the square root of number averaged.

Backscatter measurements

Backscatter coefficient measurements were made on the layer phantoms using the reference phantom method and deformation compounding. For each phantom the echo signal power spectrum was computed for an ROI and data from a reference phantom were used to account for system dependent factors (Yao et al, 1990). The reference phantom was not deformed, but elevational compounding (with 20 uncorrelated frames) was used to improve the signal to noise ratios in the reference signal spectrum. The backscatter and attenuation for the reference had been carefully measured previously (Fig. 2) using independent measurements.

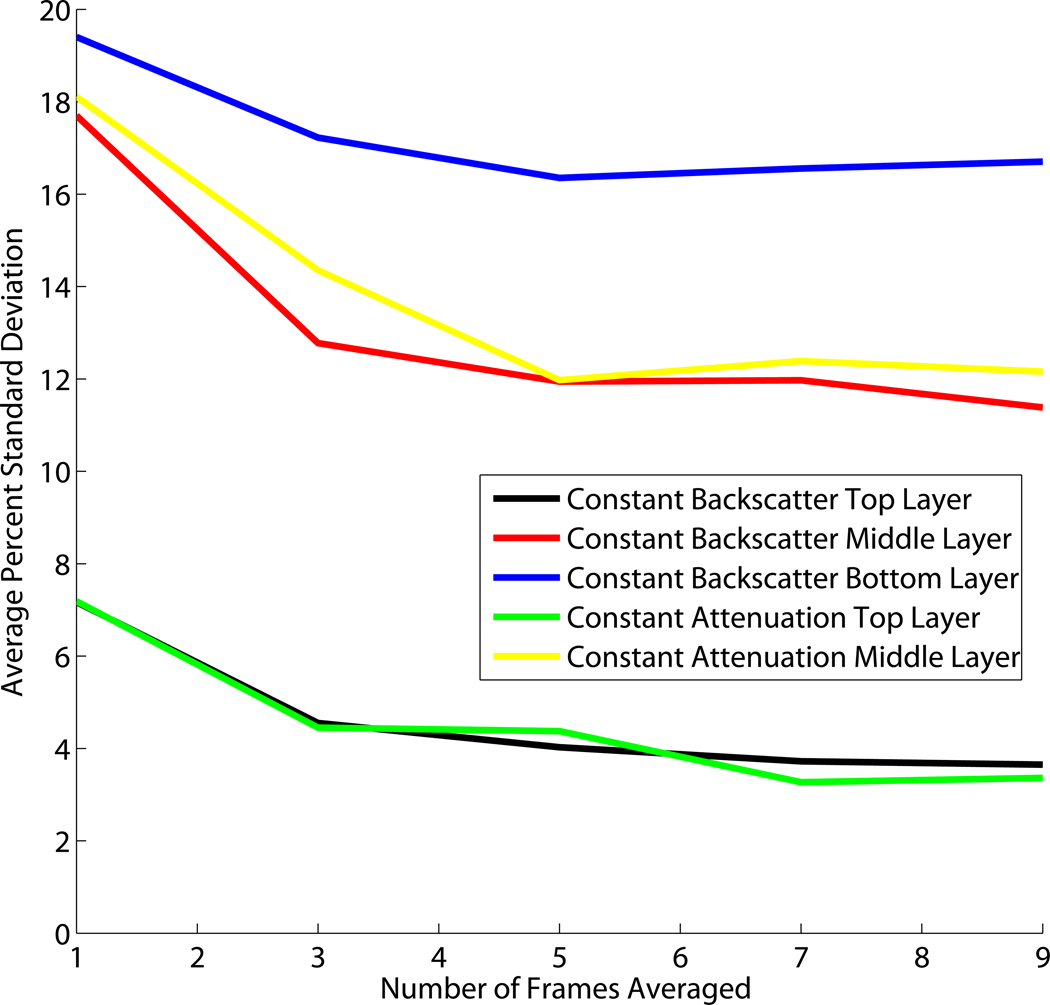
Measurements of the backscatter coefficients were made for all layers of both the constant attenuation and constant backscatter phantoms. These measurements were made with a single ROI of 5mm by 5mm, and using deformation compounding over 3, 5, 7, and 9 frames. Figure 7 shows the average percent standard deviation of the backscatter coefficients for each of these measurements. In all cases deformation compounding reduces the noise in the backscatter measurements. The deeper layers show a higher fractional standard deviation in power spectral density estimates since there is less signal with increasing depth and electronic noise contributes more to the spectral estimate uncertainty.

Figure 7.

Average percent standard deviation in the backscatter measurements for each phantom layer compared to the number of power spectra averaged using deformation compounding. The averaged frames have have correlation values less than 0.2.

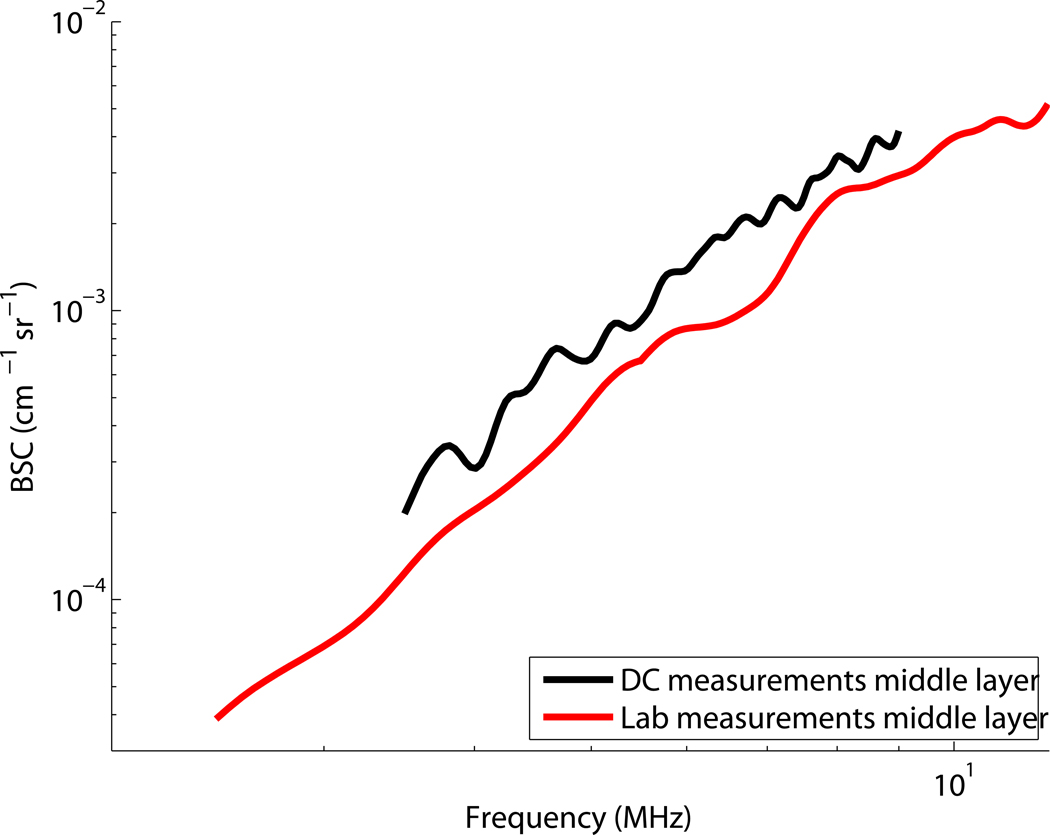
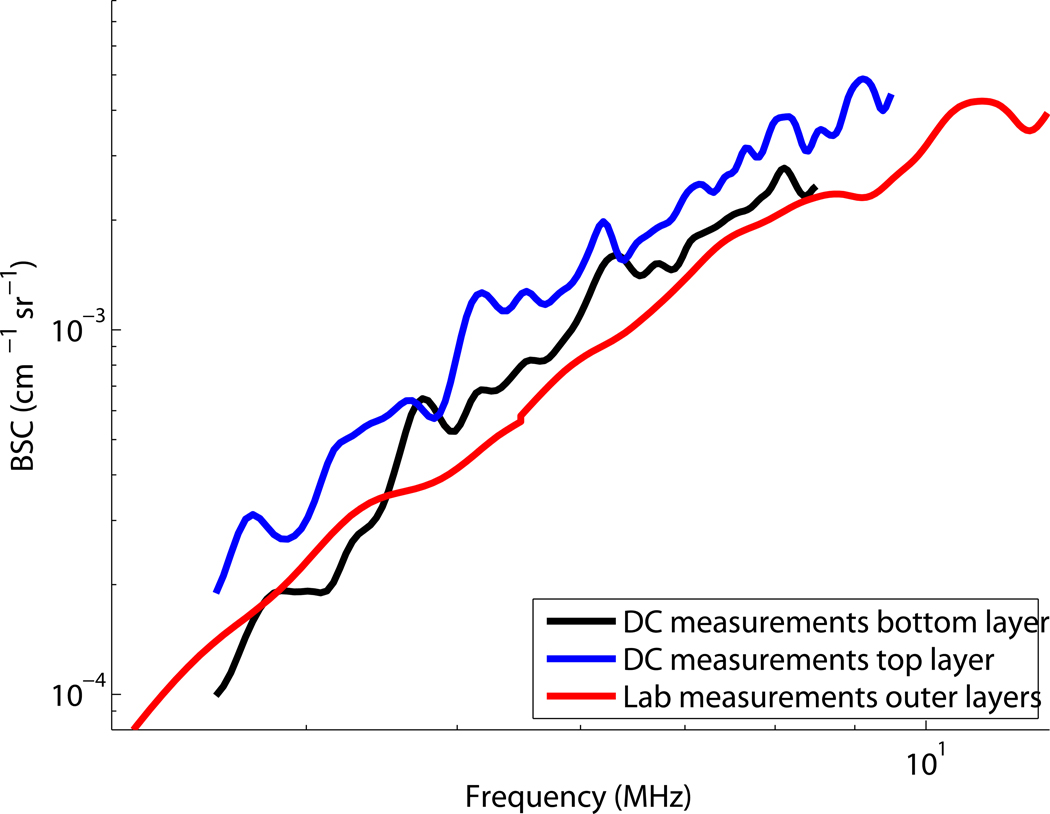
Figure 8 shows a graph of the backscatter coefficients obtained with deformation compounding (with 9 frames) compared to the independently measured values (shown in fig. 2). In (a) BSC measurements are compared for the middle layer of the constant backscatter phantom. In (b) the measurement results of the outer layers of the constant backscatter phantom are compared. The independent lab-based measurement uses a sample of the mixture poured at the same time as the phantom. Because the phantom material for those two layers is the same, only one measurement is made. With deformation compounding we scan the phantom with an imaging system and are making measurements at those two distinct depths. In (c) the BSC of outer layers of the constant attenuation phantom are shown. Here only the top layer is measured with deformation compounding. Here only the top layer is measured with deformation compounding. Last, in (d) the BSC for the middle layer of the constant attenuation phantom is shown.

Figure 8.

Comparison of backscatter measurements using deformation compounding to backscatter measurements using laboratory methods Chen et al (1990) for the: (a) middle layer of the “constant backscatter phantom,” (b) top and bottom layers of the “constant backscatter phantom,” (c) middle layer of the “constant attenuation phantom,” (d) top layer of the “constant attenuation phantom”.

Discussion and Conclusions

Deformation compounding is an effective method to reduce variance in tissue property measurements derived from echo signal data. It is particularly useful for estimates of tissue properties in small areas where other methods of spatial averaging are not viable. Measurements using deformation compounding are accurate, and there is a marked reduction in estimate variance compared to the case of no compounding. This improvement is not proportional to the square root of the number of frames averaged because of the residual correlation between frames when using deformation compounding. It is possible to see improvement in parameter estimate statistics for relatively small strains since power spectral estimates from individual frames can be effectively averaged when there is only 2 % frame to frame strain.

When using deformation compounding, the power spectra should be monitored as a function of strain to assure there is no notable change in overall frequency dependence of scattering, such as reported by Insana et al (2001). This is more important when a large (incremental) strain range is used. With large strains the scatterers themselves may be deformed, in addition to being rearranged, which would effect their scattering properties and therefore some tissue property estimates (Insana et al, 2001). For all of our data the power spectra were monitored and showed negligible shape variation due to strain. For example, correlations were calculated between the initial frame and subsequent deformed frames for an ROI in the uniform phantom. The mean correlation was 0.98 and the standard deviation between correlations was 0.007.

Deformation compounding is a promising method of averaging echo signal power spectra for small regions of interest, and further tests on soft scatterers and clinical data are called for. It is potentially an excellent tool to isolate small regions of interest for acoustic property estimation in heterogeneous tissue.

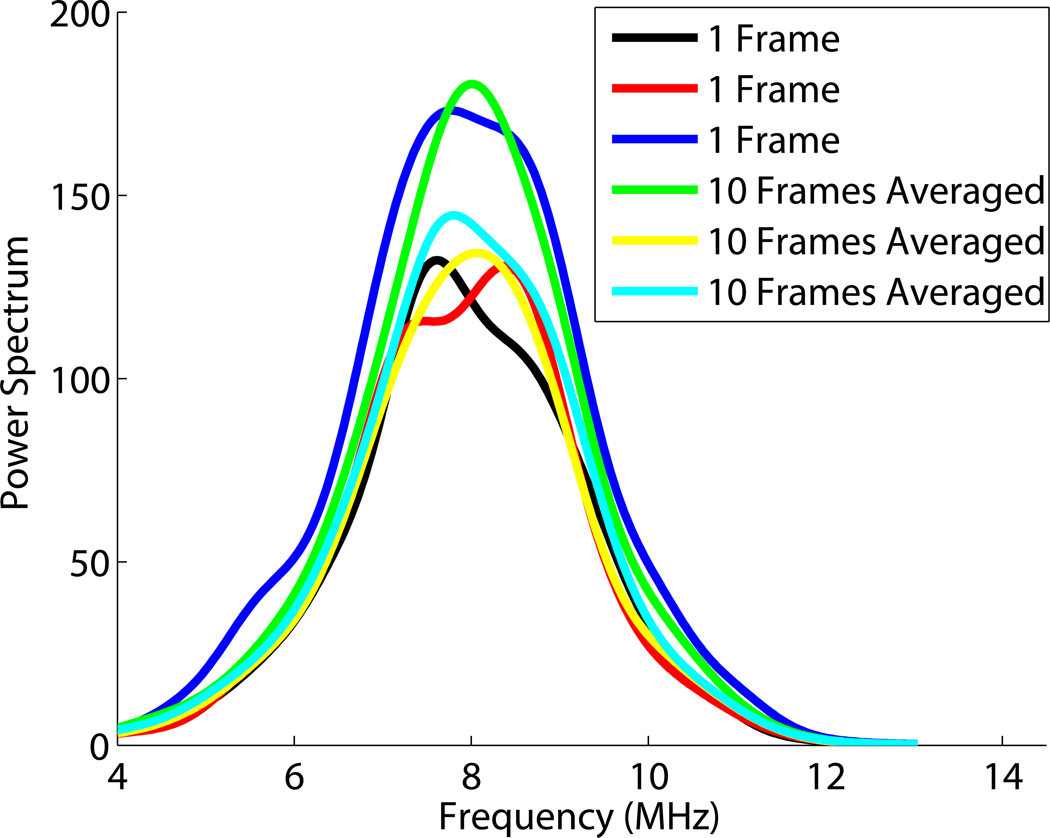
Figure 5.

Example power spectra obtained from a set of phantom data. Three different uncorrelated frames of data were used to compute power spectra for a single frame. Similarly, three different sets of 10 uncorrelated frames of data were used to estimate the average power spectrum.