Hierarchical Representations in the Auditory Cortex

Abstract

Understanding the neural mechanisms of invariant object recognition remains one of the major unsolved problems in neuroscience. A common solution that is thought to be employed by diverse sensory systems is to create hierarchical representations of increasing complexity and tolerance. However, in the mammalian auditory system many aspects of this hierarchical organization remain undiscovered, including the prominent classes of high-level representations (that would be analogous to face selectivity in the visual system or selectivity to bird’s own song in the bird) and the dominant types of invariant transformations. Here we review the recent progress that begins to probe the hierarchy of auditory representations, and the computational approaches that can be helpful in achieving this feat.

Introduction

Although object recognition seems effortless, it is a challenging computational problem [1]. The difficulty arises because of the dual need to be able to discriminate stimuli based on potentially subtle yet important clues [2,3], such as discriminating between different syllables, regardless of how fast they are spoken or the speaker’s voice. This suggests that peripheral representations might be recoded in a form that is tolerant, or “invariant” to “identity-preserving” transformations [1]. Computer science studies show that increasing the number of processing layers can broaden the range of recognition tasks that the circuit can handle, while simultaneously improving performance, learning time, and exponentially reducing the number of neurons (reviewed in [4**]). However, finding the right hierarchical structure for broad recognition systems that can match human performance regarding object recognition in natural environments remains an open problem.

Characterizing feature selectivity

How can we systematically characterize the preferred stimulus features along the auditory hierarchy? In the visual system, progress was made possible by Hubel and Weisel’s discovery that bars and edges represent a close-to-optimal stimulus feature for many cells in the primary visual cortex (V1), and by the discoveries of other researchers that preferred stimulus features further along the hierarchy include curved contours [5], followed by hands and faces [6]. In the auditory system, one can use neuroethology to help guess the optimal stimulus [7]. For example, selectivity for a bird’s own song was demonstrated within areas of avian auditory systems that are homologous to mammalian secondary auditory cortices. However, analogous stimuli for mammalian auditory neurons have been difficult to identify. For example, when vocalizations are played in forward and reverse directions, the differences between the responses are less robust in auditory cortical areas [8-11] compared to those found in the avian song selective areas. Based on the presumed complexity of representations at the level of the primary auditory cortex (A1), it has been argued that A1 is less similar to primary visual cortex and more similar to the final stages of visual processing located in the inferotemporal cortex [12]. This viewpoint is further supported by observation that neural responses are less redundant in auditory cortex and thalamus than they are in inferior colliculus [13**]. By comparison, neurons in the output layers of V1 are more correlated than in the input V1 layers [14], suggesting the redundancy among V1 neurons is higher than at the earlier visual stations.

One-dimensional models

Without an ethologically guided guess of what the best stimulus might be, there are two types of statistical approaches for characterizing auditory feature selectivity. One family of approaches relies on adaptive search procedures whereby the stimulus is generated according to the responses to past stimuli in an effort to increase the strength of the response [15-17]. Theoretical work continues on improving methods for adaptive stimulus design [18], making it a promising research direction for the characterization of neurons with complex feature selectivity.

The second family of statistical methods consists in recording the responses of neurons to large numbers of sounds. After the experiment, one correlates which stimuli elicited a spike and which did not. In its simplest form, this procedure involves computing the spike-triggered average (STA) – the difference between the average of all segments of stimuli that elicited a spike and the average of all presented stimuli [19-23]. Pioneered by de Boer [19], this approach has been generalized to characterize spectrotemporal filtering properties of neurons from the auditory periphery to A1 [20,22,23], as well as in other sensory modalities (for a review focused on the visual system see [24]). Applying this approach in A1, one study found that neurons of awake primates were particularly selective for frequency modulations [25**]. This was later confirmed using synthetic stimuli termed “drifting dynamic ripples” [26*]. Other studies in A1 found simpler features that often consisted of a single excitatory region surrounded by one or more inhibitory regions [27,28]. Additionally, when relevant spectrotemporal features have been obtained with linear models, a range of context-dependent phenomena have been observed: in some cases the features were very similar across different stimulus ensembles [29], in other cases essential nonlinearities were observed [30**, 31-32], and in some there was a reduced fraction of explained variance [33,34].

How can we reconcile these findings? It turns out that the complexity of relevant stimulus features and the degree to which neural responses can be described by a linear model varies systematically across the cortical column in A1 (Figure 1). Granular layers have preferred stimulus features that are more separable in frequency/time space than those in supra- or infra-granular layers. Furthermore, responses in granular layers were more “linear”, i.e. they were better described by a model with one relevant stimulus feature than neurons in output layers [35*,36]. These findings can help explain the observed range of complexity in feature selectivity of A1 neurons and how well linear models account for their responses (see also [34,37]).

Figure 1. A schematic of the hierarchical transformation of feature selectivity in the auditory system.

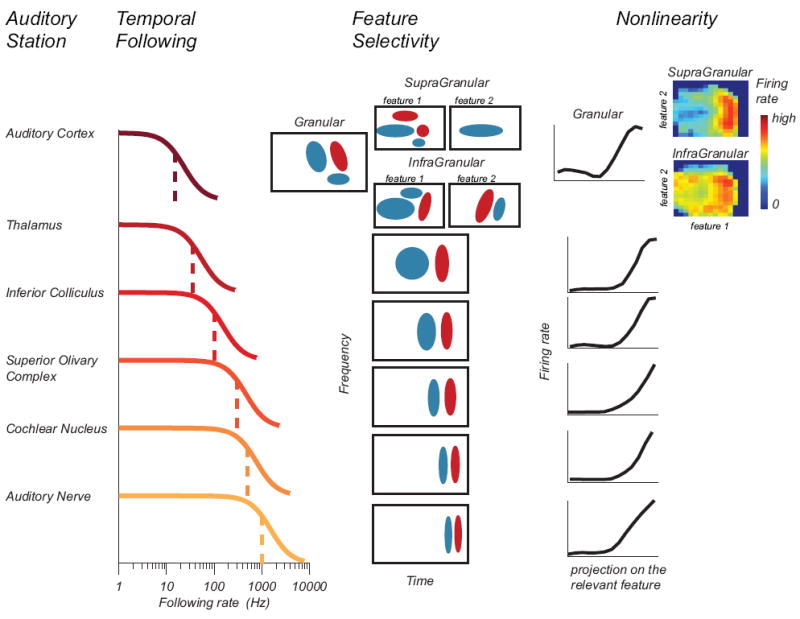
Columns from left to right are: name of the auditory station, the range over which neurons can follow the rate of temporal changes in auditory stimuli, types of relevant auditory features (positive and negative values are denoted with red and blue), and nonlinearities that describe the neural firing rate as a function of stimulus projections on the relevant stimulus features. In supra- and infra-granular layers of A1, at least two features become relevant (heat map shows nonlinearity with respect to two relevant components). In addition, relevant features become more spectrotemporally inseparable with the synaptic distance from the input A1 layer.

One of the advantages of spike-triggered methods is that they provide not only the estimate of the preferred stimulus feature (spectrotemporal receptive field, STRF) but also the nonlinear gain function (nonlinearity) that describes how spiking probability changes as a function of the similarity between the presented stimuli and the optimal stimulus feature. The nonlinearity can capture some inherent neural response properties, such as rectification (firing rate cannot be negative) and saturation (firing rate is limited by the refractory period). These effects become increasingly more pronounced along the auditory neuroaxis (Figure 1). Incorporation of the nonlinearity into models can improve the accuracy of neural response predictions [38]. Crucially, it can help reconcile the observed fast rise times and short response durations in neural responses to frequency modulated (FM) tones with the relatively slow time course of STRFs. Although in many cases the presence of the nonlinearity does not affect STRF estimation [19,39-42], (but see [43-45] for exceptions to this rule; dimensionality reduction methods are summarized in Figure 2), taking the nonlinearity into account can sharpen the predicted tuning. This effect alone could account for differences in the dynamics of V1 responses and their relevant spatiotemporal features [46,47] (reviewed in [48**]). It would be exciting to see if similarly simple calculations that take the nonlinearity into account can resolve the analogous controversies in the auditory research.

Figure 2. A summary of stimuli often used to characterize feature selectivity of auditory neurons, the stimulus statistical properties, and methods currently available.

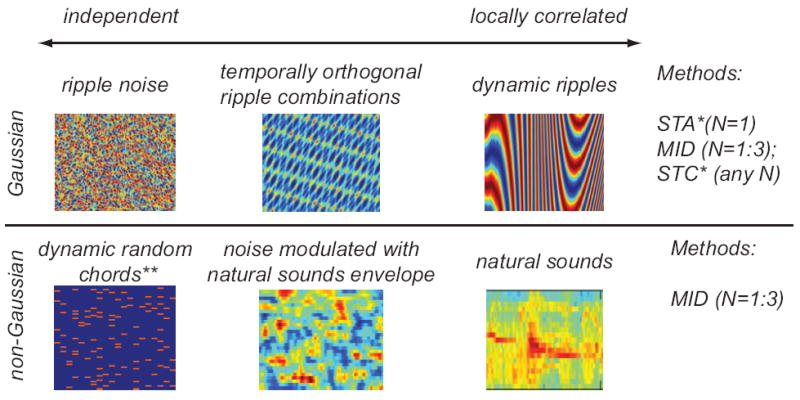
For independent Gaussian stimuli, relevant stimulus features can be computed as spike-triggered average (STA) or by diagonalizing the spike-triggered covariance (STC) matrix. STA yields only one of the relevant features, whereas STC yields all of N them. *If stimuli are Gaussian but globally correlated, then both methods can still be used, provided the features are normalized by the second-order stimulus covariance matrix [41,42]. If stimuli are non-Gaussian (or equivalently exhibit correlations between more than two points in the spectrotemporal space, as in the case of natural sounds), then relevant features can be found as those that account for maximal amount of information in the neural response. The process of searching for maximally informative dimensions (MID) corrects for stimulus correlations of any order, works with flexible nonlinearities, can be extended to multiple stimulus features (currently up to N=3 features can be estimated [84]). **Although dynamic random chords stimuli are often non-Gaussian, these effects often become negligible as a result filtering transformations within the auditory system following the rules of the central limit theorem in the absence of correlations. This allows the use of STA and STC with random chord stimuli.

Multidimensional models

However successful, models based on one stimulus feature are problematic from the standpoint of invariant sound identification. For example, any 1D model will confound responses to a suboptimal feature presented loudly with an optimal feature presented softly. Similarly, a 1D model cannot implement invariance to cadence, because the stretching in time will alter the match with any given STRF. There are two types of general strategies for solving the context-independent sound identification problem. One is to expand the stimulus space, treating the same stimuli as different depending on the value of a contextual variable. This approach is comprehensive, but can be done only for a few well defined context variables, such as mean sound level. Multilinear models that work in the three dimensional stimulus space defined by time lag, frequency, and sound level provide good descriptions of A1 responses [49*]. Mean sound level holds special importance in auditory perception, and could thus justify the expansion of stimulus dimensionality. The second strategy for solving the object recognition problem is not to explicitly expand the stimulus space, but to use combinations of different features. For example, phenomena such as two-tone masking (one tone affects the response to another simultaneously present tone) and forward suppression (a preceding tone suppresses the response to a following tone) [50-53] can be seen as building blocks of invariant sound identification [54]. These classic auditory phenomena can be accounted for by multidimensional LN models with a nonlinearity that depends on stimulus components along two (or more) relevant stimulus features. The form of nonlinearity is not restricted, and can characterize both cooperative and suppressive effects between the relevant components. A variety of computations with respect to two features have been observed in A1 [55,56*] (Figure 1).

The presence of multiple relevant stimulus features is consistent with other nonlinear and context-dependent effects observed throughout the hierarchy of auditory representations. For example, multidimensional descriptions of neural coding may provide a complementary way to account for the dynamic effects of first spike latency [57]. While 1D models with a fixed threshold applied to low-pass filtered sound amplitude could account for much of the latency data [57**], the introduction of a time-dependent threshold was necessary for a full description. A two-dimensional model with a fixed threshold that is a function of both the low-pass filtered amplitude and its first time derivative may provide another way of accounting for this phenomenon. Another example concerns the hypersensitivity of auditory cortical neurons to small perturbations of their acoustic input [31], as well as the large effect that naturalistic background noise can have on the responses [30]. These effects are difficult to explain based on a single relevant stimulus feature, but they can be explained with a multidimensional LN model [55,56*]. Curiously, the hypersensitivity of auditory neurons as manifested by strong suppression of the responses from the addition of a subthreshold tone is not observed in the inferior colliculus; it first appears in the medial geniculate body and is present in A1 [58]. This suggests that multidimensional feature selectivity – an essential property for performing object recognition – appears as a result of hierarchical auditory processing.

The emergence of ‘multiplexed’ temporal coding

The temporal dimension is central to the sense of hearing, and is reflected in the sensitivity to different time-scales of information in auditory signals, perhaps as the spatial dimensions are to the sense of vision [2,3]. In both modalities, neurons are able to integrate information over long scales while also remaining sensitive to fine details. In the visual system, invariance to image translation is one of the prominent characteristics of high-level neurons. Face-selective neurons in the inferotemporal cortex integrate visual signals across large regions of the visual space while maintaining fine spatial sensitivity (which is necessary to distinguish between different faces). Analogously, acoustic stimuli can also be characterized on multiple temporal scales such as the “envelope” (the contour of amplitude modulations (AM) of the spectral components) and the “fine-structure” (the cycle-by-cycle variations of the spectral components that contribute to the time waveform). Along the auditory neuroaxis, which extends from the peripheral stations to A1, there is a progressively increasing emphasis on encoding at coarser temporal resolution, as well as increased tolerance to other stimulus parameters, such as sound pressure level or modulation depth [59]. However, neurons maintain the ability for precise spike timing. Spike timing with single millisecond precision has been observed for sound onset detection [60,61] and with precision of a few milliseconds for a variety of other auditory stimuli, including tones [62,63], AM sounds [64], their combinations [65**], as well as natural stimuli [11,66] (although the utilized temporal precision is coarser than found in peripheral or subcortical auditory structures [66]). Thus, a picture is emerging A1 neurons use a relatively wide range of temporal cues, in a manner that is reminiscent of the wide range of spatial scales that characterize responses of high-level visual neurons.

Though there may be a shift from a temporal code to an average rate and place code along the neuroaxis, both types of information may still be utilized. On one hand, the rate coding of AM sounds in the auditory cortex carries significant information in A1, and it has been suggested that rate information alone is sufficient to explain the behavioral performance of monkeys in a low-AM discrimination task [67] (but see [68]). On the other hand, much of the amplitude modulation information is reflected in the timing of cortical responses (e.g., [69]). For example, spike-doublets with <15ms interspike intervals (ISIs) were shown to convey more event information than long-ISI spikes. Pairs of short-ISI spikes express over three times as much information as long-ISI spikes, well over what would be expected from summing two independent information sources [70]. Therefore, short-ISI spikes appear to be particularly important in A1 stimulus encoding and have the potential to provide low-noise, robust, and efficient representations of sound features. It is also possible that different populations of A1 neurons use distinct encoding schemes, either synchronized (temporal coding) or non-synchronized (rate-coding) [71-73]. A recent study expanded on this issue by demonstrating mixed schemes with synchronized responses at some modulation frequencies and non-synchronized responses at others [74]. Accordingly, cortical neurons are capable of carrying multiple signals via different codes with regard to AM. The information conveyed by these different codes (rate and time) is likely non-redundant, in that a joint code of rate and timing parameters provides more information than either code alone, as demonstrated for high modulation frequencies [75]. A similar observation has been made for low modulations frequencies (<60Hz) that dominate temporally encoded A1 activity [76]. Here, repetition–rate information carried jointly by firing rate and inter-stimulus intervals exceeded that of either code alone, thus indicating non-redundant contributions of the two codes.

Concurrently employed codes may also provide complementary information, as demonstrated for LFP and spiking signals for natural sounds [77**]. Further analysis showed that the angular phase of the LFP at the time of spike generation adds significant extra information, beyond that contained in the firing rate alone [78]. These findings provide further credence to the notion of ‘multiplexed’ coding at different timescales [79], with each code carrying complementary information.

While the impact of hierarchical and parallel schemes of information processing beyond A1 on ‘multiplexed’ coding is still unresolved, there is evidence of hierarchical processing within A1, namely across the different cortical layers. Here, granular layers phase-lock to the highest pure-tone frequencies [62]. Additionally, granular layers may also follow faster amplitude modulations, and outside of the main thalamic input zone the following rates generally decrease [80].

Outlook

The emerging picture is that auditory processing becomes increasingly multidimensional. This is expected on computational grounds because the invariant representation of auditory objects requires that neural responses be tuned to conjunctions of features. For example, David Marr argued that to detect an edge [81] one should measure both the presence of an oriented element and the absence of an oriented element of the perpendicular orientation. Mechanisms of forward- and two-tone masking may serve as examples with a similar computational purpose. Additionally, since there is a high degree of tolerance and selectivity at the level of A1, neural responses may be simultaneously sensitive to a large number of stimuli. Thus, the full understanding of auditory representations will likely require the development of new statistical methods that can recover large numbers of relevant stimulus features from responses to naturalistic sounds. The development of these methods may be guided by the construction of Bayesian methods for model selection [49*,82], especially for building minimal nonlinear models [83]. In addition, to achieve a full understanding of temporal processing, temporal aspects of neural coding for the same stimulus need to be separated from stimulus dynamics. This requires that the information content of the stimulus be quantified, and then compared to the content in the neural response. In this way the maximally achievable stimulus information may be compared to the encoding that is actually provided by the neuron.