Vector Autoregression, Structural Equation Modeling, and Their Synthesis in Neuroimaging Data Analysis

Abstract

Vector autoregression (VAR) and structural equation modeling (SEM) are two popular brain-network modeling tools. VAR, which is a data-driven approach, assumes that connected regions exert time-lagged influences on one another. In contrast, the hypothesis-driven SEM is used to validate an existing connectivity model where connected regions have contemporaneous interactions among them. We present the two models in detail and discuss their applicability to FMRI data, and interpretational limits. We also propose a unified approach that models both lagged and contemporaneous effects. The unifying model, structural vector autoregression (SVAR), may improve statistical and explanatory power, and avoids some prevalent pitfalls that can occur when VAR and SEM are utilized separately.

Introduction

The traditional approach of massively univariate modeling in FMRI data analysis has been relatively reliable and robust as it now matures into its second decade. However, it provides little or no information about communication among regions of the brain comprising a neural network. There have been a variety of analytical tools proposed for modeling connectivity among regions implicated in specific cognitive/perceptual conditions or the resting state; these tools have provided complementary evidence for organization, specialization, and integration within these specialized networks. The methods include simple correlation, context-dependent correlation or psychophysiological interaction (PPI) analysis [1], Granger causality modeling through vector autoregressive (VAR) analysis [2], path analysis or structural equation modeling (SEM) [3][49], and dynamic causal modeling (DCM) [4].

These methods are loosely categorized into two classes: “functional” and “effective” connectivity [5]. In functional connectivity analyses, the identified relation among regions can arise from a range of neural phenomena including direct anatomical connectivity to non-directional or reciprocal excitatory neurotransmission [6]. Generally such results do not convey causal or directional connections. On the other hand, if all regions in a network are known from a prior considerations, an effective connectivity modeling approach may be adopted to statistically validate the connectivity in the network and derive directional paths (and their strengths) among the regions in the specialized network.

Under this classification system, simple correlation and PPI analyses are used for functional connectivity analysis, while SEM, VAR, and DCM are used for estimating effective connectivity. Moreover, these two approaches may complement one other. For example, an exploratory functional connectivity analysis can be used to identify regions of interest (ROIs) for subsequent effective connectivity modeling.

Alternatively, from a methodological perspective, we can divide the connectivity analysis approaches into two major classes. One is a seed-based ROI search method in which a seed region is chosen and target regions are statistically inferred/identified if their time courses are significantly correlated with the seed. The seed region is typically selected based on prior knowledge that it may serve as network hub. The second approach is a network-based one in which we can either validate/confirm the presumed connections among the regions that may form a network based on previous studies, or modify and search for a model that better accounts for the available data in terms of various fit indices [22][25]. Although this classification overlaps with the conventional functional/effective connectivity dichotomy, they are not exactly the same. For example, simple correlation and PPI analyses are typically performed through ROI search with a seed-based approach. However, VAR can also be used for ROI search using a seed region. Once all the regions in a network are identified, a network-based modeling can be further pursued through VAR or another analytical methodology.

Connectivity tools such as simple correlation and PPI analyses of FMRI data have been adopted widely as exploratory approaches for locating regions that are functionally associated with each other. In addition, there are more advanced approaches such as activation likelihood meta-analysis [50][51]. However, it is rarely considered that standard regression models assume that the regressors are idealized predictors, or that they have been measured exactly and/or observed without error. This assumption of no measurement error is unlikely to be valid in typical connectivity analysis, given both that FMRI data are noisy and that there are often errors embedded in the deconvolution process involved in the PPI analysis. This unaccounted-for estimation error in the regressors may lead to inconsistent results and a potential underestimation of the association between the seed and target region–known as the attenuation bias or regression dilution [7]. Furthermore, simple correlation and PPI analyses assume roughly the same hemodynamic response across regions as well as instantaneous interactions among regions. Importantly, the reliability and robustness of these analyses are therefore compromised to some unknown extent when hemodynamic response varies significantly or when there is a time lag in activation between regions.

The tools currently available for conducting VAR and SEM range from generic to those specialized for brain imaging data, and from proprietary to open-source. Here we focus on and present three specific connectivity-modeling methodologies implemented in the FMRI data analysis package AFNI [8]: a) VAR, which can be used for seed-region-based ROI search (program 3dGC) and for network modeling (program 1dGC) of lagged effects; b) SEM that is solely suited for a network-based approach (1dSEM and 1dSEMr) on instantaneous effects; and c) structural vector autoregression (SVAR) that is the combination of VAR and SEM techniques (program 1dSVAR). It is this third method of analysis, merging the strengths of instantaneous and delayed network analyses, SVAR, that we believe will prove most fruitful for connectivity analysis of neuroimaging and brain electrical activity data.

All relevant software packages presented here are in open-source code and freely available for download. In this article we will introduce theoretical aspects of the three models, and discuss the meaning of the connectivity measures as well as the kinds of information they convey about neural network from brain imaging data. Also presented are the underlying assumptions, applicability, and limitations of each of these methodologies.

Methodology

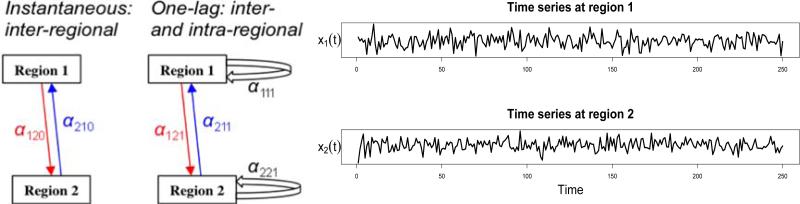
Suppose two regions in the brain, 1 and 2, form a simple network in which the history of each region affects its and the other's current state, and in which each region simultaneously affects the other (Fig. 1, left). In this example we use a lag of one sample. The evolutionary and dynamic interactions between the two regions can be intuitively represented with the following toy model of two equations for the observed time series x₁(t) and x₂(t),

$$\begin{array}{cc}\hfill x_1\left(t\right)& =c_1+{\alpha }_{120}{x}_2\left(t\right)+{\alpha }_{111}{x}_1(t-1)+{\alpha }_{121}{x}_2(t-1)+{\epsilon }_1\left(t\right)\hfill \\ \hfill x_2\left(t\right)& =c_2+{\alpha }_{210}{x}_1\left(t\right)+{\alpha }_{211}{x}_1(t-1)+{\alpha }_{221}{x}_2(t-1)+{\epsilon }_2\left(t\right),\hfill \end{array}$$ (1)

where the constants or intercepts, c₁ and c₂, are the baseline values, ε₁(t) and ε₂(t) are the residuals or noise terms, α₁₂₀ and α₂₁₀ reflect the instantaneous cross-region effects, α₁₁₁ and α₂₂₁ code for the lagged within-region effects, while α₁₂₁ and α₂₁₁ represent the lagged cross-region effects. The subscripts of each effect (α_ijk) encode target (i), the source (j), and lag (k). α_ijk indicates the amount of change of the target region i, when region j experiences a unit change at k-th lag in the past; and its sign (positive or negative) indicates excitatory or inhibitory effects, respectively. It is worth noting that we will be drawing distinctions between instantaneous effects (k=0) and lagged ones (k≥1). The distinction reflects the dichotomy in modeling approaches in common use with brain imaging. Because all of the temporal and interregional correlations have been considered in the model (1), we can reasonably assume that the residual terms, ε₁(t) and ε₁(t), are serially and mutually independent with a Gaussian distribution.

Figure 1.

(Left) A hypothesized network of two regions, 1 and 2, with excitatory (red) instantaneous and one-lag effect of region 1 on region 2, and inhibitory (blue) instantaneous and one-lag effect of region 2 on region 1. (Right) Based on two time series of 250 data points with a sampling interval of 1.2 seconds acquired from both regions under resting state, can we derive the interregional relations?

With x₁(t) and x₂(t), we can examine this two-region system from two perspectives. In the first, we impose constraints of interregional connections based on a priori knowledge of brain connectivity, say from anatomical studies, MR tractography data, or activation meta-analysis. With the connections pre-specified, we estimate the corresponding connection coefficients and perform tests to determine whether the observed data can be explained by our model. In the second perspective, we drop the connectivity constraints and attempt to find a set of connections and model coefficients that best explain the data, allowing one to assess whether a connection is present and estimate its effects. This second approach is more data driven compared to the first. Both approaches will be discussed and their differences examined.

Vector Autoregressive (VAR) modeling

Suppose that we do not explicitly model the instantaneous effects between the two regions in the model (1), but, instead, leave them in the residuals,

$$\begin{array}{cc}\hfill x_1\left(t\right)& =c_1+{\alpha }_{111}{x}_1(t-1)+{\alpha }_{121}{x}_2(t-1)+{\epsilon }_1\left(t\right)\hfill \\ \hfill x_2\left(t\right)& =c_2+{\alpha }_{211}{x}_1(t-1)+{\alpha }_{221}{x}_2(t-1)+{\epsilon }_2\left(t\right).\hfill \end{array}$$

As a result of relegating the instantaneous effects to the residuals, we cannot assume that ε₁(t) and ε₂(t) are both serially and mutually independent. With this formulation, the system is called Vector Autoregressive (VAR) model [9], capturing the temporal and cross-region interactions among multiple regions with delayed effects of one or multiple lags in a network. For a network of n ROIs, it can be modeled with a p-th order vector autoregressive model VAR(p),

$$\begin{array}{cc}\hfill & x_1\left(t\right)=c_1+\sum _{k=1}^p{\alpha }_{11k}{x}_1(t-k)+\sum _{k=1}^p{\alpha }_{12k}{x}_2(t-k)+\cdots +\sum _{k=1}^p{\alpha }_{1nk}{x}_n(t-k)+{\epsilon }_1\left(t\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill & x_n\left(t\right)=c_n+\sum _{k=1}^p{\alpha }_{n1k}{x}_1(t-k)+\sum _{k=1}^p{\alpha }_{n2k}{x}_2(t-k)+\cdots +\sum _{k=1}^p{\alpha }_{nnk}{x}_n(t-k)+{\epsilon }_n\left(t\right)\hfill \end{array}$$

where the endogenous variable x_i(t) is the time series from a given subject at region i, α_ijk indicates the effect of region j on region i with a lag of k time points, and ε_i(t) is the residual time series at region i.The order of the VAR model, p, shows how long we are tracing back in the history that could affect the current state of the endogenous variables. The constant or intercept C_i is the baseline value of x_i(t).

With the following denotation,

$$X\left(t\right)=\left[\begin{array}{c}{x}_1\left(t\right)\hfill \\ ⋮\hfill \\ x_n\left(t\right)\hfill \end{array}\right],\mathbf{c}=\left[\begin{array}{c}{c}_1\hfill \\ ⋮\hfill \\ c_n\hfill \end{array}\right],A_i=\left[\begin{array}{ccc}\hfill {\alpha }_{11i}\hfill & \hfill \cdots \hfill & \hfill {\alpha }_{1ni}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\alpha }_{n1i}\hfill & \hfill \cdots \hfill & \hfill {\alpha }_{nni}\hfill \end{array}\right],\epsilon \left(t\right)=\left[\begin{array}{c}{\epsilon }_1\left(t\right)\hfill \\ ⋮\hfill \\ {\epsilon }_n\left(t\right)\hfill \end{array}\right],$$

we can rewrite the model as:

$$X\left(t\right)=\mathbf{c}+A_{1}X\left(t\text{-}1\right)+\dots +A_{p}X\left(t\text{-}p\right)+\epsilon \left(t\right).$$ (2)

The residuals vector, ε(t), an n-dimensional process, is assumed to be white noise or an innovation process. More specifically, the error terms have a zero mean and a time invariant positive definite covariance matrix E[ε(t)ε(t)^T], with no correlation across time, including no autocorrelation in each of the individual error terms. The nonzero off-diagonal elements reflect the fact that we do not explicitly model the simultaneous cross-region effects in the model (2). It can be shown [9] that E[X(t)] = (I_n×n - A₁-...-A_p)^-1c, which relates the baseline to the unconditional mean of each regional time series, where I_n×n is an n×n identity matrix. This relation also allows us to reformat the model (2) to,

$$X\left(t\right)-E\left[X\left(t\right)\right]=A_1\left\{X\left(t\text{-}1\right)\text{-}E\left[X\left(t\right)\right]\right\}+\dots +A_p\left\{X\left(t\text{-}p\right)\text{-}E\left[X\left(t\right)\right]\right\}+\epsilon \left(t\right),$$

If we center the time series by replacing the unconditional mean E[X(t)] with the sample mean X̄, we can reduce the model (2) to,

$$X^{\ast }\left(t\right)=A_1{X}^{\ast }\left(t\text{-}1\right)+\dots +A_p{X}^{\ast }\left(t\text{-}p\right)+\epsilon \left(t\right),$$ (3)

where X*(t) = X(t) – X̄. Such a replacement is valid in practice if the sample size (the number of time points in the time series, N) is big enough and if the data are stationary. More specifically, the solutions in model (3) are asymptotically equivalent to the ones in model (2) if all of the assumptions about sample size and stationarity are met [9]. However, the replacement is problematic when the sample size is moderate or small, or when stationarity assumption is not well satisfied, which will add sizable sampling error in the model. Model (3) is usually presented in the literature mostly without explicitly stating that the data are assumed to be zero-mean through the replacement of the unconditional mean with the sample mean [10,11,12,13]. We prefer model (2)to(3) because it keeps the constant term that will be estimated through solving (2): we prefer this for three reasons: a) as seen below, the model (2) allows us to further include confounding effects; b) unlike the zero-mean model (3), the path estimates and their inferences in model (2) will be still relatively more reliable and robust even if the stationarity assumption is not met or when the sample size is inadequate; and c) the model (2) is more appropriate in overall model inferences such as model validation, comparison and search through maximum likelihood testing when, from a frequentist perspective, the asymptotic property of the data is violated.

Furthermore, through the following stacking,

$$\tilde{X}\left(t\right)={\left[\begin{array}{c}X\left(t\right)\hfill \\ X(t-1)\hfill \\ ⋮\hfill \\ X(t-p+1)\hfill \end{array}\right]}_{pn\times 1}$$

and the notations (0_n×1 and 0_n×n are an n-dimensional zero vector and an n×n zero matrix respectively),

$$\tilde{C}={\left[\begin{array}{c}\hfill \mathbf{c}\hfill \\ \hfill 0_{n\times 1}\hfill \\ \hfill ⋮\hfill \\ \hfill 0_{n\times 1}\hfill \end{array}\right]}_{pn\times 1},\tilde{A}={\left[\begin{array}{cccc}\hfill A_1\hfill & \hfill \cdots \hfill & \hfill A_{p-1}\hfill & \hfill A_p\hfill \\ \hfill I_{n\times n}\hfill & \hfill \cdots \hfill & \hfill 0_{n\times n}\hfill & \hfill 0_{n\times n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0_{n\times n}\hfill & \hfill \cdots \hfill & \hfill I_{n\times n}\hfill & \hfill 0_{n\times n}\hfill \end{array}\right]}_{pn\times pn},\tilde{\epsilon }\left(t\right)={\left[\begin{array}{c}\hfill \epsilon \left(t\right)\hfill \\ \hfill 0_{n\times 1}\hfill \\ \hfill ⋮\hfill \\ \hfill 0_{n\times 1}\hfill \end{array}\right]}_{pn\times 1},$$

we obtain a concise VAR model with the number of lags hidden [9],

$$\tilde{X}\left(t\right)=\tilde{C}+\tilde{A}\tilde{X}\left(t\right)+\tilde{\epsilon }\left(t\right),$$ (4)

which is convenient for analytical derivations and compact statements. Finally, we can even condense the VAR(p) model (2) into a regression form with regions, lags, and time all hiden,

$$Y=A^{\ast }Z+U,$$ (5)

where Y = [X(p+1),X(p+2),...,X(N)],A* =[C, A₁, A₂,..., A_p],

$$Z=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill X\left(p\right)\hfill & \hfill X(p+1)\hfill & \hfill \cdots \hfill & \hfill X(N-1)\hfill \\ \hfill X(p-1)\hfill & \hfill X\left(p\right)\hfill & \hfill \cdots \hfill & \hfill X(N-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill X\left(1\right)\hfill & \hfill X\left(2\right)\hfill & \hfill \cdots \hfill & \hfill X(N-p)\hfill \end{array}\right],U=[\epsilon (p+1),\epsilon (p+2),\cdots ,\epsilon \left(N\right)].$$

Model format (5) not only looks more concise, but also lends itself to an ordinary least squares (OLS) solution [9] for the estimate of the lagged effects A*, providing a straightforward form for the numerical solution,

$${\widehat{A}}^{\ast }=Y{Z}^T{\left(Z{Z}^T\right)}^{-1}.$$

It should be noted in VAR modeling, as shown through the OLS solution above, that the only content of model specification lies in defining all the regions involved in a network and the number of lags to include. Once the ROIs are determined, it is the data that lead to the statistical inference of temporal and interregional associations.

VAR modeling has been widely applied to various fields such as macroeconomics [14], political science [15], international relationships, geophysical systems, molecular dynamics, genetic networks, signal pathways, and neural systems. In the context of FMRI VAR modeling, confounding effects such as slow drift, head motion, physiological fluctuations, or other effects of no interest are present in the data. In addition, acquisition constraints preclude very long time series. Combining multiple time series to increase the number of samples also necessitates the modeling of time axis discontinuities. There are two approaches for modeling these nuisance parameters. They are either removed from the ROI time series before they are applied in the VAR model (2) [2,13], or explicitly modeled within the VAR by adding exogenous variables in model (2). Explicit modeling is more desirable because confounding effects are not necessarily independent of the simultaneous and lagged effects among the regions [20]. The modeling of confounds is done by incorporating q exogenous variables (covariates, deterministic or confounding effects), z₁(t), ..., z_q(t), into the model (2),

$$X\left(t\right)=A_{1}X\left(t\text{-}1\right)+\dots +A_{p}X\left(t\text{-}p\right)+{\mathbf{c}}_1{z}_1\left(t\right)+\dots +{\mathbf{c}}_q{z}_q\left(t\right)+\epsilon \left(t\right).$$ (6)

where c_j is the effect vector of size n×1 for the j-th covariate (j = 1, ..., q). Notice that the constant term c in (2) is generally of no interest and, to avoid distraction, has been incorporated as part of the covariates in model (6). To solve the extended VAR(p) model (6), we simply augment the definition of A* by appending c₁, ..., c_q, and obtain the OLS estimates of A_i and c_j.

The exogenous variables z₁(t), ..., z_q(t), are observable, and usually determined outside of the network mechanism. The incorporation of exogenous variables into (6) not only allows minimum pre-processing of the data (slice timing and head motion correction are sufficient) with no need of band-pass filtering or removal of confounds (e.g., physiological data) before the VAR modeling, but also provides a statistically more robust model.

In addition, the inclusion of exogenous variables in (6) affords it the capability to address complexities inherent in modeling BOLD data. For example, if censoring time points (e.g., spikes) is desirable, one can create, for each censored time point, a covariate in (6) with the same length as the time series composed of a 1 at the censored time point and zero at all other time points, and. Another important feature is that, if there are multiple segments of time series data at each ROI from various blocks, runs, or sessions, these segments can be concatenated with gains in statistical power. To account for discontinuities in the extended VAR(p) model, we define at each time discontinuity t_b the following dummy variables, called unit impulse functions in signal processing,

$${\mathbf{d}}_k\left(t\right)=\{\begin{array}{c}{1}_{p\times 1},t=t_b+k’\hfill \\ 0_{p\times 1},t\ne t_b+k\hfill \end{array}\phantom{\}}$$

where k = 1,..., p, and include these p dummy variables for each time break as exogenous processes in the model (6), we can easily stack all of the separate time series of each ROI into one, and solve one VAR system.

In FMRI, VAR modeling is used for the purpose of evaluating Granger causality (GC) between regions [2,10]. GC is assessed from an F-statistic, proposed by [16], which is composed of three components, one for all the lagged effects from region A to B, one for all the lagged effects from B to A, and one for the instantaneous influence. Like the F-statistic for the main effect and interaction in the conventional ANOVA framework, the F-statistics from the model (6) or the logarithm of F-statistics of the two directional components [10] provides a concise summary about the relationship between the two regions. However, these statistics lose three types of information: the contributions of the three separate components, the contributions of different lags, and the sign (positive/negative or excitatory/inhibitory) of each directional path. Another consequence of using the F-statistic is the current practice of running group analysis with the logarithm of the F-statistic from individual subjects [10,6], which is problematic in two respects: it results in additional information loss at group level, and it is questionable to assume a Gaussian distribution for the logarithm of the F-statistic. Put differently, in the GC analysis, the estimated lagged effects embedded in the A_i matrices are treated as parameters of no interest, and instead the focus is on the “Granger causality” between any two regions. Instead of using the GC F-statistic, our method yields a Student t-statistic for each directional path per lag in the model (6). This also allows us to run a mixed-effects group analysis [17] by combining two pieces of information: a) the lagged path coefficient, i.e., the effect estimate of each direction per lag, and b) the precision of the effect estimate, embedded in the corresponding t-statistic. Such an approach preserves more information from individual subjects to the group level, which is not available with the conventional F-statistic-based approaches [2,10,18].

The above methodology has been implemented in two programs in the open-source statistical language R [19], using packages vars [20] and network [21]: 3dGC for whole-brain ROI search based on specification of leading and lagging relations with time series data from a pre-selected seed region, and 1dGC for network modeling with the time series from each of the regions predefined in the network of interest.

The exploratory approach, 3dGC, adopts a bivariate autoregressive model for estimating prior and posterior relations between a pre-defined seed region and the rest of the brain, similar to [2]. It differs from [2] in the following three ways: confounding regressors are incorporated, with minimum pre-processing, in both seed and brain time-series data; significance is denoted by a t-statistic for each directional path per lag instead of one F-statistic to characterize the connectivity across all lags between the seed and the target regions; and group analysis can be performed on a per-lag basis using a linear mixed-effects meta-analysis approach that incorporates information from path coefficients and from the corresponding t-statistics as input [17].

If the network ROIs are already known, 1dGC can be used to find out the path strength and significance per lag. The program assists in selecting the order, p, of the VAR model by providing four criteria [20]: Akaike Information Criterion (AIC), Final Prediction Error (FPE), Hannan-Quinn (HQ), and Bayesian information criterion (BIC) or Schwartz Criterion (SC). In addition, a stationarity test is available by examining the roots of the characteristic polynomials det(I_n-A₁z-...-A_pz^p) (where z is an eigenvalue of the companion coefficient matrices) based on the following property [9]: The necessary and sufficient condition for the stability of a stationary VAR(p) system is that all the characteristic roots lie outside the unit circle.

1dGC provides significance testing for both lagged effects and confounding variables. If a particular covariate is not essential under some significance level, the model can be tuned by trimming the non-significant variable. A few plotting tools are available, including the network at each lag with all the directional paths thresholded at a user-specified significance level. It can also plot at each region the residual time series, the autocorrelation function (ACF) and partial autocorrelation function (PACF) of the residual time series, as well as the fitted time series versus the original time series.

Several diagnostic tests [9,20] are available in 1dGC to aid in determining whether the assumptions about the residuals are met. Normality can be checked in the residual time series with three tests: Jarque-Bera, skewness (symmetric or tilted), and the kurtosis (leptokurtic or spread-out). Additionally, three tests are available for estimating serial correlation in the regional residuals: Breusch-Godfrey Lagrange multiplier χ²-test; Edgerton-Shukur F-test; and asymptotic and adjusted Portmanteau χ²-test. 1dGC also provides autoregressive conditional heteroskedasticity (ARCH) test for time-varying volatility. Structural stability can also be tested with eight empirical fluctuation process (EFP) types.

We have cross-validated 1dGC with Causal Connectivity Analysis Toolbox in Matlab (version 1.1) [10]. Because the Matlab toolbox does not allow exogenous variables, we tested both programs with a dataset of six ROI time series with a VAR(1) model in (2) and obtained the same path coefficients and the corresponding F-statistics.

Path analysis or structural equation modeling (SEM)

Now we consider a different aspect of the model (1), where we suppose there are no lagged effects between the two regions, and we focus, instead, on the instantaneous effects,

$$\begin{array}{cc}\hfill x_1\left(t\right)& =c_1+{\alpha }_{120}{x}_2\left(t\right)+{\epsilon }_1\left(t\right)\hfill \\ \hfill x_2\left(t\right)& =c_2+{\alpha }_{210}{x}_1\left(t\right)+{\epsilon }_2\left(t\right).\hfill \end{array}$$

Because of the assumption of no lagged effects, the residual terms, ε₁(t) and ε₂(t), in this simple SEM system are serially and mutually independent of each other¹. Generally, SEM is a multivariate regression analysis for detecting contemporaneous interactions among the variables [23]. Following the notation of the model in (2), a generic SEM model can be represented as,

$$X\left(t\right)=\mathbf{c}+A_{0}X\left(t\right)+\epsilon \left(t\right),$$ (7)

where X(t) and ε(t) are defined the same as in (2), c is a constant for the baseline, A₀ is the instantaneous path matrix,

$$A_0=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill {\alpha }_{120}\hfill & \hfill \cdots \hfill & \hfill {\alpha }_{1n0}\hfill \\ \hfill {\alpha }_{210}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\alpha }_{2n0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\alpha }_{n10}\hfill & \hfill {\alpha }_{n20}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right).$$

The components {α_ij0} in A₀ specify all the possible contemporaneous effects (some of them may be specified as zero if the connections are assumed non-existent) among the n regions. The residual term ε(t) is assumed to follow a multivariate Gaussian distribution, accounting for the latent causes (exogenous variables) in the network. In addition, the residuals (error terms) in ε(t) are assumed to be uncorrelated with the endogenous variables and with each other. These assumptions are often violated in FMRI data, for reasons that we discuss later.

It can be shown that the baseline satisfies c=(I – A₀)E[X(t)], and, therefore model (7) can be reduced to,

$$X\left(t\right)-EX\left(t\right)=A_0\{X\left(t\right)-E\left[X\left(t\right)\right]\}+\epsilon \left(t\right).$$ (8)

With the mean vector E[X(t)] replaced by the vector of sample means, we center X(t) around its sample mean, X̄ , and further reduce model (8) to

$$X^{\ast }\left(t\right)=A_0{X}^{\ast }\left(t\right)+\epsilon \left(t\right).$$ (9)

where X*(t) = X(t) – X̄. Model format (9) is typically presented in the literature without explicitly stating the centering issue involved [22,12], but, similar to the situation with VAR, it is worth noting that such a replacement is valid if the number of time points is sufficiently large.

With the multivariate regression model (9), we can predict the covariance structure Σ among the n regions with:

$$\Sigma ={(I-A_0)}^{-1}\epsilon {\epsilon }^T{(I-A_0)}^{-T}={(I-A_0)}^{-1}\Psi {(I-A_0)}^{-T},$$

where ψ is the covariance matrix of the residuals that model the unaccounted variability in the latent variables. Because of the assumption that the disturbance terms are independent of each other, ψ is a diagonal matrix. By comparing Σ with the covariance matrix estimate C, estimated from the data, we can adopt the maximum likelihood (ML) approach to minimize the discrepancy or cost function between the two covariance structures (tr denotes the trace of a matrix),

$$D\left(\Sigma \right)=\ln \left[\det \left(\Sigma \right)\right]+tr\left(C{\Sigma }^{-1}\right)-\ln \left[\det \left(C\right)\right]-n$$ (10)

and obtain the estimate of the path matrix A₀ [23].

Although typically referred to as structural equation modeling, the approach adopted in FMRI data modeling is more accurately referred as path analysis, a special kind of SEM [24] that contains only observed variables. In other words, unlike the generic SEM, a path analysis model does not consider unobserved or latent variables except for residuals or disturbance terms.

We have implemented two path-analysis modules available for open use in AFNI: 1dSEM and 1dSEMr. 1dSEM combines two approaches: the optimization scheme by [22] that used two proprietary packages, S-Plus and LISREL, and a modified version in Matlab by [25]. Written in C, 1dSEM takes interregional correlations and residual variances of pooled data from multiple subjects as input [22] and estimates the path strengths among the regions in the network. To address the limitations of 1dSEM in which only group-level analysis is possible and residual variances are part of the input, we developed 1dSEMr in R with the sem package [26] that can be applied at either the individual or the group level, and with or without residual variances as input.

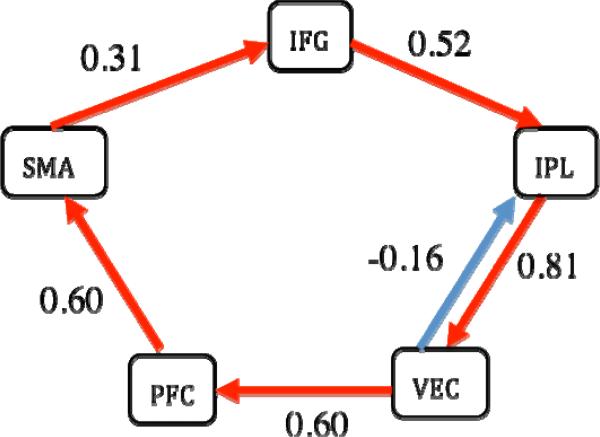
1dSEM has two modes of function: confirmatory and exploratory. In the confirmatory mode, the user specifies the regions in the brain and their connections, and obtains the path coefficient at each connection and model fit indices including the ML χ²-test. In the exploratory mode, the user can compare two nested models in which one model has more connections than the other; moreover, the user can specify the regions involved as well as minimum connections and obtain additional connections and their path coefficients based on various optimization criteria. Instead of using adaptive simulated annealing, as in [25], we adopted a nonlinear optimization scheme, NEWUOA [27], for minimizing the ML cost function. This method allows us achieve higher efficiency and speed. We also modified the original NEWUOA to allow search constraints and to search along multiple paths so that it is less likely to get trapped at a local minimum. Compared to LISREL's optimization method, our method gave better or equal fits. Indeed, our method confirmed two models (the articulatory system in [22], and the 2-back working memory network in [28]), but generated a better fit in two other cases (the 1-back and 3-back working memory networks in [28]). In addition, our optimization algorithm has been validated with data and a theoretical model of five regions and six paths from [22] involving the sequential engagement of rehearsal and monitoring components of the articulatory network (Fig. 2).

Fig. 2.

Validation of the optimization scheme in 1dSEM with data and a theoretical model from [22] with five regions: supplementary motor area (SMA), inferior frontal gyrus (IFG), inferior parietal lobule (IPL), ventral extrastriate cortex (VEC), and prefrontal cortex (PFC). The estimated path coefficients are equivalent to the published results within an accuracy of 10^-3. Runtime was about 1 s on a Mac OS X with a 2 × 2.66 GHz dual-core Intel Xeon processor. χ²(9) = 12.4, p = 0.183, AIC index = 24.57, Bollen's parsimonious fit index = 0.71.

On the other hand, for the two models fitted with LISREL (version 8) in [28], the 1-back and 3-back working memory networks, 1dSEM achieves a minimum cost of 0.157 and 0.602, respectively, in (10) which were also confirmed with 1dSEMr with a different optimization scheme, two-stage least squares, while the results in [28] show a minimum cost of 0.207 and 0.606, respectively. Furthermore, 1dSEM yielded a totally different set of path coefficients for both models; in fact, some of the path coefficients even have a different sign.

The most commonly used algorithm for model search in SEM is a perturbation method via modification index, or Lagrange multiplier in packages such as LISREL. However, our approach utilizes two more straightforward alternatives to model modification by simply searching for a model with the lowest minimized ML discrepancy: “tree growth” and “forest growth”. In tree growth, an extra path grows as a new branch on the previous model tree and the new branch with the best fit among all possible paths is chosen. In other words, each progressive model includes the directional coefficients of the simpler, previous model as the model grows by a single coefficient at a time. In contrast, forest growth is a simple brute-force method that searches through the vast array of all possible networks with a specific number of paths and selects the network with the best fit. That is, 1dSEM searches over all possible path combinations by comparing models at incrementally increasing numbers of path coefficients. There is no requirement that a previous directional coefficient with a good fit will be included in progressive iterations.

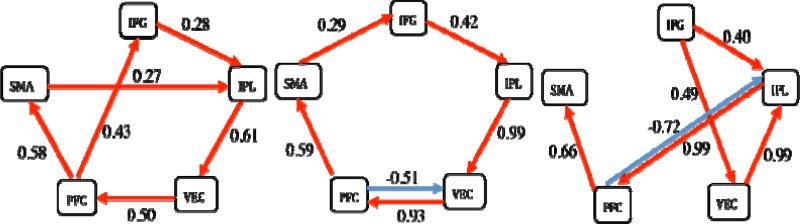
Using the data from [22], both “tree growth” (Fig. 3, middle and right) and “forest growth” in 1dSEM revealed optimal models with improved fit compared to the one identified by “tree growth” in [22] (Fig. 3, left) in terms of ML discrepancy, statistics and fit indices, indicating that our optimization algorithm performed better than the LISREL-based setup.

Fig. 3.

(Left) An optimal model of 6 paths found through automated tree growth search in LISREL by [22]. χ²(9) = 11.19 (p = 0.26), AIC index = 23.19, Bollen's parsimonious fit index = 0.75. The same path coefficients, statistics and fit indices were verified for this specific model with 1dSEM and 1dSEMr. (Middle) An optimal network of six paths identified based on “tree growth” with 1dSEM. Runtime = 4 s on a Mac OS X with a 2 × 2.66 GHz dual-core Intel Xeon processor. χ²(9) = 6.55 (p = 0.69), AIC = 18.55, Bollen's parsimonious fit index = 0.85. (Right) An optimal model of six paths found through automated “forest growth” in 1dSEM. Runtime = 42.5 s on the same Mac. χ²(9) = 5.34 (p = 0.88), AIC = 17.36, Bollen's parsimonious fit index = 0.93. Notice the χ² value (or discrepancy) and AIC index of both the “tree growth” and “forest growth” networks are lower than the optimal model in [22] while the parsimonious fit index is higher, indicating our optimization algorithm is more robust than the LISREL setup adopted in [22].

Structural vector autoregressive (SVAR) modeling

The striking difference between the VAR model (6) and the SEM equation (7) is that, whereas the former explicitly captures the effects of the history of the regions in the network on the current state, the SEM approach focuses on the instantaneous effects of neural regions. Each approach can identify some features of the network, but they each fail to model other characteristics of the network. For example, the instantaneous correlation among the regions of the network in the VAR model (6) is deemed of no interest and relegated to the residual terms, as evidenced by the residual covariance structure, a time-invariant positive definite matrix E(ε(t)ε(t)^T) with nonzero off-diagonal components. In contrast, SEM assumes that all neural interactions are assumed to be instantaneous and no lagged correlation is considered within and across region, an assumption apparently violated with FMRI data. Because the lagged effects may overwhelm the interregional interactions, the covariance structure estimated from the data might not reflect the true interregional associations, leading to the failed validation of a network and to a biased estimation of path coefficients.

A more realistic brain network would include both ongoing and lagged interactions, as shown in the toy model (1) with two regions. Combining the VAR system (6) and the SEM equations (7), we get

$$X\left(t\right)=A_{0}X\left(t\right)+A_{1}X\left(t\text{-}1\right)+\dots +A_{p}X\left(t\text{-}p\right)+{\mathbf{c}}_1{z}_1\left(t\right)+\dots +{\mathbf{c}}_q{z}_q\left(t\right)+\epsilon \left(t\right).$$

An important property of the above model is that, through a proper choice of A₀, one can have a diagonal covariance matrix for ε(t), unlike the time-invariant positive definite matrix in the VAR model (6). We can further generalize the above model to the following by adding a B matrix in the residuals,

$$X\left(t\right)=A_{0}X\left(t\right)+A_{1}X\left(t\text{-}1\right)+\dots +A_{p}X\left(t\text{-}p\right)+{\mathbf{c}}_1{z}_1\left(t\right)+\dots +{\mathbf{c}}_q{z}_q\left(t\right)+B\epsilon \left(t\right),$$ (11)

where ε(t) ~ N(0, I_n×n), and B is a matrix with n free parameters for the diagonals and zero off-diagonal elements, B = diag(b₁, b₂, ..., b_n). The general system (11) is typically called a structural vector autoregressive (SVAR) model in empirical macroeconomics [14]. A₀ can be viewed as an indicator of the similar contemporaneous effects as in the SEM equation (7) while A₁, ..., A_p are the lagged effects as in the VAR model (6). Essentially, the instantaneous effects among the regions in a network are moved from the residual terms in the VAR model (6) to what is embodied in the elements of A₀ in the model (11). The n diagonal elements of B serve as scaling factors for the residual terms, playing a similar role of the n free parameters for the error variance matrix ψ in the SEM system in (7). With B so defined, the diagonals of A₀ can be fixed to zero so that the instantaneous impact of a region onto itself is relegated to the corresponding diagonal of B. In addition to the assumptions under the VAR model (6), now the residuals of model (11) are mutually independent and therefore uncorrelated with each other; that is, ε(t) ~ N(0, I_n×n). Similar to the VAR and SEM systems (6) and (7), we keep the intercept in (11) without pre-centering the data. These assumptions reflect the fact that the model (11) captures the system dynamics with both instantaneous and lagged effect simultaneously and mutually accounted for in one model.

Model (11) can be reduced to a VAR model,

$$X\left(t\right)=A_1^{\ast }X(t-1)+\dots +A_p^{\ast }X(t-p)+{\mathbf{c}}_1^{\ast }{z}_1\left(t\right)+\dots +{\mathbf{c}}_q^{\ast }{z}_q\left(t\right)+{\epsilon }^{\ast }\left(t\right),$$ (12)

where $A_i^{\ast }={(I-A_0)}^{-1}{A}_i,i=1,\dots ,p;{\mathbf{c}}_j^{\ast }={(I-A_0)}^{-1}{\mathbf{c}}_j,j=1,\dots ,q$; and ε*(t)=(I – A₀)^-1Bε(t). The reduction step shifts the contemporaneous effects from the SVAR model (11) into the parameterization of the residual covariance structure in this reduced VAR system (12). This shows not only that both VAR and SEM are just two special cases under the SVAR scheme (11), but also that an SVAR model can be reformulated as a VAR model with a transformation of matrix A_i into $A_i^{\ast }$. This transformation allows us to solve equation (12) using the VAR machinery, and then retrieve the parameters of (11) in a second step.

The equivalence between the SVAR model (11) and its reduced version (12) provides a convenient means for model validation with instantaneous effects. As the covariance structure of the residuals ε*(t) = (I - A₀)^-1Bε(t) in the reduced VAR system (12) is (I – A₀)^–1BB^T (I – A₀)^–T, we can solve the model (11) by first analyzing its reduced VAR version (12) and obtain the estimated $A_i^{\ast }$, $B_j^{\ast }$, and the covariance matrix of the residuals ε*(t), Σ_ε*. Since the elements in A₀ and B satisfy the following n(n+1)/2 simultaneous equations (not n² due to the symmetry of the covariance matrix),

$${(I-A_0)}^{-1}B{B}^T{(I-A_0)}^{-T}={\Sigma }_{{\epsilon }^{\ast }},$$ (13)

the free parameters in A₀ and B can be estimated by minimizing a negative concentrated loglikelihood function [9,20], similar to the process in SEM. Finally the estimation of A_i and c_j in the system (11) can be obtained through $A_i=(I-A_0)A_i^{\ast }$ and ${\mathbf{c}}_j=(I-A_0){\mathbf{c}}_i^{\ast }$.

Similar to the situation in SEM, the n(n+1)/2 simultaneous equations in (13) put an upper limit on the number of elements in A₀ and B (the number of simultaneous effects or paths in the network) that we could allow to vary and estimate. In other words, we need to fix at least 2n² - n(n+1)/2 elements in the two matrices A₀ and B to identify all the elements in A₀ and B. Because B is a diagonal matrix, this leaves us with at most n(n-1)/2 free parameters in A₀ (or free paths in the instantaneous network) the system (11) could identify; the simultaneous system (13) is called under-, just-, or over-identified if the number of free parameters is less than, equal to, or more than this upper bound of n(n-1)/2. Each element in A₀, if not free, can be set to either 0 or some constant (e.g., when a path strength is known). An over-identification likelihood ratio χ² test with n(n-1)/2 - k degrees of freedom is available for calculating the goodness-of-fit, where k is the number of free parameters in A₀ [20]. It is the a priori structural restrictions placed in A₀ that provide structural meaning in SVAR.

Suppose we have a hypothesis about a network of instantaneous effects with k paths (k < n(n-1)/2). By allowing the corresponding k elements in A₀ to vary while keeping the rest fixed to constants (known value or zero), we can test with the over-identification likelihood ratio χ²-test whether the proposed instantaneous network is supported by the data, and simultaneously obtain the estimates of the k paths, if the model holds. Unlike the SEM approach for instantaneous network validation, the SVAR model validates the network accounting for the lagged within- and cross-region correlations.

Similar to the situation with SEM, we can also adopt a model comparison or model search approach with the instantaneous network coded in the A₀ matrix based on the over-identification likelihood ratio χ²-test or on various other fit indices.

On the other hand, an SVAR model can also be converted to, and thus is equivalent to, an SEM system, allowing us to validate both the instantaneous (A₀) and lagged (A_i, i = 1, ..., p) effects. This equivalence also opens up the possibility of model comparison and model search for both the instantaneous (A₀) and lagged (A_i, i = 1, ..., p) networks through the reduced SEM format of an SVAR model.

We have implemented the above modeling approach with SVAR in a program, 1dSVAR, in the open source language R [20] using the packages vars for SVAR modeling [20] and network for path drawing [21]. The solution of the equations (13) is achieved through either a scoring algorithm for the maximum likelihood (ML) estimates or an optimization scheme based on Nelder-Mead, quasi-Newton and conjugate-gradient algorithms [20]. Such an implementation allows us not only to combine two modeling methodologies, VAR and SEM, and two modeling strategies, data-driven and model validation, into one model framework, but also to estimate both historical and immediate effects in one consistent system. Compared to SEM, this should improve statistical power in detecting instantaneous effects among the regions in a given network. Similar to SEM, SVAR needs enough number of data points (e.g., at least 100 [24]) in each ROI time series to obtain stable results.

Another group introduced a similar approach in a visual attention experiment with data possessing a time resolution of 3 seconds [11], but their approach differs from ours in the following respects.

1. The approach in [11] adopted a pure model validation approach with both instantaneous and lagged paths pre-selected, while 1dSVAR with the model (11) has the flexibility of various uses, for example, the mixture of a data-driven approach for lagged effects (A_i, i = 1, ..., p) and model validation for instantaneous effects (A₀), a data-driven approach for lagged effects combined with model comparison or model search for instantaneous effects, model validation for both instantaneous and lagged effects, model comparison and model validation for both instantaneous and lagged effects.

2. The instantaneous paths in A₀ of the system (11) can be specified after the reduced form VAR is estimated, as opposed to simultaneous specification in [11]. A potential benefit is that the lagged effects in the reduced model (12) may provide guidance in specifying the instantaneous paths. Unlike the model specification in [11], the instantaneous effects matrix A₀ in system (11) does not have to bear the same structure as the lagged matrices A_i, = 1, 2, ..., p (i.e., the lagged effects), and there is no strong reason to believe that the two structures must be the same (see more in the Discussion section). The SVAR approach allows for more flexibility in modeling instantaneous and lagged effects. In the end, however, the choice of model parameters depends on the network at hand, data modality, and knowledge of prior connectivity. These decisions are left to the researcher.

3. Model (11) is capable of addressing confounds that account for effects irrelevant to system dynamics, such confounds include temporal discontinuities (e.g., data concatenation) that were not properly modeled in [11], and other covariates like head motion effects, slow drift, task/condition effects of no interest, physiological fluctuations, and irregularities. Addressing these factors at the modeling stage allows for minimal pre-processing. In addition, 1dSVAR does not require pre-centering the regional time series before the analysis.

4. 1dSVAR is specifically written for SVAR modeling in the open source language R while the analysis in [11] was performed with a generic procedure in a commercial package, SAS PROC CALIS.

Application

We applied the VAR modeling approach to the data from 14 control subjects and 16 major depressive disorder (MDD) subjects from a resting-state experiment [29]. BOLD data were acquired on a 3.0 Tesla GE Signa scanner with 18 axial slices, a voxel size of 3.44 × 3.44 × 5 mm³, repetition time (TR) = 1200 ms, echo time TE = 30 ms, flip angle = 77°, field of view (FOV) = 220 mm, scanning time = 5 minutes (250 brain volumes in the time series). The parameters for the structural data are: voxel size = 0.859 × 0.859 × 1.2 mm³, 124 axial slices. Further information about the data can be found in [29].

The spiral image time-series data were preprocessed in AFNI [8] with the following steps: slice timing correction relative to the middle axial slice, head motion correction through alignment using Fourier interpolation and a two-pass registration algorithm, spatial smoothing with a full width at half maximum of 4 mm, and spatial normalization of all 30 subjects into Talairach space.

The primary objective of the analysis was to conduct VAR analysis on a network of structures found to exhibit anomalous function in depression. Identification of this network assumed the ventral anterior cingulate cortex (vACC) is a primary convergence zone of aberrant neural function in depression, an assumption that has been confirmed in prior research [30,31]. This network was identified in three steps: a) localizing a vACC region that was over-recruited in the default mode network (DMN) [32] in depression, as has been previously found [33]; b) conducting first-order bivariate autoregressive analysis with 3dGC on the data from each subject using vACC as a seed region and obtaining the vACC-to-whole-brain and whole-brain-to-vACC path estimates and their t-statistics; and c) conducting voxel-wise comparisons of the resulting t-statistic maps from MDD and control groups to identify regions with abnormal advance prediction of vACC activity in depression as well as regions in which activity was predicted by vACC activity differentially in depressed relative to control subjects.

[33] showed that the vACC is over-recruited in the DMN in MDD. We sought to replicate this finding in order to identify the vACC seed region for this study. First, we identified the DMN in each participant by conducting a seed region-to-whole brain time-series correlation analysis with AFNI's 3dDeconvolve. We then compared vACC involvement in this network in both MDD and control subjects. To identify the DMN in each subject, we averaged BOLD time-series data from medial prefrontal and posterior cingulate seed regions (12 mm diameter, centered at (-1, 47, -4) and (-5, -49, 42), respectively) into a single time series and correlated this time series against preprocessed voxel time-series data from the rest of the brain. Nuisance covariates included in the regression model were three translational, three rotational head-motion estimates and third-order polynomials for slow baseline drift. To remove physiological noise from voxel time series, we also included as a nuisance covariate of average time-series data from a grey matter mask drawn on the Montreal Neurological Institute N27 brain. The correlation maps resulting from this procedure were then Fisher Z-transformed and compared voxel-wise, between groups, using a two-sample t-test with 3dttest in AFNI over the full extent of the vACC. The vACC was defined as the portion of the Talairach-defined [34] cingulate gyrus inferior to the most anterior aspect of the genu of the corpus callosum. The statistical threshold was set corresponding to p = 0.05, corrected for multiple comparisons across vACC voxels with cluster thresholds set through Monte Carlo simulations with AlphaSim in AFNI.

We used 3dGC to explore and identify regions whose time courses predicted subsequent vACC activity and regions whose activity was predicted by preceding vACC activity abnormally in depression in a first-order bivariate autoregressive model. Nuisance variables in the regression model were the same as those used to identify the vACC ROI: six orthogonal motion estimates, third-order polynomials, and averaged gray-matter signal. The seed region time-series in the model was preprocessed BOLD signal extracted from a sphere centered on the peak of the vACC ROI (5 mm diameter, centered at (-2, 6, -7)) identified in the manner described above. We estimated time-directed prediction between BOLD time-series across a lag of one TR (1200 ms) in order to maximize the temporal resolution of our estimates of neural influence. Finally, voxel-wise comparisons of resulting path coefficients across diagnostic groups were performed using a two-sample t-test (p = 0.05, corrected) across the whole imaging volume with 3dttest.

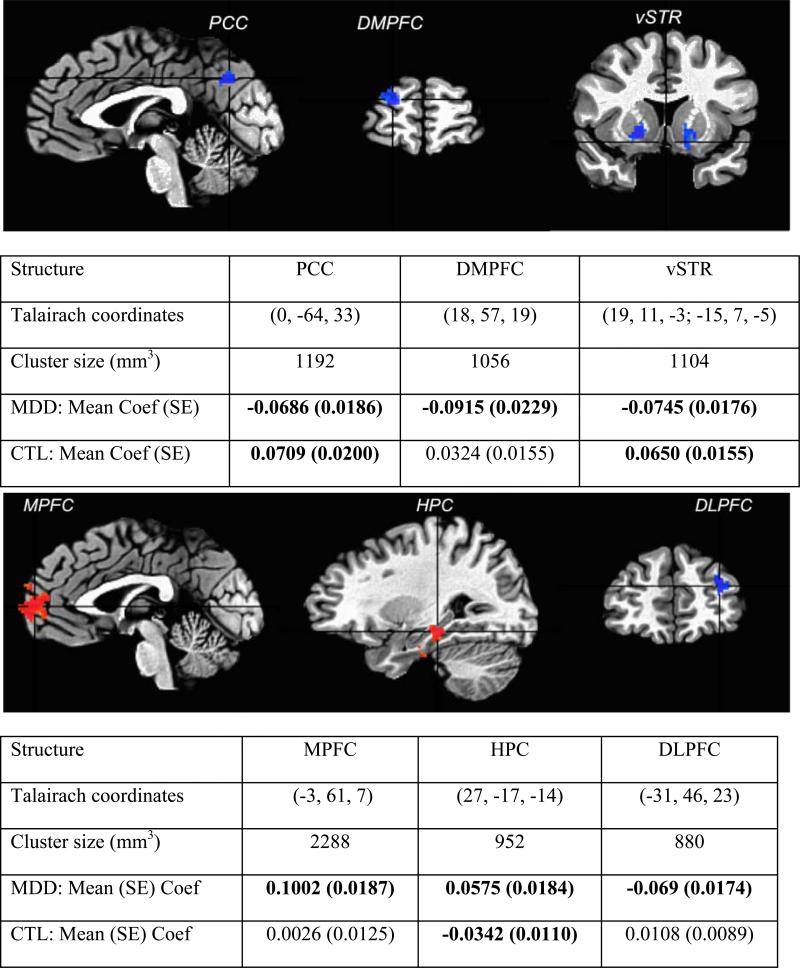
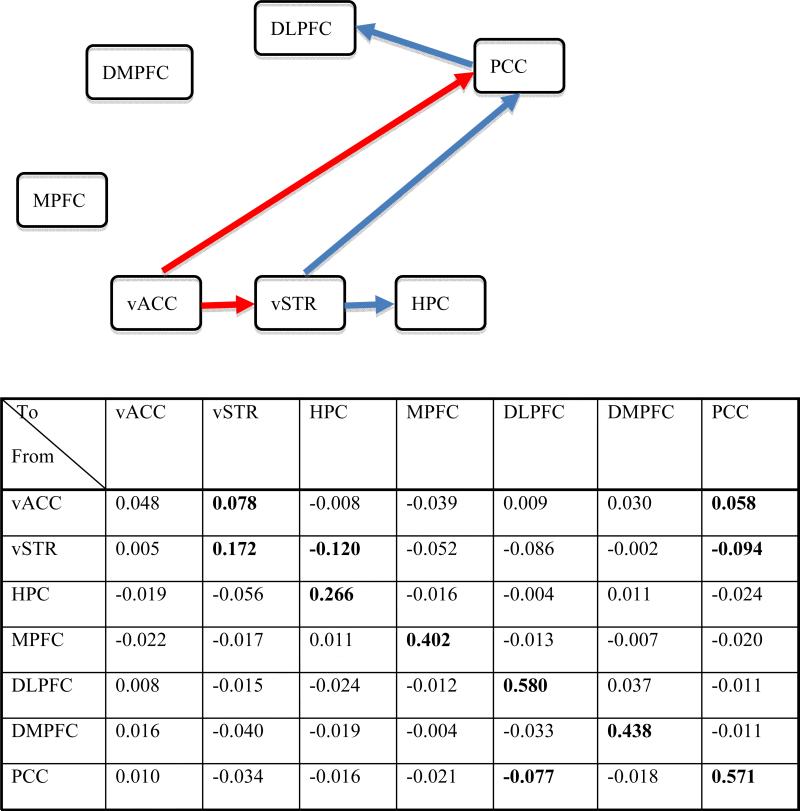
For each subject, preprocessed time-series were extracted, using 3dmaskave in AFNI, from peak voxel locations in the regions that showed differential temporal relations with vACC between the MDD and control subjects. Six regions were identified (Fig. 4): hippocampus (HPC), medial prefrontal cortex (MPFC), dorsolateral prefrontal cortex (DLPFC), dorsomedial prefrontal cortex (DMPFC), and posterior cingulated/cuneus (PCC), and ventral striatum (vSTR). These time-series for each subject were then extracted and entered into further VAR analysis.

Fig. 4.

Six regions showing between-groups differences in leading and lagging temporal association with vACC. The individual subject analyses were performed with a first-order bivariate autoregression in 3dGC. Among the six regions, three are one-lag effects from seed (vACC) to the rest of the brain (upper panel), while the other three are from the rest of the brain (lower panel) to the seed identified. Bold numbers in the tables indicate a significance level of p < 0.05, FWE corrected. The color, red, in the brain images means the path strength contrast is positive between the MDD and control (CTL) groups, and vice versa for the blue color.

For demonstration, we only present network modeling with data from the control group. A VAR(1) model was chosen based on four criterion indices provided by 1dGC which suggested appropriate lag orders of 1 or 2. The time series data from the seven ROIs were analyzed in 1dGC for each of the 14 control subjects with a VAR(1) model in (6) with seven regions as endogenous variables plus second-order polynomials, six head motion parameters and averaged gray matter signal as exogenous variables. The resulting path coefficients characterizing the strength and direction of one-lag effects among the regions, and their corresponding t-statistics from each subject, were then entered into group analysis, using a linear mixed-effects multilevel model [17]. Five interregional paths of one-lag effect were identified (p < 0.05, uncorrected) at group level (Fig. 5). Correction for multiple tests on lagged coefficients (VAR and lagged component of SVAR) is problematic because of the large number of parameters estimated. A simple VAR(1) with n regions would involve at least 2ⁿ parameter estimates, if one is to adopt the conservative Bonferroni approach. Although the parameters are not independent, there is no current approach for multiple comparisons correction.

Fig. 5.

The table shows the group-level one-lag path coefficients estimated with 1dGC for the control subjects. Each number along the diagonal shows the within-region effect while each off-diagonal value indicates the path strength from the region in the row to the region in the column. The numbers in bold indicate a significance level of two-tailed p < 0.05, uncorrected. All regions except vACC have significant serial correlation, while the VAR(1) model indicates five significant directional paths: vACC → vSTR, vACC → PCC, vSTR → HPC, vSTR → PCC, and PCC → DLPFC. The network is shown with only interregional paths because serial correlation within a region is general not of interest: red, excitatory effect; blue, inhibitory effect. In control subjects, MPFC and DMPFC are not identified to be involved in the network.

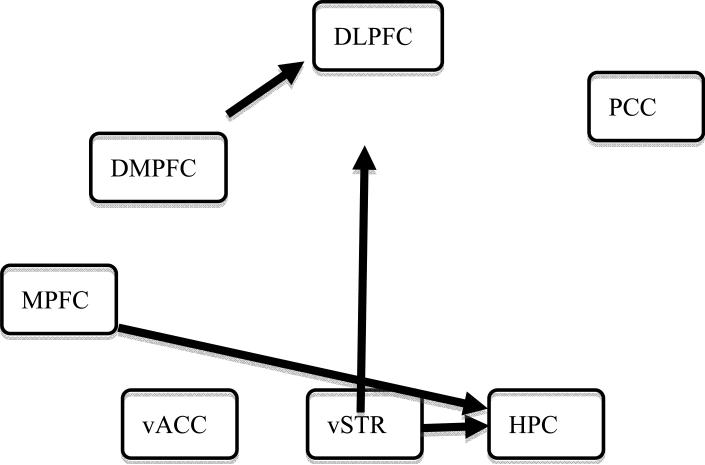
For comparison, we also conducted group analysis with the approach usually adopted in the literature [10] by taking the logarithm of the path F-statistic from each subject as input. The result (Fig. 6) is dramatically different from the one observed with 1dGC (Fig. 5). Importantly, no information regarding the path strength and its sign is available. Further, such a practice is problematic as it assumes a Gaussian distribution of the logarithm of the path F-statistic.

Fig. 6.

Path diagram identified with a one-sample t-test on the logarithm of the F-statistics from 14 control subjects, as typically done for group analysis (e.g., [10]). The network revealed is very different from the one (Fig. 5) identified with 1dGC, and the path strength at the group level cannot be identified since such information is not considered as input for group analysis with this approach. Information about the sign of the paths is also lost.

With the one-lag network identified from group analysis in 1dGC (Fig. 5), we ran SEM at group level with 1dSEM and 1dSEMr. The processing scheme of individual subject ROI time-series data was the same as in [22]. This analysis estimated path strengths of instantaneous effects that are quite different in terms of both magnitude and sign from the lagged effects in 1dGC (Table 1); moreover, the one-lag network was rejected as a reasonable model for the instantaneous network with (χ²(16) = 331, p < 10^-16). That is, SEM did not validate the contemporaneous network suggested from the one-lag paths identified with the VAR(1) model. This is not really unexpected, considering the fact that some values (e.g., between vACC and vSTR, vACC and PCC, etc.) in the contemporaneous correlation matrix are relatively low (Table 1, upper), including the ones that correspond to the paths specified in the to-be-validated network. There are a few possibilities for this failure: a) many cross-region associations are not contemporaneous; b) most variability in the data is from within-region temporal effects, cross-region delayed effects, or confounding factors that are unaccounted for in the SEM system; c) the time resolution of 1.2 s is likely too coarse to identify the real lagged network with VAR(1) in the first place; and d) the instantaneous network may not be the same as the one-TR lagged network.

Table 1.

Correlation matrix of the seven regions estimated with data from 14 control subjects.

To From	vACC	vSTR	HPC	MPFC	DLPFC	DMPFC	PCC
vACC	1	0.094	-0.044	0.035	-0.006	0.058	-0.039
vSTR	0.094	1	0.0498	-0.166	0.009	-0.050	-0.207
HPC	-0.044	0.0498	1	-0.034	0.337	0.194	0.202
MPFC	0.035	-0.166	-0.034	1	0.008	-0.046	-0.002
DLPFC	-0.006	0.009	0.337	0.008	1	0.607	0.253
DMPFC	0.058	-0.050	0.194	-0.046	0.607	1	0.135
PCC	-0.039	-0.207	0.202	-0.002	0.135	0	1

The instantaneous path coefficients estimated by path analysis with 1dSEM are: vACC → vSTR: 0.094; vSTR → HPC: 0.0498; PCC → DLPFC: 0.2535; vACC → PCC: -0.0195; vSTR → PCC: -0.2055. Model specification was based on a one-TR lagged network identified from a VAR(1) model (Fig. 5). The SEM analysis failed to validate the model as an instantaneous network. Although 1dSEMr shows two significant paths (p < 0.05, uncorrected), PCC → DLPFC and vSTR → PCC, the significance is not reliable when correlation coefficients are provided as input in path analysis (see details in the Discussion section).

None declared.

We proceeded to run a SVAR(1) model with the same endogenous and exogenous variables as we did with 1dGC. All the one-TR lagged effects were set as free parameters in 1dSVAR, while the free parameters for the instantaneous effects in A₀ matrix in (11) were preselected based on the result from the one-TR lagged network identified from 1dGC; all other path coefficients were set to zero. Such specification of the instantaneous effects is purely for demonstration, as we do not have any prior knowledge of the instantaneous network.

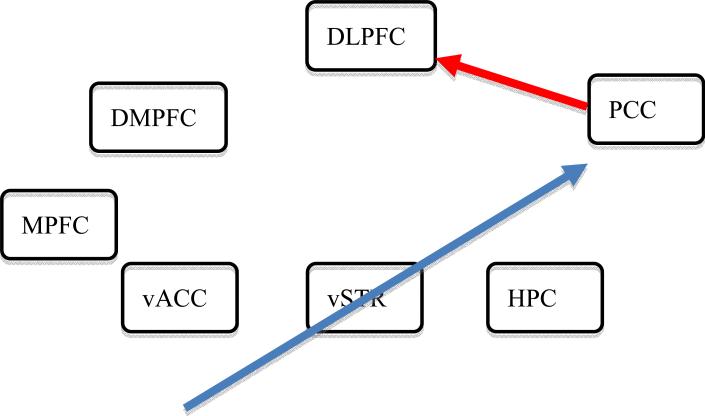
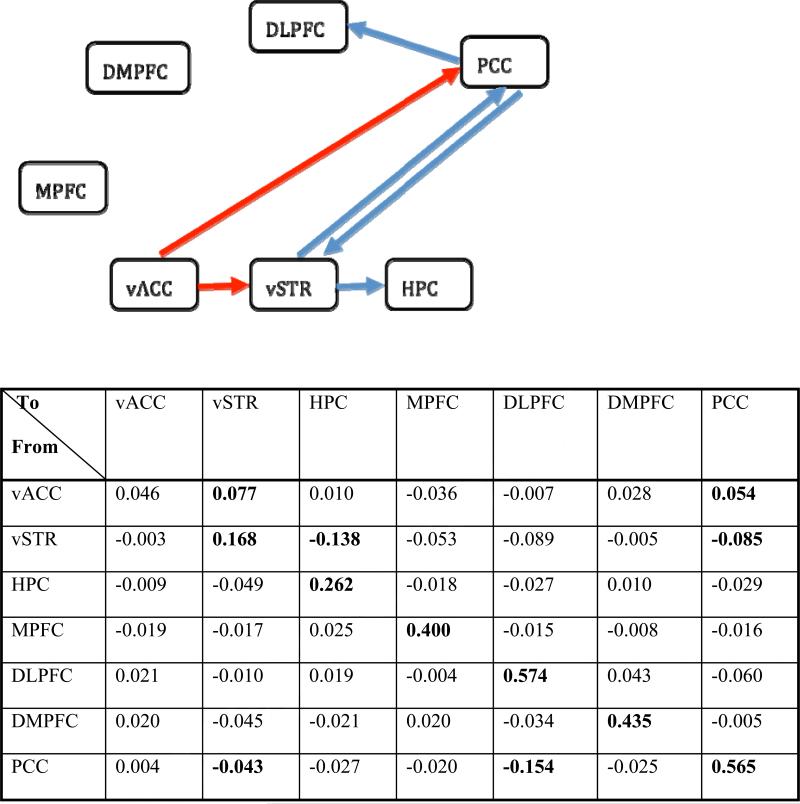
With the lagged effects accounted for, the instantaneous effects at the group level among the seven regions (Fig. 7) from the SVAR(1) model have the same signs as the SEM analysis showed, even though the values are different. Furthermore, two instantaneous paths are identified at a significance level of two-tailed 0.05 (uncorrected). Normally, a Bonferroni correction should be made with the number of multiple comparisons being the number of paths tested. A correction on our illustrative example would fail to show significant paths. This may be due to an incorrect network model or to the low power due to the limited sample size (13 subjects) in this example. With the instantaneous effects accounted for, the one-TR lagged effects among the seven regions (Fig. 8) are relatively close to what the VAR(1) analysis showed (Fig. 5) except that the path PCC → vSTR was identified with 1dSVAR (p = 0.023), but not with 1dGC (p = 0.073), which shows that modeling the instantaneous effects increases the inference power for the lagged effects.

Fig. 7.

Group-level instantaneous effects identified in 1dSVAR for control subjects with a model incorporating the lagged effects revealed through VAR(1) in 1dGC are: vACC → vSTR, 0.047; vSTR → HPC, 0.055; PCC → DLPFC: 0.064; vACC → PCC: -0.060; vSTR → PCC: -0.058. Each value indicates the path strength from the row region to the column one. Two paths (shown in the network), vACC → PCC and PCC → DLPFC, were identified at a significance level of p < 0.05 (two-tailed), uncorrected; excitatory effects are shown in red and inhibitory effects in blue.

Fig. 8.

The table shows the one-lag path coefficients for the control group estimated with 1dSVAR. Each diagonal number shows a within-region effect while each off-diagonal value indicates a cross-region strength from the row region to the column region. The numbers in bold indicate a significance level of two-tailed p < 0.05, uncorrected. All regions except vACC have significant intraregional serial correlation, while the SVAR(1) model indicates five significant directional paths: vACC → vSTR, vACC → PCC, vSTR → HPC, vSTR → PCC, and PCC → DLPFC. The network is shown with only interregional paths: red, excitatory effect; blue, inhibitory effect. MPFC and DMPFC are not identified to be involved in the network among control subjects. The path strengths and network are similar to the ones identified with 1dGC (Fig. 5) except for the one-lag path PCC → vSTR identified with 1dSVAR (p = 0.023), but not with 1dGC (p = 0.073).

It is noteworthy that the two paths in the instantaneous network (Fig. 7) that were revealed through the SVAR(1) model have the opposite sign relative to their counterparts in the one-TR lagged network identified in the same analysis. This may appear strange, but could occur because the network for the instantaneous effects specification was adopted from the one-lag network revealed from the VAR(1) analysis, which might not be a valid model for the instantaneous network.

Discussion

VAR and SEM are two popular connectivity methodologies to make inferences about connectivity from BOLD time-series data. Each captures unique network features. With VAR we adopt a purely data-driven approach and look for the lagged effects among the regions. It is worth emphasizing that the focus on the lagged effects in VAR does not mean the contemporaneous effects are not properly handled in the system; instead, they are accounted for as effects of no interest in the residuals. Such lagged effects, if significant, are usually interpreted as the popularized Granger causality relation. In contrast, SEM assumes no lagged effects and models the contemporaneous interactions among regions. Its main capability is its hypothesis-oriented core, checking and validating a model derived from prior knowledge regarding connectivity. In addition, when such prior knowledge is scarce, we can use SEM as an exploratory tool to compare alternative models based on various fit indices. This model comparison methodology can be extended to model growth by exhaustively searching all possible alternatives, and to provide a speculative or null hypothesis for further exploration.

The SVAR model, combining both VAR and SEM, accounts, under one model framework, for the variability in the data from both contemporaneous and lagged effects. This merging not only improves model fit, but also likely introduces gains in statistical power by revealing potential causal effects among the regions in the network. Not only does it benefit from the modeling power and explanatory capability of its component approaches, but, as we will now discuss, it also avoids serious limitations and assumption violations inherent to each approach when applied alone.

Lagged effects account for delayed influence of one region on itself and others. Whether these effects stem form actual connectivity or from confounding effects, it is best to include them in the connectivity model. One of the assumptions in SEM is that there is no temporal autocorrelation in each region's data; indeed such an assumption of independent observations is a prerequisite for ML estimation. However, even the residuals in the ROI time series are significantly auto-correlated due to factors such as physiological effects. The correlation in the time-series data acquired under a task or condition is obviously even more substantial. This raises a serious issue concerning the reliability and robustness of the SEM results; this is either ignored or unrealized in the FMRI community. Work-round solutions were proposed to counter this problem and involved artificially reducing the degrees of freedom by using either: a) the ratio of residual variance to the total variance in the principal component, averaged across all regions [22]; or b) with a factor of $\frac{1-r}{1+r}$ averaged across all regions [25], where r is the first-order autocorrelation coefficient of regional time-series data. Such compensation leads to a decrease in the model χ²-test, making it easier to accept the model. Nevertheless, this will not correct for the bias embedded in the path coefficient estimates that is due to the variability unaccounted for in the serially correlated data in a typical SEM analysis, which, itself, will decrease the statistical power, leading to a failure to validate the hypothesis. With the SVAR approach, lagged effects are explicitly modeled by the VAR component, thereby improving the power of the SEM component.

The choice of lag order depends on a number of factors including the time series sampling rate, the transfer function from neuronal to observed signals (HRF in FMRI), and the underlying biological model. For a given network, our implementation of VAR and SVAR provides guidance from criteria in choosing lag order: AIC, FPE, HQ, and SC (or BIC). Whereas incorporating too many lags will sacrifice model efficiency, too few lags may leave some interregional interactions unaccounted for. Each of the four criteria differ slightly in how they penalize model complexity, but in general, AIC and FPE tend to overestimate the lag order with relatively a large number of data points, while the most parsimonious SC (or BIC) usually performs well for low-order VAR or SVAR. In practice, for whole-brain FMRI experiments, limitations introduced by the sampling rate constrain the lag order to 1 or 2.

As part of the input for solving an SEM model, one needs to provide either a covariance or a correlation matrix of observations. This choice significantly affects the interpretation of the model coefficients as well as the statistical inferences made about these coefficients. When covariance matrices are used, a path coefficient from region A to B reflects the amount of change at region B, in units of standard deviation of region B, if region A changes by one standard deviation, while controlling all other regions in the network. Such an interpretation of path strength hinges on ML estimates being scale free (i.e., linearity is maintained when a variable is scaled) and the ML function being scale invariant (i.e., ML remains unchanged regardless of variable scale [24]). In contrast, when a correlation matrix is used, thereby standardizing the observations at each region, the ML estimation is no longer scale free or scale invariant. Moreover, the strength of a connection from region A to region B now indicates not only the presumed effect of region A on region B, but also the effects of other connections in the model [35]. Because of this interdependence, the magnitude of a connection between two regions can no longer be readily comparable from one group to another or from one study to another. With correlation matrices, [24] proposed reducing the path strengths to three levels, “small” (~0.1), “medium” (~0.3), or “large” (≥ 0.5). Despite their shortcomings, correlation matrices are commonly used in FMRI (e.g., [22,28,25,36,37]), including 1dSEM. Moreover, confidence intervals and the Student t-tests for path coefficients, whenever provided, are neither meaningful nor interpretable [38]. To circumvent this problem, bootstrapping [25], constrained estimation [24], and the delta method [39] can be used.

The prevalent use of correlation coefficients in SEM stems from their capacity to confer an apparent reduction in the number of parameters to be estimated. Tests result in a χ²(n(n -1)/2 – k) goodness-of-fit test, where k is the total number of paths or nonzero parameters in the path matrix plus the number of regions in the network, n. With regional observations standardized with correlation, the model has fewer parameters to estimate. The upper bound on network complexity, that is, the number of paths that can be considered, rises to n(n+1)/2 path coefficients (e.g., [22,28,25], instead of n(n-1)/2 (e.g., [37]). However, this increase in degrees of freedom is artificial, as variances have already been estimated from the same data. Other reasons exist for standardizing observations prior to conducting SEM, but those typically occur when the variables have different units [24].

Confounding effects such as head motion, slow baseline drift, physiological fluctuations, and temporal discontinuities, must be modeled; otherwise, they become part of the residual term, potentially distorting statistical inferences including path identification and network interpretation. These confounds are optimally incorporated into the connectivity model, as they are typically not independent of the model's effects of interest. However, in most SEM implementations, these confounds are not a direct part of the model, and are regressed out of the data prior to the estimation of the covariance/correlation matrix. This approach can bring about biased estimates and incorrect χ² values for model validation. In contrast, the VAR or SVAR models do allow for a direct incorporation of confounds in the model. Therefore, even when the prior interest is an SEM model, it is best to use the SVAR framework which better handles confounding effects. In this case, the number of data preprocessing steps, such as slice timing correction, should be kept to a minimum; band-pass filtering, if necessary, should be handled directly in the model.

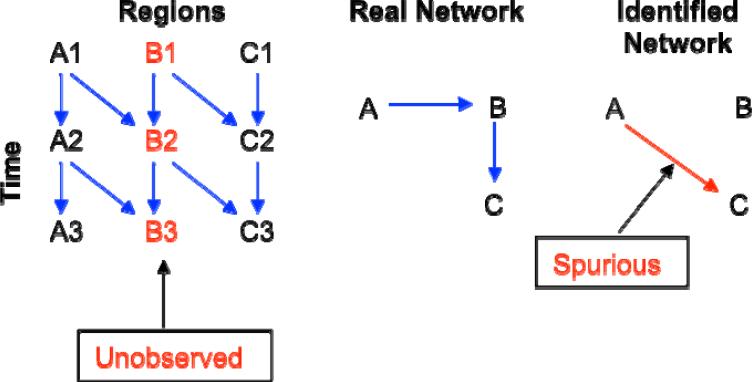
Suppose that three regions form a network of A → B → C, as illustrated in Fig. 9. If area B were not included in the network model, then a bivariate model would detect a significant path from A to C. While the result is informative in showing a connection between A and C, the path and its strength could be completely different if B had been considered in the model. Such a failure to include an essential region in the model underscores the importance of network building (Fig. 9) and the consideration of alternate models.

Fig. 9.

Suppose that a network with three regions has a true causal relationship of A → B → C (middle), and that data collected with appropriate temporal resolution (left) reveal the real network of delayed effects with a lag of one time unit. However, if region B is not included in a VAR or SVAR model, we would identify only the path A → C (right) in the network of delayed effects with a lag of two time units, leading to a spurious finding (red arrow in the right map).

Exclusion of regions can also affect SEM models [24]; consider instantaneous, instead of lagged effects between the regions depicted in Fig. 9. Regardless of the model used, one can improve the model by adding new candidate regions to it. If unsure about inclusion of a region, one can run two models, one with and the other without the region, and examine how their explanatory significance differs at both whole-model and individual-path levels.

It can be argued that no region in the brain can exert an instantaneous effect on another region. If the sampling rate is high, then the interactions are best captured by a model incorporating lagged coefficients (e.g., VAR). VAR modeling has been successfully applied in the analysis of FMRI data with high spatial resolution and short TR (e.g., single slice data in rats with a TR of 200 ms [40]) or other brain imaging or electrical activity data such as MEG and EEG. When the sampling rate is too coarse relative to the expected lags, interactions appear instantaneous and are best captured with a model with instantaneous coefficients (e.g., SEM). SVAR can handle both situations, and the user is left to decide which part of the model is of interest. However, much like the case with a missing region in the model (Fig. 9), a coarse sampling rate, which might miss an interaction [41], can result in a distorted rendering of the actual network. Fig. 10 illustrates this point. With inadequate temporal sampling, a network with connections from A → B → C can look like one with connections from A → C only.

Fig. 10.

Suppose that a network with three regions has a true causal relationship of A → B → C (middle), and that data with adequate temporal resolution (left) reveal the real network with a VAR or SVAR model incorporating a lag of one time unit. However, if the middle time point is not available, we would identify the path A → C (right) with a lag of two time units, leading to a spurious finding (red arrow in the right map).

With model validation, we begin with a predetermined network model and validate whether the data can support such a model (i.e. whether we fail to reject the model). The analysis does not constitute proof of connectivity. In conventional statistical testing, it is usually the rejection of the null hypothesis (e.g., no difference between the activation of two conditions), which is controlled through a type I error or significance level, that is of interest to researchers. However, in model confirmation the null hypothesis is H₀: the model is correct, and it is the failure to reject H₀ that is of interest to the investigator. This difference from typical null hypothesis rejection requires extra caution when performing model validation. Because of this subtle difference, the goodness-of-fit χ²-test might be better called “badness-of-fit” test because the higher the statistic value, the worse the fit. When a model is validated, statistically it means that the model (6) is not rejected based on a relatively small χ² value (e.g., p is greater, not less, than 0.05), it does not necessarily indicate that the data provides a proof for the assertion of causality in the model. This is so because the data may also provide equivalent support for many other different models, even ones that render a lower χ² value. In other words, the same data are very likely consistent with many potential models, and a currently accepted network is only a “not-disproved” model. Connectivity is usually determined by also using information from other sources [38] such as DTI or invasive axon tracing studies.

An alternate approach is to relax connection constraints and perform a search for connections that provide the best fit. Whether such a search is more appropriate than the model validation approach is an open question. Automated model search has acquired some popularity in SEM with FMRI data [22,42,25,43] and in SVAR [12]. However, searching based purely on the ML discrepancy measure is problematic. First, it is unclear when it is appropriate to stop the search, other than at the upper limit of free parameters, n(n+1)/2. Adding paths always lower the discrepancy, presenting a “better” model. Even if a fit criterion is adopted with a compromise between model fit and complexity/parsimony, various versions of such criteria may provide different stop points. Furthermore, a “best” model revealed through a numerically optimized process would most likely be one among a huge number of possible models, and these models could also be supported by the same data with a relatively small “badness-of-fit” χ² value. Some of these models may have roughly equivalent fits even if the “best” one wins out by a tiny discrepancy measure, but it is not clear that this small difference in the fit measure means anything. Also troubling is the possibility that these models can lead to substantially different interpretations about the underlying network. In other words, an “optimal” network from a given model search is usually not stable because a different search method, or different software package, will most likely lead to a different model, as clearly shown in Fig. 3.

On some occasions, model comparison may be justified, especially when the compared models are nested (e.g., trimming or building) and the associated χ²-test is meaningful. For example, if one is not sure about one specific path, a comparison between the two models, one with and the other without the path in question, will yield a χ²-difference statistic, showing whether the two models differ statistically. In addition, various fit indices are available to assess model comparisons, such as Akaike's Information Criterion (AIC), root mean square error of approximation (RMSEA), comparative fit index (CIF), goodness fit index (GIF), and others [24], are available to compare models,. These fit measures differently weight model fit and the model parsimony/complexity, and may result in different “better” or “best” models.

The three models presented here assume that the hemodynamic response function is uniform across regions. However, this is demonstrably not always the case in the task-related FMRI time-series data [44]. To the extent that such variations are not reflective of brain function (e.g., they may merely reflect regional differences in neurovascular coupling), they can yield spurious connectivity results when lagged effects are of interest [45]. Furthermore, HRF variability across regions affects SEM and the instantaneous component of SVAR by making them less likely to validate a model.

In making group-level model inferences, the fixed effects approach [22,28,42,25,12] combines observations from all the subjects and fits one model to them. However, fixed-effects analysis limits the generalization of the results to individual cases instead of to a greater population. Group-level inferences are better made with random effects analysis, assuming sufficiently many subjects are studied. Furthermore, it is best to carry both effect size and variance to second-level linear mixed-effects meta-analysis [17]. This two-tier approach allows us to account for both within- and cross-subject variability, and to make more robust population-level generalizations.

Networks are typically modeled from data obtained during a single state. For example, for a simple experiment with two alternating tasks, the observations used are only those collected during execution of one of the tasks. A task could also be a rest condition, provided proper pre-processing is used [46]. For single-task experiments, including resting-state FMRI, selection is not a problem. In block design FMRI experiments, one could select observations from steady state periods during performance of the task of interest, assuming temporal discontinuities are properly handled. For fast, event-related experiments, this selection is not possible because of overlapping responses between experimental conditions. One approach in addressing this problem is to model remaining task-related activity as a confounding factor. This approach is imperfect because trial-to-trial variability of all tasks remains unaccounted for.

SVAR modeling of neural networks permits a more accurate account of causality than VAR alone. It is the controllability of one region by another, not just the temporal precedence, that is the hallmark of causal relationship. The SVAR approach is particularly useful when the time interval in the data is of concern and considered too long, when the hemodynamic response varies too much across regions, and/or when confounding effects such as vascular response may complicate the delayed effects. Although lagged effects are still estimated, each lagged path is only suggestive, as shown in Fig. 10 when the time resolution is too coarse to identify the actual lags in the network. When interregional connectivity for the instantaneous effects is unknown, a new approach [47] is possible whereby non-Gaussianity for the residuals and acyclicity for the paths are assumed in the SVAR model. Compared to SEM, this SVAR approach to modeling instantaneous effects has three substantial benefits. First, the analysis is performed at the individual subject level, and group effects are analyzed through linear mixed-effects meta-analysis instead of fixed-effects analysis [22,25]. Moreover, with the regional time series as input in SVAR, the controversial issue of correlation versus covariance for SEM is easily addressed through simultaneous equations (13) involving the covariance structure, confidence interval and t-statistic for each individual path, which can be obtained without the complications involved in SEM. Second, the troubling assumptions of temporally and mutually independent data in SEM are no longer a concern in SVAR in which the temporal correlations are modeled through the lagged effects, and there is no need for a kludge solution of adjusting degrees of freedom. Finally, unlike SEM, SVAR allows for minimal pre-processing; confounding effects such as data discontinuities and task/condition effects of no interest are better handled as covariates in the model.

Granger causality modeling is a popular term in the FMRI community for VAR [2,18,6,13]. It is undergirded by two specific concepts: a) causes must temporally precede effects; and b) causality can be inferred from an F- or χ²-test that shows the amount of variability of lagged effects accounted for by each connection. However, as we have discussed, temporal precedence may fail to be detected if the temporal resolution is not fine enough; instead, simultaneity may appear [48]. Thus, Granger no-causality does not necessarily mean that the regions in a network are not correlated with each other. Explicitly incorporating the instantaneous effects into an SVAR model permits a more accurate account of network causality than VAR alone in terms of network modeling. It is the controllability of one region by another, not just the temporal precedence, that bears the hallmark of causal relationship.

Moreover, although the overall F- or χ²-test serves its purpose well in a bivariate autoregressive model when using a seed region to search for other regions that may have lagged effects with the seed, such a test value loses the sign information (excitation or inhibition) when taken to group analysis. Similar to the meaning of the coefficient in a univariate regression model, the lagged path coefficient from region A to B in a VAR(p) or SVAR(p) models shows the amount of change at the current moment in region B when region A varies by one unit at a given lag. That is, a path coefficient is an indicator of the effect of the history of one region on the current state of another region. The path coefficient and its t-test preserve all the necessary information at the individual level and provide more accurate information in group analysis. It is because of these two improvements that we avoid the conventional usage of the term “Granger causality” to denote the current approach.

Summary

Connectivity analysis in FMRI data explores the interactions of brain regions under various perceptual, cognitive, and affective conditions. With a seed-based approach, we seek to identify regions that have causal relations with the seed. In an ROI-based connectivity analysis, causal effects of one region on another are inferred from a model of inter-regional interactions among a predetermined set of regions. In addition, some alternative models can be explored, cautiously, through model comparison and model search. In this paper we discuss two primary connectivity approaches, VAR and SEM, that are widely adopted in both seed-based and ROI-based network modeling, and explain the meaning of these connectivity measures and the kinds of information they convey about brain function. Their strengths and limitations are presented, and, to address these difficulties, we introduce the SVAR approach that combines the two models. This synthesis opens up a flexible platform for various modeling strategies. We emphasize strongly that model validation, comparison, and search should be led as much as possible by theory as opposed to purely numerical optimization [24]. We also present our open-source programs freely available in AFNI for download, two programs for VAR modeling (3dGC and 1dGC), two for SEM (1dSEM and 1dSEMr), and one for SVAR (1dSVAR). We believe that the SVAR modeling strategy holds great promise for modeling simultaneous and lagged effects in neural network.