Density minimum in supercooled confined water

Recent papers in PNAS, here labeled I (1) and II (2), have proposed that when water confined in the porous silica matrix MCM-41-S with a 15-Å pore diameter is supercooled, it reaches a density minimum at around 200 K. The evidence for this assertion is based on the observed intensity of the (100) Bragg diffraction peak, which arises from the hexagonal arrangement of the cylindrical pores, as a function of temperature. In I, it is further found that the density profile as function of temperature shows significant hysteresis between heating and cooling at different pressures. Both results are used to speculate on a possible liquid-liquid transition in supercooled confined water.

These papers contain inconsistencies that potentially undermine the stated conclusions. At the heart of the data analysis are the assumptions that (a) the distribution of water density across the pore does not change with temperature and (b) all the water absorbed by the silica is contained in the pores and not on the surface of the silica particles. Assumption a is not justified based on recent atomistic simulations of the wider angle scattering data from these materials (3), where it is shown that the density distribution across the pore can change with temperature. Recently, I have shown that this, in turn, leads to a change in Bragg peak intensity (4), even when the overall density stays constant.

Assumption b is not justified based on the numbers quoted in the papers. The position of the (100) peak for a hexagonal lattice is given by 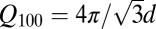, where d is the spacing between the holes and the cross-sectional area of the hexagonal unit cell is 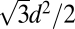. If r is the radius of the pore and ρ_w = 1.1 g/cm³ and ρ_s = 2.2 g/cm³ are the densities of (heavy) water and silica, respectively, the ratio of mass of water in pore to mass of silica is given by 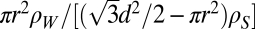. Putting Q₁₀₀ = 0.21 Å⁻¹ as in I gives d = 34.5 Å, such that with r = 7.5 Å, as stated in that paper, the maximum amount of water that can be contained in the pores is ∼0.1 gD₂O/gSiO₂. This is much smaller than the stated water absorption of 0.5 gD₂O/gSiO₂. Hence, one has to conclude either that much of the adsorbed water is not in the pores themselves but on the surface of the silica particles or that the pore radius is significantly larger than stated. A similar conclusion can be drawn from the numbers quoted in II.

Water on the surface of the silica particles will behave differently from water in the pore when cooled below the normal freezing point but has the potential to affect both the intensity of Bragg lines as well as the observed dynamics of the confined water (5). Hence, any conclusions regarding the dynamics and thermodynamics of supercooled confined water based on these scattering experiments are unreliable until a full characterization of the samples has been completed.