Nanostructure of cellulose microfibrils in spruce wood

Abstract

The structure of cellulose microfibrils in wood is not known in detail, despite the abundance of cellulose in woody biomass and its importance for biology, energy, and engineering. The structure of the microfibrils of spruce wood cellulose was investigated using a range of spectroscopic methods coupled to small-angle neutron and wide-angle X-ray scattering. The scattering data were consistent with 24-chain microfibrils and favored a “rectangular” model with both hydrophobic and hydrophilic surfaces exposed. Disorder in chain packing and hydrogen bonding was shown to increase outwards from the microfibril center. The extent of disorder blurred the distinction between the I alpha and I beta allomorphs. Chains at the surface were distinct in conformation, with high levels of conformational disorder at C-6, less intramolecular hydrogen bonding and more outward-directed hydrogen bonding. Axial disorder could be explained in terms of twisting of the microfibrils, with implications for their biosynthesis.

Cellulose makes up about half of the mass of wood, and wood cellulose is therefore more abundant than any other material in the biosphere (1). Cellulose synthesis is the key to the living world’s buffering of atmospheric carbon dioxide levels and its utilization will be crucial to our efforts to find substitutes for fossil fuels (2). Nevertheless we have much to learn about the nature of cellulose and about how its structure relates to its function. Wood cellulose is composed of long microfibrils, each a few nanometers in thickness (3). These microfibrils contain both ordered and disordered components (4–6), but their structure is not known in detail.

Within each microfibril there are domains that conform approximately (4, 7, 8) to the cellulose Iα and Iβ forms found in much more crystalline algal and tunicate celluloses (9–11). Distinguishing these two forms is difficult in wood, but it has been suggested that cellulose resembling the Iβ form predominates in softwoods (8, 12). Also present are partially ordered cellulose chains (7) and chains that differ conformationally from crystalline cellulose (5, 6, 13). Other polysaccharides, particularly glucomannans, may be closely enough associated with the microfibrils to be considered as a part of their structure (14, 15).

There is evidence that the cellulose microfibrils of conifer wood are assembled into aggregates in the region of 10–20 nm across (16). In cross-section the wood cell wall is so dense that these microfibril aggregates are not readily visible, but they have been imaged by atomic force microscopy (17) and electron tomography (3), which showed their structures to be somewhat irregular and interspersed to a limited degree with other polymers. In SEM images of transversely fractured wood the fracture planes cut cleanly across each microfibril aggregate but also run between aggregates for short distances, giving a stepped topography (18). In mechanical terms, therefore, the microfibril aggregate appears to be the basic cohesive unit of the dry wood cell wall in the sense that it does not readily fray into its constituent microfibrils during fracture.

The above description does not include precise dimensions of microfibrils and their aggregates, nor the number of chains in each microfibril, nor the disposition of its component crystalline and noncrystalline fractions. These details have been elusive. The determination of microfibril diameters in wood has been addressed frequently by a variety of techniques, particularly wide-angle X-ray scattering (WAXS) and solid-state ¹³C NMR (19–22). However each technique has drawbacks and agreement has not been generally good. Diameters suggested have ranged from 2.2 nm to 3.6 nm (20, 23). These upper and lower limits correspond to about 12 and 32 chains (πr²/0.317) if it is assumed that the wood microfibrils are approximately circular in cross-section and each chain occupies 0.317 nm² as in cellulose Iβ (9).

EM images suggest that each microfibril is synthesized by a terminal complex that takes the shape of a six-lobed “rosette” (24). Each terminal complex contains multiple cellulose synthase subunits. Distinct groups of cellulose synthases participate in the synthesis of primary (growing) and secondary (woody) cell walls (25). If it is correct that one terminal complex makes one microfibril, it would seem to follow that microfibrils synthesized during primary and secondary cell-wall formation should contain fixed numbers of cellulose chains, divisible by six. A 36-chain model is frequently suggested (25), although the evidence on which this was originally based is very indirect (26) and a 36-chain microfibril would be larger than the spectroscopic and WAXS evidence suggests, about 3.8 nm diameter (2√(36 × 0.317)/π) or 3 × 5 nm (27).

Microfibrils synthesized in a matrix with few noncellulosic polymers, as in cotton, flax, and angiosperm tension wood, have considerably larger and apparently variable dimensions (20, 28, 29) suggesting coalescence of newly synthesized microfibrils. Microfibrils appeared to split apart along the 002 crystal plane when subjected to vigorous acoustic degradation (30) and there is evidence that in some fruits the primary-wall microfibrils are less than 2 nm thick in their native state (31). When the diameter of wood microfibrils has been explored by a single technique, its variability has been small (19, 21) and might be explained by contributions from noncellulosic material. Thus although in certain circumstances the number of chains in a microfibril appears to vary and to differ from the number synthesized by each terminal complex (27), evidence that this applies also to normal wood microfibrils is lacking.

With these uncertainties, the number of chains in a microfibril is relevant to our understanding of cellulose biosynthesis, which is in turn closely entwined with the development of plant form (32) and function (33). The diameter of the cellulose fibrils and the proportion of crystalline material are key inputs into our understanding of the mechanical performance of cellulose (34–36) and into calculations of the strength of wood, textile fibers, and cellulose-based nanocomposite materials (37, 38). In addition cellulose “crystallinity” and aggregation control accessibility to glucanase enzymes (39) and are thus important but rather poorly defined questions in the technology of liquid biofuel production from cellulosic biomass.

Here we explore the questions of microfibril structure, diameter, and aggregation in spruce wood, from multiple experimental directions. Using WAXS in combination with small-angle neutron scattering, we constrained the microfibril dimensions within limits that are tighter than has previously been possible. We used deuteration-FTIR experiments to identify cellulose chains on microfibril surfaces accessible to water and two independent ¹³C NMR approaches to characterize their conformation and location.

Results

Lateral Packing and Diameter of Microfibrils: Small-Angle Neutron Scattering (SANS).

Microfibrils close-packed in a regular array would be expected to diffract radiation transverse to the microfibril axis, at angles an order of magnitude smaller than in conventional diffraction from crystal planes. It may be asked whether such small-angle scattering is expected from microfibril arrays with less ordered packing. In scattering models developed for collagen (40) and adapted for celery cellulose (41) a coherent scattering peak of this kind was constructed for a partially ordered array of parallel microfibrils with a range of spacings based on a modified Lennard-Jones function, the lower limit being fixed by contact and higher-order peaks being absent due to mingling with the contribution of the shape of the individual microfibrils (the form function) (41).

The smallest spacing would then be the center-to-center distance between microfibrils touching one another. Coherent small-angle scattering of X-rays has been observed from the loosely arrayed microfibrils of primary-wall cellulose in celery collenchyma (41). It was necessary to separate this interference contribution from that of the form function, but the q value of the interference peak provided a more direct measure of physical diameter than either the Scherrer dimensions calculated from WAXS data or the surface:volume ratios from spectroscopic measurements.

This approach does not work for wood. X-ray scattering from wood in its native state is dominated by the form function. Jakob, et al. (23) succeeded in extracting an interference contribution numerically, but it was small and difficult to characterize. From this observation it may be concluded that either the packing of wood microfibrils is too irregular to diffract strongly (42) or there is insufficient X-ray contrast between the microfibrils and any interstitial material (23). Intriguingly, an equatorial X-ray diffraction peak like that from celery cellulose microfibrils was observed after spruce wood was vigorously oxidized by chlorite/acetic acid (42).

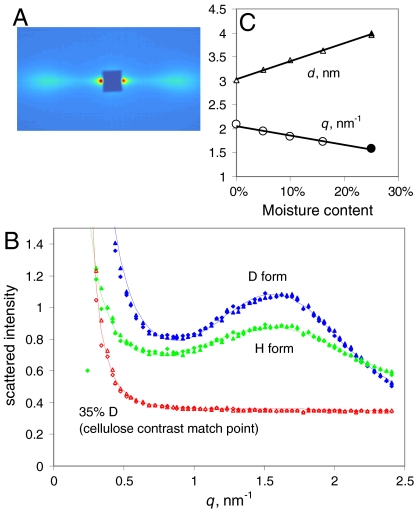
Neutron and X-ray scattering intensities show different dependence on composition. The total neutron scattering cross-section of cellulose calculated from its elemental composition lies between those of H₂O and D₂O, and matches a 35∶65 D₂O∶H₂O mixture (43). It would therefore be predicted that if either H₂O or D₂O penetrated between regularly packed cellulose microfibrils they would provide neutron scattering contrast and would allow any interference contribution to be observed. Fig. 1 shows that Sitka spruce wood, saturated with either H₂O or D₂O, gave a strong lateral SANS peak centered on q = 1.6 nm^-1, quite similar to that observed for celery cellulose by SAXS (44). As predicted from elemental composition, the intensity of the interference peak was greater for wood saturated with D₂O than with H₂O and became zero in 35∶65 D₂O∶H₂O mixture (Fig. 1). No detectable features were observed on the fiber axis.

Fig. 1.

SANS from spruce wood. (A). SANS pattern at 25% hydration with D₂O, showing equatorial Bragg reflections at q = 1.6 nm^-1. The fiber axis is vertical. (B). Radial profiles of SANS intensity at 25% hydration with D₂O, H₂O and a 35∶65 mixture of D₂O with H₂O, matching the scattering length density of cellulose based on its elemental composition. (C). Variation in position of the center of the fitted radial intensity peak with the level of hydration with D₂O, and the corresponding d-spacings between microfibril centers.

When the D₂O content of the wood was reduced from the saturation point of 0.25 g/g the position of the lateral interference peak moved to higher q (Fig. 1) and its intensity diminished. In fully dry spruce wood exchanged with D₂O the interference peak was just discernible at q = 2.1 nm^-1 but it was absent from the scattering pattern from dry wood in the H form. The corresponding mean center-to-center spacings were from 3.0 nm in the dry state to 4.0 nm when saturated with either H₂O or D₂O.

These observations imply that drying reduced the microfibril spacing as H₂O or D₂O was removed, until the microfibrils were packed so densely in the dry H state that there was insufficient contrasting material (or space) to permit measurable interference, whereas in the dry D state deuterium exchange left sufficient deuteroxyl groups at each microfibril surface to provide a small amount of contrast with the H-rich microfibril interior.

Microfibril Dimensions and Disorder: Wide-Angle X-Ray Scattering (WAXS).

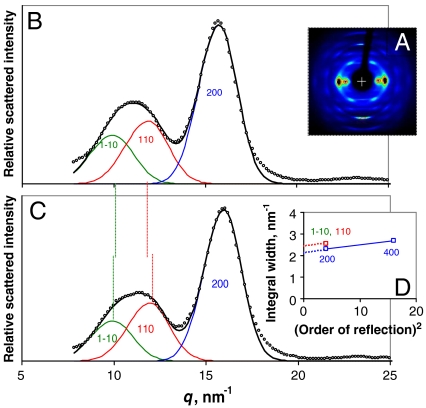
X-ray diffraction patterns from wood with very well oriented microfibrils resemble the fiber diffraction pattern from crystalline cellulose Iα and Iβ but are much more diffuse (19, 23, 39). At such a low level of resolution it is not possible to distinguish the Iα and Iβ forms by crystallographic means (45) and for clarity all reflections are indexed here on the Iβ lattice. The radial width of the 200 reflection, corresponding to the intersheet spacing in cellulose Iβ, has been widely used as a guide to the diameter of the crystalline part of the microfibril through the Scherrer equation which relates peak broadening inversely to the number of diffracting lattice planes (13, 19, 39). The dimension so obtained is in one direction only, at 90° to the ring planes, and even in that direction it may differ from the true diameter for two reasons. First, the Scherrer dimension represents not the overall diameter but the weighted-mean column length in the direction normal to the lattice plane concerned, and thus depends on the shape of the microfibril. Also, peak broadening depends on disorder as well as on small lattice dimensions. Radial disorder in cellulose, although its existence is inferred from NMR data (4, 6, 13, 28), is difficult to estimate quantitatively. The radial profile of each reflection contains information on the nature and extent of disorder (46) but in practice the asymmetry of the radial profiles means that most of the available models do not fit well. We introduced an asymmetry term to account for part of the disorder and then modeled the remaining disorder as follows.

If the 400 reflection can be measured, it is possible to correct for disorder-related broadening by assuming that the amount of broadening depends on the square of the reflection order (47). With this correction (Fig. 2) a mean column length of 3.29 ± 0.13 nm normal to the (200) plane was calculated for native spruce wood samples in the dry state, or 2.93 ± 0.05 nm when saturated with water (n = 4 in each case). In the diffraction patterns from wood cellulose the 1–10 and 110 reflections overlap strongly. The spacing between centers is controlled by the monoclinic angle γ of the cellulose Iβ lattice (or the corresponding angle in the triclinic Iα lattice) so that it is difficult to extract the widths of these reflections and γ simultaneously. Taking advantage of the fact that γ increases on hydration (36), we recorded diffraction patterns from water-saturated wood samples in which the 1–10 and 110 reflections were centered just far enough apart to be characterized independently (Fig. 2). Allowing for the asymmetry of the reflection profiles γ was determined as 101° ± 0.5° at saturation, greater than the maximum value calculated previously (36). Assuming that both reflections were of equal width and applying the same disorder correction as for the 200 reflection, the mean Scherrer dimension normal to the (1–10) and (110) planes was 2.6 ± 0.1 nm (n = 4).

Fig. 2.

Wide-angle X-ray scattering from spruce wood. (A). WAXS pattern from dry spruce wood. (B). Background-corrected equatorial WAXS profiles from dry spruce wood with the 1–10, 110, and 200 reflections fitted by asymmetric functions, using the approximation that the widths of the overlapping 1–10 and 110 reflections were equal. (C). Background-corrected equatorial WAXS profiles from hydrated spruce wood, processed as (B). (D). Variation of the widths of the equatorial reflections with the square of the reflection order. The slope of the line connecting the widths of the 200 and 400 reflections depends on the mean value of the disorder factor and its intercept approximates to the disorder-corrected width. In the absence of measurable higher-order reflections the intercept was estimated for the 1–10 and 110 reflections using the same slope.

The reduced (200) column length on hydration might suggest that surface chains became detached or disordered, but should be interpreted with caution because these data are sensitive to the background correction, and the backgrounds were much more intense and more complex from wood samples in the wet state. The (200) column lengths for dry samples were slightly greater than reported (without correction for disorder) by Andersson, et al. (19) and considerably greater than reported by Jakob, et al. (23).

The use of an asymmetric model for the reflection profiles permitted much better fits to the observed data than have previously been obtained (Fig. 2), but the accuracy of the Scherrer dimensions is likely to be reduced by a number of approximations that are not reflected in the standard deviations quoted. In particular, deviations from the Bragg equation, and apparently also from the Scherrer equation, become significant in lattices with as few crystal planes as those examined here (48). Also the above value for the mean of the dimensions in the directions normal to (1–10) and (110) depends on the assumption that the disorder parameter is the same in all radial directions; and all estimates of radial broadening, even that of the 200 reflection, depend strongly on the function assumed for the noncrystalline background. We used a background function measured in the region away from the equator, whereas others have derived model backgrounds from disordered materials such as lignin (19, 49) or joined minima in the radial profiles (36).

The Iα and Iβ crystalline forms differ in the longitudinal stagger between successive sheets of chains (50). The (102) lattice plane (as indexed on the Iβ structure) follows this stagger. A line normal to this plane would be interrupted, and the corresponding Scherrer dimension would then be reduced, if any transition between the two crystalline forms were present across a single microfibril. Using the 3.3 nm Scherrer dimension calculated from the 200 reflection and an estimated axial dimension of about 11 nm calculated from the width of the 004 reflection uncorrected for disorder, the predicted Scherrer dimension for the 102 reflection was 5.4 nm when calculated as described (23). However the observed width of the 102 reflection corresponded to a Scherrer dimension of only 3.6 nm, suggesting that there was significant disorder in the intersheet stagger that differentiates the Iα and Iβ lattices.

C-6 Conformation and Local Mobility from ¹³C NMR Experiments.

The ¹³C cross polarization, magic-angle spinning (CP-MAS) NMR spectrum from spruce wood (Fig. 3) resembled those obtained from other conifers (6) with distinct groups of C-4 and C-6 signals from well-ordered and disordered cellulose, the latter in particular being overlapped by hemicellulose signals. In ¹³C spectra from highly crystalline cellulose the Iα and Iβ forms are readily distinguished by the position of their C-4 doublets in the 89 ppm region. In wood spectra the C-4 doublets merge with an intermediate signal that has been attributed to “paracrystalline” cellulose (7). Including this intermediate signal the signal intensity from well ordered cellulose amounted to about 40% of the C-4 total, but precise estimation was difficult due to overlap with hemicellulose signals in the 82–84 ppm region.

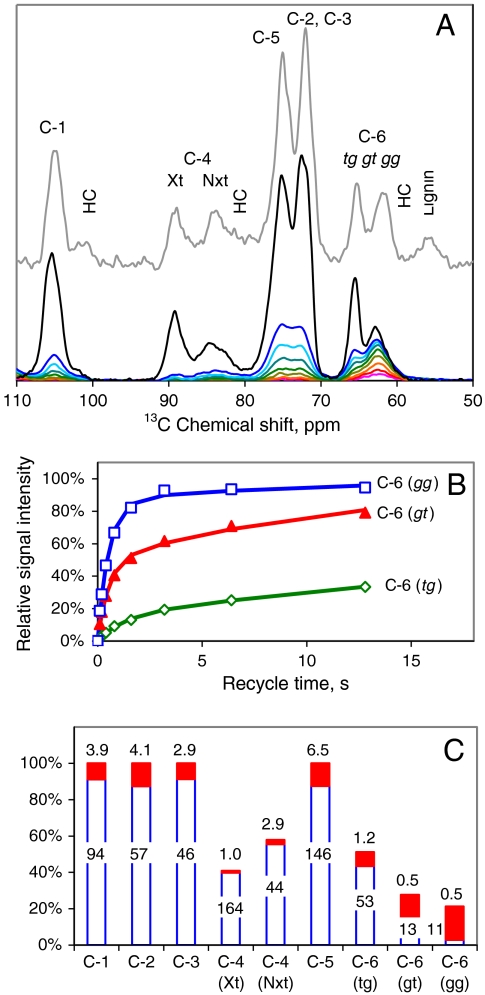
Fig. 3.

¹³C spin-lattice NMR relaxation experiments on spruce cellulose. (A). All cellulose chains are represented in the CP-MAS spectra of spruce wood (top spectrum) and cellulose isolated from it (second top). Shortening the recycle times in the MOST experiment restricted the spectral contribution progressively to the most mobile carbon atoms, particularly C-6. The MOST recycle times were (third to bottom) 12.8, 6.4, 3.2, 1.6, 0.8, 0.4, 0.2, and 0.1 s. The scaling of the CP-MAS spectra relative to the MOST spectra is arbitrary. (B). Relative intensity of the deconvoluted tg, gt, and gg components of the C-6 signal from isolated spruce cellulose as a function of recycle time in the MOST experiment, with dual-exponential fitted curves. (C). Dual-exponential fitted parameters. The histogram shows the proportions of the long-T₁ and short-T₁ components of each signal and the figures are the corresponding T₁ values in s.

In partially ordered solids ¹³C spin-lattice relaxation times (¹³C T₁), are a measure of local thermal motion on the 10^-8 s time scale, and are therefore useful in distinguishing rigid and flexible parts of nanoscale structures. Here, ¹³C T₁ relaxation times were measured using the MOST (Measurement of Short T₁s) saturation experiment (28, 51). Any ¹³C atoms in less ordered domains with some freedom of movement have short ¹³C T₁ and their signal intensity builds up quickly with increasing recycle time, whereas ¹³C atoms in rigidly ordered domains have longer ¹³C T₁ and their signal intensity builds up more slowly (28). The MOST experiment has been used previously for primary-wall cellulose but only the C-6 signal was then examined (28). Here we extended the recycle times to include all carbon atoms.

The MOST experiment is only suitable for isolated cellulose, not for intact wood samples where signals originating from more mobile cellulose domains would be swamped by hemicellulose signals. Structural changes during isolation of the cellulose were therefore an issue. The CP-MAS spectrum from the isolated cellulose (Fig. 3) not only shows the loss of hemicelluloses and lignin but also indicates that a smaller percentage of the cellulose chains were disordered in the isolated cellulose than in the original wood sample, as has been observed when cellulose crystallinity and microfibril diameter increase during pulping (52, 53).

The evolution of signal intensity with recycle time is shown in Fig. 3. The C-1, C-2, C-3, and C-5 signals each contained overlapping contributions from well ordered and disordered cellulose (28). However based on their ¹³C T₁ each of these signals could be divided into two components (Fig. 3); a major rigid component with ¹³C T₁ about 1–2 min and a minor mobile component, around 10% of the total, with ¹³C T₁ about 5 s. Further subdivision was not feasible with the signal:noise ratio available. The 89 ppm group of signals corresponding to C-4 in well ordered forms of cellulose showed a uniformly long ¹³C T₁ of nearly 2 min. The MOST experiment is not well suited to such long T₁ values but within the limitations of signal: noise there was no sign of components greater or less in mobility within this group of signals (Fig. 3). Most of the signal intensity centered on 84 ppm, assigned to C-4 in disordered forms of cellulose, showed slightly more mobility than the 89 ppm signals but a minor fraction was much more mobile with ¹³C T₁ around 3 s.

Judging from the mobility of the ring carbons C-1 to C-5, > 90% of the cellulose chains were rather rigid, including disordered as well as ordered forms. In contrast to these ring carbon atoms, C-6 has some freedom to rotate between the tg, gt, and gg conformers unless restrained by stable hydrogen bonding (54). Rotational freedom means that the mobility of C-6 is greater and that each C-6 conformer potentially gives a separate signal. The Iα and Iβ crystalline forms of cellulose have C-6 fixed in the tg conformation (9–11).

Fitting a two-component curve to each of these C-6 signals yielded several groups of ¹³C T₁ values (Fig. 3). The major component of the signal from the tg conformer had a long ¹³C T₁ comparable with the rigid component of the ring carbons and consistent with a crystal-lattice location. This rigid tg fraction amounted to 40% of the total C-6 signal. The remainder of the C-6 signal intensity can therefore be assigned to less ordered forms of cellulose, but these varied in mobility. About half of the gt signal and a minor fraction of the gg signal had ¹³C T₁ values around 10 s indicating moderate mobility. The remainder of the gt signal, most of the gg signal, and a small fraction of the tg signal had ¹³C T₁ values of about 1 s or less indicating high mobility.

The MOST data make it clear that motions of the main cellulose chain must be distinguished from C-6 rotation. In total about 40% of the C-6 signal, including all three conformers, showed strong signs of rotational motion and a further 20%, mainly in the gt conformation, showed clear but more restricted motion. In contrast significant main-chain motion was restricted to < 10% of the cellulose, all within the disordered fraction. Thus a substantial proportion of disordered chains were relatively immobile except for rotation of C-6, which appeared to be permitted by hydrogen-bonding environments less ordered than those found in crystalline cellulose. The gg conformer at C-6 predominated in the most mobile environments and the gt conformer in environments with somewhat less mobility.

These data refer to the isolated cellulose in which the disordered chains comprised a smaller fraction of the total cellulose than in the intact wood cell walls. However all the same C-4 and C-6 signals were present in the CP-MAS spectrum of spruce wood, at slightly different relative intensities, and it is reasonable to suppose that the associated mobilities were similar in relative terms.

Relative Locations of Polymer Domains: Spin-Diffusion Experiments.

Information on the spatial disposition of cell-wall polymers can be extracted from NMR experiments measuring proton spin diffusion (15, 55, 56). Proton magnetization gradients are first set up by allowing partial spin relaxation, which occurs at different rates in rigid and mobile domains. The proton magnetization is then allowed to reequilibrate between domains by spin diffusion and measured through the ¹³C spectrum. The length of time required for proton spin diffusion between two domains depends on the square of the distance between them (55, 56).

Results from experiments of this type are normally represented as curves of local magnetization evolving with spin diffusion time and converging when initially distinct domains equilibrate (15). The area enclosed between two such equilibration curves should in principle provide the basis for a two-dimensional (2D) representation of the experiment, in which cross peaks would represent spatially distant pairs of domains. Fig. 4 shows the 2D representation of such an experiment on hydrated spruce early wood, using spin-spin relaxation to set up the initial magnetization gradient. Under these conditions the principal initial reservoirs of magnetization are water molecules and mobile hydrated polymers (56). Late wood gave a similar 2D spectrum (Fig. S1A). An experiment in which rotating-frame spin-lattice relaxation was used gave a similar but less well defined 2D spectrum (Fig. S1B). Each cross peak in Fig. 4 corresponds to the signals from ¹³C atoms in two domains that differed in initial magnetization and were sufficiently separated from one another to require a measurable time (several ms) for spin diffusion to restore their magnetization to equality.

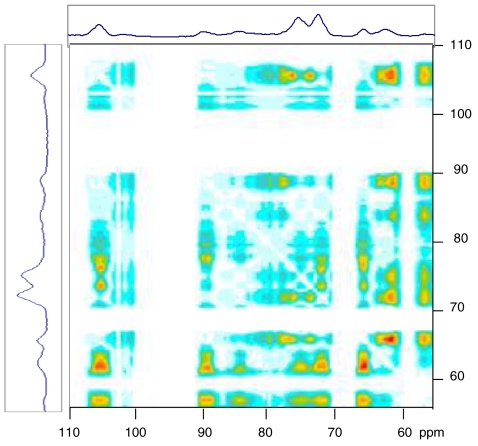
Fig. 4.

2D representation of spectral data from a proton spin-diffusion experiment on hydrated spruce wood. The ¹³C spectra are shown at top and side. Cross peaks correspond to the relative area enclosed between the T₁-corrected spin equilibration curves for the signals at the two chemical shifts concerned. For a cross peak to be generated between two ¹³C signals the initial levels of proton magnetization around the two ¹³C nuclei must differ and significant time must elapse before they equilibrate by proton spin diffusion. That is, the two ¹³C nuclei must be spatially separated.

Three groups of signals can be identified in the 2D spectrum (Fig. 4): (a) signals assigned to well-ordered cellulose at 105, 89, 75, 72, and 66 ppm; (b) signals assigned to conformationally disordered cellulose at 105, 84, 75, 72, 63, and 61 ppm; and (c) signals assigned to hemicelluloses and lignin at 101, 80, 70, and 61 ppm (hemicelluloses) and 56 ppm (lignin). Signals in bold are specific for the group to which they belong, although clearly there is overlap between these groups. Within each group there were no cross peaks. Cross peaks between group (a) and group (b) were weak as expected from the rather small difference in initial magnetization between well-ordered and disordered cellulose. Cross peaks from group (c) to group (a) were considerably stronger, relative to the peak intensities, than cross peaks from group (c) to group (b). This finding implies that, on average, the disordered cellulose was closer than well-ordered cellulose to lignin, hemicelluloses, and water.

With respect to their cross peaks to group (c), there was no sign of any difference between individual regions of the 89 ppm cluster assignable to C-4 in cellulose Iα and Iβ. The implication is not that these crystalline forms, if distinct, occupied domains close to one another, but simply that they were at similar average distances from the nearest water molecules or lignin-hemicellulose domains. The behavior of the central part of the 89 ppm cluster, assigned to “paracrystalline” cellulose (7) was consistent with its inclusion along with material resembling cellulose Iα and Iβ in the well ordered fraction and its cross peaks with the C-6 region of the spectrum indicated a tg conformation.

The 2D spectra are not easily reconciled with models in which each microfibril has crystalline and noncrystalline domains alternating along its length (57) because these would be at similar distances from the lignin-hemicellulose matrix in contradiction to our observations. Nor are the 2D spectra consistent with models in which the Iα and Iβ crystalline forms are concentric (4, 56). The results were consistent with a model in which well ordered cellulose forms the core of each microfibril and much of the less ordered cellulose is at the surface, as has been suggested previously on the basis of NMR experiments (6, 15, 58).

Accessibility to Water: Deuteration-FTIR.

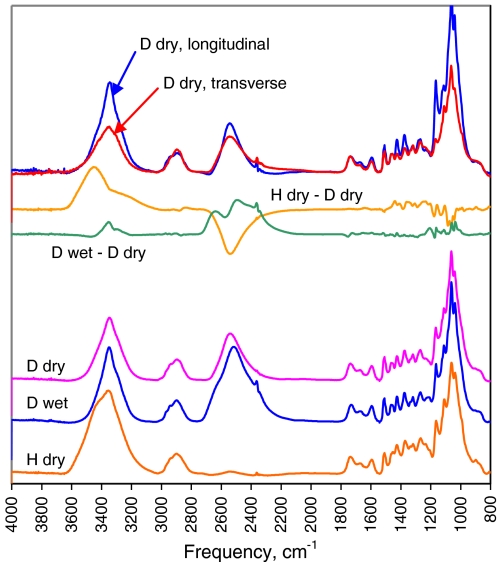
Cellulose chains accessible to water can be identified by vapor-phase deuterium exchange (28). The OH groups on C-2, C-3, and C-6 of chains accessible to hydration are replaced by OD, as are hemicellulosic OH groups. The O-H stretching bands around 3,300 cm^-1 in the FTIR spectrum are replaced by O-D stretching bands around 2,500 cm^-1 (28, 59), allowing the degree of accessibility to water to be measured and revealing the hydrogen-bonding pattern in the water-inaccessible domains.

The intensity removed from the O-H stretching region by deuteration was in a clearly defined band centered on 3,440 cm^-1 and tailing in the direction of lower frequency. A corresponding band appeared in the O-D stretching region with its maximum at 2,530 cm^-1 and slight longitudinal polarization (Fig. 5). These bands corresponded to exchangeable hydroxyl groups on hemicelluloses and water-accessible cellulose surfaces and signified a hydrogen-bonding pattern completely different from crystalline cellulose, with lower mean hydrogen-bond strength and near-random hydroxyl orientation. The extent of deuterium exchange at saturation, using a presoak with liquid D₂O followed by drying in rigorously dry air (Fig. S2), amounted to 45% ± 2% of the total hydroxyl groups (n = 3). When allowance was made for deuteration of hemicelluloses it could be calculated that 28% of the cellulosic hydroxyl groups were exchangeable. An edge-bound surface chain exchanges the hydroxyls on its outer side only (60), so approximately 56% of the cellulose chains had their outer edges accessible in this way in D₂O-saturated wood.

Fig. 5.

Baseline-corrected transmission FTIR spectra of spruce wood. From bottom; in the dry state (H dry), then equilibrated with D₂O (D wet) and then dried without access to H₂O (D dry). Deuteration moved the O-H stretching bands from accessible hydroxyl groups (3,200–3,500 cm^-1) to the O-D stretching region (2,300–2,600 cm^-1). Difference spectra show effects of deuteration (H dry—D dry) and of drying in the deuterated state (D wet—D dry). Top: polarized spectra after deuteration and drying.

When the presoak was omitted the amount of D₂O absorbed from the D₂O-saturated vapor-phase was slightly less than the saturation level and the extent of deuterium exchange was smaller and more variable, as has been noted (61). When the D₂O-saturated wood cell walls were dried there was a minor redistribution of O-H stretching intensity from the crystalline to the noncrystalline pattern. This effect is attributed to a slight distortion of the structure caused by drying stresses.

The residual O-H stretching intensity from cellulose chains inaccessible to water included the longitudinally polarized peak at 3,340 cm^-1 assigned to O-3 hydrogen bonded to O-5’ as in crystalline cellulose Iα and Iβ, but the flanking intensity assigned to O2-H and O6-H stretching vibrations was much more diffuse than in these crystalline forms (Fig. 5). In particular, there was little sign of the sharp, longitudinally oriented bands at 3,240 and 3,270 cm^-1, characteristic of the dominant hydrogen-bonding systems between O2 and O6 of successive glucosyl units in the same chain of, respectively, cellulose Iα and cellulose Iβ (28, 62). These two bands were dispersed within a broad, longitudinally polarized shoulder.

Discussion

Relative Abundance of Crystalline and Disordered Domains.

How much of the spruce cellulose was “crystalline” depends on how crystalline cellulose is defined or, more realistically, on how it is measured. ¹³C NMR is sensitive to the conformation of individual chains. WAXS is principally sensitive to how the chains are oriented and how regularly they are packed together within the microfibril. FTIR is sensitive to the hydrogen-bonding patterns that provide cohesion to the chain packing. Data on highly crystalline algal or tunicate celluloses have been obtained by all these methods (6, 9, 10, 59). In principle any such method could be used to define and quantify crystalline cellulose in spruce wood as cellulose similar to algal or tunicate cellulose. However the resemblance was never exact and the criteria for crystallinity differ so much from one method to another that agreement is not to be expected (20).

The CP-MAS NMR spectra indicated that about 40% of the cellulose chains could loosely be called cellulose I, with flat-ribbon chains and C-6 in the tg conformation. This fraction includes the form that has been called paracrystalline (7) as well as forms resembling cellulose Iα and Iβ. The remaining 60% with different conformations identifiable by NMR approximately matched in abundance (about 56%) the water-accessible surface chains engaged, on their outer sides, in hydrogen-bonding patterns clearly distinguishable from crystalline cellulose by FTIR. The NMR spin-diffusion data were consistent with a predominantly surface location for these chains. Close proximity of the water accessible and inaccessible chains is implied by deuterium exchange between these under the stress of drying. This finding would not be expected if, for example, water-accessible and inaccessible domains alternated along the length of the microfibril.

Estimating the percentage of crystalline cellulose from WAXS data is problematic, for example due to the difficulty of finding an appropriate “amorphous” calibration standard (49). From the nature of the crystallographic disorder in spruce cellulose it is evident that crystalline merges into disordered and both contribute to the diffraction patterns. The proportion of crystalline cellulose in spruce wood has been estimated at 30% (19), equivalent to about 60% of the total cellulose. This fraction appears to be more than the 40% of cellulose I as defined conformationally by NMR as described above. Both measurements are approximations, but the implication is that at least some of the conformationally disordered chains are located close enough to the corresponding lattice points, and are in approximately the right axial and rotational orientations, to contribute to the crystalline part of the WAXS pattern even though they differ conformationally.

Structure of Crystalline and Related Domains.

From the WAXS data it was deduced that many of the cellulose chains were packed similarly to the Iα and Iβ forms but with considerable statistical disorder. Overall, the asymmetry of the equatorial reflections indicated a tendency to looser packing and in the presence of water the monoclinic angle was greater.

Any attempt to establish the relative abundance of the Iα and Iβ forms within this fraction is made difficult by the inclusion of intermediate material termed paracrystalline (7) [note that this term has a different meaning in diffuse diffraction (47)]. As was found previously (7) much of the C-4 signal intensity around 89 ppm in the NMR spectra was somewhat diffuse and was not assignable to the known cellulose Iα and Iβ doublets. The tg conformation at C-6, identified by NMR, can accommodate a number of alternative hydrogen-bonding arrangements involving O2 and O6’. A more or less continuous range of hydrogen-bond geometry spanning across the corresponding spectral region was shown to be present by FTIR. Because the coherence of the (102) lattice plane did not extend to the full distance across each microfibril, it cannot even be demonstrated that any one segment of a microfibril was occupied solely by one of the two crystalline forms. Thus although about 40% of the cellulose might reasonably be classed as cellulose I on the grounds of chain conformation, this fraction contained enough hydrogen-bonding disorder within sheets of chains, and enough stacking disorder between sheets, to make it impracticable to distinguish clearly between the Iα and Iβ forms (45).

Disordered Domains.

Almost all the cellulose chains were at least moderately well oriented, as shown by both WAXS and polarized FTIR, but the disordered chains differed in conformation from the well ordered material as previously shown by NMR (5, 13). Mostly the disordered chains retained the O3H-O5’ hydrogen bond that ensures chain rigidity, as shown by the hydroxyl stretching region in FTIR, but they had a dynamic mixture of all three possible conformations at C-6. These chains resembled the oriented but disordered cellulose that has been prepared by partial dissolution in LiCl/DMAc (63, 64).

On the outer edges of chains accessible enough for D₂O exchange, as in the hemicelluloses, the hydrogen bonding was almost randomly oriented and on average weaker than in crystalline cellulose or liquid water. All three C-6 conformers were present in comparable abundance and probably in dynamic equilibrium, at least in the most mobile fraction of the isolated cellulose. However only a small fraction of this material showed significant mobility of the whole cellulose chain. The gt conformation at C-6 predominated in a further fraction with lower mobility that may be tentatively identified with the inner edges of surface chains.

Transverse Dimensions of Microfibrils.

It was not, strictly, the microfibril diameter that was obtained from the SANS and WAXS experiments. The SANS experiment yielded a range of center-to-center distances, culminating in a mean minimum distance of 3.0 nm assumed to represent lateral contact in the dry state. On a simple circular model, a diameter of 3.0 nm gives a cross sectional area sufficient for 22 chains packed as in cellulose Iβ.

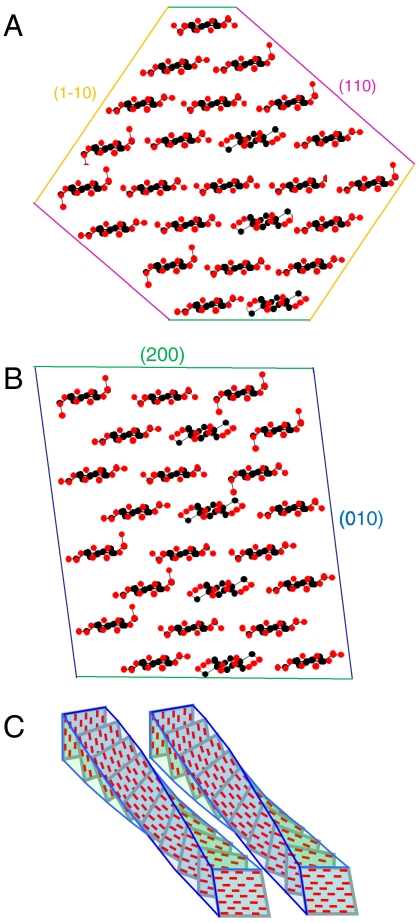
The WAXS experiments yielded Scherrer column lengths in three transverse directions, that is the dimension in each of these directions averaged across the orthogonal width of the microfibril. Constructing models from these data requires assumptions about the shape of the microfibrils. Microfibrils of, for example, the highly crystalline cellulose from Valonia have the (110) and (1–10) crystal faces exposed (60, 65) (for clarity the cellulose Iβ lattice notation is used here even though cellulose Iα predominates in Valonia cellulose). Here this shape is called the “diamond” shape whereas an alternative with the (200) and (010) faces exposed is called a “rectangular” shape. It has usually been assumed that the smaller microfibrils of cellulose from higher plants share the diamond shape found in more crystalline celluloses.

Based on this assumption, two distinct ¹³C T₁ values for the 84 ppm C-4 doublet in the NMR spectrum have been assigned to the exposed (1–10) and (110) faces (6) and simulated in MD studies (66), even though Valonia cellulose is now known to give a more complex group of four signals in the 84 ppm region (67). However Family 1 cellulose binding domains bind to cellulose in coniferous wood (68) and Arabidopsis secondary cell walls (69) through a planar hydrophobic binding region that is specific for the (200) face when these proteins bind to crystalline celluloses (70) [again we use the Iβ indexing: the same face is indexed as (110) on the Iα lattice]. These findings suggest that cellulose microfibrils in higher plants may have the (200) faces exposed as in the rectangular model, contrary to what has often been assumed.

Initial model-building trials using the mean d-spacings and the measured monoclinic angle from the WAXS images showed that the diamond shape gave smaller column lengths normal to the (200) plane than the mean column length normal to the (110) and (1–10) planes. This relationship was indeed observed for Valonia cellulose (Fig. S3). However for water-saturated spruce cellulose the observed column lengths were 2.9 nm normal to the (200) plane and a mean of 2.6 nm normal to the (110) and (1–10) planes. In the dry state the 200 Scherrer dimension increased to 3.3 nm, probably due to either coalescence of partially detached chains or some degree of crystallographic stacking of adjacent microfibrils over short lengths where the 200 planes were aligned.

The column lengths for the wet state could not be matched by the diamond shape but were matched by the rectangular shape (Fig. 6) if the dimensions parallel and orthogonal to the (200) plane were chosen appropriately. Our diffraction data therefore favored the rectangular shape, but should be viewed with caution because disorder may not be rotationally symmetric and because deviations from the Scherrer equation may be observed in such small crystallites (48). The two model structures shown in Fig. 6 have 24 chains, based on the common assumption that the chain number is fixed and divisible by six to match the symmetry of the terminal complex. If not, these models might represent mean structures. An alternative 18-chain model with additional glucomannan chains would fit the SANS data but would be a poorer match to the WAXS data.

Fig. 6.

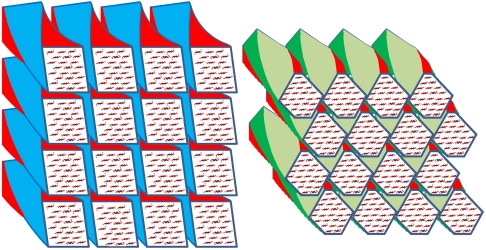
Chain packing arrangements for alternative shapes of spruce cellulose microfibrils. (A). Diamond shape. 24 chains, overall dimensions 3.2 × 3.9 nm. Weighted-mean column lengths normal to lattice planes (002), 2.7 nm; (1–10), 3.2 nm, (110), 2.6 nm. (B). Rectangular shape. 24 chains, overall dimensions 3.2 × 3.1 nm. Weighted-mean column lengths normal to lattice planes (002), 3.2 nm; (1–10), 2.8 nm, (110), 2.5 nm. Shape (B) is in closer accord with the observed Scherrer dimensions corrected for disorder. (C) Schematic diagram of two adjacent twisted microfibrils. Even if they have the same helical pitch, the ability of any crystal face to bind against the corresponding crystal face in the next microfibril is progressively lost with distance along the microfibril axis.

Microfibril diameters are calculated from NMR estimates of surface area (20, 71) by assuming that all disordered chains are at the surface and that the mean thickness of the surface monolayer is 0.56 nm, averaged from the (110) and (1–10) d-spacings of cellulose Iβ (9). But a monolayer exposed at the (010) face in the rectangular model would be 0.82 nm thick, and these dimensions may in any case be altered by disorder. We therefore avoided this approach to deducing absolute diameters, although trends calculated in this way agree with other methods (20). Both 24-chain models have over 60% of the chains at hydrophilic surfaces. If these surface chains were mostly disordered as defined by NMR there would be little scope for further disordered cellulose in the microfibril core, but localized discontinuities, at least, must exist at chain ends. Assuming DP = 10,000 (72) there is one such discontinuity on average per 200 nm of a 24-chain microfibril. Spruce cellulose when hydrolyzed with sulphuric acid breaks down into whiskers 200–400 nm long, with significant simultaneous loss of noncrystalline material assumed to come from extensive, acid-labile amorphous segments between them (73). However localized regions of disorder at chain ends might be sufficient to initiate acid cleavage of microfibrils, with disordered surface cellulose being hydrolyzed or crystallized independently.

The comparison between wood and primary-wall cellulose is of interest. Primary-wall microfibrils from celery collenchyma are about 3 nm in diameter as estimated by methods similar to those used here (28, 41). Other primary-wall microfibrils are either similar (74) or smaller (31, 71, 74) in diameter. C-6 conformations and H-bonding patterns in the disordered fraction of celery cellulose (28) were qualitatively similar to those reported here but primary-wall celluloses show consistent crystallographic differences, particularly the reduced monoclinic angle that has led these celluloses to be described as cellulose IV (48).

Axial Coherence and Twist.

It has been suggested that alternation between crystalline and disordered segments defines the length over which longitudinal crystallographic coherence is maintained. This length was only about 11 nm in the present experiments, uncorrected for disorder. Published axial Scherrer dimensions vary (19) as the width of the 004 reflection is often little greater than the instrumental broadening, but this dimension is clearly less than the length of nanocrystals prepared from wood cellulose (75) or isolated single sheets of chains (30). Some other feature must therefore contribute to the loss of axial coherence.

Considering how little variation is reported in the c dimension of the unit cell (19, 23, 76), the most likely contributor is twisting of the microfibril, which has been observed (3, 77–79) and simulated by MD (54), but see ref. 80. The mean helical pitch would probably need to be at least an order of magnitude greater than the resulting column length and would therefore be too long to give rise to small-angle axial scattering features within the q range of our SANS experiments.

Microfibril Aggregation.

The SANS data for dry spruce cellulose clearly demonstrated aggregation of microfibrils into larger units. Both the SANS and the FTIR experiments showed that at increasing moisture content, increasing amounts of water penetrated between the microfibrils within each aggregate. The data implied the separation of some segments by up to about 1 nm (4.0 nm-3.0 nm) at 25% D₂O by mass, but if all microfibrils were at this spacing it would imply a greater volume increase on hydration than is known to take place. More probably spacings were irregular (3) and the coherent SANS intensity was dominated by spacings greater than the mean, because the SANS contrast is expected to be greater for well separated pairs of microfibrils with D₂O between them.

Penetration of water into microfibril aggregates was unexpected, because aggregation of microfibrils was first suggested on the evidence that cellulose surfaces within such aggregates were inaccessible to solvents (6). But the solvents concerned did not include water, and water has much greater ability to separate and dissolve polysaccharide chains than, for example, the lower alcohols. Most of the outward-facing hydroxyl groups on the microfibril surfaces appeared to be accessible to deuterium exchange at saturation, although in the presence of smaller amounts of water many of the interfaces between microfibrils clearly remained dry. As the exchange process was probably dynamic it does not imply that a layer of water was permanently interposed between microfibrils, nor that the cohesion of the aggregates was completely disrupted, but only that water molecules could penetrate between microfibrils over some of their length in the hydrated state.

Conclusions

Our data suggest microfibrils with about 24 chains, possibly twisted and with considerable disorder increasing towards the surfaces. Less extensive disordered regions probably exist within the core of each microfibril. Tight lateral binding is facilitated by the hydrogen-bonding pattern of the surface chains, at only a small cost in tensile stiffness due to the loss of intramolecular hydrogen bonding between O2 and O6 (81). The surface location of these disordered chains means that a parallel mechanical model with tight lateral bonding to the ordered core is more appropriate than a series model, consistent with FTIR observations (35). The twisting of adjacent microfibrils may explain why they do not come into crystallographic register with one another over enough of their length to coalesce.

It is not certain that the number of chains in one microfibril is fixed and corresponds to the number synthesized by one terminal complex (27, 31), but if so each lobe of the terminal complex would be likely to synthesise four chains rather than six as has been assumed. As it travels through the cell membrane the terminal complex would seem to have to rotate, so that it leaves the microfibril twisted behind it (32). Rotation of densely arrayed terminal complexes might lead to mechanical interference between them with implications for the parallel, oriented deposition required for morphogenesis of secondary plant tissues (32, 33).

A rectangular model is favored for spruce microfibrils, differing from more crystalline celluloses in having one hydrophobic and one hydrophilic face exposed (54). It is not clear how other polymers restrict access of cellulases to the hydrophobic surfaces, but impacts of the structure and aggregation of microfibrils on the recalcitrance of woody biomass are to be expected (82).

Materials and Methods

Materials.

Mature earlywood from Sitka spruce [Picea sitchensis (Bong.) Carr.] was prepared as described (15) and longitudinal-tangential sections 20 μm in thickness were prepared wet on a sledge microtome. A three-stage extraction process (see SI Text) was used to isolate cellulose from this material for the NMR relaxation experiment.

SANS.

SANS analysis was conducted on beamline D11 at the Institut Laue-Langevin (ILL), Grenoble. Scattered neutrons were detected on a 96 × 96 cm CERCA ³He gas detector, at a sample-to-detector distance of 2 m and collimation length 8 m. The neutron wavelength was 0.6 nm with a dispersion of 9–10%. The q range covered in this experiment extended from 0.3 nm^-1 to 2.4 nm^-1. Samples 2 mm in thickness were adjusted to the desired moisture content by saturating with H₂O, D₂O, or 35∶65 D₂O∶H₂O (see SI Text) then equilibrating with phosphorus pentoxide and encapsulating in aluminum foil, with an empty foil container used as background.

WAXS.

X-ray diffraction patterns were obtained at ambient temperature using a Rigaku R-axis/RAPID image plate diffractometer. A Mo Kα (λ = 0.07071 nm) source was used, with the beam collimated to a diameter of 0.5 mm. Scattering angles were expressed as q = 4π sin θ/λ. Samples were 1 mm or 2 mm thick in the direction parallel to the beam and their other dimensions exceeded the beam diameter. The hydrated samples were saturated with H₂O and then moisture adjusted as above and encapsulated in polyethylene film. The diffraction patterns were collected in perpendicular transmission mode except for tilting experiments to measure the width of the axial reflections. Radial profiles of scattered intensity I as a function of q were integrated over an azimuthal angle of 5° on either side of the equator and meridian, using the AreaMax software package (Rigaku/MSC). See SI Text for background correction procedures and fitting of asymmetric peak functions to the equatorial profiles. It was assumed that a plot of peak width F against the square of the order of reflection r² is linear (47) with, at the intercept, the Scherrer dimension (mean column length) L = kλ/F cos θ where the Scherrer constant k = 0.94 as appropriate for a cylindrical crystallite.

FTIR Microscopy.

Longitudinal-tangential 20 μm sections were used for transmission FTIR spectroscopy with vapor-phase deuterium exchange as described previously (28) (See SI Text). For full saturation with D₂O the sample was presoaked with D₂O (1 μL) and the upper window of the cell was immediately replaced, with an uninterrupted flow of D₂O vapor. The data reported here were recorded during experiments in which the OH : OD ratio remained constant for at least 30 min under rigorously dry conditions, much longer than required to collect the spectra (Fig. S2).

Solid-State NMR.

CP-MAS spectra were obtained on a Varian VNMRS spectrometer operating at 100.56 MHz for ¹³C with a MAS rate of 8 kHz and two-pulse phase modulation decoupling at 96.2 kHz. A linear CP ramp was used with contact time 1 ms. Recycle time was 4 s. Spectral referencing was with respect to tetramethylsilane.

Single-pulse-excitation (SP-MAS) ¹³C NMR spectra were obtained from isolated spruce cellulose using the MOST multiple-pulse proton decoupling sequence (28, 51). See SI Text for details.

Spin-diffusion experiments with initial proton magnetization gradient set up using spin-spin relaxation were carried out as reported previously (15). For the derivation of the 2D representation of this experiment see SI Text.