Flow characteristics in a canine aneurysm model: A comparison of 4D accelerated phase-contrast MR measurements and computational fluid dynamics simulations

Abstract

Purpose: Our purpose was to compare quantitatively velocity fields in and around experimental canine aneurysms as measured using an accelerated 4D PC-MR angiography (MRA) method and calculated based on animal-specific CFD simulations.

Methods: Two animals with a surgically created bifurcation aneurysm were imaged using an accelerated 4D PC-MRA method. Meshes were created based on the geometries obtained from the PC-MRA and simulations using “subject-specific” pulsatile velocity waveforms and geometries were then solved using a commercial CFD solver. Qualitative visual assessments and quantitative comparisons of the time-resolved velocity fields obtained from the PC-MRA measurements and the CFD simulations were performed using a defined similarity metric combining both angular and magnitude differences of vector fields.

Results: PC-MRA and image-based CFD not only yielded visually consistent representations of 3D streamlines in and around both aneurysms, but also showed good agreement with regard to the spatial velocity distributions. The estimated similarity between time-resolved velocity fields from both techniques was reasonably high (mean value >0.60; one being the highest and zero being the lowest). Relative differences in inflow and outflow zones among selected planes were also reasonable (on the order of 10%–20%). The correlation between CFD-calculated and PC-MRA-measured time-averaged wall shear stresses was low (0.22 and 0.31, p < 0.001).

Conclusions: In two experimental canine aneurysms, PC-MRA and image-based CFD showed favorable agreement in intra-aneurismal velocity fields. Combining these two complementary techniques likely will further improve the ability to characterize and interpret the complex flow that occurs in human intracranial aneurysms.

INTRODUCTION

The origin and natural history of intracranial aneurysms (IAs) are closely associated with disturbed hemodynamic flow conditions; however, exact mechanisms are unknown.^{1, 2} Consequently, blood flow parameters either measured from imaging^{3, 4, 5} or obtained through subject-specific computational fluid dynamics (CFD) simulations^{6, 7, 8} may provide insight not only into factors relevant to the development and progression of IAs but also into their short and long term responses to therapeutic interventions (e.g., coil embolization and stent deployment).

“Subject-specific” CFD (Refs. ^{6, 8}) often utilizes vascular geometry derived from angiographic images and physiological conditions (e.g., blood flow rate, velocity, and/or pressure) adjacent to the vasculature of interest as inputs (known as boundary conditions in engineering and applied mathematics literature) to calculate 4D velocity fields by solving a set of partial differential equations, namely, the Navier–Stokes equations. Tremendous developments in computational modeling and medical imaging over the last fifteen years allow not only creation of geometrically accurate models^{6, 8} of cerebral aneurysms but also utilization of subject-specific flow information during the solution of these computer models. These computational tools provide a means to investigate variations in the hemodynamics among aneurysms of different types. For example, Cebral and coworkers recently found that small velocity jets with complex unstable flow patterns were more commonly seen in ruptured aneurysms than in unruptured ones through CFD simulations.⁸ There remains, however, a need to further document the consistency, reliability and accuracy of these methods in capturing the relevant features of intra-aneurismal flow.⁹

In parallel with advances in CFD capabilities, improvements in time-resolved three-dimensional (i.e., 4D) PC-MRA combined with three-directional velocity encoding have greatly improved achievable spatial resolutions.^{10, 11, 12} PC-MRA techniques have been applied to measure blood flow patterns in vivo in human subjects with IAs.^{5, 13, 14} In addition to blood velocities, other parameters, e.g., pressure gradients^{13, 15} and wall shear stress (WSS) (Refs. ^{5, 16}) have been quantified using PC-MRA velocity measurements. One limitation in using clinical PC-MRA to measure intra-aneurismal flow is its spatial resolution (on the order of 1-mm) since individual protons having incoherent velocities (at the subgrid level) cannot be resolved by one “averaged” velocity measurement from a relatively large resolution cell (i.e., voxel). Furthermore, disturbed flow could also lead to intravoxel dephasing where spins within the resolution cell become randomly oriented such that the accuracy of velocity measurements is significantly affected.¹⁷ Since velocity is the fundamental variable needed for calculating the WSS and the pressure gradient, it is thus essential to understand whether or not PC-MRA velocity measurements have adequate accuracy and resolution to provide results that are of clinical relevance.

A few studies have addressed this issue by comparing in vivo measurements of intracranial hemodynamic using PC-MRI with CFD simulations.^{16, 18, 19, 20, 21, 22} Two very recent studies qualitatively compared velocity fields measured with 4D PC-MRA and determined from CFD simulations in normal intracranial arteries of healthy volunteers²¹ and, in patients with IAs.¹⁶ In current study, the accelerated phase-contrast technique, PC-VIPR (Phase-Contrast Vastly undersampled isotropic projection reconstruction),¹² provides improved spatial resolution (i.e., the worst resolution has been improved to 0.525–0.62 mm from 1.6 mm reported by two above-mentioned studies^{16, 21} where different 4D PC-MRA techniques^{11, 23} were used). It is well known that complex flow rapidly changes in and around aneurysms.²⁴ Thus, enhanced isotropic resolution might improve the ability to resolve more detailed flow features.

To this end, our first objective was to extend velocity comparisons by first quantitatively comparing time-resolved velocity fields obtained using the accelerated PC-VIPR technique from two experimental canine bifurcation aneurysms.²⁶ More specifically, such comparisons are performed with spatially-registered velocity vector fields in a point-to-point manner. To our knowledge, this is the first study to compare “animal-specific” CFD simulation results with flow measurements from the accelerated PC-VIPR approach such a rigorous fashion. It is worth noting that validations of the PC-VIPR MRA technique were initially reported by comparing with conventional 2D PC-MRA measurements¹² and then by using flow phantoms under constant flow rates.²⁵ In the latter study²⁵ by Nett and colleagues, they reported that the steady flow rates estimated by the PC-VIPR technique (Venc = 120 cm/s) from a tubing phantom were, on average, only 0.4% less than the known flow rate. However, the PC-VIPR technique has not been rigorously validated for in vivo conditions, in particular, involving in disturbed pusatile flow. Our second objective was to quantitatively assess and visualize the consistency among WSSs values that were derived from the velocity fields in these two aneurysms. This is also the first study where MRA-based WSS is compared with CFD-based WSS to investigate the impact of MRA resolution and velocity measurement noise.

MATERIALS AND METHODS

Creation of canine experimental aneurysms

Under an institutionally approved animal protocol, bifurcation aneurysms (Fig. 1) were created in two adult female Beagles using a technique originally described by German and Black²⁷ and later modified in our laboratory.³ The basic geometrical parameters of these two aneurysms are listed in Table Table I.. At least three weeks after the aneurysm was produced, animals were anesthetized and then subjected to an accelerated 4D PC MRA flow study with a radially undersampled acquisition approach, PC-VIPR.^{12, 28} High resolution 3D-DSA studies were also performed within 24 h of MRA imaging for each animal and were used to verify subsequent geometrical reconstruction of the relevant vasculture. Hereafter, these two aneurysms are referred to as aneurysms A and B.

Figure 1.

Segmented and meshed geometries of the two aneurysms from PC-VIPR MRA registered with adjacent soft tissue: (a) Aneurysm A and (b) aneurysm B.

Table 1.

Basic geometrical and flow parameters of Aneurysms A and B. The aspect ratio is defined as the ratio between the aneurysm height and the neck width.

Aneurysm	Inlet diameter (mm)	Averaged flow rate (mL/s)	Height (mm)	Width (mm)	Aspect Ratio	Volume (mm3)	Ostium area (mm2)
A	2.9	4.9	9.7	4.4	2.20	235.4	14.52
B	3.2	3.5	9.4	4.3	2.18	254.3	17.10

Description and calibration of the accelerated PC-VIPR MRA technique

The 3D phase-contrast Vastly undersampled isotropic projection reconstruction (PC-VIPR) MR acquisition is a highly undersampled 3D radial acquisition that provides isotropic voxel dimensions.¹² PC-VIPR MRA exploits the sparsity of the vascular data sets and allows for accelerated imaging as compared to conventional Cartesian PC-MRA.¹² All MR imaging was performed with a 1.5 T clinical scanner (Signa HD, GE Healthcare, Waukesha, WI, USA). A standard eight-channel knee coil was used for imaging. An optimized PC-VIPR MRA method²⁸ provided us with time-resolved 3D voxel data, each of which has three-directional flow velocity components, using the following parameters: a TE/TR of 3.6/14.0 ms, retrospective ECG gating, a bandwidth of ±31.25 kHz, temporal resolution of approximately 35 ms, and scan time of 8 min. The scan time was short because an accelerated PC-MRA technique was used. More details can be found in previous publications.^{12, 28} The field of views (FOVs) were 13 × 13 × 13 cm³ and 16 × 16 × 16 cm³ for aneurysms A and B, respectively, thereby resulting in isotropic spatial resolution of 0.525 × 0.525 × 0.525 mm³ and 0.62 × 0.62 × 0.62 mm³ for aneurysms A and B, respectively.

The above-mentioned 3D PC-VIPR scans were performed twice using both a high (1.5 m/s) VENC and a low VENC (0.5 m/s) in order to better capture both the high velocity jets and areas of slow flow known to be present in and around these experimental aneurysms. Both VENCs were chosen along each of the three principal axes so that all three components of the velocity vector fields were measured by converting measured phase angles to velocity magnitudes. All data acquisition was directed by experienced MR physicists (K. J. or O. W.).

Description of “animal-specific” CFD simulations

Temporally-averaged MRA velocity magnitude data from the acquisitions described above were transferred to an offline personal workstation (Dell Precision 390, Dell Inc., Austin, TX). These data were then interpolated to achieve isotropic voxel sizes of 0.225 × 0.225 × 0.225 mm³ from their native resolutions (0.525 × 0.525 × 0.525 mm³ and 0.62 × 0.62 ×  0.62 mm³ for Aneurysms A and B, respectively). Segmentation of the volume of interest (VOI) was accomplished with a commercially available package, ScanIP (Simpleware Inc., Exeter, United Kingdom).²⁹ To verify the realism of the geometries reconstructed from MRA data, these were visually compared to the ones derived from 3D-DSA data using an open source visualization package (Paraview, Kitware Inc., NY). Besides ensuring visual consistency, geometrical measurements (aneurysm height, width, surface area, and volume) were taken from both the MRA-based and 3D-DSA-based geometries. The averaged differences are less than 10% for both aneurysms. The reconstructed geometry was imported to a voxel-based mesh generator³⁰ ScanFE (Simpleware Inc., Exeter, United Kingdom) to create an unstructured mesh.

To compute velocity waveforms in and around the aneurism, we solved the time-dependent incompressible, 3D Navier–Stokes equations [i.e., Eqs. 1, 2] for the 3D meshed vessel geometry using FLUENT software, a commercial computational fluid dynamic (CFD) solver (version 12.0; ANSYS-FLUENT Inc., Lebanon, NH). The equations for velocity are written as

$$\overrightarrow{\nabla }•\overrightarrow{u}=0,$$ (1)

$$\rho \frac{\partial \overrightarrow{u}}{\partial t}+\rho (\overrightarrow{u}•\overrightarrow{\nabla })\overrightarrow{u}=-\overrightarrow{\nabla }p+\mu {\nabla }^2\overrightarrow{u},$$ (2)

where $\overrightarrow{u}$ is the three-dimensional velocity vector, ρ is the blood density, p is the pressure and μ is the viscosity. The pressure–velocity coupling in Eqs. 1, 2 is obtained using the SIMPLEC algorithm. The explicit time-marching second-order scheme with a time step 2 × 10⁻³ s (approximately 350 steps per cardiac cycle) was used for the computations. Although this time step is relatively coarse, it seems adequate to capture gross flow features.⁸ For both aneurysms A and B, approximately 0.75 million tetrahedral cells were used to simulate transient flow [see Eqs. 1, 2] using the finite volume method by the FLUENT Solver. The average size of tetrahedral cells is approximately 0.0035 mm³. We also verified that sufficiently fine (approximately 0.03 mm layer thickness) boundary layers were created by the SCANFE software.

In Eqs. 1, 2, blood was modeled as an incompressible laminar fluid with a density of 1050 kg/m³. Both non-Newtonian and Newtonian viscosity models were used for CFD simulations. In the Newtonian viscosity model, a constant dynamic viscosity of 0.0035 kg/m s was assumed. Non-Newtonian blood behavior, which could have important effects on the flow in low shear rate ($\stackrel{·}{\gamma }$) regions, was taken into account by use of a Carreau-Yasuda viscosity model as follows:

$$\frac{\mu -{\mu }_{\infty }}{{\mu }_0-{\mu }_{\infty }}={[1+{\left(\lambda \stackrel{·}{\gamma }\right)}^2]}^{n-1∕2},$$ (3)

where μ₀ and μ_∞ are the zero and infinite shear rate limit viscosities, respectively, λ is the relaxation time constant and n is the power law index. The Carreau model values adopted³¹ are as follows: μ₀=0.0035  kg∕m∕s (which corresponds to the value of viscosity used in the Newtonian flow simulations), μ_∞=0.056  kg∕m∕s, λ=3.313  s, and n = 0.3568. Hereafter, we referred non-Newtonian and Newtonian CFD simulations as to CFD₁ and CFD₂, respectively.

An inlet flow boundary condition was chosen from PC-MRA measurements made in the artery upstream (approximately 4 cm) from the aneurysms. Time-dependent flow rates were obtained by integrating the through-plane PC-MRA velocity component over the artery lumen on a slice perpendicular to its long axis. It is reported that uncertainties of in vivo conventional PC-MRA in terms of flow rate range from 3 to 13%.^{32, 33, 34} This accuracy remains adequate for use in establishing boundary conditions for CFD calculations.³⁵ Outlet boundary conditions of the flow volume ratios of the two outlet branches were based on the PC-MRA measurements. More specifically, user defined functions (UDFs) (ANSYS-FLUENT Inc., Lebanon, NH) were used to define time-varying flow rates based on PC-MRA measurements at the inlet and at one of the outlets by assuming parabolic velocity profiles. Therefore, the flow volume division ratio between the two outlet branches was a variable and consistent to the MRA-measured flow rates (approximately 1:1). A “no-slip” boundary condition and rigid wall were assumed. Convergence criteria for continuity and velocity were both set to 10^-3 (relative to the largest value in the first five iterations) and were satisfied for each simulation. Sensitivity tests on mesh size, step size, and convergence thresholds in terms of simulated velocity values and wall shear stresses at selected locations were performed similar to methods described by Valencia et al.³⁶

Since a steady state computation was used by ANSYS FLUENT 12.0 as the initial guess for the transient simulation, multiple cardiac cycles were necessary for the result to be considered as fully periodic in time. For each simulation, we computed flow over a total of three cardiac cycles and results corresponding to the last cycle simulated will be reported below. We verified that the periodicity was reached after the second cycle.

Off-line visualization and data analysis

Comparison between PC-MRA measured and CFD-simulated velocity fields

As shown in Fig. 1, we first verified that the segmented geometries (i.e., meshed surfaces) were spatially-registered with the PC-MRA signal magnitude data as well as the phase-contrast velocity data. Then, for point-to-point and temporally-matched comparisons between the PC-MRA measurements and the CFD-calculated velocity fields, all velocity data were interpolated onto a rectilinear grid at an isotropic spatial resolution of approximately 0.6 mm (which corresponds to the spatial resolution of MRA velocity measurements) using MATLAB (Mathworks Inc., Natick, MA). As described before, we repeated velocity data acquisition for each animal using two VENC settings to capture both low-velocity and high velocity flows. In this step, we simply used MRA measurements with the low VENC value for comparisons with simulated velocity values by the CFD unless velocity aliasing was identified. In the other words, with the presence of velocity aliasing in certain spatial locations, matched MRA velocity measurements acquired under the high VENC were then used to replace these aliased velocity measurements in these locations. The potential beat-by-beat variations (e.g., slight heart rate change) accompanied by two data acquisitions were not accounted for in this study.

To quantify the degree of similarity between the MRA-measured and the CFD-synthesized velocity fields, we adopted a similarity metric between vector fields related to that developed by Li and Shen.³⁷ This similarity metric is normalized between 0 and 1, 1 being the highest degree of similarity. More details are provided in Appendix A. Similarity values were calculated for three pairs of velocity vector fields: MRA versus non-Newtonian CFD simulations (CFD₁), MRA versus Newtonian CFD simulations (CFD₂) and CFD₁ versus CFD₂. We also estimated the absolute magnitude (unit: m/s) and angular (unit: degree) differences for these three pairs of velocity vector fields.

Prior to quantitative comparisons of the CFD-simulated and the MRA-measured velocity fields, CFD-simulated velocity data were first interpolated from an unstructured/irregular grid onto a 3D uniform rectilinear grid (0.1-mm voxel size). These re-interpolated velocity fields were then convolved with a 3D isotropic Gaussian kernel (1.2 × 1.2 × 1.2 mm with a sigma of 0.7) to mimic the “averaging/smoothing” effect by a point-spread function of the MRA system as reported in the literature.³⁸ Finally, the “convolved” velocity data by the above-mentioned Gaussian Kernel were interpolated to a desirable resolution for similarity comparison as described above.

Of note, the velocity comparisons between CFD₁ and CFD₂ were done in a fine grid (0.1-mm voxel size consistent to the CFD mesh density), while the velocity comparisons for the other two pairs were performed at a coarse grid (approximately 0.6-mm consistent to the MRA voxel size).

Generation of 3D streamlines

Three-dimensional (3D) streamlines (i.e., lines of tangent to instantaneous velocity vectors) of both CFD-simulated and MRA-measured velocity vectors approximately at 20 phases of the cardiac cycle (i.e., 17 and 22 phases per cardiac cycle for aneurysms A and B, respectively) were generated using a commercial software package (AMIRA 5.3, Mercury Computer System Inc., MA). To calculate 3D streamlines, all CFD-simulated velocity vector fields were resampled/downsampled onto a rectilinear grid at an isotropic spatial resolution of approximately 0.6 mm (which corresponds to the spatial resolution of MRA velocity measurements). The origins of all streamlines were first placed at the inlet of each aneurysm model and then computed in the downstream direction using a published algorithm.³⁹

Comparison of wall shear stress obtained from the PC-MRA measured and CFD-simulated velocity fields

Wall shear stress (WSS) was derived from respective velocity fields by a polynomial interpolation of values near the vessel wall.¹⁶ For completeness, a brief description is provided in Appendix B.

To understand how two key factors, namely imaging resolution (voxel size) and velocity accuracy, affect the PC-MRA WSS estimation, we first arbitrarily selected one 3D CFD-simulated velocity field from aneurysm A. Then, this CFD-simulated velocity data set was interpolated from an unstructured/irregular grid onto a 3D uniform rectilinear grid. To mimic 3D PC-MRA measured velocity fields with different resolutions, the grid spacing was varied from 0.03 to 1 mm during the interpolation. Gaussian-distributed (White) noise with a zero mean was added to the resampled CFD velocity fields to simulate velocity measurement noise. Since the additive noise has a zero mean, standard deviation becomes the only varying parameter. From a statistical perspective, when the signal-to-noise ratio (SNR) is high (>5), the noise in PC-MRA can be approximated by a Gaussian distribution for practical purposes.⁴⁰ We verified that the high-SNR assumption and the Gaussian noise distribution were true by measuring the background tissue noise in our data. Next, the WSS values were estimated using the method described in Appendix B. Finally, these estimated WSS values were compared with the CFD-calculated WSS values based on the same velocity field (gold standard). The similarity between the CFD-calculated WSS values and the estimated WSS values were assessed by the linear correlation, with 1 being the value for highest satisfactory performance.

Statistical analysis

Pearson’s correlation coefficients were calculated between quantities derived from MRA and CFD velocity data to determine their linear correlation. Student’s t-tests were performed to assess the statistical significance of the observed correlation values. In this study, a p-value of 0.05 or less indicated statistical significance.

RESULTS AND INTERPRETATION

Similarity of velocity vector fields

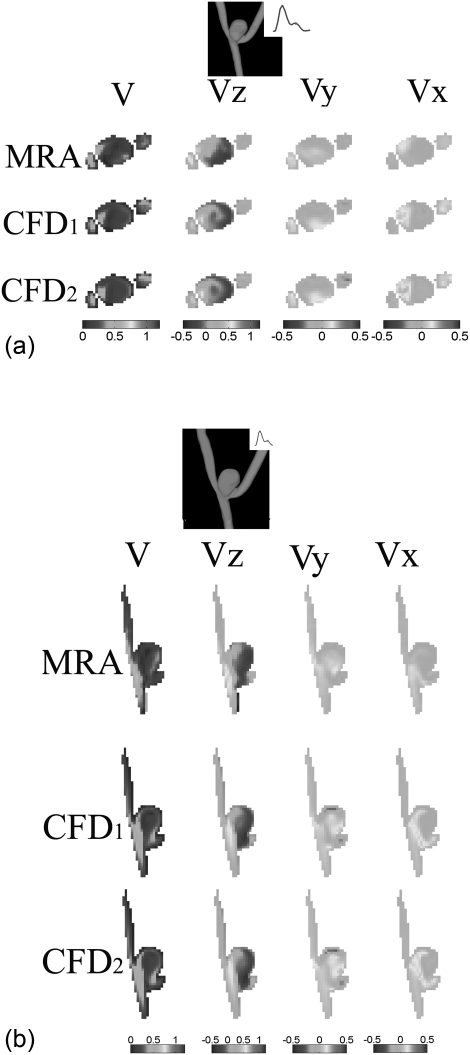
For approximately 20 phases (i.e., 17 and 22 phases per cardiac cycle for Aneurysms A and B, respectively) per cardiac cycle, point-to-point comparisons between the temporally-matched MRA-measured and CFD-simulated velocity fields were performed at four longitudinal and four transverse planes of each aneurysm. Figures 2a, 2b shows examples of spatially-registered and temporally-matched (between MRA and CFD) velocity fields during diastole for one of the transverse and one of the longitudinal planes from aneurysm A. In each figure, three components (Vx, Vy, Vz) and the velocity amplitude map for this plane are compared, respectively.

Figure 2.

Comparison of 3D velocity vector fields at diastole [three components Vx, Vy, and Vz and the velocity amplitude V] obtained from subject-specific CFD simulations and PC-VIPR MRA measurements for (a) a transverse plane and (b) a longitudinal plane in aneurysm A. In both plots, CFD₁ and CFD₂ denote non-Newtonian and Newtonian CFD simulations, respectively. Color bars corresponding to three plots of each column are shown at the end of each column. The unit used for velocity is m/s for all plots in (a) and (b).

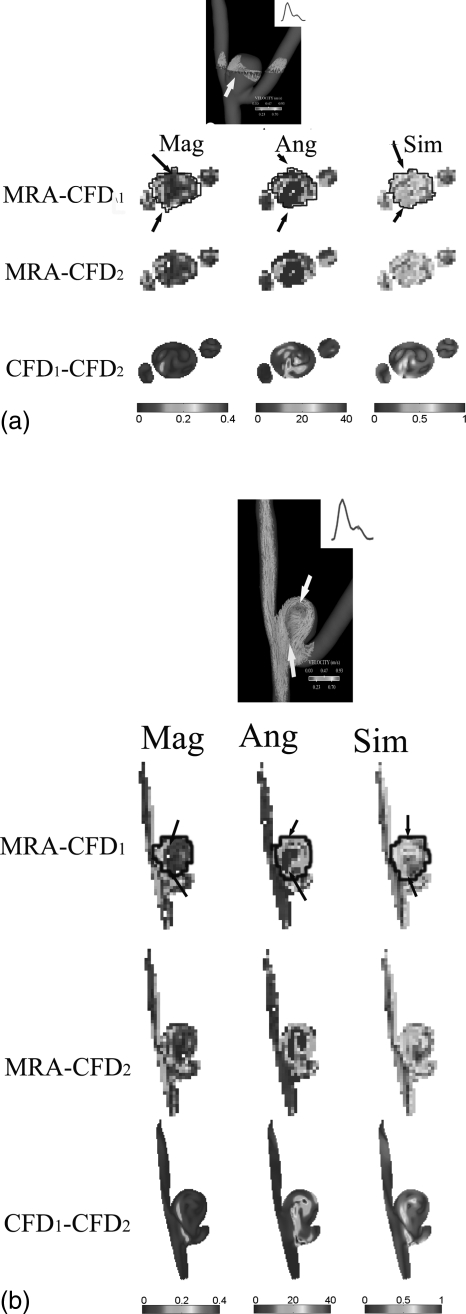
Quantitatively, the similarity metric defined by Eq. A1 in Appendix A as well as the absolute magnitude and angular differences were calculated at the same transverse and longitudinal planes illustrated in Figs. 2a, 2b between the MRA-measured and CFD-simulated (both Newtonian and non-Newtonian) velocity fields as well as between CFD-simulated velocity fields. Then, these spatially-varying similarity and, absolute magnitude and angular difference values were displayed in Figs. 3a, 3b. It is easy to see, from Figs. 23, that spatial velocity distributions between the MRA measurements and CFD simulations were in favorable agreement. We also calculated spatially-averaged similarity values within the aneurysm dome (i.e., the outlined areas in the respective similarity maps of Figs. 3a, 3b), the spatially-averaged similarity values within the dome of the transverse plane are 0.67 and 0.66 between the MRA-measured and the CFD₁, and between the MRA-measured and CFD₂, respectively, in Fig. 3a, while the spatially-averaged similarity values with the dome of the longitudinal plane are 0.72 and 0.70 between the MRA-measured and the CFD₁, and between the MRA-measured and CFD₂, respectively, in Fig. 3b. However, the similarity values between the non-Newtonian (CFD₁) and Newtonian (CFD₂) are higher as clearly illustrated in Figs. 3a, 3b. The spatially-averaged similarity values with the dome of the transverse and longitudinal planes are 0.89 and 0.91, respectively, between the CFD₁ and CFD₂ simulations.

Figure 3.

The estimated similarity values [see Eq. A1], absolute magnitude and angular differences between three pairs of velocity fields [MRA vs. CFD₁, MRA vs. CFD₂, and CFD₁ vs. CFD₂] for (a) the transverse and (b) the longitudinal planes in aneurysm A illustrated in Figs. 2a, 2b, respectively. The velocity data correspond to a phase at the diastole. Arrows on 3D velocity vector plots [top plots of both (a) and (b)] indicate a border region between the velocity jet and the low-velocity recirculation zone. In this figure, CFD₁ and CFD₂ denote non-Newtonian and Newtonian CFD simulations, respectively. Manually-delineated contours on both (a) and (b) indicate regions within the aneurysm dome. Mag (m/s), Ang (degree) and Sim [0-1] denote the absolute magnitude and angular differences, and the similarity metric between two velocity vectors, respectively. The arrows in the similarity plots (left lower three columns) point to low similarity values, where arrows in the absolute magnitude (right lower three columns) and angular (middle lower three columns) difference plots point to large discrepancies in both magnitude and direction of two sets of comparing vectors.

The averaged absolute magnitude differences between the CFD-simulated and the MRA-measured velocities are approximately 0.10 m/s, while the averaged absolute angular differences range from 20.0 to 33.8°, as shown in Figs. 23. Similarly, the absolute magnitude (roughly 0.02 m/s) and angular (roughly 6°) differences between the non-Newtonian (CFD₁) and Newtonian (CFD₂) velocities are lower.

Similar to what illustrated in Figs. 23, we analyzed the similarity values within the domes of the two aneurysms for all phases of the cardiac cycle at four transverse and four longitudinal planes. Results are listed in Table Table II. below.

Table 2.

Estimated absolute magnitude and angular differences, and similarity values with two aneurysm sacs for three pairs of velocity vector fields: MRA versus non-Newtonian CFD simulations (CFD₁), MRA versus Newtonian CFD simulations (CFD₂) and CFD₁ versus CFD₂. The mean values (±one standard deviation) were estimated within the manually-segmented aneurysm domes [see Figs. 3a, 3b].

	Aneurysm A			Aneurysm B
	Magnitude (m/s)	Angular (degree)	Similarity	Magnitude (m/s)	Angular (degree)	Similarity
MRA-CFD1	0.09 ± 0.03	38.4 ± 7.4	0.64 ± 0.04	0.08 ± 0.03	40.0 ± 7.4	0.64 ± 0.04
MRA-CFD2	0.09 ± 0.03	40.7 ± 7.5	0.62 ± 0.04	0.07 ± 0.03	39.6 ± 8.0	0.65 ± 0.04
CFD1-CFD2	0.03 ± 0.01	11.2 ± 3.0	0.85 ± 0.04	0.03 ± 0.01	22.9 ± 7.4	0.78 ± 0.06

Overall, there was a moderately high similarity (>0.6) between the MRA-measured and CFD-calculated velocity vector fields. The absolute magnitude and angular differences were approximately 0.09 m/s and 40°, respectively. Consistent with the visual perception shown in Figs. 3a, 3b, the averaged similarity values of velocity vector fields between the CFD₁ and CFD₂ simulations were 0.85 ± 0.04 and 0.78 ± 0.06 for Aneurysms A and B, respectively. Consistent to this observation, the absolute magnitude differences between the CFD₁ and CFD₂ simulations were approximately 0.03 m/s and therefore were significantly lower (p < 0.05), as compared to these between the MRA-measured and CFD-calculated velocity vector fields. The similarities between the CFD₁ and CFD₂ simulations were significantly higher (p < 0.05). Interestingly, the absolute angular differences between the CFD₁ and CFD₂ simulations in aneurysm B were significantly (p < 0.05) higher than these in aneurysm A. However, in both aneurysms, there was no statistically significantly difference among similarity values in the diastole and systole.

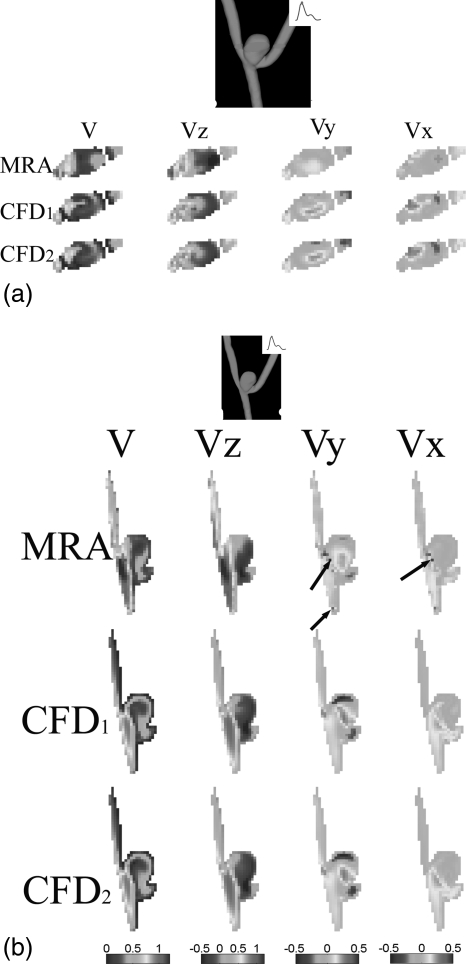
Spatially-registered and temporally-matched velocity fields at the peak systole for the same transverse and longitudinal planes shown in Fig. 2a, 2b are shown in Figs. 4a, 4b.

Figure 4.

Comparison of 3D velocity vector fields at the peak systole (three components Vx, Vy and Vz and the velocity amplitude V) obtained from subject-specific CFD simulations and PC-VIPR MRA measurements for (a) a transverse plane and (b) a longitudinal plane in aneurysm A. In both plots, CFD₁ and CFD₂ denote non-Newtonian and Newtonian CFD simulations, respectively. Color bars corresponding to three plots of each column are shown at the end of each column. The unit used for velocity is m/s for all plots in (a) and (b). The arrow in (b) points to possible MRA measurement errors.

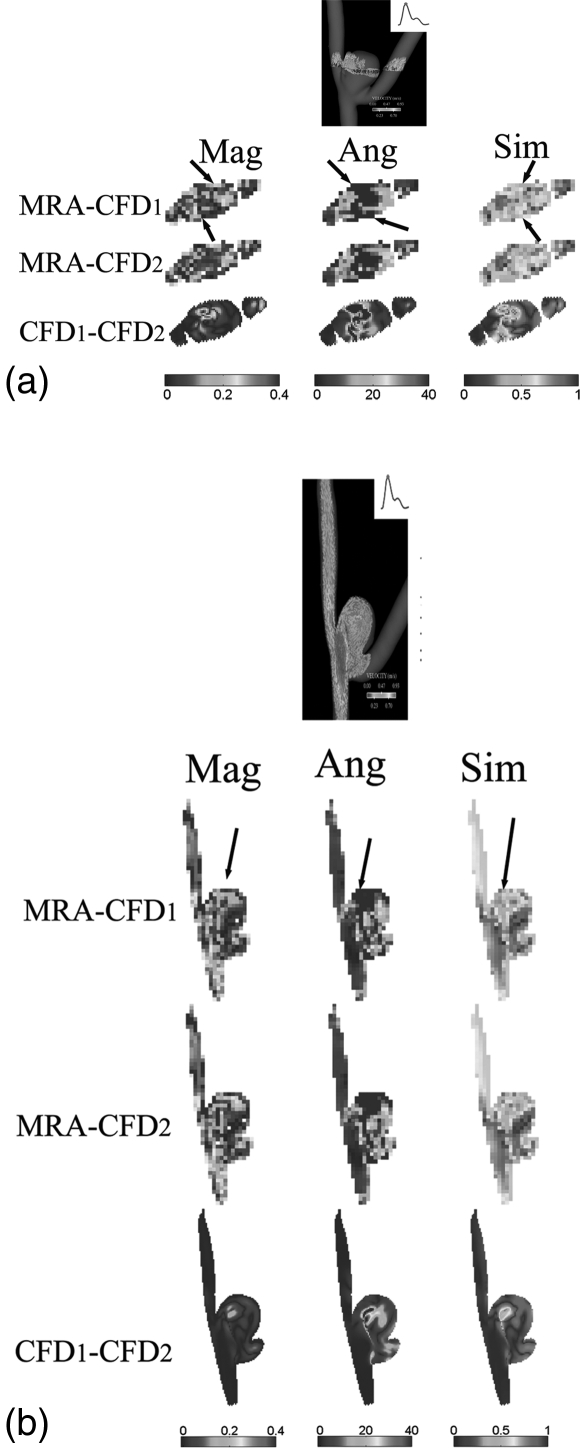
The corresponding similarity, and absolute magnitude and angular difference plots at the peak systole are shown in Figs. 5a, 5b above. As compared to values during diastole [Figs. 3a, 3b], the spatially-averaged similarity values within the aneurysm dome between the MRA-measured and the CFD₁ velocity fields were comparable (0.65 and 0.68 for Figs. 5a, 5b, respectively), whereas the spatially-averaged similarity values within the aneurysm dome between the MRA-measured and the CFD₂ velocity fields were reduced to 0.67 and 0.66 in Figs. 5a, 5b, respectively. In Figs. 5a, 5b, the similarity values of velocity vector fields between the CFD₁ and CFD₂ were 0.84 and 0.94, respectively. It is also worth noting that, consistent to Figs. 3a, 3b, discrepancies between the MRA measurements and CFD simulations shown in Figs. 5a, 5b also occurred at the border zone between the velocity jet and the low-velocity recirculation area where the velocity gradient and shear rate are also high. Similarly, the effect of the non-Newtonian properties of blood also seemed important in these border regions with high velocity gradients as shown in Figs. 35.

Figure 5.

The estimated similarity values [see Eq. A1], absolute magnitude and angular differences between three pairs of velocity fields [MRA vs. CFD₁, MRA vs. CFD₂, and CFD₁ vs. CFD₂] for (a) the transverse and (b) the longitudinal planes in aneurysm A illustrated in Figs. 2a, 2b, respectively. The velocity data correspond to the peak systole. In this figure, CFD₁ and CFD₂ denote non-Newtonian and Newtonian CFD simulations, respectively. Mag (m/s), Ang (degree) and Sim [0-1] denote the absolute magnitude and angular differences, and the similarity metric between two velocity vectors, respectively. The arrow in the similarity plots (left lower three columns) points to low similarity values, where arrows in the absolute magnitude (right lower three columns) and angular (middle lower three columns) difference plots point to large discrepancies in both magnitude and direction of two sets of comparing vectors.

In any aneurysm, two major flow areas can be defined: flow coming into the aneurysms, i.e., the inflow into the aneurysm and flow leaving the aneurysm, i.e., the outflow out of the aneurysm (hereafter referred as to inflow and outflow for simplicity). Using transverse planes oriented nearly perpendicular to the flow direction [Figs 3a, 5a] we estimated, during each phase of the cardiac cycle, the size of the inflow and outflow zones (hereafter referred as to inflow or outflow area) for four such transverse planes in each of the two aneurysms. The averaged absolute percent area differences (AAPAD) between the MRA measurements and the CFD predictions were calculated as follows: abs[(measured value—CFD prediction)/measured value]. Relative differences between the inflow areas were relatively large (average 13.9 and 15.1% for inflow areas for aneurysms A and B, respectively) between the MRA-measurements and the CFD₁ predictions. However, the discrepancy was even larger (average 17.2 and 20.4% for inflow areas for aneurysms A and B, respectively) between the MRA-measurements and the CFD₂ predications. Our values were slightly higher but comparable to 12% of average differences reported by Karmonik et al.¹⁹

When all (normal) velocities were integrated over inflow or outflow areas for the four transverse planes, in CFD simulations made with a rigid wall assumption, the differences between inflow and outflow volumes were approximately 1%. There were, however, larger imbalances in the PC-VIPR MRA measured values between the ratios of the inflow and outflow volumes [35.8 ± 23.4% (mean ± standard  deviation) for aneurysm A and 24.2 ± 17.1%, for aneurysm B, respectively].

Visualization of 3D streamlines

In Figs. 6a, 6b, instantaneous streamlines at the peak systole were calculated using MRA-measured and CFD-simulated velocity fields for both aneurysms. Although Figs. 6a, 6b only show the streamline flow patterns during the peak systole, these patterns were found to be stable over the entire cardiac cycle. As would be expected, since both aneurysms were geometrically similar, the gross flow patterns were also quite similar. There was a jet-like stream oriented parallel to the upstream segment of the parent artery immediately below the aneurysm ostium which enters the aneurysm along its left side, reaches the top of the dome, then spins clockwise around and across the dome to finally exit from the aneurysm almost exclusively into the branch on the right side. Qualitatively, these streamline visualizations show good correspondence between major flow features in and around both aneurysms as determined from the MRA measurements and the CFD calculations.

Figure 6.

Plots of streamlines (i.e., lines of tangent to instantaneous velocity vectors) of CFD simulated and PC-MRA measured velocity vectors at diastole for (a) Aneurysms A and (b) B, respectively. Streamlines were color encoded using velocity amplitude (0–0.8 m/s). In this figure, CFD₁ and CFD₂ denote non-Newtonian and Newtonian CFD simulations, respectively.

Two main differences were, however, noted. First, a 3D streamline illustrates the trajectory a zero-mass particle takes through an instantaneous flow field. Because of the presence of MRA-measurement noise, there were fewer trajectories calculated when the MRA-measured velocity fields were used as compared to both the CFD₁ and CFD₂ simulations. Second, areas of recirculation were not as well captured by the MRA-measured velocity fields as was the case with those obtained using the CFD calculations. Along the upper portions of the dome, some streamlines in the MRA based models were seen to stop at a segment of an arterial wall or at a margin of a surface in the aneurysm domes [arrows in Figs. 6a, 6b]. At the center of the dome, considerably weaker secondary/rotational flows (nonaxial velocity components) were observed in the MRA-measured velocity fields than in the calculated velocity fields.

Comparisons of WSS

The results of temporally-averaged wall shear stress (TA-WSS) estimations of both aneurysms are illustrated in Figs. 7a, 7b. In both aneurysms the TA-WSS distributions obtained from CFD (both CFD₁ and CFD₂) simulations and MRA measurements showed that the high WSS zones were along the top of the aneurysm domes where the inflow jet impacted the aneurysm wall [see Figs. 6a, 6b]. However, there were low correlations between the CFD simulations and the MRA-measurements. We found that the linear correlation values between the TA-WSS values obtained from the CFD₁ simulations and the MRA measurements were 0.32 (p < 0.05) and 0.21 (p < 0.05) for aneurysms A and B, respectively. The linear correlations between the CFD₂ and the MRA measurements were comparable (0.31 and 0.22 for aneurysms A and B [p < 0.05], respectively). As shown in Figs. 7a, 7b, there were noticeable local differences among the TA-WSS simulated by CFD₁ and CFD₂. However, overall patterns of the TA-WSS distributions between Non-Newtonian (CFD₁) and Newtonian (CFD₂) fluids are similar. In other words, the TA-WSSs obtained by the CFD₁ and the CFD₂ simulations are nearly linearly dependent (correlations of 0.95 and 0.97 in Aneurysms A and B, respectively).

Figure 7.

Side-by-side comparisons for TA-WSS values derived from PC-MRA-estimated and CFD. Arrows points to the likely locations where the inflow jets impinge the walls.

Accuracy of WSS estimation versus image resolution and noise

As described before, we resampled one CFD₂-simulated velocity field to a set of rectilinear grids to mimic the underlying MRA-measured velocity fields that were acquired with different voxel sizes. Gaussian-distributed white (zero mean) noise was added to each of these resampled CFD₂ velocity fields to simulate MRA measurement noise. In this numerical experiment, the simulated voxel size ranged from 0.03 to 1.0 mm, while the simulated standard deviation (STD) of velocity noise varied from 0 to 120 mm/s. We empirically chose the correlation between the CFD-calculated WSSs (gold standard) and the WSSs estimated by the method described in Appendix B to determine how well the WSS estimation was performed. It is easy to see, from Fig. 8, the adoption of this correlation metric seems consistent with our visual perception.

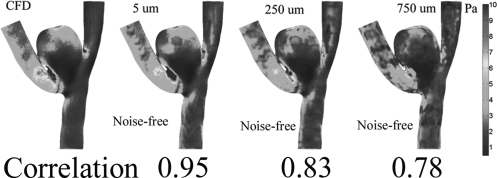
Figure 8.

Selected images of the estimated WSS under noise-free for three different voxel sizes (5, 250 and 750 μm) and their estimated correlation values.

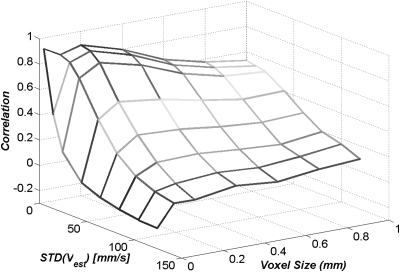
The estimated correlation values are displayed with respect to the simulated voxel sizes and the simulated standard deviations of velocity measurements in Fig. 9. Figure 9 suggests that, as the voxel size and measurement noise increase there is decreasing accuracy in the WSS estimation, resulting in lower correlation values between the CFD-calculated and the MRA-estimated WSSs. Our data also indicate that there is an “optimal” voxel size to maximize the correlation between the CFD-calculated and the MRA-estimated WSSs depends on the given measurement noise level.

Figure 9.

A plot of the estimated correlation values with respect to different simulated voxel sizes and measurement noise. Ten realizations were used to obtain each data point displayed in this plot.

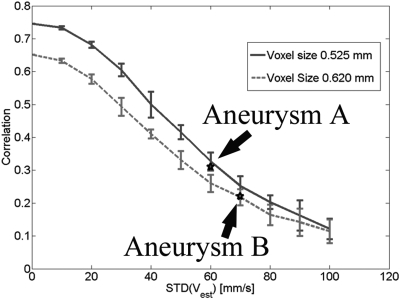
In Fig. 10, we plotted out the estimated correlation values with respect to measurement noise levels for two image resolutions that were comparable to these during data acquisition for Aneurysms A and B. The measurement noise levels (standard deviations of velocity errors) in Aneurysms A and B were approximately 60 and 70 mm/s, respectively, by measuring the velocity amplitudes in background tissues. We found that the low correlation values for the TA-WSS in Aneurysms A and B were consistent with our numerical predictions as shown in Fig. 10.

Figure 10.

Estimated correlation values for simulated velocity data with voxel sizes of 0.525 mm and 0.620 mm that are comparable to MRA-measured velocity data in Aneurysms A and B, respectively. Each data point was obtained by ten realizations and error bars stand for one standard deviation. Two black stars denote two data points for the correlation values corresponding to these TA-WSS estimates shown in Figs. 7a, 7b.

DISCUSSION

Our results (Figs. 2, 4, and 6) show, in both aneurysms, gross aneurismal flow patterns obtained by the MRA-measurements and the CFD simulations are similar. Especially, CFD models may exhibit different velocity magnitudes than the corresponding MRA data (on average 0.1 m/s within the aneurysm sac). However, regions of low and high blood flow, location of velocity jets are in good agreement. This finding is consistent with what were reported in Rayz et al.¹⁸ where they compared CFD-simulated velocity with in vivo cine 2D PC-MRI measurements. We also found that the absolute angular differences were approximately 40° between the CFD simulations and the MRA-measurements within the aneurysm sacs. This has not been reported in the literature. Although reasonably high similarities between the MRA-measured and the CFD-simulated velocity fields were found, correlations between the MRA-estimated and CFD-calculated TAWSS were low (0.22–0.31; p < 0.01). Our correlations are comparable to what was reported by Isoda et al. in human IA cases¹⁶ and our own numerical verifications (see Fig. 10).

The ability to quantitatively and noninvasively measure or predict lesion-specific hemodynamic parameters such as WSS, particle residence time and arterial inputs (e.g., pressure, flow impingement force, etc.) in vivo would dramatically enhance the capability to explore the significance of these parameters on development and progression of many vascular abnormalities. This capability would also be of potential value as a tool both for selecting lesion-specific treatment options for some of these vascular disorders and for monitoring the impact of various implants, e.g., stents on flow in and around aneurysms and stenoses.⁴¹

Along with our results, other recent studies have demonstrated that the spatial (<1 mm) and temporal (30–40 ms) resolution of the state-of-art 4D PC-MRA is adequate for velocity measurement.^{14, 16, 42} Combining these data in conjunction with visualization software, time-resolved flow in a volume of interest can be viewed in throughout the cardiac cycle.^{11, 42} Thus, these MR techniques not only provide quantitative and clinically-relevant velocity/flow rate information, but also allow visualization of blood flow in such a way that physicians and researchers may develop intuitions regarding the general features of blood flow in various disease states.

Detailed assessment of hemodynamics using the 4D PC-MRA technique is still, however, limited primarily because of limitations in spatial resolution and the inaccuracies caused by disturbed or turbulent flow.¹⁷ Even at 3T, current PC-MRA techniques do not provide sufficient details to allow full assessment of small aneurysms⁵ or stenoses in small vessels.¹⁴ Furthermore, researchers are now attempting to quantitatively map hemodynamic variables such as WSS in human aneurysms.^{5, 16} For relatively straight and large vessels, estimations of the wall shear stress can be obtained by fitting a parabolic profile through the axial velocity profile.⁴³ However, for irregular vasculatures such as aneurysms or curved tortuous vessels, fitting a parabolic profile through the axial velocity profile will likely yield poor results. Thus, a wall shear stress estimation method similar to what described in Appendix B has to be adopted. In other words, accurate estimations require not only that there be much improved spatial resolution but also enhanced SNR to allow for near-wall velocity measurements. The low correlation (0.22–0.31; p < 0.01) between the MRA-estimated and CFD-calculated TAWSS discussed early, despite velocity fields that were reasonably similar serves as an example of this limitation. In future work, we will explore this topic further by use of the improved spatial resolution and SNR provided by imaging at 3T.

Interestingly, we found that non-Newtonian properties of blood could influenced wall shear stress calculations in certain regions (see Fig. 7) but did not affect the overall patterns of the wall shear stress distribution in and around two bifurcation aneurysms as evident by high correlation values (>0.95 in Aneurysms A and B) between the wall shear stresses calculated using the Newtonian and the non-Newtonian flow. This observation is consistent with an early simulation study by Valencia et al.⁴⁴ On the other hand, in the presence of high velocity gradients, velocity vector fields obtained using Newtonian and non-Newtonian fluids may differs significantly. Further studies are needed to address this issue.

Image segmentation algorithms (e.g., the well known marching-cube algorithm⁴⁵) together with imaging data quality may affect the wall shear stress calculations.²¹ In our experience, given good imaging data (i.e., good resolution, contrast, and signal quality) and a vessel surface reconstruction algorithm, CFD-based wall shear stress calculations are fairly reproducible and accurate. This observation is consistent with results reported by Agust et al.⁴⁶ This issue requires further investigations once the representation of vessel geometry may be compromised due to low quality imaging data.

We found that there were significant discrepancies (on average 25%–35%) between MRA-measured flow entering and leaving aneurysms. On the one hand, as shown in Figs. 2345, significant discrepancies between the MRA-measured and CFD-simulated velocity fields occurred at regions where the velocity jet interfaced with the low-velocity recirculation zone. In these areas, there is the presence of high spatial velocity gradients. It is well known that high velocity gradients, especially nonlinear velocity gradients, lead to intravoxel dephasing which can bias the velocity values.¹⁷ Additionally, small uncompensated background phase from eddy currents are well known to cause large errors in flow measurements.^{47, 48} On the other hand, probable volume changes of aneurysms under pulsation⁴⁹ were not accounted for in this study.

We recognize that CFD-calculated flow is not sufficient to serve as the gold standard²¹ to validate such 4D PC-MRA measurements. However, they do, in our opinion, serve as a tool for performing valid comparisons of measured flow parameters. For instance, by comparing to CFD-simulated velocity fields, we, among others,²¹ found that MRA-measurement velocity fields resemble/capture less secondary flow (rotational and nonaxial) effects and therefore are less disturbed. As a result of insufficient spatial and temporal resolution, nonaxial components of the velocity field that often have lower amplitudes might suffer more an averaging processes both in spatial and time domains.

Tremendous developments in computer techniques and medical imaging (e.g., 3D DSA and MRA) have greatly enhanced the ability using CFD simulations to produce clinically-relevant subject-specific calculations of blood flow.⁸ One advantage of the CFD simulation technique is that, once the complex 3D unsteady velocity fields associated with a particular vascular abnormality are obtained, then, many hemodynamic parameters such as WSS, pressure, and particle residence time can be easily extracted, assessed and visualized using the same numerical model. Other advantages of CFD include the ability to observe the differences in hemodynamics that occur before and after embedding of a virtual device intended for treatment of a particular vascular lesion, e.g., flow diverter⁵⁰ and, to use simulations done at varying hear rate to assess the importance of heart rate on hemodynamic stresses.⁵¹ These advantages are not available when flow is examined with the 4D PC-MRA technique. Because of the complexities of the vascular tree and flowing blood CFD calculations will remain dependent on numerous assumptions regarding boundary conditions, vessel wall structure and blood properties. Unfortunately, the potential errors caused by the inadequacy of a subject-specific CFD model based on such assumptions are still largely unknown.^{18, 52, 53} Comparisons of patient specific CFD results to those measured by 4D PC-MRA seem well suited to improve the utility of both techniques in a clinical setting.

We believe that combining 4D PC-MRA with CFD simulations, will enhance the ability to analyze, interpret, and visualize complex but disturbed areas of flow such as occur in and around intracranial aneurysms. In our future work, we will also enforce a compromise between CFD-simulated and MRA-measured velocity fields using certain mathematical frameworks.^{54, 55}

In our study, two velocity fields were compared in terms of the relative angular and magnitude differences by an empirical equation³⁷ to obtain a single summary measure of the overall similarity. In future study, more rigorous measures of similarity between vector data need to be further explored. Other limitations to the present study include the small number of animals and lack of a gold standard for comparison.

CONCLUSION

Four-dimensional Velocity fields obtained from two experimental bifurcation aneurysms using PC-VIPR MRA and subject-specific CFD simulations were in favorable agreement. Results, however, suggest that there are still large discrepancies in the WSS values derived from the PC-MRA velocity fields and the CFD simulations largely because of the combination of noise and limited PC- MRA spatial resolution. Similar to what had already been reported,⁴⁴ we also found that similar bulk flow patterns were obtained from CFD simulations with Newtonian and non-Newtonian flow for data investigated. Although there were subtle differences between the Newtonian and non-Newtonian CFD simulations, the bulk flow patterns and overall distributions of blood velocities were nearly the same in two aneurysms investigated. These results are encouraging and warrant further study involving a larger number of subjects. Combining PC-MRA measured and CFD calculated hemodynamic values has promise to enhance the utility of both techniques.

Abbreviations

IA = 

intracranial aneurysm

3D-DSA = 

Three-dimensional digital subtraction angiography

CFD = 

computational fluid dynamics

ECG = 

electrocardiogram

FOV = 

field of view

MRA = 

magnetic resonance angiography

PC-MRA = 

phase-contrast magnetic resonance angiography

PC-MRI = 

phase-contrast magnetic resonance imaging

PC-VIPR = 

phase-contrast vastly undersampled isotropic projection reconstruction

TA-WSS = 

time-averaged wall shear stress

TE = 

echo time

TR = 

repetition time

WSS = 

wall shear stress

VENC = 

velocity encoding sensitivity

STD = 

standard deviation

STL = 

stereolithography

SNR = 

signal-to-noise ratio

APPENDIX A: SIMILARITY METRIC FOR COMPARING VECTOR FIELDS

In this study, we adopted a similarity metric between vector fields similar to that was developed by Li and Shen³⁷. The similarity metric S accounts both the angular and magnitude differences between two vectors V_i and V_j

$$S(V_i,V_j)=\beta •e^{-2a}+\gamma •e^{-m},$$ (A1)

where β and γ are positive weighting constants, β+γ=1, and a and m represent the normalized angular and relative magnitude differences between two velocity vector V_i and V_j, respectively. The angular difference m in Eq. A1 was normalized by using the antisine function value of the angular difference between two vectors. In this study, we selected both β and γ to be 0.5. It is easy to see this metric [Eq. A1] is on a scale from 0 to 1, 1 being the highest. This metric will be estimated in a point-to-point fashion and be displayed as a spatially-registered image.

APPENDIX B: WSS CALCULATION

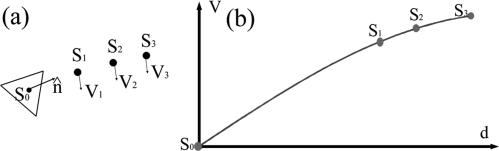
WSS is calculated by its definition in Newtonian fluid: the multiplication of fluid viscosity and shear rate at the vessel wall.⁵⁶ Similar to that was used by Isoda,¹⁶ our WSS estimation method consists of: (1) determination of the vessel wall and (2) approximation of the derivative of the blood velocity function by curve fitting. Specifically, in step 1, the STL file representing tri-angularized vessel surface extracted from a set of MR images (described in the Method Section before) is used to determine the vessel wall. In step 2, as illustrated in Fig. 11 , we selected the center of a triangle as one WSS calculation point (S₀) and three reference points (S₁–S₃) that are in the nearest vicinity of S₀. The distances between the triangle and all three reference points (d₁ to d₃) were calculated. Velocity components perpendicular to $\stackrel{\wedge }{n}$ between S₀ and S₃ were interpolated using a 1D radial basis function method.⁵⁷ The slope of the velocity amplitudes parallel to the vessel wall (perpendicular to $\stackrel{\wedge }{n}$) at S₀ was the wall shear rate at S₀ by definition. WSS amplitude at S₀ was calculated by multiplying viscosity (0.004 Pas in this study) by the wall shear rate and assigned to the location S₀. This procedure will be repeated until all points of interest are calculated.

Figure 11.

Illustrations of the calculation of WSS.