Skip to main content
PMC home page
Springer logoLink to Springer
. 2011 Nov 18;49(12):1471–1479. doi: 10.1007/s11517-011-0845-9

Comparison of four mathematical models to analyze indicator-dilution curves in the coronary circulation

Judith Brands 1,2, Hans Vink 1, Jurgen W G E Van Teeffelen 1,✉
PMCID: PMC3223587  PMID: 22095316

Abstract

While several models have proven to result in accurate estimations when measuring cardiac output using indicator dilution, the mono-exponential model has primarily been chosen for deriving coronary blood/plasma volume. In this study, we compared four models to derive coronary plasma volume using indicator dilution; the mono-exponential, power-law, gamma-variate, and local density random walk (LDRW) model. In anesthetized goats (N = 14), we determined the distribution volume of high molecular weight (2,000 kDa) dextrans. A bolus injection (1.0 ml, 0.65 mg/ml) was given intracoronary and coronary venous blood samples were taken every 0.5–1.0 s; outflow curves were analyzed using the four aforementioned models. Measurements were done at baseline and during adenosine infusion. Absolute coronary plasma volume estimates varied by ~25% between models, while the relative volume increase during adenosine infusion was similar for all models. The gamma-variate, LDRW, and mono-exponential model resulted in volumes corresponding with literature, whereas the power-model seemed to overestimate the coronary plasma volume. The gamma-variate and LDRW model appear to be suitable alternative models to the mono-exponential model to analyze coronary indicator-dilution curves, particularly since these models are minimally influenced by outliers and do not depend on data of the descending slope of the curve only.

Keywords: Coronary indicator-dilution technique, Mono-exponential model, Power-law model, Gamma-variate model, Local density random walk model

Introduction

The indicator-dilution technique was first used for the measurement of cardiac output. Later, this technique was extended to measurements of regional blood flow and to measure the blood volume in the circulation of the heart and lungs [22, 35]. Recently, we applied the indicator-dilution technique to determine the contribution of the endothelial glycocalyx to adenosine-induced changes in coronary blood volume. Coronary blood volume at baseline and during coronary administration of adenosine was compared, before and after hyaluronidase treatment of the glycocalyx [5]. We observed that, in contrast to control conditions during which adenosine-induced increases in coronary blood volume and flow appeared to be nicely matched, enzymatic degradation of the glycocalyx was associated with an impaired increase in volume yet unaltered flow response during adenosine infusion compared to corresponding baseline [5]. Because a mismatch in the increase in blood volume versus the increase in flow during exercise may be expected to be associated with an impaired coupling of nutrient exchange in the capillaries to nutrient delivery by blood flow, it might be of clinical relevance to measure coronary blood volume (reserve) in addition to coronary blood flow (reserve) in patients that are at risk for development of glycocalyx damage.

In these previous experiments, fluorescently labeled 2,000-kDa dextrans (as plasma tracer) and labeled red blood cells were injected in the left main coronary artery and blood was collected from the great cardiac vein; tracer outflow curves were constructed for determination of the mean transit time (MTT) of both tracers, and, together with the measured coronary blood flow, ultimately coronary blood volume. Blood samples were taken every 0.5 s, resulting in a limited amount of data on the descending part of the curve before the onset of recirculation. Because of this, the indicator-dilution curves were analyzed using a local density random walk (LDRW) model, rather than the commonly used mono-exponential model, since it requires less data of the descending slope of the curve. Using the LDRW model, coronary blood volumes of 18.9 ± 1.1 ml/100 g heart tissue were derived at baseline, while the volumes during adenosine infusion were increased to 33.2 ± 5.3 ml/100 g. After hyaluronidase, the volume was 26.3 ± 2.7 ml/100 g in control and 33.9 ± 6.8 ml/100 g during adenosine infusion, indicating an impaired ability for adenosine to recruit blood volume. In this study, we wanted to know how the used model contributed to the calculated volumes.

Although, the LDRW fit has been recognized in the past for the fit of indicator-dilution curves, e.g., for determination of cardiac output [26], this model has not been used for the fit of coronary indicator-dilution curves so far. With respect to the coronary circulation, the mono-exponential fit has typically been used, and the following volumes have been reported: 9.4–14.8 ml/100 g tissue at perfusion flows of 40–220 ml/min/100 g in the study of Ziegler and Goresky [33] and 15.6 ml/100 g in the studies of Hirsche and Lochner [11] as well as Morgenstern et al. [27]. The gamma-variate and LDRW fits, could, however, be more suitable for coronary volume estimations since the parameters of these models are based on the ascending and descending slope of the data curve, while the mono-exponential model is solely based on a selection of the descending slope. The power-law [1], also based only on part of the descending slope, has in one previous study been applied to measurements of water washout in isolated hearts. Although, the results were very promising, the model has never been applied to an intravascular tracer in an in situ setup. In this study, we, therefore, decided to compare a selection of these 4 indicator-dilution models to our experimental data, to determine what the influence of the model used is on the outcome of our coronary blood volume estimations and which of these four models is best suitable (based on practicability and signal-to-noise ratio) to fit tracer outflow curves when measuring coronary volumes using the indicator-dilution technique.

Methods

General surgery and anesthesia

All procedures and protocols were approved by the animal care and use committee of Maastricht University. The investigations described were conformed with the Guide for the Care and Use of Laboratory Animals. The data being analyzed in this study was from experiments on adult female goats of 18–28 kg (N = 14) in which adenosine-induced increases in coronary blood volume were measured. They included N = 6 experiments presented and described in our previous study [5]. In short, after a left thoracotomy, the great cardiac vein was cannulated via the azygos vein to obtain coronary venous blood samples. Subsequently, the left carotid artery was cannulated and a stainless steel Gregg cannula was inserted in the aorta via a purse string. The Gregg cannula was ligated into the left main coronary artery, without disrupting the coronary flow. Coronary perfusion was controlled using a roller pump perfusion system (total volume 110 ml) [30], see Fig. 1. The perfusion pressure (P perf) was measured at the tip of the Gregg cannula. An inline flow probe (6 mm Transonic flowprobe, Transonic Systems Inc.) was interpositioned into the perfusion line of the perfusion system to measure coronary blood flow (Q perf). The femoral blood pressure (P fem), left ventricle pressure (P lv), P perf, Q perf, and heart rate (HR, determined from P lv) were stored on a personal computer for off-line analysis (IDEEQ 250 Hz, IDEE). At the end of the experimental procedures a battery was placed on the heart to induce ventricular fibrillation. At the end of the experiment, the left main coronary artery was injected with a mixture of gelatin and white paint (latex) at 37°C. After cooling, the colored tissue could be dissected and weighed.

Fig. 1.

Fig. 1

Open in a new tab

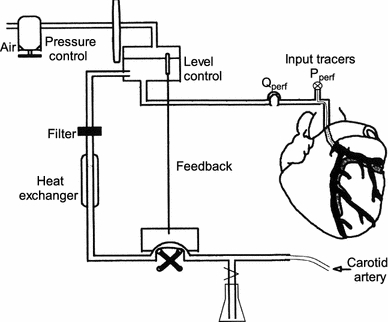
Arterial coronary perfusion system. Blood collected from the left carotid artery was heated and filtered, and circulated with a roller pump via a reservoir into the left main coronary artery. Blood level and pressure in the reservoir were kept constant. Perfusion pressure (P perf) was measured at the tip of the Gregg cannula. An inline flow probe was interpositioned into the perfusion system to measure coronary blood flow (Q perf)

Experimental protocol

After surgery, the preparation was allowed to equilibrate for 30 min. In each animal, the distribution volume of the plasma tracer FITC-labeled dextrans with a molecular weight (MW) of 2,000 kDa (Dex-2000, Sigma-Aldrich, 0.65 mg/ml) was measured using the indicator-dilution technique. A bolus injection of tracer (1.0 ml) was given by hand into the left main via the perfusion pressure catheter at the tip of the Gregg cannula. The catheter in the great cardiac vein was connected to a roller pump enabling coronary venous blood to be collected at a rate of 24.2 ml/min (205S Watson Marlow), the total volume of the sampling system was 4 ml. Blood was sampled in consecutive 1.5 ml tubes at intervals of 0.5–1 s for 50 s; the first 10 and last 20 samples were taken at an interval of 1 s, while the 40 samples in between, where the major part of the indicator-dilution curve is expected, were taken every half a second. Therefore, a total of 70 samples per volume measurement were obtained after the tracer injection. Blood was subsequently centrifuged, and plasma Dex-2000 concentration was analyzed using fluorometry (Victor3; Perkin Elmer). In 12 experiments, the measurement was repeated during intracoronary adenosine infusion (0.47 ± 0.03 mg/kg/h), to detect imposed changes in coronary plasma volume by this vasodilator.

Data analysis

Analysis of the samples resulted in 70 coronary venous plasma dextran concentrations over time per coronary volume measurement. All measured data were corrected for the background value (average value of the first three samples) and the transfer function, h(t), was obtained by dividing the measured concentration (mg/ml) times the carrier (plasma) flow (ml/s) by the amount that was injected (mg). Plasma flow was determined from coronary blood flow and hematocrit. The Dex-2000 transfer curves were fitted with four different models using Matlab® (the MathWorks, Inc., Natick, MA).

Models based on the descending slope

The mono-exponential [9, 10] and power-law model [1] are solely based on information obtained from a selection of the descending part of the transfer curve. The mono-exponential function assumes an exponential outflow of the tracer and the power-law function assumes that the outflow can be approached as being a fractal process. For the mono-exponential model, the logarithm of the transfer function was taken, while for the power-law model, both the logarithm of the transfer function and time were required. To obtain the model parameters, a straight line, using robust linear regression, was drawn through the data from one point above 70% up to 30% [12] of the peak height on the descending slope of the transfer function (Fig. 2a–d). Subsequently, for the mono-exponential model, the curve was fitted, from one point above 70% of the peak height forward, according to Eq. 1.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ h(t)_{ \exp } = e^{a} e^{bt} = Ae^{bt} . $$\end{document} 1

Fig. 2.

Fig. 2

Open in a new tab

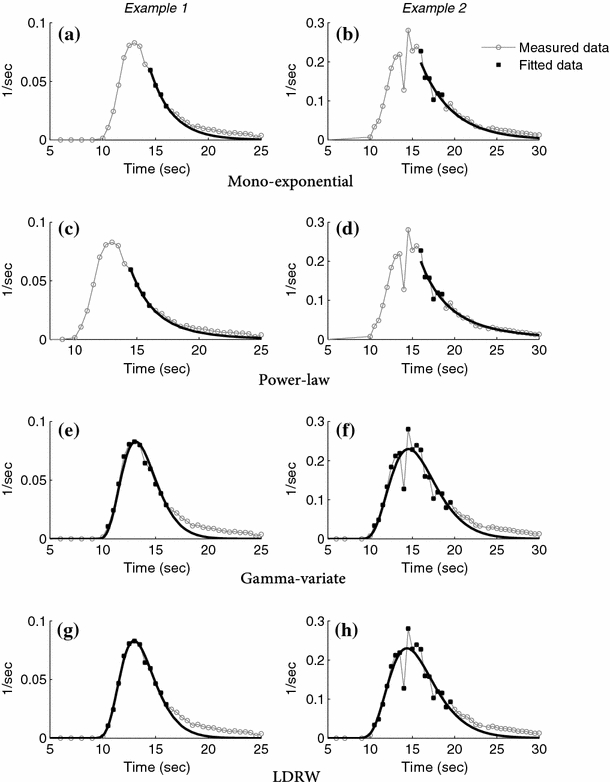
Two examples (left and right) of a transfer function fitted with the four different models a, b mono-exponential, c, d power-law, e, f gamma-variate, and g, h LDRW model. The measured data is indicated by the open circle and gray line, the black lines are fitted curves based on the data one point above 70 up to 30% of the height of the peak on the descending slope of the transfer function (a–d) and all data up to 30% of the peak height on the descending slope of the transfer function (e–h). The data used by the models are marked by closed squares. Data not yet corrected for the transit time of the sampling catheter (9.9 s)

The transfer function according the power-law was fitted using Eq. 2.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ h(t)_{\text{PL}} = B\alpha t^{ - \alpha - 1} . $$\end{document} 2

Models based on both ascending and descending slope

The gamma-variate model [21, 26] and LDRW model [3, 26] take, in addition to the descending part, the ascending part and peak of the curve into account as well. Fitting the transfer function by the gamma-variate model was done by using Eq. 3.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ h(t)_{\gamma } = h_{ \max } (t_{ \max } - t_{0} )^{ - \beta } e^{\beta } (t - t_{0} )^{\beta } e^{{\frac{{ - \beta (t - t_{0} )}}{{(t_{ \max } - t_{0} )}}}} . $$\end{document} 3

The parameters (h max, the maximal value of h(t), t max, the time at which h(t) is at maximum, t 0, the delay time from t = 0 to the time the function begins, and β, a free parameter) in Eq. 3 are independent of each other [21] meaning that one parameter can change without having an influence on any of the other parameters. The LDRW model is described by Eq. 4,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ h(t)_{\text{LDRW}} = \frac{m}{\mu \theta }e^{\lambda } \sqrt {\frac{\lambda \mu }{{2\pi (t - t_{0} )}}} e^{{\frac{ - \lambda }{2}\left( {\frac{{(t - t_{0} )}}{\mu } + \frac{\mu }{{(t - t_{0} )}}} \right)}} . $$\end{document} 4

and the parameters are defined as, m is the mass of the injected tracer, μ is the transit time of the median indicator particle, θ is the flow of the carrier, λ being a dimensionless parameter equal to the ratio between convection and diffusion in the dilution system (related to the skewness or asymmetry of the curve), and t 0 represents the zero time of the distribution [25, 26].

To prevent that the fitting based on these models converges into local minima, we used multiple linear regression as described by Mischi et al. [25]. Data between 5% of the peak height on the ascending slope up to 30% of the maximum peak value on the descending slope of the transfer function curve were compared with the data obtained from the model [24, 26], Fig. 2e–h. To determine how well the fit of the gamma-variate and LDRW models corresponded with the transfer function, the determination coefficient (R 2) was calculated over the selection used to determine the model parameters.

The quality of the fit in correspondence with the transfer function was evaluated by measuring the difference between fit and data for that part of the curve that was fitted by all four models. To do so, the area under the curve from one point above 70% of the peak height on the descending slope forward was calculated and expressed as percentage of the area under the curve of the coronary transfer function \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left( {\frac{{{\text{Area}}_{\text{fit}} }}{{{\text{Area}}_{\text{transfer}} }} \times 100\% } \right). $$\end{document}

Calculation of coronary plasma volume

Using the data from the fitted curve the MTT was calculated according to Eq. 5 [22, 25], in which C(t) is the fitted Dex-2000 outflow concentration.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{MTT}} = \frac{{\int {tC(t){\text{d}}t} }}{{\int {C(t){\text{d}}t} }}. $$\end{document} 5

The MTT of the tracer was corrected for the volume of the sampling catheter by subtraction of the sampling transit time (9.9 s), i.e., dividing the sampling catheter volume (4 ml) by the sampling flow (24.2 ml/min). Multiplying the corrected MTT with the tracer carrier flow (plasma flow) gave the distribution volume of the tracer [22].

Statistics

Differences in MTT, volume, area under the curve and, for the gamma-variate and LDRW model, the determination coefficient were tested between the four models using a t test, for both conditions (i.e., baseline and adenosine). In addition, differences between data obtained at baseline and during adenosine infusion were tested using a t test as well. Results were considered statistically significant with P < 0.05. Summary data are reported as mean ± SEM.

Results

Hemodynamic parameters of the measurements are presented in Tables 1 and 2. During the infusion of adenosine in the left main coronary artery Q perf was significantly increased, in spite of the fact that the perfusion pressure was reduced (P < 0.05). The prevailing flows differed substantially between experiments (range 63.5–424.6 ml/min/100 g at baseline and 236.0–539.5 ml/min/100 g during adenosine infusion). These flows were associated with an estimated time of onset of recirculation, determined from the volume of the perfusion system (110 ml) divided by the coronary flow, of 42.6 ± 5.5 s, with a range of 20.7–95.5 s, at baseline and 22.7 ± 1.9 s (range 13.3–33.4 s) during adenosine infusion.

Table 1.

Hemodynamic parameters (mean ± SE)

Baseline (N = 14) Adenosine (N = 12)
P lv (mmHg) 114.8 ± 11.4 114.5 ± 11.2
P fem (mmHg) 94.7 ± 12.5 87.7 ± 11.8
Q perf (ml/min/100g) 225.7 ± 25.5 388.4 ± 27.2*
P perf (mmHg) 128.0 ± 4.0 93.6 ± 4.7*
HR (BPM) 132.1 ± 7.5 129.7 ± 8.7
Htc (venous) (%) 23.3 ± 2.1 22.5 ± 1.9
Open in a new tab

Values are mean ± SE

* Significant from baseline measurement (P < 0.05)

Table 2.

Accuracy of the fits (mean ± SE)

Model Determination coefficient
Baseline Adenosine
Gamma-variate 0.97 ± 0.01 0.94 ± 0.02
LDRW 0.97 ± 0.01 0.94 ± 0.02
Open in a new tab

Values are mean ± SE

Figure 2 shows two examples of transfer functions obtained during baseline conditions, and the way they are fitted by the four models, i.e., the mono-exponential (a, b), power-law (c, d), gamma-variate (e–f), and LDRW (g, h) model. Two differences are evident when comparing the results of the mono-exponential and power-law model versus the results of the gamma-variate and LDRW model. First, the difference in descending slopes of the curves. The gamma-variate and LDRW model derived fits appear to have a steeper descending slope than their transfer functions (see Fig. 2e–h), while this difference was less for the models solely based on the descending slope. Nevertheless, the tail of all four models is below the actual measured data, as represented by the area under curve of the fitted data as percentage of area under coronary transfer curve in Fig. 3. Second, the fits by the mono-exponential and power-law model were found to contain more irregularities since they did not fit the entire (ascending and descending) curve (Fig. 2b, d).

Fig. 3.

Fig. 3

Open in a new tab

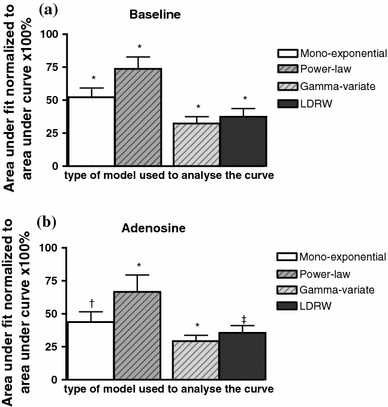
The area under the curve from one point above 70% of the peak height on the descending slope forward normalized to the area under the curve of the measured data at baseline (a) and during adenosine infusion (b). *P < 0.05 compared to all other models, † P < 0.05 compared to the power-law and gamma-variate model, ‡ P < 0.05 compared to the power-law and gamma-variate model

For one experiment during adenosine infusion there were not enough data points on the selected part of the descending slope of the transfer function to perform robust regression. This experiment was, therefore, not included in the further comparisons of MTT and volume between the models. The derived MTTs of the experiments are given in Fig. 4. Compared to baseline, there was no change in MTT of all four models during adenosine infusion. The paired volume estimates (MTT times the coronary plasma flow) are shown in Fig. 5. In line with the higher MTTs, the coronary plasma volume per 100 g heart tissue at baseline and during adenosine infusion determined using the power-law model were significantly larger than the volumes estimated using the other three models, while the mono-exponential model-derived coronary plasma volume was significant larger than those from the gamma-variate and at baseline from the LDRW model. During adenosine infusion, the estimated coronary plasma volume was equally increased (P < 0.05) for the mono-exponential, gamma-variate, and LDRW model, a 1.6 times increase in volume was measured. For the power-law model, there was a trend toward an increase in coronary plasma volume during adenosine infusion compared to baseline (P = 0.055).

Fig. 4.

Fig. 4

Open in a new tab

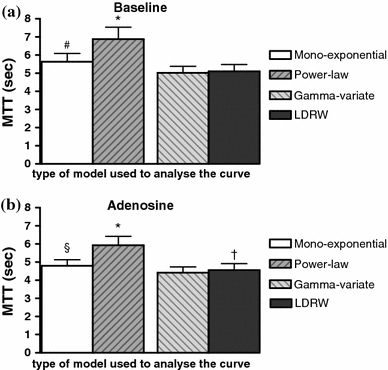
The derived MTT (N = 11) for all four models at baseline (a) and during adenosine infusion (b). *P < 0.05 compared to mono-exponential, gamma-variate, and LDRW model, # P < 0.05 compared to power-law, gamma-variate, and LDRW model, § P < 0.05 compared to power-law and gamma-variate model, † P < 0.05 compared to gamma-variate model

Fig. 5.

Fig. 5

Open in a new tab

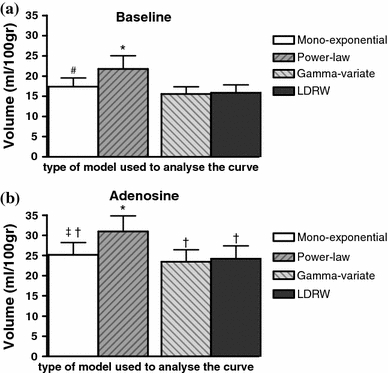
The derived coronary plasma volumes per 100 g heart tissue (N = 11) for all four models at baseline (a) and during adenosine infusion (b). *P < 0.05 compared to mono-exponential, gamma-variate, and LDRW model, # P < 0.05 compared to power-law, gamma-variate, and LDRW model, ‡ P < 0.05 compared to power-law and gamma-variate model, † P < 0.05 compared to corresponding baseline measurement

Discussion

In this study, four indicator-dilution models were compared for determination of coronary plasma volumes in the in situ goat heart. Significant differences in obtained MTTs and volumes were found between the models, illustrating the contribution of the used model in determination of coronary volume when using tracer dilution. However, when interested in relative changes during vasodilator infusion, the mono-exponential, gamma-variate, and LDRW model were equally suitable to detect a change in coronary plasma volume (baseline compared to adenosine, P < 0.05). The relative increase in coronary plasma volume found using the power-law model was less conclusive (P = 0.055). Our data suggest that, in addition to the contemporary mono-exponential model, alternative models, such as the gamma-variate and LDRW model, are well suited for the analyses of coronary indicator-dilution models, particularly in conditions of a limited sampling rate.

Indicator-dilution technique

The theory and requirements of the indicator-dilution technique have been reviewed by Meier et al. [22] and Zierler [35]. Indicator dilution is based on the principle that the flow through a system or the volume of that system can be measured by injection of a known quantity of an indicator into the system and measuring its concentration over time at a specific point in the system (i.e., the indicator-dilution curve). Using the indicator-dilution curve, the MTT, denoting the average time it takes for the indicator to travel from the point of injection to the point of sampling, can be derived. Multiplying the MTT with the indicator flow through the system, results in the distribution volume of the indicator. One important assumption, no recirculation, is normally violated in in vivo measurements. In this in situ study, we used a perfusion system with a relative large volume that delayed recirculation. The estimated moment of recirculation ranged from a minimum of 13.3 to a maximum of 95.5 s. The time it takes for the blood to circulate from the great cardiac vein (outflow of the heart) to the carotid artery (entrance of the perfusion system) was not taken into account in these numbers. Recirculation (based on the perfusion flow and volume of the perfusion system: 42.6 ± 5.5 s at baseline and 22.7 ± 1.9 s during adenosine infusion) appeared in this study at least 5 s after the last sample that was selected for the determination of the model parameters (7.8 ± 0.5 and 7.1 ± 0.4 s at baseline and during adenosine infusion, respectively). Therefore, a contribution of recirculation to the fits can be neglected in this study.

Tail of the curve

All four models tested provided a fit through the data in which the tail of the curve was below the measured data. The power-law model provided fits corresponding best with the measured data (see Fig. 3) while the fits of the LDRW and in particular the gamma-variate model differed significantly more from the measured data (area of the fit was 37.4 ± 6.2 and 32.3 ± 5.2% of the area under the curve for the LDRW and gamma-variate model, respectively). As discussed in the previous paragraph, the difference between fit and data cannot be explained by recirculation of the tracer. A possible cause for the difference is the organ of interest, the coronary vasculature. Bassingthwaighte and coworkers [20] have studied indicator-dilution curves in single vessels, as well as in the coronary, renal, and pulmonary circulation. They suggested that the late, slowly decreasing tails observed when studying the coronary circulation, causing a difference between model and measured data, could only be explained by the coronary bed itself [20]. For example, local arterial reversed flow with pulsatile intramyocardial tension development could cause changes in the tail of transfer curves that cannot be described accurately by any of the models. Mischi et al. [26] found in an in vitro setup and in patients (left and right ventricle) using the LDRW fit a much better agreement between the measured and estimated data, including the lower part of the curves, supporting the idea that the coronary bed, instead of the choice of model, may be an important contributor to the difference between model and measured data in this and previous studies. Therefore, it must be noted that a better fit of the tail of coronary indicator-dilution curves might not necessarily result in more accurate volume estimations.

Nevertheless, a steeper descending slope for the LDRW and gamma-variate model compared to measured data, although less than in the coronary vasculature, was also observed by Millard [24] and Thompson et al. [31], while Mischi et al. [26] showed that the estimated volume by these models provided underestimations for larger volumes (3.4 and 7.4% at a volume of 1,080 ml, for the gamma-variate and LDRW model, respectively), in their in vitro and in vivo measurements for cardiac output.

Ascending slope

The gamma-variate and LDRW model fit and explain not only the descending part of the transfer curve but the ascending part of the curve, the peak, and the start of the descending slope of the transfer curve as well. As a result, these fits are less sensitive to noise and irregularities. Bogaard et al. [4] found in their study that the results of the mono-exponential method were seriously affected by noise in the data, introducing a systematic error (overestimation of MTT) which considerably reduced the accuracy of this model. On the contrary, noise in the data did not have a significant effect on the outcome of the LDRW model in their study. In addition, the number of data points used for the fit is much larger for the gamma-variate and LDRW model compared to the mono-exponential and power-law model. Although, already one point above 70% of peak height was included to determine the model parameters, one of the experiments still lacked sufficient data to perform robust linear regression. Selection of less data, inevitable when no or a low volume perfusion system is used, seems, therefore, not an option for the mono-exponential and power-law model. In contrast, the gamma-variate and LDRW model require only few data points of the descending slope since these models take the ascending slope into consideration as well.

Coronary plasma volume

Certainly, based on our data it cannot be determined which model provides the most accurate volume estimations, particularly because a reliable in vitro setup of the coronary vasculature is not available for testing. A large range of coronary vascular volumes has been reported in the literature (4 up to 17.8 ml/100 g [11, 18, 27, 33]). The differences in reported values can be explained by the fact that either plasma or blood volume were measured, by differences in experimental conditions (in vivo [6, 11, 27, 33], beating isolated hearts [29] or arrested isolated hearts [16–18]) and the techniques used (histological measurements [8], the use of a silicone cast [16–18], and the dilution of specific blood or plasma indicators [6, 11, 27, 33]). Our reported coronary baseline blood volume of 14–19 ml/100 g is in the range of coronary plasma volumes (from 11 up to 17.8 ml/100 g) [11, 27, 33] found in literature using indicator dilution. The measured volumes depend on perfusion pressure and coronary blood flow [27]. In this study, we measured a baseline blood flow of 225.7 ± 25.5 ml/min/100 g. Whereas baseline coronary blood flows reported in anesthetized large animals in the literature are typically ~100 ml/min/100 g [7], the higher flows in this study seem explained by a reduction in basal vasomotor tone of the resistance vessels due to the instrumentation of the heart, including the use of a perfusion system, and the relatively high HRs and perfusion pressures. The calculated MTTs, independent of the flow, are significantly lower than the MTT per 100 g heart tissue found by Ziegler and Goresky [33] in the dog heart, except for the power-law model. In their study, these investigators found a MTT of 7.3 ± 0.4 s using exponential extrapolation of the data. In this study, we determined MTTs of 5.6 ± 0.5, 6.9 ± 0.7, 5.0 ± 0.4, and 5.1 ± 0.4 s for the mono-exponential, power-law, gamma-variate, and LDRW model, respectively. The differences in MTT might be explained by species and experimental differences, such as a different anesthesia and perfusion system, as well as a different tracer used to determine coronary plasma volume. In this study, dextrans with a MW of 2,000 kDa were used while Ziegler and Goresky [33] used albumin, a tracer which has been suggested to not only distribute in the plasma but to access a part of the endothelial glycocalyx as well [32]. It cannot be ruled out that the additional distribution in the glycocalyx compartment might have resulted in a prolonged MTT and coronary plasma volume [32].

As far as we know, in the literature, there have been no reports of indicator dilution-based coronary volumes during maximal vasodilation using adenosine. We found that the relative increase in coronary plasma volume during adenosine infusion compared to baseline volume was not different for the mono-exponential, gamma-variate, and LDRW model, i.e., appeared to be model independent. A similar trend was observed for the power-law model. The 1.6 times increase in coronary plasma volume measured during adenosine infusion corresponds well with reported coronary volume increases during adenosine infusion-induced vasodilation measured using X-ray contrast enhancement (1.68-fold increase) [13] and myocardial radioactivity (1.75-fold increase) [6].

While this data show that increases in coronary plasma volume and flow occur concomitantly in response to adenosine infusion, we found in our previous study that these increases in coronary blood volume versus flow become uncoupled after enzymatic degradation of the endothelial glycocalyx [5]. These data indicate the importance of measuring coronary blood volume in addition to flow in humans that are at risk for glycocalyx degradation, i.e., patients with diabetes or hypercholesterolemia [23, 28]. However, coronary blood volume measurements are currently not routinely applied in the clinic. Dye or radioactive labeling techniques and extensive catheterization cannot be used in humans or performed repeatedly to assess dynamic changes. Nevertheless, myocardial blood volume can be measured non-invasively in humans using myocardial contrast echocardiography [14]; MRI and electron-beam CT have this potential as well. The latter two techniques have already been used in combination with indicator dilution for measurement of myocardial perfusion [2, 15, 19, 34, 35], and to do so, a fit through the indicator concentration data is required, similar as for the volume measurement. Therefore, the comparison of the different models for fitting the indicator concentration data, as done in this study, is useful for the measurement of both coronary blood volume as well as perfusion.

In conclusion, when determining coronary blood or plasma volume using the indicator-dilution technique, the gamma-variate and LDRW model appear to be good alternatives to the mono-exponential model, with the advantage that these models take both ascending and descending slope of the curve into account (and therefore less data of descending slope is required), and are less sensitive to noise. A shortcoming of these models, however, appears to be that they tend to underestimate the tail of the indicator-dilution curve more than the mono-exponential and power-law model.

Acknowledgments

The authors would like to thank Marion Kuiper, Anniek Lampert, Arne van Hunnik, Bart Eskens, and Hanneke Cobelens for their assistance. This study was supported by the Netherlands Heart Foundation [grant numbers 2005T073, 2003B181].

Conflict of interest

None.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  • 1.Bassingthwaighte JB, Beard DA. Fractal 15O-labeled water washout from the heart. Circ Res. 1995;77(6):1212–1221. doi: 10.1161/01.res.77.6.1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Bell MR, Lerman LO, Rumberger JA. Validation of minimally invasive measurement of myocardial perfusion using electron beam computed tomography and application in human volunteers. Heart. 1999;81(6):628–635. doi: 10.1136/hrt.81.6.628. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Bogaard JM, Smith SJ, Versprille A, Wise ME, Hagemeijer F. Physiological interpretation of the skewness of indicator-dilution curves; theoretical considerations and a practical application. Basic Res Cardiol. 1984;79(4):479–493. doi: 10.1007/BF01908149. [DOI] [PubMed] [Google Scholar]
  • 4.Bogaard JM, van Duyl WA, Versprille A, Wise ME. Influence of random noise on the accuracy of the indicator-dilution method. Clin Phys Physiol Meas. 1985;6(1):59–64. doi: 10.1088/0143-0815/6/1/006. [DOI] [PubMed] [Google Scholar]
  • 5.Brands J, Spaan JA, Van den Berg BM, Vink H, VanTeeffelen JW. Acute attenuation of glycocalyx barrier properties increases coronary blood volume independently of coronary flow reserve. Am J Physiol Heart Circ Physiol. 2010;298(2):H515–H523. doi: 10.1152/ajpheart.01306.2008. [DOI] [PubMed] [Google Scholar]
  • 6.Crystal GJ, Downey HF, Bashour FA. Small vessel and total coronary blood volume during intracoronary adenosine. Am J Physiol. 1981;241(2):H194–H201. doi: 10.1152/ajpheart.1981.241.2.H194. [DOI] [PubMed] [Google Scholar]
  • 7.Feigl EO. Coronary physiology. Physiol Rev. 1983;63(1):1–205. doi: 10.1152/physrev.1983.63.1.1. [DOI] [PubMed] [Google Scholar]
  • 8.Frank JS, Langer GA. The myocardial interstitium: its structure and its role in ionic exchange. J Cell Biol. 1974;60(3):586–601. doi: 10.1083/jcb.60.3.586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Hamilton WF, Moore JW, Kinsman JM, Spurling RG. Simultaneous determination of the pulmonary and systemic circulation times in man and of a figure related to the cardiac output. Am J Physiol. 1928;84(2):338–344. [Google Scholar]
  • 10.Hamilton WF, Moore JW, Kinsman JM, Spurling RG. Studies on the circulation. IV. Further analysis of the injection method, and of changes in hemodynamics under physiological and pathological conditions. Am J Physiol. 1932;99(3):534–551. [Google Scholar]
  • 11.Hirche H, Lochner W. Measurement of the blood flow and blood filling of the coronary vascular bed with the test substance injection method on the anesthetized dog with closed thorax. Pflugers Arch Gesamte Physiol Menschen Tiere. 1962;274:624–632. doi: 10.1007/BF00363150. [DOI] [PubMed] [Google Scholar]
  • 12.Hoeft A, Schorn B, Weyland A, Scholz M, Buhre W, Stepanek E, Allen SJ, Sonntag H. Bedside assessment of intravascular volume status in patients undergoing coronary bypass surgery. Anesthesiology. 1994;81(1):76–86. doi: 10.1097/00000542-199407000-00012. [DOI] [PubMed] [Google Scholar]
  • 13.Hoffman EA, Ritman EL. Intramyocardial blood volume implications for analysis of myocardial mechanical characteristics via in vivo imaging of the heart. In: Sideman S, Beyar R, editors. Activation, metabolism and perfusion of the heart. Dordrecht: Martinus Nujhoff Publishers; 1987. pp. 421–431. [Google Scholar]
  • 14.Indermuhle A, Vogel R, Meier P, Zbinden R, Seiler C (2011) Myocardial blood volume and coronary resistance during and after coronary angioplasty [Research Support, Non-US Gov’t]. Am J Physiol Heart Circ Physiol 300(3): H1119–H1124. doi:10.1152/ajpheart.01022.2010 [DOI] [PubMed]
  • 15.Jerosch-Herold M, Seethamraju RT, Swingen CM, Wilke NM, Stillman AE. Analysis of myocardial perfusion MRI. J Magn Reson Imaging. 2004;19(6):758–770. doi: 10.1002/jmri.20065. [DOI] [PubMed] [Google Scholar]
  • 16.Kassab GS, Fung YC. Topology and dimensions of pig coronary capillary network. Am J Physiol. 1994;267(1 Pt 2):H319–H325. doi: 10.1152/ajpheart.1994.267.1.H319. [DOI] [PubMed] [Google Scholar]
  • 17.Kassab GS, Rider CA, Tang NJ, Fung YC. Morphometry of pig coronary arterial trees. Am J Physiol. 1993;265(1 Pt 2):H350–H365. doi: 10.1152/ajpheart.1993.265.1.H350. [DOI] [PubMed] [Google Scholar]
  • 18.Kassab GS, Lin DH, Fung YC. Morphometry of pig coronary venous system. Am J Physiol. 1994;267((6 Pt 2)):H2100–H2113. doi: 10.1152/ajpheart.1994.267.6.H2100. [DOI] [PubMed] [Google Scholar]
  • 19.Keijer JT, van Rossum AC, van Eenige MJ, Karreman AJ, Hofman MB, Valk J, Visser CA. Semiquantitation of regional myocardial blood flow in normal human subjects by first-pass magnetic resonance imaging. Am Heart J. 1995;130(4):893–901. doi: 10.1016/0002-8703(95)90092-6. [DOI] [PubMed] [Google Scholar]
  • 20.Knopp TJ, Dobbs WA, Greenleaf JF, Bassingthwaighte JB. Transcoronary intravascular transport functions obtained via a stable deconvolution technique. Ann Biomed Eng. 1976;4(1):44–59. doi: 10.1007/BF02363557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Madsen MT. A simplified formulation of the gamma variate function. Phys Med Biol. 1992;37(7):1597–1600. doi: 10.1088/0031-9155/37/7/010. [DOI] [Google Scholar]
  • 22.Meier P, Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol. 1954;6(12):731–744. doi: 10.1152/jappl.1954.6.12.731. [DOI] [PubMed] [Google Scholar]
  • 23.Meuwese MC, Mooij HL, Nieuwdorp M, van Lith B, Marck R, Vink H, Kastelein JJ, Stroes ES. Partial recovery of the endothelial glycocalyx upon rosuvastatin therapy in patients with heterozygous familial hypercholesterolemia. J Lipid Res. 2009;50(1):148–153. doi: 10.1194/jlr.P800025-JLR200. [DOI] [PubMed] [Google Scholar]
  • 24.Millard RK. Indicator-dilution dispersion models and cardiac output computing methods. Am J Physiol. 1997;272((4 Pt 2)):H2004–H2012. doi: 10.1152/ajpheart.1997.272.4.H2004. [DOI] [PubMed] [Google Scholar]
  • 25.Mischi M, Kalker T, Korsten HH. Videodensitometric methods for cardiac output measurements. EURASIP J Appl Signal Process. 2003;2003:479–489. doi: 10.1155/S1110865703211185. [DOI] [Google Scholar]
  • 26.Mischi M, den Boer JA, Korsten HH. On the physical and stochastic representation of an indicator dilution curve as a gamma variate. Physiol Meas. 2008;29(3):281–294. doi: 10.1088/0967-3334/29/3/001. [DOI] [PubMed] [Google Scholar]
  • 27.Morgenstern C, Holjes U, Arnold G, Lochner W. The influence of coronary pressure and coronary flow on intracoronary blood volume and geometry of the left ventricle. Pflugers Arch. 1973;340(2):101–111. doi: 10.1007/BF00588169. [DOI] [PubMed] [Google Scholar]
  • 28.Nieuwdorp M, Mooij HL, Kroon J, Atasever B, Spaan JA, Ince C, Holleman F, Diamant M, Heine RJ, Hoekstra JB, Kastelein JJ, Stroes ES, Vink H. Endothelial glycocalyx damage coincides with microalbuminuria in type 1 diabetes. Diabetes. 2006;55(4):1127–1132. doi: 10.2337/diabetes.55.04.06.db05-1619. [DOI] [PubMed] [Google Scholar]
  • 29.Salisbury PF, Cross CE, Rieben PA. Physiological factors influencing coronary blood volume in isolated dog hearts. Am J Physiol. 1961;200:633–636. doi: 10.1152/ajplegacy.1961.200.3.633. [DOI] [PubMed] [Google Scholar]
  • 30.Spaan JA, Breuls NP, Laird JD. Forward coronary flow normally seen in systole is the result of both forward and concealed back flow. Basic Res Cardiol. 1981;76(5):582–586. doi: 10.1007/BF01908365. [DOI] [PubMed] [Google Scholar]
  • 31.Thompson HK, Jr, Starmer CF, Whalen RE, McIntosh HD. Indicator transit time considered as a gamma variate. Circ Res. 1964;14:502–515. doi: 10.1161/01.res.14.6.502. [DOI] [PubMed] [Google Scholar]
  • 32.Vink H, Duling BR. Capillary endothelial surface layer selectively reduces plasma solute distribution volume. Am J Physiol Heart Circ Physiol. 2000;278(1):H285–H289. doi: 10.1152/ajpheart.2000.278.1.H285. [DOI] [PubMed] [Google Scholar]
  • 33.Ziegler WH, Goresky CA. Transcapillary exchange in the working left ventricle of the dog. Circ Res. 1971;29(2):181–207. doi: 10.1161/01.res.29.2.181. [DOI] [PubMed] [Google Scholar]
  • 34.Zierler KL. Theoretical basis of indicator-dilution methods for measuring flow and volume. Circ Res. 1962;10(3):393–407. [Google Scholar]
  • 35.Zierler K. Indicator dilution methods for measuring blood flow, volume, and other properties of biological systems: a brief history and memoir. Ann Biomed Eng. 2000;28(8):836–848. doi: 10.1114/1.1308496. [DOI] [PubMed] [Google Scholar]

Articles from Medical & Biological Engineering & Computing are provided here courtesy of Springer

RESOURCES