Abstract
Chlamydia trachomatis is the most common bacterial sexually transmitted infection (STI) in many developed countries. The highest prevalence rates are found among young adults who have frequent partner change rates. Three published individual-based models have incorporated a detailed description of age-specific sexual behaviour in order to quantify the transmission of C. trachomatis in the population and to assess the impact of screening interventions. Owing to varying assumptions about sexual partnership formation and dissolution and the great uncertainty about critical parameters, such models show conflicting results about the impact of preventive interventions. Here, we perform a detailed evaluation of these models by comparing the partnership formation and dissolution dynamics with data from Natsal 2000, a population-based probability sample survey of sexual attitudes and lifestyles in Britain. The data also allow us to describe the dispersion of C. trachomatis infections as a function of sexual behaviour, using the Gini coefficient. We suggest that the Gini coefficient is a useful measure for calibrating infectious disease models that include risk structure and highlight the need to estimate this measure for other STIs.
Keywords: Chlamydia trachomatis, sexual partnerships, individual-based model, Natsal 2000, Gini coefficient
1. Introduction
Chlamydia trachomatis is the most common curable sexually transmitted infection (STI) in many developed countries [1]. It is most prevalent among sexually active young adults, with the majority of infections being asymptomatic and remaining undiagnosed [2]. In women, infection can ascend to the upper genital tract, causing pelvic inflammatory disease, which can then lead to tubal factor infertility, ectopic pregnancy and chronic pelvic pain [3]. It is therefore essential to understand the transmission dynamics of C. trachomatis in order to develop appropriate interventions aimed at reducing the incidence and prevalence of infections.
Mathematical and computational models of infectious disease dynamics are widely used to study transmission and predict the impact of public health interventions [4–6]. With respect to C. trachomatis, such models can help us to understand the potential impact of screening, a population-level intervention that aims to reducing chlamydia prevalence and associated complications through the regular detection and treatment of asymptomatically infected cases. There are no empirical studies that show what levels of coverage and frequency of screening are necessary to achieve a specified reduction in C. trachomatis prevalence. The predictions from modelling studies can therefore be influential in guiding health policy decisions about chlamydia screening [7].
The models that have been developed to investigate the impact of screening have used either deterministic, population-based [8–10] or stochastic, individual-based approaches [11–13]. The latter approach is sometimes favoured, because it allows the detailed description of sexual partnership dynamics. Taking sexual partnerships explicitly into account has been suggested as an important feature of models of chlamydia transmission to capture re-infection within partnerships and investigate the effect of partner notification [10,14]. In spite of these advantages, it is challenging to appropriately parameterize individual-based models and analysis and interpretation of the results is generally difficult [15,16]. As a matter of fact, the three individual-based models of C. trachomatis transmission, which were designed to evaluate different screening interventions in the UK and The Netherlands, can show marked differences in the predictions which complicates their use in informing public health policy-making. The study by Kretzschmar et al. [17] described key features of each model and compared the effect of implementing the same screening scenario in the three models. The predicted reductions in chlamydia prevalence in women after 10 years of the intervention were 85 per cent [12], 25 per cent [11] and 5 per cent [13].
The contrasting predictions between the three individual-based models are a result of different assumptions about the sexual partnership dynamics and the infection parameters of C. trachomatis. These are key determinants that are believed to affect the spread of STIs. Chlamydia trachomatis, like many other STIs, is primarily found among sexually active young adults who change sexual partners frequently. This is a prerequisite for sustaining transmission of bacterial STIs with infectious periods between several months to years. Further key determinants are the duration of sexual partnerships, the gap interval between subsequent partnerships, concurrent partnerships and heterogeneity in sexual behaviour [18–20]. In order to model the spread of C. trachomatis within the population, and to obtain reasonable predictions of screening interventions, a solid comprehension of these behavioural characteristics is necessary.
Novel insights into the dynamics of sexual contacts have been gained during the last decade [21–23] but no clear formalism to describe the individual's sexual behaviour has been established so far. Also, the necessary parameters that define duration of partnerships, concurrency or age-specific behaviour are exceedingly difficult to obtain and implement in mathematical and computational models. As an additional complication, many of these behavioural characteristics are generated by a multitude of parameters. In order to assess the ‘realism’ of such models, it is therefore necessary to evaluate them in light of empirical data. On the one hand, this allows decisions about which models and predictions should be favoured over others. On the other hand, the features and structure of the most ‘realistic’ models can also give insights into the underlying mechanisms of sexual partnership formation. One of the most comprehensive data sets available to date is Natsal 2000, a population-based probability sample survey of sexual attitudes and lifestyles in Britain [24]. The large sample size of the survey allows the derivation of the characteristic distributions of measures of sexual behaviour in a population. In addition, C. trachomatis prevalence was measured in a subset of sexually active respondents [19]. Natsal 2000 therefore provides a unique opportunity to study certain characteristics of sexual behaviour and link them to the prevalence of C. trachomatis.
In this paper, we aim to explain the key differences of the three individual-based models that resulted in contrasting predictions of the impact of screening interventions against C. trachomatis [11–13,17]. By comparing the sexual partnership dynamics of the models to data from Natsal 2000, we find several properties that can affect the transmission of C. trachomatis. We illustrate the various assumptions made when describing sexual partnerships and discuss their implications for the spread of C. trachomatis and the impact of a standardized screening intervention. This allows us to report the most reasonable prediction from a specific screening intervention. As a useful summary measure to evaluate models of STI transmission, we propose that the distribution of infections among individuals with different levels of sexual activity should be described using the Gini coefficient.
2. Methods
2.1. Individual-based models
A detailed comparison of key features of the three models has been presented previously [17].
2.1.1. Kretzschmar model
The Kretzschmar model was developed at the Dutch National Institute of Public Health and the Environment, to evaluate strategies for controlling C. trachomatis and Neisseria gonorrhoeae [11]. The simulated population in the model consists of 15–64 year olds who belong to one of the two sexual activity groups; a small core group (5%) of younger adults (<35 years) who, in addition to steady relationships, undergo casual relationships that can be concurrent (with a maximum of two partners at any given time), and the other group who are either in a steady or (less likely) in a casual relationship.
2.1.2. Turner model
The Turner model was originally developed at the Health Protection Agency (HPA), London, UK [12], based on an earlier model for N. gonorrhoeae transmission developed by Ghani et al. [25]. The model simulates heterosexual partnership formation between 16 and 44 year olds. Individuals in the population have a preference for either short or longer duration partnerships. Additionally, a small core-group (5%) can undergo a concurrent partnership as long as they are younger than 35 years.
2.1.3. ClaSS model
The Chlamydia Screening Studies (ClaSS) model was developed in the UK as part of the ClaSS project [13]. The simulated population consists of 12–65 year olds who undergo heterosexual partnership formation. Individuals' sexual behaviour is divided into three activity classes with all people older than 35 year moving into the lowest activity class. The partnership duration and the possibility of forming concurrent partnerships (with up to eight concurrent partners) depend on the activity classes of both individuals. For this study, the ClaSS model was implemented in the package Rstisim (manuscript in preparation) of the R software environment for statistical computing [26].
2.1.4. Chlamydia trachomatis transmission and screening intervention
We simulate transmission of C. trachomatis in the three individual-based models to study the endemic steady-state prevalence and the impact of a standardized intervention programme. We have shown recently that different assumptions about the transmission dynamics and turnover of C. trachomatis can affect the predicted impact of a screening programme [9]. Therefore, we use a harmonized parameter set to describe the duration of infection and the proportion of symptomatic and asymptomatic cases (table 1). The values chosen are based on a recent evaluation of parameters that have been used in previous mathematical and computational models [9] and on consensus between the authors. We then adjust the transmission probability per sex act in each model in order to obtain the same baseline prevalence. After running the models such that the partnership dynamics and the baseline prevalence have equilibrated, we introduce a standardized intervention programme to reduce the prevalence of C. trachomatis. Eligible for screening are all sexually active people younger than 25 years. The proportion of people that gets screened at least once a year, p, is 20 per cent. From the relation p = 1 − e−ct, we obtain a screening rate of c = 0.223 yr−1. Note that some people can receive screening more than once a year. If people have a positive chlamydia test result, 40 per cent of their current or most recent partners will be notified and successfully treated. The predicted impact on the prevalence of C. trachomatis is reported after 5 and 10 years.
Table 1.
Parameters describing infection with C. trachomatis. Assuming the same average duration of the infection ensures that the baseline turnover of C. trachomatis is the same in all three individual-based models. However, we adjust the transmission rate per sex act to obtain a similar C. trachomatis prevalence. Analysis of data from Natsal 2000 results in a prevalence of 1.7% (95% CI: 1.3–2.1) for people aged 18–44 years and 2.9% (95% CI: 1.3–2.1) for people aged 18–29 years [19]. For a detailed evaluation of disease-specific parameters, see Althaus et al. [9]. Note that the Turner model does not include an incubation time.
| parameters | value |
|---|---|
| infection stages | |
| incubation time, i.e. the time people are infected but not yet infectious | 14 days |
| fraction of infections becoming asymptomatic | 0.75 |
| duration of symptomatic period | 35 days |
| duration of asymptomatic period | 433 days |
| transmission rate per sex act | |
| Kretzschmar model | 4.4% |
| Turner model | 3.5% |
| ClaSS model | 2.2% |
| average interval between sex acts | |
| during the first two weeks of a partnership | 2 days |
| after the first two weeks of a partnership | 7 days |
2.2. Sexual behaviour data
We use data from Natsal 2000, a population-based probability sample survey of sexual attitudes and lifestyles in Britain [24]. The sample consists of 11 161 women and men aged 16–44 years. Urine samples for ligase chain reaction testing for C. trachomatis are available for a subset of 3569 sexually active respondents aged 18–44 years [19]. Weighted data (to adjust for unequal selection probabilities and to correct for the age and gender profile in the population) were used to derive measures of sexual behaviour and C. trachomatis prevalence. We consider the following measures of sexual partnerships: lifetime number of heterosexual partners; number of heterosexual partners during the last year and the date of first and last heterosexual intercourse with the most recent and second most recent partner. The latter allow us to obtain the distribution of partnership durations and the length of gaps or overlaps between two partnerships. All data were analysed using the R software environment.
2.3. Estimating partnership and gap durations
In cross-sectional surveys, the start of a sexual partnership can, in principle, be clearly defined. However, information about the end of a partnership is more difficult to obtain as reported partnerships might be ongoing. This results in an oversampling of longer partnerships and inflated partnership durations [27–29]. We focus our analysis on the second most recent partnership, which allows us to capture short partnership durations as well. In Natsal 2000, the duration of the second most recent partnership was defined as the time in months between first and last sexual intercourse with the second most recent partner within the last 5 years. We further define the duration of the gap between the most recent and second most recent partnership as the later date of first sexual intercourse in either partnership minus the date of last sexual intercourse with the second most recent partner. Thus, we obtain the gap durations for three different scenarios: the first scenario is when the second most recent partnership has ended before the most recent partnership begins, resulting in a positive gap duration (figure 1a); in the second, the second most recent partnership has not ended yet before the most recent partnership begins, resulting in a negative gap duration or overlap (concurrent partnership) (figure 1b); in the third, the second most recent partnership begins and ends during the duration of the most recent partnership, also resulting in an overlap (figure 1c). Since the dates of first and last sexual intercourse are reported in months, a gap duration of zero months can result from a short gap of less than or equal to 1 month or a short overlap of not more than a month.
Figure 1.
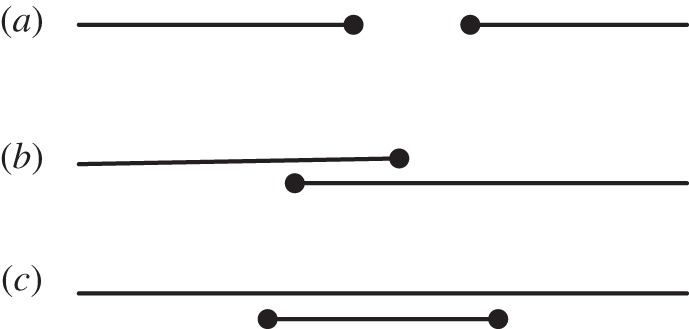
Schematic illustration of gaps and overlaps between sexual partnerships. (a) A positive gap duration results from two consecutive partnerships where the previous one has ended before the new one begins. (b) A new partnership that begins before the previous one has ended results in a negative gap duration or overlap. (c) It can also happen that a person engages in a short period of concurrency during a longer lasting partnership, also resulting in a negative gap duration.
The analysis of sexual partnership durations can be prone to additional selection biases [30]. However, our primary interest is not to estimate the true duration of partnerships and gaps but rather to compare the simulated data with empirical data. We therefore perform the same cross-sectional survey as Natsal 2000 in the three individual-based models. The following algorithm was applied to the simulated population of 16–44 year olds to obtain the partnership duration and gap length: (1) all current and past partnerships of an individual are sorted by their end date in descending order; (2) if partnerships are ongoing, the end date of the partnership is the time at cross-section; (3) the second most recent partnership is defined as the one with the second most recent end date. However, if more than one partnership is ongoing, one will be randomly selected as the second most recent; (4) the duration of the second most recent partnership is given as the time between the start and end date of the second most recent partnership; and (5) the duration of the gap between the most recent and second most recent partnership is defined as the later start date of both partnerships minus the end date of the second most recent partnership.
2.4. Lorenz curve and Gini coefficient
The Lorenz curve is a graphical representation of an empirical cumulative probability distribution. It is most well known as a method for representing inequality in income or wealth [31]. Recently, it has been applied to visualize the geographical distribution of several bacterial STIs at different levels [32–35] and over time [36]. In a mathematical modelling study, it has also been used as a method to describe the distribution of infections across certain subpopulations [37]. Here, we adopt this framework and use the Lorenz curve to represent the asymmetric distribution of C. trachomatis infections among individuals with n different levels of sexual activity. Thus, the Lorenz curve represents the cumulative proportion of C. trachomatis infections (yi) as a function of the cumulative proportion of the population (xi), after population sub-groups i (i = 1, 2, … , n) have been ranked in the order of their sexual activity level (i.e. number of partners within the last year). The diagonal line on a Lorenz curve plot denotes perfect equality, i.e. every population sub-group has the same prevalence of C. trachomatis. As a summary measure for the asymmetrically distributed infections, we can calculate the Gini coefficient [38]. It is defined as the area between the line of equality and the Lorenz curve over the total area below the line of equality:
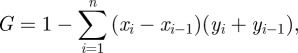 |
where x0 = y0 = 0 and xn = yn = 1. A Gini coefficient of 0 represents perfect equality, whereas a Gini coefficient close to 1 implies that only a small proportion of the population that exhibits a high level of sexual activity is infected with C. trachomatis. We plot the Lorenz curve and estimate the Gini coefficient for the empirical data from Natsal 2000 together with the distribution of C. trachomatis infections that we obtain from the three individual-based models.
3. Results
3.1. Sexual partnership dynamics
In order to gain insights into differences between the three individual-based models, we compare them to four characteristic patterns of sexual partnership dynamics from Natsal 2000: the lifetime number of partners; the number of partners in the last year; the duration of partnerships; and the duration of gaps between partnerships.
3.1.1. Lifetime number of partners
Empirical data about the distribution of the lifetime number of partners have been found to resemble a power-law, suggesting that sexual-contact networks exhibit features of scale-free networks [21,39]. While there is an ongoing debate as to what extent sexual networks have such an underlying structure [40–42], the primary feature of the distribution of the lifetime number of partners is that there is a small fraction of people with a very high number of partners; more than would be expected if individuals engaged in sexual contacts at random. Although mechanisms that would generate such a pattern have been proposed [22,23], the individual-based models that we evaluate here are based on the classical assumption that individuals in different ‘risk’ groups exhibit a certain degree of assortative mixing. It can be seen that assuming two (Kretzschmar model) or three (ClaSS model) risk groups can approximate the empirical distribution to a certain extent (figure 2). In contrast, the Turner model assumes more random mixing, which results in a Poisson-like degree distribution. All models clearly fail to describe individuals with a very high number of partners to date (>500) which is mainly due to the limited population size in the simulations. However, it is unlikely that those people contribute substantially to the transmission of C. trachomatis. Very high numbers of lifetime partners are generally reached when individuals are beyond the age where they significantly contribute to the transmission of C. trachomatis.
Figure 2.
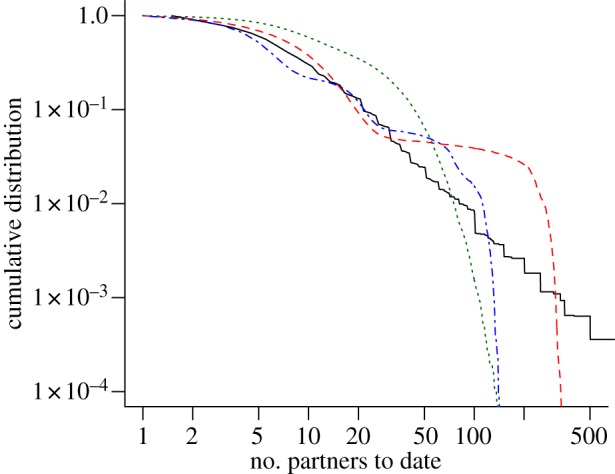
Cumulative distribution of the lifetime number of heterosexual partners to date. Data from Natsal 2000 exhibit a scale-free distribution (black solid line). Assortative mixing between risk groups in the Kretzschmar model (red dashed line) and the ClaSS model (blue dashed-dotted line) can approximate this property to a certain extent. More random mixing in the Turner model results in a Poisson-like degree distribution (green dotted line). The graph represents data from all women and men aged 16–44 years. (Online version in colour.)
3.1.2. Number of partners within the last year
An important characteristic of C. trachomatis is that most transmission occurs among sexually active young adults. One of the aims of individual-based models is to account for age-specific sexual behaviour. Empirical data from Natsal 2000 show an increase in the average number of heterosexual partners within the last year for people between the ages of 16 and 19 years (figure 3). The partner change rate decreases thereafter and stabilizes after the age of 35 at an average of around one partner per year. The Kretzschmar model does not explicitly include age-specific partner change rates, but instead uses a relatively simple algorithm where a small fraction of individuals (5%) belongs to a core group with increased sexual activity. At the age of 35 years, everyone moves into the low-risk population. The ClaSS model incorporates detailed age-specific sexual behaviour which follows a similar pattern to that shown in the empirical data. However, it underestimates the average number of partners, especially for individuals older than 35 years. Although the Turner model captures the partner change rates of individuals older than 20 years relatively well, it greatly overestimates the sexual contact rates for people of age 16–19 years. This feature of the model has been noted previously and results in an overestimation of C. trachomatis transmission among young people [17].
Figure 3.
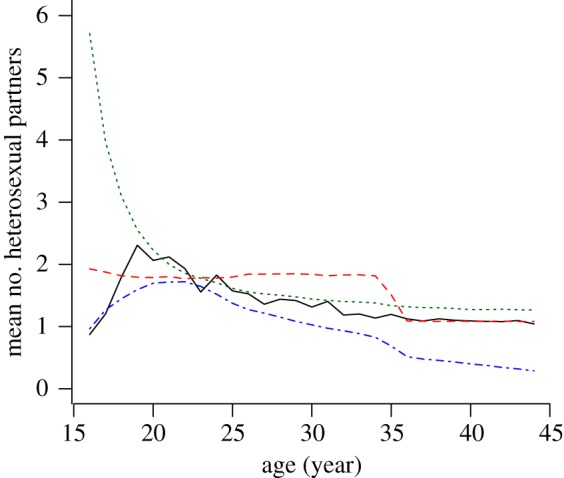
Mean number of heterosexual partners within the last year as a function of age. Data from Natsal 2000 show an initial increase in the number of partners, which peaks in 19 year olds (black solid line). Afterwards it decreases and stabilizes around 1.0%. The results from individual-based models illustrate the difficulties of closely mimicking such behaviour. Simulated data represent the means of all women and men sample at 100 time points. The red dashed line denotes the Kretzschmar model, the green dotted line denotes the Turner model and the blue dashed-dotted line denotes the ClaSS model. (Online version in colour.)
3.1.3. Duration of sexual partnerships
The duration of sexual partnerships is critically important for the transmission of C. trachomatis. Individuals with frequent partner change rates are expected to have many short-term (casual) partnerships. On the other hand, the probability of C. trachomatis transmission increases in long-term (steady) partnerships because of the higher number of sex acts. The cumulative distribution of sexual partnership durations in Natsal 2000 shows a biphasic pattern with a large proportion of casual partnerships (50.5% last less than a month) and a subsequent steady decay for casual partnerships (figure 4). This pattern of partnership durations has been found previously for a group of 18 to 39 year olds in Seattle [27]. Limiting the data from Natsal 2000 to the same age group results in a striking similarity of the cumulative distribution, indicating similar sexual behaviour (results not shown). The Kretzschmar and Turner models distinguish between casual and steady partnerships and can approximate the empirical data to a certain extent. In contrast, the distribution of partnerships in the ClaSS model appears to follow a single exponential distribution, underestimating the proportion of casual and steady partnerships. The continuously decreasing slope in the distribution of partnership durations with ongoing time indicates a certain degree of robustness. This property could be taken into account in individual-based models by setting the probability that a partnership dissolves as a function of the duration of the partnership.
Figure 4.
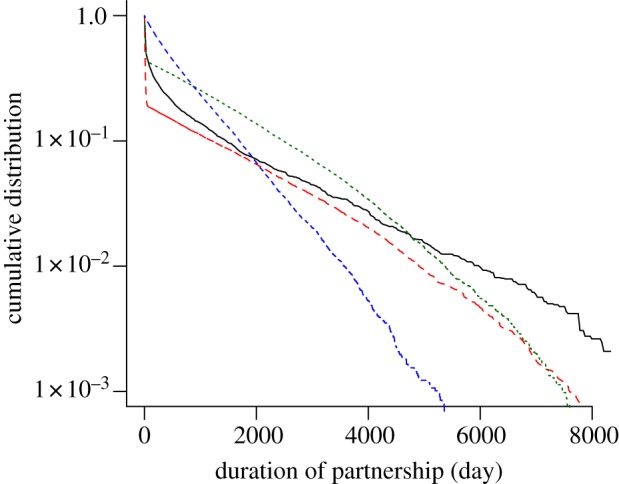
Cumulative distribution of the sexual partnership duration. The survival curve of partnerships from Natsal 2000 shows a large proportion of short partnerships and exhibits a long tail for longer partnerships (black solid line). Individual-based models generally assume exponential distributions of partnership duration and only mimic the empirical data if they explicitly account for short (casual) partnerships, such as the Kretzschmar model (red dashed line) and the Turner model (green dotted line). The blue dashed-dotted line denotes the ClaSS model. The graph represents data from the second most recent heterosexual partnership of all women and men aged 16–44 years. (Online version in colour.)
3.1.4. Duration of gaps and overlaps
Non-monogamy results in either serial or concurrent sexual partnerships. Both are considered to be risk factors for acquiring bacterial STIs [43,44]. The duration of gaps and overlaps in serial and concurrent sexual partnerships, respectively, has been found to be a particularly important determinant for the transmission of bacterial STIs [27,45,46]. All three individual-based models that we investigate exhibit serial sexual partnerships, concurrent sexual partnerships and mutual concurrency. Therefore, it is crucial that the sexual partnership dynamics in the three models exhibit a realistic distribution of gaps and overlaps between partnerships. The Kretzschmar model underestimates the amount of concurrency but results in a good description of the positive gaps between partnerships (figure 5). The Turner model also somewhat underestimates the amount of concurrency. In contrast to the other two models, individuals do not seek for sexual partnerships at a given rate, but have a predefined gap until they engage in a new partnership. Since the mean of this gap was assumed to be short (14 days), the model fails to reasonably account for the observed gap durations between partnerships. The ClaSS model captures the reported overlaps from Natsal 2000 reasonably well, but it greatly overestimates the duration of gaps between partnerships, indicating that individuals remain single for too long.
Figure 5.
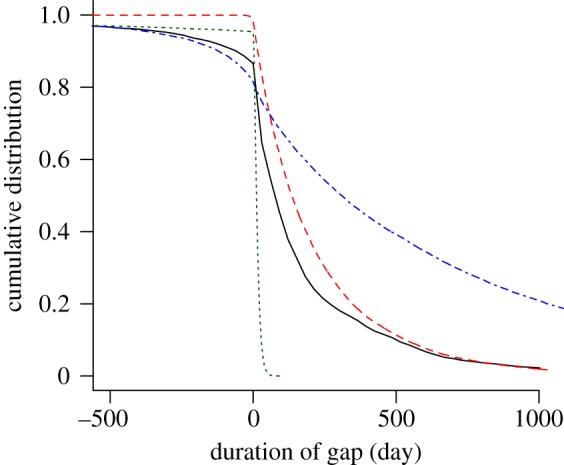
Cumulative distribution of the gap length. Negative gaps denote overlaps between partnerships and positive gaps denote waiting times until new partnerships are formed. Owing to different assumptions of the partnership formation process, individual-based models exhibit different gaps and overlaps. The graph represents data about gaps or overlaps between the most recent and the second most recent heterosexual partnership from all women and men aged 16–44 years. The black solid line denotes Natsal 2000; the red dashed line denotes the Kretzschmar model; the green dotted line denotes the Turner model and the blue dashed-dotted line denotes the ClaSS model. (Online version in colour.)
3.2. Dispersion of C. trachomatis infections
Given that the sexual partnership dynamics between the three individual-based models can vary widely, it is natural to investigate how C. trachomatis spreads in the simulated populations. In previous studies, the three models have used different assumptions about the duration of infection and the proportion of symptomatic and asymptomatic cases [17]. Here, we use a harmonized set of C. trachomatis infection parameters, which is based on a thorough evaluation of the parameter ranges in the literature and a recent estimate of the duration of the asymptomatic period (table 1). By adjusting the transmission rate per sex act in the three individual-based models, we can roughly reproduce the estimated prevalence of C. trachomatis from Natsal 2000 (1.7% (95% CI: 1.3–2.1) for people aged 18–44 years and 2.9% (95% CI: 1.3–2.1) for people aged 18–29 years) [19].
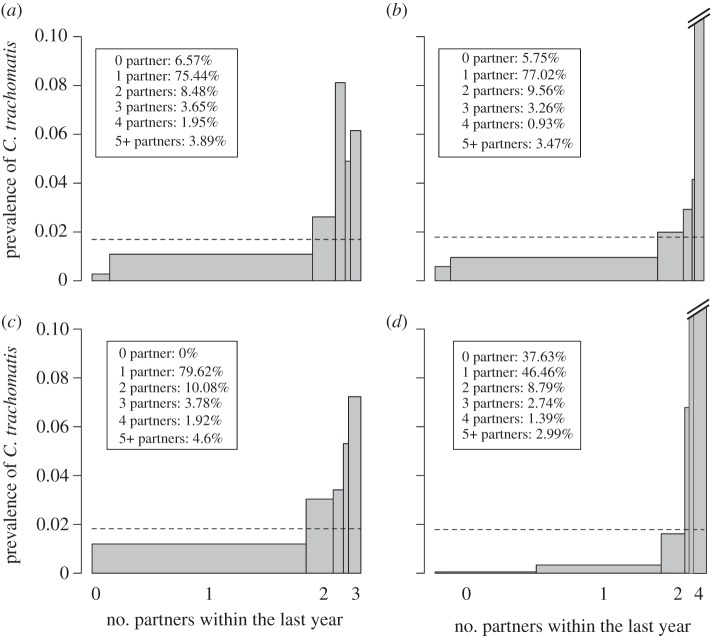
The C. trachomatis prevalence data in Natsal 2000 are unique, because we have detailed information on the sexual behaviour of each individual. This gives us the opportunity to study the dispersion of C. trachomatis infections across the population and the fraction of infections that is concentrated in individuals that exhibit frequent partner change rates. Not unexpectedly, the prevalence of C. trachomatis increases with an increasing number of heterosexual partners within the last year (figure 6a). This corroborates the concept of a ‘core group’, illustrated in the seminal work about N. gonorrhoeae by Hethcote & Yorke [47]. However, C. trachomatis seems to be less concentrated in ‘high-risk’ individuals compared with N. gonorrhoeae with 48 per cent of all chlamydia infections being among individuals with not more than one partner during the last year. Comparing the data from Natsal 2000 with the distribution of infections in the three individual-based models provides important information. The Kretzschmar model captures the overall distribution reasonably well and provides a striking resemblance of the proportion of people in each ‘risk category’ (compare the legend of figure 6a,b). The prevalence in the group of individuals with five or more partners within the last year is somewhat overestimated, however. The Turner model also captures the overall distribution of C. trachomatis infections reasonably well, with the exception that no individual remains without a partner during the period of 1 year. However, we have shown above that the Turner model assumes an unusually high partner change rate for young adults aged 16–19 years (figure 3). This behaviour is not captured in figure 6c as we only consider individuals aged 18–44 years, reflecting the age group for which C. trachomatis positivity is available in Natsal 2000. In contrast to the other two models, C. trachomatis infections are too heavily concentrated among ‘high-risk’ individuals in the ClaSS model (figure 6d). Further, it becomes apparent that the sexual partnership dynamics are not captured well as too many individuals remain single during the period of 1 year, corroborating the long duration of gaps in this model.
Figure 6.
Asymmetric distribution of C. trachomatis infections among individuals with different levels of sexual activity. The width of each bar represents the proportion of people that have had a given number of sexual partners within the last year (the legend shows the distribution of sexual partner numbers). The height of the bar indicates the prevalence of C. trachomatis in each group. Note that the prevalence in the group with highest activity (five or more partners) is 20% in the Kretzschmar model and 34% in the ClaSS model. Overall prevalence is given by the dashed line and is approximately the same in all graphs (1.7%). Data are given for women and men aged 18–44 years. (a) Natsal 2000; (b) Kretzschmar model; (c) Turner model and (d) ClaSS model.
Given the empirical and simulated data from figure 6, we can plot the Lorenz curve that represents the cumulative proportion of C. trachomatis infections as a function of the cumulative proportion of the population, after population sub-groups have been ranked in the order of their sexual activity during the last year (figure 7). From the Lorenz curve, we can calculate the Gini coefficient, which gives us a statistical measure for the strength of asymmetry in the distribution of C. trachomatis (see §2). The Kretzschmar (0.46) and the Turner models (0.32) are close to the estimated Gini coefficient from Natsal 2000 (0.38), whereas the ClaSS model has a much higher Gini coefficient (0.84).
Figure 7.
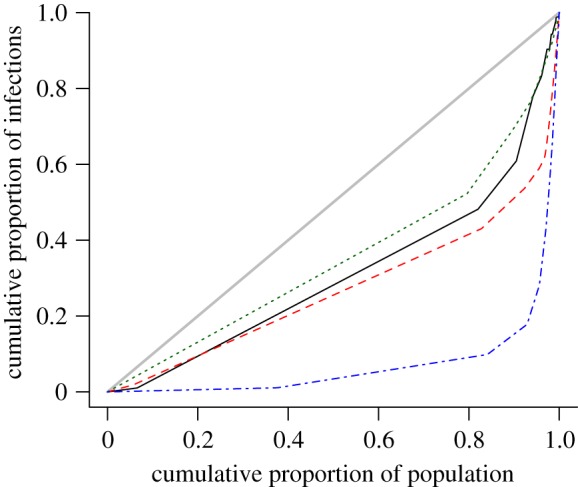
Lorenz curve representing the cumulative proportion of C. trachomatis infections as a function of the cumulative proportion of the population, after population sub-groups have been ranked in the order of their sexual activity during the last year. Natsal 2000 (G = 0.38), Kretzschmar model (G = 0.46 (mean) ± 0.03 (SD)), Turner model (G = 0.32 ± 0.04), ClaSS model (G = 0.84 ± 0.02). The line y = x denotes perfect equality, i.e. an equal dispersion of the infection within the population (thick gray line). The Lorenz curves represent data from all women and men aged 18–44 years. The black solid line denotes Natsal 2000; the red dashed line denotes the Kretzschmar model; the green dotted line denotes the Turner model and the blue dashed-dotted line denotes the ClaSS model. (Online version in colour.)
3.3. Impact of screening interventions
Given the different dispersion of C. trachomatis infections in the three models, we aim to explain the different results that these models show upon introduction of a standardized screening programme [17]. We implement the same standardized intervention (see §2) and compare the predicted impact after 5 and 10 years of intervention (figure 8). In the previous study, the Turner model predicted the strongest impact of an intervention, whereas the ClaSS model showed almost no impact at all [17]. Since we use a harmonized disease-specific parameter set between the models, we now find more similar results for the Kretzschmar and the ClaSS models. However, the Turner model still predicts a much stronger impact of the same intervention. One reason for this discrepancy in the Turner model is the overestimation of partner change rates among young adults (figure 3). The unrealistically high partner change rates imply that a large proportion of C. trachomatis transmission occurs in exactly those individuals who become eligible for screening, rendering the intervention more powerful. A second reason could be the short duration of gaps between partnerships, which results in very few individuals remaining single. Thus, infected individuals are usually engaged in a partnership with the possibility of transmitting the infection. Screening and treatment of an index case will therefore result in a reduction of C. trachomatis transmission at the population level. In contrast to the Turner model, the ClaSS model overestimates the proportion of individuals that are single. Chlamydia trachomatis infections in those individuals are likely to clear naturally before they engage in a new partnership. Thus, screening and treatment of infected singles in the ClaSS model has less effect as it does not necessarily reduce transmission at the population level.
Figure 8.
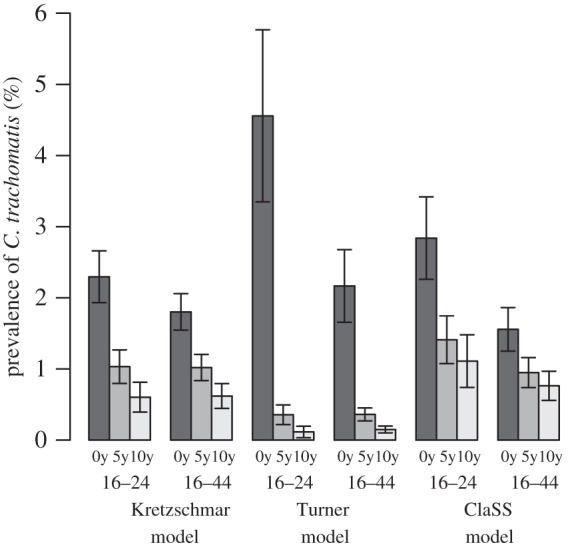
Impact of a standardized screening programme on the prevalence of C. trachomatis. The effect after screening for 5 and 10 years is shown for all women and men aged 16–24 years and 16–44 years. The proportion of eligible people receiving screening at least once a year is 20% and 40% of the current or most recent partners of an index case are successfully notified and treated. Means of 100 simulations runs are shown together with the standard deviation.
We can also express the reduction in the prevalence of C. trachomatis as a percentage of the pre-intervention steady state. After 10 years of screening, we obtain the same order for the group of 16–24 year olds (ClaSS: 39%, Kretzschmar: 26%, Turner: 3%) and the 16–44 year olds (ClaSS: 49%, Kretzschmar: 34%, Turner: 7%). Interestingly, we find the same order for the Gini coefficients obtained in §3.2 and hypothesize that these coefficients are one determinant of the predicted impact of an organized screening programme. A high Gini coefficient suggests that most C. trachomatis infections are concentrated in a small fraction of the population that exhibits high partner change rates. Thus, after infected individuals are treated for C. trachomatis, they rapidly engage in new sexual partnerships where they can contract the infection again, diminishing the effect of a screening programme. In contrast, a low Gini coefficient derives from a more equal dispersion of C. trachomatis infections among individuals with different numbers of partners. A large proportion of all infections is concentrated among individuals with low partner change rates. These individuals are less likely to contract the infection after treatment and partner notification becomes increasingly efficient as it reduces the risk of re-infection in an ongoing relationship.
4. Discussion
Our evaluation of the three individual-based models allowed us to find key reasons that affect the transmission of C. trachomatis and result in contrasting predictions of the impact of screening interventions. Different assumptions about the individual's sexual behaviour give rise to a widely different pattern of the sexual partnership dynamics between the models. This illustrates that describing some critical characteristics of the sexual partnership dynamics between individuals remains a challenging goal. Although all models capture some aspects reasonably well, they can fail in others. Overall, we find that the Kretzschmar model performs best in describing the sexual partnership dynamics as well as the transmission of C. trachomatis. This is striking, because it was the first model of its kind and its description is based on relatively simple algorithms and a moderate number of parameters. This shows that the most essential characteristics of the sexual partnership dynamics at the population level can be reasonably captured if simulated individuals are subjected to a small set of rules. It also emphasizes the fact that care should be taken if one wants to increase the complexity of models in order to achieve more ‘realism’. As several processes of the sexual partnership dynamics and their corresponding parameters at the individual level are not well understood, such attempts can result in models with ‘unrealistic’ outcomes. A critical point is that sexual behaviour surveys do not necessarily provide the data to parameterize single individuals in a model. We therefore suggest a careful comparison of the sexual partnership dynamics that emerge from individuals' behaviours in individual-based models, with the corresponding population-based data from sexual behaviour surveys.
The models that we have evaluated here are based on the classical framework where individuals are divided into subpopulations (compartments) such as risk groups that exhibit characteristic properties. This classification is often made arbitrarily and does not allow the individual's heterogeneity to be fully taken into account. The individual-based paradigm, however, allows this framework to be extended. Individuals do not need to belong to a certain subpopulation or group that will define their behaviour. Instead, the behaviour of an individual can emerge from a simple set of rules that takes into account their own and their partner's history. De Blasio et al. [23] have shown that the previous sexual history of individuals determines their future sexual contacts to a certain degree. It will be interesting to apply such mechanisms to STI modelling as they can account for a wider variation in sexual behaviour, compared to classical approaches.
The last decade has shown an increasing trend towards sophisticated and detailed computational models to describe the transmission of various infectious diseases and to assess the potential impact of public health interventions [15]. Often, different models are being built for the same purpose, which makes comparisons important to assess the reliability of their results and predictions. For example, the increasing number of models describing influenza pandemics has resulted in some formal comparison studies [48,49]. Such comparison studies can help to understand the impact of key assumptions in the models. As we have shown here, it is also necessary to re-evaluate models in light of more recent and more detailed data. The present study advances the findings of our previous comparison of the individual-based models of C. trachomatis transmission [17]. By harmonizing the disease-specific parameters, the differences in the predicted impact of screening are reduced.
In addition, the transmission of C. trachomatis is affected by the marked differences in the sexual partnership dynamics that we find between the models. These differences can at least partly explain the differences in the outcomes between the models that we find here and that have been previously described [17]. Overall, we find that the Kretzschmar model generally performs best in terms of describing the sexual partnership dynamics and the dispersion of C. trachomatis infections within the population. We therefore conclude that its predictions are likely to be the most reasonable. The predicted reductions in prevalence in the Kretzschmar model are comparable to those from simpler deterministic models of C. trachomatis transmission that examine similar screening interventions [8–10]. This is an important finding, which shows that many questions regarding the impact of public health interventions against C. trachomatis can be reasonably investigated with simpler mathematical models [50]. In terms of public health policy-making, the results suggest that screening all sexually active young adults at intervals of 2–5 years (corresponding to a yearly coverage of about 20–40%) for 5–10 years could potentially reduce the prevalence of C. trachomatis substantially. Unfortunately, there are still no empirical data from randomized controlled trials of chlamydia screening interventions to show that this kind of reduction in chlamydia prevalence is achievable in practice.
Finally, we have introduced a new summary measure to describe the distribution of C. trachomatis infections across the population as a function of people's sexual behaviour. By combining epidemiological data with behavioural data, this measure, which can be expressed as a Gini coefficient, provides insight into both the sexual partnership dynamics and the transmission of C. trachomatis. Owing to the difficulties in parameterizing individual-based models, such summary measures are especially suited to evaluation of the properties of such models. In particular, age- and gender-specific Gini coefficients will provide further insight into the transmission of C. trachomatis and public health interventions could be designed accordingly. We suggest that the Gini coefficient is a useful measure for calibrating infectious disease models that include risk structure and highlight the need to estimate this measure for other STIs.
Acknowledgements
We thank Catherine Mercer and the other investigators of the Natsal 2000 study for providing access to the data. This project was funded by the NIHR Health Technology Assessment programme (project number 07/42/02) and will be published in full in the Health Technology Assessment journal series. Visit the HTA programme website for more details (www.hta.ac.uk/1722). The views and opinions expressed therein are those of the authors and do not necessarily reflect those of the Department of Health. K.M.E.T. has received additional funding from an NIHR research fellowship. J.C.M.H. is funded by the Swiss National Science Foundation (project number 320030-118424).
References
- 1.World Health Organization 2001. Global prevalence and incidence of selected curable sexually transmitted infections: overview and estimates. Geneva: World Health Organization [Google Scholar]
- 2.Miller W. C., Ford C. A., Morris M., Handcock M. S., Schmitz J. L., Hobbs M. M., Cohen M. S., Harris K. M., Udry J. R. 2004. Prevalence of chlamydial and gonococcal infections among young adults in the United States. J. Am. Med. Assoc. 291, 2229–2236 10.1001/jama.291.18.2229 (doi:10.1001/jama.291.18.2229) [DOI] [PubMed] [Google Scholar]
- 3.Cates W. J., Wasserheit J. N. 1991. Genital chlamydial infections: epidemiology and reproductive sequelae. Am. J. Obstet. Gynecol. 164, 1771–1781 [DOI] [PubMed] [Google Scholar]
- 4.Anderson R. M., May R. M. 1991. Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press [Google Scholar]
- 5.Diekmann O., Heesterbeek J. A. P. 2000. Mathematical epidemiology of infectious diseases: model building, analysis, and interpretation. Chichester: John Wiley [Google Scholar]
- 6.Keeling M. J., Rohani P. 2008. Modeling infectious diseases in humans and animals. Princeton: Princeton University Press [Google Scholar]
- 7.National Audit Office 2009. Department of Health. Young people's sexual health: the National Chlamydia Screening Programme. London: TSO (The Stationery Office) [Google Scholar]
- 8.Regan D. G., Wilson D. P., Hocking J. S. 2008. Coverage is the key for effective screening of Chlamydia trachomatis in Australia. J. Infect. Dis. 198, 349–358 10.1086/589883 (doi:10.1086/589883) [DOI] [PubMed] [Google Scholar]
- 9.Althaus C. L., Heijne J. C., Roellin A., Low N. 2010. Transmission dynamics of Chlamydia trachomatis affect the impact of screening programmes. Epidemics 2, 123–131 10.1016/j.epidem.2010.04.002 (doi:10.1016/j.epidem.2010.04.002) [DOI] [PubMed] [Google Scholar]
- 10.Heijne J. C. M., Althaus C. L., Herzog S. A., Kretzschmar M., Low N. 2011. The role of reinfection and partner notification in the efficacy of Chlamydia screening programs. J. Infect. Dis. 203, 372–377 10.1093/infdis/jiq050 (doi:10.1093/infdis/jiq050) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kretzschmar M., van Duynhoven Y. T., Severijnen A. J. 1996. Modeling prevention strategies for gonorrhea and Chlamydia using stochastic network simulations. Am. J. Epidemiol. 144, 306–317 [DOI] [PubMed] [Google Scholar]
- 12.Turner K. M. E., Adams E. J., Gay N., Ghani A. C., Mercer C., Edmunds W. J. 2006. Developing a realistic sexual network model of chlamydia transmission in Britain. Theor. Biol. Med. Model. 3, 3. 10.1186/1742-4682-3-3 (doi:10.1186/1742-4682-3-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Low N., et al. 2007. Epidemiological, social, diagnostic and economic evaluation of population screening for genital chlamydial infection. Health Technol. Assess. 11, iii–iv, ix–xii, 1–165 10.3310/hta11080 (doi:10.3310/hta11080) [DOI] [PubMed] [Google Scholar]
- 14.Low N., Heijne J. C. M., Kretzschmar M. 2009. Use of mathematical modeling to inform Chlamydia screening policy decisions. J. Infect. Dis. 199, 767–768 10.1086/596744 (doi:10.1086/596744) [DOI] [PubMed] [Google Scholar]
- 15.Levin S. A., Grenfell B., Hastings A., Perelson A. S. 1997. Mathematical and computational challenges in population biology and ecosystems science. Science 275, 334–343 10.1126/science.275.5298.334 (doi:10.1126/science.275.5298.334) [DOI] [PubMed] [Google Scholar]
- 16.May R. M. 2004. Uses and abuses of mathematics in biology. Science 303, 790–793 10.1126/science.1094442 (doi:10.1126/science.1094442) [DOI] [PubMed] [Google Scholar]
- 17.Kretzschmar M., Turner K. M. E., Barton P. M., Edmunds W. J., Low N. 2009. Predicting the population impact of chlamydia screening programmes: comparative mathematical modelling study. Sex Transm. Infect. 85, 359–366 10.1136/sti.2009.036251 (doi:10.1136/sti.2009.036251) [DOI] [PubMed] [Google Scholar]
- 18.Kretzschmar M., Jager J. C., Reinking D. P., Van Zessen G., Brouwers H. 1994. The basic reproduction ratio R0 for a sexually transmitted disease in a pair formation model with two types of pairs. Math. Biosci. 124, 181–205 10.1016/0025-5564(94)90042-6 (doi:10.1016/0025-5564(94)90042-6) [DOI] [PubMed] [Google Scholar]
- 19.Fenton K. A., et al. 2001. Sexual behaviour in Britain: reported sexually transmitted infections and prevalent genital Chlamydia trachomatis infection. Lancet 358, 1851–1854 10.1016/S0140-6736(01)06886-6 (doi:10.1016/S0140-6736(01)06886-6) [DOI] [PubMed] [Google Scholar]
- 20.Kraut-Becher J. R., Aral S. O. 2003. Gap length: an important factor in sexually transmitted disease transmission. Sex Transm. Dis. 30, 221–225 10.1097/00007435-200303000-00009 (doi:10.1097/00007435-200303000-00009) [DOI] [PubMed] [Google Scholar]
- 21.Liljeros F., Edling C. R., Amaral L. A., Stanley H. E., Aberg Y. 2001. The web of human sexual contacts. Nature 411, 907–908 10.1038/35082140 (doi:10.1038/35082140) [DOI] [PubMed] [Google Scholar]
- 22.Jones J. H., Handcock M. S. 2003. An assessment of preferential attachment as a mechanism for human sexual network formation. Proc. R. Soc. Lond. B 270, 1123–1128 10.1098/rspb.2003.2369 (doi:10.1098/rspb.2003.2369) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.De Blasio B. F., Svensson A., Liljeros F. 2007. Preferential attachment in sexual networks. Proc. Natl Acad. Sci. USA 104, 10 762–10 767 10.1073/pnas.0611337104 (doi:10.1073/pnas.0611337104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Johnson A. M., et al. 2001. Sexual behaviour in Britain: partnerships, practices, and HIV risk behaviours. Lancet 358, 1835–1842 10.1016/S0140-6736(01)06883-0 (doi:10.1016/S0140-6736(01)06883-0) [DOI] [PubMed] [Google Scholar]
- 25.Ghani A. C., Swinton J., Garnett G. P. 1997. The role of sexual partnership networks in the epidemiology of gonorrhea. Sex. Transm. Dis. 24, 45–56 10.1097/00007435-199701000-00009 (doi:10.1097/00007435-199701000-00009) [DOI] [PubMed] [Google Scholar]
- 26.R Development Core Team 2009. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing [Google Scholar]
- 27.Foxman B., Newman M., Percha B., Holmes K. K., Aral S. O. 2006. Measures of sexual partnerships: lengths, gaps, overlaps, and sexually transmitted infection. Sex. Transm. Dis. 33, 209–214 10.1097/01.olq.0000191318.95873.8a (doi:10.1097/01.olq.0000191318.95873.8a) [DOI] [PubMed] [Google Scholar]
- 28.Burington B., Hughes J. P., Whittington W. L. H., Stoner B., Garnett G., Aral S. O., Holmes K. K. 2010. Estimating duration in partnership studies: issues, methods and examples. Sex. Transm. Infect. 86, 84–89 10.1136/sti.2009.037960 (doi:10.1136/sti.2009.037960) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nelson S. J., Hughes J. P., Foxman B., Aral S. O., Holmes K. K., White P. J., Golden M. R. 2010. Age- and gender-specific estimates of partnership formation and dissolution rates in the Seattle sex survey. Ann. Epidemiol. 20, 308–317 10.1016/j.annepidem.2009.11.003 (doi:10.1016/j.annepidem.2009.11.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Copas A. J., Mercer C. H., Farewell V. T., Nanchahal K., Johnson A. M. 2009. Recent heterosexual partnerships and patterns of condom use: a weighted analysis. Epidemiology 20, 44–51 10.1097/EDE.0b013e318187ac81 (doi:10.1097/EDE.0b013e318187ac81) [DOI] [PubMed] [Google Scholar]
- 31.Lorenz M. O. 1905. Methods of measuring the concentration of wealth. J. Am. Statist. Assoc. 9, 209–219 [Google Scholar]
- 32.Elliott L. J., Blanchard J. F., Beaudoin C. M., Green C. G., Nowicki D. L., Matusko P., Moses S. 2002. Geographical variations in the epidemiology of bacterial sexually transmitted infections in Manitoba, Canada. Sex. Transm. Infect. 78(Suppl. 1), i139–i144 10.1136/sti.78.suppl_1.i139 (doi:10.1136/sti.78.suppl_1.i139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kerani R. P., Handcock M. S., Handsfield H. H., Holmes K. K. 2005. Comparative geographic concentrations of 4 sexually transmitted infections. Am. J. Public Health 95, 324–330 10.2105/AJPH.2003.029413 (doi:10.2105/AJPH.2003.029413) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Monteiro E. F., Lacey C. J. N., Merrick D. 2005. The interrelation of demographic and geospatial risk factors between four common sexually transmitted diseases. Sex. Transm. Infect. 81, 41–46 10.1136/sti.2004.009431 (doi:10.1136/sti.2004.009431) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chesson H. W., Sternberg M., Leichliter J. S., Aral S. O. 2010. The distribution of chlamydia, gonorrhoea and syphilis cases across states and counties in the USA, 2007. Sex. Transm. Infect. 86(Suppl. 3), iii52–iii57 10.1136/sti.2009.040873 (doi:10.1136/sti.2009.040873) [DOI] [PubMed] [Google Scholar]
- 36.Chesson H. W., Sternberg M., Leichliter J. S., Aral S. O. 2010. Changes in the state-level distribution of primary and secondary syphilis in the USA, 1985–2007 Sex. Transm. Infect. 86(Suppl. 3), ii58–iii62 10.1136/sti.2009.040865 (doi:10.1136/sti.2009.040865) [DOI] [PubMed] [Google Scholar]
- 37.Chen M. I., Ghani A. C., Edmunds W. J. 2009. A metapopulation modelling framework for gonorrhoea and other sexually transmitted infections in heterosexual populations. J. R. Soc. Interface 6, 775–791 10.1098/rsif.2008.0394 (doi:10.1098/rsif.2008.0394) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gini C. W. 1912. Variability and mutability, contribution to the study of statistical distributions and relations. Studi Economico-Giuridici della R. Universita de Cagliari. [Google Scholar]
- 39.Schneeberger A., Mercer C. H., Gregson S. A. J., Ferguson N. M., Nyamukapa C. A., Anderson R. M., Johnson A. M., Garnett G. P. 2004. Scale-free networks and sexually transmitted diseases: a description of observed patterns of sexual contacts in Britain and Zimbabwe. Sex. Transm. Dis. 31, 380–387 10.1097/00007435-200406000-00012 (doi:10.1097/00007435-200406000-00012) [DOI] [PubMed] [Google Scholar]
- 40.Jones J. H., Handcock M. S. 2003. Social networks: sexual contacts and epidemic thresholds. Nature 423, 605–606 10.1038/423605a (doi:10.1038/423605a) [DOI] [PubMed] [Google Scholar]
- 41.May R. M. 2006. Network structure and the biology of populations. Trends Ecol. Evol. 21, 394–399 10.1016/j.tree.2006.03.013 (doi:10.1016/j.tree.2006.03.013) [DOI] [PubMed] [Google Scholar]
- 42.Hamilton D. T., Handcock M. S., Morris M. 2008. Degree distributions in sexual networks: a framework for evaluating evidence. Sex. Transm. Dis. 35, 30–40 10.1097/OLQ.0b013e3181453a84 (doi:10.1097/OLQ.0b013e3181453a84) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Aral S. O., Leichliter J. S. 2010. Non-monogamy: risk factor for STI transmission and acquisition and determinant of STI spread in populations. Sex. Transm. Infect. 86(Suppl. 3), iii29–iii36 10.1136/sti.2010.044149 (doi:10.1136/sti.2010.044149) [DOI] [PubMed] [Google Scholar]
- 44.Canchihuaman F. A., Carcamo C. P., Garcia P. J., Aral S. O., Whittington W. L. H., Hawes S. E., Hughes J. P., Holmes K. K. 2010. Non-monogamy and risk of infection with Chlamydia trachomatis and Trichomonas vaginalis among young adults and their cohabiting partners in Peru. Sex. Transm. Infect. 86(Suppl. 3), iii37–iii44 10.1136/sti.2010.045310 (doi:10.1136/sti.2010.045310) [DOI] [PubMed] [Google Scholar]
- 45.Chen M. I., Ghani A. C., Edmunds J. 2008. Mind the gap: the role of time between sex with two consecutive partners on the transmission dynamics of gonorrhea. Sex. Transm. Dis. 35, 435–444 10.1097/OLQ.0b013e3181612d33 (doi:10.1097/OLQ.0b013e3181612d33) [DOI] [PubMed] [Google Scholar]
- 46.Chen M. I., Ghani A. C. 2010. Populations and partnerships: insights from metapopulation and pair models into the epidemiology of gonorrhoea and other sexually transmitted infections. Sex. Transm. Infect. 86, 433–439 10.1136/sti.2009.040238 (doi:10.1136/sti.2009.040238) [DOI] [PubMed] [Google Scholar]
- 47.Hethcote H. W., Yorke J. A. 1984. Gonorrhea transmission dynamics and control. Lecture Notes in Biomathematics Berlin: Springer-Verlag [Google Scholar]
- 48.Halloran M. E., et al. 2008. Modeling targeted layered containment of an influenza pandemic in the United States. Proc. Natl Acad. Sci. USA 105, 4639–4644 10.1073/pnas.0706849105 (doi:10.1073/pnas.0706849105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ajelli M., Gonçalves B., Balcan D., Colizza V., Hu H., Ramasco J. J., Merler S., Vespignani A. 2010. Comparing large-scale computational approaches to epidemic modeling: agent-based versus structured metapopulation models. BMC Infect. Dis. 10, 190. 10.1186/1471-2334-10-190 (doi:10.1186/1471-2334-10-190) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Regan D. G., Wilson D. P. 2008. Modelling sexually transmitted infections: less is usually more for informing public health policy. Trans. R. Soc. Trop. Med. Hyg. 102, 207–208 10.1016/j.trstmh.2007.08.009 (doi:10.1016/j.trstmh.2007.08.009) [DOI] [PubMed] [Google Scholar]