Evolutionary optimization of material properties of a tropical seed

Abstract

Here, we show how the mechanical properties of a thick-shelled tropical seed are adapted to permit them to germinate while preventing their predation. The seed has evolved a complex heterogeneous microstructure resulting in hardness, stiffness and fracture toughness values that place the structure at the intersection of these competing selective constraints. Analyses of different damage mechanisms inflicted by beetles, squirrels and orangutans illustrate that cellular shapes and orientations ensure damage resistance to predation forces imposed across a broad range of length scales. This resistance is shown to be around the upper limit that allows cracking the shell via internal turgor pressure (i.e. germination). Thus, the seed appears to strike an exquisitely delicate adaptive balance between multiple selection pressures.

1. Introduction

Research into the structure and properties of biological tissues benefits enormously from knowledge of ecological and evolutionary contexts because consideration of the selective pressures to which a tissue is exposed can give important insights into its design [1,2].

This is particularly true for seeds of angiosperms. The seed is one of the most dramatic innovations in the evolution of land plants, consisting of the embryo, food reserve and seed coat. The nutritious embryo and its often lipid-rich food supply (endosperm) are highly attractive to predators [3,4].

Many seeds possess an architecture precariously balancing the avoidance of damage via a protective seed coat or shell (integument) with the ability to germinate [5]. In general, there is an evolutionary trend in the simplification of the seed coat in angiosperm families involving the reduction of the integument layers from two to one [6]. However, 40 million years ago or even earlier, a third layer called the middle integument evolved in the ancestor of a few southeast Asian members of the palaeodicot family Annonaceae [7–10]. The extra complexity that this layer provides suggests a need for an extraordinary level of embryonic protection. Indeed, the large seed studied here is known to be subject to predation by highly diverse groups of predators ranging from invertebrates (beetles) to rodents (squirrels) to primates (orangutans).

Here, we provide a mechanical analysis showing that protection from predation while retaining the ability to germinate is achieved in one thick-shelled tropical species (Mezzettia parviflora Becc.) by adaptation of the cellular structure of its shell. This shows a sophistication far beyond shells analysed to date [11–14]. We establish links between the architecture of the shell, its material properties, defined following standard materials science conventions [15], and the mechanisms of shell ‘failure’ perpetrated by predators. Our use of the term ‘fracture toughness’ refers generically to the critical energy release rate, symbolized here as R [16,17]. These properties are then used with the shell dimensions to estimate forces and stresses involved in predation–germination interactions.

The question naturally arises whether shell properties are sufficiently high to prevent predation. Complications arise because, as we show, such properties are involved in varying combinations depending on the scale of attack. There are known rules about property variation in composite structures, but biological materials are very complex composites, making it difficult to predict how individual properties might vary with construction geometry. Furthermore, most properties of biological tissues depend on scale owing to their heterogeneous structure. For example, fracture toughness increases in many materials with crack length (this is called an R-curve [17]). Thus, it is necessary to estimate the properties at a length scale similar to the predation mechanism. A major theme of our paper is the need to use tests appropriate to the length scales involved in the different events.

Beyond all this, predicting the occurrence of a specific mechanism in biological materials is complicated by their significant variability. Here, we estimate properties with the understanding that a deterministic approach with great precision is not possible. Nevertheless, we confront the question: are shell properties tailored to allow germination while hindering predators from consuming the nutritious contents, which are costly to produce?

2. Material and methods

The M. parviflora tree produces a large green fleshy fruit containing two seeds, each resembling an oblate hemisphere (figure 1). Average seed dimensions depend on location being 35 mm (Singapore) or 29 mm (Sabangau, Central Kalimantan) in length, 25 mm (width) and 17 mm in thickness. Except where indicated, seeds were collected inside fruits from Bukit Timah Nature Reserve, Singapore. Germination tests, taking 11 weeks, confirmed seed maturity.

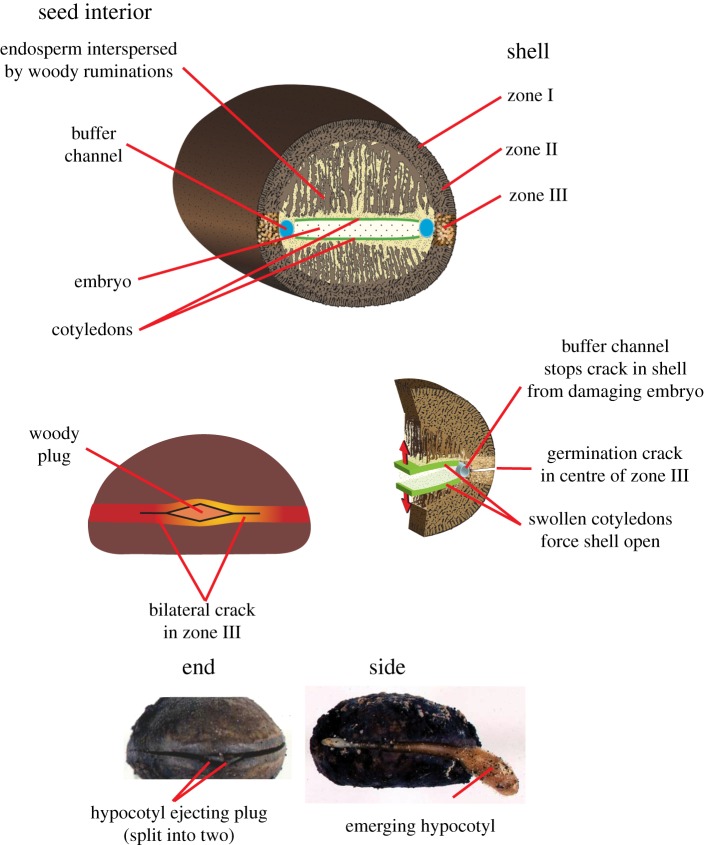
Figure 1.

Structure of the M. parviflora seed and its germination mechanism. Above, a plate-like embryo, sheathed by its cotyledons, is surrounded by a fat-rich endosperm that fuels germination but lures predators. The endosperm is partitioned by numerous thin woody struts (ruminations) that connect the complex shell formed from the middle integument. Fibres in the outer one-third of the shell run perpendicular to the surface (zone I). Otherwise, randomly oriented fibre bundles fill most of this shell (zone II). A ring of short stubby cells about 0.5 mm high encircles the shell and is critical for germination (zone III). Below, the seed imbibes water creating an internal pressure: note the buffer channel. A 5 mm long diamond-shaped woody plug at one end of zone III creates the flaw from which a bilateral crack initiates, slowly growing around the seed and allowing it to open like a mollusc shell. After the embryo differentiates, the hypocotyl emerges and pushes the plug out of its way.

Seed shell structure was investigated using light microscopy (LM), in both reflection and by transmission through sub-micrometre thick semi-thin sections, by laser confocal scanning microscopy using the natural fluorescence of the material and by scanning electron microscopy. Three structurally distinct zones of the shell (figures 1 and 2) could be observed. Macroscopic materials tests on these regions were conducted on fresh seeds (moisture content 14–16% of fresh weight) in the National University of Singapore [18]. Data of modulus and fracture toughness were obtained mainly from three-point bending tests using a universal testing machine (UTM), with either un-notched (for modulus E; restricted to zone II because of size constraints) or notched (for work of fracture R) specimens. Tests were run at UTM crosshead speeds of 0.4–2.0 mm s⁻¹. Un-notched beams were cut from shells with span-to-depth ratios of 13–77. Variation in the ratio was a deliberate attempt to ensure a true tensile modulus E, as affected minimally by shear. No variation in E with span-to-depth ratio was observed within these limits. Fifteen tests were run in total. Notched beams had span-to-depth ratios of 4.3–10.3 to encourage stable fracture and were notched from their undersurface to between 0.34 and 0.81 of their depth. Notches were made with a diamond saw, and then sharpened with a fresh razor blade prior to testing. The method was that of work area: a crack was formed, and then elongated by lowering the crosshead. The UTM crosshead was then reversed to return all unused energy in the specimen to the UTM. The work done in extending the crack was divided by the product of beam width and the crack length grown during that test to give the estimate of R. These crack lengths, always greater than 1 mm, were measured to the nearest 0.01 mm by an optical microscope. Fracture tests on zones I and III were made possible by fashioning composite beams including zone II as surrounding material. Cracks could be developed in either zones I or III in the centre of the beam. Cracks in zone I ran exclusively between fibres. Cracks in zone III ran around cells producing the appearance of rubble [18]. The total number of tests was: zone I, eight tests; zone II, 20 tests; zone III, seven tests.

Figure 2.

Light microscopic images of (a) the short stubby cells of zone III, outer part of the shell grading into the random fibre orientations of zone II, (b) the parallel fibres of zone I grading above into the random fibre orientations of zone II and (c) the short stubby cells of zone III intermingling with the random fibres of zone II.

Nanoindentation tests on M. parviflora seed shell fragments were performed at the University of Virginia on a nanoindentation system (MTS Systems Corp., Eden Prairie, MN, USA) equipped with a Berkovich diamond tip of calibrated head radius of approximately 100 nm, a similar set-up to recent studies on wood [19]. Specimen surfaces were incrementally polished down to 0.05 µm alumina prior to testing. For all tests, modulus and hardness over displacement data were made using the continuous stiffness method to a depth of 1 µm at a strain rate of 0.1 s⁻¹. A drift correction factor, as determined by a 50 s hold step at 10 per cent of the maximum load during unloading, was applied to the data to account for thermal drift during the test. Measurements reported were the average of at least 15 indentations, with 55 tests being completed on the randomly oriented fibres of zone II to ensure that variations in local material properties did not influence the global average.

The activity of beetles (the larger of two Coccotrypes spp., family Curculionidae, subfamily Scolytinae) on the seeds was monitored in a laboratory colony. The dimensions of the mandibles of adult beetles that had reached the interior were measured via optical microscopy and compared with those of developing beetles ready to exit the shell. Although tufted eared ground squirrels, Rheithrosciurus macrotis, feed on M. parviflora seeds (A. J. Marshall 2009, personal communication), no original observations are reported here. By contrast, observations on wild orangutans were made systematically in the Natural Laboratory of Peat Swamp Forest, Sabangau, Central Kalimantan (Indonesia). Orangutans were habituated to observer presence and their feeding behaviour recorded from July 2005 to June 2007 using standard behavioural methods [20,21]. Discarded remains of M. parviflora seeds consumed by orangutans were collected from beneath feeding trees and photographed at the field site. Calculations on the number of seeds consumed per year were derived from the above data of minutes per day feeding on M. parviflora, plus data on feeding rates in terms of the number of fruits consumed per minute [22].

3. Results and discussion

3.1. Measured mechanical properties

The structure of the seed shell is shown in schematic view in figure 1, with micrographs in figure 2. It possesses both thin elongate fibres and short stubby cells, but for either, the cell wall comprises approximately 95 per cent of the cell volume, leading to an overall density that is large compared with most woods [23–25]. Such a high density elevates the modulus and hardness. The spatial distribution of cellular shape and orientation leads to an important differentiation in mechanical properties. The outermost fibres run perpendicular towards the shell surface (figure 1, zone I), but most of the deeper part of the shell consists of woven randomly oriented fibre bundles (figure 1, zone II). The innermost fibres proceed centrally as woody struts extending deep into the endosperm (figure 1). In the middle of the shell, fibres are replaced by pseudospherical stubby cells that form a 0.5 mm tall germination band around the seed (figure 1, zone III). A diamond-shaped plug is positioned at one end of the band. Its boundaries have cells with thinner walls, forming a potential source for a crack (figure 1). Despite this heterogeneity, there are no gaping flaws between any of these zones (figure 2). Except behind the plug, the seed contents are separated from the germination band, by a cylindrical air-filled buffer channel (figure 1), but they are in contact in all other areas.

Measurements of shell mechanical properties at micrometre and millimetre length scales are summarized in table 1. In general, the nanoindentation tests show large scatter over small depths and asymptote to a value at depths of about 1 µm, at which depth values in table 1 were taken. Loads at this depth varied between 7.5 and 10 mN. The shell has a nearly spatially uniform hardness—the highest recorded for nut shells. While the elastic modulus varies more than hardness, the major influence is whether loading on the fibres is axial or transverse (table 1). Clearly in zone II, the mean modulus is a statistical average over a range of orientations. The most variable property was fracture toughness, with the inside of the shell away from the germination band (zone II) being the toughest by far.

Table 1.

Mechanical properties of the M. parviflora shell for different locations. Mean (s.d.).

properties	modulus, E (GPa)	hardness, H (MPa)	fracture toughness, R (J m−2)
scale of test (mm)	<0.01	<0.01	>1.0
zone I: parallel fibres	aaxial 15.7 (0.9), aparallel 7.2 (0.7)	400 (110)	250 (100)
zone II: random fibre orientation	9.4 (2.0), b7.4 (2.0)	490 (110)	2100 (1100)
zone III: pseudospherical cells	10.7 (1.1)	490 (110)	350 (55)

^aDirection of loading.

^bModulus obtained with millimetre-scale bending tests. Similar tests on zones I and III were not feasible owing to necessary specimen size.

3.2. Analysis of germination and implications

Germination is preceded by hydrostatic inflation of the two cotyledons lying either side of the embryo (figure 1). The seed imbibes water, probably via the perichalazal pad [26], elevating the intracellular turgor pressure particularly of the cotyledons [18]. This internal pressure creates a tensile stress in the shell that eventually drives a crack from the ends of the plug into the germination band (zone III), which has a lower fracture toughness than shell zone II. The germination crack grows stably as the embryo differentiates (i.e. the shell does not ‘pop’ open): the buffer channel inside the shell adjacent to the crack prevents damage from spreading to the cotyledons and embryo (figure 1). The internal pressure required to drive a crack around the germination band can be estimated by treating the shell as a thin-walled spherical pressure vessel: the critical pressure required for cracking is

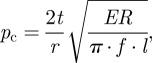where t is the shell thickness, r is the radius of the vessel, E is the elastic modulus and R is the resistance to crack growth [27]. Here, l is the crack length while f is a dimensionless correction factor that accounts for a crack length comparable to the vessel size (see appendix A [27]). Using an average modulus of E ∼ 9 GPa (table 1), fracture toughness for the germination band R = 350 J m⁻², shell thickness t = 3 mm, an effective shell radius of r ∼ 13 mm and crack length comparable to the plug size, i.e. l ∼ 6–12 mm, one predicts critical pressures in the range of approximately 1.7–3.9 MPa. This range coincides closely with internal turgor pressures measured in plant tissues, which is in the range of 1–4 MPa [28]. This strongly suggests that the shell modulus and fracture toughness are the maximum possible, since increases in either would imply that the critical pressure for germination would significantly exceed typical turgor pressures. The subsequent question naturally arises as to whether or not these properties are sufficient to provide protection against predation.

3.3. Analysis of small animal predation

Mezzettia parviflora shells are attacked by specialized seed-boring beetles (Coccotrypes spp., family Curculionidae, subfamily Scolytinae). Adult females, about 2.5 mm in body length and 1 mm in width, use their mandibles (mandibular width approx. 0.3 mm, with cusps < 0.1 mm) to bore into the shell. Following paths normal to the shell surface, they make tunnels approximately 1.5 mm in diameter. The tunnel surfaces are smooth and plastically ‘smeared’ (figure 3a,b). Once inside the shell, the females lay eggs and die, their mandibles being completely worn down during a single entry: severe wear is inevitable since the hardness of insect mandibles, even with metal impregnation [29], is comparable to that of the M. parviflora shell. Hatched larvae then feed on the seed's fatty endosperm, develop and mate.

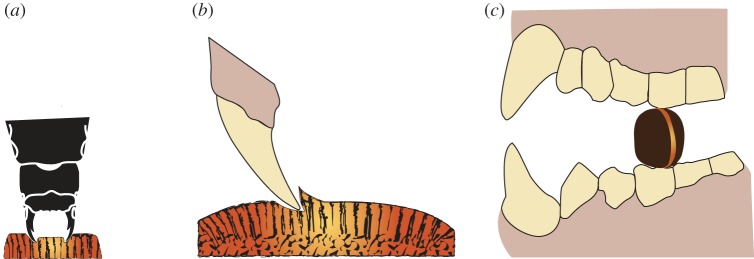
Figure 3.

Damage to M. parviflora seeds by predators: (a) entrance by burrowing beetles is random with respect to shell structure, (b) details of a 1.5 mm diameter beetle hole (by LM) suggest that burrowing is via small repetitive (plastic) gouges rather than shell fracture and (c) a seed fractured by an orangutan shows most of the fracture path following the germination band.

The force level required for the beetle to tunnel using small repetitive gouges (figure 4) can be estimated by the force to permanently damage a brittle surface via indentation. This force is described by [30]

where H is the shell hardness, E is its elastic modulus and r_m is beetle mandibular radius. We used nanoindentation, a technique involving contact radii of the order of micrometres, to obtain the hardness and elastic modulus of the shell. With the modulus taken in the direction of indentation to the tunnel sidewall (E ∼ 7 GPa), one predicts F ∼ 0.15 N for completely worn mandibles (r_m−0.3 mm). By comparison, the maximum (experimental) mandible force for various larger beetle species has been reported in the range of F ∼ 0.1–0.4 N [31]. This calculation strongly suggests that shell properties lie at the minimum required to prevent insect boring except by the most specialized species.

Figure 4.

Mechanisms of predation occur at different length scales. (a) Indentation by beetle mandibles (while burrowing) occurs at the scale of approximately 1–10 µm. (b) The size of chips produced by squirrels is constrained by the maximum bite force to be approximately 360 µm. (c) Orangutans load the whole seed along the germination band, driving cracks at the structural level of 1000 µm and above.

Squirrels eat M. parviflora seeds in other sites [32] and may be important seed destroyer-dispersers, as they can be in other tropical locations [33]. Squirrels gnaw seeds, a process akin to chipping (figure 4). Chipping (gnawing) in such rodents is predicted to be an inevitable consequence of their limited bite force, which is insufficient to crack the shell (see §3.4). The maximum bite force of Rheithrosciurus macrotis is unknown, but calculations from a regression of bite force in small mammals [34] on body mass [35] predict it could produce at least 150 N. Chipping forces in brittle materials can be estimated by [36]

where h is a measure of chip size and β is a dimensionless coefficient dictated by contact geometry (i.e. tooth shape and orientation). For E = 9 GPa, R = 2100 J m⁻² and β ∼ 5–15 (see appendix B), the chip size h is approximately 175–360 µm for a bite force of F ∼ 150 N. For the M. parviflora seed, this implies that a squirrel would need to make at least h/t bites, i.e. eight bites, with close to maximum force simply to penetrate the shell, and to make considerably more to form a hole large enough to access the embryo. Thus, although a persistent squirrel can consume the seed, the shell properties clearly are sufficient to make this a difficult, energy- and time-consuming process.

3.4. Analysis of large animal predation

Orangutans (Pongo pygmaeus), large fruit-eating great apes whose feeding behaviour has been studied intensively, eat M. parviflora seeds at a number of study sites in Borneo and Sumatra [20–22,37]. In Sabangau, Central Kalimantan, adult orangutans spent a mean 13.3–18.2% of their total monthly feeding time consuming these seeds [21], which are the hardest item they are known to consume [20]. Observations of orangutan feeding suggest two mechanisms for large animal predation, i.e. two methods to crack the seed by biting. In the first method, observed in wild orangutans in Sabangau, the seed is placed between jaws with the germination band running vertically (from bottom tooth to top tooth): the crack probably originates from the plug, which serves as a pre-crack aligned with the bite force and pointing into the germination band (figure 4). Not coincidentally, this configuration is closely aligned with a common laboratory experiment to determine fracture toughness of thin films embedded in circular discs, referred to as a ‘brazil nut fracture specimen’. The pinching force required to crack a flawed solid circular disc is given by [27]

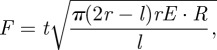where r is the radius of the disc, t is the thickness of the disc and l is the length of the initial flaw. Using the same properties as the germination study described above (i.e. in which the plug acts as a pre-crack that is approx. 6–12 mm long), the force required to crack the shell is F ∼ 1000–2000 N. This seems a reasonable lower bound: accounting for the third dimension (i.e. cracking an ellipsoid rather than a disc) dramatically increases this estimate, as does any misalignment between the germination band and the axis of pinching.

In the second biting method, observed in captive orangutans, the seed is placed between the jaws with the germination band running horizontally (parallel to the teeth or rotated 90° in figure 4). The shell cracks by unstable growth of flaws on the interior surface of the shell, which experiences tensile stresses owing to shell bending underneath the loading points. To establish the peak force at fracture, we treat the seed as a bilayer: a stiff shell surrounding an inner homogeneous core. The critical force to crack the shell is [38]

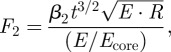where t is shell thickness and β₂ ∼ 16 is a dimensionless coefficient (see appendix C). An estimate is required for the modulus of the core: data for other seeds suggest E_core ∼ 30 MPa [10], although the seed interior of M. parviflora is undoubtedly stiffened by the woody struts. Taking E_core∼ 30–100 MPa, the shell modulus as E ∼ 9 GPa, the zone II shell fracture toughness as R ∼ 2100 J m⁻² and the shell thickness as t = 3 mm, then F₂ ∼ 5000–6000 N. There are no in vivo bite force data available for this rare great ape, but experiments using cobalt-chrome tooth replicas to break M. parviflora seeds in a UTM yielded an average fracture force of 6000 N (range 2700–8100 N) [39]. The agreement between these measurements and the above estimates provides significant confidence that the idealization of the geometry and cracking mechanics are reasonably accurate.

Despite the orangutans' success in eating seeds (field observations in Sabangau suggest they consume an average of about 120 seeds per day, with a maximum of 1001), it is clear that enormous forces are required: the force is equivalent to that exerted by the weight of one to six fairly sizable humans. The seed's properties provide remarkable resistance to biting, except for specialized predators that have evolved dramatic capabilities to win the biological arms race.

3.5. Discussion of evolutionary context for mechanical properties

The shell band has sufficiently low fracture toughness to allow turgor pressure to drive the development of germination cracks. At the same time, when combined with the intricate shell design, the fracture toughness is large enough to deter large predators. Predation by small consumers is discouraged by high cellular density that produces a relatively uniform obstacle to penetration at small scales. The seed has thus evolved highly adapted shell architecture with optimal properties, in the sense that they are tailored to balance competing performance constraints to ensure survival. There appears to be little room for property deviation. For germination, the shell needs quasi-static crack growth to give time and space for the embryo to differentiate. The calculation of internal pressure required to crack the shell suggests that shell thickness and stiffness are maximal: thicker, stiffer shells would require pressures that significantly exceed known turgor pressures, preventing germination. While softer, more compliant shells would facilitate germination (by requiring lower turgor pressures to crack the shell open), even small reductions in hardness and stiffness would leave the shell prone to burrowing by beetles. Similarly, the fracture toughness of the shell is low enough to permit germination, but not sufficiently low as to allow chipping by rodents. To resist the attack of large animals, the shell needs to be thick, stiff and, most of all, tough: rather than maximizing these properties outright, the shell has evolved a complex structure that raises these properties to upper limit indicated by the need to crack open during germination.

The calculations outlined above emphasize the critical role of the germination band: it is equally as hard as the surrounding shell, which is the principal property hindering burrowing by very small predators. At the same time, this band has a lower fracture toughness to allow for germination while being narrow enough to prevent chipping by medium-sized predators. While the low fracture toughness of the germination band implies cracking is possible by large predators, it nonetheless requires a large gape, carefully manipulated orientation and extremely large compressive forces.

It is compelling that the cellular shapes and orientations ensure resistance to predation mechanisms spanning a range of length scales from the micrometre (beetle mandible tips) to the centimetre (orangutan mouths), while still permitting germination. The above calculations clearly indicate the properties lie at the intersection of these competing constraints, a common outcome of constrained multivariate optimization. It is thus reasonable to conclude that the seed is an optimized structure given its ecological niche that favours survival by balancing multiple constraints.

The evolutionary pressures themselves are not straightforward. The Annonaceae diversified relatively early in the Cenozoic [40]. The date of evolution of the Mezzettia shell itself is unknown, but it is in several aspects paralleled by that of the smaller tritegmic seeds of Artabotrys [26], a genus of Miocene origin [7]. Coccotrypes beetles, noted for their tendency to predate large seeds [41], also evolved in Southeast Asia, probably in the early Miocene [42]. The orangutan/human split is dated at 12–15 million years ago [43], but the ancestors of orangutans had very similar dentitions [44]. This is also contemporaneous with the arrival of the earliest squirrels in Southeast Asia, which diversified rapidly [45]. Thus, it would appear that the Miocene, possibly the middle Miocene, a sub-epoch of widespread climatic change [46] and extinctions [47], might have been the critical period for the evolution of the complex plant–animal interaction we have documented. Yet clearly, further study is needed to elucidate seed dispersal syndromes in M. parviflora and to determine which evolutionary pressures were temporally matched with the evolution of shell structure.

Appendix A. Cracking due to germination

To estimate the pressure required to crack the germination band, the seed is idealized as a spherical pressure vessel: the maximum stress in the shell is given by σ = pr/2t, where p is the internal pressure, r is the radius of the vessel and t is the thickness of the vessel wall. For an elastic solid, fracture occurs when the energy released by crack extension reaches a critical value. The energy release rate for a crack in the vessel wall is given by

where E is the elastic modulus of the shell and f(l, r) = 1 + 1.41λ² +0.04λ³ is a geometry factor that accounts for the size of the crack relative to the vessel size, where λ = l/(t · r). Crack growth (fracture) occurs when G equals the critical energy release rate for the material, denoted as R in the main text. Thus, the above equation determines the critical stress for cracking in terms of the shell geometry (l, r, t) and the material fracture toughness, R: the resulting formula is given in the main text. The use of linear elastic fracture mechanics is justified when the size of the plastic zone near the crack tip is much smaller than the crack length or vessel size: the plastic zone can be estimated as r_p ≈ (RE)/(πσ_Y²), where σ_Y is an estimate of the material's yield stress. Taking E = 8.7 GPa, R = 350 J m⁻² and σ_Y ∼ H/3 = 150 MPa, the plastic zone size is approximately 0.03 mm. Since this is considerably less than the size of the plug, linear elastic fracture mechanics is justified.

Appendix B. Chipping during gnawing

The analysis of chipping in the main text is based on previous work that analysed the case of a sharp tool indenting a surface with a nearby free edge, wherein a chip is formed between the point of contact and a distance h from the free surface [36]. The scaling in the chipping equation (main text) has been validated for a broad range of geometries, with the dimensionless factor β accounting for the angle of the loading axis to the surface, the interior angle of the cutting tool (indenter) and the angle of the chip corner. This factor lies in the range of β ∼ 5–15, with the smallest values corresponding to sharp tools and shallow inclinations of the indenter relative to the surface, and the largest values for blunter tools and nearly normal indentation of the surface. This range is used to compute the range of chip sizes cited in the main text.

Appendix C. Cracking owing to biting

In the main text, the second cracking scenario involves a geometry factor that accounts for the relative size of the orangutan tooth and the shell. This factor can be approximated as β₂ ∼ 13.1 + 2.1r_c/t, where r_c is the effective radius of the contact between the tooth and the shell, and t is the shell thickness [38]. The effective radius of contact is given by 1/r_c =1/r_tooth +1/r_shell. The radius of curvature of the cusps of orangutan premolars is about r_tooth ∼ 4 mm [39]. With r_shell ∼ 14 mm, then r_c ∼ 3 mm, giving β₂ ∼ 16.