A decentralized control scheme for orchestrating versatile arm movements in ophiuroid omnidirectional locomotion

Abstract

Autonomous decentralized control is a key concept for understanding the mechanism underlying the adaptive and versatile behaviour of animals. Although the design methodology of decentralized control based on a dynamical system approach that can impart adaptability by using coupled oscillators has been proposed in previous studies, it cannot reproduce the versatility of animal behaviours comprehensively. Therefore, our objective is to understand behavioural versatility from the perspective of well-coordinated rhythmic and non-rhythmic movements. To this end, we focus on ophiuroids as a simple good model of living organisms that exhibit spontaneous role assignment of rhythmic and non-rhythmic arm movements, and we model such arm movements by using an active rotator model that can describe both oscillatory and excitatory properties. Simulation results show that the spontaneous role assignment of arm movements is successfully realized by using the proposed model, and the simulated locomotion is qualitatively equivalent to the locomotion of real ophiuroids. This fact can potentially facilitate a better understanding of the control mechanism responsible for the orchestration of versatile arm movements in ophiuroid omnidirectional locomotion.

1. Introduction

Animals exhibit adaptive, supple and versatile locomotion in real time under unpredictable real-world constraints. Such movements are achieved via spatio-temporal coordination of a significantly large number of bodily degrees of freedom. Clarifying the remarkable ability of animals to properly orchestrate and manoeuvre their numerous degrees of freedom can enable us to understand their adaptive and versatile behaviour as well as to construct truly intelligent artificial agents.

A prominent concept for addressing this issue is ‘autonomous decentralized control’, which has attracted considerable attention. This methodology is expected to provide non-trivial macroscopic functionalities that cannot be explained solely in terms of individual functionality. In fact, numerous biological findings support this concept; well-known examples include coupled biochemical oscillators in true slime moulds [1] and distributed neural networks called ‘central pattern generators’ in the spinal cords of lampreys [2,3]. These findings strongly suggest the existence of certain forms of decentralized control mechanisms that are exploited by most animals for locomotion.

These biological findings have enabled mathematicians and roboticists to employ a dynamical system approach based on decentralized control mechanisms to describe the ability of animals to perform synergetic movements. In particular, coupled oscillators or distributed neural networks have been widely used for the control systems of robotic agents [4–7]. The core idea underlying these studies is to exploit the intrinsic structural stability of a limit cycle, which induces self-organized behaviour of the entire system without any preprogrammed trajectory tracking control. Significantly, the limit cycle is constructed in the product space composed of the brain ( i.e. control system), the body ( i.e. mechanical system) and the environment, through which the generated behaviour can be adapted according to the situation.

The studies mentioned above have provided us with remarkable insights into ‘adaptability’, which is an important aspect of animal behaviour. However, animals exhibit versatile behaviour whereby rhythmic and non-rhythmic movements are well coordinated. Such behavioural ‘versatility’, which is another indispensable aspect, cannot be described solely in terms of limit cycles that exhibit rhythmicity. In summary, descriptions of movements based on limit cycles constrain behavioural versatility. In order to alleviate this problem and to realize behavioural versatility, we should refrain from the limit cycle-based approach and introduce an extended systematic design scheme that can describe rhythmic and non-rhythmic movements effectively. This requires a minimalistic approach to deal with a suitable model of a living organism that orchestrates versatile movements.

Accordingly, we focus on ‘ophiuroid omnidirectional locomotion’, in which both rhythmic and non-rhythmic movements are well coordinated for achieving efficient locomotion. As shown in figure 1, an ophiuroid consists of a central disc and five arms that radially diverge from the disc. All the five arms are functionally identical and the body is completely radially symmetric. By exploiting such bodily structure, the ophiuroid performs omnidirectional locomotion via spontaneous assignment of rhythmic and/or non-rhythmic arm movements according to the circumstances [8,9]. For example, the arms achieve propulsion by exhibiting rhythmic movement, forwards exploration and bodily support via non-rhythmic movements during locomotion; this is greatly different from the locomotion of the starfish that intensively uses its ‘tube feet’ underneath the body. Surprisingly, there is no nerve centre in the nervous system that assigns arm movements [10–13]. These unusual properties strongly suggest the existence of a simple good decentralized control mechanism that orchestrates versatile movements in ophiuroids.

Figure 1.

Complete illustration of an ophiuroid, Ophiocoma scolopendrina (Ophiuroidea, Echinodermata). It consists of a central disc and five arms. All the arms are completely identical, forming a radially symmetric shape.

Thus, our primary objective is to clarify the autonomous decentralized control mechanism that effectively explains ophiuroid omnidirectional locomotion in which the assignment of rhythmic and non-rhythmic movements to the arms can be achieved spontaneously and changed dynamically according to the situation. To this end, we employ a synthetic approach using a simulated robot as a tool to effectively achieve a better understanding of the mechanism. Synthetic approaches can facilitate the understanding of complex systems like animals; therefore, they can potentially provide us with novel insights that are hard to obtain solely through biological approaches. Using a synthetic approach, we model a maximally simplified ophiuroid robot that has five arms, each of which has only two degrees of freedom and is controlled in a fully decentralized manner. As the first step of the investigation, we carry out simulation experiments, whose results show that the spontaneous role assignment of rhythmic and non-rhythmic arm movements is successfully realized by applying attractant stimuli to the arms.

The remainder of this paper is organized as follows. In §2, we introduce the details of biological findings on ophiuroids in terms of anatomical and behavioural data. In §3, we describe the proposed ophiuroid robot based on a decentralized control method that can describe both rhythmic and non-rhythmic properties. In §4, we present the simulation results in terms of spontaneous role assignment of arm movements by applying attractant stimuli to the arms. Finally, we provide the conclusions of this paper and discuss future work in §5.

2. Related works on ophiuroids

2.1. Anatomical studies

An ophiuroid has five arms radially connected to a central disc. Each arm consists of numerous ossicles and muscles, as in the case of the spine in vertebrates. This structure enables the ophiuroid to perform back-and-forth and up-and-down arm movements. The arm movements are innervated by ‘radial nerves’ that are connected to each other through a ‘circumoral nerve ring’. Figure 2 shows the schematic of the nervous system of the ophiuroid. Interestingly, it has no nerve centre, i.e. brain [10–13].

Figure 2.

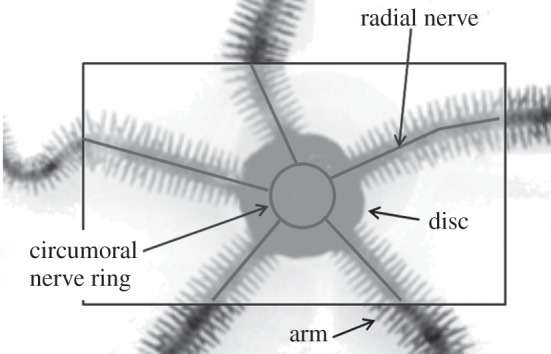
Schematic of nervous system of an ophiuroid. ‘Radial nerves’ innervate the arm movements, and they are connected to each other through a ‘circumoral nerve ring’ in the central disc.

2.2. Behavioural studies

The body of an ophiuroid is completely radially symmetric; the five arms are functionally identical. Such atypical symmetry requires coordination among the five arms for locomotion. For instance, the arms are used for propulsion, forwards exploration and bodily support. The most noteworthy locomotion pattern that clearly exhibits explicit role assignment of arm movements is described as the ‘breast stroke method’ [8,9]. As shown in figure 3, in this locomotion pattern, the ophiuroid assigns three types of roles to the arms, which can be summarized as follows:

• — ‘leading arm’: one arm that surges forwards and explores the direction of movement (non-rhythmic movement);

• — ‘side arms’: two arms that play a pivotal role for performing locomotion (rhythmic movement);

• — ‘posterior arms’: two arms that do not contribute to locomotion but passively move to support the body (non-rhythmic movement).

Figure 3.

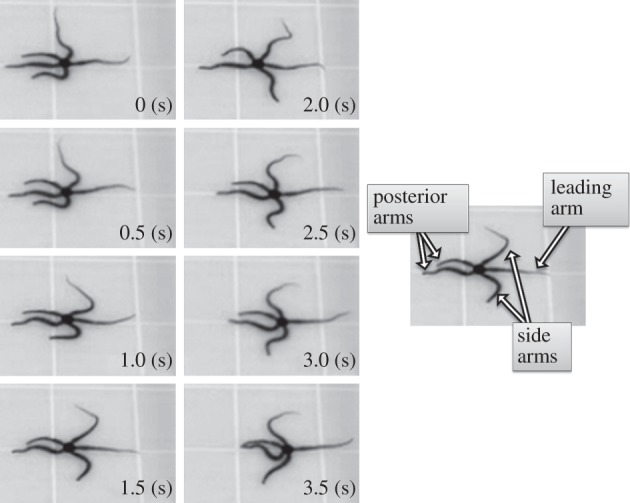
Snapshots of ophiuroid locomotion described as the ‘breast stroke method’. The five arms are functionally divided into the following three types: one ‘leading arm’ that surges forwards is used for exploration of the direction of movement (non-rhythmic); two ‘side arms’ are mainly used for performing locomotion (rhythmic); two ‘posterior arms’ are passive, and they do not contribute to locomotion (non-rhythmic).

In addition, this role assignment of arm movements can be dynamically changed when the attractant stimuli detected by the arms are changed.

2.3. Robotic studies

Lal et al. [14] developed a brittle star-like modular robot. They let the robots learn their movements by using a genetic algorithm so as to coordinate each other and generate locomotion. However, as the ‘performance phase’ of the robot is completely separated from the ‘learning phase’ that requires a certain amount of time, the robot cannot behave adaptively in real time. Moreover, this work did not refer to the orchestration of rhythmic and non-rhythmic arm movements observed in real ophiuroid locomotion.

3. The model

3.1. Mechanical system

A schematic of the ophiuroid robot employed in this study is shown in figure 4. The robot consists of a central disc and five arms. For simplicity, we design each arm by using a rigid bar with a single joint, even though the actual arms have many degrees of freedom. Two motors that can rotate in the vertical (pitch) and horizontal (yaw) direction are implemented in each joint. The joint angle is controlled according to proportional-derivative control, the details of which are explained in §3.3.

Figure 4.

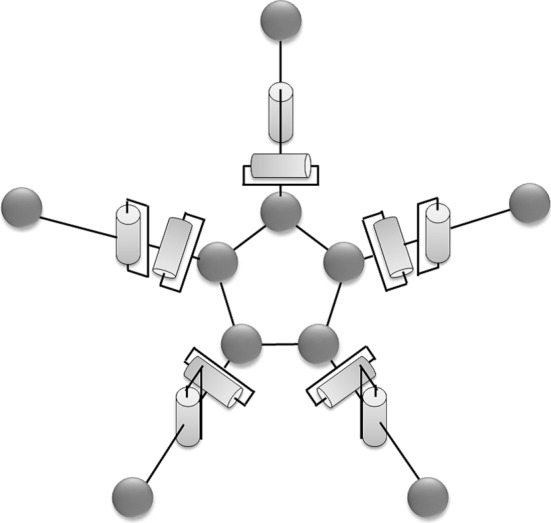
Schematic of an ophiuroid robot. The robot has five arms, each of which is driven by two motors that enable pitch and yaw rotation. The pitch and yaw joint angles are controlled according to proportional-derivative control (see §3.3).

3.2. Control system

In order to describe both rhythmic and non-rhythmic arm movements of ophiuroids, we focus on an ‘active rotator model’. An active rotator model exhibits both oscillatory and excitatory properties, and it is represented as [15]

3.1

where ϕ is the phase of the active rotator, ω is the angular frequency and a is a parameter, which determines the property of the phase dynamics.

As shown in figure 5, the behaviour of the active rotator is divided into three states. When −ω < a < ω, the active rotator exhibits oscillatory behaviour whereby it rotates along the unit circle with angular velocity ω−a cosϕ (figure 5b), resulting in rhythmic movements. On the other hand, when a<−ω and ω<a, there exists a pair of equilibrium points at which the condition ω−a cosϕ = 0 is satisfied, where one is stable and the other is unstable (figure 5a,c). In such cases, the active rotator exhibits excitatory behaviour whereby it converges to the stable equilibrium point when no external force is applied, resulting in non-rhythmic movements. By modulating the parameter a with the simple equation (3.1), we can easily switch between rhythmic and non-rhythmic movements. Hence, we design the ophiuroid with three types of arm movements such that they correspond to the oscillatory and excitatory properties, as shown in table 1.

Figure 5.

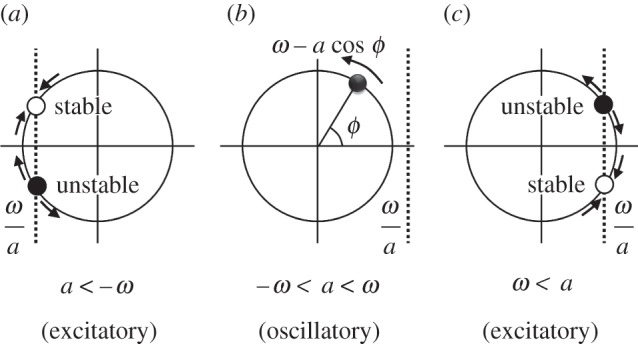
Phase dynamics of active rotator in the cases of (a) a < −ω, (b) −ω < a < ω, and (c) ω < a. The active rotator exhibits oscillatory behaviour in the case of (b) and excitatory behaviour in the cases of (a), (c).

Table 1.

Properties of the active rotator corresponding to the three types of arm movements.

arm type	property of active rotator
leading arm	excitatory (a > ω)
side arm	oscillatory (−ω < a < ω)
posterior arm	excitatory (a < −ω)

For the joints, we implement distributed control systems based on the active rotator model, as shown in figure 6. The time evolution of the phase of the active rotator embedded in the ith arm, ϕ_i, is described as

3.2

where ω is the intrinsic frequency and a_i is a parameter that determines the property of the active rotator.

Figure 6.

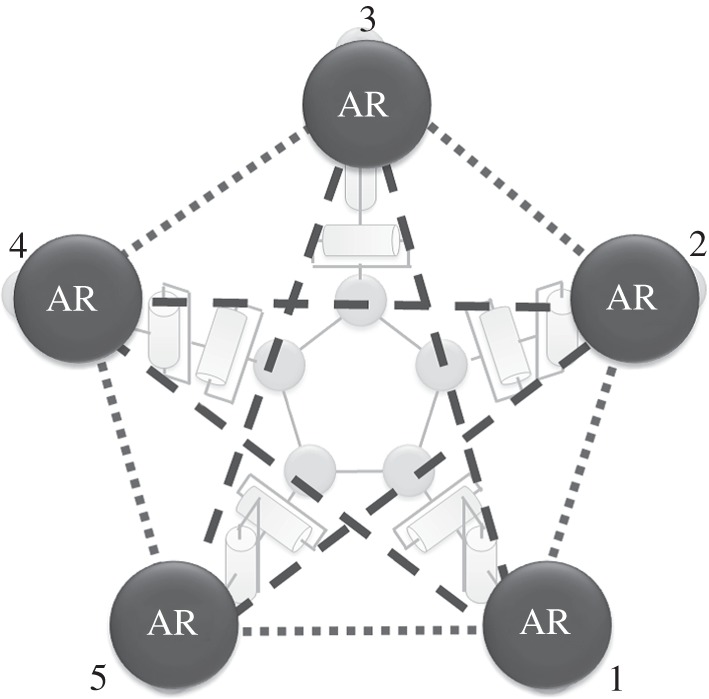
Schematic of distributed control systems in ophiuroid robot. The arm numbers are set in counterclockwise ascending order. The total interconnectivity between the active rotators (ARs) is described by two types of lines. Excitatory (dotted lines) connections between the nearest active rotators and inhibitory (dashed lines) connections between the second nearest neighbours are assumed.

In order to dynamically change the role of arm movements, we consider the time evolution of the parameter a_i by taking into account mutual interactions and sensory inputs, i.e. attractant stimuli. We assume the excitatory connections between the nearest active rotators and the inhibitory connections between the second nearest neighbours as mutual interactions, as shown in figure 6.

Accordingly, we construct the differential equation for the parameter a_i as

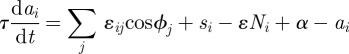3.3

and

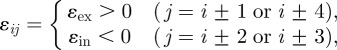3.4

where τ is the time constant and ɛ_ij is the constant that defines the coupling strength. ɛ_ex and ɛ_in are defined in the cases of connections between the nearest neighbours and the second nearest neighbours, respectively. s_i is the sensory input applied to the ith arm. The third term, ɛ N_i, is the local sensory feedback term (explained in detail in §3.3), where ɛ is a positive constant and N_i is the ground reaction force acting on the ith arm. α is a constant to which a_i converges when there exist no mutual interactions and sensory inputs.

3.3. Interaction between control and mechanical systems

The pitch and yaw joint angles of the ophiuroid robot are controlled according to proportional-derivative control. The target angles of the two motors in the ith arm are set as

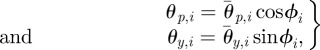3.5

where θ_p,i and θ_y,i are the target angles in the vertical (pitch) and horizontal (yaw) directions, respectively, an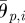d and 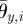are the corresponding amplitudes of rotation. θ_p,i > 0 and θ_y,i > 0 imply that the ith arm rotates upward and is close to the (i + 1)th arm, respectively. Owing to these controls, the arms trace an ellipsoidal orbit as shown in figure 7. An arm tends to be in the swing phase when −π/2 < ϕ_i < π/2 and in the stance phase when π/2 < ϕ_i < 3π/2. Note that only the side arms perform this rotative movement.

Figure 7.

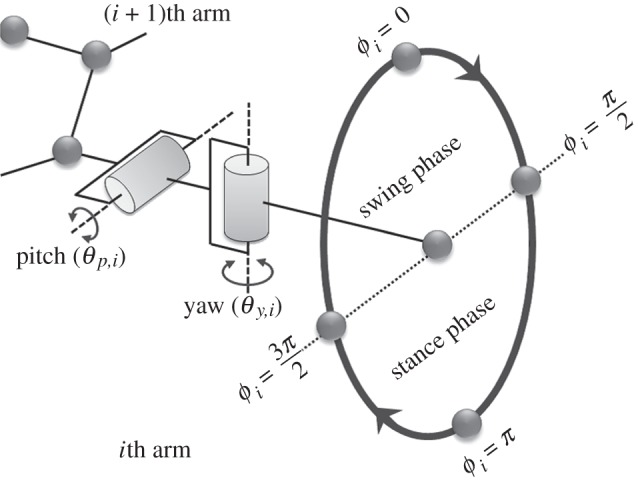
Ellipsoidal orbit of arm movement. Note that the direction of rotation of the ith arm changes according to the sign of 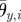( 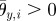in this figure).

In ophiuroid locomotion, both side arms rotate towards the leading arm in the swing phase (figure 3). To realize this property, the amplitudes 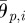and 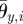are determined by using the phases of adjacent active rotators,

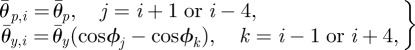3.6

where 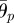and 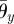are positive constants.

Moreover, in efficient ophiuroid locomotion via the breast stroke method, the rhythmic movements of two side arms are in phase. To successfully realize the in-phase movements of two side arms, local sensory feedback control based on the ground reaction force is employed (equation 3.3). As shown in figure 8, the local sensory feedback term causes the phase ϕ_i to approach π/2 when the ith arm is in the stance phase. Note that N_i increases when the other arm is in the swing phase. This causes the phase of the side arm in the stance phase to remain around π/2 until the other arm in the swing phase enters the stance phase. Thus, synchronization of the side arms' movements can be realized through such physical interaction.

Figure 8.

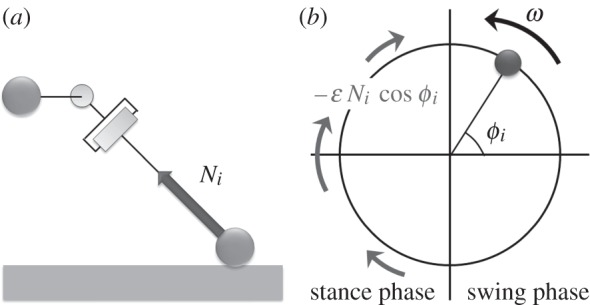
Schematic of local sensory feedback: (a) ground reaction force N_i and (b) phase modification. The phase ϕ_i approaches π/2 when the ith arm is in the stance phase.

4. Simulation results

We conducted simulations to verify the validity of the proposed model. In the simulation experiment, we applied the attractant stimulus to only one arm, and we checked whether spontaneous role assignment could be achieved. We also examined whether the roles of the arms were successfully changed when the applied attractant stimulus was switched from one arm to the other arm. The simulation parameters and the initial values of the variables are listed in table 2. These parameters were set so that a_i converges within one of the following ranges: a_i < −ω (posterior arm), −ω < a_i < ω (side arm) and ω < a_i (leading arm) as a result of the mutual interaction between the active rotators (table 1).

Table 2.

Simulation parameters.

parameter	value
ω	0.5
τ	12.5
ɛex	0.15
ɛin	−0.20
α	−0.5
si	1.2
ɛ	0.002
ϕi (initial value)	0 ≤ϕi ≤ 2π (random)
ai (initial value)	−0.5 ≤ ai ≤ 0.5 (random)

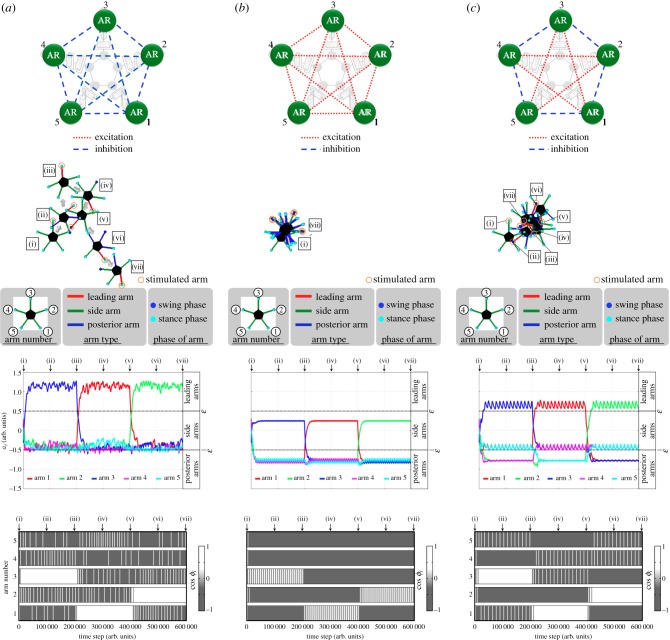
Figure 9 shows snapshots of the simulated locomotion of the ophiuroid robot. In the interval (i)–(iii), the attractant stimulus was applied to arm 3; it was switched to arm 1 at (iii) and to arm 2 at (v). As observed, the stimulated arm became the leading arm, and the robot moved in the leading direction with role assignment of the three types of arm movements in the intervals (i)–(iii), (iii)–(v) and (v)–(vii). Snapshots of one locomotion cycle are shown in figure 10.

Figure 9.

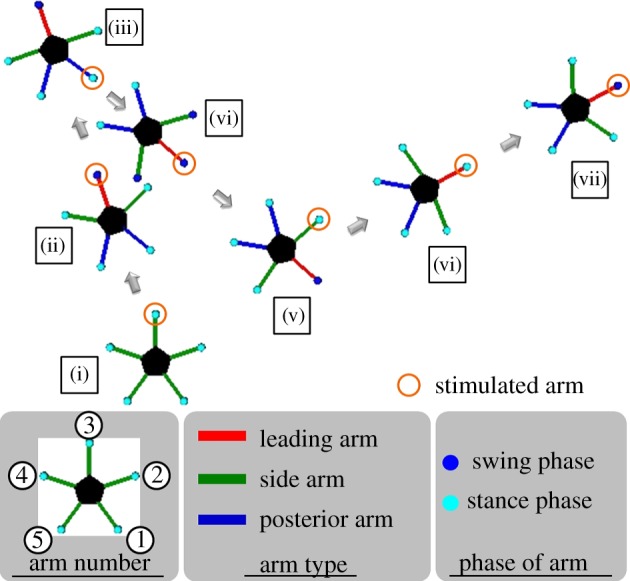
Snapshots of the simulated locomotion of the ophiuroid robot. These were obtained for every 100 000 time steps in the simulation, corresponding to the symbols (i)–(vii). First, in the interval (i)–(iii), the attractant stimulus is applied to arm 3. Next, it is switched to arm 1 at (iii) and applied to it in the interval (iii)–(v). Finally, arm 2 is stimulated from (v) to (vii).

Figure 10.

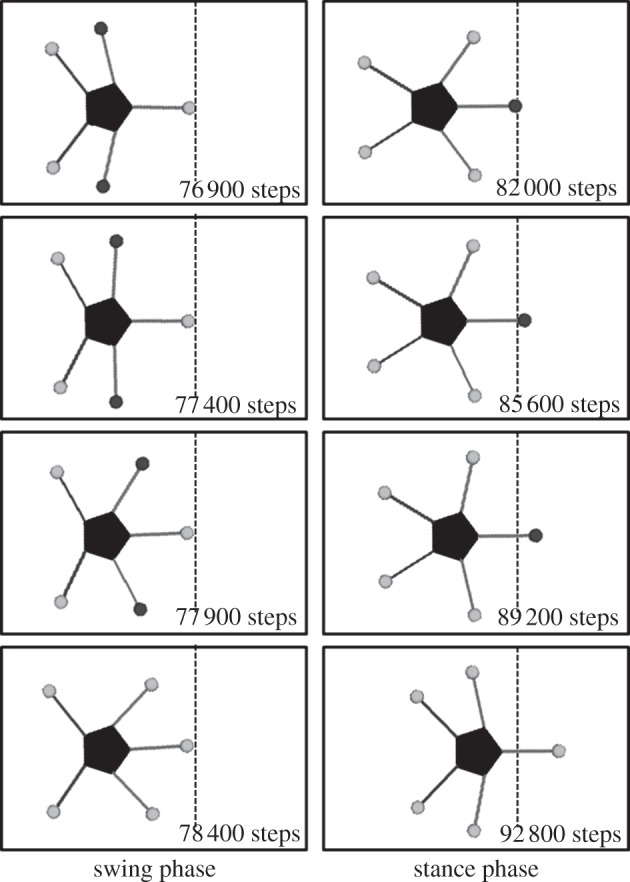
Snapshots of locomotion in a cycle. The dashed line denotes the edge of the leading arm in step 76 900. This simulated locomotion is qualitatively equivalent to real ophiuroid locomotion (figure 3).

Such simulated locomotion is qualitatively equivalent to the locomotion of a real ophiuroid (figure 3). Such spontaneous role assignment is clearly represented by the time evolutions of the parameters a_i and the phases ϕ_i, as shown in figures 11 and 12. As shown in figure 11, it is confirmed that the conditions a_i > ω, −ω < a_i±1 < ω and a_i±2 < −ω are satisfied when the attractant stimulus is applied to the ith arm. Note that the role of each arm changes immediately when the attractant stimulus is switched.

Figure 11.

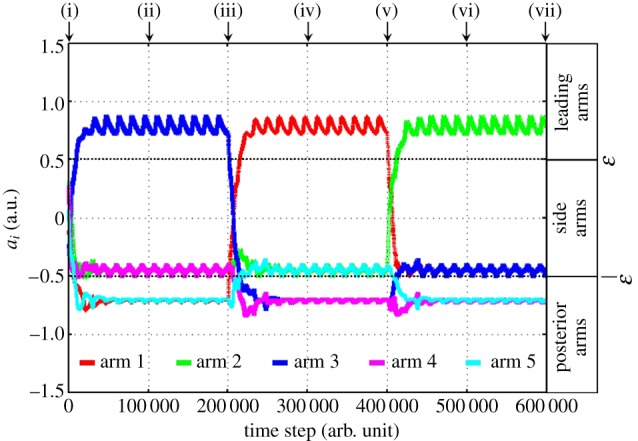
Time evolution of the parameter a_i. The arms exhibit their roles immediately after the attractant stimulus is switched.

Figure 12.

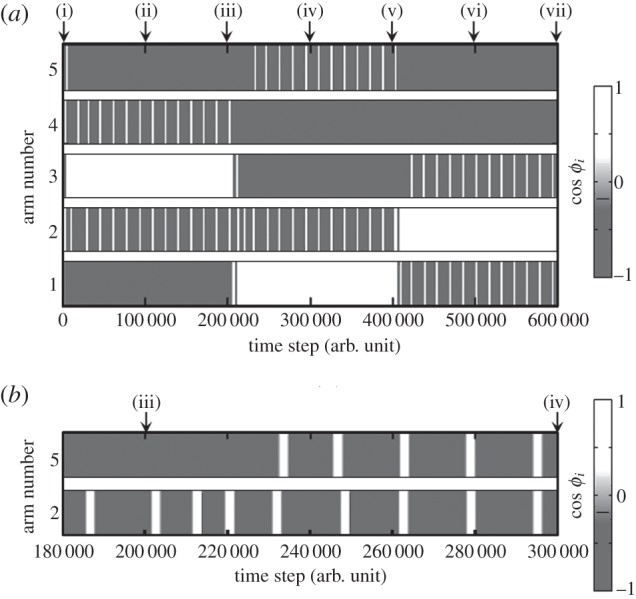
Time evolution of the phase ϕ_i: (a) from the beginning to the end of the experiment, and (b) around the time step 200 000 (iii). After (iii), at which the attractant stimulus switches from arm 3 to arm 1, the phases of the two side arms (arm 2 and arm 5) are steadily in phase.

Figure 12a shows that the phase ϕ_i of the side arms varies periodically, whereas those of the leading arm and posterior arms have a steady-state value. This clearly implies that the role assignment of rhythmic and non-rhythmic movements among the arms is realized spontaneously. Moreover, figure 12b clearly shows that the phases of the two side arms steadily become in phase; thus, local sensory feedback control based on the ground reaction force is suitable for the phase modulation of active rotators.

In order to verify the validity of the proposed network connectivity between active rotators, we intensively searched possible solution by changing the structure of neural circuit. The typical results are shown in figure 13. As shown in the figure, in all cases, appropriate role assignment of arm movements cannot be realized. These results indicate that the proposed network connectivity is more plausible than the other possible connections.

Figure 13.

Simulation results with respect to the different network connectivity. From the top to bottom, the network connectivity, the snapshots and the time evolution of a_i and ϕ_i are shown: (a) all the connections are inhibitory, (b) all the connections are excitatory, and (c) the connections between the nearest neighbours are inhibitory and the connections between the second nearest neighbours are excitatory.

5. Discussion

The objective of this study was to understand the mechanism of emergence of behavioural versatility, which is an indispensable property of animal behaviour. To this end, we intended to adopt autonomous decentralized control of ophiuroid omnidirectional locomotion, whereby ophiuroids realize spontaneous role assignment of their rhythmic and non-rhythmic arm movements. As the first step of the investigation, we constructed an autonomous decentralized control model for ophiuroid locomotion on the basis of the active rotator model, which can describe both oscillatory and excitatory properties. The validity of the proposed model was verified through simulation experiments, whereby the attractant stimulus was applied to a single arm and switched to the other arms. Simulation results showed that the proposed model can successfully realize spontaneous role assignment of rhythmic and non-rhythmic arm movements according to the attractant stimulus. The simulated locomotion is qualitatively equivalent to actual locomotion (figures 3 and 10).

Other possible mathematical models for describing behavioural versatility have been investigated, e.g. coupled chaotic systems [16–18] or coherence resonance and noise-induced synchronization in Hodgkin–Huxley neurons [19,20]. However, owing to the complexity of the individual components in these models, it is difficult to extract the essential mechanism in terms of versatility. In order to alleviate this problem, we employed a minimalistic approach to deal with an ophiuroids as a simple good model living organism because it has a simple body and neural systems. Furthermore, we described ophiuroid omnidirectional locomotion by using an active rotator model as a highly simplified individual component. These are the novel aspects of this study, and it is noteworthy that the simplicity enables us to extract the essence more easily.

The proposed model can realize the coordination between rhythmic and non-rhythmic arm movements as well as proper role assignment. We defined excitatory connections among the nearest neighbour active rotators and inhibitory connections among the second nearest neighbours in the model. Although it is known that axon bundles of neurons can reach only the nearest neighbours and no evidence based on anatomical experiments is available for connections among the second nearest neighbours [11], the assumption of existence of interneurons makes our design compatible with such findings. We designed the interconnection by means of a trial-and-error approach because the actual function of the circumoral nerve ring in ophiuroids has not been understood thus far. Hence, further neurophysiological and electrophysiological verification of neural systems is required to evaluate the validity of the proposed model.

Moreover, ophiuroids can respond to lesions of bodily parts, e.g. amputation of arms, by changing the role assignment of arm movements [9]. However, the proposed model cannot describe such responses because the force sensory system is too simple; hence, the detected force information does not influence the control system effectively. Therefore, it is necessary to consider an extended methodology whereby rich force sensors and feedback mechanisms that use these sensory inputs are implemented. Furthermore, we plan to develop a real ophiuroid robot equipped with this mathematical model and to verify the validity of the control system in real-world conditions on the basis of the active rotator model.