Flexibility and binding affinity in protein–ligand, protein–protein and multi-component protein interactions: limitations of current computational approaches

Abstract

The recognition process between a protein and a partner represents a significant theoretical challenge. In silico structure-based drug design carried out with nothing more than the three-dimensional structure of the protein has led to the introduction of many compounds into clinical trials and numerous drug approvals. Central to guiding the discovery process is to recognize active among non-active compounds. While large-scale computer simulations of compounds taken from a library (virtual screening) or designed de novo are highly desirable in the post-genomic area, many technical problems remain to be adequately addressed. This article presents an overview and discusses the limits of current computational methods for predicting the correct binding pose and accurate binding affinity. It also presents the performances of the most popular algorithms for exploring binary and multi-body protein interactions.

1. Introduction

Top pharmaceutical companies use both biophysical and computational methods for small ligand screening and drug design. Biophysical methods including nuclear magnetic resonance (NMR), mass spectrometry and fluorescence-based techniques allow the qualitative detection of a small molecule binding to a target and the quantitative determination of physical parameters associated with binding [1]. Drug design methods include structure-based virtual screening, where the three-dimensional protein structure is known [2,3], and ligand/pharmacophore-based virtual screening in the absence of a known receptor structure in order to identify and exploit the spatial configuration of essential features that enable a ligand to interact with a specific receptor [4,5]. Recent years have also seen the emergence of chemogenomics with the aim of understanding the recognition between all possible ligands and the full space of proteins by using traditional ligand-based approaches and biological information on drug targets [6] or by requiring only protein sequence and chemical structure data [7].

In this review, we focus on the current approaches aimed at structure-based virtual screening that circumvent the time, labour and material costs associated with experimental binding essays and have led to success stories for specific targets [8–10]. In a typical virtual screening experiment, ligands can be generated de novo using combinatorial chemistry or taken from a library of chemical compounds. The resulting ensemble of thousands to millions of small molecules are then optimally docked to the target protein and subsequently ranked according to their calculated binding energies [11]. There are two main bottlenecks in this procedure. The first one is related to the propensity to generate native or native-like docking poses. In the first chapter of this review, we report our current understanding of biomolecular recognition and the methods used for sampling the conformations of proteins and low molecular weight molecules separately. The second bottleneck in virtual screening is related to the correlation between the experimental and predicted binding affinities. Numerous studies predict false-positives or compounds with poor affinities. In the second chapter, particular emphasis is placed on advanced methods for predicting three-dimensional ligand-binding pockets, determining binding energies from physics-based interactions, and sampling the configurational space of protein–ligand complexes. Reviews on the effectiveness of empirical scores and knowledge-based functions to evaluate the interaction between ligands and rigid proteins with a continuum description of solvent can be found elsewhere [12–14].

Finally, the last chapter focuses on the field of binary and multi-component protein interactions. In many cases, the design of ligands must be envisioned in the context of a network of interacting molecules that have well-defined three-dimensional structures in isolation or become folded upon either binding to one partner or polymerization. Aggregation of several proteins constitutes a major societal challenge, as it is connected to human neurodegenerative diseases such as Alzheimer's disease (AD).

2. Protein and ligand plasticity

It is well established that proteins, while adopting well-defined structures in aqueous solution, are in constant motion and display conformational heterogeneity [15,16]. Experimental and theoretical studies also show that proteins can fluctuate between open and closed forms in the absence of ligand [17] and protein domains are dynamic with movements including the hinge bending and the shear motions [18]. Looking at molecular recognition, involving the non-covalent association of ligands (either low molecular weight molecules or proteins) to large macromolecules with high affinity and specificity, two mechanisms have been considered for a long time. In the Fisher's ‘lock-and-key’ model, the protein displacements are limited to a few residues within the catalytic pocket and thus each partner essentially binds in its lowest free energy conformation [19]. In contrast, the Koshland's ‘induced-fit’ model posits that the bound protein conformation forms only after interaction with a binding partner [20].

Very recently, based on a large number of NMR observables and the energy landscape theory of protein structure and dynamics, a new molecular recognition paradigm has emerged. The so-called ‘conformational selection’ model postulates that many protein conformations including the bound state pre-exist, and the binding interaction leads to a Boltzmann population shift, redistributing the conformational states [21]. This concept is rather bad news for drug design and makes the docking exercise harder, because the available protein structures in the absence of small ligands or protein-binding partners are no longer the final targets. In addition, the size of the conformational ensemble for docking will depend on the shape of the free energy landscape and it is possible that very large amplitude motions occur with virtually no expense in energy so that docking becomes very complicated. The ‘conformational selection’ paradigm is also challenged by intrinsically disordered proteins (IDPs), which are expected to represent 30 per cent of eukaryotic genome-encoded proteins with wholly or partially unstructured domains [22]. In many cases, IDPs undergo folding, in whole or in part, upon binding to their biological targets. This transition, referred to as ‘coupled folding and binding’ [23], may shift the minima in the conformational space by introducing new conformations.

There is a wide spectrum of theoretical approaches to tackle the functional motions of proteins ranging from normal mode analysis, which determines small vibration motion around a local minimum by means of the Wilson GF method [24] to molecular dynamics (MD)-based methods [25] that explore the configurational space by solving the Newton equations of motion. All these methods can use an all-atom or a coarser description of the target with explicit or implicit solvent representations. Coarse-grained (CG) models, which make use of beads to represent groups of atoms, reduce the number of degrees of freedom and extend the size of the systems to be studied. For example, one protein can be represented by interacting centres at the C_α atom positions (one-bead model), C_α atom and centroid positions of the side-chains (two-bead model), and three to six bead positions [26–31].

Normal mode analysis calculates with high accuracy the lowest vibrational frequency modes which very often resemble the conformational change between the unbound and bound protein forms [32]. By using a set of 20 proteins that undergo large conformational change upon association (>2 Å C_α RMSD), a single low-frequency normal mode was found that describes well the direction of the observed conformational change only in 35 per cent of the proteins studied starting from the unbound form [33]. Since these collective motions are related to the form and topology of the protein of interest [34], they are invariant to the details of the energy function [35] and can be obtained using elementary representations, opening the study of very large systems, such as the ribosome [36]. A more robust description of protein-collective motions can be obtained using ‘consensus’ normal modes from a set of related structures [37]. The drawback of normal mode analysis is that sampling is carried out in the vicinity of the starting structure and therefore it neither gives the real amplitude of the motion nor does it provide any information on the thermodynamics and kinetics of the transition.

It is possible to go beyond harmonic motions by various stochastic methods using constraint theory [38], activation–relaxation [39] or path-planning approaches [40,41]. The activation–relaxation technique in internal coordinate space, ARTIST [39] was found to be efficient for exploring conformational space in densely packed environments by successive identifications and crossings of well-defined saddle points connecting minima, i.e. energy minimized structures that are accepted/rejected using the Metropolis criterion. ARTIST is not sensitive to the heights of the barriers and can therefore move through the configurational space. It lacks, however, a proper thermodynamical basis [39]. Path-planning is a classical problem in robotics. It consists of computing feasible motions for a mechanical system in a workspace cluttered by obstacles. Within this approach, molecules are modelled as articulated mechanisms. Groups of rigidly bonded atoms form the bodies of the mechanism and the articulations between bodies correspond to bond torsions. These torsions are the molecular degrees of freedom. The capabilities of path-planning for exploring protein motion were recently demonstrated for long flexible loops and domains [40,41].

At the other end of the spectrum, the most widely used approach for exploring the functional motions of proteins is all-atom MD simulation with explicit treatment of solvent and ions [25]. These simulations, which typically cover a timescale of 20–200 ns depending on the protein size and the available computer resources, cannot routinely explore large conformational changes occurring in the microsecond–millisecond timescale. Using Anton, a specially built supercomputer, atomic folding characterization of three proteins up to 56 amino acids was however recently reported for 100–1000 µs [42].

Other techniques offer a unique alternative to bridge detailed intermolecular interactions and motions occurring at larger spatial scales and longer timescales. The temperature replica exchange molecular dynamics (T-REMD) simulation consists of running N MD simulations in parallel (or replicas) at N increasing values of temperature [43]. At regular intervals, two MD, at adjacent temperatures, exchange their conformations according to the Metropolis criterion. The rationale underlying this method is that simulating at high temperatures allows the replicas to cross free energy barriers that are trapped at low temperatures. All of these sampled data can be used in the weighted histogram method (WHAM [44]) to obtain the full thermodynamics properties of the system, such as the heat capacity. Because the number of replicas scales with the number of degrees of freedom, all-atom T-REMD in explicit solvent is not routinely performed on large proteins consisting of more than 100 amino acids [45]. To accelerate sampling for large systems, we can resort to T-REMD with CG protein models [46] or use alternative all-atom approaches such as Hamiltonian replica exchange molecular dynamics (H-REMD) or temperature-accelerated molecular dynamics (TAMD). H-REMD uses several related Hamiltonians for different replicas, where only some of the terms of the potential energy function are modified across replicas through scaling parameters [47–49]. On the other hand, TAMD rapidly explores the important regions in the free energy landscape associated with a set of continuous collective variables (CVs). As CVs, we may select for instance hinge bending angles or low-frequency normal modes. By using CVs related to the Cartesian coordinates of the centres of contiguous domains, TAMD applied to the GroEL subunit, a 55-kDa, three-domain protein and the HIV-1 gp120 unit, has led to large-scale conformational change that may be useful in the development of inhibitors and immunogens [50]. It is also possible to perform all-atom explicit solvent metadynamics using a large number of CVs without any knowledge of the bound form, as described in §3, or run discrete (discontinuous) molecular dynamics (DMD) using all-atom [51] or CG [52–54] models. DMD does not require numerical integration of Newton's equations but rather computes and sorts collision times, resulting in an improved computational efficiency.

Finally, for large proteins, it would also be possible to follow a hierarchical procedure consisting of T-REMD simulations with a CG model and multiple short all-atom MD simulations in explicit solvent starting from the predicted lowest energy CG conformations [55].

In principle, the biologically active conformations of any low molecular weight molecule in isolation can be determined by MD-based or stochastic methods. While feasible for a small number of targets, they are too slow for high-throughout screening, and techniques using an ensemble of discrete states [56–58] or sampling dictionaries of rotatable bonds [59–61] are preferable. An example of such a fast technique for large-scale de novo peptide structure prediction is PEP-FOLD [62]. This WEB-server approach takes advantage of the concept of structural alphabet [63], in which protein backbones are described as a series of consecutive fragments of four residues. By predicting a limited series of local conformations along the sequence, the folding problem is turned into an assembly of rigid fragment conformations using a chain growth or greedy method [64,65]. Although the progressive assembly poses numerous questions, particularly for the analytical form of the Van der Waals interactions to be used since steric clashes occur much more frequently in a discrete space than in a continuous space, PEP-FOLD folded 25 peptides of 9–25 amino acids with α-helix, β-strand or random coil character accurately (RMSD of 2.3 Å on the peptide NMR rigid cores) and very rapidly (in a few minutes). This result opens new perspectives for the design of small peptides and even mini-proteins [66] and indicates that discretization is feasible for any ligand types and biomolecular systems, including polyRNA and oligosaccharides if it is accompanied by further consistent non-polarizable [67–74] and polarizable [75,76] force field improvements.

3. Protein–ligand interaction

An important and very active issue in protein–ligand recognition, where the ligand is a small molecule, is to predict three-dimensional ligand-binding pockets. Numerous structure-based methods, in particular for in silico screening of small compounds, have been developed to detect pockets, clefts or cavities in proteins [77–88]. Starting from the experimental structures, current approaches can be classified as geometric, energetic and with or without any consideration of evolutionary information.

Geometric approaches for locating cavities use either Voronoi diagrams such as CASTp [77] or fpocket [78] or three-dimensional grid-based approaches such as VICE [79], PocketPicker [81] and LigSite [82] that search for grid points that are not situated within the protein and satisfy some conditions. For instance, the scanning procedure in PocketPicker [81] comprises the calculation of ‘buriedness’ of probe points installed in the grid to determine their atom environment. The accessibility of a grid probe is calculated by scanning the molecular surrounding along 30 search rays of length 10 Å and width 0.9 Å. As a result, the calculated buriedness indices range from 0 to 30 indicating a growing buriedness of the probe in a protein. The clustering of grid probes for pocket identification is restricted to those probes with buriedness indices ranging from 16 to 26. In LigSite [82], the protein is mapped onto a three-dimensional grid. A grid point is part of the protein if it is within 3 Å of an atom coordinate; otherwise it is solvent. Next, the x, y and z-axes plus the four cubic diagonals are scanned for pockets, which are characterized as a sequence of grid points, which start and end with the label protein and a period of solvent grid points in between. These sequences are called protein–solvent–protein (PSP) events. Pockets are then defined using as regions of grid points with a minimum number of PSP events. In practice, a threshold of two PSP events yields good results.

Energetic approaches are based on the calculation of interaction energies between the protein and one or a collection of probes or chemical groups. For instance, Laurie & Jackson [83] use a methyl probe at grid points, while An et al. [84] calculate a grid potential map using a carbon atom probe. Brenke et al. use an approach based on fast-Fourier techniques to map 16 small probes (ethanol, ispropanol, urea, etc.) to identify the hot spots of interaction, i.e. regions that are likely to bind small drug-like compounds with more affinity than the rest of a pocket [85]. Finally, combining evolutionary sequence conservations and three-dimensional structure-based methods has proven of interest for identifying surface cavities [80], and ConCavity [86] was found to outperform many approaches on a large set of single- and multi-chain protein structures.

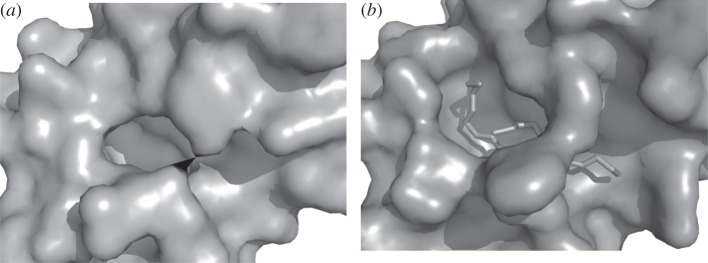
The static view used by all previous pocket detection methods meets, however, three major limitations. Firstly, the methods will identify more than one candidate. Although the largest pocket frequently matches the experimental ligand-binding site (e.g. [87]), this rule cannot be generalized, and the question of ranking the pockets in terms of druggability remains to be determined. Secondly, algorithms will usually identify regions larger than the effective interacting area on the protein surface and a finer delimitation of pockets is important in the context of in silico screening. Thirdly, pocket detection from ligand-free protein conformation can be misleading because the bound and unbound protein conformations can differ [88] as seen in figure 1. In addition, the traditional active site pocket concept meets its limits in the emerging field of protein–protein interaction inhibitor design where the notion of cavity becomes fuzzier and the observation of transient pockets at protein–protein interfaces for instance is particularly challenging [89,90]. The pocket-detection approach can be however tackled using simulation approaches. In particular, CG normal modes [91] and Brownian dynamics [92] have been shown to be useful for the prediction of functional sites. Recent approaches also start to track pockets in MD trajectories. The analysis of protein flexibility is expected to provide better understanding of pocket properties.

Figure 1.

Protein adaptation to ligand binding. (a) Conformation of the phospholipase A2 without ligand (PDB 3p2p). (b) Conformation bound to an inhibitor (PDB: 5p2p). The protein orientations are strictly identical. Images generated using pymol.

Along with pocket identification approaches, several docking methods are available to screen and evaluate a library of ligands [93–96]. These algorithms, which can allow full flexibility of the ligands, trade accuracy for CPU time and suffer therefore from three drawbacks.

Firstly, the limited sampling of the thermodynamically accessible protein conformations can be responsible for the failure to find the docked pose. One way of incorporating protein backbone flexibility is to consider a conformational ensemble using experimental data (for instance, different X-ray crystal or NMR-derived structures) and/or simulations (for instance, short MD simulations and normal mode analysis). This pre-generated protein ensemble is not sufficient when the target undergoes extensive rearrangement and only the crystal structure of its apo-structure is available [97]. However, inclusion of multiple protein and ligand conformations may also increase the ability of scoring functions to eliminate false-positives, as highlighted by the recent LigMatch approach [98].

Secondly, analysis of a large number of incorrect ligand–receptor docking poses indicates many other sources of error beyond receptor flexibility. They include improperly assigned histidine tautomers, charged states for aspartate, glutamate and histidine [96] and absence of water molecules in the binding region [99].

Thirdly, calculating binding free energy between a protein and a ligand in quantitative agreement with experiments, one of the most ambitious goals of structure-based drug design, is difficult to reach for high-throughput screening. In a recent study, Kim and Skolnick studied the quality of the BLEEP (knowledge-based), FlexX and X-Score (empirical) and AutoDock scores in various situations, including co-crystallized complex structures, cross-docking of ligands to their non-co-crystallized receptors, docking of thermally unfolded receptor decoys to their ligands and complex structures with ‘randomized’ ligand decoys. In all cases, the correlation of the raw docking score with the affinity is generally poor [100], confirming earlier studies [101] even in congeneric series [93]. Improving the correlation is a hard task and moves at a slow pace. In 2008, MedusaScore, based on models of physical interactions including van der Waals, solvation and hydrogen-bonding energies, was found to outperform the 11 scoring functions that are widely used in virtual screening for docking decoy recognition and binding affinity prediction [102]. However, the Pearson correlation coefficient between the score and the experimental dissociation constant pKd for the PDBBind database is only 0.63, matching the performance of the RosettaLigand procedure developed in 2006 [103]. Finally, by analysing the performance of six docking programs (DOCK, FlexX, GLIDE, ICM, PhDOCK and Surflex), Cross et al. [104] reported general trends in accuracy that are specific for particular protein families, suggesting that expert knowledge is critical for optimizing the accuracy of these methods.

All-atom MD simulations have long been discarded for virtual drug screening because they require a significant effort to calculate accurate residual charges and torsional energy barriers for all possible compounds, although progress has recently been made in this direction for small organic molecules [105]. More importantly, while the binding free energy can be deduced from the probability to find a ligand in interaction or not with its target during an MD simulation, exploring the relevant space of configurations is very time consuming because of the necessity to simulate rare events associated with crossing activation barriers. Yet, significant progresses have been achieved in making MD more tractable for drug design: increase of computer power and design of special machines [106–108] and development of two MD-based families to estimate in order to compute binding free energies: endpoint and pathway methods [109,110].

Special machines, such as Anton [106,107] or MD engines running on graphical processing units [108], have been able to sample the full binding pathways of how a drug finds its target binding site, for example the cancer drug dasatinib with the Src kinase protein within 15 µs [106], an irreversible agonist-β2 adrenoceptor complex within 30 µs [107], and the enzyme–inhibitor complex trypsin–benzamidine using a total time of 49.5 µs [108].

Endpoint free energy methods, such as the Molecular Mechanics Poisson–Boltzmann Surface Area (MM/PBSA) model, have received much attention because they benefit from computational efficiency as only the initial and final states of the system are evaluated. In the MM/PBSA approach, an explicit solvent simulation of the bound state is carried out. Then the simulation is post-processed to determine the enthalpic differences between the bound and unbound solute states. The solvation-free energy is the sum of a polar solvation term using the Poisson model and a non-polar term estimated by solvent-accessible surface area (SASA). The conformational entropy change is usually computed by normal mode analysis.

In a pioneering study, MM/PBSA was used to rank the binding affinities of 12 TIBO-like HIV-1 RT inhibitors. Good agreement between MM/PBSA results and experiments was obtained not only for the relative binding free energies, but also for the absolute ones, which have a root mean square deviation of 1.0 kcal mol⁻¹ and a maximum error of 1.9 kcal mol⁻¹ [111]. The quality of the agreement depends, however, on the target families studied. For instance, the free energy of binding between avidin and seven biotin analogues led to a mean absolute error of 2.3–4.5 kcal mol⁻¹, arising mainly from the entropy contribution [110]. Enhanced performance to recognize active among non-active compounds may be achieved by combining massive MD simulations of protein–ligand conformations obtained by molecular docking and MM/PBSA. This was confirmed by a recent study in which, trypsin, HIV-1 protease and acetylcholine esterase were each subjected to a 700 ps MD simulation using each of the top-ranking 1000 compounds obtained by docking. This pre-generated MD protein–ligand conformation ensemble was not, however, sufficient for cyclin-dependent kinase-2 [112].

There exist a few faster variants to the MM/PBSA method, such as MM/GBSA, in which the generalized Born (GB) solvent model is used to score the structures. A survey of recent literature reports various degrees of success. On the one hand, the docking poses a diverse set of pharmaceutically relevant targets, including CDK2, Factor Xa, thrombin and HIV-RT were re-evaluated using MM/GBSA and the correlation in all cases between the MM/GBSA results and the –log(IC50) experimental data, where IC50 represents the compound/substance concentration required for 50 per cent inhibition, was satisfactory [113]. Accurate prediction of the relative potencies of members of a series of kinase inhibitors was also reported using molecular docking and MM/GBSA scoring [114]. Overall, these methods are less expensive than those that use an explicit representation of the solvent. However, they can be fully unreliable when interfacial water molecules are present between the ligand and the cavity [99,115], and when the ligand-reorganization free energy is not taken into account. Using the X-linked inhibitor of apoptosis (XIAP) protein and 31 small ligands, major improvement was achieved when the free-energy change for ligands between their free- and bound-states, or ligand-reorganization free energy, was included in the MM/GBSA calculation, with the linear correlation coefficient value between the predicted and the experimentally determined affinities increasing from 0.36 to 0.66 [116].

Finally, it is of interest to compare the performances of the MM/PBSA and MM/GBSA methods. One recent study based on an ensemble of 59 ligands interacting with six different proteins showed that MM/PBSA gave better correlations than MM/GBSA with experiment, and MM/PBSA performed better in calculating absolute, but not necessarily relative, binding free energies [117]. However, the performances of PBSA are very sensitive to the solute dielectric constant and the characteristics of the interface, while the performances of GBSA depend on the GB model used. Considering its ability to be used in MD simulations, GBSA could serve as a powerful tool in drug design.

The second MD-based family to calculate free energy includes the rigorous, but computationally expensive pathway MD methods [118]. The most widely known is the alchemical double decoupling method, where the interactions of the ligand with the protein and bulk solvent are progressively turned off. Alternatively, it is possible to use a potential of mean force (PMF) method, where the ligand moves along a reaction path from the binding site to the bulk solution [93,119]. In both of these computational approaches, various restraining potentials may be turned on and off to explore more efficiently the translational, rotational and conformational changes of the ligand and protein upon binding, and their effects are removed to yield an unbiased binding free energy. Alchemical decoupling approaches have been shown to provide reliable binding free energies within an accuracy of 1 kcal mol⁻¹ if the protein conformational changes upon ligand binding are small, the ligand is uncharged and its solvation free energy is not very large. They are preferable if the ligand binds to buried sites or cavities, and a simple path for ligand association cannot be found. In contrast, PMF-based approaches are preferable if the solvation free energy of the ligand is very large [119]. Interestingly, in a recent blind test, the binding free energies of 50 neutral compounds to the JNK kinase were computed. The free energy computations correctly predicted two of the top five binders, as well as six of the 10 worst binders. The computed binding free energies range from −16 to −3 kcal mol⁻¹, while the experimental values range from −8.6 to −5.5 kcal mol⁻¹. The error in some cases amounts to 7 kcal mol⁻¹, emphasizing again the impact of large protein motion and/or wrong side-chain rotameric states on free energy calculations [119]. For large and flexible protein–ligand system, such as the protein plasmepsin of PM II and several exo-3-amino-7-azabicyclo[2,2,1] heptanes, the use of replica exchange-based free energy methods resulted in enhanced convergence, but still failed to reproduce experimental data [120].

Metadynamics or Hill's method is occupying a place of choice in pathway MD methods [121]. Metadynamics, which accelerates the sampling of rare events, maps out the free energy landscape as a function of a small number of CVs. This method is a modification of a standard MD simulation in which restraints are imposed on appropriately selected CVs of the system by a history-dependent potential. The history-dependent potential, by summing up Gaussian functions at regular time intervals along the trajectory, disfavours already visited configurations. Metadynamics was successfully applied to several ligand–protein interactions leading to a better understanding of specific interactions in molecular recognition and binding affinities [122–125]. However, calculating the free energy projected on CVs is computationally intensive. Clearly, the accuracy of the free energy surface will depend on the force field used, but more importantly on the CVs used to describe the slow degrees of freedom associated with molecular recognition. In particular, it is important to explore the internal degrees of the protein (e.g. loop motions, large-scale motion and possible structured/disordered transitions in specific regions) and the degrees of freedom associated with the in and out motion of the ligand from the protein active site. The choice of these independent CVs is non-trivial and target–ligand-dependent.

Finally, by providing the energy and the position of transition states, the PMF method and metadynamics offer the perspective to extract not only thermodynamic, but also kinetic properties such as the association and dissociation constant rates that impact the efficacy and action time of drugs and have been mostly out of reach of simulations thus far [106–108,126].

4. Protein–protein and multi-component protein interactions

The field of protein–protein interactions has rapidly progressed in the past 10 years [127]. Proteins seldom act alone and most cellular functions are regulated through intricate protein–protein interaction networks. Large efforts have been made to unveil these interactions in a high-throughput manner, with the first interactome maps for several model organisms [128,129]. We can identify binary interactions—that involve only two proteins by multiple methods such as array technology, cross-linking study, cytoplasmic complementation assay, NMR, two hybrid or X-ray crystallography)—and multi-component interactions [130,131]. It is to be noted that if the experimental protein–protein structures are known, there are computer-based tools available to design proteins to bind faster and tighter to their protein-complex partner by electrostatic optimization between the two proteins [132,133].

Protein–protein docking aims to predict the three-dimensional structure of a complex from the knowledge of the structure of the individual proteins in aqueous solution. Many docking methods are now able to predict the three-dimensional structure of binary assemblies if the protein partners do not display important conformational changes between their bound and unbound forms [134–137]. However, large-scale motion upon binding is still a major and unresolved problem in the absence of experimental constraints. This motion generally involves the displacement or the internal rearrangement of loops or domains and can also be characterized by the simultaneous movement of several flexible parts (up to three in known cases). For instance, by using all-atom metadynamics, the transition between the bound and unbound structures of the cyclin-dependent kinase 5 (CDK5) reveals that the large-scale movement has a two-step mechanism: first, the αC-helix rotates by 45°, allowing the interaction between Glu51 and Arg149; then the CDK5 activation loop refolds to assume the closed conformation [138]. As a result, the binding interface can be completely remodelled from the two unbound forms and it is therefore necessary to take flexibility into account at the beginning of the docking simulations. Collective movements of lower amplitudes have a less dramatic impact on the quality of the predictions but still can bias the results. Clearly, if the structure of the complex with homologous partners is available, this enhances the probability to have native-like conformations in the heap of states.

In the current docking programs, the first stage is aimed at a systematic exploration of the possible geometries of association and is performed either under rigid body approximation [139–142] using all-atom or CG representations or by using a limited sampling of protein backbone conformations. These latter methods involve: (i) the use of CG models [143] with either normal modes [144] or multi-copy approaches where discrete possible loop conformations are taken into account simultaneously [145]; (ii) multi-component docking of flexible domains that are kept rigid using geometric hashing [146]; (iii) Monte Carlo searches of backbone conformations and rigid-body degrees of freedom [147]; and (iv) pre-identification of binding interface and use of more time-consuming search approaches like MD, restricted in space [148].

The second refinement stage of most current docking programs introduces some flexibility by optimizing the side-chain interactions and the rigid body orientations and generates thousands of solution candidates that are ranked using a scoring function. Other programs or web servers introduce, however, backbone flexibility, and not only side-chains and rigid-body orientations. For example, in FiberDock, backbone mobility is modelled by an unlimited number of low and frequency normal modes [149], while in ATTRACT, it is modelled by the first few lowest frequency modes [143]. As reported in §3, precise evaluation of the binding free energy requires highly time-consuming exploration of all the details of the interaction at atomic precision and accurate information on binding affinities is therefore out of reach of all current docking methods.

The performances of state-of-the-art docking strategies producing rigid body solutions were recently evaluated by using a benchmark of 124 interacting pairs for which a high-resolution structure of the complex and the individual components exist [150]. Docking poses for all pairs were generated using FTDock [151] and ZDOCK3 [139], together with one of the most successful docking scoring schemes (pyDock [152]). While ZDOCK3 outperformed FTDOCK, ZDOCK3 obtained an acceptable solution among the top three for only 20 per cent of the cases. This low accuracy poses questions on the usefulness of these programs to study in high-throughput cross-docking manner protein–protein interactions without any knowledge of the interacting pairs [153]. The same conclusion was reached by a more recent study which concluded that there is a poor correlation between measured binding energies and nine commonly used scoring algorithms including pyDock for 81 complexes [154]. There is strong evidence that running docking experiments using homology models of the individual proteins is likely to decrease the success rate [153].

Coupling orientation procedures with flexibility of the protein backbone and the side-chains during the first stage of protein docking is a challenge. It is well known that side-chain rotamers are dependent on the main-chain conformation and side-chain rotamer transitions frequently occur at protein–protein interfaces [155]. Recently, a total of 64 groups and 12 web servers submitted docking predictions for 11 protein complexes and their performances were analysed in Critical Assessment of PRediction of Interactions (CAPRI) 2009 [156]. Overall, the evaluation reveals that eight groups produced high- and medium-accuracy models for six targets with medium conformational changes (1.5–2 Å; RMSD) upon interaction but exploring larger backbone and loop rearrangements, and improving the criteria for selecting promising solutions need to be addressed [137].

Significant progress was also reported by the Symmdock procedure for complexes with Cn symmetry (with a vertical n-fold axis of symmetry) by geometry-based docking [146] and the Rosetta ‘fold-and-dock’ procedure for symmetrical homodimeric complexes starting from fully extended monomer chains using symmetrical constraints [157]. A multi-scale approach based on Brownian dynamics simulations starting from X-ray crystal structures of the unbound proteins, incorporation of relevant biochemical data followed by all-atom MD simulations, in nine out of 10 cases yielded structures of protein–protein complexes close to those determined experimentally with the percentage of correct contacts > 30% and interface backbone RMSD < 4 Å; [158]. Good results could be obtained for large-scale simulations if multiple protein conformations were pre-stored in a library using various techniques. These include the all-atom activation–relaxation technique in internal coordinate space, ARTIST, with a continuum solvent model [159] and CG models coupled to Brownian dynamics [160] or MD simulations [161] if the protein fold is not too much maintained using the elastic network model.

Clearly, the field of protein interactions goes beyond docking and scoring two entities and three issues pose numerous challenges. Determining whether two given proteins interact is an extremely difficult in silico problem [162]. Current docking strategies often give high scores for proteins that do not interact experimentally. Little work has been reported in this cross-docking area, but an important result on protein surfaces is that the optimal orientations of the partners tend to lie within the largest cluster of docking results [163]. More recently, it was found that simply studying the interaction of all potential protein pairs within a dataset can provide significant insights into the identification of the correct interfaces [164]. The second issue lies in the development of algorithms able to dock proteins with well-defined three-dimensional structures beyond binary interactions. This field has attracted recent attention, leading to a combinatorial docking approach [165], the Rosetta ‘fold-and-dock’ procedure [157]) and the HADDOCK multi-body docking program up to six molecules using experimental and/or bioinformatics to drive modelling [166].

Finally, and more complex and urgent is the case where random coil proteins aggregate first into soluble oligomers and then to insoluble amyloid fibrils, leading to misfolding diseases such as AD, the most common form of senile dementia. With increased life expectancy and an ageing population, the number of patients with AD is expected to reach 80 million in 2040. The hypothesis for AD causation for which the greatest clinical and experimental support exists is that oligomeric forms of the β-amyloid protein with 39–43 amino acids are the proximate neurotoxic agents [167]. Thus far, no disease-modifying treatments exist and current structural biology methods have failed to reveal three-dimensional target structures of the Aβ oligomers. This is an extremely difficult problem as the low molecular weight aggregates are transient and in dynamic equilibrium between many species ranging from dimers to dodecamers [168].

A number of theoretical studies have recently determined the transmembrane structures of Aβ oligomers [169], and the structures of Aβ oligomers in aqueous solution by using multiple simulation approaches described in §2 [170–176]. To increase our knowledge on the exact mechanism of action for known Aβ drugs, several modelling studies were conducted [177–182]. For instance, all-atom MD/REMD studies looked at the impact of organic molecules, such as naproxen, on Aβ dimers [178] and protofilaments [179] or the impact of N-methylated peptide-based inhibitors [180,181] and the Pittsburg compound on Aβ protofilaments [182].

Other modelling studies along with transmission electron microscopy and spectroscopic circular dichroism (CD) experiments, cell viability essays [183–185] and even in vivo experiments [186] helped in the rational design of beta-sheet ligands against Aβ42-induced toxicity. For instance, formation of Aβ42 oligomer in the presence of C-terminal Aβ inhibitors has been studied by the DMD approach starting from spatially separated monomeric mixtures of Aβ42 and inhibitors. It was found that Aβ31–42 and Aβ39–42 are leads for obtaining mechanism-based drugs for treatment of AD using a systematic structure–activity approach [184]. Additional DMD simulations suggest that region Asp1–Arg5, which is more exposed to the solvent in Aβ42 than in Aβ40 oligomers, is involved in mediating Aβ42 oligomer neurotoxicity [185].

Overall, there is increasing evidence that very long CG and all-atom simulations, if coupled to low-resolution experimental data, may soon provide the transient Aβ42/Aβ40 oligomeric structures at an atomic level of detail, a prerequisite for the discovery and optimization of more efficient drugs against AD.

5. Conclusions

We have reviewed current in silico methodologies for predicting the correct binding pose and affinity measures in protein–ligand and protein–protein complexes. While an increasing number of studies have reported success stories in both areas [157,187,188], the size of the libraries requiring screening and the possibility of several interaction sites per protein still argue in favour of using mostly rigid body approximations and empirical scoring functions in order to select a small number of targets (<20) for experimental validation and further learning [14]. This procedure is not optimal for two reasons. Firstly, the methods cannot filter out all false-positives and expert knowledge is highly desirable to obtain compounds that bind selectively to their target receptors and do not cause side-effects by binding to other systems [104,189]. It is to be noted that false-positives are not available to the scientific community while they would help adjust the current methodologies. Secondly, optimization of the thermodynamic and kinetic properties is out of reach using standard computer resources if the experimental protein–ligand and protein–protein structures are not known.

The treatment of very large conformational changes in the receptor induced by ligand or protein-binding remains one of the biggest challenges in calculations of binding free energies. Finding the relevant rotational, translational and conformational degrees of freedom or CVs for a binary complex is far from being trivial, but this would be achievable for less than 20 candidates with the increase of computer power using a multi-scale approach that moves through different levels of complexity and precision. In the first step, approximate docking pathways could be sampled with rapid methods such as elastic network models, path-planning approaches and short replica exchange MD simulations based on CG representations of the systems. Next, these pathways could be refined and optimized with metadynamics or other rigorous techniques by retaining a full atomistic description of the system only in regions of interest while describing the rest of the system with elastic network models.

Much work remains to be done in the field of multiple-component docking of either well-defined structured proteins or proteins that fold, in whole or in part, upon binding or polymerization. All these stimulating challenges will undoubtedly involve extensive research.