Trophic network structure emerges through antagonistic coevolution in temporally varying environments

Abstract

Understanding the mechanisms underlying ecological specialization is central to our understanding of community ecology and evolution. Although theoretical work has investigated how variable environments may affect specialization in single species, little is known about how such variation impacts bipartite network structure in antagonistically coevolving systems. Here, we develop and analyse a general model of victim–enemy coevolution that explicitly includes resource and population dynamics. We investigate how temporal environmental heterogeneity affects the evolution of specialization and associated community structure. Environmental productivity influences victim investment in resistance, which will shape patterns of specialization through its regulating effect on enemy investment in infectivity. We also investigate the epidemiological consequences of environmental variability and show that enemy population density is maximized for intermediate lengths of productive seasons, which corresponds to situations where enemies can evolve higher infectivity than victims can evolve defence. We discuss our results in the light of empirical studies, and further highlight ways in which our model applies to a range of natural systems.

1. Introduction

Specificity can be defined as the range of tasks that an organism can accomplish, or as differential preference or performance in these activities [1,2]. Specificity is an emergent, complex trait, influenced by evolutionary and ecological processes [3]. Ecological specialization (i.e. the process leading to the selective exploitation of a subset of the resources or environments encountered) originates in the selection of organisms based on their ability to exploit and perform on one or more resources. Specificity is therefore influenced by diverse constraints [4] and trade-offs [5], which may be linked to abiotic and biotic components of the environment [6]. Biological constraints may be caused by physical and physiological sources [7]. Ecological factors include spatial heterogeneity in resource density [8], temporal environmental heterogeneity [9], and the distribution and abundances of competitors and natural enemies [10].

The selective pressures involved in specialization are due to changes in abiotic or biotic components of the environment, the latter involving change in the abundances, behaviours or spatial distributions of interacting species. In the case of host–pathogen associations, hosts can either evolve independently of, or coevolve with, the enemy. Understanding the causes of specificity in coevolving symbiotic interactions is particularly important, since these are thought to exhibit some of the most extreme cases of specialized adaptations [11]. This is likely to be challenging, because of the potentially complex spatio-temporal feedbacks that characterize antagonistic co-evolutionary processes. For example, in host–pathogen systems, changes in the frequency or density of one or both antagonists can have ramifications for the level of adaptation to all genotypes present [12]. As such, the dynamics and consequences of specialization in coevolving associations are different from situations involving interactions with abiotic environments. However, most of our understanding of the evolution of specificity comes either from abiotic interactions (see [2] for a review), or from biotic interactions of low complexity [13] (i.e. simplified communities with few interacting species).

Despite considerable theoretical investigation of the dynamics of antagonistic coevolution [14–16], the drivers of specialization in such interactions remain largely unknown, although we know that changes in productivity or biotic complexity can strongly affect specificity in symbiotic communities [17]. Levels of reciprocal selection within and across patches could be seen as indicators of specialization, since strong local reciprocal selection can initiate the divergence of a single generalist into multiple specialists [18]. Links between reciprocal selection and specificity will be influenced by the availability of novel genotypes via mutation or migration [19], drift (although its impact is expected to be weak if reciprocal selection is strong), trait matching [20] and trade-offs with other fitness-determining traits [21]. A central prediction of coevolutionary theory is that, in tightly coupled associations, the strength of frequency-dependent cycles will depend on the degree of specialization in interacting genotypes [22], or cost-based trade-offs leading to fixed host ranges [23], the latter being consistent with a multi-locus gene-for-gene interaction.

Despite the impact of environmental productivity on coevolution [23,24] and the recognition that the dynamics of resource supply can affect diversification even with a non-evolving resource [25,26], no study to our knowledge has explicitly investigated their joint impact on the evolution of specialization and the structure of antagonist communities. Accounting for resource dynamics is likely to be important to understanding coevolutionary patterns in nature. Recent work on a naturally occurring microbial community suggests an ecological mechanism linking resource availability to specialization of enemies on their victims and the range of exploitable victim types [27]. Limiting resource supply reduces victim population growth (and/or carrying capacity), resulting in reduced rates of enemy multiplication and a decrease in the number of victims encountered. Reduced encounter rates have been shown to decrease the propensity of antagonistic coevolution to alter the interactive traits of enemies and victims [28].

We develop and analyse a model of antagonistic coevolution between enemies and their victims in situations where the availability of resources consumed by the victim changes through time. In particular, we explore situations in which resources regulating the growth of the basal species (victim) exhibit periodic or stochastic temporal dynamics. Variable resource input is common in nature [29], applying broadly to a range of interactions (e.g. bacteria and phage [30,31], phytoplankton and mussels [32], and herbivores and predators [33]). Evolution and coevolution in our system can be influenced by reciprocal genetic interactions between enemies and victims, and costs and constraints of trait evolution, including resource limitation directly affecting the victim population. Environmental variability occurs in the form of seasonality in resource input that regulates the potential for investment in costly interactive traits. Overall, we find a strong effect of environmental variation that regulates the amount of resources available to victims, and thus their investment in costly resistance. This selects, in turn, for different levels of investment in enemy attack. Thus, the structure and diversity of enemy–victim communities are partly dependent on the interaction between coevolutionary processes and conditions that regulate the possibility of investment in defences and diversification. These results are discussed in light of recent empirical data.

2. Model development

Our model describes the dynamics of three trophic levels: a resource (R), a victim species (V) and an enemy species (E), where the latter two populations are each composed of multiple genotypes (see below and electronic supplementary material, figure S1a). We define ‘enemy’ to represent the trophic level that specifically preys on the ‘victim’, which itself exploits an underlying resource. As such this excludes other antagonistic interactions such as competition.

We assume that resource input into the system does not directly depend on past resource levels, as would be the case for organic or inorganic nutrients, and density-independent immigration of prey items that do not reproduce in the modelled patch. Specifically, we assume that resource input I_R{t} fluctuates through time as a step function with a basal entry rate of S for T_L time steps, and an elevated entry rate of S + A (the ‘productive period’) for T_R time steps (the ‘frequency of resource input’; electronic supplementary material, figure S1b).

The differential equations are

1.1a

1.1b

1.1c

Resources are consumed by victims at a per capita rate γ and converted into victim biomass (ɛ). Enemies kill victims at rate ϕ and convert them into enemy biomass (β). Victims and enemies die owing to extrinsic factors at per capita rates ρ_V and ρ_E, respectively. We make the simplifying assumption that the enemy species only consumes the victim species, and the latter only consumes the resource. Parameter values employed in simulations are given in table 1.

Table 1.

Model parameters, their meanings and values used in the numerical simulations. For a sensitivity analysis of the model to parameters involved in resource dynamics, see electronic supplementary material, appendix S2.

parameter	meaning	value and range explored
TR+ TL	length of epoch	40
TR	length of productive season	1 to 40
S	basal resource supply	0.01
A	amount of resource during TR	0.1 to 10 (log scale)
ρR	resource degradation rate	0.1 (main text), 0.5
ρV	victim mortality rate	0.1 (main text), 0.2, 0.5
ρE	enemy mortality rate	0.1 (main text), 0.2, 0.5
ɛ	victim conversion rate	10
Φ0	basal attack rate	0.01
γ0	victim consumption rate	0.01
β0	progeny size (enemy)	3
∂	baseline cost of adaptation	0.4
w	non-optimal attack score	0.2
kV	victim cost of defence	0.25 (main text), 0.5
kE	enemy cost of attack	0.25 (main text), 0.5

The model assumes all trophic levels exploit and are exploited in a manner consistent with a type I functional response [34]. Using saturating (e.g. type II) functional responses would limit the exploitation of resources by victims (and of victims by enemies) in patches of high productivity, which would mitigate the impact of environmental variation through reinforced density-dependent mediation of exploitation by higher trophic levels [34,35]. Although not described in detail here, employing a type II functional response did not qualitatively affect the equilibrium results presented below (see electronic supplementary material, appendix S1), although it may affect the transient community dynamics.

(a). Multiple genotypes

We extend this model to the general case where both enemy and victim coevolve. Gene-for-gene models of antagonistic coevolution generally rely on the assumption that host resistance and pathogen infectivity also have associated costs that increase with the level of investment in defence or attack [14]. In contrast, in matching allele models, there is no differential cost in the expression of alternative alleles [36]. We employ a modified gene-for-gene interaction that allows multiple genotypes with the same number of resistance loci (and thus equal costs) to co-occur. Recent empirical work showed that a range of natural systems are best described by this type of model [37–39]. We assume a multi-genic (n genes) bi-allelic model, in which each organism carries either a 0 (cost-free) or 1 (costly infectivity for the enemy; costly resistance for the victim) allele at each locus. Moreover, we assume that competition between genotypes is indirect (i.e. exploitation competition). Genotypes are denoted by i for the victim and j for the enemy. The total number of victim and enemy genotypes is v and e, respectively.

The equations governing changes in resource density and enemy and victim genotypic densities are

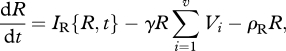2.1a

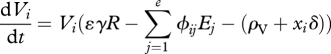2.1b

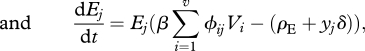2.1c

where mortalities increase owing to costs associated with resistance and infectivity alleles for the victim and enemy, respectively. Specifically, the constant δ represents the baseline cost of adaptation, which is weighted by parameters x for the victims and y for the enemies to account for carrying costly loci, such as for the enemy j

2.2

Here δ is the cost, m_j is the number of genes with costly alleles and n is the total number of genes involved in the interaction (the same formula is applied to x_iδ). The parameter k controls the strength of the trade-off, accelerating for k > 1, saturating for k < 1 and linear for k = 1 [40]. Frank [41] showed that polymorphism in enemy and victim arises if k < 1. Since we are interested in the potential for polymorphism, we assume a saturating cost with k = 0.25. Pilot numerical studies showed that employing different values of k less than unity did not qualitatively change the results.

The exploitation rate of victim i by enemy j in an interaction of n genes, denoted by ϕ_ij, is given by

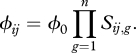2.3

S_ij,g is the interaction score of enemy j and victim i for gene g, which takes on values of (i) 1 if the enemy carries a 1 allele and the victim carries a 0, (ii) 0 if the enemy carries 0 and the victim a 1, and (iii) w for the other two combinations [41]. Equation (2.3) is a modification of classical gene-for-gene interactions [36] in which partial resistance can occur. Finally, we assume no sexual structure in our populations, as it would probably obscure the results obtained through numerical experiments by changing costs associated with specialization [42] and result in recombination, which may favour generality [21,43].

We use this model to investigate how specialization evolves in interaction traits between enemies and victims assuming gene-for-gene associations, such as is hypothesized for various enemy–victim interactions, most notably including hosts and parasites, and plants and rusts or herbivores [39,44,45]. Although specialization in predator–prey associations is generally considered to involve more complex, quantitative traits (e.g. behavioural, morphological or physiological adaptations [4,46]), it can be argued that gene-for-gene interactions are discrete versions of multi-gene quantitative trait models [15], and thus of relevance across a broad range of systems.

(b). Measures

We analyse the structure of genotypic communities of enemies and their victims by employing approaches from food web and network analysis. There are obviously limitations in analogies between the driving forces behind the structure of genotypic and species communities [47–49], and our intention is rather to employ the rich diagnostic tools that the latter have to offer. A full description of the measures used and how they are calculated is given in the electronic supplementary material.

Enemy specificity is measured for each genotype using the paired differences index [27], which builds on relative differences in exploitation performance of several victim genotypes. We use Lloyd's interspecies patchiness measure [50] to tell whether enemies are specialized on similar victim genotypes. To quantify the range (i.e. proportion) of victims exploited by an enemy, or the range of enemies able to exploit a given victim genotype, we employ the measures of generality and vulnerability [51]. The need to jointly consider generality and vulnerability stems from the fact that the potential to exploit and the potential to resist exploitation can be differently distributed in a trophic network. All of the above measures are reported as weighted averages, whereby the value of each individual genotype is weighted by its frequency in the population.

Finally, other important structural features of the enemy–victim genotypic network are reported. These measures include connectance (the proportion of potential links that are realized), richness (the number of enemy and victim genotypes) and the evenness of genotypic densities for both populations.

(c). Numerical simulation methods

For each set of conditions investigated, at least 50 replicate simulations were initiated with 1 unit of resource, one victim individual with genotype 000 and one enemy individual with genotype 000. The system was simulated for 50 epochs, each consisting of 40 generations (preliminary simulations showed that a steady state was always reached in this time span). For each epoch, the number of productive generations (T_R in electronic supplementary material, figure S1b) was fixed, and the remaining generations were non-productive.

For each simulation, we investigated the impact of changing T_R and A under different combinations of basal resource input (S) and resource degradation rate (ρ_R). We present results for conditions of weak external basal input (S = 0.01) and a resource degradation rate of 0.1 (other values of basal input and degradation rate did not qualitatively affect the results, but their impact was nonetheless quantified; see electronic supplementary material, appendix S2). All simulations were done with n = 3 genes in both enemy and victim.

3. Results

(a). The evolution of specialization, generality, vulnerability and community structure

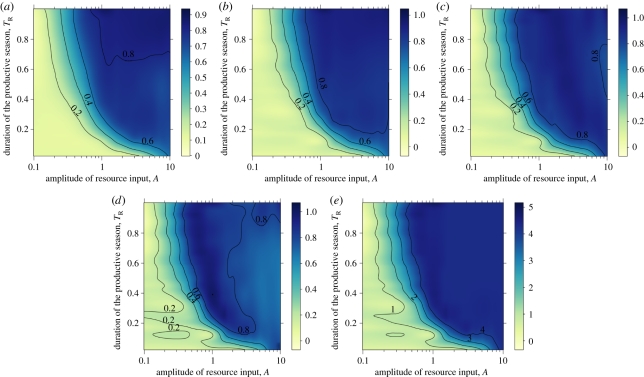
Enemy specialization increases when resources do not limit the growth of the victim population—that is, when T_R ≫ T_L (i.e. seasons with resource input are much longer than seasons without)—and for high levels of A (more resource inflow during the productive season; figure 1a). This is despite the enemy exploiting a wide victim range (figure 1b). In contrast, the proportion of enemies exploiting a given victim genotype (victim range) is maximal for longer productive seasons and for intermediate resource input (figure 1c). Connectance increases when resources are abundant (figure 1d), whereas it decreases when both T_R and A are high. Overall, connectance is maximized when both generality and vulnerability are high (i.e. enemies establish numerous links that victims are not able to prevent). It should be noted that the values of connectance we report are similar to recent experimental data on coevolving antagonistic interactions [27,39].

Figure 1.

Impacts of changing different resource dynamic parameters (see electronic supplementary material, figure S1b) on the structure of the enemy–victim community. (a) Enemy specificity (as measured by the paired differences index). (b) Enemy generality (‘victim range’). (c) Victim vulnerability. (d) Connectance. (e) Niche overlap among enemies. Results are for 10 replicate simulations of 50 values of T_R by 50 values of A. Each point is the mean of the different indicators taken over two epochs (i.e. T_R + T_L) after equilibrium. Surface plots have been smoothed using the loess quadratic fitting method [52].

Figure 1e presents the niche overlap between enemies. Strong niche overlap means that all enemies exploit a similar subset of possible victims, thus also resulting in strong competition [53]. We find that overlap is maximized at intermediate productivities, and only slightly decreases with increased specialization (figure 1a). As intuitively expected, niche overlap is maximized when victims are highly vulnerable and connectance is high. Note that niche overlap accounts for quantitative differences in levels of exploitation, and as such specialist enemies coexist on the same subset of victim genotypes at high productivity (i.e. when both T_R and A are high).

(b). Richness and evenness

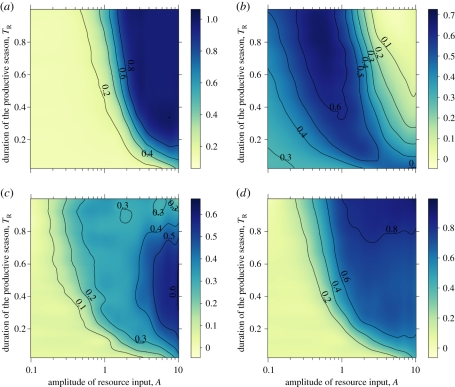
Both enemy and victim richness are maximized for high resource input (figure 2a,c). The evenness of victim genotypes does not produce a clear pattern, with maximal values at high A when T_R is short, intermediate A for intermediate T_R, and low A for long T_R (figure 2b). The lack of any strong pattern is similar for victim vulnerability (figure 1c). In contrast to victims, enemy evenness increases with both A and T_R, and is maximized in the most resource-rich environments (figure 2d). A recent theoretical study on competitive communities shows that the complex patterns of victim evenness that we report can arise owing to interactions between the frequency and intensity of environmental perturbations [54].

Figure 2.

(a) Victim richness (number of genotypes) and (b) victim evenness. (c) Enemy richness and (d) enemy evenness. See figure 1 for parameters and additional information.

(c). Patterns of investment in costly traits and epidemiological consequences

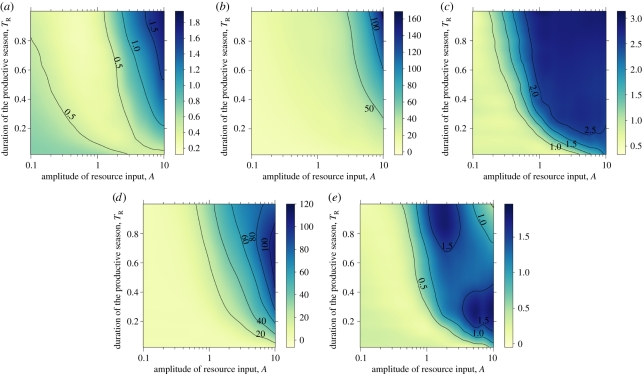
In agreement with previous studies [23], enemies and victims evolve towards higher investments in costly interactive traits in resource-rich environments (figure 3a,c). However, enemies evolve costly attack alleles at lower resource input values than those for which victims evolve costly resistance alleles (figure 3a,c). For a given subset of parameter space (intermediate availability of resources), the community is composed of enemies attacking undefended victims (numerical studies showed that varying costs of attack and defence did not qualitatively modify this result). Under these conditions, not surprisingly, victim vulnerability (figure 1c) is maximized, and community connectance starts to increase (figure 1d). In the same region of parameter space, victim evenness is high, suggesting that enemies (as opposed to competition between victim genotypes) play a strong regulatory role in victim population dynamics.

Figure 3.

(a) Victim investment in defence and (b) victim population size. (c) Enemy investment, (d) enemy population size and (e) enemy prevalence. See figure 1 for parameters and additional information.

In selecting for higher levels of victim defence, high resource input results in larger victim population sizes (figure 3b). The enemy population generally increases with resource input (figure 3d), but, in contrast to the victim, its population size is maximal for intermediate values of T_R. This is explained by the pattern of victim defence observed at high resource input: fully defended victims dominate the victim community, which reduces the abundance of all but the enemies with the highest investment in attack. The maximum population size of enemies can only be attained when they invest more in attack than their victims do in defence (figure 3a,c). Note that the pattern of investment also explains the pattern of network connectance (figure 1d), since increases in victim defence will decrease the number of established links between enemy and victim genotypes. Thus, enemy prevalence (measured here as the number of enemies per victim; figure 3e) is highest for intermediate frequencies of resource input, and follows the same pattern as victim evenness and vulnerability.

(d). Model sensitivity

We investigated the sensitivity of model behaviour to the assumption of linearity in the functional response (see electronic supplementary material, appendix S1). The employment of a saturating (type II) functional response did not qualitatively change the pattern of the metrics presented here. However, at intermediate productivities (i.e. intermediate frequency of amplitude of resource input), a saturating functional response decreased specificity and increased victim evenness relative to a linear (type I) functional response.

We also examined how variation in parameters regulating resource dynamics affected model behaviour (see electronic supplementary material, appendix 2). As is intuitive, the persistent supply of resources (S) supersedes the effects of other resource parameters. As S becomes very low, T_R and A emerge as the most influential parameters. Thus, as expected, temporal variation in resource dynamics increasingly affects community structure as resource supply decreases.

Finally, we considered how stochastic variation in both the period (time between perturbations) and amplitude of resource influx affects model predictions of enemy specificity (see electronic supplementary material, appendix 3). Stochasticity was simulated in T_R and in A by assuming a normal distribution around the means used in figure 1. We found that stochasticity slightly increased the range of parameters for which the specialization was high in the enemy population, but this result is insensitive to the variance of the distribution. The impact of stochasticity is stronger at low T_R. As expected (see electronic supplementary material, appendix 2), the variance of T_R had a greater impact on specificity than that of A. Note that adding stochasticity to the model had a stabilizing effect on the network structure (see figures in electronic supplementary material, appendix S3). In sum, although stochasticity affected quantitative predictions, it did not alter our basic conclusions concerning the impact of resource dynamics on trophic network structure.

4. Discussion

We developed a population dynamical model of enemy–victim coevolution, and used it to investigate how variation in environmental productivity for the victim affects specialization and genotypic community structure. Because we assumed asexual reproduction and rare mutation events, genotypic community structure in our model is conceptually similar to species community structure. As we argue below, previous theoretical studies on the role of fluctuating environments in determining community structure make contrasting predictions regarding the likelihood of emergence and maintenance of biotic complexity. Competitive coexistence can occur if there is sufficient temporal variability in the system [55], but this is contingent on the expression of costs affecting growth [56]. For non-coevolving two-level trophic systems in which some organisms act as resources for the other, Abrams [9] showed that coexistence requires sustained asynchrony in resource abundance (in our case, victims) and saturating functional responses in one of the consumer species (here, the enemy). In addition, increasing host population growth resulted in less coexistence among enemies. However, the impact of realistic patterns of resource dynamics (e.g. dynamic changes in environmental quality [9]) has not been addressed in previous studies. Our results demonstrate that coevolution results in communities that differ in structure depending on resource dynamics. Specifically, all else being equal, increasing productivity in the form of the amplitude and/or frequency of resource input leads to increased specialization, and promotes the assembly of complex enemy–victim communities. Niche overlap (the degree to which enemies exploit the same subset of victims) is maximized at intermediate productivities, but stays high even when specialization among enemies is greatest.

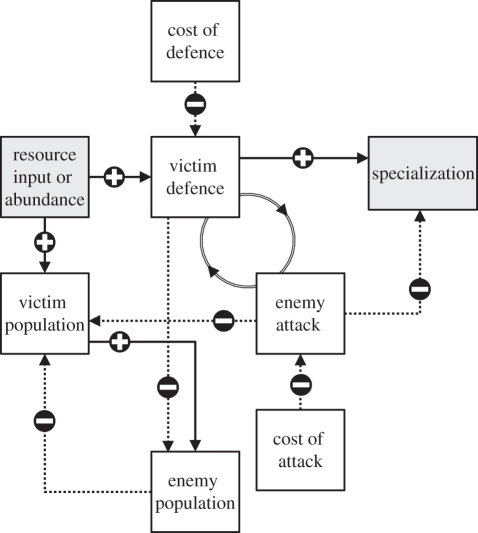
The outcome of coevolutionary dynamics is by itself difficult to predict when multiple loci are involved, owing to complex feedbacks between different processes [18,36] (figure 4). For example, changes in the structure of victim defence can modify selective pressures regulating enemy evolution (and vice versa). In addition, environmental productivity or stability will also indirectly affect enemies. Hochberg & van Baalen [23] and Lopez-Pascua et al. [57] reported that enemy generality was decreased when resources needed by its victim to grow were not readily available (a result also reported here; figure 1b). Environmental features are expected to change through time (and space, although not investigated here), and predicting patterns of community structure in coevolving systems in nature will therefore require the incorporation of such complexity in numerical experiments. It is especially important to understand the epidemiological consequences of specialization under realistic scenarios of resource dynamics, since it has been shown that the degree of specificity among enemy species can have pervasive effects on victim dynamics and diversity [58], and select for enemies with lower attack rates [59].

Figure 4.

Synthetized view of the impact of resource changes on the studied variables. Solid and dashed arrows indicate positive and negative relationships, respectively. Double arrows linking ‘enemy attack’ and ‘victim defence’ represent the coevolutionary process.

We found that enemies evolve to lower levels of specificity when resources are scarce, owing to either low or infrequent resource input (figure 1a). This pattern is in agreement with previous empirical results [57], where decreasing resource availability was shown to reduce pathogen exploitation of hosts. This resulted in enemies exploiting all of their victims at similar levels of performance. Recent theoretical and empirical studies showed that generalists were better able to persist in changing environments at ecological [27,60] as well as geological [61] timescales. Both of these findings and the results we report are congruent with the simple prediction, made by Ward [62], that species tend to specialize preferentially on stable resources (i.e. those that are less likely to go extinct). This proposition has received empirical support from studies of host–pathogen systems [63]. Victim populations evolving in resource-poor conditions support fewer individuals, increasing the risk of extinction of less-abundant genotypes (and therefore decreasing the perceived stability of victims for the enemies) and selecting for low specificity (figure 1a,b). The rapid turnover of victim genotypes translates to a highly heterogeneous environment for enemies; in these situations, it is expected that less-specialized genotypes will dominate the community [64].

One salient result of our simulations is that vulnerability and evenness followed a similar pattern: maximal evenness was associated with higher vulnerability (figures 1c and 2a). The hump-shaped pattern of victim evenness along a gradient of resource availability in the presence of enemies has been previously reported [65,66], although whether and how this result originates from coevolutionary processes is unclear. Here, we show the hump-shaped pattern emerges as a result of the shift between victim investment in defence and enemy investment in attack, the latter occurring for lower resource availability (figure 3a,b). This results in a situation where enemies overcome victim defences (high vulnerability) and therefore have a large impact on their population sizes (high evenness). Maximizing diversity in the form of higher evenness (all genotypes have equal population sizes) can lead to increased ecosystem functioning in terms of biomass production or ability to recover from perturbations, especially in fluctuating or otherwise stressful environments [67].

Our results have important implications for understanding the fate of coevolving communities across temporally heterogeneous environments. Generally, we predict that coevolution will lead to networks with higher connectance and specialization in productive environments (figure 1d). This is known to result in overall higher system stability, and is thus linked to ecosystem health and functioning [68]. Such systems are more likely to be robust to enemy extinction following the loss of specific victim genotypes [69,70], and are thought to be more productive overall [71,72].

5. Concluding remarks and future directions

Using a theoretical resource–victim–enemy model, akin to a tri-trophic resource–plant–herbivore system, we studied how different patterns of resource dynamics could impact the structure of an exploitative community. Our results show that specialized enemies are selected for in high-quality environments, while poor-quality environments select for unspecialized enemies exploiting fewer victim genotypes. Our results are important from an epidemiological standpoint in showing that environmental variation, through its impact on interaction-related traits, can alter population densities, thus affecting transmission rates and coevolutionary outcomes. Classical [73] and more recent [74] empirical results clearly demonstrate that such host range expansion is contingent on ecological and molecular changes, and can lead to rapid pathogen spread within a host population. Thus, understanding factors that influence the evolution and maintenance of enemy–victim specialization is central to assessing the impacts of natural enemies on host fitness [58], as well as the spread of infectious disease [75,76].