Decomposing variation in population growth into contributions from environment and phenotypes in an age-structured population

Abstract

Evaluating the relative importance of ecological drivers responsible for natural population fluctuations in size is challenging. Longitudinal studies where most individuals are monitored from birth to death and where environmental conditions are known provide a valuable resource to characterize complex ecological interactions. We used a recently developed approach to decompose the observed fluctuation in population growth of the red deer population on the Isle of Rum into contributions from climate, density and their interaction and to quantify their relative importance. We also quantified the contribution of individual covariates, including phenotypic and life-history traits, to population growth. Fluctuations in composition in age and sex classes ((st)age structure) of the population contributed substantially to the population dynamics. Density, climate, birth weight and reproductive status contributed less and approximately equally to the population growth. Our results support the contention that fluctuations in the population's (st)age structure have important consequences for population dynamics and underline the importance of including information on population composition to understand the effect of human-driven changes on population performance of long-lived species.

1. Introduction

Population size varies over time as a consequence of both intrinsic and extrinsic factors, as well as their interactions [1]. Understanding the relative contribution of these factors to changes in population abundance and identifying the ecological processes associated with them are of fundamental importance for conservation, wildlife management [2] and evolutionary demography [3,4]. Large long-term datasets have been invaluable in obtaining estimates of the fundamental biological processes of survival and recruitment across life-history stages in several species and in identifying the factors that generate temporal variance in these rates [5,6]. Work has proceeded on two fronts. First, studies designed to identify key demographic rates (e.g. adult survival) associated with population growth have identified common patterns in dynamics across a range of species. In birds, for example, changes in fertility were predicted to have the greatest impact on population growth rate in populations characterized by high reproductive rates, whereas changes in adult survival are expected to have the greatest impact on the growth of populations with low reproductive rates [7]. A second front has studied the relative contributions of processes such as density dependence, environmental variation and fluctuations in the demographic structure of the population [8–10]. There has been insufficient work using the second approach to draw any general conclusions for (st)age-structured populations, although it is clear that all processes can interact to contribute to the observed dynamics. Neither approach tends to consider the consequences of different distributions of phenotypic traits for populations (but see [4] and [9]).

Much work has examined how individual characteristics such as age and sex influence population growth [11,12], but we know less about the contribution of other individual attributes even though traits like body size frequently influence survival and reproduction probabilities, especially in variable environments. For populations living in a fluctuating environment, the relative importance of survival and recruitment for population growth can vary among demographic classes [13–15]. Animals of different age, sex and size often adopt different reproductive strategies [16] and the effect of environmental conditions, such as weather and density, on performance can vary between demographic classes [17]. Consequently, environmental variation can affect population composition in sex, age (hereafter named (st)age structure), phenotypic trait (including morphology or behaviour) distributions and population growth [13,17]. New analytical techniques allow the decomposition of observed fluctuation in population growth into contributions from processes such as density dependence, environmental stochasticity and age structure [18,19]. Such analyses allow one to evaluate the relative importance of density dependence, extrinsic climate fluctuation, demographic heterogeneities and phenotypic distributions for changes in population size [13,17].

In this article, we use a method developed by Coulson et al. [19] to analyse the individual-based data of the red deer population (Cervus elaphus) inhabiting the Isle of Rum, Scotland. The objective is to evaluate the relative importance of climate, density, phenotype (birth weight), life-history (reproductive status) and their interactions in shaping the population dynamics. To do so, we investigate the combined effects of density dependence, phenotype and environmental variation across all fitness components and explore their relative contributions to population growth. Secondly, we quantify the relative contribution of these factors to reproductive performance and survival for animals in different age and sex classes. Finally, we compare our results in red deer to those previously measured in a population of Soay sheep (Ovis aries), also inhabiting a Scottish island, to identify common patterns between two species of large ungulates [19].

(a). Demographical decomposition

Factors influencing age-specific survival and recruitment rates are routinely identified using regression methods [20,21]. Coulson et al. [19] demonstrated how statistical models can be combined across demographic classes to construct a statistical description of the population growth rate in year t. First, for each age/sex class, a statistical model (general linear models, generalized mixed effects models or other) is used to produce a predicted survival or reproductive outcome for each individual at each time, e.g. for survival of individual j in stage i at time t. Then, predictions for each individual are averaged to construct a statistical description of the population growth rate in year t. Coulson et al. [19] also showed how the stepwise removal of terms from these models, as is standard to assess the statistical significance of a term [22], can be used to estimate the contribution of the term to population dynamics. By applying this approach to the long-term Soay sheep dataset, they demonstrated that density dependence contributed approximately twice as much as environmental variation and fluctuations in age and sex structure in explaining variation in population dynamics [19]. However, in their analysis, they did not incorporate individual attributes other than age and sex. In this paper, we use this approach to analyse the long-term time series of a population of red deer, where we estimate the overall contribution of density, extrinsic climate fluctuation (using the North Atlantic Oscillation [23]) and (st)age-structure. In addition, we extend the approach to include individual attributes (birth weight, age and reproductive status) that are associated with fitness in this species [24–26]. To do so, we extend the method previously described by Coulson et al. [19]. We first use functions identified from regression models of survival and fecundity (respectively, g_si and g_ri) to predict the survival and reproductive rate of individual j in age class i at time t:

and

where N_t is the population size in year t, E_t is the environment in year t, P_i is the (fixed) phenotype of individual j, R_{j,t − 1} is the recruitment rate of individual j in year t − 1 and a_j,t represents the age class of individual j in year t. We then take the averages of 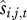and 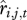across all individuals in each age class to generate a mean survival and recruitment rate for each age class,

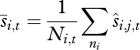and

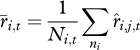where N_i,t is the total number of individuals in age class i at time t. We then combine these mean survival and recruitment rates across age classes to estimate the population growth rate at time t, λ_t

In the equations above, we assume that the regression functions are linear. However, individual survival is binomially distributed and reproduction may not be normally distributed. If generalized linear models (GLMs) are used instead of general linear models, it is necessary to estimate 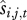and 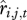on the scale of the link function, take their average and then back transform these averages to the response scale so that the mean survival and mean recruitment are in units of the number of individuals.

The functions 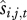and 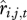can be identified using standard regression approaches where one model is individually fitted for each rate (survival and recruitment) and for each sex and age class. All demographic rates can be affected by a range of covariates, including climate, density or phenotypic traits (such as weight or life-history traits). Each statistical model can be fitted including all relevant covariates and their interactions and then non-significant terms can be dropped with a stepwise approach to obtain minimal models containing only significant terms. Alternatively, model selection could be done using Akaike Information Criteria [27]. The associations between survival and recruitment and a range of different covariates x will therefore be described for each demographic class and each class need not be influenced by the same covariates. The retrospective performance of this model can then be assessed by comparing the observed and predicted performances when parameterized with the observed data. Finally, the contribution of each variable (environmental or phenotypic) can then be assessed by comparing model predictions including and excluding each covariate. This comparison allowed us to evaluate how each covariate contributed to the correlation between the full model and observations. The contribution of (st)age-structure fluctuations can be calculated by comparing predictions generated by a model where N_i,t/N_t remains constant with time to those from a model where it varies from year to year. See Coulson et al. [19] for a complete demonstration of the demographic decomposition approach.

2. Methods

(a). Study area, population and data

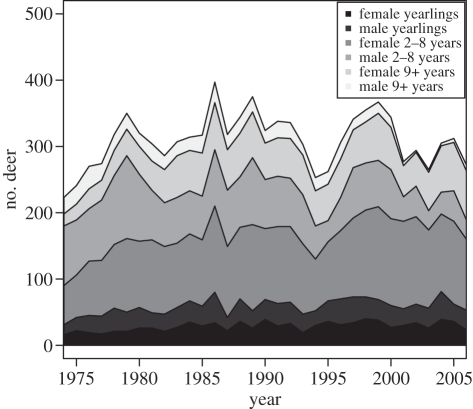
The red deer population in the North Block of the Isle of Rum, Scotland (57°01′ N, 6°17′ W), has been the subject of detailed, long-term monitoring since 1971 [28]. After the population was released from culling (1972), its density increased, reaching a maximum of 397 deer in the study area, and is now oscillating around carrying capacity (figure 1). Most calves are captured and marked a few hours after birth, and more than 95% of individuals present in the study area each year are individually recognizable with artificial marks or natural phenotypic characteristics [28]. For those individuals, complete life-history is known. In this article, we used data from 1974 (when formal censuses of the population started [28]) to 2005. In this study, the deer year runs from 15 May in year t to 14 May in year t + 1 just prior to the calving season (as in Catchpole et al. [29] and Coulson et al. [21]). In this article, we use the following definitions and variables.

Figure 1.

Population count (total number of deer) and structure of the study area population of red deer between 1974 and 2006.

(i). Life-history variables

Birth weight. Calves are typically born in May and June and are caught few hours after birth. At capture, each calf is measured and birth weight was estimated as follows: birth weight = capture weight (kg) − 0.01539 × age at capture (h) (see [28] for further details). Birth weight varied between 1.02 and 11.19 kg, with an average birth weight of 6.7 kg).

Age classes. In this population, survival is best explained by a combination of age classes rather than a fully age-dependent model [26,29]. Our analyses therefore consider three age classes for each sex: yearlings, 2–8 years (prime-age where survival is age independent) and 9 years and older (senescent individuals when survival declines with increasing age: see [29]). Within each of these (st)age classes, we also tested whether age, fitted as a continuous variable, was significant to ensure that we controlled for any other potential age effects. Calf survival to 1 year of age was modelled as the recruitment component of female fitness (see below).

Reproductive status. Hind reproductive status was a five-level factor:

• — First time breeder: primiparous hinds.

• — True yield: a hind that did not breed in the current year, but had bred previously.

• — Summer yield: a hind whose calf died between birth and 1 October.

• — Winter yield: a hind whose calf died between 1 October and 1 May.

• — Milk hind: a hind that successfully raised a calf to 1 year of age.

(ii). Demographic rates

Recruitment. For simplicity, we investigated how environment and phenotype affect the probability that a hind of breeding age in year t would raise a calf to the following May (in year t + 1). Recruitment, as defined in our study, therefore represents the product of the age-specific birth rate and calf survival from birth to 1 year of age. As age at first reproduction in deer on Rum is 3 years, we modelled recruitment for females using two age classes: 3–8 years and 9 and older. To control for age effect within these age groups, we also fitted age of the individual in each model as a continuous variable (see below). We used the same categories to model the effect of reproductive status in year t − 1 on survival and recruitment in year t. In the following text, we refer to the linear effect of age within class as ‘age effect’ and to the variation in age and sex class as ‘(st)age class effect’ to avoid confusion between our two ways of accounting for age.

Survival and emigration. Determined through repeated sightings of deer during census and recovery of dead animals. The re-sighting rate of individuals for this population was very high, ranging between 0.884 and 1—with most years between 0.955 and 1 [26,29], and individuals that have permanently emigrated are generally known. For those individuals, we assigned an emigration event in the last year they were seen in the January to May censuses.

(iii). Environmental variables

Population size. Population size each year (ranging between 244 and 397 deer) is based on sightings of individual deer during censuses. Up to five censuses are conducted each month by walking a standard route and recording all animals seen. Population size is defined as the number of deer age 1 year and older seen in at least 10% of censuses between January and May [21,29]. This definition of population size excludes transient individuals and non-resident stags that enter the study area only during the rut [21]. As the study area is of fixed size, population size can be viewed as a measure of population density. Population composition (proportion of individuals in each age and sex class) in each year was also reconstructed based on the January to May censuses (figure 1).

Northern Atlantic Oscillation. We used a large-scale index of weather, the North Atlantic Oscillation (NAO) to model the effect of climate on deer population dynamics [30]. NAO indices from December to March in each year were obtained from the Climate Analysis Section, NCAR, Boulder, USA [30]. The NAO index for year N_t refers to an average NAO for December year N_t−1 and January, February, and March year N_t. In the period studied, NAO values varied between −3.78 and 5.08. In the west coast of Scotland, high NAO values correspond to stormy and wet winters whereas low NAO values correspond to colder and dryer winters [17].

(b). Statistical analysis

(i). Demographical decomposition

Demographic rates for each age and sex class were described using GLMs. We fitted six models for survival (one for yearling, prime-age and senescent classes of each sex) and two models for recruitment (one for prime age and one for senescent hinds). Survival was modelled with a binomial error structure. The response was defined as a vector of dead (0) or surviving deer (1) in each year. We used a similar approach for modelling deer recruitment. The response was also modelled with a binomial error structure (calf surviving to the following year or not), as no female has been observed to twin in this population. For each analysis, we first fitted a full model, including density, NAO, life-history traits (calf birth weight, reproductive status in years t and t − 1 for adult females) and their interactions. These full models were then simplified using deletion tests in a backward procedure retaining only terms significant at the α < 0.05 level [22].

(ii). Predictions

Using the statistical models presented in electronic supplementary material, tables S1 (survival) and S2 (recruitment), we evaluated the contribution of each covariate (density, NAO, age and sex structure and birth weight) to the observed dynamics by deletion tests. To do this, we removed one covariate at a time from all statistical models and recalculated the ‘overall’ survival, recruitment and population growth predictions as described previously. The difference between adjusted r² values from models including and excluding a specific covariate (such as density) was interpreted as an estimate of the relative contribution of this covariate to our ability to predict the observed dynamics. The contribution of (st)age-structure fluctuations was calculated by comparing predictions between a model where N_i,t/N_t remains constant with time (we used the average proportion of individuals in each (st)age class during the study period) with predictions from a model where it varies from year to year (figure 1). To assess the goodness of fit of our models, we visually examined the associations between the yearly observed population growth, survival and recruitment and the predicted population growth, survival and recruitment rates. We also explored the association between the predicted and observed values using adjusted r² (see §3). All analyses were conducted in R, v. 2.12.0 (R Development Core Team, http://www.R-project.org).

3. Results

(a). Statistical models for each age and sex class

Factors influencing survival varied with age and sex. The effects of NAO and density on survival were most important for young and senescent red deer (electronic supplementary material, table S1). Survival of prime-age red deer (2–8 years old) of both sexes was insensitive to changes in environmental conditions. For prime-age females, only reproductive status affected short-term survival. In prime-age males, only age, fitted as a continuous variable within this (st)age class, was significant (electronic supplementary material, table S1). Birth weight had a significant effect on survival for both male and female yearlings and its effect was more pronounced in unfavourable conditions: the female yearling survival was more affected by birth weight in high-density years while the effects of birth weight on male yearlings was more pronounced during harsh winters (electronic supplementary material, table S1). Density, NAO, calf birth weight and reproductive status in the previous year affected recruitment in both prime-aged and senescent females (electronic supplementary material, table S2). For prime-aged females, there were complex interactions between NAO, density, reproductive status and calf birth weight. More specifically, in years where conditions are poor (harsh weather or high density), reproductive status in the previous year and calf weight had a greater effect on the probability of a calf reaching the following May than in years where conditions are favourable (electronic supplementary material, table S2).

(b). Relative importance of environment, demography and phenotype

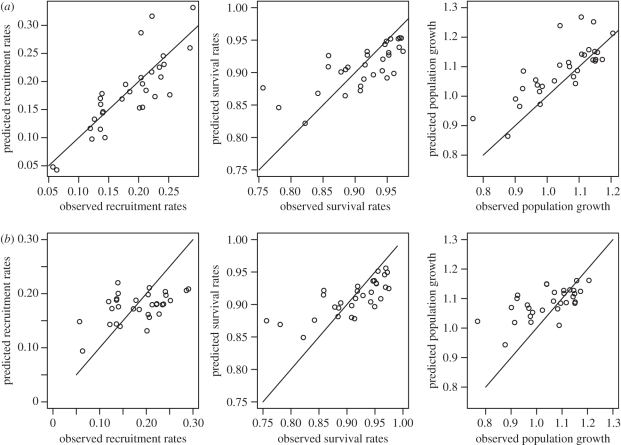
Predicted values from statistical models of survival and recruitment for each demographic class were then combined (as explained previously) to obtain predicted values of population growth at each time step. Predicted values for overall survival, recruitment and population growth were checked graphically for goodness of fit by plotting the expected values predicted from the model with the ‘observed’ values calculated from the data (figure 2). We consider that our models predicted the deer population dynamics adequately as we were able to predict the ‘ups’ and ‘downs’ in the dynamics, although our models failed at predicting the magnitude of these fluctuations (electronic supplementary material, figure S1, table 1). To determine the relative importance of each parameter in predicting survival, recruitment and population growth, we compared the correlation of predicted values versus observed values for a model excluding that specific parameter and any interactions to the same correlation based on a model including the parameter (table 1). Although life-history traits significantly affect both recruitment and survival, they had little effect on the overall population dynamics (table 1). (St)age structure appeared to be the most important variable to predict recruitment and population growth (table 1 and figure 2). For survival, only the model excluding female reproductive status gave poorer predictions (table 1).

Figure 2.

Associations between predicted and observed recruitment rates, survival rates and population growth for models using annual fluctuation in (st)age structure (a) and models for which the (st)age structure was fixed at the average observed during the study (b). Adjusted r² for models with and without yearly variation in (st)age structure are presented in table 1. The solid lines represent the theoretical association between predicted and observed rates if the adjusted r² were 1.

Table 1.

Pearson correlations (r) and proportion of variance (adjusted r²) explained between observed and predicted values from individual based models for survival (r_surv), recruitment (r_rec) and population growth (r_w). The full demographic models used are presented in electronic supplementary material, tables S1 (survival) and S2 (recruitment).

models	rsurv	rrec	rw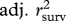
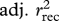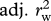full model	0.72	0.83	0.78	0.52	0.69	0.61
full model excluding (st)age structure	0.74	0.48	0.62	0.55	0.23	0.38
full model excluding density	0.68	0.82	0.77	0.46	0.67	0.59
full model excluding NAO	0.66	0.83	0.76	0.43	0.69	0.58
full model excluding birth weight	0.72	0.84	0.78	0.52	0.70	0.61
full model excluding reproductive status	0.60	0.82	0.75	0.36	0.68	0.57

4. Discussion

In this article, we have shown how to estimate the contribution of individual variation in phenotype and life history to population growth while controlling for environmental variation using a demographic approach. As ecological relationships involving climate (or other environmental changes) are typically scale dependent and multi-factored [24,25,31], a detailed knowledge of the system and species under investigation is required to decompose complex dynamics [6,32]. Here, we show that, consistent with previous results on this population of red deer, the effect of climate (as measured using the NAO index) and density on survival is age and sex dependent, with juvenile and senescent (st)age classes showing a greater reduction in survival in poor years [24,25,33]. Similarly, calf recruitment by senescent hinds was lower in years of high density and harsh winters, but the interactions between density and climate were only apparent for prime-age hinds. Our results support the common finding that climate effects are exacerbated when resources are limited [5,34] and that (st)age and sex classes are affected by the environment in very different ways [17]. For example, population dynamics of large herbivores can be strongly affected by a combination of stochastic environmental variation and density dependence: in Soay sheep on Hirta (St Kilda, Scotland), identical winter weather can result in very different dynamics, depending on the population density and sex and/or age structure [17,19,35].

Coulson et al. [21] have argued that, because the red deer population fluctuates around carrying capacity, and has done so for most of the study period (after 1980), the detection of density dependence is now difficult. Our results support this view as we have found significant, but weak, density dependence. Our decomposition of the relative contributions of density dependence, environmental variation and demographic heterogeneity reveals that, for this red deer population, (st)age structure contributes almost 1.5 times more to the population dynamics we can explain in a simple model than density, NAO, birth weight and reproductive status. This effect occurs principally because (st)age structure is a strong predictor of recruitment in this population. Indeed, when excluding fluctuations in the (st)age structure to predict recruitment, the model performs at least twice as poorly as a model accounting for (st)age structure. This effect was not observed when considering only the survival components, suggesting that most of the (st)age effect is driven by the variation in age-specific reproductive performance in female deer. Indeed, when there are fewer prime-age hinds, the population has a lower reproductive rate. NAO and density were important to survival, reducing the variance explained in the observed survival by (respectively) 8.1 and 5.5 per cent. The exclusion of these two terms (NAO and density), however, only had a limited effect on the power to predict the observed population dynamics. This result, however, does not mean that the effect of environment is trivial. Indeed, in this deer population, variation in environment (such as climate and density) generates fluctuations in sex and age structure. Thus, observed fluctuations in (st)age structure account indirectly for some effect of the environment. Finally, similar to a previous study on this population, we found evidence for a cost of reproduction in female hinds [26,29,36]. This cost was more evident for the senescent (st)age class. This factor was important in explaining female survival and its inclusion increased the proportion of variation explained in adult female survival by 14.7 per cent.

Our results on the red deer are in sharp contrast with a recent study on Soay sheep [19]. When applying the same approach to decompose the observed variation in population growth in Soay sheep, Coulson et al. [19] reported that density dependence contributed approximately twice as much to population growth than environmental variation and fluctuations in the age-structure of the population, whereas in the red deer population fluctuation in (st)age structure appears to be very important. Why do we find such contrasting patterns for species with relatively similar life-histories? Are (st)age structure fluctuations likely to be stronger in more long-lived species? We suggest that these contrasting patterns arise partly because of the difference in fecundity and maturation and thus, demography between these two populations [37,38]. In red deer, a large proportion of the population is composed of females 2 years and older (45.4%), while the proportion of calves and yearlings is around 20 per cent. In the Soay sheep, the population is composed of 35 per cent (and up to 40%) juveniles on average. In ungulates, juvenile survival is typically more sensitive to degradation of environmental conditions while adult survival is high and shows low variability [5], which might explain why density and climate drivers appear stronger in the sheep. In addition, on average, 13.5 per cent of Soay sheep females can produce twins [39] while red deer hinds produce only one calf a year and therefore the reproductive potential of sheep in a given year is higher. A strong effect of age structure on population dynamics was also reported for three populations of alpine ungulates (two populations of bighorn sheep, Ovis canadensis, and one population of mountain goats, Oreamnos americanus) inhabiting the Canadian Rockies [40]. Festa-Bianchet et al. [40] showed that as density increases, recruitment decreases and the age structure was skewed towards older females, giving an impression of density dependence in adult female survival when age effects were not taken in account.

Variation in senescence of survival and recruitment may also explain the contrasting results in the importance of the (st)age effects between the sheep and the deer. Deer are longer lived than the sheep and the senescence period in the deer is also longer [41]. In order to generalize whether (st)age effects are likely to be stronger in long-lived species, it would be interesting to see how the relative importance of age, climate and density varies for a range of systems with contrasting life-histories and population structures. Finally, we also found that the overall adjusted r² values of the models predicting population dynamics are much smaller in the deer than in the sheep. This is likely to be due to the different dynamics of the populations. The sheep population is characterized by high fluctuation in population size [1,17,42], while the red deer increased in density in the late 1970s, reaching more than 300 deer in the study area (figure 1) with small between year fluctuations [21]. This low variation in population size and growth from one year to the next might limit our ability to predict some vital rates accurately. For example, our model predicting survival was qualitatively able to predict good and bad survival years; however, it was poor at predicting the magnitude of the change in survival. Another explanation for the lower explanatory power of the survival model is that, in our analyses, we are looking at the immediate effects of environment on survival, recruitment and population growth. However, the (st)age-structure effect suggests that environmental variation also generates cohort effects that yield immediate effects on the population growth rate, but could also have delayed effects which were not considered in these analyses. For example, female deer born at high density tend to have faster senescent rates than the ones born at low density [43]. Consequences of these long-term cohort effects of population growth remain to be assessed.

Although birth weight is an important determinant of survival in juvenile red deer [24,25], inter-year variation in calf birth weight explained little variation in the observed population growth. A potential explanation is that birth weight integrates the effect of environment (climate and density [24,25]), thus including both types of variables in our models do not increase the accuracy of our predictions. Additionally, as red deer are only captured once in their lifetime, we could not evaluate the contribution of yearly weight to the dynamics, which might not be negligible. As weight is a very plastic trait which varies both across ontogeny and between years [44], including only birth weight may underestimate the real contribution of weight to population dynamics. For example, in Soay sheep, body size variation explains nearly 20% of variation in population growth in harsh years [4]. In addition, as yearly variation in weight distribution is affected by a variety of factors [9] including selection (e.g. smallest individuals have already died), using only birth weight might have underestimate the importance of this trait in explaining population growth fluctuation.

Studies investigating the relative importance of different ecological processes (e.g. age structure, climate and density) on population dynamics are invaluable to understanding complex ecological interactions. In this article, using detailed longitudinal data on marked animals, we applied a recently developed approach to decompose observed population dynamics into the contributions of processes including density dependence and population structure, and we demonstrated how the approach can be expanded to include individual covariates. Our analyses provide new insights into population biology as they allow us to quantify the relative importance of ecological and evolutionary variables. We found that (st)age structure explained a substantial amount of variation in observed population fluctuations and we suggest that population structure is likely to play a large role on the population dynamics of long-lived species living in a fluctuating environment.