Fishing destabilizes the biomass flow in the marine size spectrum

Abstract

Fishing impacts on marine food webs are predicted by simulations of a size spectrum community model. In this model, predation is determined by predator and prey size and abundance, and drives predator growth and prey mortality. Fishing amplifies temporal oscillations in the biomass flow. Oscillations appear at lower fishing intensity and have wider amplitude when fishing is selective (removes a narrow size range) and/or when large fish are targeted, than when fishing is more balanced (catching a larger size range) or when small fish are targeted. A novel index of size diversity is developed, and is shown to be sensitive to both fishing intensity and selectivity. To avoid unstable food web dynamics with potential harmful consequences for fisheries, limiting both fishing intensity and selectivity might be an appropriate exploitation strategy.

1. Introduction

Fishing magnifies fluctuations in fish stock abundances, because age-truncated populations have more variable dynamics [1]. Selective harvesting of old individuals alters the basic dynamics of exploited populations and favours booms and busts that can ultimately lead to stock collapses. This might also apply to higher organization levels. If selective removals destabilize population dynamics, could they affect the stability of community trophic dynamics? Fishing indeed is selective at the community level: valuable species are preferentially targeted; many of these species are large-sized; within species, large size classes are usually preferred and minimum size limits are often used as management tools [2]. Although most fisheries catch various amounts of unwanted size classes or species [3,4], any fishing gear is selective because catch composition is different from that of the fish population, or community, in the area where the gear is used [5]: many animals escape owing to their size or behaviour. There is a general belief that the more selective the better (e.g. [6,7]), and gear technologists generally see their goal as ‘perfect gear selectivity’ [8].

However, attention has recently been drawn to the idea that selective fishing might alter biodiversity and ecosystem function [9]. Evidence accumulates that, because not all sizes are targeted, fishing affects the size-structure of communities, both directly by removing large fish [10] and indirectly by increasing the abundance of smaller fish released from predation [11–13]. Not only is selective fishing ecologically disruptive, unselective fishing might be economically beneficial. For example, in prawn fisheries, the removal and discarding of small fish that are prawn predators or competitors probably increases prawn production [14]. Within species, it is now well established that size-selective fishing creates an evolutionary selective pressure that drives generally counter-productive genetic changes in populations [15,16]; for example, targeting large individuals induces evolution towards smaller sizes and slower growth [17].

Size is recognized as a key feature in marine ecological processes and, because fishing is size-selective, the size distribution of marine populations and assemblages is often used to monitor fishing impacts at various organization levels [18]. In particular, the ‘size-spectrum theory’ has been developed for marine ecosystems [19–22]. This class of models describes the ecological processes underlying the biomass size spectrum, the distribution of biomass across body size classes, where each individual is defined by size regardless of species. When the energy transfer is governed by size-dependent predation, which determines prey mortality and predator growth, unfished size spectra have two classes of dynamics depending on assumed prey size preferences: either a steady state (also called stable spectrum hereafter), or an oscillatory solution in which waves move over time along the size spectrum from small to large body size [23]. The question is, how does fishing affect these dynamics? The shape of the size spectrum is known to be sensitive to fishing intensity [24,25]. Intuitively, selective fishing might generate gaps that would disturb the biomass flow and potentially favour oscillatory dynamics, creating temporal variations in biomass and catch. Clearly, both fishing intensity and selectivity interact to determine the impact of fishing on size-spectrum dynamics.

Here, we use Benoît & Rochet's [20] model to predict how various fishing intensities and selectivities affect the marine food web. Measures of fishing impacts include indices of both the spectrum shape and temporal variations. We first recall the main assumptions of the Benoît & Rochet [20] model, slightly modified to account for recruitment depending on the reproductive biomass in the ecosystem. We then introduce a series of fishing scenarios, and various measures of fishing effects. We present simulation results and discuss the consequences of our findings for fisheries management at the ecosystem scale.

2. Methods

(a). A size-spectrum model

As in the Benoît & Rochet [20] model, we assume that predation is the force driving growth and mortality and that size determines all processes. Here, size is measured by body-weight w log-transformed to x = log w/w₀ (see all variable and parameter definitions in table 1). The probability φ of a predation event after encounter of two individuals with log-weight x and y only depends on the ratio of their weights q = y − x. Here, we use

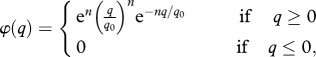a positive, dome-shaped function that peaks at q₀; the larger the n, the sharper the peak. Encounter rate is determined by the volume searched by the predator, an allometric function of predator weight Ae^αy where A and α are constant. Any predation event generates prey mortality and predator growth with constant growth efficiency K. In summary, as in Benoît & Rochet [20] the dynamics of fish density is given by

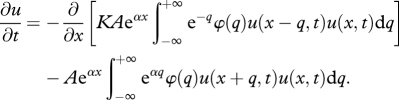2.1

There exists a unique slope λ such that u(x) = u₀e^λx is a stationary solution of equation (2.1), the linear size spectrum. The model is defined for x varying from −∞ to +∞. In simulations x varies on a bounded interval [x_min, x_max] and boundary conditions need to be specified. First, energy is input to the system by a size-structured plankton population with size [x_Pmin, x_min]. Fish eat plankton with the weight ratio-dependent predation probability φ; predation events generate predator growth but no prey mortality. Second, a population of ‘sea monsters’ with size [x_max, x_Mmax] exerts predation on large fish. Sea monsters mimic both intrinsic mortality owing to senescence [28], and extrinsic mortality. The latter is caused by large predators whose growth and mortality differ from those of fish and are therefore not included in the spectrum dynamics, e.g. marine mammals. This mortality prevents biomass accumulation in large sizes and improves the stability and regularity of the size spectrum. Predation events by sea monsters have probability φ again. For the sake of parsimony, both the plankton and sea monster populations are time-invariant, independent of the size spectrum u, and set as a linear size spectrum with slope λ. Third, to calculate the lower boundary condition u(x_min), the recruitment of fish at minimum size x_min is assumed to depend on the number of fish above a constant reproduction size x_mat according to 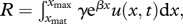where γ and β are parameters of a weight–fecundity relationship. In this model, energy devoted to reproduction is constant, and density-dependence in recruitment is described by the predation exerted by larger fish on recruits.

Table 1.

Definition of the model variables and parameters.

variable/parameter	definition	unit	reference value
w	weight of a fish	g
x	logarithm of w/w0 with w0 = 1g
t	time	year = yr
u(x,t)	number of fish at time t by unit volume, by unit of x	m−3
φ(q)	probability of predation when a predator size x meets a prey size x − q
α	exponent of weight in volume water searched	—	0.82a
A	volume searched by unit weight	m3 yr−1	640a
eq0	modal ratio of predator to prey size	—	100a
n	an inverse measure of the width of the predator–prey size-ratio distribution	—	5a
K	growth efficiency	—	0.2a
xmin	minimum size of fish		−3 ln(10)
xmax	maximum size of fish		6 ln(10)
xmat	log-weight at first reproduction		2.7 ln(10)b (500 g)
γ	number of eggs spawned by unit weight	yr−1	100b
β	exponent of fecundity–weight relationship	—	1.2b
	plankton spectrum	m−3	0.01 exp(−1.05x)a
	sea monster spectrum	m−3	0.01 exp(−1.05x)a
	initial fish spectrum	m−3	0.01 exp(−1.05x)a
μf(x)	fishing mortality rate	yr−1
C0	total catch from unexploited spectrum	g m−3 yr−1	0.01 (table 2)
a	fishing mortality multiplier	yr−1
s	selectivity of fishing: inverse width of the selection curve		1.44
w0	reference weight for size	g	1
xf = log10(wf/w0)	modal size of the selection curve		2 ln(10)
δ	size difference for which the distance in the size diversity index is 1 − 1/e		2 ln(10)
μs	starvation mortality rate	yr−1
μ0	starvation mortality rate when food supply is just sufficient (g = gst)	yr−1	0.1
θ	coefficient of starvation mortality rate	—	5
κ	coefficient for standard metabolism	yr−1	4c
p	exponent of standard metabolism	—	3/4c
σd	diffusion coefficient	yr−1	0.1

^a[20].

^b[26].

^c[27].

(b). Fishing selectivity

For a target species, size-selectivity of a gear is described by its selection curve, that is, the probability that an individual with a given length be caught by that gear. Traditionally, selection curves are taken as sigmoid functions, with the probability of being caught monotonically increasing with size up to 1, so that large fish present in the area will certainly be caught [5]. However, the assumption that all large fish are caught is related to the design of most trawl selectivity experiments using small mesh covers over codends, twin or trouser trawls, which cannot account for the presence of larger, uncaught fish in the area. But recent comparisons of catches by several types of gear have shown that trawls do not catch large animals that are taken in the same area by other gears like gillnets, hooks or traps; this applies to various species of fish (e.g. [29–31]) and crustaceans (e.g. [32]), or to the fish community [33]. Fish behaviour greatly influences catchability and some species are able to avoid the gear [34,35]; for those swimming away from mobile gears, probability of escape is positively related to swimming speed, that is, to body size [34]. Beside trawls and other towed gears, dome-shaped selection curves are relevant for other gears such as gillnets, or hooks [36]. At the community level, a dome-shaped selection curve might be representative of the multi-species catches relative to video estimates of total abundance [37]. Thus, we used a dome-shaped, Gaussian fishing mortality:

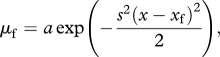2.2

where selectivity is described by two parameters, x_f catch modal size or target size, and s inverse width of the selection curve or fishing selectivity stricto sensu. Larger s values imply narrower selection curves that is, more selective fishing. The traditional view of improving selectivity by increasing mesh size to let smaller fish escape [38] could imply either increasing target size x_f, or increasing selectivity stricto sensu s, or both. Parameter a is a fishing mortality multiplier.

(c). Indices of fishing effects

Many solutions of equation (2.1) do not converge to a stable spectrum but oscillate in time. Therefore, measures of fishing effects cannot be taken at any particular time and need to be summarized over a time period after the system reached a stationary limit, either steady or oscillatory (below: over years 130–150). To detect fishing effects on the size spectrum including disturbances of the biomass flow, we calculated the range of total biomass in the system and total catch, and their median.

To describe spectrum regularity, we developed a measure of size diversity. To take account of size classes being ordered, an index including some measure of distance like the taxonomic diversity indices of Clarke & Warwick [39] is required. We sought a nonlinear distance metric, which would be zero for animals the same size, small when size difference is low and reach a maximum 1 when size difference increases—two animals with a weight ratio of 10 would be approximately as distant as when the weight ratio is five. We used a ‘V-shaped’ distance d(x,y) = 1 − exp(−|y − x|/δ) between two log-weights x and y, where δ determines the ‘V’ width (electronic supplementary material, figure S1a). As d is a function of y − x, two fish with a given weight ratio have a similar distance, irrespective of their individual weight. Size diversity is then the expected size-distance between two random biomass units,

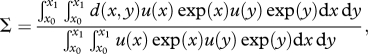where u(x)dx is the number of individuals with size in [x,x + dx]. In this definition, the denominator is set so that the index is 1 when all individuals are distant by d(x,y) = 1. Using the distance between two biomass units rather than two individuals by multiplying by exp(x) and exp(y) gives more weight to larger individuals. The diversity of a linear biomass spectrum increases as δ decreases, and peaks when the spectrum slope is −1 (electronic supplementary material, figure S1b). Peaks or gaps in the size spectrum lower its diversity. Below size diversity is calculated over the fish size range from x₀ = 0 to x₁ = 4 ln10.

(d). Numerical simulations

Parameters for the predation dynamics were set to the reference values used in Benoît & Rochet [20] (table 1). Preliminary simulations showed that this choice of parameters led to sustained oscillations over time with low amplitude in the unfished spectrum. This is consistent with the findings of Law et al. [23] who concluded that a Hopf bifurcation from a steady state to oscillatory solution occurs at values of volume searched (parameter A) lower than the one used here. A wide range of fishing scenarios was explored. Fishing selectivity varied from unselective fishing s = 0.25, where the typical weight ratio of a large to a small fish caught is close to exp(1/s) = 55, to selective fishing s = 4 where this ratio is 1.28. Target sizes span from 100 g (as forage fish targeted by industrial fisheries for fish meal, or small crustaceans such as prawn) to 10 kg (a large size in modern fisheries). Actual fishing gears such as hooks, gillnets and large-mesh trawls would have a 2–50 kg target size with a selectivity parameter s between 0.5 and 1.5; small mesh trawls (e.g. used to catch small crustaceans) target 20–200 g sizes with a low selectivity s ≈ 0.5; traps have a higher selectivity (s ≈ 1.5) and their target size depends on the target species. All these are educated guesses based on references cited in §1b rather than true estimates; data at the community level are lacking. Highly selective fishing s = 4 would describe an ideally selective fishing gear and does probably not reflect any existing gear. As for fishing intensity, parameter a was set so that applying the resulting fishing mortality rate to a so far unexploited ecosystem would yield a total reference catch C₀ spanning the range 0.00125–0.08 g m⁻³. The simulated catch varied as a result of the spectrum dynamics and was lower than C₀, encompassing realistic values of total catch taken from actual ecosystems, estimated between 0.002 and 0.02 g m⁻³ (table 2). We explored the phase-portrait in the fishing intensity–selectivity space for two target sizes.

Table 2.

Estimated total catch and surface area from exploited marine ecosystems. Catch per unit volume is approximated assuming that most fishing effort is deployed in a 200 m layer near surface, except for Baltic Sea which is shallower, thus we used total volume.

area	total catch (106 tonnes yr−1)	area (106 km2) or volume	catch/water volume (10−3 g m–3 yr−1)
Mediterranean	1–2a	2.5c	2–4
northwest Atlantic	2–5a	6.3c	2–4
northeast Atlantic	6–12a	14.4c	2–4
North Sea	2.7b	0.58b	23
Baltic Sea	0.5b	21.7 103 km3d	23

^a[40].

^b[41].

^chttp://www.fao.org/fishery/area/search/fr

^dhttp://www.marbef.org/wiki/Baltic_Sea

To guard against numerical artefacts, three simulation methods were used. The classical Euler and Runge–Kutta methods approximate the dynamic system du/dt = A(u) by the discrete system u(t + dt) = u(t) + A_d(u(t))dt with a time step dt, where A_d is A discretized into fixed steps dx, starting from a given initial value. Third, we used the method of characteristics, which consists in following the evolution of cohorts. This method is more adapted to the structure of the ecological problem, as the step dx varies with log-weight x. Similar results were found with the three methods using various integration steps (from dx = 0.02 ln(10) to 0.05 ln(10) and from dt = 0.2/360 to 2/360). Results converged towards identical solutions as step lengths were reduced (electronic supplementary material, figure S2). All figures shown were obtained with the characteristics method unless otherwise specified. The influence of the choice of boundary conditions was also examined by increasing the maximum size of fish x_max from 6 ln(10) to 9 ln(10); the spectrum dynamics were not qualitatively affected.

(e). Model variants

The size-spectrum model of equation (2.1) is an idealized food web, where size determines all processes and food availability is linearly reflected in growth. The lack of diversity in processes and of density-dependence might generate non-realistic instability. To investigate the impact of fishing on more stable spectra, we simulated a restricted set of fishing scenarios on size spectra stabilized by either of two ways. First, we included starvation mortality, for at low food density, growth does not just slow down: some fish die. The starvation mortality rate was μ_s = μ₀ exp(θ(g_st − g)/g_st) where μ₀ and θ are coefficients, g is assimilated food and g_st = κ exp(px) is energy required for standard metabolism. θ was chosen large such that μ_s ∼ 0 when food is sufficient, and increases steeply when food becomes scarce. Second, as a proxy to growth diversity among individuals, we added a diffusion term σ_d∂²u/∂x² to equation (2.1). This mimics diversity in growth whereby two fish, the same size eating the same ration, have lognormally distributed growth rates, and stabilizes the size spectrum [20]. The diffusion coefficient σ_d was chosen just sufficient to stabilize the unfished size spectrum. In a third model variant, we acknowledge that equation (2.1) is a first-order approximation of a more realistic model with jump-growth [42]. Simulations including the second-order term showed no significant difference with the first-order approximation, because the size ratio between prey and predator is small enough.

3. Results

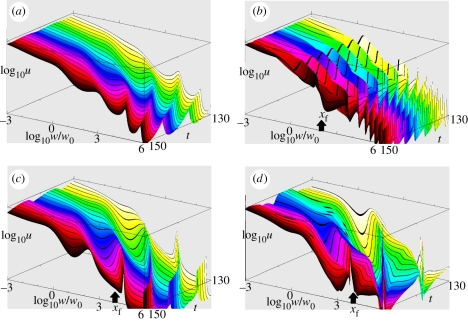
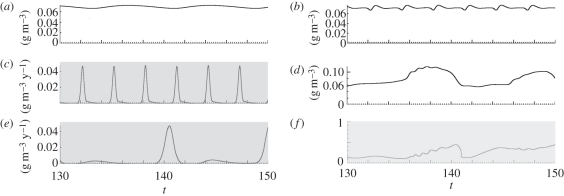
Without fishing, the size spectrum oscillated lightly within a wavy-shaped contour (figure 1a). This spectrum was not linear as in Benoît & Rochet [20] model because of the discontinuity at minimum fish size x_min between the plankton and the fish spectra. This discontinuity occurs because we did not force recruitment parameters to be consistent with the plankton spectrum density. Our purpose was not to obtain a linear spectrum and we rather selected the ‘most realistic’ parameters; wavy size spectra are commonly observed when size classes are small enough (e.g. [10,43]). Fishing mortality destabilized the spectrum—wave amplitude increased. Selectively targeting small sizes created a step at the target size and decreased wave period in larger sizes (figure 1b); when large sizes were targeted unselectively, waves with sharper peaks propagated both top-down and bottom-up (figure 1c); when large sizes were targeted selectively, waves increased again in amplitude and became less regular (figure 1d). High, selective fishing depleted biomass at the target size; as a consequence, predators feeding on this size range grew very slowly, and their biomass accumulated, which still amplified the depletion at the target size; similarly, biomass accumulated in size ranges normally preyed upon by the target size. The biomass flow, choked with these accumulations, became oscillatory. These oscillations were sustained as shown by the time series of summary indices (figure 2): total biomass oscillated with low amplitude and a simple pattern with no fishing (figure 2a); when small fish were targeted selectively (figure 2b,c), the time period was shorter, the oscillations were wider and total catch peaked sharply; when large fish were targeted selectively, biomass had wider and less regular oscillations (figure 2d), catch showed the widest oscillations from very low values to high and steep peaks (figure 2e), and size diversity showed a complex oscillatory pattern (figure 2f).

Figure 1.

Examples of simulated size spectra (parameters from table 1) over years 130 to 150. (a) No fishing; (b) selectively fishing small fish (s = 4, log₁₀(w_f/w₀) = 2, C₀ = 0.01); (c) non-selectively targeting large fish (s = 0.25, log₁₀(w_f/w₀) = 4, C₀ = 0.01); and (d) selectively fishing large fish (s = 4, log₁₀(w_f/w₀) = 4, C₀ = 0.01). Colours vary from yellow to black from year 130 to year 150. Arrows show the size targeted by fishing.

Figure 2.

Examples of simulated time series of normalized biomass, catch and size diversity (parameters from table 1) over years 130 to 150. (a) Total biomass with no fishing; (b) total biomass, and (c) total catch with selectively fishing small fish (s = 4, log₁₀(w_f/w₀) = 2, C₀ = 0.01); (d) total biomass, (e) total catch, and (f) size diversity with selectively fishing large fish (s = 4, log₁₀(w_f/w₀) = 4, C₀ = 0.01).

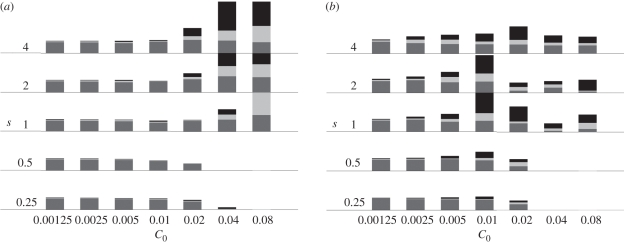
Fishing lightly with low selectivity and targeting small sizes (left area in figure 3a) did not destabilize the spectrum much: minimum, average and maximum biomass were almost the same. When fishing intensity was increased with high selectivity (s > 1), oscillations amplitude increased. Oscillations widened at lower fishing intensity when fishing was more selective (top area in figure 3a). Fishing with high intensity and low selectivity was unsustainable and left no fish in the system (bottom right corner in figure 3a). When a large size was targeted, biomass oscillations appeared at lower fishing intensity and selectivity, and their amplitude at a given combination of fishing selectivity and intensity was higher, except at highest fishing intensity where both amplitude and biomass in the system decreased (figure 3b).

Figure 3.

Summary of biomass variations as a function of fishing selectivity and intensity when target size is (a) log₁₀(w_f/w₀) = 2 or (b) log₁₀(w_f/w₀) = 4. The x-axis spans fishing intensity measured by expected catch C₀ that is, the catch that would be produced by applying the fishing effort to the unfished spectrum (C₀ is used to calculate the fishing mortality multiplier a). The y-axis spans fishing selectivity s. Each bar shows: minimum (dark grey), median (light grey), and maximum (black) biomass (over simulated years 130–150). Median biomass ≈0.07 g m⁻³ for C₀ = 0.00125. Empty cells correspond to total extinction of biomass in the system.

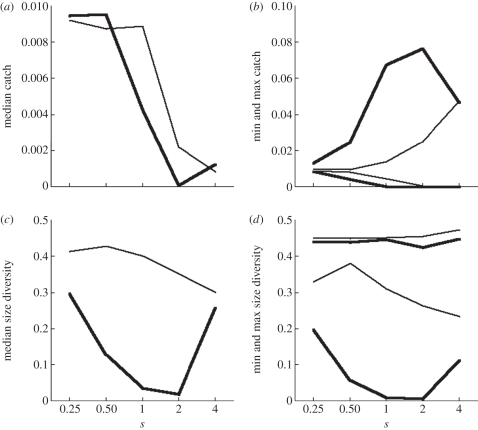
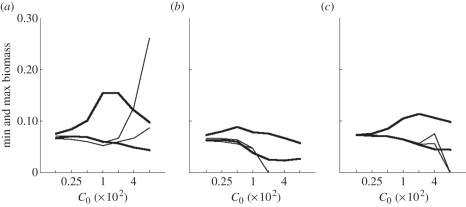
Maximum catch could be very large when fishing selectively, especially when large sizes were targeted (figure 4b). However, in that case minimum catch was almost zero (figure 4b), and median catch was low (figure 4a), because the high catches only happened on isolated peaks (figure 2c). Catch range was much smaller and median catch higher when fishing unselectively, especially when small fish was targeted (figure 4a,b). Maximum size diversity was insensitive to fishing selectivity (figure 4d), but minimum and median size diversity were lower when large sizes were targeted (figure 4c,d).

Figure 4.

Community metrics as a function of fishing selectivity when targeting small (log₁₀(w_f/w₀) = 2, thin lines) or large (log₁₀(w_f/w₀) = 4, bold lines) fish with moderate fishing intensity (C₀ = 0.01), over years 130 to 150. (a) Median catch, (b) minimum and maximum catch, (c) median size diversity, and (d) minimum and maximum size diversity.

Starvation mortality moderately stabilized the unfished spectrum, which oscillated within a narrower contour (not shown). Under all combinations of fishing selectivity and intensity, oscillations were less wide and there was slightly less biomass in the stabilized spectrum than without starvation mortality (figure 5a,b). Diffusion was stabilizing as well, and resulted in a stable spectrum with no or moderate fishing (minimum and maximum biomass superimposed on figure 5c). Oscillations were less wide in the stabilized spectrum than without diffusion (figure 5a,c). The effects of fishing selectivity on spectrum dynamics were qualitatively similar, whether or not the spectrum was stabilized by either mechanism (not shown).

Figure 5.

The effects of stabilizing spectrum dynamics on biomass amplitude: minimum and maximum biomass as a function of fishing intensity when targeting small (log₁₀(w_f/w₀) = 2, thin lines) or large (log₁₀(w_f/w₀) = 4, bold lines) fish with moderate fishing selectivity (s = 1), over years 130–150 (Euler method). (a) Non-stabilized spectrum, (b) spectrum with starvation mortality, and (c) spectrum with diffusion.

4. Discussion

(a). Which fishing attributes destabilize the size spectrum?

Strong, non-selective fishing can eliminate the biomass from the ecosystem, while a low fishing intensity has low impact, irrespective of selectivity. All other combinations of fishing selectivity and intensity destabilize the size spectrum, that is, amplify temporal oscillations in the biomass flow. When fishing is selective and/or when large fish are targeted, oscillations appear at lower intensity; for a given intensity, oscillations have wider amplitude.

Size-spectrum models can be unstable when all processes are determined by size only. Silvert & Platt [44] showed that owing to the nonlinear feedback, a wave-like instability that would damp at infinite time was created by, for example, a perturbation in plankton input. Law et al. [23] found a Hopf bifurcation in unexploited size spectra, depending on the parameters of the feeding regime. Here, we started with parameters yielding a slightly wavy size spectrum with no fishing, and showed that fishing-induced waves amplify these oscillatory dynamics. More realistic models show that various processes stabilize size spectra in the real world. A diffusion term mimicking variability in food assimilation efficiency, or a non-predation mortality term, improve the stability of the linear size spectrum [20]. A more explicit modelling of biodiversity with life histories (growth and reproduction) determined by asymptotic size leads to stable size spectra [27]. Dynamic interactions between benthic and pelagic size spectra also improve the food web stability and resilience [45]. However, our simulations show that fishing generates oscillations even in more realistic spectra stabilized by either diffusion or starvation mortality. Thus, the result that fishing destabilizes the trophic flow in size-based food webs might be quite general.

Whether actual size spectra exhibit oscillations over time is difficult to examine, because many published observations are averaged across years, or summarized by slopes or other statistics which overlook oscillations. However, a few publications show time series of survey-based demersal fish biomass size spectra that suggest oscillations with a period from a few years on Georges Bank [46] to a decade on Scotian Shelf [47]. This is also suggested by groundfish trawl surveys in French waters, which exhibit oscillations of various amplitude with periods of 5–10 years: peaks move along the size-axis over time (electronic supplementary material, figure S3). A systematic analysis of size spectra time series with appropriate tools is required to ascertain these visual results.

(b). Is size diversity affected by fishing?

The size diversity index is sensitive to both fishing intensity and selectivity, especially when large fish are targeted. High fishing intensity or selectivity generate waves; in addition, selective fishing creates gaps in the size spectrum; both lower the size diversity index. This result is consistent with the results of a size-spectrum model with distinct life histories determined by asymptotic size [27]. With this model, exploiting limited, either large or small, size ranges generated gaps in the exploited range and stable peaks and valleys in the adjacent sizes, thus would lower the size diversity index; this effect was stronger when fishing intensity was higher.

As size is related to many life-history traits and largely determines ecological role in trophic chains [18], size diversity provides a proxy for functional diversity. Our results imply that both fishing intensity and selectivity affect biodiversity components of conservation interest.

(c). Consequences for fisheries management

Sustained oscillations in the size-spectrum result in oscillations in the catch that can be wide when fishing is selective, especially when large fish are targeted. This has potential ecological and economic consequences. Biomass oscillations are hazardous because unstable dynamics increase the risk of change in ecosystem state and dynamics. For example, oscillations might increase system sensitivity to environmental variability—the co-occurrence of low or very high biomass and unfavourable environmental conditions increasing the probability of collapses. Catch oscillations are not desirable economically and socially as stable landings will favour stable profits and employment. Stabilizing fisheries has long been taken as a management objective (e.g. [48]), and for example, in the European Union, relative stability is one of the basic principles of the Common Fisheries Policy [49].

However, a high variability is observed in European landings, especially when fishing mortality is high [50]. This variability could be due to unstable fish stocks, or unstable food web dynamics, or the interplay of both. Without waiting for the investigations necessary to determine the main factor of variability, actions to stabilize either of those dynamics could be taken to stabilize landings. The results of our simulations suggest that, rather than just reducing fishing pressure as usually advised (e.g. [7,50,51]), it might be wise to reduce fishing selectivity at the same time. The idea that exploitation should be balanced across trophic levels to maintain the ecosystem trophic structure has already been put forward [52]. Actually, fishing the size spectrum less selectively protects both large species [53] and large individuals within species, which would also reduce the destabilizing effect of fishing on stock dynamics [1]. Regulations to prevent the capture of small fish, either minimum landing size or mesh size regulations, have long proven less beneficial than generally expected [54]. Our results suggest that this is because the expected benefit was wrong to start with. Of course, catching and discarding small fish is sacrificing their future growth, a waste both ecologically [55] and economically [2]. Developing bycatch utilization [56,57] or using a wide diversity of gears each targeting different ecosystem components [58] might be better ways forward than striving to avoid catching small-sized individuals and/or species.