Positive feedback and alternative stable states in inbreeding, cooperation, sex roles and other evolutionary processes

Abstract

A large proportion of studies in systems science focus on processes involving a mixture of positive and negative feedbacks, which are also common themes in evolutionary ecology. Examples of negative feedback are density dependence (population regulation) and frequency-dependent selection (polymorphisms). Positive feedback, in turn, plays a role in Fisherian ‘runaway’ sexual selection, the evolution of cooperation, selfing and inbreeding tolerance under purging of deleterious alleles, and the evolution of sex differences in parental care. All these examples feature self-reinforcing processes where the increase in the value of a trait selects for further increases, sometimes via a coevolutionary feedback loop with another trait. Positive feedback often leads to alternative stable states (evolutionary endpoints), making the interpretation of evolutionary predictions challenging. Here, we discuss conceptual issues such as the relationship between self-reinforcing selection and disruptive selection. We also present an extension of a previous model on parental care, focusing on the relationship between the operational sex ratio and sexual selection, and the influence of this relationship on the evolution of biparental or uniparental care.

1. Introduction

Negative feedback is a common theme in evolutionary ecology as a stabilizing factor. Positive feedback, in contrast, describes self-reinforcing, de-stabilizing processes; by favouring a type that is already common, it often leads to alternative stable states. Much of systems science can be characterized as the study of regulatory processes involving a mixture of positive and negative feedbacks [1–3].

In ecology, alternative stable states ([4], review) often differ greatly in their practical consequences. Examples include near irreversible collapses of fish stocks from their original states of abundance [5,6], or disease outbreaks as a result of compromised herd immunity when too small a proportion of individuals is vaccinated [7]. Inverse density dependence—a form of positive feedback (better per capita growth in larger than small populations)—can drive a population extinct via an Allee effect. Here, a population that has experienced a stochastic reduction in its size may now be within the basin of attraction of extinction (these basins outline which of the alternative equilibria are reached from given starting conditions). Allee effects can be created in many ways [8], including a positive feedback where overexploitation of rare species becomes self-reinforcing because humans attribute value to rarity [9].

Studies of alternative stable states in evolutionary biology (our focus here) are scarcer than in ecology, despite many examples featuring positive feedback [10]. We describe connections between alternative stable states and disruptive selection, followed by examples of alternative stable states in evolutionary processes, with new theory on parental sex roles. Finally, we will comment on the challenges of testing evolutionary predictions that feature alternative equilibria.

2. Is disruptive selection synonymous with positive feedback? no

Disruptive selection occurs when intermediate phenotypes have a fitness disadvantage compared with more extreme phenotypes. At first sight, it seems logical that disruptive selection would easily lead to alternative stable states at both extremes. This is, however, only partly true. Disruptive selection can be divided into two categories, one of which can indeed lead to alternative stable states, whereas the other results in protected polymorphisms [11].

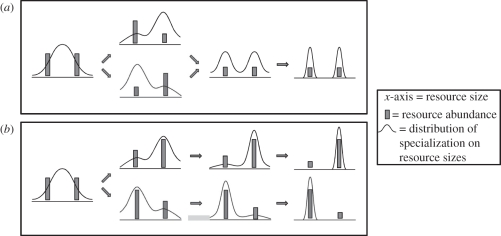
The type of disruptive selection that does not lead to alternative stable states occurs when disruptive selection is associated with negative feedback. Consider a population exploiting a resource of varying sizes (such as small and large seeds). Consumption affects the availability of the resource (figure 1a; note that size variation can also be continuous [12]). If individuals that are best at exploiting a certain seed size become relatively more abundant, then this part of the resource size range becomes depleted. Phenotypes that deviate from the majority now have an advantage. Instead of multiple equilibria, this can maintain a stable, protected polymorphism in the population. Even though two trait values (alternative strategies) coexist, the polymorphism itself is not an example of a set of alternative stable states. Instead, the population has reached one stable state, which is a polymorphism with two coexisting trait values.

Figure 1.

Why disruptive selection is not synonymous with positive feedback. (a) Disruptive selection leads to a protected polymorphism, and because all deviations from the initial state lead to the same state, there are no alternative stable states (even though the one state comprises two alternative strategies). (b) Initial deviations become reinforced, and this leads to two alternative stable states.

Of more interest are scenarios where disruptive selection (suboptimal fitness of an intermediate phenotype) combines with positive feedback (suboptimal fitness of a rare phenotype). Consider a consumer that feeds on two fruit (with large and small seeds, for example) and the plant relies on frugivory for germination (figure 1b). As before, intermediate phenotypes are not able to efficiently use either resource, which initially creates similar bimodal distributions as mentioned already, but now selection can make a population specialize on one of the two seed sizes. If the majority specializes on, say, small seeds, then the plant with small seeds is germinated more efficiently and increases in abundance. The payoff for specializing on small seeds then increases in a self-reinforcing way. In this case, there are truly two alternative stable states in the population.

From this hypothetical example, we will now move on to consider real-life examples of positive feedback and self-reinforcing selection.

3. Positive feedback on a single trait

(a). Inbreeding tolerance

Inbred offspring can inherit an identical copy of a deleterious recessive allele from both parents, which can markedly reduce offspring viability or other fitness components [13]. On the other hand, inbreeding has kin-selected benefits [14–17]: a sib-mating mother has 50 per cent genetic advantage because the offspring has a 50 per cent chance of harbouring not one but two gene copies that are identical by descent to those of the mother. The kin-selected benefit of inbreeding and the cost of inbreeding depression do not necessarily cancel out. Their balance determines whether inbreeding is adaptive [15].

Lande & Schemske [18] made it explicit that the process involves positive feedback. In plants, if only few individuals reproduce by selfing (an extreme form of inbreeding), then they will do so in a population harbouring many recessive deleterious alleles. Inbreeding depression is consequently strong, and selfing is selected against. Inbreeding depression will be much weaker, however, if the population is already inbred because harmful recessives will have been purged from the population [19]. The more there is inbreeding, the easier it is for the benefits to override the costs. This self-reinforcing nature of selection for inbreeding made Lande & Schemske [18] predict that plants should mostly reproduce by selfing, or mostly outbreed; intermediates should be unstable.

Lande & Schemske's paper [18] is a good example of work that has led to fruitful research avenues, while making predictions that are at least partially wrong. Categorizing plant species according to the frequency of selfing reveals a u-shaped frequency distribution: very low and very high selfing frequencies predominate [20]. However, about one-third of plant species have an intermediate selfing rate [20,21], which is hard to explain if positive feedback is the only factor at play. A multitude of possible explanations for such mixed mating strategies have been proposed since [22]. Without the ground-breaking work that produced the prediction that only the two ends of the distribution would be stable, the relevance of the question ‘why does mixed mating occur?’ might have remained undiscovered for quite a while.

Unsurprisingly for research focused on plants, Lande & Schemske's paper [18] has received far less attention in the animal than in the plant literature. Approximately 70 per cent of the 817 citing studies refer to plants, 20 per cent to animals and 10 per cent are modelling studies. Animal studies state commonly enough that inbreeding can prevail when inbreeding depression is mild, but the self-reinforcing nature of the process is rarely commented on (e.g. [17,23,24], but see also [25,26]).

(b). Cooperate but only if others do too…

Arguments regarding the evolution of cooperation often distinguish between the origin and maintenance of prosocial tendencies. For example, it is difficult to see why eusociality should evolve if colony-level relatedness is low, but the first eusocial insects may have avoided this problem if their queens mated monogamously—opening the door for eusociality even if queens later evolve multiple mating. This pattern is indeed found in phylogenetic studies [27], including contexts that are not strictly eusocial (cooperative breeding in birds [28]). Some animal societies have been argued to have reached ‘points of no return’ [29] or ‘dead-ends’ [30]. This occurs when an individual never develops outside a colony with highly differentiated division of labour. A complex suite of traits can then evolve; from that point, it can be difficult to evolve back to simpler lifestyles with independent breeding.

More general models of cooperation, built without a specific taxon in mind, likewise often predict alternative equilibria that differ greatly in cooperativeness. One of the classic models is the iterated Prisoner's Dilemma, where ‘tit for tat’, which starts out behaving cooperatively and then copies its partner's moves, forms a stable equilibrium—but so does ‘always defect’, which cannot be invaded by ‘tit for tat’ [31]. The finding that ‘cooperation can be difficult to get started, but becomes more robust once established’, repeats itself in many other models (e.g. the evolution of policing [32]).

Tit-for-tat games feature immediate reciprocity. Reciprocity can also occur in a broader sense: cooperative systems often feature young helpers, some of which later proceed to a dominant status and now become receivers of help. Such systems can be stable against freeriders [33], but the establishment phase is difficult: why begin helping if it is never reciprocated? This can give rise to two equilibria, with and without help [33,34]. The no-help equilibrium can become unstable and disappear, however, if there is some reason to contribute to the common good that does not depend on receiving help. Safety in numbers (in the form of predator dilution) is the simplest way to achieve such a kick-start [33,35]. Kinship is possibly the commonest, but mutualistic relationships can also evolve between unrelated species. For example, Wolbachia (an endosymbiont parasite of insects) has also been observed to reach the alternative state of an obligate mutualist in at least two independent evolutionary transitions; such an evolutionary transition again offers no easy way back to independent living [36].

4. Coevolving multiple traits: a plethora of (mostly sexual) examples

Reviewing alternative stable states in a coevolutionary context offers us a wealth of examples. The coevolving traits could belong to different species, and mutualism is not the only example; coevolution of predators and their prey is a well-studied example [37]. Alternatively, the traits can be characteristics of the same organism. Schaffer & Rosenzweig [38] present an early example where an organism can, depending on its ancestral state, evolve two or more different life histories based on the same trade-offs. The relevant set of coevolving traits is reproductive expenditure (RE) at each age. For example, RE in the first year affects the optimum RE in the second year, and vice versa, leading to coevolution where alternative stable combinations can be reached depending on the initial values: the same set of trade-offs can lead to iteroparity or semelparity (reproduction over several years or just once as a form of terminal effort).

Perhaps because of the distinctness of male and female traits, sexual interactions form the arguably best-studied examples of positive feedback, and we thus draw most of our examples from this field.

(a). Males and females… or just two types of gametes?

The evolution of maleness and femaleness provides an interesting case study of alternative stable states. Males and females do not exist in all sexually reproducing species. One speaks of ‘mating types’ if gametes of equal size fuse to form a zygote (isogamy), and the terminology of ‘males’ is only used if one gamete type evolves to be much smaller than the other (anisogamy). Disruptive selection can make sexes specialize in producing numerous, small ‘searcher’ gametes (sperm) or fewer and larger ‘resource provider’ gametes (eggs) [39,40]. Self-reinforcing selection towards small ‘searcher’ gametes may require a threshold asymmetry in gamete size. Below this threshold, gamete sizes evolve back towards equality, especially once internal fertilization evolves; above, one gamete type evolves to be much smaller than the other [41,42].

Recent modelling recognizes the importance of alternative stable states in gamete evolution [42]. The equilibrium with isogamy (equally sized gametes) can cease to be stable even in the absence of gamete competition, if gametes have trouble finding each other through low gamete production or encounter rates, or through high gamete mortality. But isogamy also breaks down if the more numerous gametes compete intensely for the less numerous ones, i.e. if there are gametes from several adults in the same locality.

Anisogamy by itself comprises two alternative stable states, because it is not predefined which mating type evolves to specialize in the production of small gametes. If there are two mating types (x and y), then the two alternative stable states are (x = male, y = female) and (x = female, y = male), despite the end results looking similar owing to symmetry. If the conditions for the evolution of anisogamy are present, then theory predicts that the type with the initially smaller gametes will be able to keep decreasing its gamete size (in evolutionary time, owing to gamete competition or possibly gamete limitation) until a minimum size is reached. The other type is simultaneously ‘forced’ to increase its gamete size in order to maintain reasonable zygote survival, which also increases zygote survival for the other mating type despite its smaller gamete size. Later, a researcher will simply choose to label the individuals with small gametes as ‘males’ because males by definition produce the small gametes. Isogamy can be a third alternative stable state [42].

(b). Sexual selection and mate choice

Once anisogamy has evolved, creating two sexes, their roles in reproduction give rise to many types of positive feedback. A sexual signal (often produced by a male) and a preference for this signal in the opposite sex form a good example. Positive feedback between these two traits has been hypothesized since the 1930s: this forms the basis of the Fisher [43] process where a trait and a preference become genetically linked and may self-reinforce each other towards greater exaggeration of the trait and the preference alike (‘runaway’ evolution [44]). Because any trait might become preferred in this way, evolving in arbitrary directions, the model has been used to make the prediction that related species should enter numerous alternative stable states and exhibit great across-species variation in their secondary sexual characteristics [45] (but see [46,47] for a critique of too simplistic models of speciation via sexual selection).

Fisherian sexual selection was initially modelled in an open-ended fashion, with no boundaries on how far a preference or a trait could go. Depending on parameter values, populations reach a neutral line along which drift occurs or experience an open-ended ‘runaway’ with its endpoint not explicitly modelled ([48]; for later models, see [44]). The process still forms the cornerstone of sexual selection for genetic (indirect) benefits [49], although it appears fragile when modified to include likely real-life phenomena, such as costs of female preference expression (even minute costs destroy the runaway, unless there is recurrent mutation [50]). A more general view of the Fisherian process avoids restricting attention to purely arbitrary traits, which require zero correlation between the trait and any other characteristic of the male. Instead, the ‘Fisher–Zahavi process’ assumes covariation with other heritable traits of the male that influence offspring reproductive value. Solutions then include stable equilibria where female preference expression can be costly, and the male trait does not exaggerate further nor does it disappear despite natural selection against the present level of exaggeration [51–53].

Again, these models feature multiple equilibria. It makes no sense for a female to evolve a costly preference if the male trait is not present and thus cannot reveal differences among males. But if females do not prefer any male over another, a male who displays a costly trait will not have its display traits selected for—a classic chicken-and-egg problem. The equilibrium of no trait, and no preference for it, is stable (e.g. figure 2 in Kokko et al. [53]) and surrounded by a basin of attraction where individuals expressing preferences or displays are selected against (much like the problem of the origin of cooperation mentioned earlier). In other words, the trivial equilibrium (no preference, no trait) and the more interesting equilibrium (sexual trait and a preference for it) are separated by a fitness valley.

Figure 2.

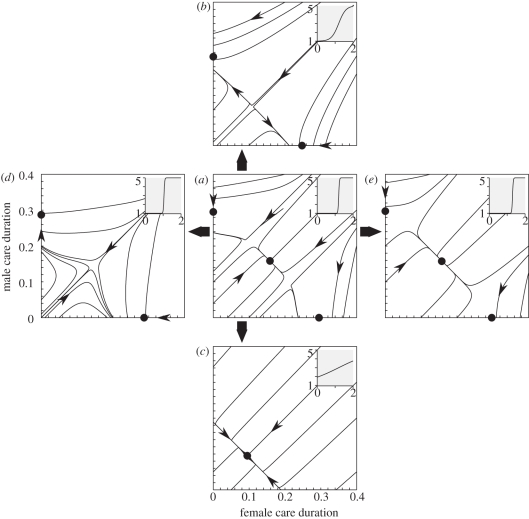
Evolutionary trajectories of coevolving parental care duration of females (x-axis) and males (y-axis), with stable alternative states indicated as dots. Small grey boxes depict the shape of the relationship between sexual selection (y-axis: 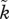ranging between 1 and 5) and the OSR (x-axis ranging between 0 and 2); for females, the relationship is mirrored (not shown; see text). This relationship is of a logistic shape in all examples, 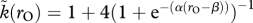, with (a) α = 50, β = 1.2, (b) α = 5, β = 1.2, (c) α = 1, β = 1.2, (d) α = 50, β = 1.05 and (e) α = 50, β = 1.3. Panels are arranged such that vertical deviations shift the slope of the OSR– 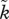curve, horizontal deviations shift it horizontally without changing the slope. There is no multiple mating (in the notation of Kokko & Jennions [54]; 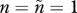) and all mortalities per time unit are equal to 0.01.

The population should somehow be displaced to jump over the valley such that the self-reinforcing process towards interesting outcomes gets its necessary kick-start [53]. A potential solution is that the non-trivial equilibrium usually predicts very asymmetric costs of male and female traits. Because indirect benefits are usually not large in magnitude [55], females are never expected to evolve very costly preferences for them. Relatively cost-free levels of preferences can nevertheless put a strong selective pressure on the male trait. For example, females who turn up at a lek at the most convenient time with respect to the females' own breeding schedules, and mate with a random male present at the time, will select for males with above-average display stamina [56].

This can make crossing fitness valleys easier: females are not heavily penalized for expressing preferences that initially yield no benefit, whereas males are strongly selected to respond to such preferences. Genetic drift on female traits, or various sensory biases that predispose females to be attracted to certain male characteristics, can help evolution cross such fitness valleys towards more interesting equilibria [53,57], but empirical tests of such ideas are largely lacking [58]—as are explicit theoretical studies of drift in this context.

(c). Same trait, different sexes? The evolution of mate searching and parental care

In our earlier-mentioned examples, the two sexes expressed very different traits. Preferences or ornaments can also be more symmetrically expressed by the sexes (for mutual mate choice, see [59,60]). There is arguably an even more interesting set of traits where it is not obvious whether males or females, or both, should develop them. Mating systems feature several tasks that should be performed by one of the two sexes or both, and good performance by one sex reduces selection for the other to put as much effort in the task. If males search for females, females do not need to [61]; if females take good care of offspring, males do not need to [62]. Mate searching and parental care are the most obvious traits that can, in principle at least, be ‘interchangeably’ performed by either parent—or jointly. Inbreeding avoidance (see §3a) belongs to the same category, if it is achieved through dispersal [63,64]. Why then is there often a sex difference in these traits?

Adult individuals of either sex can engage in mate-finding activities. It is not immediately obvious why the sex that produces sperm should also perform the majority of any mate-searching tasks. Models that lack sperm competition indeed predict two alternative stable states: either the female or the male can evolve to become the searcher [61,65] or—if search costs accelerate rapidly with search effort—both may evolve to move equally much in search of each other ([65]; this solution features no alternative stable states but a single joint solution for both sexes). Including sperm competition appears to make males the predominant searcher [65], but this conclusion appears robust only if females do not benefit as much from multiple mating as males. If females benefit greatly from multiple mating, e.g. via increased fecundity when consuming multiple nuptial gifts, then this can flip the system to an equilibrium where females are the predominant searchers [66].

(i). Uniparental or biparental care? A grand battle between positive and negative feedback

Early models on parental care [67–69] showed how the fitness of each sex depends on the behaviour of the other, but the payoffs themselves remained rather arbitrarily defined. The payoff (or probability of remating) of a deserting parent was assumed constant. Later, it was understood that the payoffs should evolve as the frequency of parenting and deserting types in the population changes. A deserter cannot gain much reproductive success if individuals of the opposite sex are busy caring for young and hence not available for matings. This negative feedback on desertion stabilizes mixed strategies where only some individuals of a given sex desert their young [70]. The importance of negative feedback has since become prominent in sex role theory: it has overturned older arguments for the prevalence of female (as opposed to male) care (see [54,71] commenting on Trivers [67]).

The essence of the argument is that it is incorrect to claim that the sex producing small gametes suffers a relatively smaller loss of fitness if offspring die because of insufficient care. Males can only reproduce if they find females to reproduce with (Fisher condition sensu [72]). If most females are busy caring, then a male cannot achieve much fitness searching for (non-existent) females ready to mate. The more there are males competing to find new mates, the more profitable does caring for young become as an alternative route to male fitness (reviewed in earlier studies [54,73]). This makes it hard to argue that there should be self-reinforcing selection that makes sex roles diverge; such selection requires positive rather than negative frequency dependence.

New models of parental sex roles [54,71,73] offer several explanations for why one sex nevertheless can end up with the lion's share of parenting duties. If there is multiple mating per brood, then males will typically have less parentage in a brood than females, and this selects against male care. Caring is also selected for in the sex that is more common in the adult sex ratio. Finally, if there is sexual selection, then this makes the sexually selected sex a less likely carer. Why? Sexual selection implies that mating success is not random. The stronger sexual selection is, the more confident mated individuals of the sexually selected sex can be of their mating success after desertion. These individuals possess traits that make their mating success a repeatable feat. This can tip the ‘care or desert?’ balance in favour of deserting if sexual selection is strong [73].

The situation as a whole combines negative feedback with the possibility of positive feedback. An overabundance of one sex in the mating pool (technically expressed as a bias in the ‘operational sex ratio’, OSR) has two effects that oppose each other. Both stem from the same fact that the sex that currently cares little is likely to be abundant in the OSR and will have trouble securing new matings. As stated earlier, negative frequency dependence (Fisher condition) selects for more care in the sex that currently cares little: ‘if it is difficult to find a new mate, make the most of the current breeding attempt’. But mating difficulties can also set the stage for sexual selection where a subset of individuals perform much better than others in a competitive situation. This creates the potential for positive frequency dependence where the less-caring sex is self-reinforcingly selected to care ever less.

The following thought process (which we here exemplify using a male perspective) gives the details of the positive feedback. Assume some initial asymmetry, e.g. males initially provide a little less care than females, say, for reasons of uncertain parentage. They thus spend more time than females in the mating pool: they are abundant in the OSR. This creates mating difficulties for males. If males also experience stronger sexual selection than females, mating success of mated males becomes repeatable, which selects for a further reduction in male care. Thus, the numbers of males keep building up in the mating pool, which again aggravate male mating difficulties.

The Achilles heel of this argument (and the reason why an explicit model is needed) can be found in the ‘if’ in the above paragraph. It may sound plausible that traits that improve mating success only become relevant when matings are hard to achieve, i.e. when the OSR is biased towards the focal sex—to the extent that some authors have recommended OSR as a measure of sexual selection itself ([74]; for data on widespread usage to date see [75]). However, one should not conflate difficulties of obtaining matings (captured by the OSR) with the statement that mating success is repeatable (not captured by the OSR). The latter requires not only that matings are difficult to achieve but also that success is predicted by properties that vary across individuals [75]. Therefore, there is no specific fixed relationship between these factors, and the strength of sexual selection could even decrease with increasing OSR [76].

The relevant aspect of sexual selection for parental sex roles is the extent to which mating is a predictor of an individual's future mating success [54]. This determines whether a mated individual (an individual in the position to desert or to care for its young) expects high enough mating success so that abandoning the current young is favoured. In Kokko & Jennions [54], sexual selection was measured as k (or 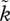for males), the future success of any mated individual, if it returns to the mating pool, compared with the average success of individuals of this sex in the mating pool. Thus, if k = 1, then there is no difference and mating is random. If individuals vary in, for example, body size, and mated individuals are larger than average, then individuals observed to mate once also enjoy above-average mating success in the future, expressed as k > 1. This value was fixed for each scenario investigated by Kokko & Jennions [54].

Earlier, we have stated the need to examine how sexual selection varies with the OSR. Although a precise, universal mathematical relationship relating OSR to k does not exist, we extend the basic model [54] by making k and 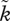functions of the OSR in a biologically plausible way (figure 2). When assuming a specific relationship between the OSR and sexual selection, we make both sexes obey the same relationship but, obviously, the relevant OSR for males is mirrored by 1/OSR for females. This is because the OSR is conventionally defined as r_O = number of males/females that are ready to mate at a given point in time. This is clearest in an example: if we assume that two males per female creates sexual selection on males (say 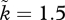) and very mild sexual selection on females (k = 1.01), then by symmetry, the condition of two females per male, all else being equal, should have 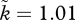and k = 1.5. The former situation has r_O = 2; the latter has 1/r_O = 2. Females become sexually selected under conditions that exactly mirror those that make males sexually selected, while the model still allows us to investigate any relationship between k and the OSR (including cases where mating is always random, or alternatively, sexual selection operates on both sexes simultaneously, as all this requires is 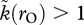and k(1/r_O) > 1). We are free to explore any function (symmetric or asymmetric) to relate OSR to sexual selection as long as 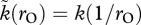for all values of r_O.

We refer the reader to Kokko & Jennions [54] for the full model description. Here, we are interested in finding out whether an increase in sexual selection (parameters k and 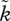) experienced by one of the sexes, once the OSR has evolved to deviate from 1 : 1, can become self-reinforcing. If it can, the positive sexual selection feedback may override the negative feedback that arises via mating difficulties of the common sex in the OSR, and sex roles can diverge.

An example of where this happens is found in figure 2a. If sexual selection targets the common sex in the OSR with increasing strength as the OSR becomes more biased (for the shape of the relationship see the grey box in figure 2a), then self-reinforcing sexual selection can indeed overcome the negative frequency dependence towards biparental solutions, but only if the ancestral state of the population is biased such that one sex already stays with the young for longer (evolutionary trajectories in figure 2a). We thus find a total of three equilibria: biparental care, and uniparental care by either the female or the male (figure 2a).

While figure 2a shows that an ancestral biparental population with OSR = 1 : 1 experiences no selection to move away from this equilibrium, this result is derived assuming that no significant sexual selection operates on either sex at OSR = 1 : 1 (grey box: 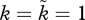at OSR = 1). But because biparental systems often feature mutual mate choice [59,77], figure 2a alone gives a restricted view on the possibilities existing in nature. By altering the slope of the OSR– 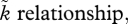we can also consider scenarios where significant sexual selection is already present at OSR = 1 : 1. We find that this can destroy biparental care, if deviations from OSR = 1 : 1 immediately strengthen sexual selection on the sex towards which the OSR becomes biased (uniparental care in figure 2b). Alternatively, it can destroy the stability of the two uniparental equilibria, if the strength of sexual selection responds only mildly to variations around OSR = 1 : 1 (biparental care in figure 2c). The intuitive reason for the difference is that the self-reinforcing process of sexual selection must kick in with strongly increasing force for the more abundant sex in the OSR, as its abundance creates negative feedback on care differences, which pulls solutions back towards biparental care. The positive feedback (strengthening sexual selection) is strong enough to overcome the negative feedback in figure 2b, while it remains too mild in figure 2c. These results complement earlier theoretical predictions that mutual mate choice can coexist with biparental care but only as long as sex differences in parental investment remain modest [16,77].

The mild slopes for the OSR–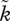 relationship in figure 2b,c assume that sexual selection remains operational on both sexes, even if one of them is clearly in the minority in the mating pool. Because this may be unrealistic for some systems, we can also opt to keep the sharp relationship of figure 2a and shift the curve leftwards towards OSR = 1. Now sexual selection begins fairly accurately at OSR = 1 and ceases to operate on the minority sex as soon as OSR is biased. This makes self-reinforcing sexual selection operate very efficiently: it now overrides the negatively frequency-dependent pull towards biparental care at all OSR values (figure 2d: only uniparental care is possible).

In contrast with figure 2d, where the smallest variations in the amount of care provided by either sex make sex roles diverge in a self-reinforcing manner, shifting the OSR–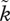 curve in the opposite direction makes the basin of attraction of biparental care wider (figure 2e). Here, sexual selection only becomes sufficiently self-reinforcing to overcome the frequency-dependent pull once the OSR is strongly biased towards one sex. Such a bias is hard to reach if there is no other a priori reason why one sex should increase or decrease its parental effort (for a discussion of possibilities though, see Kokko & Jennions [54]).

5. Discussion

(a). What does this mean for testing models?

‘However, the diverse cases, contexts, models and conjectures described here indicate that positive feedback might be remarkably widespread in evolutionary and ecological processes, although its fleeting, episodic nature makes it difficult to observe directly’. Crespi [10, p. 632]

‘We are thus faced with the prospect that more general analyses will reveal a dynamic quagmire […] If populations remain stranded at one of a multitude of local optima, then hope of accounting for observed differences between real world populations in terms of adaptation must quickly fade’. Schaffer & Rosenzweig [38, p. 68]

These two quotes express two different kinds of pessimism regarding evolutionary understanding when there are alternative stable states. In the first case, the author expresses little hope for documenting self-reinforcing selection simply because the evolutionary endpoints can be reached very quickly. This is undoubtedly true, but the evolutionary endpoints still remain observable. The latter quote states that we typically only observe one endpoint at a time for any given system (contrary to systems where alternative strategies coexist in the same population). If the very same process can predict multiple equilibria that appear fundamentally different from each other, then how can we hope to test any theory, or indeed predict what will happen in a system undergoing evolutionary change in a changing environment?

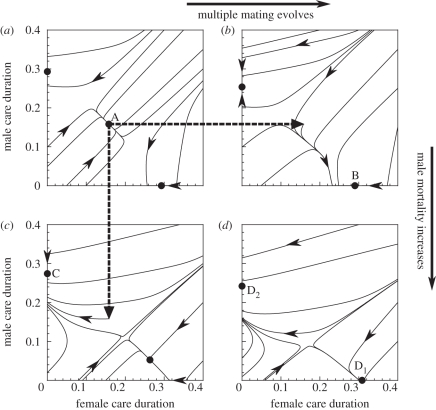
There is no easy answer, but in an attempt to highlight some issues, we will revisit our example of parental versus uniparental care (figure 3). Throughout, we now assume that the OSR–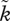 relationship follows that used in figure 2a. The symmetrical case (figure 3a) lacks multiple mating. Biparental care is stable, but so are two uniparental equilibria. Should female multiple mating now evolve for any reason [78,79], the population shifts to a basin of attraction that leads the population to female-only care (follow the horizontal dotted arrow, then the trajectory in figure 3b leading to evolutionary endpoint B). Male care is selected against because offspring are not as often true genetic descendants of the father as they are of the mother, and sexual selection on males completes the self-reinforcing process.

Figure 3.

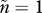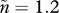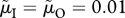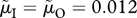Evolutionary trajectories that otherwise follow the assumptions of figure 2a but increase the mean number of males per female mating event from to (this applies in panels b,d) and/or increase male mortality by 20% (using notation of Kokko & Jennions [54], from to ; this applies in panels c,d). Straight dotted lines refer to environmental changes that shift the population from one situation, where it is originally at a stable state, to another, from which point evolution follows a trajectory to proceed to a new stable state. For clarity, we draw only two of all possible lines.

Now consider another environmental change that, for an unspecified reason, tends to kill males more often than females. The population consequently becomes female-biased. This new shift from figure 3b to figure 3d does not, however, produce much further change in behaviour; females remain the only carers at points B and D₁ alike.

One can end up from figure 3a to figure 3d via a variety of temporal routes. What happens if the extra source of male mortality arises first, and multiple mating evolves later? Now from A in figure 3a, evolution proceeds to C in figure 3c (follow the vertical dotted line, and then the evolutionary trajectory in figure 3c), uniparental care by males. There are two forces at play, both arising because the male–female difference in mortality shifts the OSR towards females. Negative feedback selects for female care (and against male care: each surviving male now has many potential female mates [54]). Simultaneously, positive feedback via sexual selection on females (owing to the OSR now being female-biased) selects against female care. In this particular example, positive feedback overrides negative feedback, and the net outcome features sex role reversal and uniparental male care. This remains unchanged when multiple mating subsequently evolves: the system now evolves from C to D₂ (figure 3c,d).

The overall conclusion? Depending on what happened first (increased male mortality or the evolution of multiple mating), the system has deterministically zreached two totally different endpoints, either uniparental female care D₁ or uniparental male care D₂. Is this a quagmire of a theory, then, as Schaffer & Rosenzweig [38] would call it? We have demonstrated hysteresis, a phenomenon where the temporal order of external influences matters for the endpoint reached. Only history can explain why of two related species one has evolved male-only care, the other female-only care, when relevant parameter values (multiple mating and sex-specific mortality) are identical between the two equilibria in figure 3d. This reminds us of the general principle that explaining the origin of a trait is not equivalent with explaining how it is currently maintained.

A partial remedy is that a large number of species (or populations) may have undergone changes in a similar nature. We discussed the earlier-mentioned two routes above as if they were equally probable, but they might not be. A biologist armed with good data on actual patterns of evolutionary variation, and the relevant environmental changes associated with such variation, will be able to detect the predominant routes of evolutionary change much better than an uninformed spectator viewing myriads of possible equilibria. This abstract point is best illustrated with an example. In principle, transitions could occur between each of the four scenarios in figure 3. Some will, however, be biologically much more likely than others, and sets of parameters are unlikely to change in isolation from each other. Consider a species that initially is at solution (b) in figure 3b. If male mortality increases, then it is probably more reasonable to consider that this might also impact the number of times an average female mates than to assume that this number remains unperturbed [80]. The system is therefore more likely to move from figure 3b to figure 3c than to figure 3d. That said, neither change is impossible. Encouragingly, however, both are in line with the general theory that states that an increase in male mortality can underlie a transition from female-only care to biparental care (here, the battle of negative and positive feedback stabilizes as biparentalism with more female than male care; figure 3c), or then no transition might materialize (interpretable as phylogenetic inertia; figure 3d). Good understanding of theory and data alike is required to create good predictions when these often follow the pattern ‘X favours Y when all else is equal, but because of the covarying process Z, all else is unlikely to be equal—but is Z strong enough to override?’.

The entire body of theory on parenting sex roles is based on several ‘all else being equal’ type predictions; this is why the factors are not meant to be studied in isolation. With a great number of species available to study, and today's sophisticated analysis methods that allow taking phylogenetic inertia into account, one can ask which of all possible patterns of covariation, each of them permissible in theory, predominate in nature. This should also improve our ability to predict evolutionary responses to new environmental condition: if a particular fitness valley often appears too wide to be crossed by populations, it is likely to remain so on a currently changing planet too. The interplay of theory and data would be enhanced if we paid explicit attention to developing methods aimed at assessing how easily systems can shift between basins of attraction of alternative equilibria. We have already mentioned drift in female choice (§4b), and complex ‘dead-ends’ (§3b) in social systems. In line with this thought, phylogenetic studies could shift some of their emphasis from analysing evolutionary transitions that did happen (for parental sex role examples, see [81–84]) to evaluating the relative stability of each alternative stable state. If some are more difficult to leave than others, more transitions will enter than leave these states.

(b). Positive feedback leads us… where?

The alternative stable states that a model predicts are not always well defined. In simple scenarios with, say, one locus and two alleles (‘reproduce by selfing, or outbreed’), definitions are simple: positive feedback implies that either allele can go to fixation. With continuous trait variation, changes in allele frequencies are replaced by tracking the population-wide mean value of the trait over time. There is then no (upper) boundary for trait values: examples include body size or weapon size in arms race models [15,16], or the length of a sexually selected bird's tail in coevolutionary models of female preferences and male traits [44]. With positive feedback, the self-reinforcing process can theoretically go on forever, which is of course impossible in reality.

The process may come to a halt once there is no more genetic variation for selection to operate on (which is conceptually similar to fixation of one allele in a ‘one locus, two alleles’ model), but the exact point at which this happens is arguably less interesting than the process that pushed the population along the runaway. When runaways are modelled by taking population size explicitly into account, they can also lead to extinction [85], or they may come to a natural halt if no further change is possible for some logical reason, such as zero parental care reached by one sex.

Alternatively, even if there is no physical or logical boundary, a runaway process can grind to a halt because positive feedback might eventually turn negative owing to some feature of the biological interaction. Figure 3c shows an example: a biparental care equilibrium where positive and negative feedback balance out. Our example of parental sex roles, where both positive and negative feedback interact with varying strength across the OSR landscape to produce a stable outcome, should not be considered an isolated example. In the study of mate choice, an explicit discussion about the nature of equilibria has led to healthy questions concerning indirect selection on female preferences: should females still prefer a male trait once its sexually selected benefit has become balanced by a naturally selected cost [55,86–89]?

Similarly, the study of sexually antagonistic variation has benefitted from explicitly deriving predictions for the ‘standstill’ points of evolutionary arms races [90]. Whether a researcher wishes to emphasize the non-equilibrium nature of the evolutionary process, or the fact that traits will not spend much time very far away from equilibria [91], it always remains a core task to disentangle the various opposing forces that jointly form the causal route to each evolutionary outcome that we are trying to understand. Systems science has taught us that this can lead to emergent properties that would be hard to predict if one considered one level of organization only. Our current examples show that the same principle extends to high-level phenomena: selection on individuals interacts in a very fundamental and important way with emergent properties of populations (e.g. adult sex ratio or the level to which deleterious alleles have been purged). Discussing the relative ease or difficulty of crossing from one basin of attraction to another ought to be a key question for empiricists and theoreticians alike, if we are to explain across-species diversity as well as the common, repeatable themes in their evolutionary trajectories.