Pattern-oriented modelling: a ‘multi-scope’ for predictive systems ecology

Abstract

Modern ecology recognizes that modelling systems across scales and at multiple levels—especially to link population and ecosystem dynamics to individual adaptive behaviour—is essential for making the science predictive. ‘Pattern-oriented modelling’ (POM) is a strategy for doing just this. POM is the multi-criteria design, selection and calibration of models of complex systems. POM starts with identifying a set of patterns observed at multiple scales and levels that characterize a system with respect to the particular problem being modelled; a model from which the patterns emerge should contain the right mechanisms to address the problem. These patterns are then used to (i) determine what scales, entities, variables and processes the model needs, (ii) test and select submodels to represent key low-level processes such as adaptive behaviour, and (iii) find useful parameter values during calibration. Patterns are already often used in these ways, but a mini-review of applications of POM confirms that making the selection and use of patterns more explicit and rigorous can facilitate the development of models with the right level of complexity to understand ecological systems and predict their response to novel conditions.

1. Introduction

How fast is ecology moving forward? If we quantify progress by how predictive ecology is, then progress has been slow and insufficient to solve many problems related to the loss of biodiversity, global changes in climate and land use and the potential collapse of ecosystem services. Ecology will not be able to solve these problems alone, but without improving its predictiveness, there might be no solutions at all.

What do we mean by ‘predictive’? Models can be more predictive just because they make more kinds of predictions about more kinds of changes. The logistic equation cannot by itself predict how a population responds to habitat loss, and a habitat selection model can predict which habitat animals use, but cannot by itself predict population responses; these simple models are not very predictive. Models can also be more predictive because they are more accurate and precise at representing system states that were not considered or used in building the model. Models more predictive in this way are more useful for science and management because they let us more confidently estimate how a system would respond to different inputs or management actions.

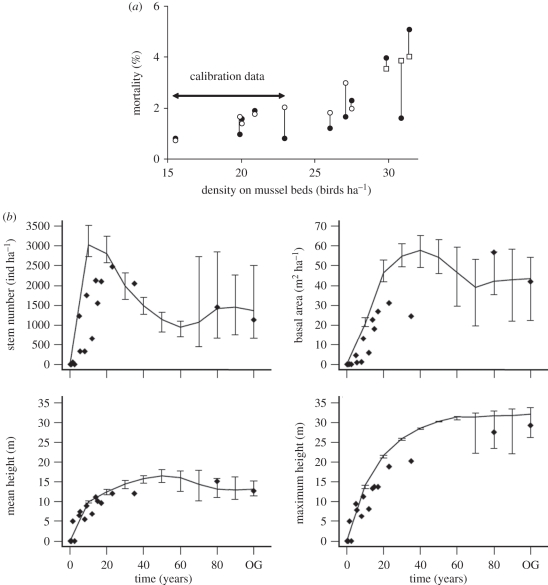
Reasons why our ability to make useful ecological predictions is limited include the complexity, large extent and slow dynamics of ecological systems, which usually prevent controlled experiments. Ecology thus often has to rely on modelling. Simulation models can indeed deliver useful predictions (figure 1), but such predictions are rather the exception than the rule in ecology. Progress in predictive modelling has been hampered by three main obstacles.

Figure 1.

Examples of predictive ecological models. (a) Predictions of overwinter mortality of oystercatchers from an individual-based model that includes optimal foraging, interference with conspecifics, tidal dynamics and varying composition of prey species [1]. Data collected for model calibration show no relation between bird density and mortality, so a statistical model would predict no increase in mortality at high densities. The model did, however, predict the observed increase in mortality at high densities, which was possible because the model is based on ‘first principles’ and individual behaviour. (Adapted from Stillman & Goss-Custard [1].) (b) Results of the forest model FORMIND parametrized for a tropical montane cloud forest in Mexico [2,3]. Lines show model predictions of forest regeneration, dots show field data on forest regeneration on abandoned pastures from 400 m² plots obtained after model predictions were made. Values at OG represent mature forests. Model predictions are strikingly good considering that no calibration to the field data shown was conducted. (From the electronic supplementary material of Rüger et al. [2].) (a) Filled circles, observed; open circles, predicted. (b) Filled diamonds, field data; thin line, simulation.

First, we cannot develop a separate model for every specific system and region. However, if we make models more generic, they become harder to tie to data. Focus in theoretical ecology has been on understanding rather than prediction and, therefore, on simple models rather than on more specific, complex ones. Second, even if we decide to develop a model realistic enough to make specific predictions, what would be the right level of complexity? A too-complex model might be too hard to parametrize, test and understand, whereas a too-simple model might not be realistic enough. Third, and most importantly, traditional ecological theory and modelling have addressed single patterns, observed at a single level of organization. Population ecology has focused on single patterns in abundance, e.g. cycles or coexistence, but ignored characteristics of both individual organisms (e.g. behaviour) and communities (e.g. species composition and nutrient cycling). Ecosystem theory has focused on nutrient cycling or primary production, but ignored characteristics of communities, populations or individuals [4].

Most current ecological theory and modelling are thus either microscopic, zooming into lower levels of organization, or macroscopic, zooming out and trying to capture entire populations, communities or ecosystems. However, these levels should not be considered separately. For example, population characteristics emerge from the properties and behaviour of individual organisms, but the behaviour of organisms is constrained by the characteristics of populations, communities and ecosystems. This mutual dependence implies that patterns observed at the individual level contain, indirectly, information about higher levels of organization, and vice versa. This indirect information could be valuable for developing and testing predictive models. Data at the macro level might not be sufficient to make a model predictive, but data from the micro level might help fill this gap, and vice versa. Therefore, we can generally assume that ecological models will be more predictive if they better capture the system's generative mechanisms—the internal organization and processes that generate the system's responses—that are relevant to the problems of interest. While there have been exceptions to this assumption, we expect that it is true much more often than not for complex systems and ecology.

Predictive ecology thus needs a ‘multi-scope’ that lets us simultaneously take into account the micro and macro levels of organization. Pattern-oriented modelling (POM) is such a multi-scope. POM is a general strategy for tying models to multiple patterns, observed at different scales and levels of organization, and thereby finding the right level of complexity and increasing the chance of capturing the internal organization of the real system, or class of systems, in question. The goal is to produce ‘structurally realistic’ models that capture, in a simple yet useful way, the system's generative mechanisms.

POM has been explained previously [5–11] and in a new textbook on agent-based modelling [12]. Here we focus, for the first time, on the use of POM as a multi-scope for predictive ecology. We also review the development and the use of POM over the past 5 years, present new examples, and provide basic protocols for using POM. We discuss current challenges to POM but also emphasize that POM can help overcome the three obstacles to predictive ecological modelling mentioned above.

2. Patterns and generative mechanisms

The primary premise of POM is that we can identify generative mechanisms by examining multiple patterns observed in the system. To demonstrate this premise, consider the following exercise, where the ‘data’ are: F_2,3 = 10, F_7,2 = 63, F_6,5 = 66, F_8,4 = 96. The exercise is to correctly predict F_9,7. The function F is the generative mechanism that we need to deduce. We intuitively start by seeking patterns in the data. The data are sorted by the output's value, which makes us wonder whether output increases with one of the inputs, which is not strictly the case, but seems to be at least the trend for the first input. A second pattern is that the output always is a multiple of the first input, but not of the second. By what factor is the first input multiplied? We most easily identify 63 as being 7 × 9, and 66 as 6 × 11 and, next, 9 as 7 + 2, and 11 as 6 + 5. Thus, the generative mechanism F is: multiply the first input by the sum of both inputs. We can then predict F_9,7 to be 144.

This exercise demonstrates that tying models to multiple patterns is an intuitive approach often used, without explicitly referring to it, by many modellers. In this example, a purely descriptive approach (e.g. graphing the result of F for each known pair of inputs), or focusing on only one pattern (that F_x,y increases with x), would not have been sufficient to deduce the mechanism. If F had been a random number generator, the output would have contained no pattern and, consequently, no information about the generative mechanism. A pattern thus can be defined as anything beyond random variation [6].

For complex systems, a single pattern is rarely enough to fully decode the internal organization and achieve structural realism. This is why there are so many conflicting models attempting to explain, for example, cycles in small mammals, coexistence of grass and trees in savannahs, species diversity in tropical forests, or heavy-tailed size distributions of forest fires. Models can easily be calibrated to reproduce a single pattern of interest, but potentially for the wrong reasons. Von Bertalanffy [13] referred to this phenomenon as ‘equifinality’, which means that ‘there are many acceptable representations that cannot be easily rejected and that should be considered in assessing the uncertainty associated with predictions’ [14, p. 21].

Thus, the central idea of POM is to use multiple patterns, observed at different levels of a system's organization and scales, to identify the system's generative mechanisms. In POM, we seek models that simultaneously reproduce a diverse set of patterns. POM can therefore be defined as: multi-criteria design, selection and calibration of models of complex systems. Each pattern used in POM can be considered a filter that helps reject unacceptable models or parametrizations. To fully exploit this idea, it is important to consider both strong and weak patterns. A strong pattern, such as cycles or spatial structure, is striking and seems to be a strong indicator of the underlying generative mechanisms. Strong patterns typically take equations and parameters, or a dataset, to describe. Weak patterns are often qualitative and can be described with a few words or numbers; examples include the direction of a trend in how one variable responds to another, the fact that a population exists over a certain time span, that some system characteristic changes seasonally, or that animals use one type of habitat more than another. A weak pattern is less striking and therefore often easier to reproduce—in isolation—by multiple models with conflicting generative mechanisms. However, multiple weak patterns, observed at different hierarchical levels and scales, can often achieve higher structural realism, with less effort, than focusing only on one strong pattern [15].

One of the main keys to success with POM is selecting patterns appropriate for the particular system and problem being modelled and predicted. These patterns should emerge from the mechanisms believed to be important for the problem addressed by the model. Patterns should be relevant to prediction context, not a response to some mechanism that may not be active under the conditions to be predicted. One way to think about relevant patterns is: if the model cannot reproduce these patterns, then you would not trust it to make the predictions you need.

Of course, patterns that characterize a system with respect to some modelling problem do not simply emerge and wait to be observed. Selecting patterns that characterize a system has to use judgement and knowledge of the system. Like any other modelling assumption, the choice of patterns for POM is experimental: we have to see how well they help us make useful predictions. The strongest indicator that the patterns used are the right ones is that the model predicts patterns that were not considered at all during model formulation, testing and calibration. Such secondary, or independent, predictions are the strongest indicator that a model is structurally realistic (and rare in the ecological literature).

Once a set of patterns has been chosen for POM, both the patterns and criteria for whether they are produced by the model need to be defined with enough precision to make analysis reproducible. For this step, it is decisive not to be overly quantitative by using too restrictive criteria. Otherwise, the potential of POM's multi-scopic view might not fully be realized. We recommend following the advice given in Platt's famous article on ‘strong inference’ [16]: ‘Many—perhaps most—of the great issues of science are qualitative, not quantitative, even in physics and chemistry. Equations and measurements are useful when and only when they are related to proof; but proof or disproof comes first … .’

3. The three elements of pattern-oriented modelling

POM comprises three interrelated elements, which are explained below with simple protocols for putting them into practice.

(a). Patterns for model structure

What entities, such as individuals, spatial units, populations and compartments of the abiotic environment, should be explicitly represented in a model, and what state variables and attributes should be used to characterize these entities? What processes should be included? Of course, the model should be as simple as possible, so the model's purpose provides the first filter. Only entities, variables and processes considered absolutely essential for this purpose are included, and others are ignored or taken into account only in a much aggregated way. For example, to explore the viability of a certain metapopulation, subpopulations might be characterized just by their abundance and the carrying capacity and location of their habitat; the abundance of other species, and the landscape between habitat patches, might be completely ignored.

However, for complex systems, a model's purpose is rarely a sufficient filter to achieve structural realism. Thus, the simple, and by no means new, idea of POM is to use multiple patterns that characterize the system, or class of systems, as an additional guide for choosing model structure. The protocol for doing so is [12]:

1. Define a structure of your model verbally, preferably following a standard format such as the ODD protocol [17], using the model's purpose as the only criterion or filter: include only those entities, state variables, attributes and processes that seem necessary to meet the model's purpose, given the current understanding of the system. This first formulation should look slightly too simple to possibly be useful.

2. Identify patterns that characterize the system and are likely related to the problem to be solved with the model. Sources for identifying patterns are the empirical observations and literature, experts and sometimes existing theory (e.g. a plant population model might need to reproduce the widely studied self-thinning trajectories [18]). Do not ignore weak patterns. The number of patterns needs to be manageable, sometimes only three or four. Include patterns that address different characteristics of the system and the entities that make it up; examples include distributions of the entities' attributes, trends in behaviour or owing to behaviour, distributions of dispersal distances, response times to certain events, ranges for state variables of different hierarchical levels or spatial patterns. Try to rank the patterns by their importance.

3. Define criteria for deciding whether the model reproduces each pattern. Start with simple qualitative criteria, for example, visual inspection of trends or whether or not average outputs are within confidence limits of observed data.

4. Revise the model structure described in step 1 as necessary so that it allows, but does not force, the patterns identified in step 2 to emerge from the model. It may be necessary to add state variables, processes, or even entities to the model. This change in orientation from just the model's purpose to the patterns may make a model a little more complex, but should also make the model much more likely to include just enough structure to become general and predictive.

Many experienced modellers work in exactly this way, but without explicitly referring to or documenting the pattern-oriented approach. Making the multi-criteria design of models explicit would make design more systematic, provide evidence of how general the model is and the purposes for which it could be useful, and facilitate the subsequent steps of POM.

(b). Patterns for model selection

The first step of POM identifies the processes to be in a model; now, how can we find useful representations of those processes? For many processes, it is straightforward to find a simple equation or algorithm. But virtually every model has one or a few key processes that we consider more important than others and that we therefore need to represent in more detail. For these key processes, the idea of POM is to formulate alternative submodels representing the process and treat them as hypotheses that we then try to falsify. Contrasting alternative models, or hypotheses, is the basis of what is called ‘scientific method’. Platt re-formulated this method and called it ‘strong inference’, stating that science advances much faster and becomes more predictive when it is used routinely and explicitly [16]. The following protocol for pattern-oriented testing of alternative submodels closely follows Platt's protocol for strong inference:

1. Identify alternative submodels that implement alternative hypotheses for the process of interest. The alternative submodels should be of varying complexity and include at least one ‘null model’ that seems unrealistically simple (e.g. decisions are made randomly; a relationship is linear instead of complex and nonlinear).

2. Implement these alternative submodels one at a time in the full model.

3. Contrast the alternatives by testing how well the full model reproduces the set of characteristic patterns defined during the pattern-oriented formulation and design of the full model, and reject submodels that cannot reproduce one or more patterns.

4. Repeat until a submodel has been found that reproduces all the patterns. This cycle can include revising the submodels and looking for (or generating, from focused experiments on the real system) additional patterns that better resolve differences among submodels.

While modellers often use an iterative or trial-and-error approach, this hypothesis-testing protocol is rarely followed systematically or documented such that peers could see how a submodel's formulation was developed and how it affects the entire model. One goal of POM is to establish a culture of systematically and explicitly following scientific method.

Often it is not trivial to identify several alternative submodels. They can be taken from previous models, from theory, from practical knowledge, or from statistical analyses. Additionally, other disciplines that cover different scales and levels of organization might provide useful approaches. For example, in trying to develop a predictive population model, we might ‘borrow’ submodels from behavioural ecology, physiology, stoichiometry or landscape ecology. Submodels need to be explored and tested thoroughly before being put into the full model; often models developed in one discipline at one level of organization need revision to perform well in multi-level or multi-scale models. Development of submodels for predictive, multi-level models is a new, relatively unexplored, yet critical field of ecology.

Of course, it is possible that this model selection cycle will fail to identify a single best representation of some key process: several alternative submodels might cause the model to reproduce observed patterns equally well. However, this analysis can be conducted as a cycle: as clearly inadequate submodels are rejected, additional patterns can be added to the analysis and used to further delineate the usefulness of the remaining alternatives. This cycle can be an excellent link between modelling and empirical research.

(c). Patterns for calibration

Pattern-oriented models tend to be of intermediate complexity, with typically 10–20 parameters. Individual submodels can often be parametrized independently from data specific to them, but usually there are several key parameters with strong effects on the entire model that cannot be evaluated independently. ‘Guestimated’ parameter values are often sufficient to make the model show the right qualitative behaviour. However, for predictive ecology, we need to calibrate models to specific systems and problems. Calibrating a model against multiple patterns, sometimes at multiple levels, can help estimate parameter values and improve model accuracy when calibration data are typically limited.

Pattern-oriented calibration works the same way as pattern-oriented model selection: each pattern is used as a filter, or criterion, for acceptance, but now it is parameter values being filtered. Sets of parameter values that do not cause the model to reproduce a pattern according to quantitative criteria are discarded. This procedure is closely related to the ‘inverse modelling’ or ‘Monte Carlo filtering’ techniques used in other disciplines. This approach has been used to parametrize a bear migration model [15], a metapopulation model from presence–absence data [9,19] and a grassland model [20].

Pattern-oriented parametrization includes the following steps:

1. Identify parameters that need to be calibrated. These are particularly uncertain parameters, and ones to which the model is particularly sensitive.

2. Identify calibration criteria. In POM, criteria for accepting a parameter set are usually categorical: we check whether a certain model output falls with a certain range. Model outputs must be as comparable as possible to the calibration data; they should be observed in the same way, for example, at the same point in time, as their real counterparts [21], and not overly affected by the model's initial conditions.

3. Design and conduct simulation experiments, using methods similar to traditional calibration. For each parameter combination, check whether model output meets all pattern acceptance criteria. Finally, examine the parameter sets that pass all the pattern filters to learn about the successful combinations.

This protocol is straightforward but computationally elaborate, often needs to go through iterations, and includes many experimental decisions regarding acceptance criteria, the set and sequence of patterns used, and whether or not to change model structure and thereby the number of parameters. Note, however, that this protocol shows strong similarities to many other traditional and innovative calibration methods [22].

4. A mini-review

The adoption of POM in the scientific community has been slow. Overview articles on POM are frequently cited but the term POM has not yet caught on. The two review articles on POM [7,9] have been cited, independently or together, 263 times through January 2011 (Web of Science database, Thomson Scientific), but only 14 articles not written by the original proponents of POM include the term ‘pattern-oriented’ in their abstract.

There seem to be several reasons for the term POM not becoming popular. First, ‘pattern-oriented’ does not emphasize the key feature of POM that modelling should be oriented towards multiple patterns. There has not yet been an explicit, one-sentence definition of POM that makes this clear. Therefore, we provide such a definition: POM is the multi-criteria design, selection and calibration of models of complex systems.

Second, it has not been clear how POM differs from what modellers and scientists do anyway. The answer is: there is no fundamental difference, but POM is designed to make the ‘multi-scope’ approach to modelling explicit and systematic. POM can help establish a new culture in ecological modelling focused on structural realism, predictions and ‘strong inference’. Third, no previous journal articles have explained in detail how POM really works.

Although POM is not yet popular as a term, its underlying ideas have been used in many studies and often led to important results. Table 1 summarizes 13 studies that explicitly refer to POM. This mini-review shows that POM can be used for all kinds of questions and systems. It also shows, strikingly, how weak patterns typically ignored in ‘monoscopic’ approaches can help infer strong insights. Patterns vary greatly in complexity and information content, ranging from system-level patterns such as disturbance–diversity relationships or frequency–area distributions of wildfires [35] to single numbers such as population size and sex ratio [31]. Time series can, even if short, contain enough information for making inference if they describe the response to a major disturbance [29] or include several state variables [25]. Patterns were taken from experiments [29,36], targeted field studies [24], databases [28] and literature reviews [31].

Table 1.

Example studies that use the pattern-oriented modelling approach and explicitly refer to it.

discipline: system	question	patterns used	use of patterns	major insights
behavioural ecology: goose foraging in farm fields [23]	how is the decision to forage in groups affected by the foragers' information on habitat quality and on group benefits?	seasonal difference in flock sizeincreasing number of geese foraging on wheat from mid-April seasonal changes in differences between roost and foraging sites higher exploitation of rice fields that are farther away from the roost seasonal pattern in the rate of fat deposition	model selection (four alternative submodels for decision making)	the submodel assuming incompletely informed foragers with benefits of group foraging best reproduced all five patterns
landscape ecology: elk foraging and habitat selection [24]	what are the effects of roads on the distribution and foraging movement of elk?	proportion of elk observations occurring within 11 road proximity intervals and six general classes of vegetation	model selection (four alternative movement models)	elk responses to growing road networks are nonlinear, exposing thresholds for road density effects
microbiology: cyanobacteria in laboratory cultures [25]	what are the biochemical mechanisms driving the circadian clock of a unicellular cyanobacterium, and how does the clock affect fitness?	time series of the concentration of 20 different types of molecules, under a variety of growth conditions	parametrization (manually and by visual inspection)	unrealistic model output led to the identification of a missing process
population ecology: European eel populations [26]	how can watershed management increase the biomass of spawning eels?	silver eel production in a watershed is not unlimiteddecreased recruitment leads to changes in sex ratios, favouring females	model designmodel selectionparametrization	recommendation for management to concentrate mitigation efforts on the downstream part of the watershed
		eel abundance in rivers decreases exponentially with distance from the sea
		sex ratio changes in favour of females with distance from the sea sex ratio changes with increasing recruitment, from purely female to purely male (related to second pattern)
plant ecology: treelines (ecotones) [27]	does the array of processes underlying tree line formation vary among sites, or do local heterogeneities and site idiosyncrasies dominate over prevailing mechanisms?	density of seedlings, adults and krummholz individualsmean height of individuals (excluding krummholz) at different locations along the treeline transect (data from field studies on four sites)	parametrization (using summary statistics, likelihood functions and Monte Carlo Markov Chain methods)model selection (based on Aikaike Information Criterion)	variation in tree line physiognomy observed at four sites reflects changes in the relative importance of certain nonlinear responses
community ecology: stream fish communities [28]	how do patterns of fish diversity emerge in river networks?	local species richnesss (LSR) in different geographical regions which directly drain to a group of streams (mean LSR as a function of topological distance to outlet; frequency distribution of LSR)	model designmodel selection (dispersal kernel)parametrization	neutral theory, implemented via meta-community models, can reproduce biodiversity patterns of stream fish in dendritic river networks (if appropriate dispersal kernel and local capacities are assumed)
		species occupancies in this regions (rank-occupancy curve)
		between-community, or β, diversity (Jaccard's similarity index as a function of the topological distance between region pairs)
population ecology: mangrove crab habitat selection and population dynamics [29]	what explains movement of mangrove crab into new areas, and how does movement effect recovery after fishing?	recolonization dynamics on experimentally cleared plots with/out leaving crab burrows intact (abundance versus time)	model selectionparametrization	local competition among crabs explains recovery better than a null model
plant ecology: tree architecture [30]	how do trees regulate their structure in response to changing light conditions during growth?	growth in size, shape, and biomass follows a sigmoid curve ending in a steady stateindividual trees have more leaves where there is more lighttrees remain at a size below their physiological limits	validation (secondary predictions)	trees change their structure during growth in response to changing light gradients to maximize carbon gain by optimal placement of structural elements, taking into account basic morphological properties and carbon balance
		allometric relations such as leaf to plant mass ratio were constant during a tree's growth, but trees in different light environments had different scaling exponents
		trees strongly adjust their reproductive investment to the prevailing forest light environment
conservation biology: amphibian populations [31]	will a population increase or decrease, considering the high uncertainty in census data?	final population size final adult sex ratioproportion of toads returning to their natal pondmean maximum distance moved	model selection (of 16 full models which differ only in parameter values)	the range of plausible survival estimates can be narrowed the previously unknown over-winter survival of metamorphs can be estimated the uncertainty in population projections can at least be quantified
marine ecology: mussel beds [32]	does self-organization explain regular spatial patterns in mussel beds?	spatial patterns (cluster size, point pattern statistics) changes in spatial patterns with density relation between cluster size and movement speed	model selection (additional submodel needed to explain patterns)	interactions among individuals explained observed spatial patterns, supporting the self-organization hypothesis
plant ecology: savannahs [33]	what is the role of asymmetric competition and spatial patterns on the self-thinning trajectory?	self-thinning line degree of size inequalityaverage size of the population at which a certain degree of size inequality is reached	model design (starting with simple model version and generic patterns, proceeding to refined versions and specific patterns)	asymmetric competition and spatial distribution of individuals contribute to size inequality and their contribution varies greatly
			model selection
plant ecology: treelines (ecotones) [34]	what causes differences between commonly observed treeline types (abrupt/smooth; with/without krummholz)?	abruptness in tree density and tree height along altitudinal gradient (data from fields study on two sites)	parametrization model selection (only certain combinations of processes, represented by certain parameter ranges, allowed for certain	positive feedback and strongly increasing growth inhibition required for high krummholz densities abruptness in adult tree density positively correlated with facilitation strength and growth inhibition
			patterns to emerge)	treelines with abrupt height transitions require both low growth inhibition and a strongly increasing mortality
plant ecology: forest fire spread and extent [35]	do forest fire models from ecology and statistical physics produce the same results, for the same reasons?	characteristics of burnt area (shape index, edge index, unburned area, median size of unburned ‘islands’)frequency–area distribution of wildfires (slope of the ‘power law’)hump-shaped relationship between disturbance intensity (annual area burned) and diversity of successional stages	model design model selectionparametrization	seemingly different models are essentially identical a unified model includes two key processes the unified models fails to reproduce observed variation in the slope of frequency–area distributions and presumably is missing a key process

The column ‘patterns used’ in table 1 indicates that the core of POM is creativity in identifying and combining patterns. The creativity lies in combining information not previously considered together, or looking at data from a new perspective, or by collecting new data specifically to test the model. There are famous examples of such creativity: Watson and Crick combined different patterns from different kinds of chemical analysis to narrow down possible structures of DNA, and Mendeleev inferred the periodic table of elements by identifying patterns in their physico-chemical properties. These discoveries resulted from creatively seeking and combining various pieces of evidence as a detective does. POM thus requires that we, as ecology detectives, combine systematic ‘dragnet investigations’ with the creative attitude of Sherlock Holmes.

Table 1 indicates that POM is less often used explicitly for model design. This is probably because patterns usually are taken into account in model design implicitly or intuitively. Modellers often decide that a certain entity, state variable or process should be in a model for it to capture the real system's key features. Still, explicitly following the POM model design protocol would force us to adopt the multi-scope view and remind us of the Sherlock Holmes part of science.

5. Examples

There has been much more sound POM in ecology than captured by our mini-review: many highly predictive, and theoretical, models have been developed and analysed according to one or more of POM's three elements without referring explicitly to POM. For example, models of fish schools and bird flocks are clearly based on multi-criteria model selection, having evolved over a long series of increasingly sophisticated field observations and simulation experiments that contrasted alternative submodels [37–39]. The highly predictive shorebird models of Stillman, Goss-Custard and co-workers [1,40] reproduce numerous patterns at multiple levels of organization, but these patterns have not been comprehensively listed and discussed. The following sections highlight studies illustrating the potential of POM for predictive ecology.

(a). Forest fire models

The size–frequency distribution of forest fires has been observed in many kinds of ecosystems to robustly follow a power law (the log of fire frequency decreases linearly with the log of fire size). Statistical physicists have used very abstract models to explain this distribution, linking it to the theory of ‘self-organized criticality’ (SOC): systems can organize themselves into a state characterized by self-similarity and, hence, a power law in the size frequency distribution of disturbance events. The classical model in this field includes a grid of cells that can be empty or contain a tree [41]. Cells are subject to lightning strikes which, if they hit a tree, spark a fire. Fire spreads deterministically to neighbouring cells with trees and destroys the trees. New trees emerge stochastically on empty grid cells. In contrast, generic wildfire models from ecology assume that fire spread is stochastic, that the flammability of a grid cell depends on the time since the cell burn the last time, and that succession and, hence, the local increase of flammability is deterministic [42,43].

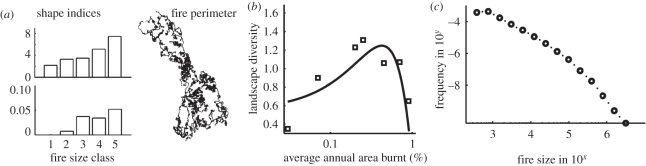
Thus, these two types of model seem completely different: deterministic fires and stochastic regrowth of vegetation in the physicists' model, stochastic fires and deterministic regrowth in the ecologists' models. The advantage of the physicists' model is that many of its features can be deduced analytically, whereas the ecologists' models are more realistic. In particular, Ratz [42] showed that his model not only reproduces the key power-law pattern, but also two additional patterns: the typical size and shape of unburned ‘forest islands’ within burnt areas, and a hump-shaped relationship between disturbance intensity (average annual area burned) and diversity of successional stages (figure 2).

Figure 2.

Three patterns reproduced by generic forest fire models that include a ‘memory effect’, i.e. local flammability that depends on the time since the site last burned, and assume fire spread is only limited by fuel availability. (a) Shape indices of fires of different size classes. (b) Hump-shaped relationship between disturbance intensity (average annual area burnt) and the diversity of successional stages. (c) Heavy-tailed, power-law-like frequency distribution of fire sizes. (Adapted from Zinck & Grimm [35]; © 2009 The University of Chicago). (b) Squares, data: Suffling (1988), Ontario; thick line, least-squares fit.

Zinck & Grimm showed that these two additional patterns are also produced by the physicists' model if grid cells represent entire tree stands of several hectares instead of individual trees [35,44]. They also showed that the key process for reproducing all three patterns is a ‘memory effect’: flammability increases with the time since a site last burned. Interestingly, this unified model did not reproduce a fourth pattern: that the slope of fire size distributions observed in different ecoregions varies between −1.9 and −1.3. The unified model instead consistently produces a slope of −1.5. This failure indicated that the true generative mechanisms underlying wildfire regimes were not yet fully captured.

In subsequent work, Zinck et al. [45] found that the fire models' assumption that fire spread is controlled only by fuel availability produces the unrealistic results. Fire spread is also affected by soil moisture, topography, species composition and other regional factors. A parameter for average spread success controls the slope of fire size distributions and the qualitative characteristics of fire regimes, and even separates two quantitatively and qualitatively distinct fire regimes. Thus, environmental changes can induce a sudden change in the characteristics of a forest system, a result that cannot be produced by the SOC models.

This example shows how considering additional, very simple, patterns can falsify models that, while not completely wrong, lack the key processes needed to understand ecosystem response to environmental change. While both the physics and ecology models could reproduce the first three patterns, the fourth pattern could be reproduced only by the ecology model's deterministic depiction of succession.

(b). Snowshoe hare cycles

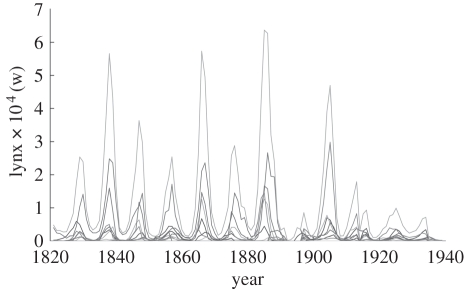
The census time series of the Canadian lynx and one of its main prey, the snowshoe hare, are among the longest available, spanning 200 years. They are included in many textbooks as a classical example of predator–prey cycles. However, different models can explain predator–prey cycles, so the single pattern that cycles exist is not sufficient to determine which models contain the mechanisms that actually produce the cycles. Blasius et al. [46] plotted the time series not for all of Canada, but separately for seven regions (figure 3). They found two new simple but decisive patterns: cycle length was constant in all regions, whereas amplitude varied chaotically. They then searched the literature on dynamic systems for equations that would reproduce these two patterns. The system they found could be interpreted as a tri-trophic system that also represents the hare's food. Interestingly, the dynamic system had one critical term that could be attributable to prey-switching by lynx at low hare densities. In fact, lynx switch to squirrels in such situations. Here again, the use of multiple patterns allowed the key mechanisms of the system to be inferred and a more realistic model to be developed.

Figure 3.

Time series of lynx abundance in six regions in Canada. (Adapted from Blasius et al. [46]; data from Elton & Nicholson [47].)

(c). Adaptive rangeland management

Two schemes for semi-arid rangeland management have been debated for decades. Livestock density can be kept constant, or management can be adaptive by adjusting livestock density to the available vegetation biomass, which varies from year to year owing to rainfall variation. Predicting which scheme is most effective requires an accurate model of how livestock production depends on rainfall.

Jakoby [48] developed a generic difference equation model that has state variables for green, brown and storage biomass; rainfall in rainy and dry seasons; and the number of livestock. To calibrate this model, Jakoby used pattern-oriented parametrization. From the literature, he identified four very general patterns characterizing an acceptable representation of semi-arid rangelands in general. These patterns specify (i) the long-term conditions of overgrazing under which the rangeland system degrades and (ii) the rainfall and reduced grazing conditions under which the system recovers. Furthermore, (iii) some level of grazing is sustainable under average conditions, so that constant livestock management is possible in principle; and (iv) within certain limits, green biomass increases with annual rainfall.

Out of 10⁹ parameter sets tested, 11 316 reproduced all four patterns simultaneously. The structure of the successful parameter sets provided important insights. Most importantly, adaptive management was predicted to be substantially more effective than constant management when using the successful parameter sets but not when using random parameter sets. This example shows that pattern-oriented calibration can be beneficial even for simple generic models. In the absence of site-specific data, the POM filtering process narrowed the range of parameter values enough for the model to produce useful conclusions.

(d). Reverse pattern-oriented modelling for evaluating existing models

While POM is intended primarily as an approach for designing models, it can also be used in reverse to assess existing models: which models reproduce characteristic patterns well enough that we should have confidence in them? An example is available from the business economics literature. Heine et al. [49] evaluated four models addressing one problem: the ‘Groves mechanism’ is designed to make division managers of a big company report their profits honestly instead of overstating them (by rewarding managers by how well the whole company as well as their own division performs). However, the Groves mechanism can be undermined by collusion among managers. Models from simple game theory to more complex simulators have been used to explore the conditions likely to produce such collusion. Heine et al. noticed ‘ad hocery’ in the models' design and tried to evaluate their structural realism. They identified six broad patterns, for example, that collusion is favoured under long time horizons and when group composition is stable, and determined whether each of the models reproduced the patterns—or even had enough structure to address the pattern. One model addressed only one pattern and contradicted it; two models addressed two patterns; the most convincing model addressed three patterns and reproduced two of them partially and one convincingly. Only this last model was considered structurally realistic enough to leave ‘little room for arbitrary model design or questionable parameter calibration’ [49].

This reverse application of POM can be an important tool for determining what processes and structures are needed to predict widely studied phenomena. Given a set of models varying in complexity and structure and a set of characteristic patterns, POM can be used to identify the structure models need to make predictions about the system.

6. Discussion

POM has long been used implicitly in many convincing modelling studies, but its explicit use is an important way to make ecological models more structurally realistic and predictive. This article is intended to promote explicit use of POM by providing specific guidance (as does, in greater detail, a new book [12]). The following sections discuss important challenges, and how predictive systems ecology could change through wider use of POM.

(a). Challenges

One of the most important benefits of POM is making model design less ad hoc, but the selection and assessment of patterns in POM can seem itself to be ad hoc. If two teams of modellers independently identified characteristic patterns for a savannah model, would they select the same ones? Part of the answer is that the model's purpose is a decisive criterion for what patterns are useful. If both teams addressed the same question, for example, explaining tree–grass coexistence or setting limits on grazing rates to prevent shrub encroachment, the set of patterns they choose should be similar, but probably would not be identical.

This remaining variability can be productive. If different people consider different patterns characteristic, then the argument is about data and observations, not ad hoc assumptions. And, because POM leads to mechanistically realistic models that can produce a variety of predictions, the ultimate comparison of competing models is available: which is most predictive of new patterns not considered in its development?

Pattern-oriented parametrization of complex models is powerful but includes many experimental decisions regarding the sequence in which patterns are used as filters, the criteria for pattern matching and the importance of different patterns. Computational feasibility can also be a limitation. When calibrating many parameters, simple algorithms such as random search or Latin hypercube design may not be feasible, but a variety of techniques from the optimization literature are available [22].

Finally, it will not always be clear whether a model developed via POM should really be used to predict system responses to novel environmental conditions. The answer is clearly no if the model's key mechanisms are determined mainly by parameters estimated by calibration to observations, but can be yes if instead the model's dynamics emerge from lower level processes (such as physiology and adaptive behaviour) that can be parametrized and tested independently of the whole model. If the submodels representing such lower level processes can be parametrized for wide ranges of environmental conditions—which is often possible using laboratory experiments on individuals—then the model may be well suited to predict system responses to such conditions. The two models underlying figure 1 are such models, where the underlying mechanisms are optimal foraging and photosynthesis.

(b). Outlook

While POM is still catching on as an explicit framework for ecological modelling, the science of ecology is primed for its use. Ecologists have long realized that what we call theory and models has been of limited use for predicting how populations and ecosystems respond to disturbance and environmental change [50]. Like the other complex sciences, ecology is struggling to develop theory of the type used in physical sciences: models that are accepted as theory because they have been tested and proved useful for making predictions and solving real problems. One approach to such theory is sophisticated analysis of long data time series, but this approach is insufficient for ecological problems because we rarely have long and accurate time series, especially for novel and even unobserved conditions such as climate change. A second approach is to analyse and model systems at several levels at once. The need for cross-scale and multi-level analyses, especially the linking of individual behaviours and interactions to system dynamics, is clearly recognized by modern ecologists [51]. This paper is about how to do such analyses, by using POM as a multi-scope that lets us see enough about the different levels of a system to identify and understand the processes that produce its dynamics.

Using POM does not require a significant change in how people build models and do ecology. Instead, it provides a framework within which the various ways of doing ecology, from studying behaviour, physiology and autecology to modelling populations, communities and systems can be tied together into a productive process that leads to reliable predictions. Multi-level models produced via POM tend to be more complex than the traditional models of theoretical ecology, but because they can contain information observed at multiple levels their uncertainty need not always increase inexorably with complexity and their applicability need not be limited to conditions under which system-level parameters have been fit. In fact, our experience has been that POM can inspire empirical research targeted to reduce the most important uncertainties in our understanding of a system. If a model fails to reproduce some observed pattern, why? POM can both identify the mechanisms that most need research and provide a way to make use of the new information effectively.

This kind of modelling requires expertise in both lower and higher levels of a system and, often, on the physical and environmental processes that are external drivers of the system, plus the computer science needed to build a reliable simulator. Hence, predictive ecology may not be the province of the individual graduate student or mathematician but (as the successes so far indicate) may often require an interdisciplinary team that conducts field research as well as modelling while seeking new ideas and methods from other such teams. Predictive systems ecology may not require ‘big science’ but perhaps bigger science than the tradition of researchers working in isolation on small, highly simplified problems.

The mini-review of POM, plus the authors' experience, indicates that multi-scale and multi-level modelling is a rapidly developing approach with many exciting prospects for important discoveries. For many well-studied systems and problems, a wealth of knowledge is already available at the different levels and only the key links between levels—often, useful submodels for adaptive individual behaviour—are needed to create highly realistic and powerful models.