Dielectric Boundary Forces in Numerical Poisson-Boltzmann Methods: Theory and Numerical Strategies

Abstract

Continuum modeling of electrostatic interactions based upon the numerical solutions of the Poisson-Boltzmann equation has been widely adopted in biomolecular applications. To extend their applications to molecular dynamics and energy minimization, robust and efficient methodologies to compute solvation forces must be developed. In this study, we have first reviewed the theory for the computation of dielectric boundary forces based on the definition of the Maxwell stress tensor. This is followed by a new formulation of the dielectric boundary force suitable for the finite-difference Poisson-Boltzmann methods. We have validated the new formulation with idealized analytical systems and realistic molecular systems.

I. Introduction

Solvation interaction is one of the essential determinants of the structure and function of proteins and nucleic acids [1-5]. It has been shown that continuum electrostatics represents an effective and physically sound approach to account for a number of phenomena involving solvent electrostatic effects on the function of biological macromolecules [6-9]. Due to the availability of high performance computing resources, continuum modeling of electrostatic interactions, which is based upon the numerical solutions of the Poisson-Boltzmann equation (PBE), has been widely adopted in biomolecular applications [3-5,9-11]. Among the numerical solution methods for PBE, finite difference methods (FDM) [12-17], finite element methods (FEM) [18-21], and boundary element methods (BEM) [22-28] are mostly used.

A disadvantage of the numerical PBE methods is that it is conceptually difficult to incorporate them into molecular mechanics algorithms, mainly because of the problem of assigning solvation forces [19,29-34]. Along with other limitations, the numerical PBE methods are mostly used for static conformations of biomolecules in practical applications. To extend the application of these methods to molecular dynamics and energy minimization, robust and efficient methodologies to compute solvation forces must be developed. It has been shown that solvation forces can be divided into two components: reaction field forces and dielectric boundary forces [19,29-34]. Reaction field forces are straightforward to compute, but accurate computation of dielectric boundary forces (DBF) is a challenge. To date, it is still impossible to achieve energy-conserved molecular dynamics simulations when the numerical PBE methods are used, especially at realistic spatial discretization resolution of 0.25 to 0.50 Å.

Many efforts have been invested to calculate the DBF [29-32,34]. The “virtual work” method is, in a sense, the most definitive [29]. In the “virtual work” method the electrostatic energy G is recalculated for small displacements d of each atom in the x, y, and z directions, respectively. The numerical force is then −ΔG / d for each direction. The limitation of this approach, however, is that at least four full numerical calculations are required in order to calculate each force vector. Apparently, this is only realistic for molecules treated as rigid bodies. In addition, the numerical forces, defined as the negative finite-difference derivatives, are very difficult to converge when the electrostatic energies are computed numerically due to the cancellation of significant digits in the subtraction of two large numbers.

Davis and McCammon proposed a DBF formulation by examining the integration of the Maxwell stress tensor for the classical two-dielectric model. The DBF surface density was shown as [29]

$${\mathbf{f}}_{DBF}=\frac{1}{4\pi }({\epsilon }_o-{\epsilon }_i)({\mathbf{E}}_o\cdot {\mathbf{E}}_i)\widehat{\mathbf{n}},$$ (1)

where ε_o and ε_i are the dielectric constants of the solvent and the solute, respectively, and E_o and E_i are the electric field evaluated on the solvent and solute sides of the molecular surface, respectively. Note that use of eqn (1) is difficult for the FDM solutions because the grid potentials close to the solute/solvent dielectric interface are the least accurate. In addition, it requires a numerical surface integration that can be very expensive within the FDM. Recently Che et al. revisited the DBF calculation through a variational strategy in the classical two-dielectric model [34]. Given the assumption that the normal surface field contributes predominantly to DBF, they showed that the DBF surface density can be formulated as

$${\mathbf{f}}_{DBF}=\frac{1}{8\pi }\left(\frac{1}{{\epsilon }_i}-\frac{1}{{\epsilon }_o}\right){\mid \epsilon \nabla \phi \mid }^2\widehat{\mathbf{n}},$$ (2)

where ε∇φ represents the continuous normal dielectric displacement vector on the solute/solvent dielectric interface.

The BEM is another promising approach to incorporate the continuum electrostatics into molecular mechanics simulations [35]. The DBF calculation in the BEM using a polarization charge method was first described by Zauhar [30], who showed that the DBF surface density can be calculated as

$${\mathbf{f}}_{DBF}=\left[2\pi {\sigma }^2{\epsilon }_i+\frac{1}{8\pi }({\epsilon }_o-{\epsilon }_i){\mid {\mathbf{E}}_o\mid }^2\right]\widehat{\mathbf{n}},$$ (3)

where σ is the surface polarization charge density. This expression was derived from eqn (1). Use of the surface polarization charge density is straightforward in certain types of BEM where the Poisson's equation can be solved through the iteration of the surface polarization charge density. Cortis et al. also tried to compute the DBF via the Maxwell stress tensor for their FEM leading to the same formulation as that of Zauhar [19].

Gilson et al. presented a variational approach for the DBF [31], and it was further tailored into a numerical algorithm for the FDM. Their expression for the DBF volume density can be expressed as

$${\mathbf{g}}_{DBF}=-\frac{1}{8\pi }{\mid \mathbf{E}\mid }^2\nabla \epsilon ,$$ (4)

where ε is the dielectric constant and E is the electric field. Note that the direction of the DBF in eqn (4) is consistent with that in eqn (1) and its equivalent formulations because the gradient of dielectric transition is in the normal direction of the dielectric interface. Im et al. proposed a method equivalent to eqn (4) as [32]

$${\mathbf{g}}_{DBF}=\left[\frac{1}{8\pi }\varphi \nabla \cdot \left(\frac{\partial \epsilon }{\partial \epsilon }\nabla \varphi \right)\right]\widehat{\mathbf{n}},$$ (5)

where ϕ is the total electrostatic potential, r represents the atomic coordinates. Apparently both eqn (4) and (5) require smoothly varying dielectric constants for stable numerical performance [33]. This excludes the classical two-dielectric model where ∇ε is infinite on the dielectric interface. Even if the harmonic average is used, direct numerical calculation of ∇ε is still unstable in molecular dynamics. This leads to large and unstable DBF that often does not satisfy the “virtual work” principle. Numerical approximation of ∇ε may alleviate the problem, but instability cannot be completely eliminated in molecular dynamics simulations [31,36].

Even with these pioneer developmental efforts, the DBF calculation remains to be a bottleneck that limits the wide application of numerical PBE methods in molecular simulations. Nevertheless, these prior efforts have laid down the foundation for us to develop more accurate and robust methods. In this study, we intend to resolve the challenge within the FDM and classical two-dielectric framework, which, in recent comparative analyses of PB-based solvent models and the explicit solvent models, can reasonably reproduce the solvation electrostatic potential, energies, and forces simulated in the explicit solvents for a wide variety of biomolecules [37-41]. However, the proposed method can also be applied to other types of dielectric models with smoothly varying dielectric constants [32,33,42]. In the following we first review the theory for the DBF calculation based on the Maxwell stress tensor. This is followed by the development of a new algorithm particularly designed for the FDM solutions. The performance of the new algorithm is then analyzed in detail and is compared with the analytical method and the virtual work principle [29,31].

II. Methods

A. Theory

It is well known that the electrostatic force volume density (g) can be derived from the divergence of the Maxwell stress tensor (P) as [43]

$$\begin{array}{cc}\hfill \mathbf{g}=\nabla \cdot \mathbf{P}& =\frac{\partial }{\partial x}(\widehat{\mathbf{i}}\cdot \mathbf{P})+\frac{\partial }{\partial y}(\widehat{\mathbf{j}}\cdot \mathbf{P})+\frac{\partial }{\partial z}(\widehat{\mathbf{k}}\cdot \mathbf{P})\hfill \\ \hfill & ={\rho }^f\mathbf{E}-\frac{1}{8\pi }{\mid \mathbf{E}\mid }^2\nabla \epsilon -\Delta \Pi \nabla \lambda ,\hfill \end{array}$$ (6)

where ρ^f is the fixed charge density, E is the electric field, ε is the dielectric constant, and ΔΠ is the excess osmotic pressure [44], λ is the Stern layer defined so that it is 1 in the regions accessible to the mobile ions and 0 elsewhere. This is consistent with the formulation of Gilson et al. [31] derived from the variation of the total electrostatic free energy. Here the second term of eqn (6) is responsible for the DBF

$${\mathbf{g}}_{DBF}=-\frac{1}{8\pi }{\mid \mathbf{E}\mid }^2\nabla \epsilon .$$ (7)

To remove the potential numerical instability in ∇ε and develop a new formulation that is more suitable for the FDM, we utilize a revised PBE. In the vicinity of the dielectric boundary ρ^f = 0, we have

$$\nabla \cdot \left(\epsilon \mathbf{E}\right)=0.$$ (8)

Differentiation by parts of the left hand side of eqn (8) gives

$$\nabla \epsilon \cdot \mathbf{E}+\epsilon \nabla \cdot \mathbf{E}=0.$$ (9)

The second term of eqn (9) can be rewritten as

$$\epsilon \nabla \cdot \mathbf{E}=\epsilon \nabla \cdot ({\mathbf{E}}_c+{\mathbf{E}}_{RF}),$$ (10)

where E_c is the Coulomb field and E_RF is the reaction field. Since ∇·E_c = 4πρ^f = 0 in the vicinity of the dielectric boundary, eqn (10) can be simplified as

$$\epsilon \nabla \cdot \mathbf{E}=\epsilon \nabla \cdot {\mathbf{E}}_{RF}=4\pi \epsilon {\rho }^{pol},$$ (11)

where ${\rho }^{pol}=\frac{1}{4\pi }\nabla \cdot {\mathbf{E}}_{RF}$ is the polarization charge density on the dielectric boundary. With eqn (9) and (11), ∇ε·E can be written as

$$\nabla \epsilon \cdot \mathbf{E}=-\epsilon \nabla \cdot \mathbf{E}=-4\pi \epsilon {\rho }^{pol}.$$ (12)

To utilize the above conclusion to eqn (7), we first transform eqn (7) via a dot-product by E on both sides

$${\mathbf{g}}_{DBF}\cdot \mathbf{E}=-\frac{1}{8\pi }{\mid \mathbf{E}\mid }^2\nabla \epsilon \cdot \mathbf{E}=\frac{1}{2}\epsilon {\rho }^{pol}{\mid \mathbf{E}\mid }^2.$$ (13)

Since the direction of g_DBF follows the gradient of the dielectric constant, i.e. the normal direction of the surface (n̂), the left hand side of eqn (13) can be further transformed as

$${\mathbf{g}}_{DBF}\cdot \mathbf{E}=g_{DBF}\widehat{\mathbf{n}}\cdot \mathbf{E}=g_{DBF}{E}_n,$$ (14)

where E_n is the normal component of the surface field. Therefore

$$g_{DBF}=\frac{{\mathbf{g}}_{DBF}\cdot \mathbf{E}}{E_n}=\frac{\frac{1}{2}\epsilon {\rho }^{pol}{\mid \mathbf{E}\mid }^2}{\mathbf{E}\cdot \widehat{\mathbf{n}}}.$$ (15)

Thus g_DBF can finally be written as

$${\mathbf{g}}_{DBF}=g_{DBF}\widehat{\mathbf{n}}=\frac{1}{2}{\rho }^{pol}\frac{\epsilon {\mid \mathbf{E}\mid }^2}{E_n}\widehat{\mathbf{n}}=\frac{1}{2}{\rho }^{pol}\frac{\epsilon {\mid \mathbf{E}\mid }^2}{\mathbf{E}\cdot \widehat{\mathbf{n}}}\widehat{\mathbf{n}}.$$ (16)

An equivalent form of eqn (16) is, by noting that D = εE and D_n = εE_n,

$${\mathbf{g}}_{DBF}=\frac{1}{2}{\rho }^{pol}\frac{\mathbf{D}\cdot \mathbf{E}}{E_n}\widehat{\mathbf{n}}=\frac{1}{2}{\rho }^{pol}\frac{{\mid \mathbf{D}\mid }^2}{D_n}\widehat{\mathbf{n}}.$$ (17)

B. Numerical algorithm

Because of the large jump in the dielectric constant between the solute and the solvent (typically, in water the dielectric constant is about 80, and in molecules it is set to be 1 - 4), the tangential components of the electric field are trivial and eqn (16)/(17) can be replaced by

$${\mathbf{g}}_{DBF}=\frac{1}{2}{\rho }^{pol}\frac{{\mid \mathbf{D}\mid }^2}{D_n}\widehat{\mathbf{n}}\approx \frac{1}{2}{\rho }^{pol}{D}_n\widehat{\mathbf{n}}=\frac{1}{2}\epsilon {\rho }^{pol}{E}_n\widehat{\mathbf{n}}.$$ (18)

Eqn (18) also rules out the possibility of the large numerical error induced by a small electrical displacement. Use of eqn (18) requires the electric field or the electric displacement at the grid points, but in the FDM, they are defined on the grid edge centers, equal to the finite difference derivative of the potential of neighboring grid points. There are different ways of interpolating the electric field or the electric displacement. In the contact region of the surface, we used the one-sided least-square interpolation method to interpolate the electric field [45]. In the reentrant region, due to the indefinite variation trend of the electric field between adjacent grid points, especially at coarser grid spacings, we used the weighted summation of the electrical displacement at nearby intersection points of the molecular surface and the grid edges.

In the FDM, the surface polarization charges can be regarded as being located at the dielectric boundary grid points [46]. They are computed using the Gauss's law and the grid potential obtained from the FDM. It will be shown below that the grid-based polarization charges are very good numerical representations of the dielectric interface polarization charges and converge very well. Their errors are particularly small when typical grid spacings, i.e. 0.25 ~ 0.50 Å, are used. Given this numerical representation of the polarization charges and eqn (18), the total DBF in the solution system, G_DBF , can be computed numerically as

$${\mathbf{G}}_{DBF}=\int {\mathbf{g}}_{DBF}d\nu \approx \frac{1}{2}\sum _{i=1}^{nbnd}{q}_i^{pol}{D}_{n,i}{\widehat{\mathbf{n}}}_i=\frac{1}{2}\sum _{i=1}^{nbnd}{\epsilon }_i{q}_i^{pol}{E}_{n,i}{\widehat{\mathbf{n}}}_i,$$ (19)

where nbnd is the number of the solute/solvent dielectric boundary grid points where the polarization charges are located. Of course the polarization charges are zero on all other grid points where there is no dielectric variation. $q_i^{pol}$, D_n,i, E_n,i, and n̂_i are, respectively, the polarization charge, normal electric displacement, normal surface field, and surface normal unit vector at dielectric boundary grid point i.

C. Computational details

The PBE methods require the surface definition that seperates the solute in atomic details from the continuum solvent. In the solvent excluded surface definition, the surface is defined as the union of atomic spheres and probe spheres. The accuracy of the finite-difference Poisson-Boltzmann method at a certain finite difference grid spacing can be improved by increasing the number of probe centers, and the probes that are in concurrent contact with three atoms and are responsible for the spherical triangles in the reentrant region are of particular importance to achieving high accuracy in surface areas, electrostatic energies, and forces. We always guarantee the inclusion of the probes in contact with three atoms no matter what density of the probes is. In the case of probes in contact with more than three atoms, the associtated reentrant region is divided into multiple spherical triangles, each of which is dealt with its own probe.

The numerical force elements need to be assigned to atoms. If the force element is exerted on the contact region of the surface, it can be directly assigned to the atom which the contact region belongs to. If the force element is exerted on the reentrant region of the surface, we can apply the singular value decomposition (SVD) method to assign the force to the atoms that form the reentrant region. When the probe contacts two atoms, the SVD method is equivalent to the method introduced by Gilson et al. [31], i.e., the force component that is in the plane defined by the centers of the probe and the two atoms is retained and distributed to the two atoms according to the parallelogram law, while the force component that is out of the plane is left out. When the probe contacts three atoms, the force element is distributed to the three atoms by solving a complete linear system.

An issue important for stable dynamics simulations is the numerical uncertainty of solvation forces when the finite-difference grid is randomly positioned. Sensitivity of grid positions with respect to the solute molecule has been a particularly annoying limitation in current numerical FDM solutions. If not specified otherwise, a total of 96 randomized rotations and translations were used to reduce the numerical uncertainty.

The dielectric constant outside was set as 80.0, and the dielectric constant inside was set as 1.0. The probe radius was 1.4 Å. The grid spacing was chosen from 1/2 Å to 1/16 Å. The finite-difference convergence criterion was set to be 10^-9. The PBE was solved with the charge singularity removed [47]. All molecular structures were first processed with Leap in AMBER 10 [48] and the modified Bondi radii were used except the radii of all hydrogen atoms were changed to 1.0 Å. No electrostatic focusing was used. Other parameters were set to be default as in the PBSA program [17,49,50] of AMBER 10.

In the test section, we will compare the new formulation with the virtual work principle. Both methods were used to compute the force on a base of a base pair. The virtual work force was calculated in the following way. First, the total electrostatic energy was computed by the numerical reaction field energy at given grid spacings plus the analytical Coulomb energy in small distance increments between the two bases. Next the discrete electrostatic energy was processed with spline curve fitting. The electrostatic force on one of the two bases was obtained by taking the first derivative of the smoothed electrostatic energy with respect to the distance between the two bases. Then the van der Waals force was computed using the 6-12 Lennard Jones fomula. Finally the nonbonded virtual work force was the summation of the electrostatic forces and the van der Waals forces.

III. Results and discussion

A. Model systems

We first used a well-studied testing system, a single dielectric sphere imbedded with point charges, to study the validity of the new formulation. The radius of the sphere is 2.0 Å, about the size of a united carbon atom, centered at (0, 0, 0). Three typical situations are considered: (a) charged system with a unit positive charge positioned at (0.5, 0, 0); (b) dipolar system with two unit charges located at (-0.5, 0, 0) and (0.5, 0, 0), respectively. (c) quadrupolar system with four unit charges located at (-0.5, 0.5, 0), (-0.5, -0.5, 0), (0.5, -0.5, 0) and (0.5, 0.5, 0).

It is clear that in all three test cases the DBF distributions converge to the analytical values as the grid spacing is reduced from 1/2 Å to 1/16 Å. Note too that the DBF distributions deviate noticeably from the analytical values at the coarsest grid spacing of 1/2 Å, and the deviation is reduced as the grid spacing is reduced. More quantitatively the average standard deviations and average root-mean-squared (RMS) deviations (between the mean and the analytical forces) of the DBF decrease with a factor of 2 – 4, as the grid spacing is reduced by half (Table 1).

Table 1.

Convergence of dielectric boundary forces (kcal/(mol Å)) in the spherical analytical systems. σ and rmsd are, respectively, the average standard deviations of dielectric boundary forces and average root mean squared deviations of dielectric boundary forces from analytical values. Both σ and rmsd are computed over the 30 bins used to divide the spherical surface.

	1/h	This work
		σ	rmsd
single-charged	2	0.334	0.117
	4	0.101	0.023
	8	0.036	0.009
	16	0.013	0.005
dipolar-charged	2	0.285	0.060
	4	0.083	0.011
	8	0.031	0.008
	16	0.012	0.006
quadrupolar-charged	2	0.215	0.322
	4	0.042	0.042
	8	0.015	0.011
	16	0.005	0.006

B. Molecular systems

Atomic polarization charges

We used two salt-bridging amino acid side chain pairs RD and KD to analyze the convergence of the atomic polarization charges. This is an important issue in our “charge-based” approach. The average deviations (versus the values at 1/16 Å) in Table 2 indicate that the mean polarization charge on each atom converges with reducing grid spacings. It is interesting to note that the mean polarization charge is already quite accurate at the grid spacing of 1/2 Å. Average standard deviations of the atomic polarization charges are also analyzed and shown in Table 2.

Table 2.

Convergence and uncertainty of atomic polarization charges (e) for salt-bridging amino acid side chain dimers RD and KD. σ and rmsd are, respectively, the average standard deviations of atomic polarization charges and the average root mean squared deviations of atomic polarization charges from those computed with the finest tested grid spacing.

	1/h	σ (×10-3)	rmsd (×10-3)
RD	2	2.74	2.28
	4	1.02	1.45
	8	.379	.659
	16	.142	NA
KD	2	3.30	1.69
	4	1.20	.794
	8	.473	.501
	16	.168	NA

Convergence of Atomic dielectric boundary forces

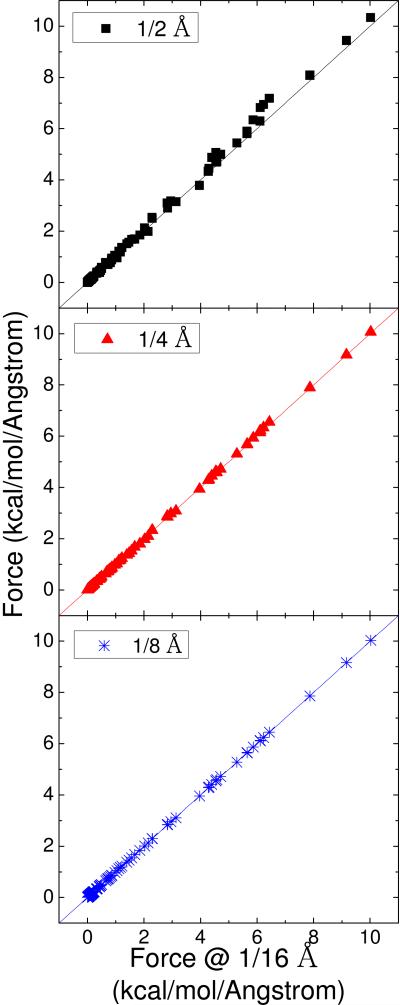
We selected additional hydrogen-bonding base pairs (GC and AT), together with the two salt-bridging amino acid side chain pairs (RD and KD), to test the new DBF formulation. Figure 1 plots the correlations between the atomic DBF at relatively coarse grids (1/2 Å, 1/4 Å, 1/8 Å) and those at 1/16 Å for the four pairs. The relative errors in atomic dielectric boundary forces are a few percentages at 1/2 Å, except the forces on several hydrogen atoms, which are as high as 10% mainly because of the small radius of the atom, 1 Å, and the low ratio of 2 between the radius and grid spacing. At the grid spacings of 1/4 Å and 1/8 Å, the atomic DBFs are quite consistent with the forces at 1/16 Å, suggesting a rapid convergence of the DBFs computed by the new formulation.

Figure 1.

Correlations between atomic dielectric boundary forces (kcal/(mol Å)) computed at the grid spacings of 1/2 Å, 1/4 Å, and 1/8 Å, respectively, and those at the grid spacing of 1/16 Å for the GC dimer and AT dimer.

Comparison with the virtual work principle

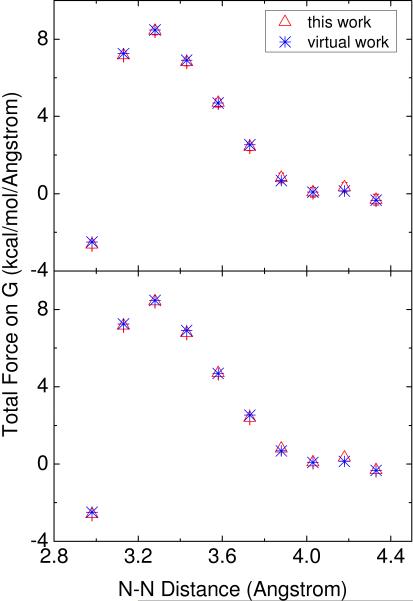
Next we used the GC dimer test case to assess the agreement between the new method and the virtual work principle in reproducing the total nonbonded force between the two bases. Figure 2 plots the total nonbonded force on base G versus the base pair distance (the distance between N-1 of guanine and N-3 of cytosine). The forces by the new formulation were computed at 1/4 Å and 1/16 Å, respectively. Clearly, there is an overall high level of agreement between the new method and the virtual work principle, and the figure also shows the rapid convergence of the new formulation because the results change very little when the grid spacing is changed from 1/4 Å to 1/16 Å.

Figure 2.

Total nonbonded force (kcal/(mol Å)) on base G of the GC dimer with respect to the N-N distance (the distance between N-1 of guanine and N-3 of cytosine). The results of this work are shown in red triangle, and the results of the virtual work method are shown in blue star. The error bar means the standard error of the means. The data were collected with the grid spacings of 1/4 Å (top) and 1/16 Å (bottom).

Singularity removal in field interpolation

Finally, we would like to highlight the importance of the charge singularity removal with a test on the salt-bridging side-chain pairs (RD and KD). Table 3 shows that the standard deviations of the computed forces are smaller with singularity removal than those without singularity removal, indicating a more stable algorithm performance. In addition, RMS deviations and correlation coefficients (CC) of the forces at coarser grid spacings with respect to the forces computed at the grid spacing of 1/16 Å clearly converge faster with singularity removal than those without singularity removal.

Table 3.

Convergence and uncertainty of atomic dielectric boundary forces (kcal/(mol Å)) for salt-bridging amino acid side chain dimers RD and KD with and without singularity removal. σ and rmsd are, respectively, the average standard deviations of atomic dielectric boundary forces and the average root mean squared deviations of atomic dielectric boundary forces from those computed with the finest tested grid spacing.

		w/o singularity			with singularity
	1/h	CC	rmsd	σ	CC	rmsd	σ
RD	2	.995702	.207	.109	.991407	1.05	.307
	4	.999824	.063	.034	.998444	.382	.053
	8	.999959	.024	.013	.999851	.110	.016
	16	N/A	N/A	.005	N/A	N/A	.006
KD	2	.995221	.205	.091	.992494	1.26	.243
	4	.999585	.080	.035	.998621	.395	.051
	8	.999917	.028	.014	.999871	.117	.017
	16	N/A	N/A	.006	N/A	N/A	.007

(CC: correlation coefficient)

C. Limitations of the new formulation and future directions

As we have discussed in the methods, there is no need to worry about the infinite derivative of the dielectric constant in the new formulation that utilizes the dielectric boundary charges. The test results have demonstrated high level of agreement between the new formulation and the analytical method as well as the virtual work principle. However, use of the surface charges has a disadvantage, that is, its scaling, in the order of O(N_atom × N_bnd), is clearly worse than O(N²_atom) because there are always far more dielectric boundary grid points than atoms. Fortunately, the pairwise interaction between the atoms and boundary grid points only needs to be computed once for both the reaction field force and the DBF. Nevertheless, the total cost of the numerical forces can exceed that of the numerical FDM solution in dynamics simulations if a well-optimized solver is used. This shows that better-scaled methods are still needed.

Another difficulty in the DBF calculation comes from the geometric complexity of the widely used molecular surface definition: i.e. there are two types of surface, contact surface from the van der Waals hard sphere surface and reentrant surface from the solvent probe. There are two consequences resulted from the complexity. The first consequence is its unsmooth nature, i.e. the surface curvature is not always continuous. Indeed, discontinuity always occurs where the contact surface joins the reentrant surface. Even more seriously, the curvature does not exist when the reentrant surface is reduced to a point in some geometric arrangements. When the numerical integration of the DBF is evaluated on such a surface, certain loss of numerical stability can be expected even if the new formulation is used.

An apparent possibility is to implement our algorithm for the smooth dielectric transition models that allow surface derivatives to be defined. However there is indeed good physics in the solvent excluded surface definition as recent literatures have suggested. Given these considerations, we are exploring to revise analytical/differentiable molecular surface definitions so that they are consistent with the solvent excluded surface definition.

IV. Conclusion

Numerical PBE methods have been shown to be successful in a wide range of biomolecular applications, but their applications are quite limited in molecular mechanics simulations, in part due to the difficulty in the calculation of the DBF. In this work, we first review the theory for the DBF calculation based on the Maxwell stress tensor. Then a new algorithm is developed for the FDM solutions based on the concept of polarization charges. The performance of the new algorithm is then analyzed in detail and compared with the analytical method and the virtual work principle.

Our analysis shows that the mean polarization charges converge well. We then tested the new DBF formulation with multiple small molecules. The results show that the new formulation is consistent with the analytical method and the virtual work principle. The advantage of the new method is its fast convergence of atomic forces at coarser grid spacings. We also analyzed the effect of charge singularity removal in the computation of the DBF and noticed a significant improvement when the charge singularity is removed.

It should be pointed out that the pleasant numerical behavior of the new formulation comes at a cost, that is, its scaling, in the order of O(N_atom × N_bnd, is clearly worse than O(N²_atom) because there are always far more dielectric boundary grid points than atoms. Nevertheless, the pair-wise interaction between the atoms and boundary grid points only needs to be computed once for both the reaction field force and the DBF.

• Existing methods to compute dielectric boundary forces (DBF) are reviewed.

• New formulation of DBF suitable for the finite difference method is proposed.

• The new method is validated with tests on idealized systems and real molecules.