Abstract
Markov State Models provide a framework for understanding the fundamental states and rates in the conformational dynamics of biomolecules. We describe an improved protocol for constructing Markov State Models from molecular dynamics simulations. The new protocol includes advances in clustering, data preparation, and model estimation; these improvements lead to significant increases in model accuracy, as assessed by the ability to recapitulate equilibrium and kinetic properties of reference systems. A high-performance implementation of this protocol, provided in MSMBuilder2, is validated on dynamics ranging from picoseconds to milliseconds.
1 Introduction
Conformational changes such as myosin procession,1 protein folding,2 and ligand binding3 have long occupied the attention of biophysicists. A predictive, first-principles understanding of conformational dynamics could elucidate these processes in atomic detail, with broad applications in engineering and medicine. Many biophysical experiments probe the fundamental states and rates of a system. For example, the dominant conformational state of a biomolecule can be determined experimentally by NMR spectroscopy4 or X-ray crystallography,5 while the existence of intermediate states can be demonstrated by kinetic studies.6,7 Even at the single-molecule level, dynamics between multiple conformational states can be tracked by monitoring observables (e.g. FRET)8 that report on the conformational details of a molecule. Conformational states and their rates of interconversion remain a unifying paradigm of biophysical studies.
Discrete-time Master equations, or Markov State Models,9–11 formalize this paradigm. In a Markov State Model, one defines a set of conformational states and models the dynamics between them as a Markov jump process on that state space. Predicted conformational states and rates can be extracted from atomistic molecular dynamics simulations of biomolecular dynamics under ambient conditions.12–14 Here we describe an improved protocol for constructing Markov State Models from an ensemble of molecular dynamics simulations. This enhanced protocol has been implemented as version 2.0 of the freely available MSMBuilder software package, available at https://simtk.org/home/msmbuilder. The improvements in MSMBuilder2 include more accurate state definition through hybrid k-centers k-medoids clustering, improved estimates of kinetic and equilibrium properties via a reversible maximum likelihood estimator,9,11 and an extensible Python implementation allowing facile customization. We validate and benchmark the protocol on proteins spanning a range of timescales and sizes.
2 Theory
A Markov State Model9,10,15–17 consists of a set of state definitions and a transition probability matrix characterizing the kinetics on this state space. In this work, we adopt the following conventions. States are labeled integers {1,2, …,n}. Transition matrix entry ij gives the conditional probability of jumping from state i to state j during a time interval (lagtime) τ:
| (1) |
where σ(x) is a function mapping the conformation x onto the state space. Equilibrium conformational dynamics are expected to satisfy detailed balance: that is, πiTij = πjTji, where πi is the equilibrium population of state i. Because of the symmetry of the detailed balance equation, we define a symmetric matrix Xij = Xji = πiTij. This matrix gives the counts between states i and j at equilibrium, normalized such that ∑ijXij = 1. With this definition, the transition matrix can be expressed as T = D−1X, where D = diag(π) is a diagonal matrix of equilibrium populations.
The eigenvalues and eigenvectors of a transition matrix have special significance. Let (λi, vi) be an eigenvalue-eigenvector pair for T (e.g. Tvi = λivi). By comparison to the eigenvalues of a continuous-time master equation rate matrix K, one can show that the eigenvalues of a transition matrix are related to the relaxation timescales (τi) of a master equation via λi = exp(−τ/τi), where τ is the lagtime use to estimate the transition matrix.15,18 For systems satisfying detailed balance, the eigenvalues λi must be real, as the eigenvalue equation can be written as a symmetric generalized eigenproblem: Xvi = λiDvi. We point out that a recent work9 provides an excellent review of the theory of MSMs; another review covers both theoretical and experimental aspects as applied to protein folding.19
To estimate a transition matrix, one must fix a lagtime, which we signify by writing transition matrices with explicit lagtime dependence T(τ). Because they describe physical observables, relaxation timescales should be insensitive to changes in lagtime. However, projecting dynamics onto a finite state space results in dynamics that are only approximately Markovian. Thus, a common test of model consistency is to calculate the relaxation timescales for a sequence of lagtimes.9,10,18 In practice, discretization error manifests itself as erroneously fast timescales for short lagtimes. Indeed, it has been shown9,20 that increasing either the number of states or the lagtime will lead to more accurate models; however, finite sampling and computational resources place limits on the number of states and lagtime.
3 Methods
This paper presents the recent advances in MSMBuilder2. Below, we discuss these advances, both in terms of the nature of the improvement as well as its motivation. We propose the following new protocol for MSM construction, which shares some characteristics with ones previously developed by ourselves and others.9,11,21
Cluster molecular dynamics trajectories using a hybrid k-centers k-medoids algorithm.
Restrict data to its maximal ergodic subgraph.
Estimate transition and count matrices (T(τ), C(τ)) using a maximum likelihood reversible estimator.
While this protocol is similar to previous approaches in broad strokes, these key refinements make the approach more quantitative without increasing computational cost. We note that MSMBuilder2 also allows non-reversible maximum likelihood estimation for systems where reversibility is not desired.
3.1 Hybrid k-centers k-medoids clustering
The first step in MSM construction is to identify conformational states. Because MSM accuracy depends on the quality of state decomposition, enhanced clustering is a natural way to improve MSM methods. In MSMBuilder2, as in other MSM methods, it is vital to achieve kinetic clustering–that is, states sufficiently fine so as to be free from internal kinetic barriers.
Previous work9,11 used an O(kN) approximate k-centers clustering,22 where k denotes the desired number of clusters and N denotes the number of conformations. That algorithm can be viewed as an approximate solution to the problem:
| (2) |
Here, σ(x) is the “assignment” function that maps a conformation to the nearest cluster center. d(x, y) is the distance between two conformations x and y, measured via the RMSD metric.23 The minimization occurs over all clusterings (σ) with k states, subject to some choice of initial center. Finally, the max is taken over all conformations in the dataset.
The k-centers approach minimizes the worst-case clustering error, as quantified by the objective function fmax(σ) = maxid(xi, σ(xi)). Considering only the worst-case clustering error is problematic for conformational dynamics, particularly in protein folding, as the worst-case error is often determined by extended (unfolded) conformations with very small populations. Furthermore, cluster centers generated by this algorithm are often non-central, that is, they often do not represent the geometric center of their associated data.
Alternatively, k-medoids clustering24 approximately minimizes . With sufficient sampling, constant temperature molecular dynamics draws Boltzmann-weighted conformations; thus, by averaging over all conformations, fmed(σ) is an objective function that penalizes the (approximately) ensemble-averaged deviation from cluster centers. The resulting clusters tend to be centrally located within their respective data–i.e. they are medoids.25 However, for folded proteins, strict Boltzmann weighting yields few unfolded states, often leaving unfolded conformations assigned to folded states. This deficiency can be explained in terms of fmax(σ). A clustering that minimizes fmed(σ) may in fact be worse when evaluated by fmax(σ); conversely, minimizing fmax(σ) could increase fmed(σ). For accurate kinetic clustering of biomolecule dynamics, one should consider both the worst case (fmax) and average case (fmed) clustering error.
Simultaneously optimizing both the average and worst-case error can be achieved by combining the k-centers and k-medoid algorithms. Let ε be some desired worst-case clustering error. Define the set
| (3) |
Thus, S(ε) is the set of all clusterings that have worst-case errors of ε (or better). We now apply a k-medoids clustering algorithm, but restricted to the set S(ε). In practice, we use a two step approach:
Apply approximate k-centers to return initial clusters gi, terminating when fmax(σ) ≤ ε.
Apply approximate k-medoids to the result, but rejecting all moves that increase fmax(σ).
For (2), we employ a modification of the Partitioning Across Medoids algorithm.24 For each cluster gi, we randomly select a conformation xi assigned to that state. The clustering errors (fmed, fmax) are calculated and compared to the values that would be obtained were xi instead the cluster center of that state. If fmed is improved and fmax is improved (or unchanged), the move is accepted. In practice, fmax decreases insignificantly during this process, but fmed decreases dramatically over a handful of iterations. As described, the hybrid algorithm tends to preserve the overall distribution of clusters, essentially refining k-centers to be more “central“; this is desirable because k-centers is known22 to provide a reasonable partition of conformation space.
3.2 Improved Estimators for Reversible Transition and Count Matrices
Since equilibrium conformational dynamics obeys detail balance, it is important for MSMs to satisfy detailed balance (also called reversibility). A positive reversible MSM guarantees positive real eigenvalues λ, which can be interpreted as relaxation timescales through the relation . Previous work11 has used the symmetrized counts–so called because the count matrix is symmetrized via the equation –to estimate a reversible count matrix. Though the resulting MSMs satisfy detailed balance, this estimator can introduce artifacts in both equilibrium and kinetic properties;15,21 this error is pronounced for short trajectories started from a distribution far from the system’s equilibrium. A recent work21 recommends estimating a transition matrix using the unsymmetrized counts after restricting the data to its maximal ergodic subgraph. Thus, after clustering, one must first identify the maximal ergodic (i.e. strongly connected) subgraph–that is, a (maximal) set of states M such that if i ∈ M and j ∈ M, then there exists a path from i → j and from j → i. That approach eliminates artifacts in equilibrium estimates, but yields transition matrices that may not satisfy detailed balance. To enforce detailed balance while preserving accurate estimation of equilibrium properties, we have implemented the following protocol:
Apply Tarjan’s algorithm,26 restricting data to the maximal ergodic subgraph.
Estimate a reversible count matrix using a maximum likelihood estimator.
The theory of reversible estimation has been discussed previously;9,11,16,27,28 however, several implementation issues have limited its general use. First, the reversible MLE estimator is only well-defined for ergodic MSMs, so the trimming procedure is critical. Second, the iterative procedure sometimes converges slowly for many-state models; in Appendix 8.2, we discuss an efficient implementation that allows scaling to biological systems with tens of thousands of states.
4 Results
We now validate the revised MSM protocol. First, we show that improved clustering results in more self-consistent models, as measured by either relaxation timescales or correlation function analysis. Second, we show that improved transition matrix estimators result in improved ability to recapitulate kinetic and equilibrium properties of a known reference model.
4.1 Hybrid k-centers k-medoids clustering improves state definitions
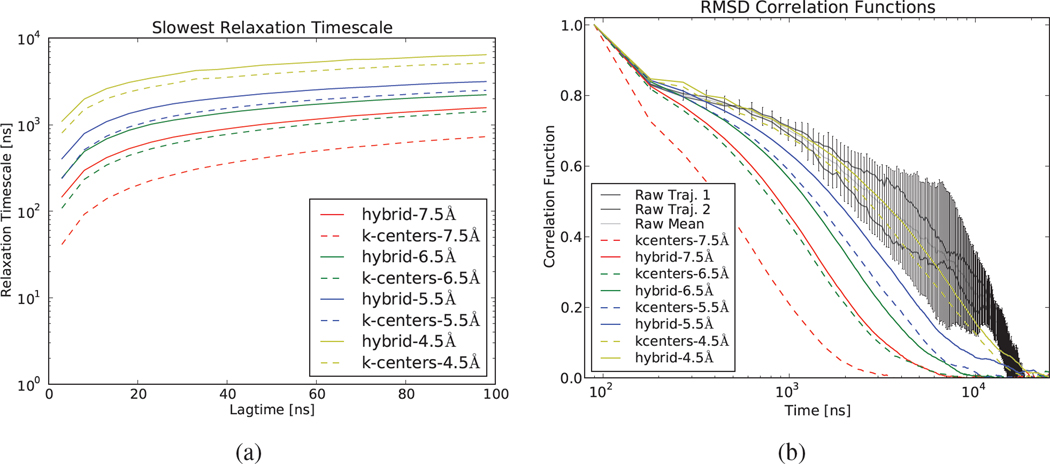
Projecting onto a finite state space results in dynamics that are only approximately Markovian. One way to evaluate model consistency is by calculating the relaxation timescales for a sequence of lagtimes; as observables, these timescales should be approximately lagtime-independent. As compared to models constructed with k-centers clustering, hybrid clustering yields relaxation timescales that are slower (Figure 1a) and less lagtime-dependent. For models with few states (fmax = 5.5 Å – 7.5 Å; Table 1), hybrid clustering performs considerably better than k-centers. In particular, a hybrid model with a fixed number of states (e.g. 176 states, or fmax=7.5 Å) performs comparably with a k-centers model with considerably more states (e.g. 806 states, or fmax=6.5 Å). In the limit of many states, hybrid and k-centers perform comparably, as eventually both k-centers and hybrid yield 1 state per sampled conformation; however, statistically accurate estimation is impossible when the number of states approaches the total number of available conformations. For this reason, it is desirable to achieve accurate models with as few states as possible.
Figure 1.
(a). Relaxation timescales of models constructed with k-centers and hybrid clustering. (b). RMSD correlation functions as calculated by different clusterings. MSMs in (b) constructed with 90 ns lagtime. MSMs constructed from simulations of the WW protein; see Appendix 1.
Table 1.
Models constructed from WW domain simulations were used to compare structural properties of k-centers and hybrid clusterings. The number of states for each model was determined by k-centers convergence based on a pre-specified fmax; hybrid clusterings use the same k-centers clusters and iteratively improve them by the algorithm described above.
| Model | # States | fmax (Å) | fmed(Å) |
|---|---|---|---|
| k-centers | 26104 | 4.5 | 2.97 |
| hybrid | 26104 | 4.5 | 2.21 |
| k-centers | 5135 | 5.50 | 4.21 |
| hybrid | 5135 | 5.50 | 2.97 |
| k-centers | 806 | 6.50 | 4.76 |
| hybrid | 806 | 6.48 | 3.60 |
| k-centers | 175 | 7.48 | 6.03 |
| hybrid | 175 | 7.47 | 3.97 |
The lack of a true reference value makes relaxation timescales an incomplete validation of MSM kinetics. Correlation function analysis offers an orthogonal check with a known reference value. The RMSD correlation function is given by , where s(t) = r(t)− < r(t) > and r(t) is the RMSD to a reference structure, here taken to be the native conformation. For the MSM calculation, the transition matrix was used to first calculate a pseudo-trajectory of 100,000 lagtimes (9,000,000 ns). For each frame in the pseudo-trajectory, an RMSD value was randomly selected from the collection of RMSD values observed for that state. This approach models intrastate dynamics by the random selection of each RMSD value.
As compared to the reference (calculated from the raw data), MSMs with few states show erroneously fast kinetics (Figure 1b); hybrid clustering partially mitigates this error. With sufficiently many states (e.g. fmax ≤ 4.5), the dynamics is accurately captured by the MSM. Both raw and MSM RMSD correlation functions decay on a timescale comparable to the folding-unfolding dynamics of the protein. Further increasing the number of states is not feasible due to increased statistical uncertainty (Appendix 8.5). We observe similar results for Alanine dipeptide (Appendix 8.6).
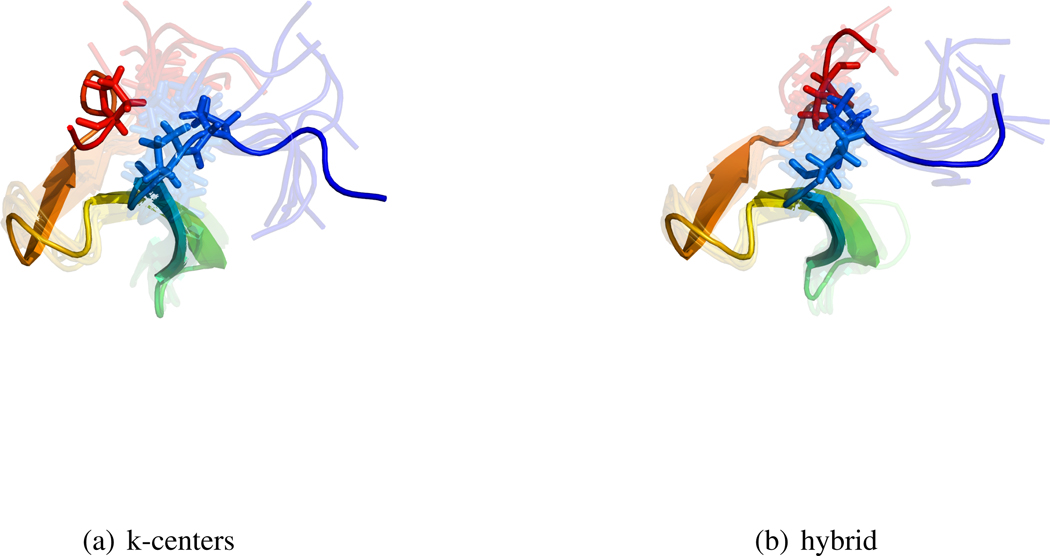
In addition to enabling kinetic calculations, clustering provides an important tool for exploratory data analysis, which benefits from cluster centers that are representative of their associated data. Yet, with k-centers clustering, the fmax objective function is inherently insensitive to local or average structural properties. This leads to state definitions that tend to be useful only as partitions of conformation space–in particular, minimizing fmax does not ensure that cluster centers are central within their associated data. When applied to simulations of the WW protein, hybrid clustering decreases the average clustering error significantly, as quantified by the fmed objective function (Table 1). The hybrid clusters show less structural heterogeneity (Figure 2). Furthermore, the k-centers cluster center lacks a critical proline contact (sticks) that defines the native fold; the hybrid cluster center retains this key structural feature.
Figure 2.
Cluster centers (opaque) and randomly sampled conformations (transparent) are displayed for the most populated state from models based on the k-centers and hybrid clustering algorithms. Both models are based on simulations of the WW domain. The hybrid clusters (b) were constructed by improving the initial k-centers clustering in (a). Both clusterings have 806 states (fmax = 6.5Å).
4.2 Improved Estimators for Reversible Transition and Count Matrices
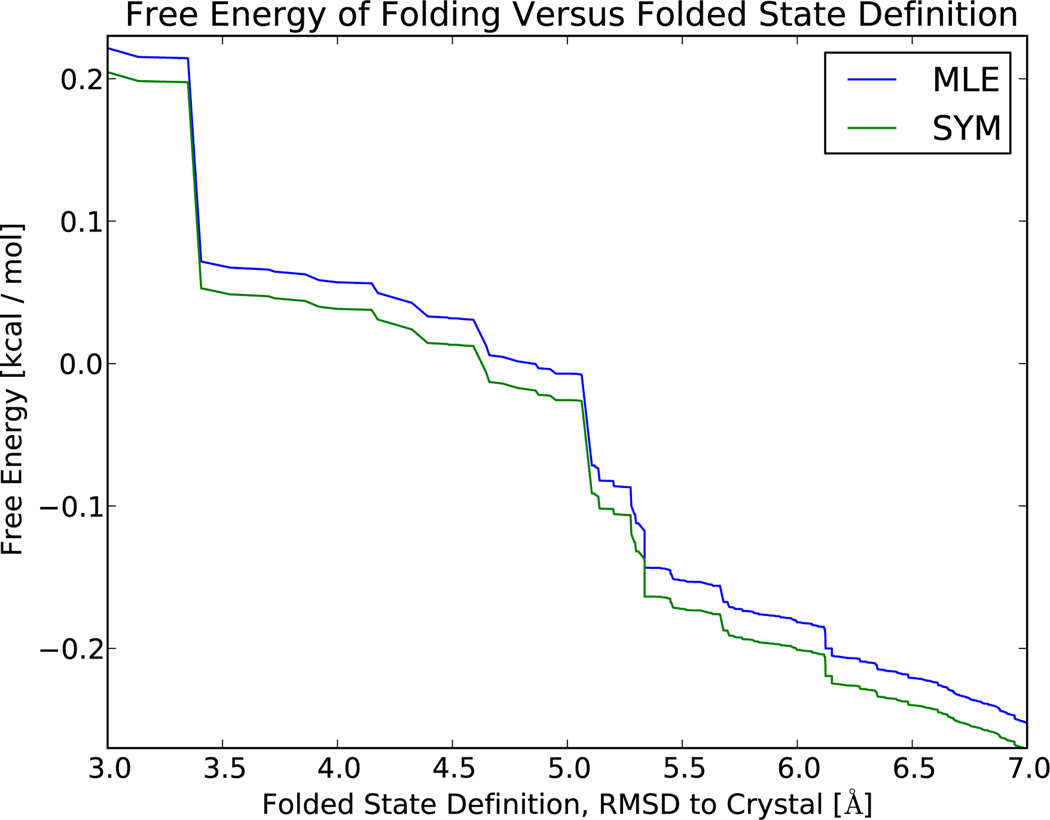
The reversible MLE yields improved estimates of equilibrium and kinetic properties. As a preliminary control, the MLE and symmetrized estimators are compared on a dataset consisting of two trajectories that are long (100 µs) relative to the folding and unfolding timescales (≈ 10 µs); as expected, the resulting free energies show good agreement (Figure 3).
Figure 3.
Simulations of the WW protein12 were used to compare the performance of the symmetrized and MLE protocols. Folding free energies calculated using a two-state approximation , show good agreement (Δ ≤ 0.03 kcal / mol) between models constructed using the symmetrized and MLE protocols, as expected for long trajectories. The near-zero folding free energy is expected, as the simulations were performed near the melting temperature;12 the exact free energy depends weakly on how one defines the folded state. Here, the folded state is defined as all states with an RMSD (to crystal structure) below some cutoff value; the unfolded state is defined as the remaining states. The large RMSD values observed are due to the large conformational fluctuations observed in the high temperature (393 K) simulations.
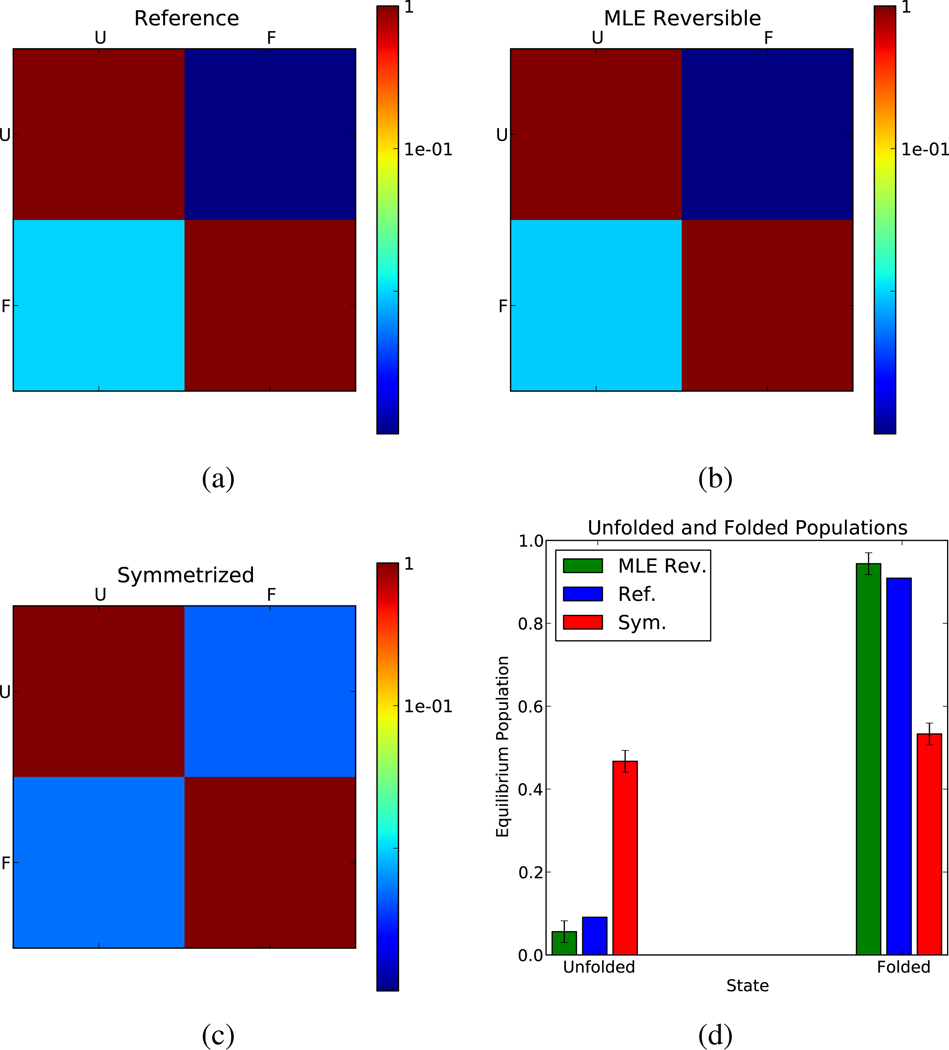
In a more demanding test, we generate an ensemble of two-state folding trajectories from a model with a folding timescale of 100 steps and an unfolding timescale of 1000 steps (see Appendix 4). This approximates the scenario of running MD simulations from an ensemble of unfolded conformations. Because the trajectory length is comparable to the folding timescale, the symmetrized estimator biases results towards the starting distribution of conformations, which in this case is entirely unfolded.
Using the model data, transition and count matrices were estimated using the MLE and symmetrized procedures (Figure 4). The reversible MLE accurately estimates the kinetic (a–b) and equilibrium (d) properties of the reference model. However, the symmetrized estimator shows equilibrium properties that are biased towards the unfolded state (d). Furthermore, the symmetrized unfolding timescale is erroneously high (c). This symmetrization bias reduced the accuracy of some previous MSMs, as pointed out in;29 reversible estimation eliminates this bias.
Figure 4.
Simulated two-state folding simulations generated from a reference transition matrix (a) were used to estimate transition matrices. The MLE reversible procedure (b) shows good agreement with the reference transition matrix, while the symmetrized procedure (c) shows poor agreement with the reference. Furthermore, as compared to the symmetrized estimate, the MLE estimate better recapitulates the reference equilibrium properties (d).
4.3 Improved Scaling and Performance
MSM construction relies on the clustering and analysis of vast simulation datasets. For the clustering algorithms in this work, RMSD evaluations are rate limiting; further inspection shows that RMSD is bottlenecked by a matrix multiplication involving an m × 3 matrix of atomic coordinates, where m is the number of atoms in each conformation. Using an SSE3-optimized matrix multiply routine30 with OpenMP parallelization, we have accelerated RMSD and clustering calculations by 20× over the previous versions of MSMBuilder. MSMBuilder2 has been successfully applied to systems spanning a broad range of timescales and sizes; Table 2 reports the computational cost of MSM construction for various protein systems. In all cases, the cost of the MD simulations is considerably greater than the cost of MSM analysis.
Table 2.
MSMBuilder2 was applied to various protein systems, ranging from alanine dipeptide to the λ-repressor protein. Walltimes include the cost of reading all conformations into memory, applying k-centers until convergence, and applying 10 iterations of hybrid k-medoids. The number of states is determined by applying k-centers clustering until the desired maximum cluster size fmax is achieved; the hybrid step typically produces little change in fmax. The slowest observed relaxation τslow is calculated by , where λ is the largest nonstationary eigenvalue of the model. τlag gives a lower bound on the timescales accessible to a given model; τslow gives an upper bound on the timescales observed in a given dataset. These data suggest that the present methods can successfully model conformational dynamics from the picosecond to millisecond timescales.
| System | # Atoms | # Frames | Walltime | Cluster Size (fmax) | nstates | τlag | τslow |
|---|---|---|---|---|---|---|---|
| ALA | 22 | 250000 | 1.0m | 0.35 Å | 82 | 10ps | 202 ps |
| WW | 562 | 200000 | 11.6h | 5.50 Å | 26104 | 90ns | 5.9 µs |
| HP35 (300K) | 576 | 109674 | 2.25h | 4.00 Å | 9328 | 10ns | 7.6 µs |
| λ | 1258 | 700133 | 1.80d | 4.00 Å | 20599 | 20ns | 2.0 ms |
5 Discussion
5.1 MSMBuilder2 Protocol
As shown above, the protocol validated in this work presents several clear advantages over previous methods. These advances are evolutionary in nature, building upon previous work. The overall MSM construction protocol has retained the following key steps: perform molecular dynamics simulations, cluster data, and estimate a transition matrix. We continue to work with the RMSD metric, as its simple distance interpretation provides a physically-motived state decomposition. RMSD is a widely used distance metric for comparing biomolecular conformations;23,31,32 this common use allows a biophysical intuition for RMSD, which is one reason for our choice of this metric. Furthermore, previous work found that, for alanine dipeptide, RMSD-based state decompositions yielded models that paralleled ones based on manual state decompositions.10 We note that some systems may benefit from other metrics; the MSMBuilder2 framework is extensible to such situations.
The procedure of kinetic clustering, whereby one leverages fine structural clustering to produce states free from kinetic barriers,9,10,15 benefits from the improved clustering algorithm. In kinetic clustering, it is critical to validate state decompositions using kinetic metrics; here, we have applied tests based on both relaxation timescales and correlation functions. Another key motivation for the hybrid algorithm is performance. Hybrid clustering achieves improved clusters with only 10× worse computational cost than the simple k-centers algorithm; this cost is more than offset by the accelerated RMSD calculation.
The reversible MLE protocol builds upon previous work9,11,21 to build accurate reversible models. Besides enforcing reversibility, the reversible MLE has other subtle benefits. First, reversibility improves statistics; because a reversible MSM is defined by a symmetric matrix Xij, the number of possible parameters drops from n2 to . Second, the counts matrix X can be visualized to gain intuition on the connectivity properties of a system. Previously, this has typically been done using transition path theory (TPT).33 However, TPT requires a priori definition of initial and final states, while visualizing the counts matrix can be done in a hypothesis-free manner.
5.2 MSMBuilder2 Implementation
MSMBuilder2 is implemented as a library using the Python34 language and achieves high performance by using optimized libraries (Numpy,35 Scipy, Pytables36) whenever possible. The rate-limiting step in clustering, the 3 × n matrix multiply, is written as a small C library with Python wrappings. This design framework allows both flexibility and performance; indeed, benchmarks30 suggest that the clustering code approaches the published peak efficiency of the benchmark machines. We suspect that the MSMBuilder2 library will be a useful starting point for other researchers interested in methods development. For researchers interested in applying MSMBuilder2 to analyze their simulations, the current protocol is captured by a set of command-line scripts and tutorial at (https://simtk.org/home/msmbuilder/).
5.3 Future Challenges
The advances in MSMBuilder2 represent significant advantages over previous methods; however, future work will likely lead to further improvements. Clustering remains a compromise between accuracy and speed. For full protein datasets (≥ 100,000 conformations), performance worse than O(kN) will generally be unacceptable, but other methods may further improve the results shown here. Estimation of reversible transition matrices may benefit from a Bayesian framework;16,27,28 accelerating such schemes for use in biological systems remains a key challenge. In addition to incremental improvements in the current protocol, more drastic changes have also been explored. In particular, other groups have shown some success working with incomplete partitions of conformation space and continuous time (Master Equation) modeling.15,18 Finally, existing frameworks consider clustering, ergodic trimming, and model estimation as three distinct steps. However, these steps are coupled and jointly contribute to modeling uncertainty. Methods that consider model accuracy and finite sampling statistics during all stages of model construction may further reduce modeling error.
6 Conclusion
Although modeling conformational change at atomic resolution remains challenging, the MSMBuilder2 protocol yields significant improvements in model accuracy, structural insight, and computational performance. With system sizes ranging from 22 atoms to 1258 atoms and timescales ranging from 10 picoseconds to 2 milliseconds, the model systems considered here suggest that MSMBuilder2 may facilitate simulation studies of previously inaccessible biomolecular systems.
Acknowledgements
We thank Rhiju Das, Sergio Bacallado, and the members of the Das and Pande labs for helpful discussions. We gratefully acknowledge D. E. Shaw Research for providing the WW domain simulations. We thank NSF CNS-0619926 for computing resources and NIH R01.-GM062868, NSF-DMS-0900700, and NSF-MCB-0954714 for funding. Finally, we thank Folding@Home donors for providing the computational resources for the HP35 simulation. KAB was supported by a Stanford Graduate Fellowship. We acknowledge the following award for providing computing resources that have contributed to the research results reported within this paper: MRI-R2: Acquisition of a Hybrid CPU/GPU and Visualization Cluster for Multidisciplinary Studies in Transport Physics with Uncertainty Quantification http://www.nsf.gov/awardsearch/showAward.do?AwardNumber=0960306. This award is funded under the American Recovery and Reinvestment Act of 2009 (Public Law 111-5).
8 Appendices
8.1 Simulation Details
Alanine dipeptide was simulated using using Gromacs 4.5.337 with the AMBER96 force field and GBSA implicit solvent. One trajectory of length 50ns was analyzed; snapshots were stored every 200fs.
The WW domain38,39 simulations were described previously;12 the authors of that work have graciously provided the trajectories on their web site. Simulations were performed using the AMBER99sb-ILDN40 force field at 395K. For MSM construction, data were stored at every 1ns; two trajectories of length 100 µs were analyzed.
The HP35 dataset includes more than 600 simulations (minimum length 700ns) at 300K. Simulations were performed using Gromacs 4.5.3 with the Amber99sb-ILDN force field and TIP3P water. Conformations were stored at 1ns intervals. Conformations were started from more than 600 different folded and unfolded conformations.
The λ-repressor simulations have been described previously.41 More than 700 simulations of minimum length 600ns were analyzed; conformations were stored at 1ns intervals. Simulations were performed at 370K, using the ff03 force field with TIP3P water.
8.2 Maximum Likelihood Estimator for Reversible MSMs
Suppose one has observed a matrix of counts Cij; this is typically output from the clustering and assignment stages of model construction. To estimate a general (possibly non-reversible) transition matrix T, one formulates the log-likelihood function
| (4) |
Maximizing this likelihood (e.g.9) leads to the following MLE estimator of the transition matrix:
| (5) |
Suppose one knows that the underlying data is reversible. In that case, there exists a symmetric count matrix Xij = Xji such that
| (6) |
Inserting this equation into f(T) yields a likelihood function for X, where the row sums of X are defined as Xi = ∑j Xij and the row sums of C are defined as Ni = ∑jCij:
| (7) |
To maximize this function, one requires the partial derivatives with respect to parameters Xij, which are given by (a ≠ b)
| (8) |
| (9) |
Setting partial derivatives to zero:
| (10) |
| (11) |
This expression can be used in an iterative update procedure. While others9 have suggested an approach using the quadratic formula, we find that the current formula is effective because it can be expressed entirely as simple vector and (sparse) matrix operations. In practice, we typically see convergence within 100000 iterations; we terminate iteration when ‖πk+1−πk‖ ≤ 10−10.
For situations with limited data, MLE estimation may require some regularization or prior to avoid overpopulating states that are strongly metastable but have been inadequately sampled. Methods to achieve regularization are discussed in the following section.
8.3 Incorporating prior pseudocounts into the reversible MLE
It is sometimes useful to perform estimation with some nonzero prior; in practice, this involves adding a uniform matrix of pseudocounts to the observed count matrix: . This procedure generally destroys sparsity structure, preventing its use for large systems. Below we show a method to maintain sparsity while incorporating prior pseudocounts.
The update equation can be expressed in terms of the observed counts Cab, the observed row sums Na, the prior pseudocount (α) added at each matrix position, and the number of states, n.
| (12) |
| (13) |
To simplify the computation, define two intermediate variables Qab and Rab:
| (14) |
| (15) |
The update formula is now
| (16) |
The key is that Qab is sparse, and Rab has a simple functional form that is the result of vector operations. Furthermore, the iterative update does not require each Rab, but rather ∑iRib.
In practice, we find that this protocol remains limited by computational performance. As an alternative, the following regularization scheme appears to work well in practice.
Starting with the matrix Cij of counts, we construct a matrix Sij such that Sij = 1 if Cij > 0 or Cji > 0. Thus, S is a sparse matrix with ones for every count that was observed in either forward or reverse direction. When performing the MLE estimation, we use the matrix C′ =C+αS. The effect of this is to prevent transitions with limited statistics from being too strongly favored in one direction. In practice, α must be chosen such that α ∑ijSij ≤ ∑ijCij; for the datasets in this work, α ≈ 0.1 leads to . The advantages of this regularization are threefold. First, the data remains sparse, which allows scaling up to hundreds of thousands of states. Second, transitions that are nearly irreversible but inadequately sampled are smoothed. Third, this method adds pseudocounts only to transitions that were observed in the data (albeit in either the forward or reverse directions); thus, this method cannot introduce artifactual pathways.
8.4 Two State Model for Comparing Transition Matrix Estimators
The two state model in Figure 4 is based on the transition matrix
| (17) |
where p = 0.99 and q = 0.999. Thus, folding (100 timesteps) is approximately 10× faster than unfolding (1000 timesteps); this is similar to the fast-folding variants of HP3542 under mildly denaturing conditions (with 1 timestep corresponding to 10ns). Using this transition matrix, 100 trajectories of length 200 were generated and used to estimate transition and count matrices using either the symmetrized or reversible MLE protocols.
8.5 Balancing Kinetic Accuracy and Statistical Reliability
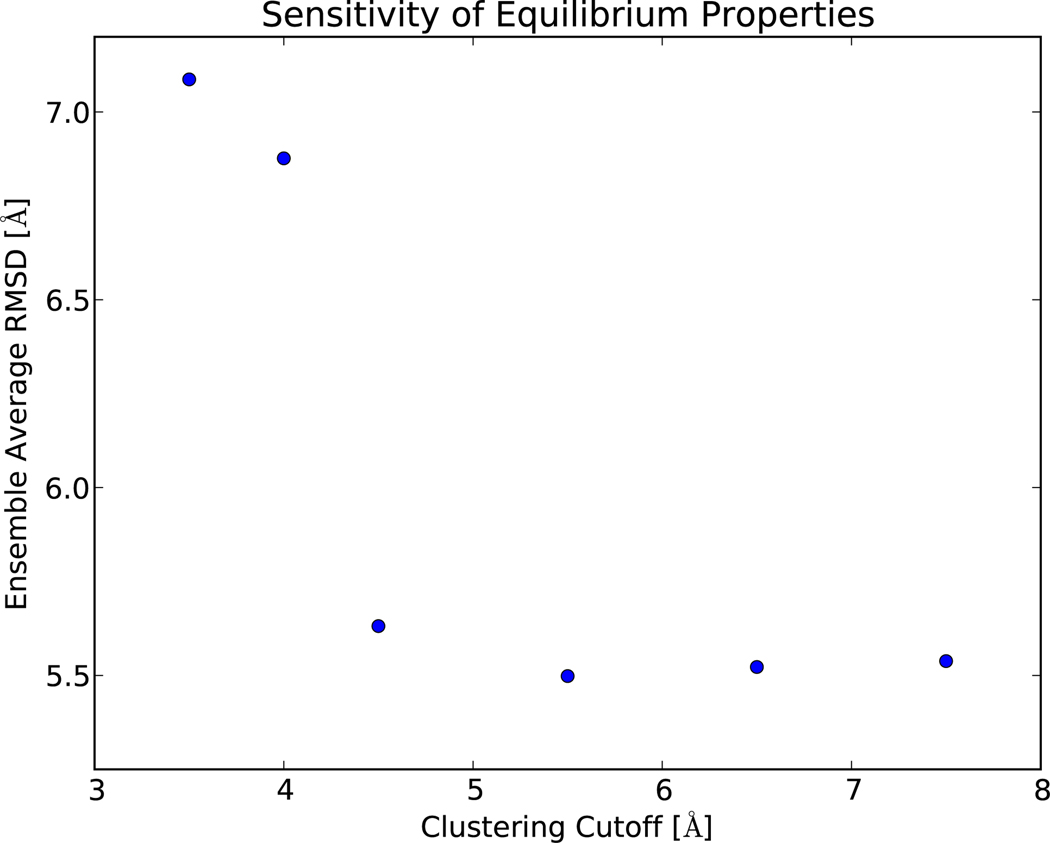
Discretization error in MSM construction is reduced by increasing either the number of states or the lagtime.9 However, these solutions lead to statistical uncertainty due to increasing the number of model parameters or decreasing the amount of independent data, respectively. Thus, accurate model construction requires a careful balance between discretization and statistical error. A useful test is to consider the equilibrium properties of a sequence of models (Figure 5). We have calculated the ensemble average RMSD to native, which gives a smooth estimate of the stability of the folded state. For the WW protein, well-folded conformations typically show RMSD values of 0–4 Å, with unfolded conformations ranging from 5 to 10 Å. Models with few states (fmax ≥ 4.5 Å) appear near the folding midpoint, with an ensemble average RMSD of 5.54 ± 0.05 Å; models with more states (fmax = 3.5,4.0) appear considerably less folded, with an RMSD of 6.98 ± 0.1 Å. In general, state decompositions that are too fine will lead to spurious irreversible transitions and inaccurate equilibrium estimates. For the present dataset (200,000 conformations), the 3.5 Å model has 47,684 states and lies well-within the data-poor regime. The lack of agreement with coarser models leads us to reject the 3.5 and 4.0 Å models. The 4.5 Å model is the best model for the WW data, as measured by relaxation timescale consistency (Figure 1a), correlation function analysis (Figure 1b), and equilibrium robustness (Figure 5). Constructing a sequence of models with increasingly many states helps identify models that minimize both discretization and statistical error.
Figure 5.
Ensemble average RMSD to native is calculated for a sequence of models constructed from WW simulations.
8.6 Relaxation Timescale Analysis of Alanine Dipeptide
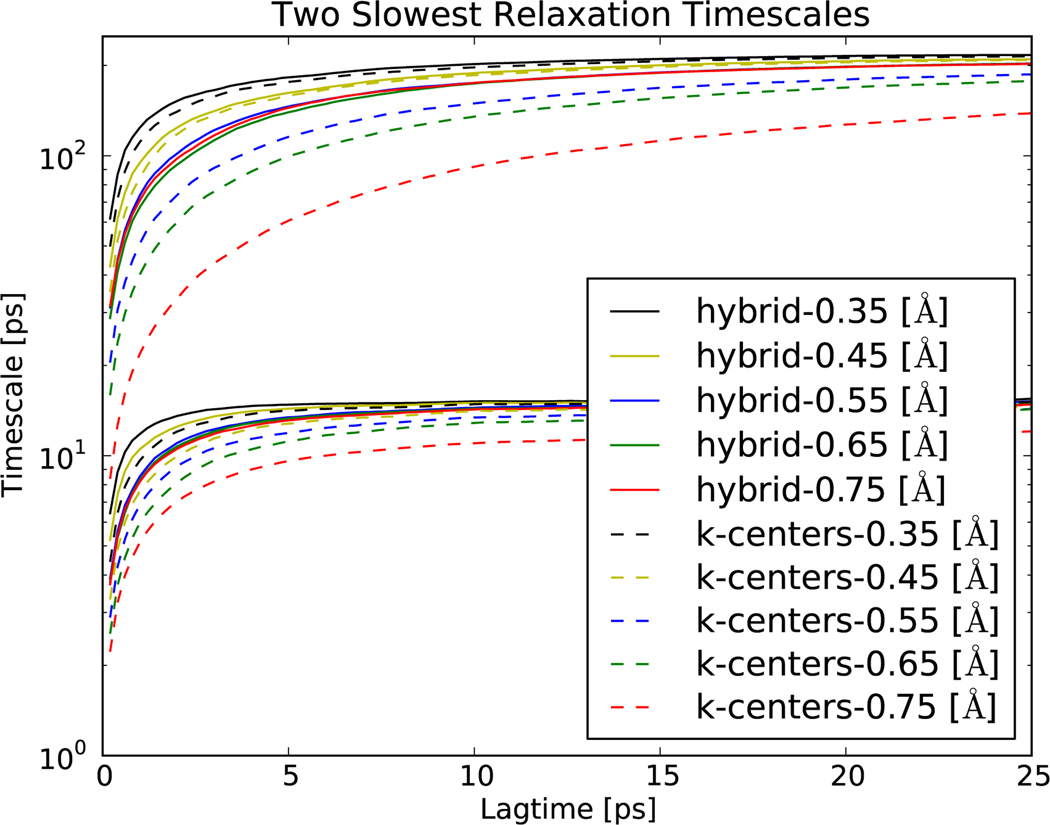
We present a relaxation timescale analysis (Figure 6) of a single (50 ns) alanine dipeptide simulation at 300K in GBSA implicit solvent. In this example, the hybrid clustering provides improved performance for all choices of clustering diameter. Furthermore, the high-resolution models (ε ≤ 0.45 Å) converge to a slowest relaxation of 200 ps. The hybrid clusterings approach this value at shorter lagtimes, particularly for the lower-resolution models (ε ≈ 0.65 Å). The second-slowest timescale also suggests improved performance by the hybrid clustering.
Figure 6.
The two slowest relaxation timescales for alanine dipeptide are plotted as a function of lagtime.
References
- 1.Inoue A, Saito J, Ikebe R, Ikebe M. Nat. Cell Biol. 2002;4:302–306. doi: 10.1038/ncb774. [DOI] [PubMed] [Google Scholar]
- 2.Anfinsen C. Science. 1973;181:223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 3.Buch I, Giorgino T, De Fabritiis G. Proc. Natl. Acad. Sci. U. S. A. 2011;108:10184–10189. doi: 10.1073/pnas.1103547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wüthrich K. J. Biol. Chem. 1990;265:22059–22062. [PubMed] [Google Scholar]
- 5.Kendrew J, Bodo G, Dintzis H, Parrish R, Wyckoff H, Phillips D. Nature. 1958;181:662–666. doi: 10.1038/181662a0. [DOI] [PubMed] [Google Scholar]
- 6.Kim P, Baldwin R. Annu. Rev. Biochem. 1982;51:459–489. doi: 10.1146/annurev.bi.51.070182.002331. [DOI] [PubMed] [Google Scholar]
- 7.Bai Y, Sosnick T, Mayne L, Englander SW. Science. 1995;269:192–197. doi: 10.1126/science.7618079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schuler B, Eaton W. Curr. Opin. Struct. Biol. 2008;18:16–26. doi: 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Prinz J, Wu H, Sarich M, Keller B, Senne M, Held M, Chodera J, Schütte C, Noé F. J. Chem. Phys. 2011;134:174105–174128. doi: 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- 10.Chodera J, Singhal N, Pande V, Dill K, Swope W. J. Chem. Phys. 2007;126:155101–155118. doi: 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- 11.Bowman G, Beauchamp K, Boxer G, Pande V. J. Chem. Phys. 2009;131:124101–124112. doi: 10.1063/1.3216567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, Wriggers W. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- 13.Voelz V, Bowman G, Beauchamp K, Pande V. J. Am. Chem. Soc. 2010;132:1526–1528. doi: 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lei H, Wu C, Liu H, Duan Y. Proc. Natl. Acad. Sci. U. S. A. 2007;104:4925–4930. doi: 10.1073/pnas.0608432104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Buchete N, Hummer G. J. Phys. Chem. B. 2008;112:6057–6069. doi: 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- 16.Noé F, Fischer S. Curr. Opin. Struct. Biol. 2008;18:154–162. doi: 10.1016/j.sbi.2008.01.008. [DOI] [PubMed] [Google Scholar]
- 17.Pan A, Roux B. J. Chem. Phys. 2008;129:064107–064115. doi: 10.1063/1.2959573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schütte C, Noé F, Lu J, Sarich M, Vanden-Eijnden E. J. Chem. Phys. 2011;134:204105–204120. doi: 10.1063/1.3590108. [DOI] [PubMed] [Google Scholar]
- 19.Buchner GS, Murphy RD, Buchete N-V, Kubelka J. Biochim. Biophys. Acta. 2011;1814:1001–1020. doi: 10.1016/j.bbapap.2010.09.013. [DOI] [PubMed] [Google Scholar]
- 20.Sarich M, Noé F, Schütte C. Multiscale Model. Simul. 2010;8:1154–1177. [Google Scholar]
- 21.Scalco R, Caflisch A. J. Phys. Chem. B. 2011;115:6358–6365. doi: 10.1021/jp2014918. [DOI] [PubMed] [Google Scholar]
- 22.Gonzalez T. Theor. Comp. Sci. 1985;38:293–306. [Google Scholar]
- 23.Theobald DL. Acta Crystallogr., A, Found. Crystallogr. 2005;61:478–480. doi: 10.1107/S0108767305015266. [DOI] [PubMed] [Google Scholar]
- 24.Kaufman L, Rousseeuw P, Corporation E. Finding groups in data: an introduction to cluster analysis. Vol. 39. Wiley Online Library; 1990. [Google Scholar]
- 25.Keller B, Daura X, van Gunsteren W. J. Chem. Phys. 2010;132:074110–074126. doi: 10.1063/1.3301140. [DOI] [PubMed] [Google Scholar]
- 26.Tarjan R. SIAM J. Comput. 1972;1:146–160. [Google Scholar]
- 27.Bacallado S, Chodera J, Pande V. J. Chem. Phys. 2009;131:045106–045116. doi: 10.1063/1.3192309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Diaconis P, Rolles S. Ann. Stat. 2006;34:1270–1292. [Google Scholar]
- 29.Cellmer T, Buscaglia M, Henry E, Hofrichter J, Eaton W. Proc. Natl. Acad. Sci. U. S. A. 2011;108:6103–6108. doi: 10.1073/pnas.1019552108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Haque I, Beauchamp K, Pande V. Submitted. 2011 [Google Scholar]
- 31.Maiorov VN, Crippen GM. J. Mol. Biol. 1994;235:625–634. doi: 10.1006/jmbi.1994.1017. [DOI] [PubMed] [Google Scholar]
- 32.Damm K, Carlson H. Biophys. J. 2006;90:4558–4573. doi: 10.1529/biophysj.105.066654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Noé F, Schütte C, Vanden-Eijnden E, Reich L, Weikl T. Proc. Natl. Acad. Sci. U. S. A. 2009;106:19011–19016. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rossum G. Python reference manual. Amsterdam, The Netherlands, The Netherlands: CWI (Centre for Mathematics and Computer Science); 1995. [Google Scholar]
- 35.Ascher D, Dubois PF, Hinsen K, Hugunin J, Oliphant T. Numerical Python. Livermore, CA: Lawrence Livermore National Laboratory; 1999. version UCRL-MA-128569. [Google Scholar]
- 36.Alted F, Vilata I. [Accessed 6-1-2011];2002 http://www.pytables.org/
- 37.Hess B, Kutzner C, Van Der Spoel D, Lindahl E. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 38.Jager M, Zhang Y, Bieschke J, Nguyen H, Dendle M, Bowman M, Noel J, Gruebele M, Kelly J. Proc. Natl. Acad. Sci. U. S. A. 2006;103:10648–10653. doi: 10.1073/pnas.0600511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Peng T, Zintsmaster J, Namanja A, Peng J. Nat. Struct. Mol. Biol. 2007;14:325–331. doi: 10.1038/nsmb1207. [DOI] [PubMed] [Google Scholar]
- 40.Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis J, Dror R, Shaw D. Proteins: Struct., Funct., Bioinf. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bowman G, Ensign D, Pande V. J. Chem. Theory Comput. 2010;6:787–794. doi: 10.1021/ct900620b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kubelka J, Chiu T, Davies D, Eaton W, Hofrichter J. J. Mol. Biol. 2006;359:546–553. doi: 10.1016/j.jmb.2006.03.034. [DOI] [PubMed] [Google Scholar]