Capturing Changes in Gene Expression Dynamics by Gene Set Differential Coordination Analysis

Abstract

Analyzing gene expression data at the gene set level greatly improves feature extraction and data interpretation. Currently most efforts in gene set analysis are focused on differential expression analysis – finding gene sets whose genes show first-order relationship with the clinical outcome. However the regulation of the biological system is complex, and much of the change in gene expression dynamics do not manifest in the form of differential expression. At the gene set level, capturing the change in expression dynamics is difficult due to the complexity and heterogeneity of the gene sets. Here we report a systematic approach to detect gene sets that show differential coordination patterns with the rest of the transcriptome, as well as pairs of gene sets that are differentially coordinated with each other. We demonstrate that the method can identify biologically relevant gene sets, many of which do not show first-order relationship with the clinical outcome.

1. INTRODUCTION

Analyzing microarray gene expression data at the gene set level, rather than single gene level, has proven to be an effective approach to extract valuable information for the elucidation of biological mechanisms, and for the selection of genes to build classification models for diseases [1]. Currently, the dominant approaches in gene set analysis focus on identifying gene sets whose genes are differentially expressed between the control and treatment groups. A number of methods compare the distribution of certain test statistics related to differential expression against the background distribution [2–5]. To address the issue of within-gene set heterogeneity, methods were developed to select subsets of genes for gene set scoring [6, 7], utilize covariance structure [8], or incorporate other types of data [9]. Some of the methods were reviewed and compared [1, 10]. Most of the gene set analysis methods can be further classified into two major sub-classes – those based on gene label permutation (competitive hypotheses), and those based on sample permutation (self-contained hypotheses) [1, 10].

The afore-mentioned approaches focus on finding gene sets showing first-order relationships with the clinical outcome. However it is well-established that higher-order relationships exist between gene expression and the clinical outcome [11]. Capturing higher-order relationships at the gene set level can yield information that is not revealed by the regular gene set analysis methods. There is difficulty capturing such higher-order relationships at the gene set level, because the majority of gene sets are not coherent in terms of expression [12]. Rather, as some authors documented, certain genes assume more important roles in the regulation at the expression level [13]. Currently there are only a few works published in the area of finding higher-order relationships at the gene set level. Choi and Kendziorski proposed a method that focuses on within-gene set correlation changes between treatment groups [14], which doesn’t consider changes of relationship between gene sets. Cho et al proposed a method to measure differential co-expression between pairs of gene sets, which is based on the similarity of sample correlations measured on individual gene sets [15]. This method doesn’t test the global hypothesis of whether a gene set is differentially regulated under different treatment conditions.

Here we present a systematic approach named Gene Set Differential Coordination Analysis (GSDCA). The reason we use the word “coordination”, rather than “co-expression”, is because of the lack of coherence in the expression of the genes within gene sets [12]. Our approach allows genes within a gene set to contribute at different levels based on the correlation structure of the data. The method systematically tests a series of hypotheses: (1) Test the hypothesis that a gene set is differentially coordinated with the rest of the transcriptome between treatment groups. (2) Test the hypothesis that a pair of gene sets are differentially coordinated with each other between treatment groups. (3) Select genes that are major contributors to the differential coordination. The R code is available at http://userwww.service.emory.edu/~tyu8/GSDCA/.

2. METHODS

2.1 The genome-wide index of correlation (GIOC) function of a gene set

In order to define a profile of a gene set that’s invariant to the number of samples in each treatment group, we use the GIOC function, which is defined on the discrete space of all the measured genes. A primitive version of the GIOC function was defined in our previous work [16]. However, we found that version of GIOC function doesn’t suit the need of hypotheses testing between treatment conditions. The main reason is that the overall distribution of the correlations between genes may be different under different treatment conditions, caused by changes in biological regulations, different levels of measurement noise, or different sample size. In the current work we define a new GIOC function and a set of testing procedures suitable for between-treatment group testing.

A key assumption of the GIOC function is that not all gene-gene correlations are biologically relevant. This is based on the fact that some genes are not regulated at the transcription level, and the majority of gene pairs are not co-regulated [12, 13, 17, 18].

First, for every gene g_i in the gene collection G of the dataset, we find its highest absolute correlation with the genes in gene set S,

$$c_i={max}_{g_k\in S}\mid \mathit{corr}(g_i,g_k)\mid .$$

This is similar to the single linkage distance measure in clustering.

Secondly, we transform the raw scores c_i using a sigmoid function,

$$s_i=1-\frac{1}{1+e^{\alpha (c_i-\delta )}}.$$

The motivation for such a transformation is to accommodate potential differences in the overall distribution of the correlations caused by varying noise levels and/or sample size difference between treatment groups. In this report, we use the 97.5^th percentile of the c_i’s of the genes not belonging to the gene set as δ, and select α such that the 95^th percentile receive the weight of 0.05 (maximum possible weight is one). Using this partially rank-based transformation, the top 2.5% of the genes receive weights between 0.5 and 1, and the next 2.5% of the genes receive weights between 0.05 and 0.5. The rest 95% of the genes receive weights of <0.05.

Thirdly, the s_i’s are normalized to have sum one,

$$w_i=s_i/{\sum }_{j\in G}{s}_j.$$

The resulting profile w, which resembles a probability distribution, is denoted the GIOC profile of gene set S.

2.2 Measuring the coordination change of a gene set between treatment groups

In order to measure the change in the GIOC profile of a gene set between different treatment groups, we use the metric distance defined by Comaniciu et al based on Bhattacharyya coefficient [19],

$$D={\left(1-{\sum }_{i\in G}\sqrt{w_i^{\mathit{group}1}{w}_i^{\mathit{group}2}}\right)}^{1/2},$$

which is normally used to measure the distance between probability distributions. We randomly permute the sample labels K times and compute the distances {D^(k)}_k=1,…,K The proportion of the sampled permutations with distance larger than the observed distance is taken as the p-value of the one-sided test,

$$p=\frac{1}{K}{\sum }_{k=1}^{K}I\left(D^{(k)}\ge D\right),$$

where I(A) is the indicator function which is 1 if A is true and 0 otherwise. The workflow is illustrated in Supporting Figure 1.

2.3 Identifying changes of coordination between pairs of gene sets

For two gene sets S₁ and S₂, we first find their GIOC profiles in treatment group 1, ${\mathit{w}}_1^{\mathit{group}1}$ and ${\mathit{w}}_2^{\mathit{group}1}$, respectively. We then find the distance between the two GIOC profiles,

$$D_{S_1,S_2}^{\mathit{group}1}={\left(1-{\sum }_{i\in G}\sqrt{w_{1,i}^{\mathit{group}1}{w}_{2,i}^{\mathit{group}1}}\right)}^{1/2}.$$

Similarly, we find the distance between their GIOC profiles in treatment group 2. We then take the difference of the distances,

$$\mathrm{\Delta }{D}_{S_1,S_2}=D_{S_1,S_2}^{\mathit{group}2}-D_{S_1,S_2}^{\mathit{group}1},$$

as a measure of change in coordination between the pair of gene sets across the treatment groups. To assess the significance of the change, we randomly permute the treatment group labels K times and compute the distances ${\left\{\mathrm{\Delta }{D}_{S_1,S2}^{(k)}\right\}}_{k=1,\dots ,K}$. We take

$$p=\frac{2}{K}\times min\left({\sum }_{k=1}^{K}I(\mathrm{\Delta }{D}^{(k)}\ge \mathrm{\Delta }D),{\sum }_{k=1}^{K}I(\mathrm{\Delta }{D}^{(k)}\le \mathrm{\Delta }D)\right)$$

as the p-value of the two-sided test. The direction of change can be determined by the tail of the distribution the observed statistic falls onto. The workflow is illustrated in Supporting Figure 2.

2.4 Identifying the genes that are major contributors to the differential coordination of a gene set

To identify genes that are major contributors to the differential coordination of a gene set, we focus on the gene-gene correlations that help define the GIOC profile. First, for every gene g_m in the gene set S, we create an indicator vector y_m to denote whether it is the nearest neighbor (highest absolute correlation) within S to other genes,

$$y_{mi}=I\left(m=arg{max}_{j\in S}|\mathit{corr}(g_j,g_i)|\right),\forall g_i\in G_{-S}.$$

Secondly, between the treatment groups, for every gene g_m in the gene set S, we find the difference between its correlations with other genes, focusing on those to which g_m is the nearest neighbor within S in either treatment group. Another indicator vector is created for this purpose,

$$z_{mi}=I(y_{mi}^{\mathit{group}1}+y_{mi}^{\mathit{group}2}\ge 1),\forall g_i\in G_{-S}$$

We then find the mean absolute difference between the absolute values of the correlation coefficients,

$$d_m=\frac{{\sum }_{i:g_i\in G_{-S}}{z}_{mi}\left|\mid \mathit{corr}{(g_m,g_i)\mid }^{\mathit{group}1}-\mid \mathit{corr}{(g_m,g_i)\mid }^{\mathit{group}2}\right|}{{\sum }_{i:g_i\in G_{-S}}{z}_{mi}}.$$

Thirdly, the significance of d_m is determined through a randomization test. We permute the sample labels K times to obtain ${\left\{d_m^{(k)}\right\}}_{k=1,\dots ,K}$. The proportion of the sampled permutations with distance larger than the observed distance is taken as the p-value of the one-sided test,

$$p_m=\frac{1}{K}{\sum }_{k=1}^{K}I(d_m^{(k)}\ge d_m).$$

2.5 Selecting gene sets for this study

We selected gene sets from the biological processes of the Gene Ontology (GO) [20]. In order to select a collection of GO terms that were relatively specific yet not too narrow, we used a heuristic procedure that examines the number of ENTREZ gene IDs assigned to each term and its direct descendants. We ignored all terms with less than 10 assigned human genes. Starting from the term “biological_process”, we examined if 40% of the term’s genes (70% if the term contains less than 500 genes) were assigned to its children terms. If the answer was yes, we abandoned the term for being too broad, and examined its children terms one-by-one using the same criterion; if the answer was no, we kept the term in the final collection. We continued this procedure until all biological process terms were exhausted. Due to the structure of the GO system, a small fraction of the terms in the collection had ancestor-descendant relations, in which case the descendant terms were eliminated.

2.6 Simulations

To achieve realistic correlation structures in simulated data, we randomly sampled 1000 genes from the yeast cell cycle dataset [21], and computed the Cholesky decomposition of the correlation matrix between genes. In every simulation, we first generated a control data matrix and a treatment data matrix. In each matrix, the gene expression values were independently drawn from the standard normal distribution. Then we multiplied each matrix with the Cholesky square root of the cell cycle data to achieve an overall distribution of correlations similar to the real data. In all the simulations, 1000 genes were simulated, and different sample sizes (50, 100, 200 samples per group) were simulated. Four gene set sizes were considered: 10, 20, 50 and 100 genes.

To simulate a gene set of size m, we first randomly drew a seed gene, and found its top 50 (or 2m, whichever is larger) neighbors based on correlation coefficient, including itself. Then we randomly selected m genes from them. This way the expressions within the simulated gene set were reasonably coherent, yet not too tightly correlated [12]. First, to confirm the size of the tests were correct, we tested for differential coordination of one gene set, and between a pair of gene sets, without any further manipulation of the data. Secondly, to assess the statistical power of GSDCA to detect differential coordination of a gene set, and the power to select contributing genes, we performed the simulation in two ways. In each simulation, the data in the treatment data matrix was further manipulated, while the control data matrix was unchanged. (1) We added noise at different signal to noise ratio (defined as the ratio between the variances of signal and noise, S/N = 2, 1, 0.5, or 0) to the expression values of a portion (10%, 20%, 30%, 40%, or 50%) of the genes in the gene set. Note that this S/N considers all pre-manipulation values as signal. The data generation process introduces a certain level of baseline noise, for which we cannot determine the exact S/N because the true noise level of the cell-cycle data is unknown. (2) We replaced the expression values of a portion (10%, 20%, 30%, 40%, or 50%) of the genes in the gene set with those of other randomly selected genes, plus different levels of noise (S/N = 2, 1, 0.5, or 0). When S/N=0, the results from the two scenarios should converge as the expression values were replaced with pure noise and the selected genes lost correlation with other genes. Thirdly, to assess the power of GSDCA to detect differential coordination between a pair of gene sets, we first drew two non-overlapping gene sets, and then replaced the expression values of a portion (10%, 20%, 30%, 40%, or 50%) of the genes in one gene set with those of randomly selected genes from the other gene set, plus different levels of noise (S/N = 2, 1, 0.5, or 0). Again this manipulation was only done to the treatment data matrix, while the control data matrix was unchanged. At each parameter setting, the simulation was run 100 times.

3. RESULTS AND DISCUSSIONS

3.1 Simulation results

When GSDCA was applied between matrices with similar correlation structure, at the alpha cutoff of 0.05, 5.7% of the gene sets were called significant, 5.8% gene set pairs were called significant, and 5.7% of the genes were called significant. There was no trend associated with sample size or gene set size. These results confirmed the size of the test is correct, with a very slight inflation of false positives.

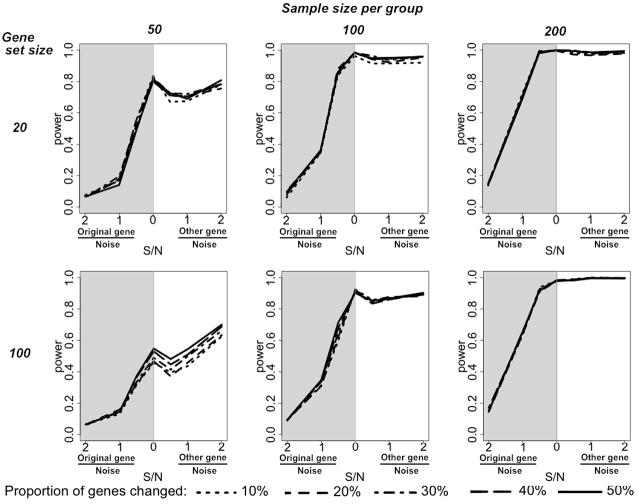
We then considered the statistical power of GSDCA to detect the differential coordination of a gene set (Fig. 1). The power is defined as the probability to call the gene set as significant when it is truly differentially coordinated. In Figure 1, each column represents a different sample size, and each row represents a different gene set size. Two gene set sizes are shown here. More complete result can be found in the Supporting Figure 3. The statistical power is plotted against signal to noise ratio (S/N). The left half (grey) of each plot shows the results from adding different levels of noise to the original gene expression values in the treatment data matrix. The effect of adding noise is causing the selected genes to lose correlation with other genes. This scenario represents situations where genes in certain pathways become dysregulated, which often happens in cancer [22]. When a gene becomes constitutively expressed, repressed, or simply uncontrolled, its variation in microarray data is mostly from biological/measurement noise, and its correlations with other genes become low. In this scenario, we can clearly see that the power rose along with the increase of noise. At higher S/N level (left), little noise was added to the original expression values. Thus the GIOC profile of the gene set changed little, and the statistical power of finding the differential coordination is close to zero. With the increase of noise, i.e. decrease of S/N ratio (right), the gene set’s GIOC profile changed more and the power of identifying the differential coordination rose. However, the power was still limited at S/N=0, when the expression of a subset of genes were replaced by pure noise. In this scenario the gene set lost part of its transcriptional connections to the rest of the transcriptome, yet didn’t gain new connections. In addition, as the simulated gene sets were relatively coherent, i.e. genes within the gene set were correlated, when gene A in the gene set lost correlation with gene B outside the gene set, gene C in the same gene set could still be correlated with gene B, thus the change of the GIOC profile of the gene set was limited.

Figure 1.

The statistical power of GSDCA to identify differentially coordinated gene sets in simulation. Each column represents a different sample size. Each row represents a different size of gene sets. The statistical power is plotted against signal to noise ratio (S/N) for the portion of genes to which noise was added. Presented are the merged results from two sets of simulations. Left half (grey) of each plot: different levels of noise were added to original gene expression values; right half (white): the expressions of a portion of genes were replaced by those of genes outside the gene set (randomly selected) plus different levels of noise. The two sets of results converge when S/N=0, where the expressions of some genes were replaced by random noise. The alpha cutoff of 0.05 was used.

On the right half of each sub-plot is the situation where the expressions of the genes were replaced by those of randomly selected genes outside the gene set plus different levels of noise. We can see that with the increase of S/N, meaning a portion of the genes inside the gene set became more and more correlated with some outside genes, the power continued to rise. When the sample size and/or the proportion of genes that change expression were reasonably large, the statistical power of detecting the differential coordination approached one.

Figure 2 shows the power of GSDCA to select major contributing genes. Two gene set sizes are shown here. More complete result can be found in the Supporting Figure 4. At the sample size of 100/group or higher, the power was high when the genes were replaced by noise, and stayed high when the signal of another gene was incorporated. When the sample size was small (50/group), the power was larger for smaller gene sets, which is expected as the contribution of each gene is large when the gene set is small. At the same time, for the portion of genes that didn’t change correlation patterns, the size of the test remained correct – 5.9% of unchanged genes were called significant, and there was no clear trend associated with sample size or gene set size (Supporting Figure 5).

Figure 2.

The statistical power of GSDCA to identify contributing genes to the differential coordination of a gene set in simulation. Each column represents a different sample size. Each row represents a different size of gene sets. The statistical power is plotted against signal to noise ratio (S/N) for the portion of genes to which noise was added. Presented are the merged results from two sets of simulations. Left half (grey) of each plot: different levels of noise were added to original gene expression values; right half (white): the expressions of a portion of genes were replaced by those of genes outside the gene set (randomly selected) plus different levels of noise. The two sets of results converge when S/N=0, where the expressions of some genes were replaced by random noise. The alpha cutoff of 0.05 was used.

Figure 3 shows the power of GSDCA to detect differential coordination between a pair of gene sets, when a subset of their genes become correlated. The power rose with the increase of gene set size, sample size, and/or the proportion of genes becoming highly correlated. More complete result can be found in the Supporting Figure 6. Biological regulation at the gene set level is complex, and our simulation only represents a few of the many possibilities. In the following text, we demonstrate the value of the approach using real data analyses.

Figure 3.

The statistical power of GSDCA to identify differentially coordinated gene set pairs in simulation. Each column represents a different sample size. Each row represents a different size of gene sets. The statistical power is plotted against signal to noise ratio (S/N). The expression of a portion of genes in one gene set were changed to that of genes in the other gene set, plus different levels of noise. The alpha cutoff of 0.05 was used.

3.2 Real data analysis – GSE18864

Using the heuristic GO term selection procedure, we selected 577 biological process terms that contain a total of 10455 genes, which accounted for 73.5% of all genes with biological process annotations. The full list of the selected gene sets are in Supporting Table 1. Given a dataset with two treatment groups, we first computed the GIOC function of every gene set in each treatment group. Secondly, for every gene set, we found the distance between its GIOC functions in the two treatment groups, and the significance level using the randomization test. Thirdly, after the most significant gene sets were selected, we examined their changes of coordination with all other gene sets under study. Fourthly, we identified the most influential genes in the differential coordination to help elucidate the mechanisms. Along with the GSDCA analysis, we also performed regular gene set analysis using one of the leading methods – GSA by Efron and Tibshirani [2]. Notice the purpose of including GSA results is not for direct competition, as the two methods aim at different goals. Rather, we wish to show that GSDCA extracts additional information that is not revealed by regular gene set analyses that focus on first-order relations.

The first dataset we analyzed was the GSE18864 dataset downloaded from the Gene Expression Omnibus (GEO; GSE18864) [23], which compares the gene expression of sporadic triple negative breast cancers (TNBC) against other types of breast cancer. TNBC is characterized by the lack of expression of estrogen receptor (ER), progesterone receptor (PgR), and the human epidermal growth factor receptor 2 (ERBB2) [24]. The data contains 24 TNBC samples and 51 samples from breast cancers of all subtypes. We selected the probesets with known ENTREZ Gene IDs. When a gene was represented by more than one probesets, we merged the corresponding probesets by taking the average expression values. The final data matrix contained 19622 rows (genes) and 75 columns (samples). The GSDCA p-values for a big proportion of the gene sets were quite small, indicating large global changes of co-expression patterns. On the other hand, the GSA p-values appeared to be uniformly distributed, indicating no strong first-order gene set differential expression (Supporting Table 2).

We transformed the p-values using Benjamini and Yekutieli’s false discovery rate (BY FDR), which is a stringent method that deals with dependency between tests [25]. We focus our discussion here on the gene sets with BY FDR less or equal to 0.05 (Table 1). We first noticed that 7 of the 27 gene sets (Table 1; superscript 1) contained at least one of the three receptors that characterize TNBC. Interestingly, although TNBC is characterized by the lack of expression of these receptors [24], only one of the 7 gene sets (GO:0048384, retinoic acid receptor signaling pathway, p-value 0.035) showed first-order relationship with the cancer type according to the GSA p-values. This indicates a more complex regulatory mechanism behind the phenotype. In five of the seven gene sets, a TNBC-related receptor, either ESR1 or PGR, was identified as one of the major contributing genes to the differential coordination (Table 1; Supporting Table 4). ESR2 and ERBB2 appeared to play a less important role in the differential coordination.

Table 1.

Gene sets with BY FDR<0.05 in the GSE18864 dataset.

GO term	name	TNBC receptor genes involved	GSDCA p-value	BY FDR	GSA p-value
GO:0030534	adult behavior		0	0	0.032
GO:0001974	3blood vessel remodeling		0	0	0.178
GO:0033059	4cellular pigmentation		0	0	0.027
GO:0043623	cellular protein complex assembly		0	0	0.095
GO:0006333	2chromatin assembly or disassembly		0	0	0.164
GO:0042384	5cilium assembly		0	0	0.002
GO:0000578	6embryonic axis specification		0	0	0.02
GO:0030855	1epithelial cell differentiation	PGR*	0	0	0.143
GO:0030520	1Estrogen receptor signaling pathway	ESR1*, ESR2	0	0	0.080
GO:0008585	1female gonad development	PGR*	0	0	0.207
GO:0042593	glucose homeostasis		0	0	0.057
GO:0006516	glycoprotein catabolic process		0	0	0.346
GO:0007030	Golgi organization		0	0	0.357
GO:0001889	1liver development	ERBB2	0	0	0.149
GO:0007093	2mitotic cell cycle checkpoint		0	0	0.387
GO:0022602	1ovulation cycle process	PGR*	0	0	0.256
GO:0007422	1peripheral nervous system development	ERBB2	0	0	0.147
GO:0045666	7positive regulation of neuron differentiation		0	0	0.041
GO:0009791	8post-embryonic development		0	0	0.143
GO:0009954	proximal/distal pattern formation		0	0	0.221
GO:0046320	regulation of fatty acid oxidation		0	0	0.494
GO:0048384	1retinoic acid receptor signaling pathway	ESR1*	0	0	0.035
GO:0006829	9zinc ion transport		0	0	0.254
GO:0000077	2DNA damage checkpoint		0.00025	0.037	0.334
GO:0045444	fat cell differentiation		0.00025	0.037	0.128
GO:0007126	2meiosis		0.00025	0.037	0.489
GO:0060491	regulation of cell projection assembly		0.00025	0.037	0.264

^*TNBC receptor genes identified as major contributors to the differential coordination of the gene sets. All five p-values were ≤ 0.0015.

Secondly, four cell-cycle/DNA replication related gene sets were among the top 27 gene sets (superscript 2), which could be related to the different growth characteristics of TNBC [26]. Some of the genes known to be associated with TNBC, or breast cancer in general, were among the top contributing genes to these gene sets’ differential coordination (Supporting Table 4). They include RAD51, whose function tends to be lower in TNBC [27]; BLM and MAD2L1, whose levels are associated with the prognosis of ER⁻ breast cancers [28]; ATM, whose level is reduced in BRCA1/BRCA2-deficient breast cancer and TNBC [29]; and RAD51L1, a genetic risk factor of breast cancer [30]. Among the other top gene sets, we also found many connections with TNBC or breast cancer in general. We briefly list some examples here. TNBC is characterized by enhanced angiogenesis, which involves genes in blood vessel remodeling such as VEGFA (superscript 3) [31]. The relationship between pigmentation and breast cancer is reviewed in [32], and polymorphisms in pigmentation gene OCA2 have been associated with ER-negative breast cancer survival (superscript 4) [33]. Cilia abnormalities have been reported in breast cancer (superscript 5) [34]. A large portion of the genes in embryonic axis specification are involved in estrogen-dependent transcription and cancer (superscript 6) [35]. It has been documented some growth factors in positive regulation of neuron differentiation, including EPO and BDNF, are related to breast cancer progression (superscript 7) [36]. The apoptosis regulating BCL2 family and the hedgehog signaling genes of the embryonic development process are known to be associated with breast cancer (superscript 8) [37]. The aberrant expression of some zinc transporters were linked to the progression of breast cancer (superscript 9) [38].

We then identified gene sets that showed differential coordination with those listed in Table 2 (BY FDR < 0.05; Fig. 4; Supporting Table 3). Because the gene sets in this study accounted for 74% of ENTREZ genes with biological process annotation, and 53% of all ENTREZ genes measured on the array, the graph (Fig. 4) only provides partial explanation to the results in Table 1. We observed a clear pattern in the distribution of the red (higher coordination in TNBC) and green (lower coordination in TNBC) edges. Interestingly, two gene sets showed both increased and decreased coordination. They were zinc ion transport (GO:0006829) and positive regulation of neuron differentiation (GO:0045666). Three gene sets were connected by a large number of green edges. They include the cell-cycle-related gene set DNA damage checkpoint (GO:0000077), as well as Golgi organization (GP:0007030) and glycoprotein catabolic process (GO:0006516). Three gene sets were connected by a large number of red edges. Two of them (GO:0030520, GO:0048384) were signaling pathways and contained ESR1, which was a major contributing gene for both gene sets. The other was mitotic cell cycle checkpoint (GO:0007093). The major contributing genes for this gene set included BLM and MAD21L1, whose levels are associated with the prognosis of ER⁻ breast cancer (Supporting Table 4) [28].

Table 2.

Top 25 differentially coordinated gene sets in response to MTX treatment.

GO term	name	GSDCA p-value	GSA p- value
GO:0031929	2TOR signaling pathway	0.001	0.245
GO:0019794	3nonprotein amino acid metabolic process	0.002	0.168
GO:0002718	1regulation of cytokine production during immune response	0.002	0.030
GO:0042228	1interleukin-8 biosynthetic process	0.002	0.018
GO:0002444	1myeloid leukocyte mediated immunity	0.002	0.007
GO:0030574	4collagen catabolic process	0.003	0.152
GO:0009620	1response to fungus	0.004	0.114
GO:0009303	rRNA transcription	0.006	0.465
GO:0007156	5homophilic cell adhesion	0.008	0.481
GO:0007009	6plasma membrane organization	0.008	0.03
GO:0042092	1T-helper 2 type immune response	0.009	0.02
GO:0006944	membrane fusion	0.01	0.104
GO:0006805	1xenobiotic metabolic process	0.01	0.338
GO:0006968	1Cellular defense response	0.011	0.006
GO:0009595	1detection of biotic stimulus	0.012	0.137
GO:0002889	1regulation of immunoglobulin mediated immune response	0.012	0.019
GO:0042742	1defense response to bacterium	0.013	0.015
GO:0006888	ER to Golgi vesicle-mediated transport	0.013	0.265
GO:0042375	quinone cofactor metabolic process	0.014	0.267
GO:0046717	9acid secretion	0.015	0.111
GO:0046131	7pyrimidine ribonucleoside metabolic process	0.017	0.046
GO:0006954	1Inflammatory response	0.017	0.018
GO:0006754	8ATP biosynthetic process	0.018	0.295
GO:0051262	protein tetramerization	0.019	0.094
GO:0032655	1Regulation of interleukin-12 production	0.021	0.041

Figure 4.

Differences in gene set coordination between the TNBC and other types of breast cancer. Node labels are GO accession numbers with preceding zeroes omitted. Cyan nodes: differentially coordinated gene sets with BY FDR<0.05; grey nodes: other gene sets. Green solid edges: higher coordination in other types of breast cancer; red dashed edges: higher coordination in TNBC. The plot was generated using Cytoscape [50].

Genes that were major contributors to the differential coordination (p-value < 0.05) are listed in Supporting Table 4. Two of the receptors that characterize TNBC, ESR1 and PGR, were among the top gene lists of five gene sets. Besides the genes we discussed above, among the known genes associated with TNBC or breast cancer in general, a number of them, such as ARL6, HOXB6, HOXD8, BDNF, BCL2 and BMP4, were also identified as major contributors to the differential coordination.

3.3 Real data analysis – GSE10255

The second dataset we studied was the gene expression in primary acute lymphoblastic leukemia (ALL) associated with methotrexate (MTX) treatment [39]. The major clinical outcome is the reduction of circulating leukemia cells after initial MTX treatment. Again we selected the probesets with known ENTREZ Gene IDs. When a gene was represented by more than one probesets, we merged the corresponding probesets by taking the average expression values. The data matrix contained 12704 rows (genes) and 161 columns (samples). In order to identify differential coordination associated with MTX treatment response, we selected samples falling into the top- and bottom- quartiles in the clinical outcome – reduction of circulating leukemia cells. Thus 82 samples were used in the analysis.

Using the one-sided randomization test, we tested the hypothesis that a gene set’s coordination with the entire transcriptome was different between the two groups. Due to the limited power caused by the limited sample size, and possibly the subtlety of the changes in gene expression dynamics, the p-values were not extremely small to undergo stringent FDR adjustment that considers dependency between tests. We used the nominal p-values as a ranking tool and picked the top 25 differentially coordinated gene sets (Table 2). For the complete list of p-values of all the gene sets, please refer to Supporting Table 5. Again the GSA p-values were close to uniformly distributed showing limited first-order relationship with the clinical outcome (Supporting Table 5).

Twelve (48%) of the top 25 gene sets were associated with stimulus response and cytokine production (Table 2; gene sets labeled with superscript 1), while only 13.8% of all the 577 gene sets under study were related to such processes. This is consistent with the immunosuppressive effect of MTX [40]. A number of these gene sets showed both differential coordination and differential expression, as evidenced by the GSA p-values.

Most notably, the top gene set found by GSDCA was the TOR signaling pathway (Table 2; superscript 2). It was documented that a number of genes in the TOR pathway play important roles in ALL development and drug resistance [41]. More importantly, synergistic effect was found between mTOR inhibitors and MTX in clinical trial [42]. This gene set was not significant in the GSA result, which supports the argument that GSDCA extracts additional useful results from the data by utilizing different information than regular gene set analysis. The second most significant gene set found by our method, nonprote-in amino acid metabolic process (Table 2; superscript 3), involves the metabolism of citrulline, ornithine and beta-alanine. The concentrations of ornithine and citrulline in gut tissues were found to be impacted by MTX treatment [43]. Among the other top gene sets, we also found many connections with MTX and/or ALL development. We briefly list some examples here. A few genes in collagen metabolism were found to be associated with leukemia [44], and the overall expression level of collagen increases with MTX treatment (superscript 4) [45]. Several cellular adhesion molecules are known to be influenced by MTX (superscript 5) [40]. In addition, diversity in adhesion molecule levels was observed in other types of leukemia [46]. A number of proteins in the membrane organization process are influenced by leukemia (superscript 6) [44, 47]. Pyrimidine metabolism is known to be affected by MTX due to its inhibition of the related purine metabolic pathway (superscript 7) [48]. Genes in the ATP biosynthesis pathway were found to be differentially expressed in a combination therapy involving MTX (superscript 8) [49].

We then identified gene sets that showed differential coordination (p-value < 0.005) with those listed in Table 2 (Fig. 5). With the increase of MTX response, seven of the top 25 gene sets, six of which belonging to the stimulus response system, showed decreased coordination (red dashed edges) with other gene sets. A large proportion of the pairs showed clear functional relationships. For example, 76.7% of the stimulus response and cytokine production gene sets associated with any of the top 25 gene sets were actually associated with one of the 12 stimulus response and cytokine production gene sets. The full list of the gene set pairs is provided in Supporting Table 6.

Figure 5.

Changes in gene set coordination between the low MTX response group and the high MTX response group. Node labels are GO accession numbers with preceding zeroes omitted. Cyan nodes: top 25 differentially coordinated gene sets; grey nodes: other gene sets. Green solid edges: increased coordination in high MTX response group; red dashed edges: decreased coordination in high MTX response group. The plot was generated using Cytoscape [50].

We further identified major gene contributors to the top differentially coordinated gene sets (Supporting Table 7). Interleukins and their receptors, especially IL10, appeared to contribute to the differential coordination of multiple gene sets. The gene set “acid secretion” was differentially coordinated (Table 1, superscript 9), yet no clear functional link to ALL or MTX was documented. The gene-level result provided an explanation - among the 8 genes of the gene set, 2 were shared with inflammatory response. One of these two genes, ANXA1, was highly significant in the test of single gene contributors (p-value 0.002).

In this manuscript, we presented a method to detect differential coordination at the gene set level, together with follow-up analysis methods. Our GSDCA method is based on the genome-wide index of correlation (GIOC) profile of a gene set, which utilizes the correlation structure between a gene set and all the genes measured in the array. Given that a large portion of the genes are without functional annotation, and a lot of other genes may have incomplete annotations, a gene set profile that utilizes all measured genes can better capture the useful information in the data.

In this study, we used a two-step procedure to analyze the datasets. First, we examined whether a gene set’s GIOC profile changed significantly between treatment groups. Secondly, for those selected gene sets from the first step, we further explored their change of coordination with other gene sets, in order to better understand the mechanistic changes at the functional group level. In this process, we avoided testing for significance of gene set pairs within one treatment group. The reason is that if we were to use randomization test for significance within one treatment group, we would have to resort to permuting gene labels, which is plagued by issues of not preserving correlation structure and favoring gene sets with certain characteristics [1, 10].

4. CONCLUSION

Overall, the proposed method is explorative and hypotheses-generating. It could help biologists identify potential functional groups/pathways that are associated with disease progression and/or drug response. Biological regulations at the gene set level are complex. Analyzing gene set level differential coordination may lead to insights into the data that complement results generated by traditional gene set analyses that focus on first-order relationships between gene sets and the clinical outcome.

Highlights.

• Some clinically relevant gene expression changes are not first-order.

• We develop a method named Gene Set Differential Coordination Analysis (GSDCA).

• GSDCA captures changes in gene expression dynamics at functional group level.