Effect of metal Ions (Ni²⁺, Cu²⁺ and Zn²⁺) and water coordination on the structure of L-phenylalanine, L-tyrosine, L-tryptophan and their zwitterionic forms

Abstract

Methods of quantum chemistry have been applied to double-charged complexes involving the transition metals Ni²⁺, Cu²⁺ and Zn²⁺ with the aromatic amino acids (AAA) phenylalanine, tyrosine and tryptophan. The effect of hydration on the relative stability and geometry of the individual species studied has been evaluated within the supermolecule approach. The interaction enthalpies, entropies and Gibbs energies of nine complexes Phe•M, Tyr•M, Trp•M, (M = Ni²⁺, Cu²⁺ and Zn²⁺) were determined at the Becke3LYP density functional level of theory. Of the transition metals studied the bivalent copper cation forms the strongest complexes with AAAs. For Ni²⁺and Cu²⁺ the most stable species are the NO coordinated cations in the AAA metal complexes, Zn²⁺cation prefers a binding to the aromatic part of the AAA (complex II). Some complexes energetically unfavored in the gas-phase are stabilized upon microsolvation.

Introduction

Aromatic amino acids (AAA) are essential to higher animals including humans. Phenylalanine and tryptophan contain phenyl and indole rings and are classified as non-polar. Due to its hydrophobicity L-phenylalanine is nearly always found buried within a protein. The indole functional group of L-tryptophan contains the N-H hydrogen bonding group, which can interact with solvent in folded proteins. L-tyrosine is a hydroxylated derivative of L-phenylalanine. The phenolic hydroxyl group of this amino acid is substantially more acidic than are the hydroxyls of aliphatic amino acids (serine, threonine) and its acidity vary depending on its environment. The body needs the essential amino acid L-phenylalanine (and L-tyrosine) to make melanine, dopamine, noradrenaline, adrenaline and thyroxine. A shortage of either of these two aromatic amino acids could cause mental disorders, including anxienty, depression, low libido, and chronic fatigue. Tryptophan is an essential amino acid that is necessary for normal growth in infants and for nitrogen balance in adults. All three aromatic amino acids can also be administered as nutraceuticals.

Both experimental and theoretical studies demonstrate that amino acids exist in the gas phase in the neutral form [1]. However, in aqueous solution the zwitterions are the predominant species [2–4]. The zwitterionic form of amino acids (⁺H₃N–CH(R)–COO^–) can be stabilized by the presence of counter ions and/or water molecules [1, 3]. In order to investigate the nature of the interaction between metal cations and aromatic amino acids, a number of theoretical and experimental studies have been conducted [5–14]. The effect of water molecules on the stability of the zwitterionic structure of phenylalanine, tyrosine and tryptophan was also investigated [3, 4]. Aromatic amino acids may, besides interaction through their polar heads, also interfere via their aromatic part of the molecule. The aromatic groups of these amino acids can be involved in non-covalent cation – π interactions with different cationic species [11, 14–17]. This kind of interaction in biological systems may play an important part, e.g., in biological recognition processes [17], selectivity and functioning of ion channels [18], or in drug-receptor interaction [19].

Despite their importance in biology and chemistry, the interactions of aromatic amino acids with metallic cations were prevailingly focused on the metallic complexes containing alkali and alkaline earth metallic cations such as Na⁺, K⁺, Mg²⁺ and Ca²⁺, which are essential for animal and human life [1, 3, 11–14, 20]. On the other hand, divalent cations of the transition metal elements, besides their important role in functioning of enzymes, proteins and other biomacromolecules, may play an important part for the formation of peptides from simpler compounds under conditions modeling those of the primordial earth [21, 22]. Divalent cations (e.g., Ni²⁺, Cu²⁺, Zn²⁺, etc.) can enhance such a formation of peptides [22–26]. Few of the previous studies considered metalation of aromatic amino acids by transition metals. They are limited to the gas-phase complexes of phenylalanine with Ag⁺ and Zn²⁺ [8]. Rimola et al. [9, 10] carried out theoretical calculations on Cu⁺ and Cu²⁺ gas-phase complexes of phenylalanine, tyrosine and tryptophan. Very recently, Larrucea et al. [7] carried out systematic calculations of microsolvated complexes of aromatic amino acids with Al³⁺. However, to the best of our knowledge, a systematic study of the aromatic amino acid – transition metal cation complexes has not been realized yet.

In this work we use several methods of theoretical chemistry to investigate the conformations and energetics of the complexes formed by transition metal cations Ni²⁺, Cu²⁺ and Zn²⁺ with phenylalanine, tyrosine and tryptophan. The solvent effect on the systems studied was evaluated within a supermolecule approach considering microsolvation of both neutral and zwitterionic species. These metal cations have numerous and important biochemical functions in living systems. Hydrated complexes with aromatic amino acids should serve as simpler models for more complex protein – metal systems in an aqueous environment

Computational details

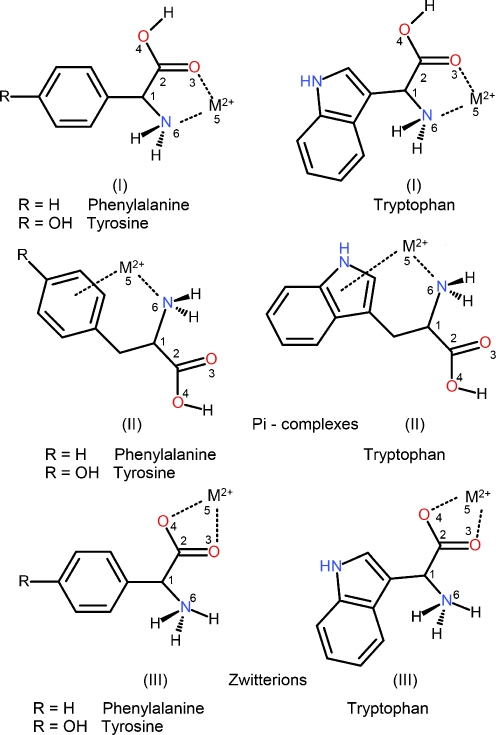
The geometries of the Phe•M, Tyr•M, Trp•M, Phe•M(H2O)₅, Tyr•M(H2O)₆, and Trp•M(H2O)₆ (M = Ni²⁺, Cu²⁺ and Zn²⁺) systems (Fig. 1) have been completely optimized with the Gaussian 03 program [27], using the density functional theory methods [28–32] Becke3LYP/6–311 + G(d,p) [31, 32] and BHandHLYP/6–311 + G(d,p) (note that these are the half-and-half functionals implemented in Gaussian 03 which are not the same as the ones proposed by Becke [33]. The formation of metal – AAA complexes can be described by reaction (A):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\hbox{M }}\left( {\hbox{g}} \right){ } + {\hbox{ AAA }}\left( {\hbox{g}} \right){ } \leftrightarrow {\hbox{ AAA}} \bullet {\hbox{M }}\left( {\hbox{g}} \right) $$\end{document} 1

Fig. 1.

Structure and atom numbering of the aromatic amino acid – metal ion complexes

M = Ni²⁺, Cu²⁺ and Zn²⁺. The gas-phase interaction enthalpy (cation binding affinity), entropy and Gibbs energy were calculated by the same way as in our previous publication [34]. The equilibrium geometries and tautomeric equilibria of AAA•M, and AAA•M(H₂O)_n, n = 5, 6 (M = Ni²⁺, Cu²⁺ and Zn²⁺) and corresponding zwitterionic forms were determined at the Becke3LYP level of theory (for Cu²⁺ complexes also BHandHLYP level of theory) and the triple-ξ basis set 6–311 + G(d,p). For Ni, Cu and Zn, we used the 6–311 + G(d,p) Wachters-Hay all electron basis set [35, 36]. Open shell calculations (Cu²⁺ complexes) have been carried out using a spin-unrestricted formalism. Ni²⁺ may exist in its complexes both in high-spin and low-spin states (triplet and singlet, respectively). Thus, for Ni²⁺ complexes the initial calculations were carried out for both low-spin and high-spin states. Cu²⁺ is an open shell system with a d⁹ (²D) ground state. Zn²⁺ is a d¹⁰ ion, so its complex is a closed-shell system with a singlet ground state. Previous investigations have shown [37–39] that the density functional theory method yields results, which compare favorably with the corresponding results obtained using the high level ab initio coupled-cluster method. Hence, DFT can sometimes be an economic alternative to ab initio methods for studying larger systems. The values of metal affinities computed using DFT are comparable to ab initio SCF results and mostly in good agreement with the corresponding experimental data [40–43]. The question of the performance of different theoretical methods to correctly describe the cation − pi interaction was discussed in several publications [9, 10, 44, 45]. It was shown, that in the case of aromatic amino acids − metal cation complexes, the hybrid (B3LYP, BHLYP) DFT model chemistries perform well compared to the highly correlated CCSD(T) and MP2 methods, respectively [9, 10, 45].

Results and discussion

Molecular structures

According to the experimental evidence [46–48] the α-amino acids and their derivatives prefer to form five-membered chelate rings with metal cations. Previous investigations [48–51] have shown that the most stable structures for a metal cation and an aliphatic amino acid are two, namely the one where the cation binds to both the N6 and the O3 sites of the neutral amino acid, and where it binds to both oxygen ends of the zwitterionic amino acid. However, aromatic amino acids can form three types of complexes with metallic cations illustrated in Fig. 1. Complex (I) represents charge-solvated systems. In those complexes the M²⁺ ion is coordinated to nitrogen and carbonyl oxygen (NO coordination) of AAAs. The aromatic ring may take part in the cation – π interaction, complex (II). The zwitterionic form of AAAs is involved in a bifurcated interaction of the negatively charged carboxyl group with the metal cation, complex (III), Fig. 1. Selected structural parameters of the metallic complexes are given in Tables 1, 2, and 3. The respective atoms are numbered according to the scheme presented in Fig. 1. An analysis of the harmonic vibrational frequencies of the optimized species proved that all of them are minima (zero number of imaginary frequencies). In the case of the isolated Phe•Ni²⁺complexes I –III the calculations were performed for the Ni²⁺cation present in both, high-spin and low-spin states (triplet and singlet, respectively). Because the singlet Ni²⁺ion and its phenylalanine complexes are higher in energy than the corresponding triplet species, the results obtained for the triplet Ni²⁺cation are discussed only. The initial conformations of the AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺) complexes were constructed on the basis of previous investigations of similar systems (phenylalanine - Zn²⁺, Polfer et al. [8], Cu²⁺ gas-phase complexes of phenylalanine, tyrosine and tryptophan determined by Rimola et al. [9]). In the neutral complex I the cation binds to both the O3 and N6 sites of the neutral AAA. This complex has been found by Rimola et al. [9] to be the most stable one. The existence of π-complexes of AAAs with monovalent metal cations was reported by several authors [1, 4, 9–14, 20]. Rimola et al. [9] examined the ability of interaction of the transition metal dication Cu²⁺ with AAAs. However, they were not able to determine a complex in which the Cu²⁺ cation interacts with the π-system of the aromatic ring. In order to check this finding, we decided to model this kind of interaction using complex II, Fig. 1. In this complex, besides π-interaction, the metal dication is stabilized via the coordination through lone pair of the N6 nitrogen atom. The conformation of this structure is further stabilized by the hydrogen bond of the NH₂•••O = C type (Fig. 1). The salt-bridge complex III represents preferable coordination of the zwitterionic AAA histidine [34].

Table 1.

B3LYP/6-311 + G(d,p) optimized relevant bond lengths (Å), bond angles (deg) and dihedral angles (deg) for the metal-coordinated and hydrated complexes of L-phenylalanine, L-tryptophan, and L-tyrosine species

Parameters	(Phe···M2+) x (H2O)n						(Trp···M2+) x (H2O)n						(Tyr···M2+) x (H2O)n
	Ni2+		Cu2+		Zn2+		Ni2+		Cu2+		Zn2+		Ni2+		Cu2+		Zn2+
	n = 0	n = 5	n = 0	n = 5	n = 0	n = 5	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6
d[C(1)–C(2)]	1.536	1.526	1.547	1.516	1.524	1.530	1.534	1.516	1.544	1.521	1.535	1.520	1.538	1.525	1.546	1.521	1.535	1.529
d[C(2)–O(3)]	1.233	1.250	1.219	1.253	1.253	1.247	1.224	1.251	1.220	1.241	1.233	1.249	1.227	1.251	1.219	1.243	1.239	1.247
d[C(2)–O(4)]	1.300	1.281	1.312	1.279	1.287	1.282	1.309	1.282	1.313	1.289	1.299	1.283	1.306	1.282	1.313	1.289	1.295	1.283
d[C(1)–N(6)]	1.500	1.496	1.485	1.501	1.512	1.494	1.494	1.501	1.488	1.491	1.486	1.495	1.495	1.496	1.487	1.495	1.491	1.495
d[N(6)···M(5)]	2.035	2.057	2.106	2.019	2.036	2.104	2.048	2.043	2.097	2.065	2.157	2.064	2.044	2.050	2.103	2.066	2.117	2.093
d[O(3)···M(5)]	1.965	2.008	2.082	1.961	1.963	2.080	1.990	1.972	2.087	2.017	2.067	2.011	1.982	2.013	2.090	2.011	2.027	2.087
Θ[C(1)–C(2)–O(3)]	122.0	119.3	122.9	120.9	123.3	119.5	123.1	121.2	123.5	121.2	122.9	121.8	122.3	119.2	123.3	121.5	122.8	119.5
Θ[C(2)–C(1)–N(6)]	108.1	107.1	109.0	108.1	110.0	107.3	108.7	108.6	109.4	108.1	108.6	109.5	108.3	107.0	109.3	108.7	108.5	107.3
Θ[C(1)–N(6)···M(5)]	108.2	105.7	109.3	111.5	109.7	106.0	108.8	110.3	109.4	110.1	109.9	108.9	108.4	105.6	109.4	110.9	109.5	106.0
Θ[C(2)–O(3)···M(5)]	113.7	113.8	113.4	115.7	110.8	113.8	113.2	115.2	112.7	115.1	115.2	113.6	113.6	113.5	113.0	115.3	114.6	113.3
Θ[O(3)···M(5)···N(6)]	84.8	81.8	81.6	83.5	87.7	79.7	84.6	83.6	82.1	81.8	80.0	83.8	84.3	81.9	81.8	82.4	81.8	79.8
Φ[O(3)–C(2)–C(1)–N(6)]	13.1	26.7	15.2	-5.3	-15.2	28.1	-11.2	-11.6	11.4	-16.7	10.9	-16.3	12.9	27.5	12.8	-12.8	10.0	28.4
Φ[C(2)–C(1)–N(6)···M(5)]	-17.8	-35.8	-20.3	1.8	16.1	-38.0	13.3	8.9	-17.2	20.2	-18.2	15.8	-17.9	-36.6	-18.4	10.4	-16.6	-38.7
Φ[C(1)–C(2)–O(3)···M(5)]	-0.5	-1.9	-0.9	6.3	4.8	-1.8	2.3	8.2	1.2	3.9	3.2	7.4	-0.2	-2.2	0.4	8.4	2.9	-1.7

Table 2.

B3LYP/6-311 + G(d,p) optimized relevant bond lengths (Å), bond angles (deg) and dihedral angles (deg) for metal-coordinated and hydrated pi-complexes of the L-phenylalanine, L-tryptophan, and L-tyrosine species

Parameters	(Phe_pi···M2+) x (H2O)n						(Trp_pi···M2+) x (H2O)n						(Tyr_pi···M2+) x (H2O)n
	Ni2+		Cu2+		Zn2+		Ni2+		Cu2+		Zn2+		Ni2+		Cu2+		Zn2+
	n = 0	n = 5	n = 0	n = 5	n = 0	n = 5	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6
d[C(1)–C(2)]	1.541	1.539	1.539	1.541	1.543	1.536	1.543	1.535	1.546	1.537	1.542	1.534	1.540	1.536	1.542	1.538	1.542	1.536
d[C(2)–O(3)]	1.203	1.220	1.204	1.218	1.204	1.224	1.203	1.219	1.201	1.217	1.206	1.220	1.203	1.219	1.202	1.217	1.205	1.220
d[C(2)–O(4)]	1.319	1.300	1.318	1.299	1.318	1.297	1.324	1.305	1.326	1.305	1.319	1.304	1.320	1.303	1.323	1.304	1.317	1.301
d[C(1)–N(6)]	1.519	1.498	1.518	1.498	1.529	1.510	1.503	1.504	1.496	1.493	1.530	1.508	1.517	1.500	1.508	1.496	1.532	1.502
d[N(6)···M(5)]	1.990	2.054	1.979	1.995	1.996	2.033	1.986	2.058	2.003	2.008	1.974	2.085	1.998	2.042	1.991	1.994	1.989	2.063
Θ[C(1)–C(2)–O(3)]	120.7	120.9	120.4	120.8	120.7	120.6	121.2	122.1	121.6	121.4	121.0	121.8	120.8	121.4	121.1	121.3	120.6	121.1
Θ[C(2)–C(1)–N(6)]	106.5	109.3	107.1	108.7	105.3	107.4	107.0	109.5	107.5	109.1	104.7	108.7	106.8	109.7	107.6	108.8	105.0	108.6
Θ[C(1)–N(6)···M(5)]	112.5	116.6	113.4	117.0	114.4	121.5	117.2	117.5	119.9	113.2	115.0	121.5	111.5	112.2	113.6	114.3	115.3	115.1
Φ[O(3)–C(2)–C(1)–N(6)]	-15.9	-21.3	-10.1	-18.2	-17.1	-12,6	-15.2	-4.5	-13.4	-12.9	-9.2	0.1	-15.3	-20.4	-12.6	-10.3	-15.1	-18.4
Φ[C(2)–C(1)–N(6)···M(5)]	154.6	138.4	155.9	137.7	155.1	110.1	152.3	113.7	147.1	127.3	132.1	105.9	152.4	135.3	155.4	124.0	146.8	130.0

Table 3.

B3LYP/6-311 + G(d,p) optimized relevant bond lengths (Å), bond angles (deg) and dihedral angles (deg) for metal-coordinated and hydrated complexes of the zwitterionic L-phenylalanine, L-tryptophan, and L-tyrosine species

Parameters	(Phe_zwitt···M2+) x (H2O)n						(Trp_ zwitt ···M2+) x (H2O)n						(Tyr_ zwitt ···M2+) x (H2O)n
	Ni2+		Cu2+		Zn2+		Ni2+		Cu2+		Zn2+		Ni2+		Cu2+		Zn2+
	n = 0	n = 5	n = 0	n = 5	n = 0	n = 5	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6	n = 0	n = 6
d[C(1)–C(2)]	1.525	1.513	1.568	1.508	1.527	1.515	1.539	1.523	1.566	1.557	1.536	1.511	1.532	1.514	1.569	1.520	1.531	1.512
d[C(2)–O(3)]	1.268	1.273	1.227	1.273	1.269	1.271	1.265	1.265	1.232	1.233	1.262	1.272	1.266	1.269	1.230	1.261	1.265	1.272
d[C(2)–O(4)]	1.256	1.271	1.271	1.274	1.263	1.271	1.247	1.263	1.267	1.272	1.256	1.272	1.252	1.271	1.267	1.268	1.259	1.272
d[C(1)–N(6)]	1.524	1.495	1.520	1.495	1.520	1.495	1.529	1.497	1.520	1.500	1.521	1.493	1.526	1.496	1.520	1.497	1.522	1.495
d[O(4)···M(5)]	2.063	2.024	1.921	1.963	2.082	2.015	2.056	2.083	1.924	1.884	2.083	2.021	2.080	2.049	1.926	2.018	2.062	2.016
d[O(3)···M(5)]	2.016	1.996	3.023	2.006	2.027	2.067	2.116	2.034	3.018	3.136	2.152	2.054	2.036	2.002	3.038	2.132	2.120	2.061
Θ[C(1)–C(2)–O(3)]	119.3	122.8	116.5	123.8	120.2	122.3	117.8	121.1	116.2	119.1	118.9	122.1	118.7	122.4	116.0	121.9	119.5	122.2
Θ[C(2)–C(1)–N(6)]	107.1	111.0	103.8	111.1	109.3	111.1	105.6	109.6	103.6	109.1	108.2	111.2	106.6	110.6	103.5	110.1	108.6	111.1
Θ[C(1)–O(4)···M(5)]	85.8	87.9	117.3	89.9	86.0	89.1	88.2	86.5	117.1	123.3	89.1	88.7	85.7	87.2	117.7	90.7	88.8	88.9
Θ[C(2)–O(3)···M(5)]	88.1	89.2	65.3	88.1	88.6	86.8	85.1	88.8	65.4	62.6	85.9	87.2	88.0	89.2	65.0	85.8	86.0	86.9
Θ[O(3)···M(5)···O(4)]	65.1	65.5	48.2	66.1	64.7	64.9	63.8	64.3	38.3	45.5	62.7	65.1	64.6	65.2	47.9	63.9	63.6	65.1
Φ[O(3)–C(2)–C(1)–N(6)]	-12.1	-17.2	7.9	-17.9	-9.1	-16.1	-2.5	-4.1	2.4	-8.6	-10.8	-13.3	-9.4	-20.5	4.9	-10.9	-5.2	-17.3
Φ[C(1)–C(2)–O(4)···M(5)]	179.9	-177.9	-177.0	177.8	-177.9	-178.2	-179.1	-179.2	-175.1	-178.1	177.4	177.3	-179.8	-178.6	177.9	179.8	178.5	177.7
Φ[C(1)–C(2)–O(3)···M(5)]	-179.8	178.1	176.6	-177.7	177.9	178.2	179.1	179.3	176.6	179.1	-177.5	-177.2	179.8	178.7	-177.3	-179.2	-178.5	-177.6

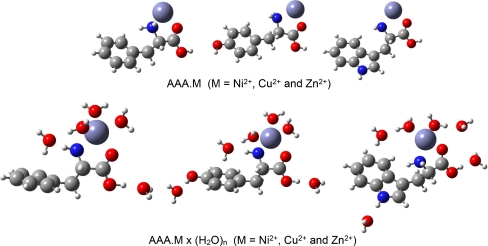
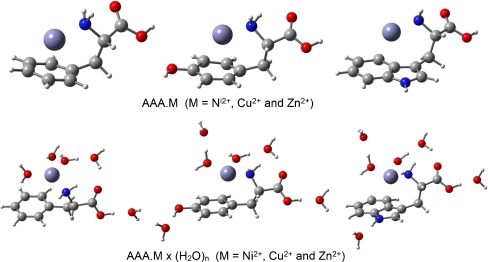
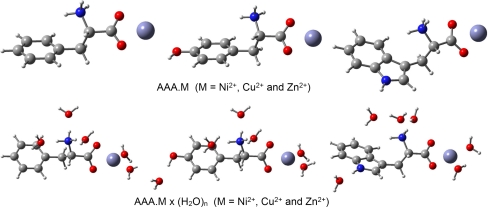
The solvent effect on the geometry and stability of individual complexes is studied making use of a supermolecule modeling of hydration. The solvation of the parent systems was investigated using the Phe•M(H₂O)₅, Tyr•M(H₂O)₆ and Trp•M(H₂O)₆ (M = Ni²⁺, Cu²⁺ and Zn²⁺) species. The water molecules were placed at the polar parts of the AAAs. Metal cations are coordinated, like in our previous work [40], by two water molecules. The optimized complexes Phe•M(H₂O)₅, Tyr•M(H₂O)₆ and Trp•M(H₂O)₆, (M = Ni²⁺, Cu²⁺ and Zn²⁺) converged to the energetically stable species stabilized by both, strong electrostatic interaction and intermolecular hydrogen bonds. For an illustration of the molecular structure of these complexes the fully optimized metal coordinated and solvated systems represented by the zinc species are shown in Figs. 2, 3 and 4. Generally, water molecules form intermolecular hydrogen bonds with polar proton donor (OH, NH, NH₂, NH₃) and proton acceptor C = O groups of neutral and zwitterionic forms of AAAs.

Fig. 2.

Overall structure of the B3LYP/6311 + G(d,p) optimized neutral complexes of chelated phenylalanine, tyrosine and tryptophan and their hydrates

Fig. 3.

Overall structure of the B3LYP/6311 + G(d,p) optimized π-complexes of chelated phenylalanine, tyrosine, tryptophan and their hydrates

Fig. 4.

Overall structure of the B3LYP/6-311 + G(d,p) optimized complexes of the chelated zwitterionic form of phenylalanine, tyrosine, tryptophan and their hydrates

Neutral complexes AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺)

In these complexes the M²⁺ ion is bicoordinated to nitrogen and carbonyl oxygen (NO coordination) of AAAs. Selected bond lengths, bond angles and dihedral angles of the fully optimized neutral metal complexes and their hydrated systems are given in Table 1. The hydration results in different changes of the molecular structure of the parent complexes. In general, the covalent bond lengths C(1)–C(2), C(2)–O(3), C(2)–O(4) and C(1)–N(6) of the AAAs are only slightly changed upon hydration. However, microsolvation results in most cases in a slight prolongation of the M²⁺···O and M²⁺···N bonds by about 0.02 – 0.05 Å. The M···O bonds are always shorter (about 0.02 – 0.07 Å) than the analogous M···N bonds (M = Ni²⁺, Cu²⁺ and Zn²⁺), indicating that these metal cations form stronger bonds to the oxygen atoms of AAAs. The equilibrium distances M···O and M···N increase in the order: Ni²⁺ < Cu²⁺ ≤ Zn²⁺. With regard to valence angles, upon hydration larger changes (by about 1 – 4^o) were observed only in the values of the valence angle C(1)–N(6)···M(5). The O(3)···M(5)···N(6) angle in the AAA complexes extends over a relatively tiny interval (80 – 85^o). The chelate rings of the metallic complexes are not planar [dihedral angles O(3)–C(2)–C(1)–N(6) and C(2)–C(1)–N(6)···M(5)], and the deviation from planarity considerably increases with microsolvation (Table 1).

Π-complexes AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺)

The role of the cation – π side chain AAA interaction was modeled using the complex in which the cation is bound to both, the Phe, Tyr or Trp π face and to the –NH₂ group (Figs. 1 and 3). Ma et al. [16] has assumed the existence of such interactions in their study of the alkali metal cation – phenylalanine complexes. We have located these conformers as minimum for all structures except for the BeckeHandHLYP calculations of the system Tyr•Cu²⁺, which collapsed to the neutral conformer I. However, the cation – π side chain interaction was preserved in the hydrated complex Tyr•Cu²⁺(H₂O)₆. Important geometric characteristics of these complexes are given in Table 2. Like in the neutral system (I), the covalent bond lengths C(1)–C(2), C(2)–O(3), C(2)–O(4) and C(1)–N(6) of the AAAs are only slightly changed upon hydration. The equilibrium distance M(5)···N(6) slightly increases in the hydrated complexes (about 0.05 Å). The valence angle C(1)–N(6)···M(5) and dihedral angles O(3)–C(2)–C(1)–N(6) and C(2)–C(1)–N(6)···M(5) change appreciably in the hydrated systems (by about 3 – 30⁰), thus solvation of π-complexes is connected with an appreciable structural rearrangement.

Complexes zwitterionic AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺)

For transition metal – AAA complexes III, Figs. 1 and 3, represent the interaction of the zwitterionic phenylalanine, tyrosine and tryptophan with metal cations. In these complexes metal cations are bicoordinated to the carboxylate group of AAAs. Recently, Rimola et al. [9] computationally predicted zwitterionic complexes of Phe•Cu²⁺ and Tyr•Cu²⁺ as the second most stable structure. Of the nine AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺) zwitterionic complexes studied, the hydrated Trp•Cu²⁺(H₂O)₆ complex represents the energetically most stable structure. The metal cation coordination to the carboxylate group of zwitterionic AAAs is almost symmetric. The only exception is the Cu²⁺cation which in the isolated systems, due to electrostatic repulsion between the copper dication and the positively charged –NH₃ group of AAAs, is coordinated unsymmetrically with the shortest Cu²⁺•••O distance of about 1.9 Å to the oxygen O(4) that is not acting as proton acceptor (Table 3). The Cu²⁺•••O(3) distances were found to be considerably longer (about 3 Å). This highly asymmetric coordination of the copper dication is also preserved in the hydrated complex Trp(zwitt)•Cu²⁺(H₂O)₆. The metal cations lie in both, isolated and hydrated complexes, in the plane of the carboxylate group (dihedral angles Φ[C(2)–C(1)–O(4)···M(5)] and Φ[C(1)–C(2)–O(3)···M(5)], Table 3). The O(3)···M(5)···O(4) angle of the bifurcated metal bond is within a relatively large interval of 40 – 65^o. Thus, the position of the metal cation at the binding site of zwitterionic AAAs depends on both, the kind of acid and environment.

Relative energies

The relative energies with reference to the most stable species of the 54 gas-phase and hydrated complexes studied are given in Table 4. As it is evident from this Table, the relative energies of the species studied vary in a relatively large energy interval (by about 5 – 80 kJ mol^-1) indicating that in most cases gas-phase complexes should exist in one most stable form. Similar net preference for one most stable structure was theoretically found for histidine metallic complexes [34]. Hydration changes the structure of the AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺) complexes significantly. Of the three types of systems investigated (I, II and III, Fig. 1), the relative stability of the gas-phase complexes computed with DFT methods suggest, with exception of the Zn²⁺system, metallic complexes I of the neutral AAAs to be the most stable species. In the most stable complex I the Ni²⁺ and Cu²⁺ cations are bicoordinated to the AAA N(6) and O(3) atoms, Figs. 1 and 2. In the gas-phase the energetically unfavored zwitterionic Trp•Cu²⁺ complex is stabilized upon solvation and represents the most stable copper complex of tryptophane in aqueous solution (Becke3LYP method, Table 4). It was recently demonstrated [9, 52] that functionals (e.g., BhandHLYP) with a larger percentage of exact exchange (50%) than the most commonly used Becke3LYP for open-shell systems compare better to the highly correlated CCSD(T) method. Thus, for the AAA – Cu²⁺ complexes, in addition to Becke3LYP we also carried out calculations with the BHandHLYP functional. BHandHLYP relative Gibbs energies are for most cases by about 10 – 30 kJ mol^-1 larger (Table 4). The discrepancy in the results of the different DFT methods used for the prediction of the relative stability of open shell systems containing Cu²⁺ cations may be explained by the shortcomings of the B3LYP method to correctly describe the delocalized nature of the Cu²⁺ complexes [43]. The cation Zn²⁺ behaves differently. Due to the large Gibbs energy gap between the most stable complex II and the other systems (I and III) the most stable complex II is dominant in the gas phase. Coordinated water shifts the absolute stability towards complex I of the Phe•Zn²⁺ and Trp•Zn²⁺ systems (Table 4). An interesting situation is observed for the Tyr•Zn²⁺ complex. In both, the gas phase and solvated state the π complex II has been found to be the global minimum (Table 4). However, due to the low energy barrier of about 5 kJ mol^-1 both species (I and II, respectively) may coexist in water.

Table 4.

B3LYP/6-311 + G(d,p) calculated relative stability ( ΔG, in kJ mol^-1) of neutral complexes (I, II) and zwitterionic (III) metal ion complexes of the AAAs studied

Cation	System	(Phe···M2+) x (H2O)5			(Trp···M2+) x (H2O)6			(Tyr···M2+) x (H2O)6
		I	II	III	I	II	III	I	II	III
Ni2+	Without water	0	6.8	44.6	0	39.9	51.3	0	49.2	39.5
	With water	0	43.6	56.3	0	4.8	46.0	0	23.1	39.2
Cu2+	Without water	0	52.6	26.5	0	47.1	28.6	0	64.4	28.7
	With water	0	48.3	19.9	21.2	23.0	0	0	11.2	14.7
	Without watera	0	87.6	36	0	65.4	35.7	0	0b	37.1
	With watera	0	63.4	42.7	0	22.1	8.6	0	33.6	40.9
Zn2+	Without water	35.6	0	27.5	66.1	0	65.2	26.4	0	14.8
	With water	0	42.4	33.4	0	13.3	72.9	5.7	0	41.8

^aBhandHLYP method

^bCollapsed to the conformer I

Interaction enthalpies, entropies and Gibbs energies

Table 5 summarizes the interaction enthalpies, entropies and Gibbs energies of the AAA•M (M = Ni²⁺, Cu²⁺ and Zn²⁺) complexes computed at the Becke3LYP level of DFT together with the data for copper complexes computed using the BHandHLYP model and the published values of interaction energies for copper complexes taken from the work by Rimola et al. [9]. As it is evident from our calculations of 54 AAA-metal cation species, the stability of the different conformers and forms of AAAs can be substantially modified by specific metal ion AAA interactions as well as by hydration. The interaction energies can be computed for individual complexes of varying relative energetic stability. However, only the results presented for the thermodynamically most stable structures have a physical meaning. The interaction energies were computed as the difference between the most stable species (Table 4). For AAAs as reference state conformers we used the conformers stabilized by means of the OH•••NH₂ hydrogen bond and an additional stabilizing interaction between the amino group and the π-electron system of the aromatic ring. These conformers have been found previously as the most stable gas phase structures of phenylalanine [53] and tryptophan [54]. The formation of AAA – metal cation complexes as described in Eq. 1 is an exothermic process. The association reaction is connected with a large and negative, destabilizing effect of entropy (Table 5). In the complexes studied this entropy effect amounts from -105 to -150 J mol^-1 K^-1. The largest entropy changes (some -150 J mol^-1 K^-1) are observed for AAA complexes with Zn²⁺. In this case, however, the Zn²⁺ – π interaction forces the polar amino group of the amino acid to bend toward the aromatic ring (Fig. 3). The importance of entropy effects for the relative stability of individual conformers of phenylalanine was recently stressed by Kaczor et al. [6]. To take the entropy effects into consideration, Gibbs energies, which describe the tendency to associate in real molecular complexes, will be discussed. The computed Gibbs energies ΔG ²⁹⁸ are negative and span a relatively narrow energy interval from -940 to -1320 kJ mol^-1. The energetic differentiation of the complexes studied based on the type of the aromatic substituent of AAAs shows an increasing interaction Gibbs energy in the order Phe < Tyr < Trp for all three metal cations studied. This ordering of stability correlates very well with the experimental gas-phase basicities and proton affinities of these aromatic amino acids [55]. For reason of comparison, Table 5 also contains computed interaction enthalpies and Gibbs energies for Cu²⁺ complexes of AAAs by Rimola et al. [9] using a slightly different basis set. The results of Rimola et al. [9] are in very good agreement with data obtained for the same complexes by us. The Gibbs interaction energies show for all three AAAs studied a decreasing binding affinity in the order Cu²⁺ > Ni²⁺ > Zn²⁺. Thus, of the transition metal cations studied, the copper dication is the most effective Lewis acid in the interaction with the basic center of AAAs. The largest interaction Gibbs energy was found for the tryptophan - Cu²⁺ complex (-1317.5 kJ mol^-1, Becke3LYP method). According to Marino et al. [41] charge transfer plays an important role in the complexation of the transition metal cations Ni²⁺, Cu²⁺, and Zn²⁺. Moreover, the Cu²⁺ cation is an open shell system, and it has been assumed that the different internal polarizability of the whole Cu²⁺ complexes is probably one of the main reasons for this difference. Rimola et al. [9] examined complexes of monovalent and divalent copper with AAAs. They showed that functionals such as BeckeHLYP with larger percentages of exact exchange (50%) than the commonly used Becke3LYP (20%) compare better to the highly correlated ab initio CCSD(T) method for these open-shell systems. We also did calculations of all open-shell Cu²⁺ complexes with the half-and-half functional BeckeHandHLYP implemented in the G03 computer code. BeckeHandHLYP relative Gibbs energies for AAA•Cu²⁺ complexes were computed to be by about 100 kJ mol^-1 lower than with B3LYP (Table 5). According to Rimola et al. [9] the variation in interaction energy using two functionals may be at least partly explained by the different results of calculations of the second ionization energy for copper using Becke3LYP and BeckeHandHLYP methods, respectively. Sousa et al. [43] explain the discrepancy in the results of the different DFT methods used for the prediction of the relative stability of open shell systems containing the Cu²⁺ cation by the shortcomings of the Becke3LYP method to correctly describe the delocalized nature of the Cu²⁺ complexes.

Table 5.

B3LYP/6-311 + G(d,p) calculated enthalpies ΔH, entropies, ΔS, and Gibbs energies ΔG, of the ion – AAA systems^a

System	Complex	ΔH 298, kJ/mol	ΔS 298, J/mol K	ΔG 298, kJ/mol
I	Phe···Ni2+	-1051.8	-120.6	-1016.1
I	Phe···Cu2+	-1199.9 (-1196.6)	-109.9	-1167.1 (-1165.7)
I b	Phe···Cu2+	-1104.1 (-1096.5)	-105.4	-1072.6 (-1066.1)
II	Phe···Zn2+	-984.1	-144.6	-940.9
I	Trp···Ni2+	-1184.6	-112.1	-1151.2
I	Trp···Cu2+	-1349.9 (-1346.0)	-108.7	-1317.5 (-1311.7)
I b	Trp···Cu2+	-1249.7 (-1243.1)	-107.6	-1217.6 (-1209.2)
II	Trp···Zn2+	-1098.1	-142.9	-1055.4
I	Tyr···Ni2+	-1117.2	-124.2	-1080.1
I	Tyr···Cu2+	-1277.5 (-1272.4)	-116.4	-1242.8 (-1238.0)
I b	Tyr···Cu2+	-1179.1 (-1171.1)	-115.2	-1144.8 (-1137.2)
II	Tyr···Zn2+	-1004.9	-154.7	-958.9

^aData in parentheses were taken from the work by Rimola et al. [9].

^bBHandHLYP method

Electronic structures

The atomic charges of the complexes studied were evaluated by natural population analysis [56, 57] using the NBO program [58]. The natural charges (NAC), Wiberg bond indices (WBI) and amount of charge transfer (CT) for the most stable species are shown in Table 6. The coordination of these transition metal cations that are borderline hard acids [59] appreciably increases polarization of AAAs studied. This polarizing effect of bivalent cations is much higher in the case of Lewis acids Ni²⁺ and Cu²⁺, respectively. These Lewis acids accept very large amount of negative charge (0.9 – 1.1e). Thus the role of charge transfer for bonding of the AAAs studied to nickel and copper dications is of particular importance.

Table 6.

Natural atomic charges (NAC), Wiberg bond indices (WBI) and amount of charge transfer (CT) from the B3LYP/6-311 + G(d,p) NBO analysis

System	Complex	NAC/e			WBI		CT/e
		O(3)	N(6)	M2+	O(3)···M2+	N(6)···M2+
I	Phe···Ni2+	-0.679	-0.912	1.089	0.1448	0.1927	0.911
I	Phe···Cu2+	-0.663	-0.917	0.936	0.0874	0.1419	1.064
I a	Phe···Cu2+	-0.700	-0.933	0.937	0.0611	0.0942	1.063
II	Phe···Zn2+		-0.982	1.585		0.3259	0.415
I	Trp···Ni2+	-0.660	-0.908	0.851	0.1264	0.1736	1.149
I	Trp···Cu2+	-0.668	-0.928	0.905	0.0871	0.1495	1.095
I a	Trp···Cu2+	-0.709	-0.936	0.934	0.0634	0.1013	1.066
II	Trp···Zn2+		-0.998	1.459		0.2856	0.545
I	Tyr···Ni2+	-0.667	-0.907	0.963	0.1313	0.1757	1.037
I	Tyr···Cu2+	-0.663	-0.928	0.907	0.0858	0.1450	1.093
I a	Tyr···Cu2+	-0.705	-0.935	0.935	0.0624	0.0982	1.065
II	Tyr···Zn2+		-0.993	1.532		0.3128	0.468

^aBHandHLYP method

More interesting situation is with the Zn²⁺ complexes. Most stable species correspond to the π complex II. The cation − π interactions are electrostatic in nature, accounting for 60 – 90% of the overall binding [16]. This fact is also manifested in our calculations of the zinc-coordinated complexes. The magnitude of charge transfer contribution is much lower (ca. 0.4 – 0.5e). However, zinc is sometimes considered a transition metal and sometimes a main group element. According to Amin and Truhlar computational chemistry requirements of zinc coordination resemble those of the main group rather than the first transition row [60]. Its interaction with aromatic amino acids through cation − π interaction resembles similar interaction of main group metal cations with aromatic motifs of amino acids [11, 13, 14].

As is evident from Table 6 the quantitative importance of CT term varies considerably among the ions. It is frequently argued that metal ion interaction energies well correlate with electron affinity of metal cation [61]. Hoyau et al. in their theoretical study of the interaction of glycine wit 15 metal cations have shown that the magnitude of charge transfer correlates well with the electron affinity (EA) of the metal ion [62]. In the case of metal cations studied by us their electron affinities (18.17, 20.29 and 17.96 eV for s Ni²⁺, Cu²⁺, and Zn²⁺, respectively [63]) exhibit irregularity with respect to CT. For transition metal cations Ni²⁺ and Cu²⁺, the larger the metal ion EA the larger the CT. Although Zn²⁺ electron affinity is large and comparable in magnitude with that for Ni²⁺ cation, its magnitude does not quantitatively correlate with charge transfer. Moreover, the amount of CT from the amino acid toward the M²⁺ ions also does not correlate with the interaction energies of the complexes investigated (Tables 5 and 6).

Summary and conclusions

This theoretical study was set out to determine stable conformers for the 54 complexes of phenylalanine, tyrosine and tryptophan with the transition metal cations Ni²⁺, Cu²⁺ and Zn²⁺ and their hydrated forms. From the results the following conclusions can be drawn.

1. For phenylalanine, tyrosine and tryptophan complexes with Ni²⁺ and Cu²⁺ the most stable structure corresponds to the complex in which the metal cation binds to the oxygen of the carbonyl group and to the nitrogen of the amine (system I).

2. The π − complexes of AAAs with metal cations studied represent a new kind of low − energy conformers. The interaction of the Zn²⁺ cation with the AAAs studied results in the π − complex II as the most stable structure.

3. Solvation changes the relative stability of individual species in several cases. Coordinated water shifts the absolute stability toward the complex I of the Phe•Zn²⁺ and Trp•Zn²⁺ systems. On the other hand, the π − complex II of the Tyr•Zn²⁺ system has been found to be the global minimum in both, gas phase and solvated state.

4. Among the Lewis acids investigated, the strongest affinity to the aromatic amino acids studied resulted for the Cu²⁺ cation. The largest interaction Gibbs energy was found for the tryptophan – Cu²⁺ complex.

This work yields quantities that may be inaccessible or complementary to experiments and represents the first quantum chemical approach in which both the gas-phase and solvated phase complexation between aromatic amino acids (phenylalanine, tyrosine and tryptophan) and transition metal cations Ni²⁺, Cu²⁺ and Zn²⁺ are considered and absolute metal ion affinities were evaluated. The results are also relevant for attempts to design peptides selectively binding different metal ions [64].