Invited Commentary: Understanding Bias Amplification

Abstract

In choosing covariates for adjustment or inclusion in propensity score analysis, researchers must weigh the benefit of reducing confounding bias carried by those covariates against the risk of amplifying residual bias carried by unmeasured confounders. The latter is characteristic of covariates that act like instrumental variables—that is, variables that are more strongly associated with the exposure than with the outcome. In this issue of the Journal (Am J Epidemiol. 2011;174(11):1213–1222), Myers et al. compare the bias amplification of a near-instrumental variable with its bias-reducing potential and suggest that, in practice, the latter outweighs the former. The author of this commentary sheds broader light on this comparison by considering the cumulative effects of conditioning on multiple covariates and showing that bias amplification may build up at a faster rate than bias reduction. The author further derives a partial order on sets of covariates which reveals preference for conditioning on outcome-related, rather than exposure-related, confounders.

THE PHENOMENON OF BIAS AMPLIFICATION

This commentary deals with a class of variables that, if conditioned on, tend to amplify confounding bias in the analysis of causal effects. This class, independently discovered by Bhattacharya and Vogt (1) and Wooldridge (2), includes instrumental variables (IVs) and variables that have greater influence on exposure than on the outcome (3).

I am pleased to see that the phenomenon of bias amplification, which until recently was practically unknown to researchers in the health sciences, has received a thorough and comprehensive treatment by Myers et al. (4), confirming and qualifying several theoretical predictions derived by Pearl (3) and White and Lu (5). I am particularly struck by Myers et al.’s description of the hip fracture study by Patrick et al. (6), in which “the strength of the IV-exposure relation in this example makes the IV easy to identify and remove by investigators” (4, p. 1218). This awareness that strong predictors of exposure may be a source of troublesome bias is perhaps the most significant impact that the theory of bias amplification has had thus far, because, as Myers et al. point out, it goes against conventional wisdom. Hirano and Imbens (7), for example, devote a major effort to choosing the strongest possible predictors for propensity score inclusion, and Rubin (8) regards the very idea of leaving an observed covariate unconditioned on as “nonscientific ad hockery.” (See my previous article (9) for an explanation.)

In this commentary, I supplement the discussion of Myers et al. (4) with several observations that might shed additional light on their conclusions, especially as they pertain to the cumulative effect of multiple near-IV confounders, and the problem of selecting a reasonable set of covariates from a massive host of promising candidates.

BIAS AMPLIFICATION WITH MULTIPLE COVARIATES

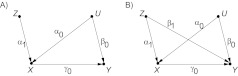
Let us examine the simple IV model depicted in Figure 1A, assuming a zero-mean, unit-variance standardization. If we retrace the derivation of the association between X and Y conditional on Z,

(1)

we find that this formula holds not only for a perfect IV but also for a near-IV, as the one depicted in Figure 1B (see my previous article (3)). Allowing a confounding path to extend from Z to Y will only change the crude association, which will increase from ${\text{γ}}_0+{\text{α}}_0{\text{β}}_0$ to ${\text{γ}}_0+{\text{α}}_0{\text{β}}_0+{\text{α}}_1{\text{β}}_1$ to reflect the added confounding path X ← Z → Y.

Figure 1.

A) A linear model with instrumental variable Z and confounder U. B) A near-instrumental variable Z that is also a confounder.

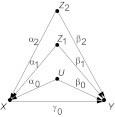
Now consider a system of multiple confounders, such as the one depicted in Figure 2, where each covariate intercepts a distinct confounding path between X and Y and for which the crude bias (without any conditioning) is

(2)

If we condition on Z₁, two modifications are required. First, the path containing Z₁ will no longer contribute to confounding and, second, whatever bias is contributed by the remaining paths, namely ${\text{α}}_0{\text{β}}_0+{\text{α}}_2{\text{β}}_2$, will be amplified by a factor of , reflecting the decreased variance of X due to fixing Z₁. Overall, the bias remaining after conditioning on Z₁ will read

(3)

Further conditioning on Z₂ will remove the factor α₂β₂ from the numerator (deactivating the path X ← Z₂ → Y) and will replace the denominator by the factor , representing the reduced variance of X, due to fixing both Z₁ and Z₂. The resulting bias will be

(4)

Figure 2.

A linear model with multiple covariates (Z₁ and Z₂) and an unobserved confounder U.

We see the general pattern that characterizes sequential conditioning on sets of covariates, organized as in Figure 2. The bias B(Z) remaining after conditioning on a set Z = (Z₁, Z₂, …, Z_k−1, Z_k) is given by the formula

(5)

which reveals 2 distinct patterns of progression, one representing confounding reduction (shown in the numerator) and one representing IV amplification (shown in the denominator). The latter increases monotonically while the former progresses nonmonotonically, since the signs of the added terms may alternate. Thus, the cumulative effect of sequential conditioning has a built-in slant towards bias amplification as compared with confounding reduction; the latter is tempered by sign cancellations, the former is not.

In deriving equation 5, we assumed that no Z_k is a collider, that each Z_k has a distinct path characterized by α_k, and that the Z_k’s are not correlated. In a general graph, where multiple paths may traverse each Z_k, B(Z) will read

(6)

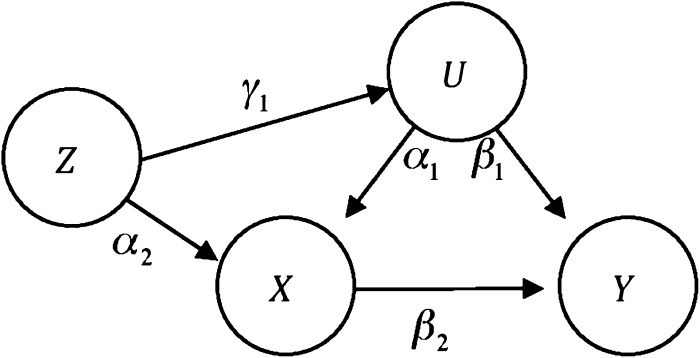
where $B_0^{-}\left(k\right)$ represents the crude bias B₀ modified by conditioning on (Z₁, Z₂, …, Z_k−1, Z_k), and ${\text{α}\prime }_k$ is the coefficient of Z_k in the regression of X on (Z₁, Z₂, …, Z_k−1, Z_k). For example, in model 5 of Myers et al. (4) (shown in Figure 3), the crude bias is

(7)

while the bias remaining after conditioning on Z reads

(8)

The numerator is obtained by setting α₂ = 0 in equation 7 and multiplying the remaining term by $(1-{\text{γ}}_1^2)$, to account for the effect that conditioning on Z has on the path X ← U → Y. The denominator invokes the factor α′ = (α₂ + γ₁α₁), which is the regression coefficient of X on Z.

Figure 3.

The model used by Myers et al. for studying near-instrumental variables. The parameter γ₁ contributes to confounding as well as to bias amplification.

We see that, in this model, γ₁ controls simultaneously the reduction of confounding bias and the amplification of residual bias, both caused by conditioning on Z. Myers et al. (4) assumed that γ₁ controls the former only.

In examining the extent to which these results are generalizable to nonlinear models, it has been shown (3) that, while in linear systems conditioning on an IV always amplifies confounding bias (if such exists), bias in nonlinear systems may be amplified as well as attenuated. Additionally, an IV may introduce new bias where none exists. This can be demonstrated if we introduce an interaction term into the model of Figure 1A, to read

With this modification, equation 1 becomes

(9)

while the crude association becomes

(10)

The resulting z-adjusted bias therefore reads

where B₀ is the unadjusted bias.

We see that, if B₀ ≥ 0 and α₀α₁δ_z > 0, we can get |B_z| < |B₀|. This means that conditioning on Z may reduce confounding bias, even though Z is a perfect instrument and both Y and X are linear in U. Note that, owing to the nonlinearity of Y(x, u), the conditional bias depends on the value of Z and, moreover, for Z = 0 we obtain the same bias amplification as in the linear case (equation 1).

We also see that conditioning on Z can introduce bias where none exists. However, this occurs only for a specific value of X,

a condition that yields B₀ = 0 and |B_z| > 0.

ON THE CHOICE BETWEEN EXPOSURE-RELATED AND OUTPUT-RELATED COVARIATES

Investigators are often faced with the need to adjust for a large number of potential confounders; some are strongly related to exposure, and some are more related to the output. Since estimation efficiency usually deteriorates with the number of covariates involved, the question arises as to which subset of potential confounders to measure and control for (see discussions by Day et al. (10), Thomas and Greenland (11), Hill (12), Austin (13), Pearl (9), White and Lu (5), Patrick et al. (6), and Myers et al. (4)).

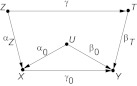
Figure 4 represents this choice formally, where T represents output-related covariates, Z represents exposure-related covariates, and U represents unmeasured confounders. We ask which set of variables should be chosen for adjustment: {Z}, {T} or {Z, T}. Morgan and Winship (14) raise the same question, and they state a preference for {Z, T}.

Figure 4.

Adjustment for an output-related covariate (T) is preferred to adjustment for a treatment-related covariate (Z) or both (Z, T). The former covariate has a lower bias-amplification potential than the latter two when U is unobserved.

Intuitively, since Z is “closer” to X, it acts more like an instrument than T, and one would expect T to yield a lower bias. Indeed, substituting the proper parameters for α_k and β_k in equation 5 confirms this preference; the biases obtained for Z and T are

(11)

and

(12)

with a clear advantage of T over Z.

As to the set {Z, T}, from equation 6 and the fact that the coefficient of T in the regression of X on Z and T vanishes, we conclude that conditioning on {Z, T} would have the same bias as conditioning on Z alone. This can also be seen from the theory of collapsibility and confounding-equivalence (15), since X ⫫ {Z, T}|Z.

Equations 5 and 6 induce a total order on covariate sets, which in theory can be used to determine (in linear systems) which among several candidate sets of covariates will result, upon adjustment, in the lowest bias. Of course, these equations are not estimable from the data because, first, the residual bias α₀β₀ is not estimable and, second, the graph structure is generally unknown. However, given a theoretically plausible graph structure, a partial order can be derived which is independent on the numerical values of the parameters. The idea is to compare sets that are known to give rise to the same numerator and for which one denominator is guaranteed to be greater than the other for all values of α_k. We have seen such a preference derived in equations 11 and 12, yet a more general condition for preferring set T over Z can be established by means of this logic, leading to the following rule:

A set T is preferred to Z if

•  1) T blocks all paths between Y and Z that do not traverse X, and

•  2) T does not block all paths between Z and X.

These two conditions are clearly satisfied in Figure 4. Complementing this partial order, Pearl and Paz (15) established a necessary and sufficient condition for 2 sets to be equally meritorious for bias reduction.

Thus far, our discussion has focused on adjustment and its effect on systematic bias, yet the harmful effect of overadjustment on precision is not less important and has been recognized by epidemiologists for at least 3 decades (10, 11). Remarkably, the ordering dictated by precision considerations coincides almost exactly with that dictated by consideration of bias amplification. Based on a result by Hahn (16) and assuming no unmeasured confounders, White and Lu (5) derived a partial order on covariates in terms of the asymptotic variance of the effect estimand. This ordering prefers covariates that do not constrain X—the more independent variation there is in the exposure, the more efficient the resulting estimator. The intuition is clear; the more latitude we allow for X to swing away from its baseline value, the fewer samples are needed to reveal the effect of that swing. Referring to Figure 4 with α₀ = 0 (no measured confounders), White and Lu (5) showed that the asymptotic variance of the estimators of γ₀ obtained by conditioning on T alone is lower than that obtained by conditioning on both T and Z, and the latter is lower than that obtained by conditioning on Z alone. This further reinforces the idea that conditioning on factors affecting X (or their proxies) is to be avoided if possible.

CONCLUSIONS AND RELATED OBSERVATIONS

The study by Myers et al. (4) confirms the general conclusions of Bhattacharya and Vogt (1), Wooldridge (2), Pearl (3), and White in Lu (5) that 1) strong predictors of exposure should be excluded from the analysis, 2) factors affecting outcome (or their proxies) are safer and more effective bias reducers than those affecting exposure, and 3) consideration of covariate selection should be grounded in structural assumptions; it cannot be left at the mercy of conventional wisdom, however entrenched.

Myers et al.’s conclusions that, under conditions prevailing in practice, the bias-reducing potential of a near-IV outweighs its bias-amplification potential should be reevaluated in light of the way that bias accumulates in sequential conditioning over large sets of potential confounders. The fact that bias amplification increases monotonically while confounding reduction progresses nonmonotonically, moderated by cancellation of positive and negative confounding paths, may result in a more pronounced effect of bias amplification than the one revealed by studying a single covariate.

The partial preference order established above on subsets of candidate covariates, though requiring basic knowledge of the graph structure, should not be easily dismissed. The basic scientific knowledge required for this determination is often far more accessible than the knowledge needed for substantiating assumptions such as “strong ignorability,” which underlie much of the propensity-score practice.

A few observations should be noted concerning the use of IVs in nonparametric models. First, IVs carry the unique (and rarely utilized) capability of detecting the presence of residual bias whenever a difference $B_0\ne B_z$ is measured. Second, conditioning on Z has no effect whatsoever on selection-induced bias unless selection is determined by causes of X (3). Finally, Bareinboim and Pearl (17) have shown that the use of an IV can, under certain weak conditions, eliminate selection bias altogether.

Glossary

Abbreviation

IV

instrumental variable