The channel-blocking action of methonium compounds on rat submandibular ganglion cells

Abstract

1. The effects of drugs of the polymethylene bis-trimethylammonium (methonium) series on the characteristics of the synaptic currents (e.s.cs) recorded from voltage-clamped rat submandibular ganglion cells have been studied. The drugs studied were from C4 to C10 (decamethonium).

2. All of the drugs except C4 shortened the initial decay phase of the e.s.c.; C9 and C10 produced an additional slowly decaying component. These effects were interpreted in terms of an open channel block mechanism, the calculated rate constants for association with the open channel at − 80 mV being fairly similar (5.9 × 10⁶ to 18.1 × 10⁶M⁻¹ s⁻¹) for all of the compounds except C4, which had no effect on the e.s.c. decay.

3. All of the compounds produced use-dependent block when tested with short trains of stimuli at 10 Hz, or with trains of ionophoretic pulses of acetylcholine, consistent with their channel blocking property. Tubocurarine had a similar effect, but not trimetaphan or mecamylamine.

4. Recovery from use-dependent block with short chain methonium compounds, up to C8, was very slow in the absence of agonist, being incomplete even after several minutes. With C9 or C10 or tubocurarine, recovery from use-dependent block was complete within a few seconds. With C6 recovery in the absence of agonist was unaffected by membrane potential, but could be accelerated by applying acetylcholine with the cell depolarized to − 40 mV. This persistent block was ascribed to the ability of the blocking molecule to become trapped by closure of the channel. With C9 and C10 it is assumed that their presence inhibits channel closure, so they can escape without the help of agonist.

5. When use-dependent block is avoided by leaving the ganglion unstimulated during equilibration with the blocking drug, the first e.s.c. elicited shows no appreciable reduction of amplitude, though with C6, C7 or C8 subsequent responses elicited at 0.1 Hz become progressively more blocked.

6. Even at 1 Mm, C6 does not prevent acetylcholine from opening ionic channels.

7. It is concluded that all of the effects on e.s.c. amplitude can be interpreted in terms of channel block, there being no evidence of any receptor blocking action.

Introduction

It has recently been shown that many drugs that block transmission at the ganglionic and neuromuscular synapses owe their actions not only to an ability to block acetylcholine (ACh) receptors, but also to an ability to block the ionic channels that are activated when ACh combines with its receptors. This channel-blocking activity has been characterized for many neuromuscular blocking drugs, such as tubocurarine (Manalis, 1977; Katz & Miledi, 1978; Colquhoun et al., 1979) as well as for a variety of other drugs, such as atropine (Feltz et al., 1977) and various local anaesthetics (Adams, 1977; Neher & Steinbach, 1978; Tiedt et al., 1979) which act at the neuromuscular junction. The contribution of this type of action to the effects of classical neuromuscular blocking drugs is probably quite small, most of their action being due to receptor block. In contrast, the ganglionic blocking action of drugs such as hexamethonium, tubocurarine and decamethonium has recently been shown to depend mainly on channel block (Ascher et al., 1979; Rang, 1982), though Rang (1982) concluded that other mechanisms may also contribute to the ganglionic blocking effect of hexamethonium. In this paper the blocking effects of the n-alkyl bis-trimethylammonium (methonium) series of drugs, from the n-butyl compound (C4) to decamethonium (C10), on the responses of rat sub-mandibular ganglion cells to ACh and to synaptic activation have been analysed in more detail, with the aim of understanding better the reasons underlying the familiar pattern of structure-activity relationships revealed by the classical studies of Paton & Zaimis (1949) who showed that C5, C6 and C7 were much more active in blocking ganglionic transmission than either shorter or longer chain compounds.

In this paper the analysis concentrates on the channel block mechanism, which was first postulated by Blackman (1959), and analysed formally by Adams (1976). The simplest model for the action of a channel-blocking drug is as follows:

In this scheme R and R* represent the closed and open states of the channel respectively, and BR* is the open but blocked state. The opening reaction is governed by the rate constants β′ (which is a function of the agonist concentration) and α. This formulation is the same as that used by Colquhoun et al., (1979) in their discussion of channel blocking drugs at the neuromuscular junction. The blocking reaction is governed by the forward and backward rate constants, k₊ and k_–, which will be characteristic of the blocking drug. One of the fundamental implications of the scheme is that the antagonist can only bind to the open form of the channel, and that the channel is therefore unable to close with the blocking molecule in situ. The predicted effects of such a blocking drug on the kinetics of synaptic current decay have been discussed by several authors (e.g. Adams, 1976; Beam, 1976a, b; Feltz et al., 1977). If the transmitter is quickly removed from the synaptic cleft (Magleby & Stevens, 1972) the number of open channels, and hence the synaptic current, will, in the absence of a blocking drug, decay exponentially with a rate constant equal to α. In the presence of a blocking drug the initial rate of decay will increase, because a channel can leave the conducting state not only by closing (rate constant α) but also by becoming blocked (rate constant k + [B1]). The model also predicts a second, slower component in the synaptic current decay, which arises because a blocked channel must unblock, and transiently conduct, before finally closing. However, under conditions where the rate of dissociation from the channel, k_– is slow with respect to (α + k₊ [B]), this component will be of low amplitude and not easily resolved. If this slow component is found to be small, therefore, the effect of the blocking agent in accelerating the decay of the synaptic current can be used to estimate the association rate constant, k₊, of drugs combining with the open channel (see Rang, 1982). This approach has been used to characterize the properties of the methonium series in this paper.

A further prediction of the channel block model is that repeated activation of the receptors with agonist in the presence of a slowly-dissociating blocking drug should result in a cumulative blockade. This phenomenon, known as ‘use-dependence’ (Courtney, 1975) because the level of block increases when the frequency at which channels are opened increases, has been observed with local anaesthetic block of sodium channels in nerve (Strichartz, 1973; Courtney, 1975; Khodorov et al., 1976; Cahalan, 1978) and skeletal muscle (Schwartz et al., 1977) and is of particular interest here as it could account for the marked dependence of the blocking effect on stimulation frequency that has been described for ganglionic blocking drugs (Paton & Zaimis, 1949; 1951; Kharkevich, 1967), and also occurs with agents that inhibit ACh action at the neuromuscular junction (Magazanik & Vyskocil, 1976; Burgermeister et al., 1977; Maleque et al., 1982). It was of interest to measure the degree of use-dependence seen with drugs of the methonium series, and to compare their actions in respect of this characteristic with those of ganglionic blocking drugs that do not act principally by blocking channels. Measuring the rate of recovery of ACh sensitivity after the blocking action has been caused to accumulate by repetitive agonist application can give information about the rate constant for dissociation, k_–, of the drug from the open channel (see Adams, 1976; 1981; Adams & Feltz, 1980), and we have investigated the methonium drugs systematically in this way.

The main conclusion of this study agrees with that of Ascher et al. (1979) and Rang (1982), namely that the methonium compounds and tubocurarine act mainly by blocking ionic channels, in contrast to trimetaphan and mecamylamine, whose action is compatible with receptor block. It is found, however, that the shorter chain members of the methonium series produce a much more persistent use-dependent block than the longer chain compounds, and that this can be ascribed to their ability to become trapped by closure of the channel with the blocking molecule in situ, an event that cannot occur, or occurs much less readily, with the longer chain compounds. A similar proposal has recently been made by Lingle (1983a, b) to account for the blocking action of chlorisondamine and certain other antagonists on the ACh responses of lobster muscle fibres.

Our evidence also shows that hexamethonium, even at high concentration, does not prevent ACh from opening ionic channels, showing that this drug does not cause appreciable receptor block.

A preliminary account of part of this work has been published (Gurney & Rang, 1981).

Methods

The methods were essentially as described by Ascher et al. (1979) and Rang (1981, 1982). Hooded Lister rats of either sex, weighing 200 g or less, were killed with chloroform and bled by perfusion of 20–30 ml of Krebs solution through the left ventricle. Submandibular ganglia were dissected, cleaned of connective tissue as thoroughly as possible, and mounted on a bed of Sylgard resin on the bottom of a 1 ml recording chamber. The chamber was perfused continuously with oxygenated Krebs solution at about 3 ml min⁻¹; the temperature was maintained at 30°C. The preparation was mounted on the stage of a Nomarski microscope and viewed through a × 40 water immersion objective.

Cells were impaled with two microelectrodes (resistance 40–60 MΩ). The recording electrode was filled with 4m potassium acetate solution, and the current passing electrode with 0.5m potassium sulphate solution. The voltage clamp circuit was the same as that used in earlier studies (Ascher et al., 1979). The current signals were passed through a low-pass filter (Barr & Stroud, Type EF3) set at 400–500 Hz for recording ionophoretic responses and at 1000–1200 Hz for recording synaptic currents. Records of membrane potential and current were stored on magnetic tape (Racal Store 4 FM) for later analysis.

For experiments involving preganglionic nerve stimulation a length of the chorda tympani nerve was drawn into a suction electrode and stimulated with 0.5 ms supramaximal pulses delivered from a Grass stimulus isolation unit. In other experiments ACh was delivered ionophoretically from a high-resistance micropipette containing 1 m acetylcholine chloride. The ionophoretic current was controlled by a constant current generator similar to that described by Dreyer & Peper (1974).

The membrane potential was normally held at −40 or −50 mV except when an experimental procedure was being carried out, this usually being close to the membrane potential of doubly-impaled cells. After control recordings were made the drug solutions were perfused through the chamber for at least 5 min before recordings were made in the presence of the antagonists. Whenever possible control records were repeated after the drug had been washed out, and the drug effect was expressed in relation to the mean of the results obtained before and after drug application. With the ionophoresis experiments it was rare for more than two or three solution changes to be achieved without the pipette moving and reducing the response amplitude, but this could be detected by a change in the rise time of the response. With ionophoretic application care was taken to position the pipette optimally in relation to sensitive spots on the post-synaptic membrane, so that the rise time was minimized. The best responses reached a peak within 20 ms following a 2 ms pulse of ACh.

Drugs and solutions

The Krebs solution had the following composition (Mm): NaCl 119, KCl 4.7, CaCl₂ 2.5, KH₂PO₄ 1.2, NaHCO₃ 25, MgSO₄ 1.2 and glucose 11. The solution was bubbled with 95% O₂: 5% CO₂ and its pH was 7.2.

Drugs used were: acetylcholine chloride (Sigma), trimetaphan camsylate (Roche), mecamylamine hydrochloride (Merck, Sharpe & Dohme), (+)-tubocurarine chloride (Sigma), hexamethonium bromide (Sigma), decamethonium iodide (Koch-Light). Additional members of the methonium series of compounds were kindly provided by Dr R.B. Barlow (University of Bristol) and Dr E.W. Gill (University of Oxford).

Results

The normal synaptic currents that are recorded from rat submandibular ganglion cells have been described in detail by Rang (1981). Although the experiments presented here were performed at a higher temperature, the general features of the excitatory synaptic currents (e.s.cs) were the same. The rise time was about 1 ms, compared with 2 ms at 20°C; the peak amplitude was somewhat greater (67 ± 5 nA; mean ± s.e.mean, membrane potential −80 mV, 50 cells), and the decay was faster. As found by Rang (1981), the decay phase consisted of two exponential components, the time constants being 6.2 ± 0.3 ms and 20.0 ± 2.0 ms respectively, at − 80 mV (18 cells). Both components were slowed by hyperpolarization, as found previously (Rang, 1981). Examples of normal synaptic currents are shown in Figures 1 and 2.

Figure 1.

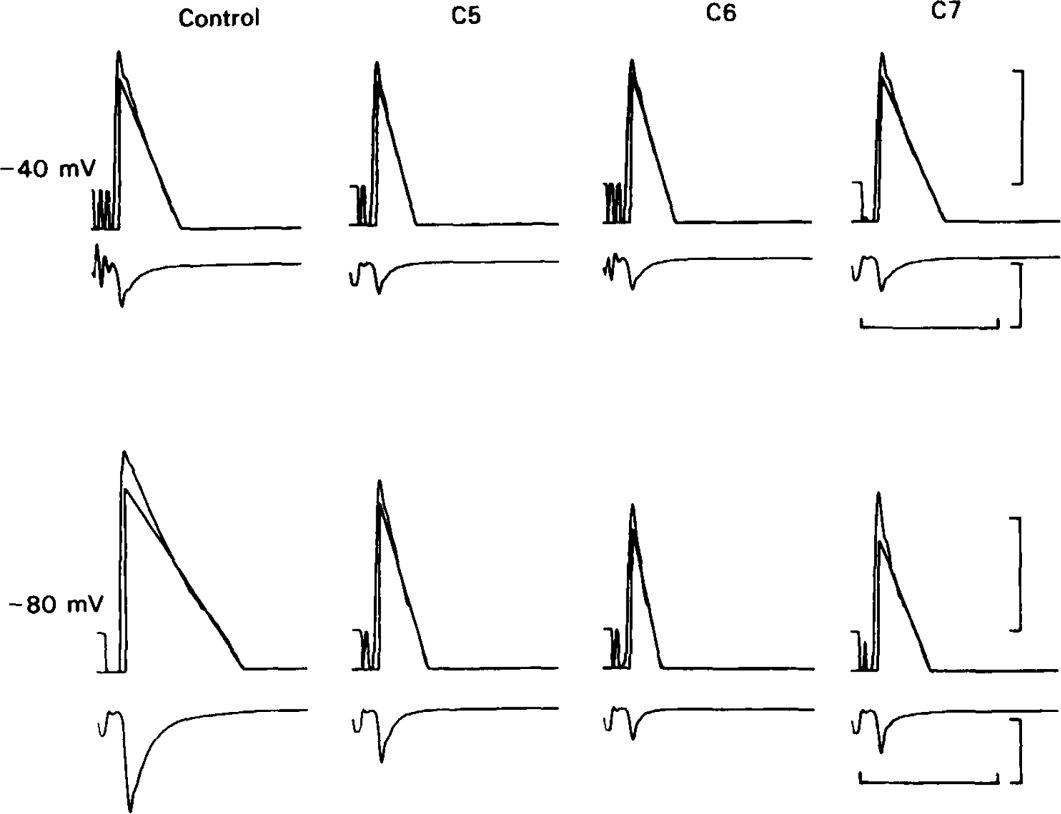
The effect of C5, C6 and C7 (20 μm in all cases) on the amplitude and decay kinetics of e.s.cs. In each pair of traces the lower record shows the e.s.c. (inward current being registered as a downward deflection) preceded by the stimulus artefact. The upper trace shows the e.s.c. plotted semi-logarithmically; points below an arbitrary level 2 log units below the peak have been suppressed and represented as a flat baseline to avoid an excessively noisy ‘tail’ to the semi-logarithmic plot. Noise has also been reduced by smoothing, with a running average procedure, applied to the tail region of the signal. Straight lines were fitted by eye to the slow component with the plots displayed on a graphics screen, the presence of a fast component being shown by the deviation of this line from the recorded signal at early times. The size of the fast component in this cell was unusually small and hard to resolve, but the effects of the blocking drugs on the slow component are clearly shown. Upper records: membrane potential −40 mV; lower records: membrane potential − 80 mV; calibrations: vertical: 1 decade; 20 nA. Horizontal: 50 ms. Note that in the controls hyperpolarization lengthens the slow component, whereas in the presence of C6 and C7 it has the opposite effect.

Figure 2.

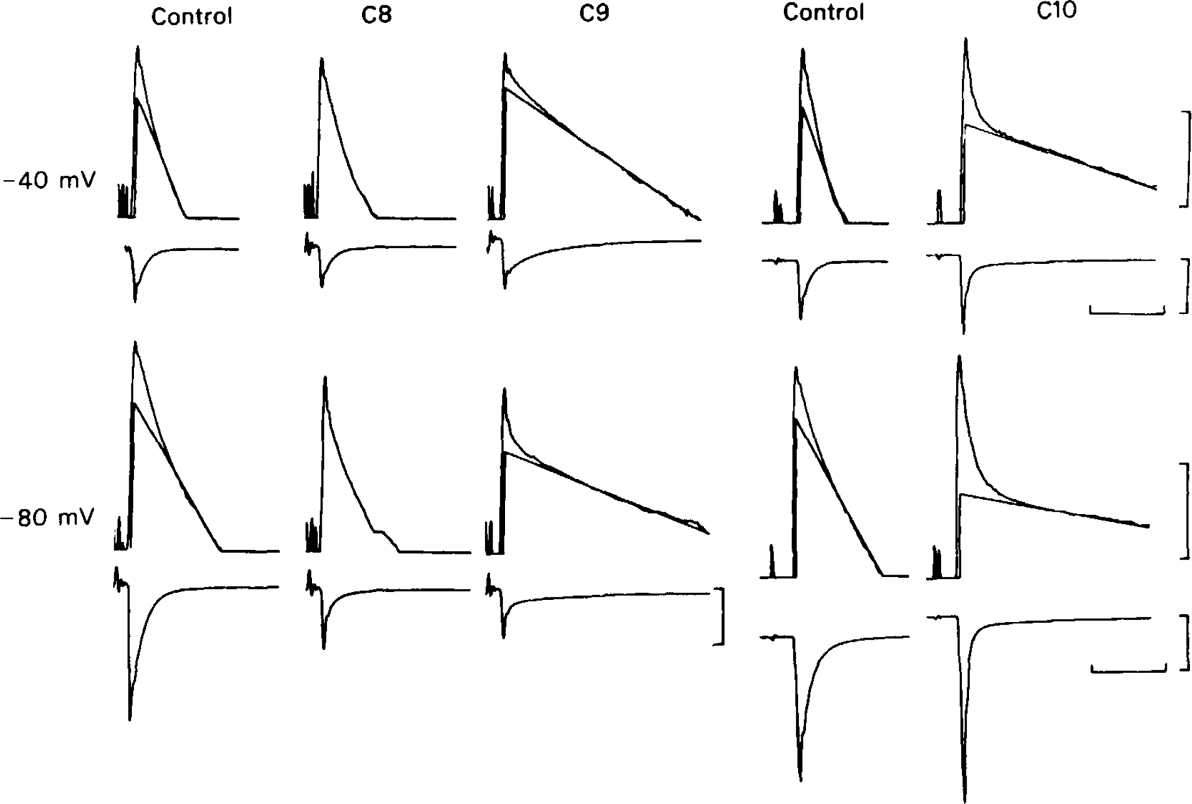
The effect of C8, C9 and C10 (20 μm in all cases) on e.s.cs, plotted as in Figure 1. C8 and C9 were tested on one cell, C10 on another. Upper records: membrane potential −40 mV; lower records: membrane potential − 80 mV. Calibrations: vertical: 1 decade; 20 nA. (The top of the 20 nA bar corresponds to zero holding current.) Horizontal: 50 ms. C8 produces a complex decay pattern, in which the exponential components cannot be resolved. C9 and C10 cause the appearance of a slow component, slower than either component of the control e.s.c., which is further lengthened by hyperpolarization. C9 caused an unusually large reduction of e.s.c. amplitude in this cell.

Effects of blocking agents on the time course of e.s.cs

The effects of hexamethonium, tubocurarine, and trimetaphan on e.s.cs have already been studied (Rang, 1982), and in this study we were concerned mainly to make a comparison of drugs of the methonium series from C4 to C10. With the exception of C10, all of the methonium compounds clearly reduced the peak amplitude of the e.s.c. and, except for C4, shortened its decay (Figures 1 and 2). With C10 (20 μm) the effect on amplitude was slight; at −80 mV the mean reduction was 19 ± 12% (n = 6; see Table 1). In the presence of C5, C6 or C7 (Figure 1) the decay usually remained bi-exponential, and both components became faster than the corresponding component of the control, this speeding becoming more pronounced as the cell was hyperpolarized. C9 and C10 produced a more complex effect (Figures 2 and 3) in which the early part of the decay was speeded up, but this was followed by a prolonged tail. It was usually necessary to include more than two exponential components to fit these responses satisfactorily (Figure 3). C8 produced an intermediate type of effect, causing a slow component to appear which was slower than any component of the normal e.s.c., but much less prolonged than that seen with C9 or C10. Because the kinetic components in the presence of C8 were not clearly separated, resolution of their time constants was uncertain.

Table 1.

Rate constants (k_+f and k_+s) for binding of methonium compounds to open ion channels at various membrane potentials estimated from e.s.c. decay kinetics, and effects on e.s.c. amplitude, expressed as Δ (= amplitude in absence of drug/amplitude in presence of drug) at drug concentration 20 μm. Stimulation frequency 0.1 Hz

Drug	Em (mV)	k+f (m−1s−1) × 10−6	k+s (m−1s−1) × 10−6	Δ − 1 (20 μm)
C4	−80	<0.4 2)	<0.1 (2)
C5	−40	3.5 ± 0.9 (4)	4.1 ± 1.0(4)	0.61 ± 0.24	0.27
	−60	5.6 ± 1.3(4)	5.2 (2)	1.13 ± 0.23	0.20
	−80	5.9 ± 0.7 (4)	4.3 ± 2.1 (3)	0.92 ± 0.18	0.16
C6	−40	4.4 ± 0.8 (5)	2.7 ± 0.6 (5)	0.43 ± 0.15	0.10
	−60	8.9 ± 2.3 (4)	7.6 ± 2.6 (5)	0.72 ± 0.34	0.08
	−80	17.9 ± 1.6(17)	10.3 ± 1.3(17)	1.38 ± 0.17	0.08
C7	−40	4.9 ± 1.4(5)	1.2 ± 0.7(5)	0.43 ± 0.15	0.09
	−60	8.8 ± 3.2 (5)	1.5 ± 0.7 (5)	0.82 ± 0.20	0.09
	−80	17.4 ± 4.8(5)	2.6 ± 0.8 (5)	1.08 ± 0.13	0.06
C8	−40	—	—	0.45 ± 0.20(5)	—
	−60	—	—	0.49 ± 0.09(5)	—
	−80	—	—	0.69 ± 0.17(6)	—
C9	−40	7.9 ± 4.8 (4)	0.8 ± 0.4 (4)*	0.06 ± 0.11	0.01
	−60	14.2 ± 1.9 (5)	2.3 ± 0.9 (5)*	0.28 ± 0.12	0.02
	−80	18.1 ± 2.3 (6)	4.5 ± 1.7 (6)*	0.45 ± 0.02	0.02
C10	−40	—	—	—	—
	−60	—	—	—	—
	−80	15.8 ± 2.4(6)	4.7 ± 1.2(6)*	0.19 ± 0.12	0.01

Values given are mean ± s.e.mean, the number of cells tested being given in parentheses.

^*Since we cannot be sure that k_−s is much greater than (α + k_+s[B]) for these drugs, the values given must be regarded as upper limits.

Figure 3.

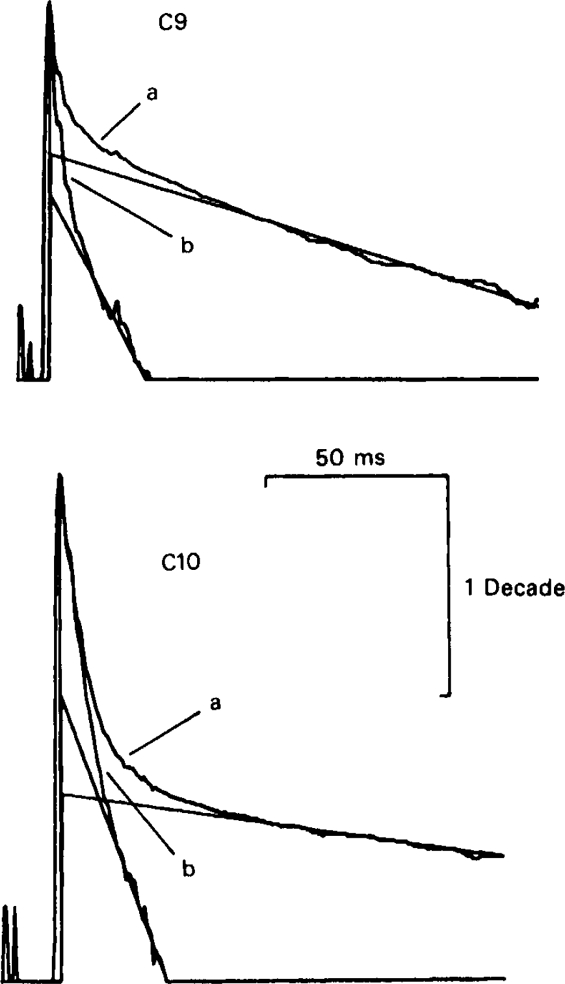
Analysis of e.s.cs recorded at − 80 mV in the presence of C9 (20 μm) and C10 (20 μm). The semi-logarithmic plots (as in Figures 1 and 2) can be split into 3 exponential components. The slow component was subtracted from the original trace (a) to produce trace (b). Trace (b) is still non-linear, implying that it consists of more than one exponential component. Straight lines have been plotted through the slowest component of traces (a) and (b).

The predicted effect of a channel blocking drug whose rate of association with the open channel is increased by hyperpolarization is that it should split the exponential decay of each component of the control response into two components, respectively faster and slower than the control, and that hyper-polarizing the cell should speed up the fast and slow down the slow component of this split decay (see Adams, 1977; Colquhoun & Hawkes, 1977; Ascher et al., 1979). Where, as with these ganglion cells, the control decay contains two components, the effect of a channel blocking drug may result in four components, making interpretation very difficult. With the shorter chain compounds, the fact that hyperpolarization speeded up both components of the decay implies that they represent, respectively, the speeded up fast and slow components of the original biexponential decay. Since, with these drugs, no slow phase appeared even when the cell was hyperpolarized, we conclude that the hypothetical slow component associated with the channel block mechanism was too small to be apparent. Under these circumstances the speeding up of the two components can be used to calculate the rate constants for association of the blocking drug with the fast and slow channels (see Rang, 1982). Thus if the control time constants for the fast and slow components of the e.s.c. are τ_f and τ_s, and these change to τ′_f and τ′_s, in the presence of drug concentration [B], then the respective association rate constants (k_+f and k_+s) will be given approximately by:

(1)

(2)

This approximation is valid so long as the dissociation rate from the open channel, k_–, is small with respect to (α + k₊ [B]). Measurements of the rate of recovery from channel block presented below show that this is the case for the shorter chain compounds, C5, C6 and C7, for which estimates of the rate of association with the open channel, based on equations (1) and (2), are given in Table 1 and Figure 4. The shortest compound tested, C4, had no observable effect at 20 μm; at 200 μm it reduced e.s.c. amplitude by about 30% (shown in Figure 11) but had no effect on the time course. The upper limits for the association rate constants given in Table 1 are calculated on the assumption that a 20% change in τ would have been detected. It is possible, however, that the ineffectiveness of C4 reflects a particularly high rate of dissociation, which might happen, for example, if the drug were able to pass straight through the channel. In this event the assumptions implicit in the use of equations (1) and (2) to calculate k₊ would be invalid, and k₊ might be seriously underestimated.

Figure 4.

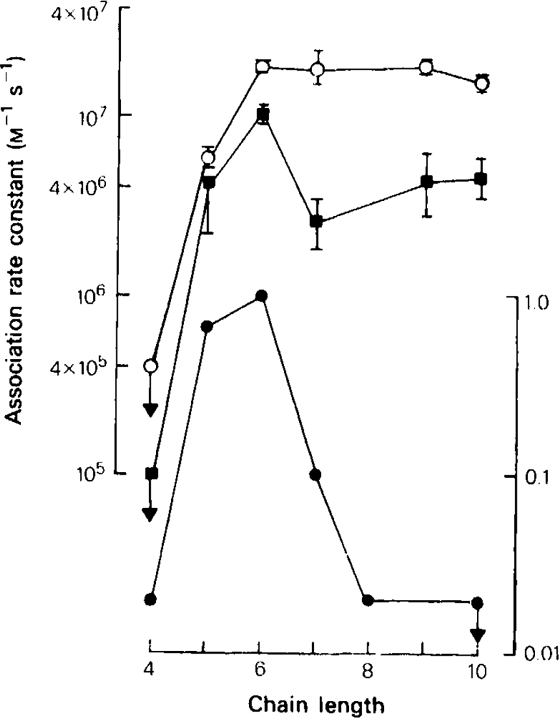
The relationship between chain length and the rate constant for association with the fast channels, k_+f, and the slow channels, k_+s, in the methonium series: (○) (left hand ordinate): k_+f; (▪) (left hand ordinate): k_+s; (•) (right hand ordinate): measurements of ganglion blocking potency (C6 = 1) on the cat superior cervical ganglion in vivo, from Paton & Zaimis (1949). Downward arrows indicate values which represent upper limits.

Figure 11.

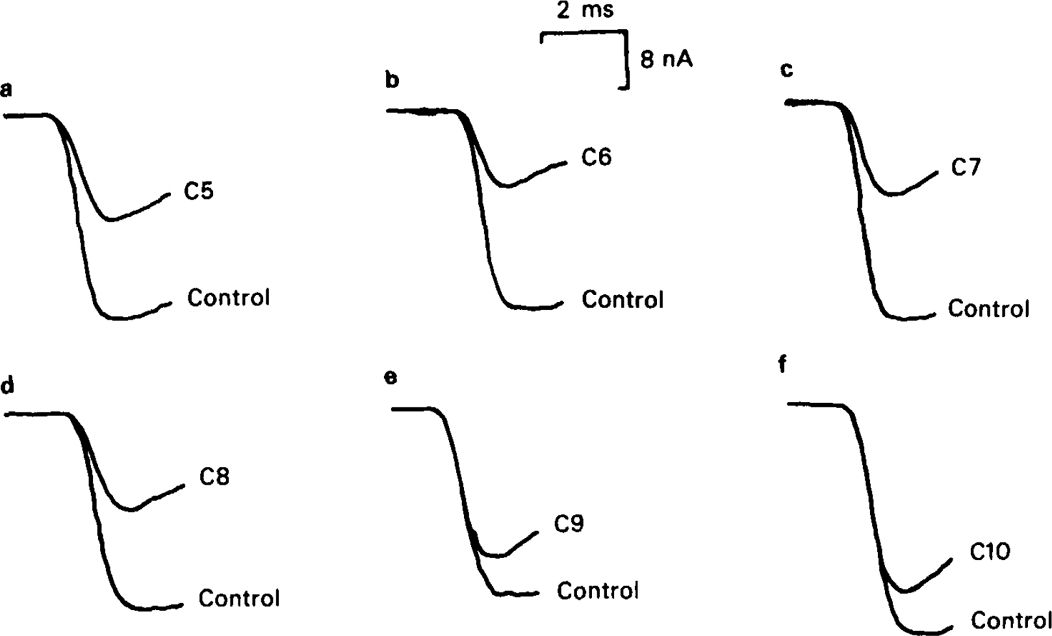
Synaptic currents recorded at − 80 mV under control conditions and in the presence of methonium compounds at 20 μm. The stimulation frequency was 0.1 Hz. Note that with compounds up to C8 the rising phase of the e.s.c. was inhibited, whereas this did not happen with C9 or C10.

The longer chain compounds, C9 and C10, often caused the decay phase to be split into three components (Figure 3). The two faster components decayed more rapidly than their counterparts in the control e.s.c., and were speeded up by hyperpolarization. These components were therefore used, as with the shorter chain compounds, to calculate k_+f and k_+s. The third component was slower, and was further slowed by hyperpolarisation (see Figure 2); it was taken to represent unblocking of open channels as the drug dissociates (Adams, 1976; Adams & Sakmann, 1978). The presence of this slow component introduces more uncertainty into the estimates of the association rate constants, partly because of the problem of resolving the three exponential components, and partly because we cannot be sure that k_– is small enough to justify the use of equations (1) and (2). Results presented below suggest that k_–f is probably small enough for the approximation to be reasonable, but we cannot reliably estimate k_–s so the association rates for C9 and C10 binding to the slow channel should be regarded as upper limits. Values were not calculated for C8 because of the difficulty of resolving the components of the e.s.c. with this drug.

The association rate constants given in Table 1 for C6 at − 80 mV are slightly higher than the corresponding values found by Rang (1982), which were 1.3 × 10⁷ m⁻¹s⁻¹ for the fast channel and 5.3 × 10⁶ m⁻¹s⁻¹ for the slow channel, which is probably due to the temperature difference. The value for decamethonium binding to the fast channel, 1.58 × 10⁷ m⁻¹s⁻¹ at −80 mV, is similar to the estimate by Adams & Sakmann (1978) of its rate of binding to ACh-operated channels at the frog neuromuscular junction measured at −130 mV (1.71 × 10⁷ m⁻¹s⁻¹). A plot of the rates of association to the two kinds of channel against the chain length of the methonium drugs (Figure 4) shows some variation but no obvious pattern in the structure-activity relationship. In Figure 4 we have superimposed on our results the well-known bell-shaped curve obtained by Paton & Zaimis (1949) which relates ganglion blocking potency measured in vivo to chain length. It is clear that variation of the rate of binding to the open channel as a function of chain length cannot account for Paton & Zaimis’ results.

Use-dependent block

The first series of experiments designed to measure the degree of use-dependence seen with different blocking drugs was carried out by recording trains of e.s.cs (usually 10 Hz for 1 s) in the absence and presence of the blocking drug. Because the rate of association of drugs with the channel (Table 1), and the equilibrium blocking effect (Ascher et al., 1979) increase with hyperpolarization, it was predicted that the degree of use-dependent block should also be sensitive to the membrane potential, and trains were recorded at − 40 mV and − 80 mV to test this point (Figure 5). When no drug is present the e.s.c. amplitude declines to about half of its initial value after 4 or 5 stimuli at 10 Hz, and then remains constant. This effect is independent of membrane potential, and presumably reflects a reduction of transmitter release during the tetanic train. In the presence of C6 (10 μm) the amplitude of the first e.s.c. in the train is reduced by about 50%. At a holding potential of − 40 mV the run-down is only slightly greater than in the control, but at − 80 mV it is much more pronounced. All of the methonium compounds tested produced a similar effect on e.s.c. run-down, as did tubocurarine which has been shown to have a similar channel blocking action on rat submandibular ganglion cells (Ascher et al., 1979; Rang, 1982). The results are shown in Figure 6, where the run-down occurring in the control trains has been allowed for by normalising each response with respect to the corresponding response in the control train at −40 mV. Trimetaphan and mecamylamine, which our earlier studies showed to lack channel blocking activity, reduced the amplitude of the e.s.c. but did not affect the pattern of run-down.

Figure 5.

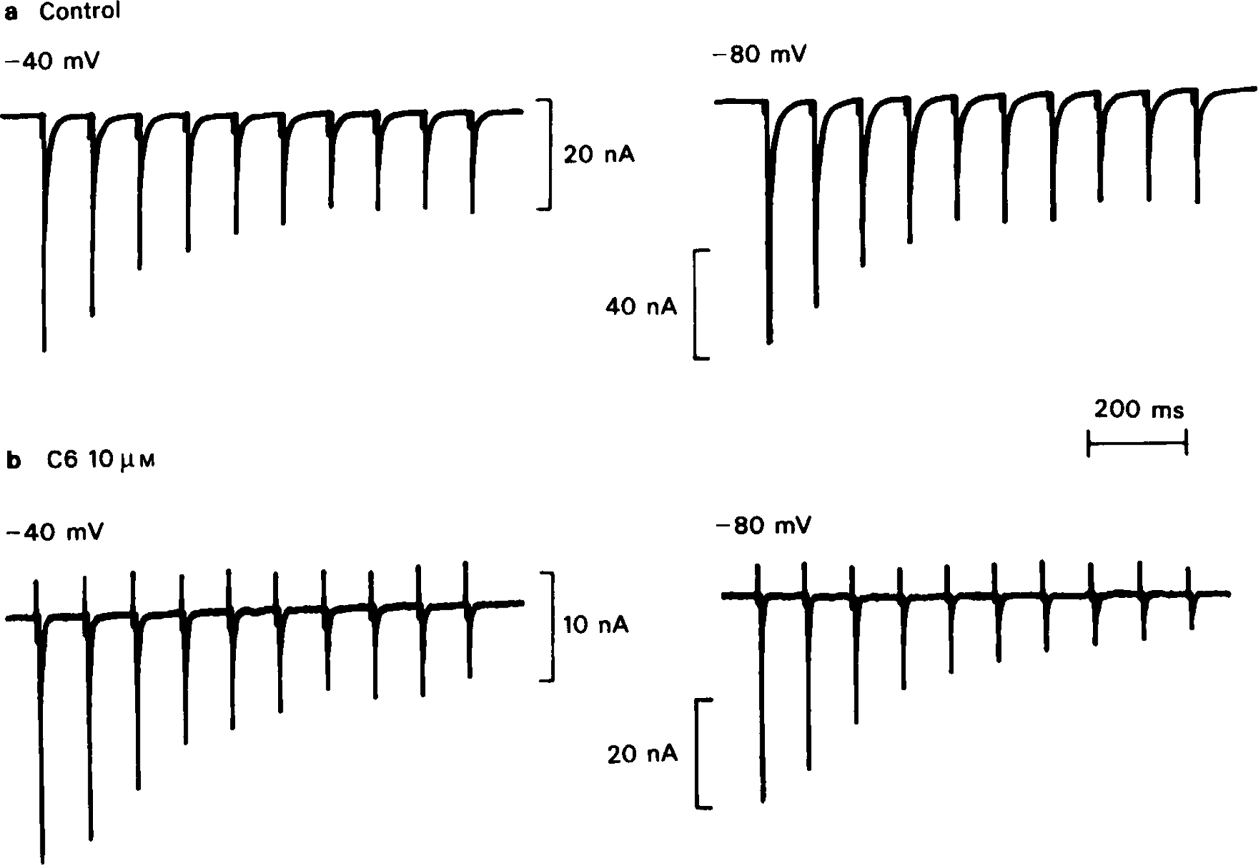
The effect of C6 (10 μm) on the run-down of e.s.c. amplitude during a 1 s train of stimuli at 10 Hz. At − 40 mV the degree of run-down occurring during the train was only slightly increased by C6, though the amplitude of the first e.s.c. in the train was reduced by about 50%. At − 80 mV the degree of run-down was clearly increased by C6. Note the different amplitude calibrations in the 4 traces.

Figure 6.

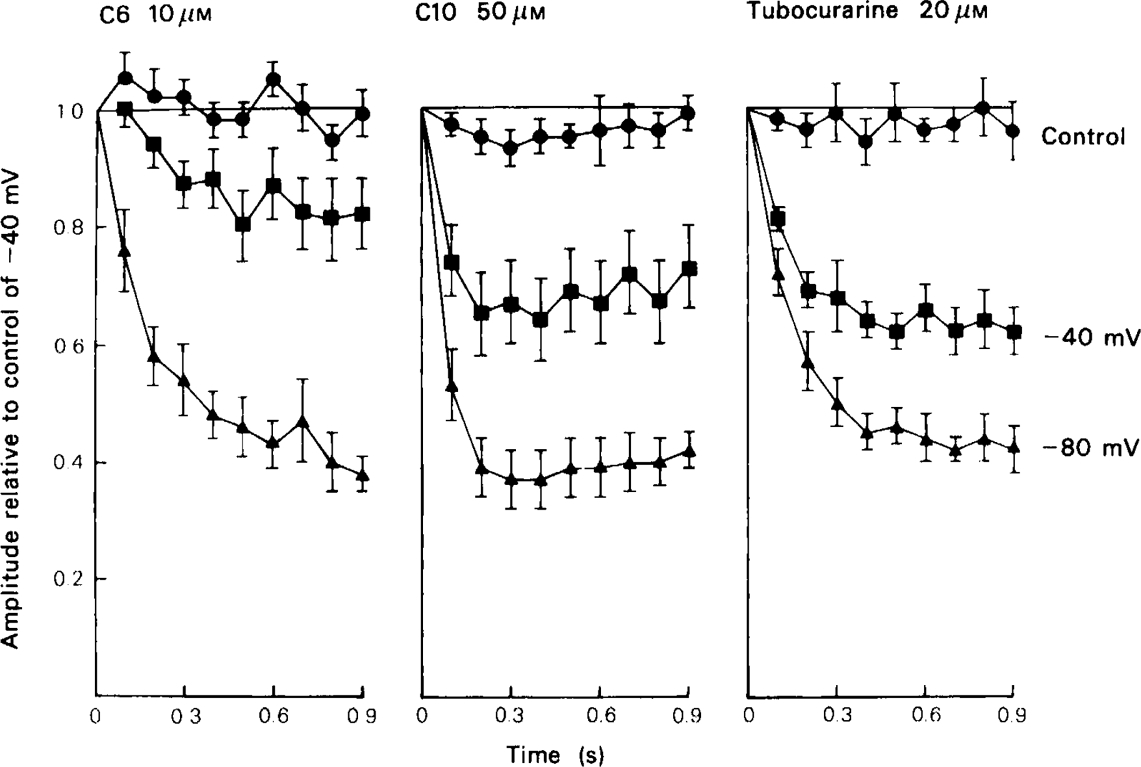
E.s.c. run-down during a 1 s train at 10 Hz in the presence of C6 (10 μm), C10 (50 μm) and tubocurarine (20 μm). The points show mean for measurements on 6–8 cells, ± s.e.mean shown by vertical lines. For each cell the responses were normalised with respect to the corresponding response in the control train at − 40 mV, the amplitude of the first response in each train being taken as unity; (•) control responses –80 mV; (▪) test responses − 40 mV; (A) test responses − 80 mV. All three drugs increased the degree of run-down during the train, the effect being greater when the cell was hyperpolarized.

Very similar results are obtained if ACh is applied ionophoretically as a train of brief pulses. This technique has the advantage that it avoids the complications of presynaptic fatigue that occur with nerve stimulation, but has the disadvantage that the relatively slow rise-time (about 20 ms) means that appreciable channel block occurs during the rising phase, so the amplitude does not simply reflect the amount of block existing at the moment when the test pulse was delivered. With a train of 2 ms pulses at 5 Hz no desensitization occurred in control runs, so each response in the test trains could be compared directly to the preceding responses without the need for normalisation. The enhanced run-down seen in the presence of various methonium drugs is plotted in Figure 7, from records similar to those shown in Figure 9, it is evident from Figures 6 and 7 that the time course of the development of use-dependent block differs appreciably among the different compounds tested, even though the concentrations were adjusted to give approximately the same final level of use-dependent block. Thus C6 produced a relatively slowly developing effect, which had not reached equilibrium by the end of the train of 10 pulses, whereas with C10 the amplitude decreased sharply within the first 2 or 3 pulses and then stayed more or less constant. The time course of use-dependent block will obviously depend not only on the rate of association of the drug with the open channel, but also on the rate of dissociation. If the dissociation rate is high, then drug molecules entering the channel during one pulse of ACh will have time to leave before the next, so use-dependence will appear slight and will reach a steady state rapidly. If dissocation is slow, however, the effect will build up gradually during a train of pulses, reaching equilibrium only when the number of channels vacated between pulses equals the number blocked during each pulse. A more formal kinetic analysis can be developed (see Gurney, 1982) but it can be seen intuitively that the results shown in Figures 6 and 7 suggest that C6 and other short chain methonium compounds dissociate more slowly than longer chain compounds such as C10.

Figure 7.

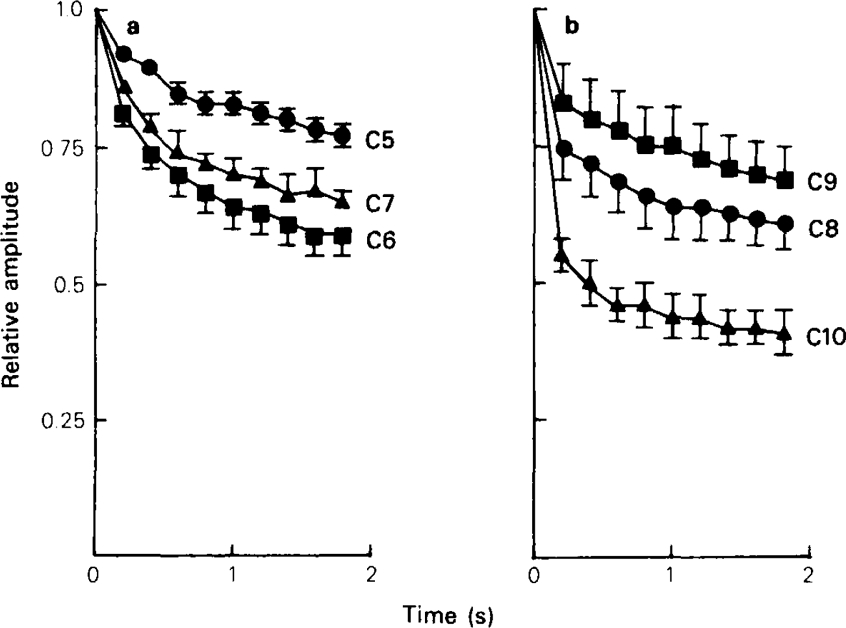
Effect of methonium compounds on the amplitude of responses to 2 ms, inophoretic pulses of ACh applied as a 2 s train of pulses at 5 Hz. Membrane potential − 80 mV. CS, C6 and C7 were tested at 1 μm; C8, C9 and C10 were tested at 10 μm. The peak amplitude of each response is expressed relative to the amplitude of the first response in each train, and each point represents the mean ± s.e.mean (vertical lines) for 4–6 cells.

Figure 9.

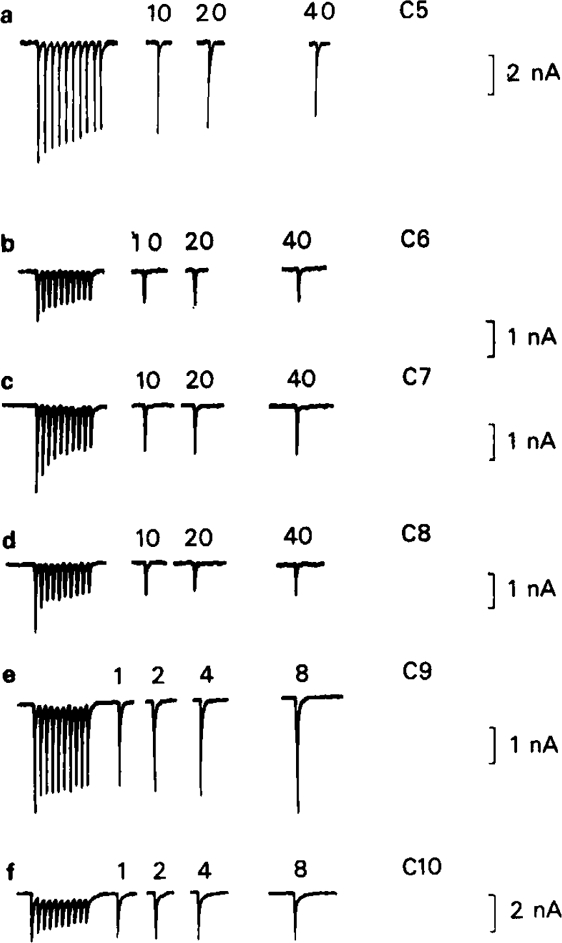
Onset and recovery from use-dependent block elicited by a 2 s train of ionophoretic pulses of ACh (duration 2 ms at 5 Hz, in the presence of C5, C6 and C7 (1 μm), C8, C9 and C10 (10 μm). Membrane potential −80 mV. Each train was repeated several times to generate the complete recovery curve, as in Figure 8. The recovery interval is indicated on the test reponses. Use-dependent block was discharged after each test by application of a 1 s pulse of ACh with the cell clamped at − 40 mV (see Figure 13).

This conclusion was tested by using the type of experimental protocol introduced by Adams (1976) and Adams & Feltz (1980), which allows the kinetics of dissociation to be measured more directly. In these experiments the preparation was equilibrated with the blocking drug at rest, then a conditioning train of ACh pulses or nerve stimuli was applied to establish a degree of use-dependent block, as in Figures 6 and 7. After a variable interval a test ACh pulse or stimulus was then applied to measure how much recovery towards the equilibrium block had occurred. By repeating the train and varying the recovery interval a plot of the recovery time course was built up. If nerve stimulation was used it was necessary to carry out this protocol under control conditions to allow for the effects of presynaptic depression on the amplitude of the test response; with ionophoretic application, the pulse train procedure had no effect on ACh responses in the absence of blocking drugs, so controls were not needed with each experiment. Figure 8 shows the time course of recovery from use-dependent block, measured with the nerve stimulation procedure, in the presence of C6, C10, and tubocurarine. Under the conditions of the experiment the drugs produced a certain amount of steady state block, as reflected in the reduction of the amplitude of the first test response, and the plots in Figure 8 have been normalised to allow for this. The use-dependent block is represented by the shaded areas, and it can be seen that tubocurarine dissociates fully in about 4s, C10 in about 10s and with C6 little recovery has occurred by the end of 15 s. With C6 we found that depolarizing the cell to − 40 mV during the recovery period (keeping it at − 80 m V during the conditioning and test stimuli) had no consistent effect on the recovery kinetics; this was not tested with any other blocking agents. Quantitative results were easier to obtain with ionophoretic ACh application, and Figure 9 shows records obtained with various methonium drugs tested on a single ganglion cell. It can be seen that with C5, C6, C7 and C8 a 20 s recovery period produced little or no increase in the amplitude of the test response compared with the response at the end of the conditioning train, whereas with C9 and C10 there was considerable recovery within 1 s and virtually complete recovery at 8 s. The results of a systematic series of experiments with ionophoretically applied ACh is shown in Figure 10. It is clear that with the methonium compounds up to and including C8 there was little or no dissociation from the channels during the 20–40 s recovery period, whereas C9 and C10 dissocated fully within about 10 s. A semilogarithmic plot of the recovery phase for these two drugs (Figure 10b) shows that part of the recovery (about 50%) occurred rapidly (time constant less than 1 s), with the remainder taking place more slowly, the estimated time constants being 9.5 s for C9 and 5.5 s for C10.

Figure 8.

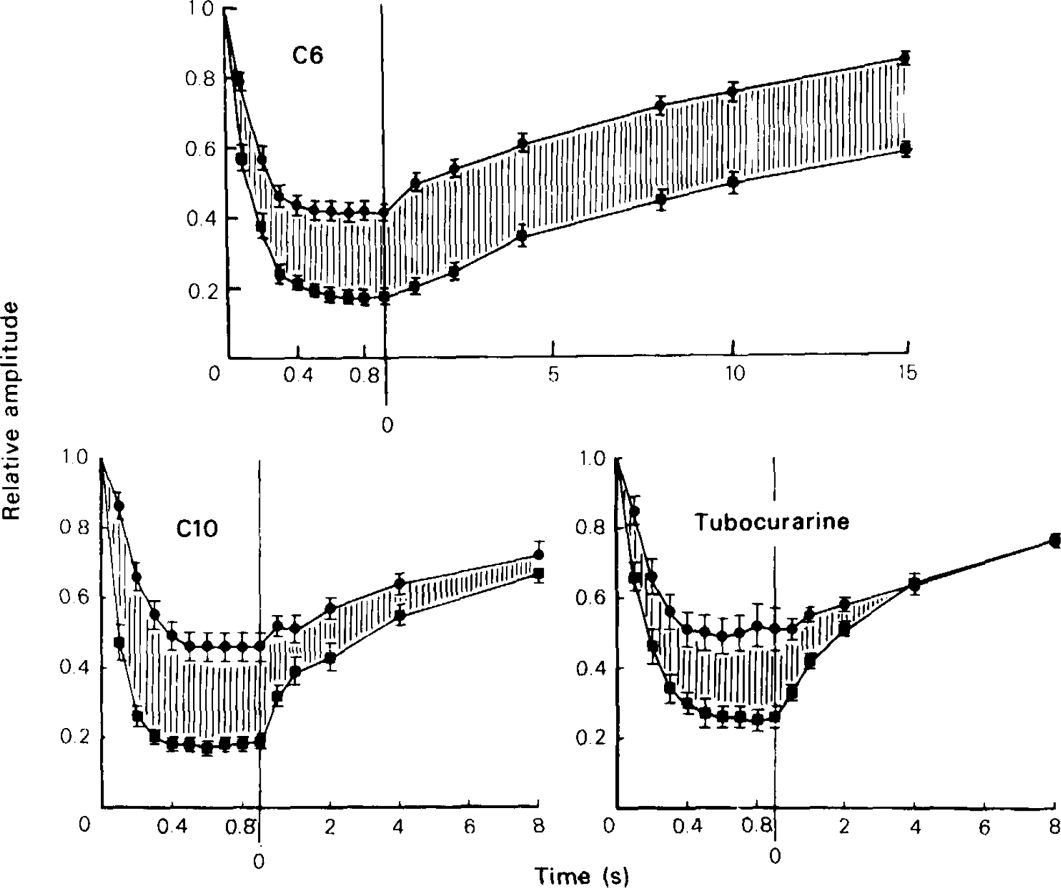
The kinetics of recovery from use-dependent block of e.s.cs at − 80 mV in the presence of C6 (20 μm), C10 (50 μm) and tubocurarin (20 μm). The left-hand section of each plot shows the decline of e.s.c. amplitude during a 1 strain of stimuli at 10 Hz, the upper curve (•) being the control and the lower curve (▪) being recorded in the presence of the drug. The response amplitude is normalised with respect to the first response in the train. The right-hand section shows the recovery time course, the abscissa being the interval between the end of the conditioning train and the application of a single test stimulus. To obtain the recovery curve, the conditioning train was repeated 5 or 6 times on each cell. The points show mean (vertical lines, s.e.mean) for 6–10 cells. The shaded area represents the degree of use-dependent block during the run-down and recovery periods. To discharge the use-dependent block fully after each test sequence a train of stimuli was applied with the cell clamped at − 40 mV (see text).

Figure 10.

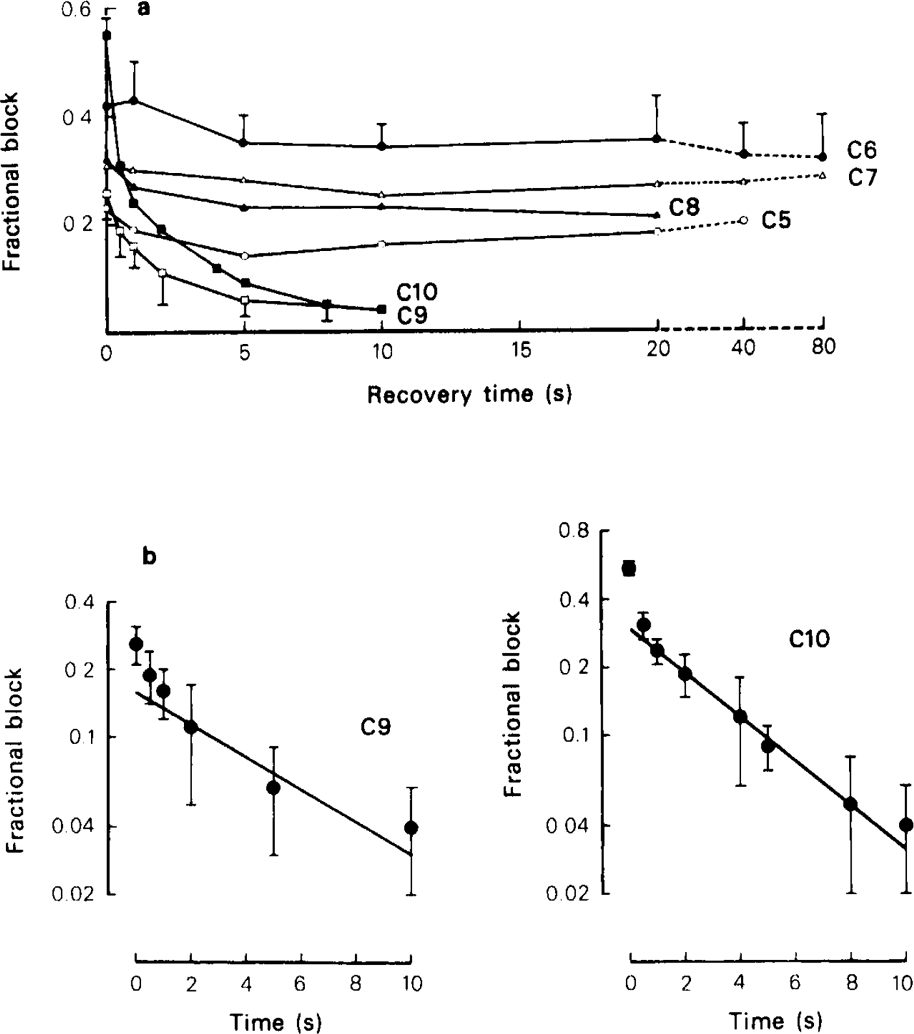
Kinetics of recovery following use-dependent block produced by a train of ionophoretic pulses of ACh (protocol as in Figure 9) at − 80 mV, in the presence of C5, C6, and C7 (1 μm), C8, C9, C10 (10 μm). (a) Overall results for 3–6 cells tested with each drug. Mean (s.e.mean shown by vertical lines) is given for C6 and C9; s.e.mean has been omitted from other curves for clarity, but was of similar magnitude in all cases. (b) Semi-logarithmic plots of recovery kinetics for C9 and C10 showing fast and slow phases. The lines fitted by eye to the slow phase correspond to time constants of 9.5 and 5.5 s respectively for C9 and C10. The time constant for the fast phase is not well defined, but appears to be less than 1 s for both drugs.

In theory, according to the simple model for open channel block shown in Scheme 1 (see Gurney, 1982) the time course of recovery from use-dependent block should consist of two exponential components with the same time constants as are present in the e.s.c. decay. The slowest e.s.c. component observed in the presence of 20 μm C9 or C10 had a time constant of a few hundred milliseconds (Figure 3), similar to that of the fast phase of recovery. The slow phase of recovery could represent the hypothetical fourth component that would result from the splitting of each of the two exponential components of the control e.s.c., but the evidence presented later suggests strongly that it reflects an additional kinetic step, not included in Scheme 1, corresponding to the closing of blocked channels.

The stability of the use-dependent block produced by the shorter chain compounds was actually such that experiments in which repeated pulse trains were tested, even at intervals of several minutes, produced a progressively increasing level of block. This would have made experiments such as that shown in Figure 9 impossible had not a means been found, as described later, of discharging the residual use-dependent block at the end of each test sequence.

In an earlier study (Rang, 1982) it was concluded that the reduction of e.s.c. amplitude caused by C6 was too great to be explained in terms of scheme 1 if it was assumed that no cumulative block was occurring during a period of stimulation at low frequency (0.1 Hz). The fact that use-dependent block by C6 and other short chain methonium compounds is very persistent caused us to re-examine this conclusion, first by measuring the effect of the various methonium compounds on e.s.c. amplitude during stimulation at 0.1 Hz, to see if the reduction of amplitude was more marked with the short chain compounds; second, by observing the effect on the first e.s.c. recorded after equilibration of the ganglion with the methonium compound under resting conditions.

Relationship between channel blocking activity and reduction of e.s.c. amplitude in the methonium series

All of the methonium compounds, tested at 20 μm, caused a reduction of e.s.c. amplitude, recorded during continuous stimulation at 0.1 Hz (Table 1), though with C10 the effect was not significant. The magnitude of this effect can conveniently be expressed by calculating Δ, defined as (amplitude in absence of drug/amplitude in presence of drug). If the reduction in amplitude were due only to open channel block according to Scheme 1, with no residual block affecting the response to successive stimuli at this frequency, Δ would be closely related to the association rate constants, k_+f and k_+s, for the decrease in amplitude would be the result of channel block occurring during the brief rising phase of the e.s.c. The results in Table 1 show that this is clearly not the case; the ratio (Δ − 1)/k_+f is greater for the short chain than for the long chain compounds, implying that short chain compounds are more effective in reducing e.s.c. amplitude in relation to their rate of binding to the channel than are long chain compounds. When e.s.cs are plotted on a fast time base so that the rising phase can be seen (Figure 11) it is clear that the short chain compounds cause inhibition of the earliest part of the rising phase, as noted by Rang (1982), whereas the long chain compounds do not; with C9 and C10 the first part of the rising phase is unaffected, as would be expected of drugs that dissociate fully between one stimulus and the next. In a number of experiments the nerve was not stimulated continuously as in the experiments summarised in Table 1 and Figure 11, but the preparation was left unstimulated for a period of 5–10 min during which drug solution was perfused through the recording chamber. The first e.s.c. elicited after equilibration with the drug solution was then compared with a control e.s.c. elicited after a similar resting period in the absence of drug (Figure 12). With C6 (20 μm) the amplitude of the first test e.s.c. was only slightly reduced relative to the control, and the initial part of the rising phase was unaffected; after a few stimuli at 0.1 Hz the reduction became much greater, and the rising phase was clearly inhibited, as described by Rang (1982). The channel blocking action of the drug is clearly evident from the marked shortening of the decay phase of the first e.s.c. in a series of experiments the mean amplitude of the first e.s.c. in the presence of 20 μm C6 relative to the control was 0.86 ± 0.04 (n = 5) at −40 mV, and 0.73 ± 0.06 (n = 24) at − 80 mV. During continuous stimulation at 0.1 Hz the corresponding values were 0.71 ± 0.07 (n = 6) at −40mV and 0.53 ± 0.05 (n = 9). C8 and C10 also caused only a small reduction in amplitude of the first test e.s.c. without affecting the initial rising phase; with C8 there was appreciable block evident during stimulation at 0.1 Hz, but with C10 no additional block was seen at this frequency (Figure 12).

Figure 12.

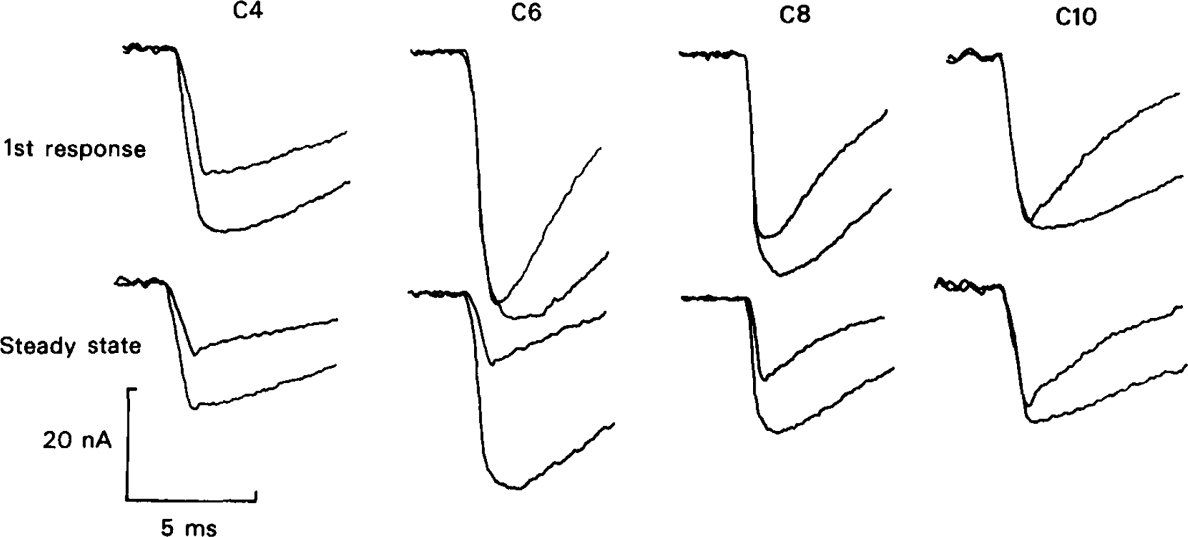
Synaptic currents recorded at − 80 mV under control conditions and in the presence of methonium compounds. C4 was tested at 200 μm, the other compounds at 20 μm. In each pair of traces the larger signal is the control e.s.c. recorded in the absence of drug and the smaller signal is the e.s.c. in the presence of drug. The upper row shows the first responses recorded after a rest of 5–8 min, during which the drug solution, or control solution, was perfused through the bath. The lower row shows responses recorded after the preparation had been stimulated for 1–2 min at 0.1 Hz.

The trapping phenomenon

The surprising difference in the recovery kinetics observed with short and long chain members of the methonium series implies that the short chain compounds result in the formation of a much more stable blocked state than occurs with the longer chain compounds, there being a fairly sharp transition in properties between C8 and C9. One explanation for this might be that the shorter chain compounds allow the channel to close with the blocking molecule inside, whereas the longer chain compounds prevent or greatly impede channel closure. If the blocking molecule can only enter or leave when the channel is in the open state, block with the short chain compounds would then persist more or less indefinitely in the absence of channel activation by agonist. This scheme can be represented more formally as an extension of the simple model represented in scheme (1), as follows:

In this model trapping of the blocking molecule occurs as a result of the transition BR* → BR, it being assumed that the rate constant, l_–, for the escape of the blocking molecule from the closed channel is very small. An important factor in determining the properties of this model is the effect of the blocking molecule on the equilibrium between the open and closed states of the channel in the absence of agonist. Normally this equilibrium (R ↔ R*) lies well over to the left if no agonist is present, but if the presence of a blocking molecule hindered closure of the channel the equilibrium would be shifted towards the open state (BR*) from which B is able to dissociate. The original channel block model proposed by Adams (Scheme 1) represents the limiting case in which channel closure is completely prevented by the binding of B, which may correspond to the situation that we have observed with tubocurarine.

This hypothesis to account for the slow recovery kinetics observed with short chain methonium compounds can be tested experimentally, for it predicts that dissociation of the blocking molecule should be expedited if agonist is applied to the cell during the recovery period, so as to promote channel opening (BR → BR*) at the same time as the cell is depolarized so that dissociation of B (BR* → R*) is favoured. Figure 13 shows the result of an experiment designed to test this prediction. A train of ionophoretic pulses of ACh applied in the presence of 1 μm C6 with the membrane potential held at −80 mV causes the usual run-down phenomenon associated with use-dependent block, and very little recovery occurs during the 5 s resting period (Figure 13a). Depolarizing the cell to −40 mV during most of the recovery period without applying agonist (Figure 13b) has no effect, but if a maintained pulse of agonist is applied with the cell depolarized (Figure 13c) the amplitude of the test pulse is fully restored during the 5 s recovery period. Though not shown in this figure, a similar agonist pulse applied during recovery with the membrane potential held at − 80 mV causes, as one would expect, a further reduction of the amplitude of the test response due to a reinforcement of the use-dependent block produced by the conditioning train. Thus, as predicted by the trapping hypothesis, both conditions, namely the presence of agonist and depolarization must be met in order to allow rapid dissociation of the blocking agent. This experiment gave the same result with all of the short chain methonium compounds, and the unblocking procedure shown in Figure 13 was used, routinely in experiments such as those shown in Figure 10 in order to discharge the block that accumulated following each conditioning train. Repetitive nerve simulation with the membrane clamped at −40 mV was also effective in unblocking the channels.

Figure 13.

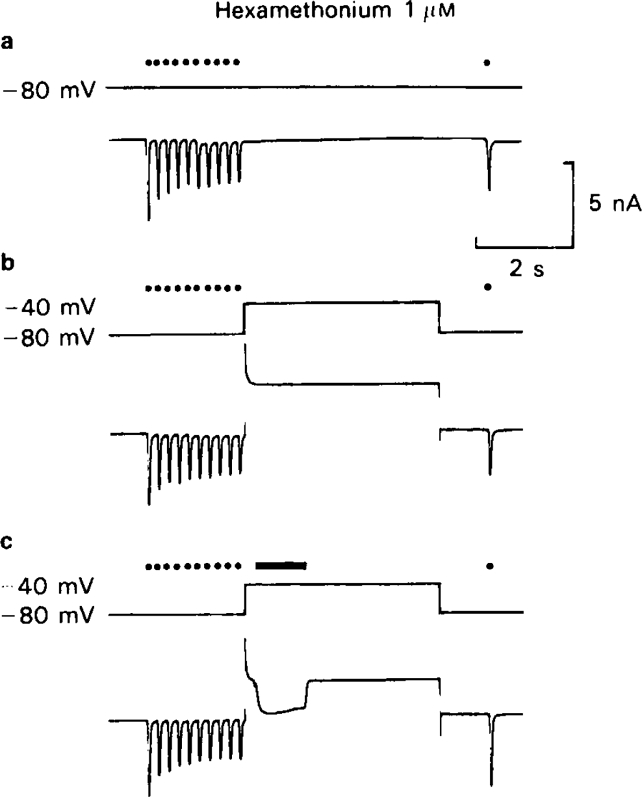
The effect of membrane potential and ACh application on the rate of recovery from use-dependent block in the presence of C6 (1 μm). Use-dependent block was elicited by a train of ACh pulses as in Figure 9, and the recovery period before the test pulse was 5 s. (a) Membrane potential held at − 80 mV during recovery period. Very little recovery at 5 s (cf. Figure 10). (b) Membrane potential held at — 40 mV during recovery period. Very little recovery at 5 s. (c) Membrane potential held at − 40 m V while a 1 s pulse of ACh was applied during recovery period. Complete reversal of block.

Does C6 inhibit channel opening by agonist?

Studies with various local anaesthetics and other drugs acting on the neuromuscular junction, e.g. procaine (Adams, 1976), QX-222 and QX-314 (Beam, 1976a), atropine (Feltz et al., 1977), benzocaine (Ogden et al., 1981), piperocaine (Tiedt et al., 1979) have shown that many of them act to prevent channel opening by agonists, as well as by blocking channels after they have been opened, and this makes them considerably more effective at inhibiting ACh responses than they otherwise would be. The evidence presented so far (e.g. Figure 12) suggests that C6 at a concentration of 20 μm has no such action, but we were interested to know whether it might have such an effect, for instance by blocking ACh receptors, when tested at higher concentrations. It would be difficult to measure such an effect directly because the channel blocking action of C6 at high concentration would itself reduce e.s.c. amplitude markedly and thus make any additional receptor blocking effect hard to detect. An indirect method, based on the trapping phenomenon, was therefore used. The protocol, shown in Figure 14, was as follows. Following a test response to a brief ionophoretic pulse of ACh in the absence of drug, the preparation was equilibrated for a few minutes with a high concentration (1 Mm) of C6. The C6 was then washed out for 5–10 min and the test pulse repeated. If no agonist was applied during the exposure to C6 (upper records in Figure 14) recovery of the test response after removal of C6 was virtually complete. If ACh was applied in the presence of C6 (lower record in Figure 14), it caused no inward current but nonetheless an appreciable blocking effect was evident after the C6 had been washed out. It was clear that this block was due to the same type of channel block mechanism as discussed previously, since it could be discharged by applying a pulse of ACh with the cell depolarized, thus restoring the test response to its control amplitude (lower record in Figure 14). Thus, even in the presence of 1 Mm C6 (about 10 times the dissociation constant measured by inhibition of α-bungarotoxin binding to ACh receptors in denervated rat muscle; Colquhoun & Rang, 1976), the conditioning pulse of acetylcholine was evidently able to open ionic channels, as judged by its ability to promote blocking by C6. Though such a qualitative experiment cannot exclude some degree of receptor block, it is unlikely that it contributes appreciably to the effect of C6 on ganglionic transmission.

Figure 14.

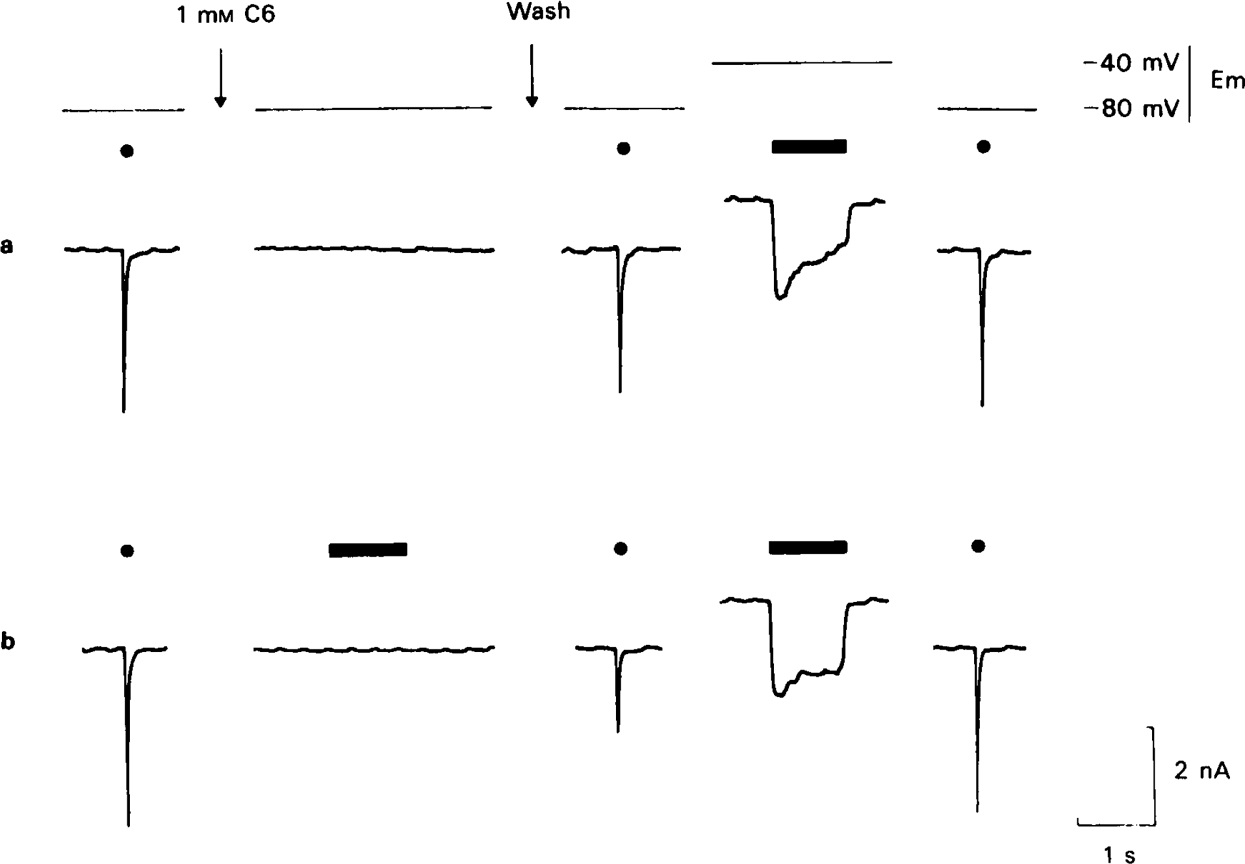
Experiment to test whether C6 at high concentration prevents acetylcholine from opening channels. Traces marked (a) and (b) represent consecutive experiments on the same cell. Test responses to a standard 2 ms ionophoretic pulse of acetylcholine (ACh) are indicated by closed circles and 1 s pulses of ACh by horizontal bars. The membrane potential is shown on the upper trace. In sequence (a) C6 (1 Mm) was applied for 5 min and then washed out for 5 min before the second test response was elicited. The second test response shows only a very slight residual block. Application of a 1 s pulse of ACh with the cell depolarized to − 40 mV produces only a small increase in the test response. In sequence (b), the same procedure was followed except that a 1 s pulse of ACh was applied in the presence of C6. Though this pulse caused no discernible inward current, it enhanced the blocking effect of C6 considerably as shown by the reduced test response. Application of the unblocking procedure (1 s ACh pulse at − 40 mV) restored the test response fully, indicating that channel block was responsible for the effect.

Discussion

The main conclusions to be drawn from the results presented in this paper concern (a) the relationship between chain length and rate of association with the ACh-operated ion channel among the methonium series, and (b) the factors affecting the rate of dissociation of these drugs from the channel.

The procedure used to calculate the association rate constant, k₊, from the degree of speeding of the two components of the e.s.c. decay is at best only an approximation. If the simple two-step kinetic model (scheme 1) is correct, and if there is only a single component in the control e.s.c., the values for both the association and dissociation rate constants can, in principle, be calculated from the rate constants of the two exponential components of the e.s.c. decay recorded in the presence of the drug (see Adams, 1976; Colquhoun & Hawkes, 1977; Colquhoun et al., 1979). There are complicating factors in the present work which make it difficult to use this analytical approach. In the first place, the e.s.c. decay is biexponential in the absence of any blocking drug, so the theoretical effect of a channel blocking drug would be to give rise to a 4-component decay, which could not be resolved satisfactorily. Secondly, there is evidence that scheme 1 is insufficient to account for the actions of the methonium compounds. The results presented in this paper show that an additional step, involving the closing of blocked channels must be postulated (scheme 2) for the shorter chain methonium drugs, and the consequences of this may need to be taken into account. An analysis of the kinetic behaviour expected of the model given in scheme 2 has been carried out by computer simulation (Gurney, 1982). The conclusion from this analysis is that inclusion of the additional reaction step (BR* → BR) predictably introduces yet another exponential component into the e.s.c. decay, but unless the rate of closing of blocked channels is close to or exceeds the normal closing rate, this reaction will produce only a very small effect on the rate of the fastest component which has been used to calculate k₊ in this study. With the short chain methonium compounds it is possible that channel closure occurs at a similar rate whether or not the blocking molecule is present; the effect of this would be to speed up slightly the fastest of the three rate constants in the e.s.c. decay, and to cause our simplified analysis (equations 1 and 2) to overestimate k₊. The fact that we did not observe a slow component in e.s.cs recorded in the presence of these drugs, however, makes it unlikely that this additional reaction was sufficiently fast to make much difference to the fast component, so the error is probably small. With C9 and C10 the additional slow component seen in the e.s.c. decay (Figure 2) whose rate decreased as the cell was hyperpolarized, could have been produced, in the context of the simple two-step blocking scheme, if the rate of dissociation from the open channel, k_–, is appreciable in relation to the blocking rate; it could also occur with the more complex model (scheme 2), according to the analysis of Gurney (1982) if the rates of opening and closing of the blocked channel are sufficiently high. The fact that the preparation contains fast and slow channels makes more detailed interpretation impossible, for it is not certain whether the slow component that we can observe relates to the behaviour of the fast or the slow channels. Its presence may invalidate the use of equations (1) and (2) to calculate k_+f for C9 and C10, the direction of the error being such that the values given in Table 1 for these drugs are likely to be overestimates. Even with these uncertainties it is clear from Figure 4 that the variations in k_+f or k_+s among the different methonium drugs cannot account for the variation in ganglion blocking potency reported by Paton & Zaimis (1949), who found C8 to be only about 1/50 as active as C6, and C10 to be inactive on the cat superior cervical ganglion. They also found C4 to be appreciably active (about 1/50 as active as C6), whereas in a few tests we found it inactive in blocking channels even at 200 μm. One possibility that could account for the apparent inactivity of C4 is that it enters the open channel, like the other members of the series, but passes freely through it. There is evidence that even much larger methonium compounds, such as C10, can cross the endplate membrane via agonist-operated channels (Creese & England, 1970), and Lingle (1983b) has found that dissociation of C6 from ACh-operated channels of lobster muscle fibres can be hastened by extreme hyperpolarization of the membrane, suggesting that it is escaping inwards rather than outwards. Studies on frog muscle have shown that organic cations such as histidine and diethylamine can permeate the ACh-operated channels at the neuromuscular junction sufficiently fast to generate an appreciable inward current (see Dwyer et al., 1980; Adams et al., 1981), implying a rate of dissociation inward through the channel greater than 10⁵ s⁻¹. A rate of permeation by C4 only 1% of this would account for its lack of apparent channel blocking activity in our experiments. Our estimates of k₊ for C6 and C10 may be compared with measurements made on the frog motor endplate. Milne & Byrne (1981) calculated a value of 1.8 × 10⁵ M⁻¹ s⁻¹ for C6 and 6.0 × 10⁶ m⁻¹ s⁻¹ for C10 at − 130 mV, whereas Adams & Sakmann (1978) estimated 1.7 × 10⁷ m⁻¹ s⁻¹ for C10 at the same potential. Our value for C10 (1.6 × 10⁷ m⁻¹ s⁻¹) agrees reasonably with these values for the motor endplate, bearing in mind that the membrane was less hyperpolarized in our experiments, and the temperature higher. The association rate constant for C6 that we have found, however, (1.8 × 10⁷ m⁻¹ s⁻¹) appears considerably greater than Milne & Byrne's estimate, which may partly account for the specificity of action of C6 at the ganglionic synapse.

The most interesting difference between the members of the methonium series that we have found concerns the rate of dissociation from the ionic channel, where several lines of evidence indicate that the short chain methonium compounds escape much more slowly than the long chain compounds (or tubocurarine, whose properties are similar to those of a long chain methonium compound). Thus 10 μm C6 is about as effective as 50 μm C10 in producing steady-state block during stimulation at 10 Hz (Figure 6), even though the rate constant for association with both fast and slow channels is similar for the two drugs. The implication is that C10 dissociates faster, a conclusion that is borne out by the more rapid achievement of a steady state with C10 than with C6, and by the more direct measurement of the dissociation rate by means of the protocol used in Figures 8 and 9. The appearance of a long tail on the e.s.c., with a time constant greater than that of any component of the normal e.s.c., with C9 and C10 (Figure 2) also suggests that these drugs dissociate relatively rapidly from the channels.

The possibility that a presynaptic effect, causing transmitter release to decline more rapidly than normal during a train (as postulated by some authors for the action of tubocurarine at the neuromuscular junction; see Hubbard & Wilson, 1973; Glavinovic, 1979) can account for the accelerated run-down of e.s.c. amplitude occurring in the presence of methonium compounds can be ruled out, because the same phenomenon occurred with ionophoretically applied ACh, and because the unblocking phenomenon (Figure 13) would be inexplicable on that basis.

Though the difference in the kinetic behaviour of long and short chain methonium compounds could simply reflect quantitative differences in the dissociation rate, without there being any fundamental difference in mechanism, two observations make this unlikely. The sharpness of the transition, around C8, between the two types of kinetic behaviour would seem unlikely in such a series if the mechanism of binding were qualitatively the same. More directly, we found that the dissociation of the short chain compounds could be greatly accelerated by opening the channels, provided the membrane was simultaneously depolarized. The most likely explanation for all of these findings is that the short chain compounds can become trapped within the channel, but that long chain compounds inhibit channel closure and thus escape more rapidly. The two-phase kinetics of recovery from use-dependent block seen with C9 and C10 (Figure 10) are consistent with this model if it is postulated that these drugs inhibit channel closure but do not prevent it completely. In terms of scheme 2 the fast phase of recovery would correspond roughly to k_– (escape from the open channel) while the slow phase would result from the opening of blocked channels in the absence of agonist, followed by escape of the blocking molecule and spontaneous closure of the channels (BR → BR* → R* → R), with channel opening presumably being the rate-limiting step. The value of k_– estimated from the fast recovery component with C9 and C10 is roughly 2 s⁻¹. With C9 the slow phase occurs at about 0.1 s⁻¹, implying that at equilibrium approximately 5% of the blocked channels are in the open state; with C10 the same calculation suggests that about 10% of the blocked channels are open. For unblocked channels we can calculate from the fact that the input conductance of a cell can increase as much as 200 fold at the peak of the e.s.c., that the proportion of open channels in the absence of agonist must be very small, certainly less than 0.5%, so the binding of C9 or C10 increases the opening probability considerably. The magnitude of the fast phase of recovery from use-dependent block (30–50% of the total amplitude in Figure 10) implies that the rate of closing of blocked channels (α_B) must be very much less than that of unblocked channels (α), for if it were not the open blocked channels would be much more likely to close than to unblock, and the amplitude of the fast phase of recovery (which we take to represent unblocking of open channels) would be negligible. In a study of the actions of tetraethylammonium derivatives on the voltage-sensitive potassium channels of squid axon, Armstrong (1971) similarly concluded that closure of the channels was considerably impeded by the presence of the blocking molecule, provided that the size of the alkyl substituent was sufficient. Tetraethylammonium itself appeared to have little effect on the gating reactions. It is not possible to say from our results whether or not channel opening is facilitated by the presence of the blocking molecule.

We found that the trapping phenomenon occurred only with the short chain methonium compounds from C5 to C8, and not with C10 or tubocurarine. Lingle (1983a, b), however, working on lobster muscle, found evidence of trapping with both C10 and tubocurarine, as well as with other drugs such as pempidine, mecamylamine and chlorisondamine, but not with C6, which appeared to be able to permeate the channel. Though this might suggest that the ACh-operated channel of lobster muscle is rather larger than that of the ganglion cell, measurements of the channel conductance (Rang, 1982; Gray & Rang, 1983; Lingle & Auerbach, 1983) give very similar values in the two preparations, although the lobster measurements were done in sea-water, whereas the ganglion measurements were done in Krebs solution.

It seems likely that the transition that occurs at about C8 between drugs that can become trapped and those that cannot is one factor that accounts for the sharp decline in ganglion blocking potency in vivo as the chain length is extended beyond C6 (Figure 2). Extrapolation from voltage clamp studies to ganglion block measured physiologically during repetitive stimulation is not, however straightforward, because both the blocking and unblocking reactions are sensitive to the membrane potential. The depolarization associated with normal transmission would be expected to discourage channel block, but the magnitude of this effect would depend critically on the kinetics and voltage-sensitivity of the blocking and unblocking reactions, as well as on the stimulation frequency; detailed quantitative information about these reactions would be needed to model the process more precisely.

In summary, our results suggest that the classical bell-shaped curve relating ganglionic blocking potency to chain length in the methonium series reflects the fact that compounds smaller than C8 either fail to enter open channels or (more likely) pass straight through them without appreciable sojourn, whereas compounds larger than C8 prevent channel closure and thus escape quickly and fail to produce a cumulative blocking effect. It is the intermediate compounds, which are too large to pass straight through, but small enough to become trapped, that are the most active.